Kapitel 5 Womit beschäftigt sich Statistik?
5.1 Wissenschaftstheoretische Einordnung
In der Statistik stehen Daten im Zentrum des Geschehens. Ob es sich nun um Temperaturmessungen handelt, radioaktive Zerfallsmessungen, Kennzahlen zur Biodiversität wie die alpha-, beta- oder gamma-Diversität, Verkehrserhebungen, Umfragen z.B. zur Bereitschaft sich für den Klimawandel einzuschränken, zum voraussichtlichen Wahlverhalten oder Untersuchungen zur Effektivität des Impschutzes und dem auftreten schwerwiegender Nebenwirkungen bei Impfungen oder Medikamenten - stets geht es um die Daten. Diese repräsentieren das, was wir über die Welt und das, was sie im innersten zusammenhält wissen. Diese Daten zu analysieren, Strukturen, Muster und Zusammenhänge zu erkennen ist Aufgabe der Statistik.
Dazu bedient sich die Statisik mathematischer Methoden, was sie nicht immer beliebt macht. Mitunter wird sie deswegen in Form von Heuristiken gelehrt, ohne die zugrundeliegenden Prinzipien wirklich zu erläutern. Dies man bequem sein, birgt jedoch die Gefahr, dass man Fehlschlüssen aufsitzt 17 Deswegen gilt es, sich der Grundlagen wenigstens soweit bewusst zu sein, dass man erkennt, wenn man sich in unruhiges Fahrwasser begibt und in Gefahr läuft Fehlschlüssen aufzusitzen.
Auch wenn in manchen Anwendungsfällen rein datengetriebene Analysen ausreichen, spielen im wissenschaftlichen Erkenntnisprozess neben Daten Hypothesen und Vorwissen (prior knowledge) eine wichtige Rolle. Ein Beispiel für die rein datengetriebene Analyse ist das Ableiten von Assoziationsregeln, was einem bei Amazon und anderen Onlinehändlern regelmäßig begegnet. Die Anbieter haben kein Interesse daran, warum gewisse Zusammenhänge bestehen, sondern einzig daran mehr Umsatz und Gewinn zu generieren. Im Gegensatz dazu ist es in der Wissenschaft in der Regel relevant zu verstehen, warum ein Zusammenhang existiert. Bekanntermaßen ging der Rückgang der Storchpopulation in Mitteleuropa mit einer Abnahme der Geburtenrate einher. Wenn man die Hypothese das der Storch die Kinder bringt als sicher falsch verwirft, wird man mit einer rein datengetriebenen Analyse schnell unzufrieden sein und sich anderen Hypothesen (wie dem Zusammenhang zwischen Industrieller Revolution, demographischem Übergang und dem Verlust von Storch-Habitat) beschäftigen und versuchen diese mit den Daten zu stützen.
Im Fall der hypothesengetriebenen Datenanalyse, sollte man sich der Aussage von Karl Popper bewusst sein, dass man Hypothesen nur falsifizieren, nicht aber verifizieren kann (Popper 1989). Einfacher ausgedrückt: eine Hypothese gilt nur solange als wahr, wie man sie nicht falsifizieren kann. Wir sollten uns auch immer bewusst sein, dass wir die komplexe Realität stets vereinfachen, wenn wie sie analysiseren. Es geht uns ja darum, generelle Zusammenhänge zu erkennen und nicht darum, vor der komplexen Realität in die Knie zu gehen (um dann am Ende irgendeinem Bauchgefühl oder sonstigen Heuristken zu folgen). Es gilt der gute alte Satz: “Alle Modelle sind falsch, aber manche sind nützlich.” (Box 1976).
Die Messdaten/Beobachtungen stehen im Fokus der empirischen Forschung. Mit Methoden der Statistik wird versucht, aus den einzelnen Beobachtungen (dem Besonderen) induktiv auf zugrundeliegende Gesetzmäßigkeiten zurückzuschließen 18. Dies passiert im Kontext vorausgegangener Untersuchungen und Experimente, auf deren Grundlage bereits Hypothesen formuliert wurden. Je nach Wissenschaftsdisziplin werden die empirischen Ergebnisse auch in deduktiv19 abgeleitete Erkenntnisse eingebettet.
Die Statistik als quantitative Wissenschaft setzt voraus, dass die Messungen objektiv quantifizierbar und untereinander vergleichbar sind. Dies ist nicht immer möglich oder sinnvoll. Bei Befragungen zu Fluchtursachen z.B. hat man es mit vielschichtigen Prozessen zu tun, die subjektiv erlebt, bewertet und geschildert werden. Auch wenn es möglich ist, solche Erhebungen zu quantifizieren, indem man z.B. die Aussagen klassifiziert, ist dies mit einem erheblichen Informationsverlust verbunden. Entsprechend eignen sich Methoden der qualitativen Sozialforschung für manche Fragestellungen besser als quantitative Fragestellungen. Es kommt stets darauf an, das richtige Werkzeug (die adäquate Methodik) zu nutzen 20
5.2 Einige Bereiche der Statisik
Die Anwendungsbereich der Statistik sind vielfältig und wir können in diesem Kurs nur einige behandeln. Einige der wichtigsten Unterteilungen sind:
- Korrelation: Ungerichtete Zusammenänge zwischen unterschiedlichen Messdaten untersuchen
- Regression: Gerichtete Zusammenhänge zwischen zu erklärender Variablen (Response) und erklärenden Variablen (Prädiktoren) untersuchen (supervised learning)
- Klassifikation: Gerichtete Zusammenhänge zwischen kategorialer zu erklärender Variablen (Response) und erklärenden Variablen (Prädiktoren) untersuchen und die wahrscheinlichste Klasse ermitteln (supervised learning)
- Multivariate Verfahren: Zusammenhänge zwischen mehrern Merkmalen oder zwischen Standorten mit mehreren Merkmalen erkennen (unsupervised learning), z.B. Hauptkomponentenanalyse, Cluster Analyse
Des weiteren unterscheidet man zwischen parametrischen und nicht-parametrischen Verfahren. Bei den parametrischen Verfahren - die hier im Mittelpunkt stehen - ist die Modellstruktur fix, d.h. ein Modell ist anhand einer fixen Anzahl von Parametern bestimmt (z.B. lineares oder generalisiertes lineares Modell). Bei parameterfreien (nicht-parametrischen) Modelle ist die Modellstruktur dagegen nicht a priori festgelegt, sondern wird aus den Daten bestimmt. Der Begriff parameterfrei bedeutet also nicht, dass solche Modelle keine Parameter besitzen - die Art und Anzahl der Parameter ist bei diesen Modellen flexibel und nicht von vornherein festgelegt. Beispiele dafür sind Entscheidungsbaumverfahren, Resamplingverfahren wie Jacknife und Bootstrap oder Support Vector Machines.
5.3 Schließende Statistik
Eines der zentralen Aufgabenfelder der Statistik ist es, anhand einer Stichprobe (Sample) auf die Grundgesamtheit (population) zu schließen. In der schließenden Statistik geht es darum, Eigenschaften der Grundgesamtheit anhand der Stichprobe zu schließen.
Man kann sich die Situation des empirisch arbeitenden Wissenschaftlers vielleicht anhand des Platonschen Höhlengleichnisses verdeutlichen. Angeketten mit dem Rücken zum Höhleneingang sieht der Wissenschaftler nur die Schatten der Ereigniss außerhalb der Höhle (die Messdaten, Stichprobe) an der Wand. Anhand derer versucht er auf die Welt außerhalb der Höhle (Grundgesamtheit) zu schließen.
Die Stichprobe ist das, was wir über die Wirklichkeit wissen. Es ist i.d.R. nicht möglich überall und ständig zu messen, da sowohl finanzielle als auch personelle Ressourcen fehlen. Deswegen existieren in Deutschland nur einige hundert Klimastationen, aus denen z.B. Veränderungen der Klimas abgeleitet werden. Ebenso werden für Umfragen nicht alle in Deutschland lebenden Personen befragt, sondern nur eine kleine Stichprobe. Kompletterfassungen im Sinne einer Volkszählung oder Zensuserhebung finden nur in großen Zeitabständen statt. Natürlich hat die Auswahl der Stichprobe Auswirkungen auf unsere Fähigkeit auf die Grundgesamtheit zu schließen. Dazu später mehr.
Umfragen, z.B. der ARD Deutschlandtrend - berichten oft wieviel Prozent der Befragten einer Meinung zustimmten oder welche Partei sie wählen würden, wenn am kommenden Sonntag Bundestagswahl wäre. Ehrlicherweise muss man jedoch sagen, dass es nicht wirklich interessant ist, was eine Stichprobe von ein paar hundert oder tausend Personen denkt oder tun würde. Implizit wird auf die Grundgesamtheit (die deutsche Wohnbevölkerung oder die Wahlberechtigten) geschlossen. Beim Schließen kommt es zu Unsicherheiten, die korrekterweise quantifiziert und mit angegeben werden müssen. Anstelle von “52% der Befragten unterstützen die Ukrainepolitik der Bundesregierung” müsste es eigentlich heißen “die Unterstützung der Wohnbevölkerung für die Ukrainepolitik der Bundesregierung beträgt zwischen 45.4% und 59.8% (95% Konfidenzintervall), wobei 50,3% der beste Schätzer ist”.21 Das mag zu komplex für eine Nachrichtensendung sein, aber für wissenschaftliche Fragestellung ist das essenziell.
Schauen wir uns das Vorgehen anhand eines fiktiven Beispiels an. Stellen wir uns vor, Sie sollten die Biomasse eines Waldstücks ermitteln, auf dem vor einigen Jahren im Rahmen einer Treibhausgaskompensationsmaßnahme Bäume gepflanzt worden sind.22 Wenn Sie abschätzen wollen, wieviel \(CO_2\) in der Vegetation gebunden ist, brauche Sie folgende Informationen: a) wieviel \(CO_2\) wird je Holzvolumen (z.B. \(cm^3\)) gebunden, b) wieviel Biomasse haben wir (z.B. Tonnen), c) die Anzahl der Bäume. Wenn wir davon ausgehen, dass nur eine Baumart oder nur wenige Baumarten gepflanzt worden sind 23, reicht es, wenn Sie einige Stammbohrungen durchführen und den \(CO_2\) Gehalt ermitteln. Da Sie schlecht die Bäume ausgraben und wiegen können, gehen wir über das Volumen vor. Alle Stämme einzeln zu vermessen ist zeitaufwendig und teuer, deswegen behelfen wir uns mit einem in den Forstwisseschaften etablierten Näherungsverfahren, dem Durchmesser in Brusthöhe. Daraus lassen sich mit ein paar Faustzahlen eine Schätzung des Volumens je Baum ausrechnen. Einfacher, aber wenn wir zehntausende von Bäumen haben, wollen Sie sicher nicht die nächsten Monate damit verbringen, alle Bäume zu messen. Deswegen behelfen wir uns mit einer Stichprobe und schließen auf die Verteilung des Durchmessers in Brusthöhe.
Hinsichtlich der Anzahl der Bäume könnten wir ähnlich vorgehen: wir erstellen zufällig Planquadrate und zählen dort die Bäume aus - da sie gepflanzt worden sind, haben wir aber vermutlich schon eine ganz gute Schätzung.
Nachfolgende Verteilung soll die wahre Verteilung der Grundgesamtheit beschreiben. Im Mittel haben die Stämme in Brusthöhe 50cm Durchmesser (alle wurden zeitgleich gefplanzt), wobei es eine gewisse Streuung gibt. Die Verteilung wird hier durch eine Normalverteilung mit Mittelwert 50 cm und einer Standardabweichung von 1 cm beschrieben.
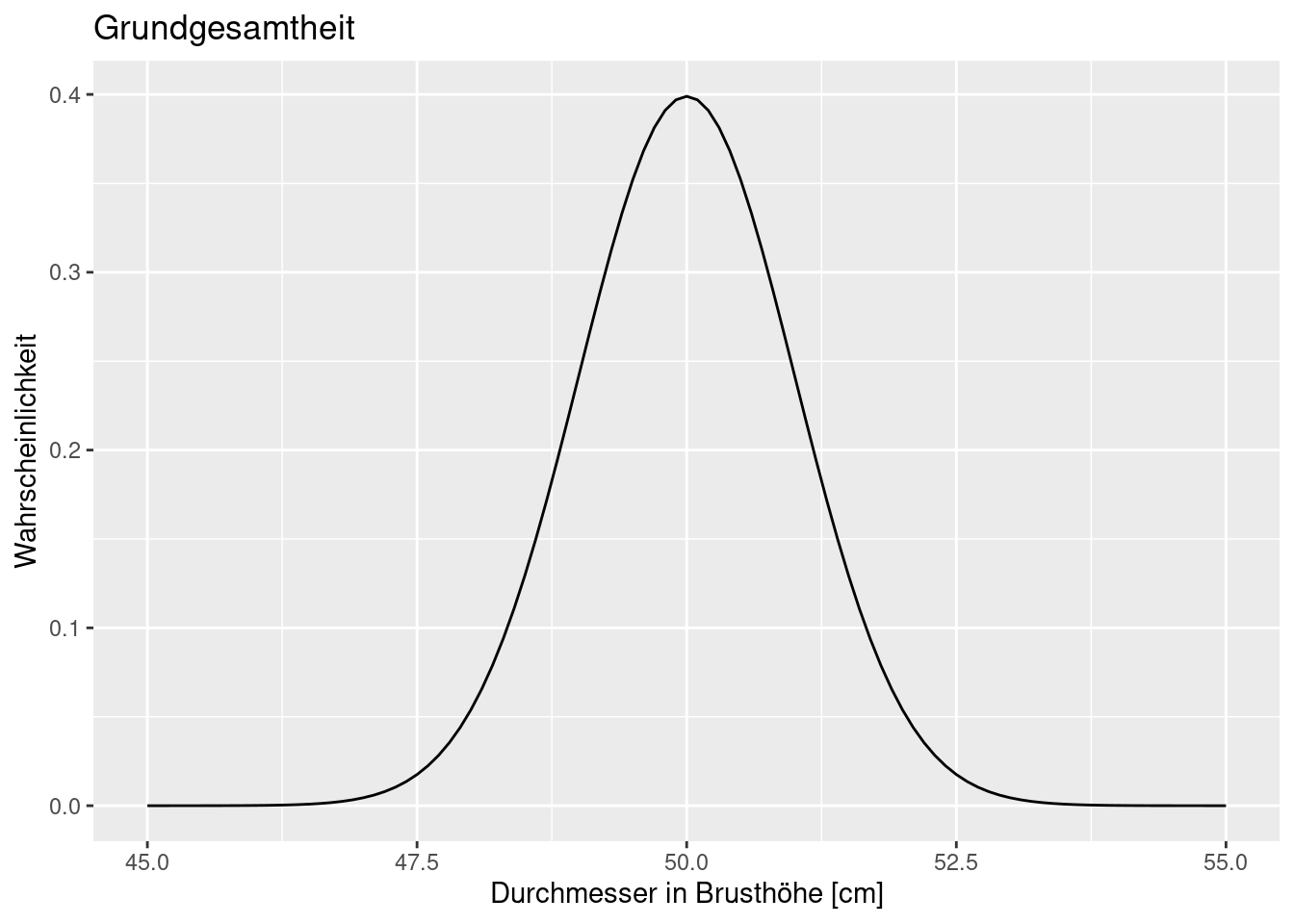
Nun stellen wir uns vor, wir hätten 50 zufällig ausgewählte Bäume eingemessen. Damit sind wir mindestens eine Tag lang beschäftigt, da die Bäume im Gebiet verteilt ausgewählt wurden.
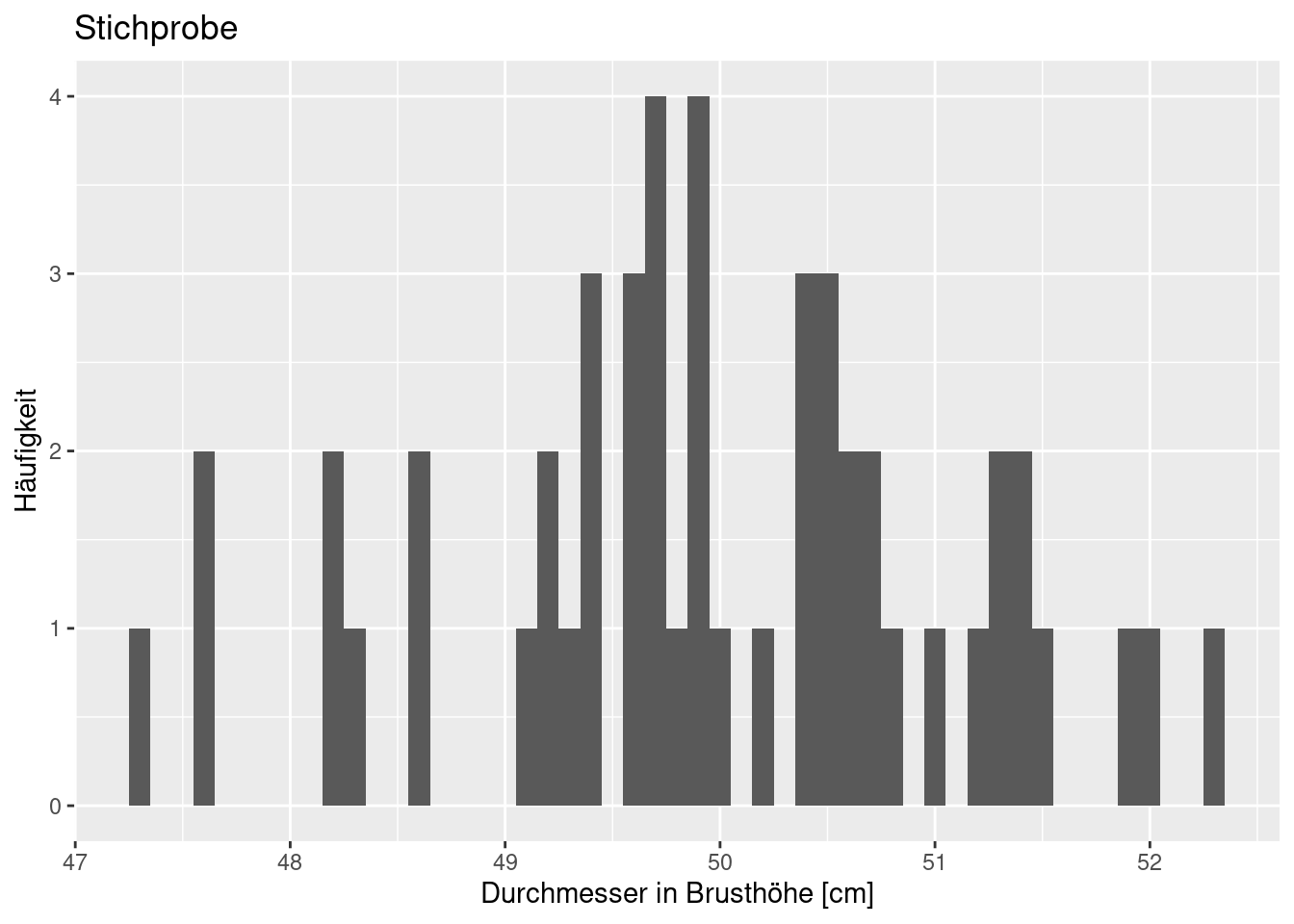
Würden wir 50 andere Bäume auswählen, sähe die Verteilung sicherlich etwas anders aus. Nachfolgend sechs weitere Stichproben, die wir erhalten würden, wenn wir unsere Stichprobe anders gewählt hätten.
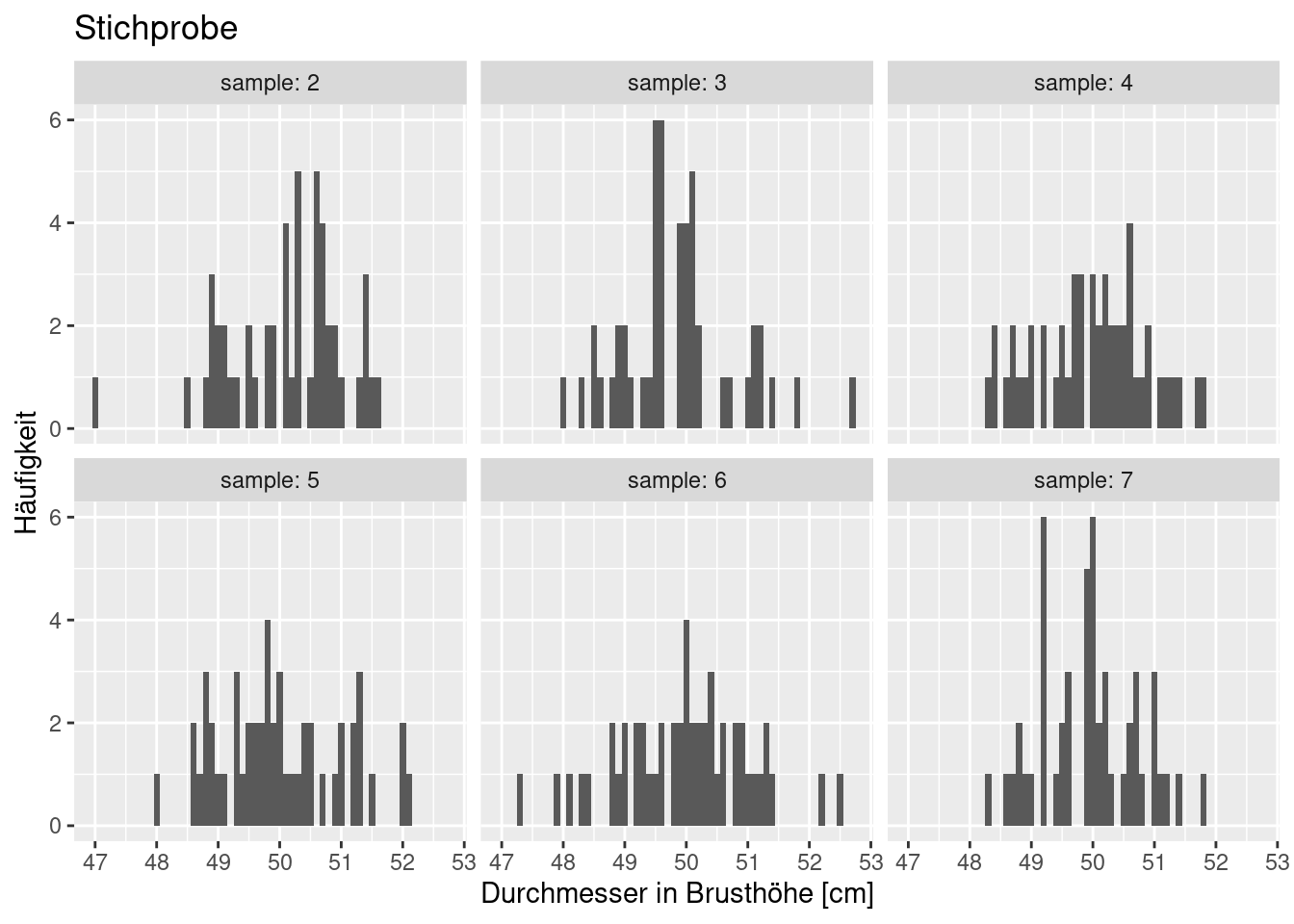
Wie wir sehen, unterscheiden sich die Verteilungen durchaus, auch wen gewisse Charakteristika erhalten bleiben.
Nun aber zum spannenden Teil: welche Parameter (Mittelwert und Standardabweichung) schätzen wir aufgrund der ersten Stichprobe?
Wenn wir davon ausgehen, dass die Werte einer Normalverteilung entspringen und die bestmögliche Normalverteilung zu unseren Daten schätzen, dann erhalten wir folgende Werte:
## mean sd
## 49.9643282 1.1399034
## ( 0.1612067) ( 0.1139903)Die erste Zeile gibt den Mittelwert und die Standardabweichung an, die zweite die Unsicherheit dieser Schätzung (der Standardfehler). Wie wir sehen, sind die Parameter der Grundgesamtheit recht gut getroffen und die Unsicherheit der Schätzung ist relativ zum geschätzten Wert gering24. Vergleichen wir einmal die Verteilung, die sich ergeben würde mit der wahren Verteilung der Grundgesamtheit:
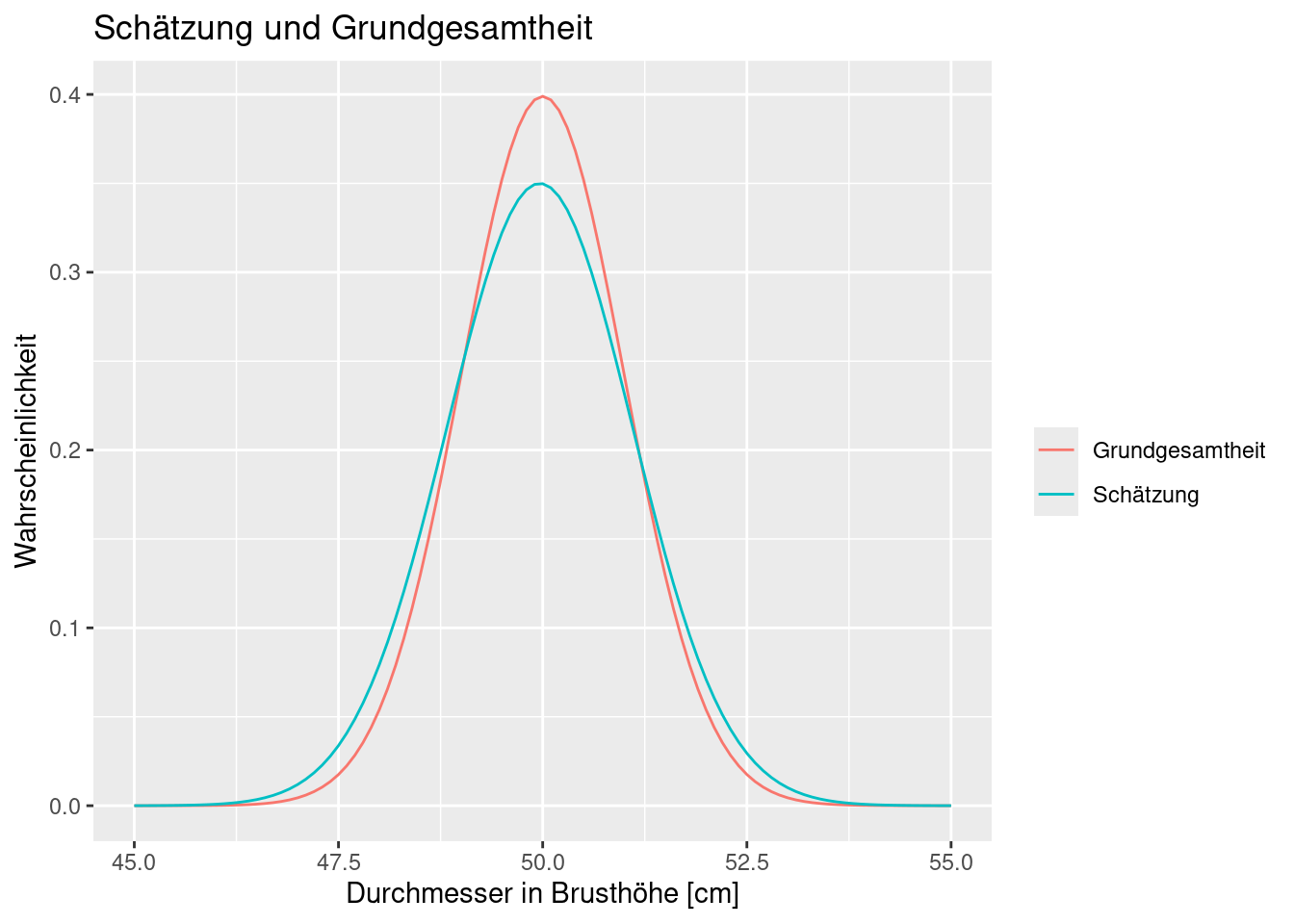
Wie wir sehen, treffen wir zwar den Mittelwert relativ genau, aber wir nehmen eine größere Streuung des Durchmessers an, wenn wir die Schätzung aufgrund der Stichprobe verwenden. Da der Mittelwert etwas kleiner ist, als der wahre Wert unterschätzen.
Aber wir müssen eigentlich auch noch die Unsicherheit bei der Parameterschätzung mit berücksichtigen. Im nachfolgenden sind noch vier Verteilungsfunktionen eingezeichnet, die entstehen, wenn wir nicht die beste Schätzung für die Parameter verwenden, sondern einen Unsicherheitsbereich verwenden. Die wahre Funktion liegt irgendwo dazwischen.
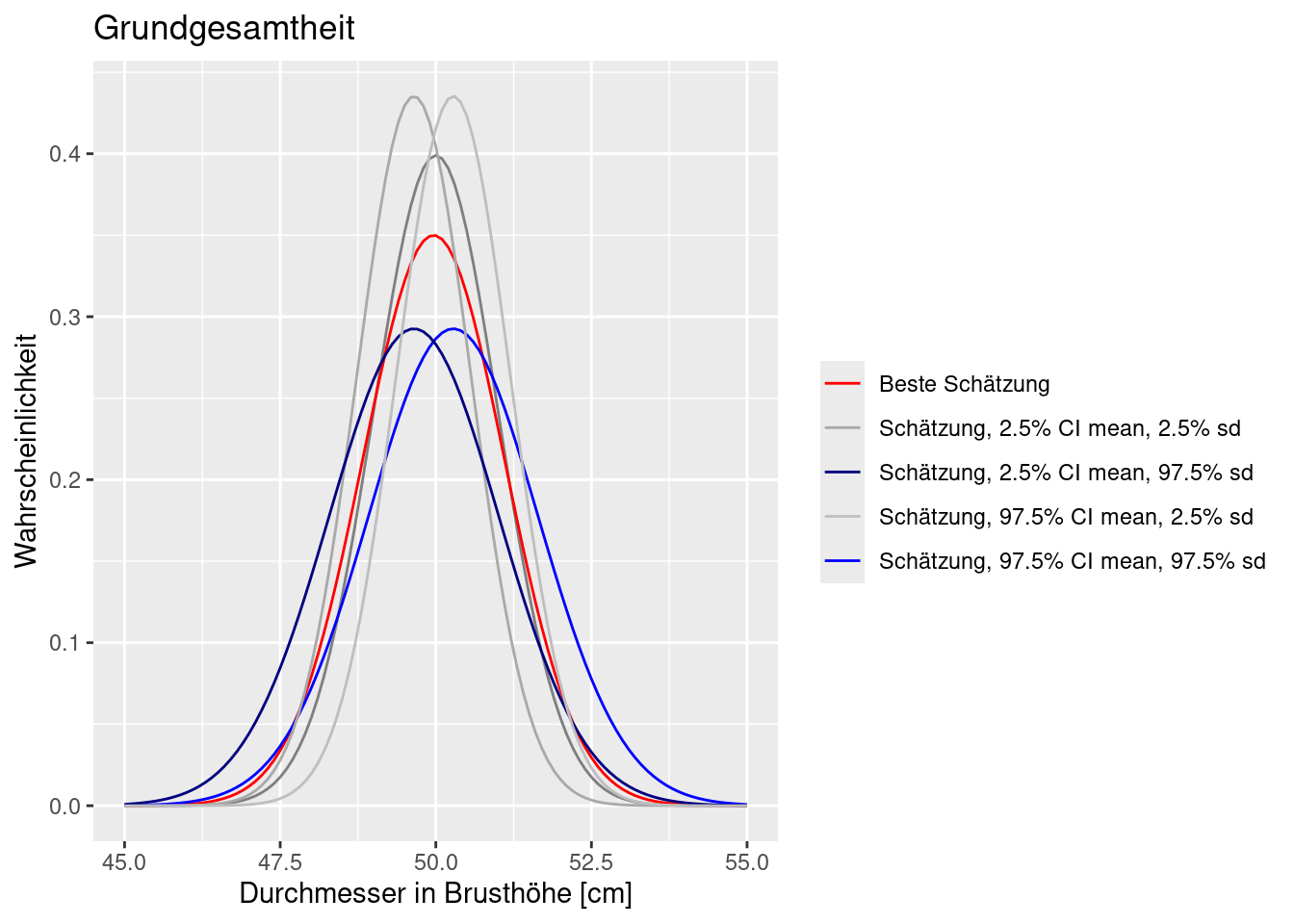
Wir sollten also beim Schließen auf die Grundgesamtheit die Unsicherheiten mitdenken. Wie das genau von statten geht, damit werden wir uns noch ausführlich beschäftigen.
Weiterführende/zitierte Literatur
Diese Gefahr gilt nicht nur für die Statistik, sondern generell, wie Kaneman (Kahneman 2011) eindrücklich nachweißt.↩︎
Wobei z.B. Karl Popper dieses induktive Schließen sehr kritisch sieht. Karl Poppers Aussagen bezogen sich vor allem auf den Bereich der Sozialwissenschaften. Während man in der Physik und der Chemie von der Existenz grundlegender Gesetze ausgehen kann, wird dies bereits in der Mikrobiologie schwieriger. In Abhängigkeit von der untersuchten Skala sind wir in der physischen Geographie sicherlich etwas weiter von zugrundeliegenden Gesetzmäßigkeiten entfernt als in der Physik. In der Humangeographie und den Sozialwissenschaften ist die Annahme allgemeingültiger Gesetzmäßigkeiten noch kritischer zu hinterfragen.↩︎
Aus dem Allgemeinen (Gesetze und Theorien) abgeleitet.↩︎
Getreu der Aussage “Wenn man einen Hammer in der Hand hält sieht vieles nach Nägeln aus, auch wenn ggf. ein Schraubenzieher besser geeignet wäre.”↩︎
Alle Zahlen sind frei erfunden.↩︎
Ob das eine sinnvolle Maßnahme ist, sei dahingestellt.↩︎
Ökologisch wäre einer höhere Vilefalt sicher besser, aber wir wollen es einfach halten.↩︎
Den Standardfehler sollten wir immer im Verhältnis zum geschätzten Parameter interpretieren.↩︎