Kapitel 17 Lineares Modell und Faktorvariablen
17.1 Kategorielle Prädiktoren in R
Bisher haben wir uns in der Hauptsache mit kontinuierlichen Prädiktoren beschäftigt. Nun wollen wir uns kategoriellen, insbesondere ordinalskalierten Prädiktoren zuwenden. Dies Variablen haben als Werte wie “hoch”, “niedrig”, “männlich”, “weiblich”. In R werden diese als sogenannte Faktoren repräsentiert. Schauen wir uns das einmal am Beispiel an:
Zunächst erstellen wir eine Variable mit Stringwerten
## [1] "A" "B" "A" "B" "A" "B" "A" "B" "A" "B"## [1] "character"Die Struktur des Vektors ist denkbar simpel:
## chr [1:10] "A" "B" "A" "B" "A" "B" "A" "B" "A" "B"Anders wird es, wenn wir die Variable in einen Faktor umwandeln:
## [1] A B A B A B A B A B
## Levels: A B## [1] "factor"## Factor w/ 2 levels "A","B": 1 2 1 2 1 2 1 2 1 2## [1] "A" "B"Wir haben nun eine etwas kompliziertere Struktur: die Werte sind als Integerwerte abgespeichert, zusätzlich ist im Objekt hinterlegt, was die Integerwerte bedeuten (welchem Faktorlevel sie zugeordnet sind).
Wenn wir wollen, können wir die Reihenfolge der Faktoren ändern:
## Factor w/ 2 levels "B","A": 2 1 2 1 2 1 2 1 2 1Level B steht nun vorne und wird als 1 kodiert, A als 2.
Wenn wir die Faktorlevel umbenennen wollen, gehen wir ähnlich vor
## Factor w/ 2 levels "Bauerwartungsland",..: 2 1 2 1 2 1 2 1 2 1Wir laden nun die bereits bekannten Daten der INKAR Kreisstatistik und wandeln zwei der als Characterfelder vorliegende Variablen in Faktorvariabelen um:
owfür die Unterteilung in die Gebiete der alten und der neuen BundesländerGEN_LANfür die 16 Bundesländer
inkar <- read.table("data/inkar_ue2_all.csv", sep=";", header = TRUE)
inkar$ow <- factor(inkar$ow)
levels(inkar$ow)## [1] "alte Länder" "neue Länder"## [1] "Baden-Württemberg" "Bayern" "Berlin"
## [4] "Brandenburg" "Bremen" "Hamburg"
## [7] "Hessen" "Mecklenburg-Vorpommern" "Niedersachsen"
## [10] "Nordrhein-Westfalen" "Rheinland-Pfalz" "Saarland"
## [13] "Sachsen" "Sachsen-Anhalt" "Schleswig-Holstein"
## [16] "Thüringen"17.2 ANOVA - Einsatz kategorieller Variablen in linearen Modellen
Wird ein lineare Modell mit einer Faktorvariable als Prädiktor gefittet, wird je Gruppe der Mittelwert gefittet (s. Abbildung 17.1). Dieser wird dann für die Vorhersage verwendet - es gibt ja auch keine Differenzierung hinsichtlich des Merkmales. Ein Kreis im INKAR Datensatz gehört zu den alten oder den neuen Bundesländern (s. Abbildung 17.2).
Klasssicherweise wird dies als ANOVA (Analysis of Variance) bezeichnet, das untersucht wird, ob sich die Varianz zwischen den Gruppen signifant unterscheidet. Die ANOVA lässt sich jedoch problemlos als Spezialfall des linearen Modells darstellen.64
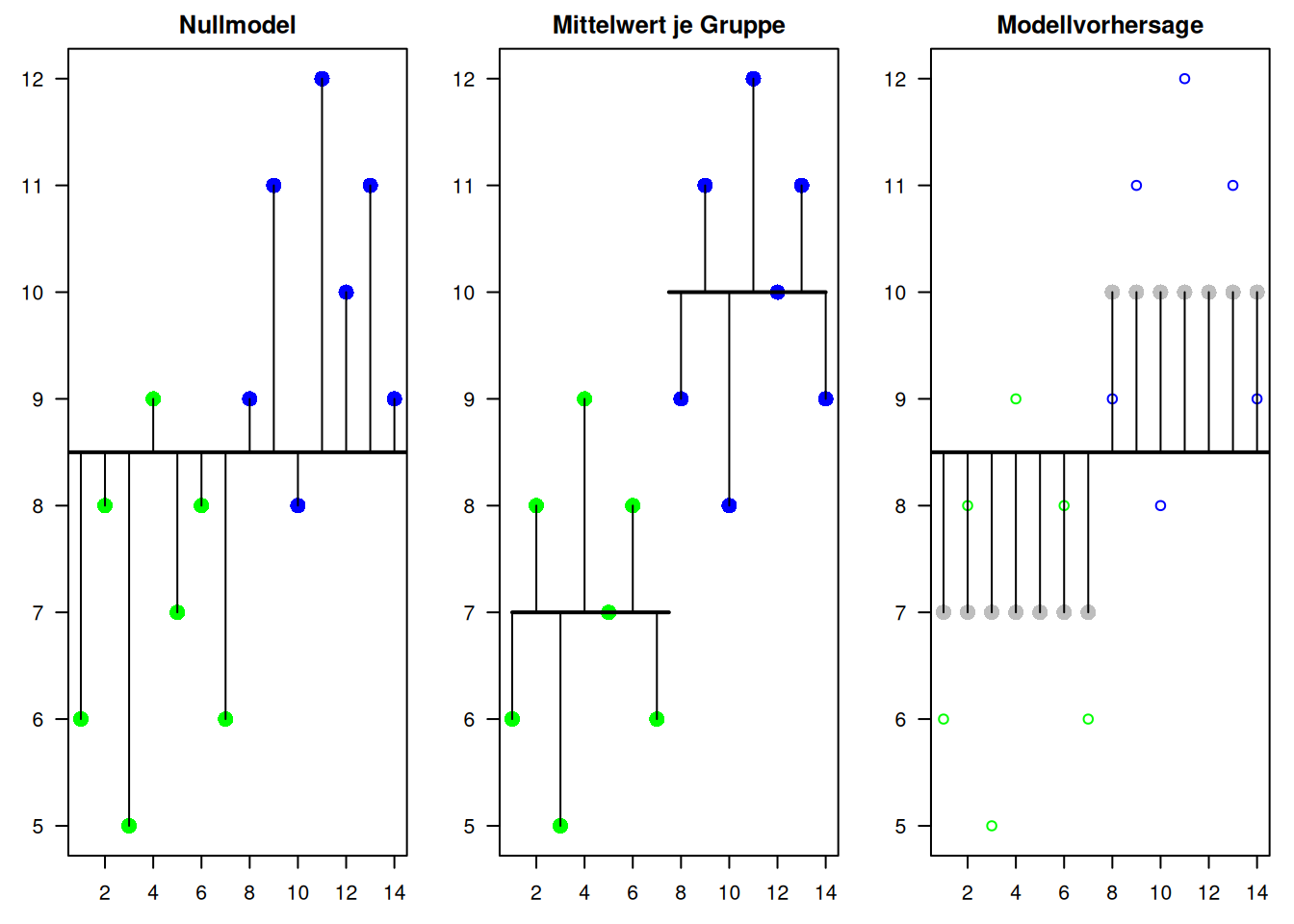
Figure 17.1: Verwendung einess kategorialen Prädiktors mit zwei Faktorleveln in einem linearen Regressionsmodell. Der linke Plot zeigt das Nullmodell, bei dem der globale Mittelwert verwendet wird, um das Systemverhalten abzubilden. Im mittleren Pannel wird der Mittelwert je Gruppe für die Vorhersage verwendent. Im rechten Plot ist die Modellvorhersage eingezeichnet. Die horizontalen Linien repräsentierten stets den Mittelwert, die Farbkodierung der Punkte gibt die Gruppenzugehörigkeit an.
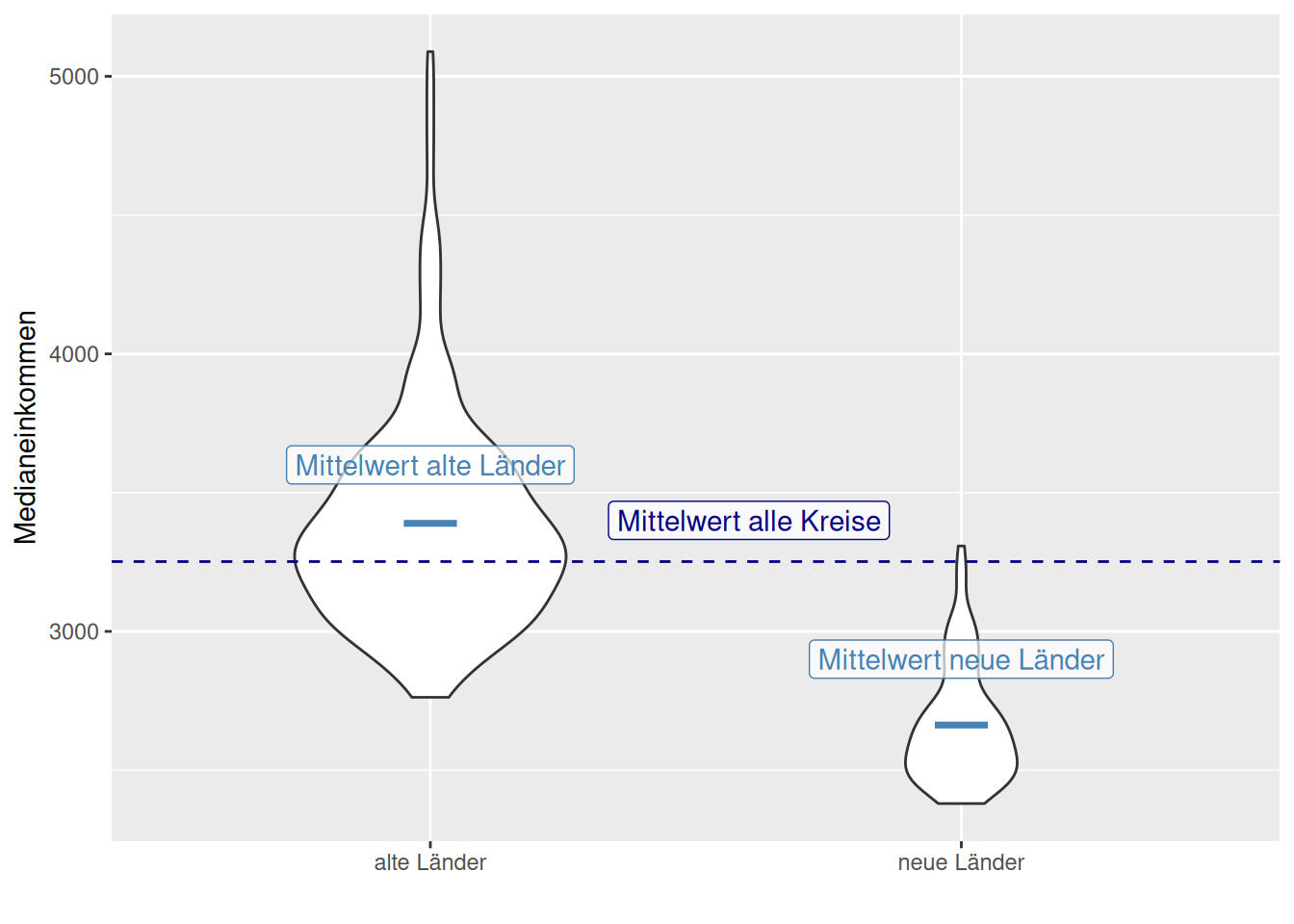
Figure 17.2: ANOVA im linearen Modell. Es wird je Gruppe der Mittelwert geschätzt und für die Vorhersage verwendet. Die Güte des Modells ergibt sich wieder aus dem Vergleich mit dem Nullmodell, bei dem der Mittelwert über alle Faktorlevel hinweg geschätzt wird. Der Violinplot zeigt die Verteilung der Daten, die horizontalen Linen den jeweiligen Mittelwert.
Das Model wird im formula Objekt von lm ganz normal definiert - die Funktion erkennt, dass es eine Faktorvariable ist und erstellt daraus die Modellmatrix. Hierbei wird die kategorische Variable (bei Verwendung der Standard Kontraste) als Dummy-Variable kodiert. Hierbei werden alle Faktorlevel bis auf das Referenzlevel (das erste Level des Faktors) in einer eigenen Variable mit 0 und 1 kodiert: 1 wird gesetzt, wenn die Beobachtung dem Faktorlevel angehört, 0 sonst.
## (Intercept) owneue Länder
## 1 1 0
## 2 1 0
## 3 1 0
## 4 1 0
## 5 1 0
## 6 1 0Entsprechend zeigt summary auch einen Regressionskoeffizienten für jedes Faktorlevel außer dem Referenzlevel65. In unserem Beispiel wird dieser als owneue Länder angezeigt. Dieser gibt die Differenz zum Referenzlevel an. Das Medianeinkommen der neuen Länder ist also 726,69€ geringer als der Mittelwert über alle Kreise.
##
## Call:
## lm(formula = Medianeinkommen ~ ow, data = inkar)
##
## Residuals:
## Min 1Q Median 3Q Max
## -626.73 -228.01 -67.85 169.76 1699.59
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3389.32 20.01 169.38 <2e-16 ***
## owneue Länder -726.69 45.96 -15.81 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 360.7 on 399 degrees of freedom
## Multiple R-squared: 0.3852, Adjusted R-squared: 0.3836
## F-statistic: 250 on 1 and 399 DF, p-value: < 2.2e-16Verwenden wir die Bundesländer als Prädiktor, werden entsprechend 15 Regressionskoeffizienten geschätzt. Da wir nichts weiter definiert haben, wird Baden-Württemberg als Referenzwert verwendet, da es bei der alphabetischen Sortierung der Faktorlevel an erster Stelle kommt.
## (Intercept) GEN_LANBayern GEN_LANBerlin GEN_LANBrandenburg GEN_LANBremen
## 1 1 0 0 0 0
## 2 1 0 0 0 0
## 3 1 0 0 0 0
## 4 1 0 0 0 0
## 5 1 0 0 0 0
## 6 1 0 0 0 0
## GEN_LANHamburg GEN_LANHessen GEN_LANMecklenburg-Vorpommern
## 1 0 0 0
## 2 0 0 0
## 3 0 0 0
## 4 0 0 0
## 5 0 0 0
## 6 0 0 0
## GEN_LANNiedersachsen GEN_LANNordrhein-Westfalen GEN_LANRheinland-Pfalz
## 1 0 0 0
## 2 0 0 0
## 3 0 0 0
## 4 0 0 0
## 5 0 0 0
## 6 0 0 0
## GEN_LANSaarland GEN_LANSachsen GEN_LANSachsen-Anhalt
## 1 0 0 0
## 2 0 0 0
## 3 0 0 0
## 4 0 0 0
## 5 0 0 0
## 6 0 0 0
## GEN_LANSchleswig-Holstein GEN_LANThüringen
## 1 1 0
## 2 1 0
## 3 1 0
## 4 1 0
## 5 1 0
## 6 1 0##
## Call:
## lm(formula = Medianeinkommen ~ GEN_LAN, data = inkar)
##
## Residuals:
## Min 1Q Median 3Q Max
## -549.51 -208.30 -68.67 122.34 1895.54
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3684.49 50.95 72.312 < 2e-16 ***
## GEN_LANBayern -317.56 61.53 -5.161 3.94e-07 ***
## GEN_LANBerlin -301.16 341.80 -0.881 0.378811
## GEN_LANBrandenburg -983.14 94.56 -10.397 < 2e-16 ***
## GEN_LANBremen -190.83 244.36 -0.781 0.435314
## GEN_LANHamburg 135.88 341.80 0.398 0.691191
## GEN_LANHessen -168.03 83.60 -2.010 0.045153 *
## GEN_LANMecklenburg-Vorpommern -1049.79 129.90 -8.081 8.37e-15 ***
## GEN_LANNiedersachsen -491.12 71.66 -6.854 2.87e-11 ***
## GEN_LANNordrhein-Westfalen -262.10 68.93 -3.802 0.000167 ***
## GEN_LANRheinland-Pfalz -388.25 75.96 -5.112 5.04e-07 ***
## GEN_LANSaarland -289.75 147.09 -1.970 0.049564 *
## GEN_LANSachsen -1051.79 106.69 -9.858 < 2e-16 ***
## GEN_LANSachsen-Anhalt -1013.74 103.71 -9.775 < 2e-16 ***
## GEN_LANSchleswig-Holstein -588.11 101.05 -5.820 1.24e-08 ***
## GEN_LANThüringen -1030.47 86.96 -11.849 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 338 on 385 degrees of freedom
## Multiple R-squared: 0.4792, Adjusted R-squared: 0.4589
## F-statistic: 23.62 on 15 and 385 DF, p-value: < 2.2e-16Schwierig ist in unserem Beispiel, dass die Anzahl der Kreise je Bundesland sehr stark streut:
## GEN_LAN
## Baden-Württemberg Bayern Berlin
## 44 96 1
## Brandenburg Bremen Hamburg
## 18 2 1
## Hessen Mecklenburg-Vorpommern Niedersachsen
## 26 8 45
## Nordrhein-Westfalen Rheinland-Pfalz Saarland
## 53 36 6
## Sachsen Sachsen-Anhalt Schleswig-Holstein
## 13 14 15
## Thüringen
## 23Entsprechend hinkt der Vergleich zwischen den Bundeländer etwas. Dies spiegelt sich auch in den p-Werten der einzelnen Koeffizienten wieder - es ist nicht nur der Unterschied zum Referenzlevel relevant, sondern auch die Anzahl der Elemente je Stichprobe.66
## Warning: Groups with fewer than two datapoints have been dropped.
## ℹ Set `drop = FALSE` to consider such groups for position adjustment purposes.
## Groups with fewer than two datapoints have been dropped.
## ℹ Set `drop = FALSE` to consider such groups for position adjustment purposes.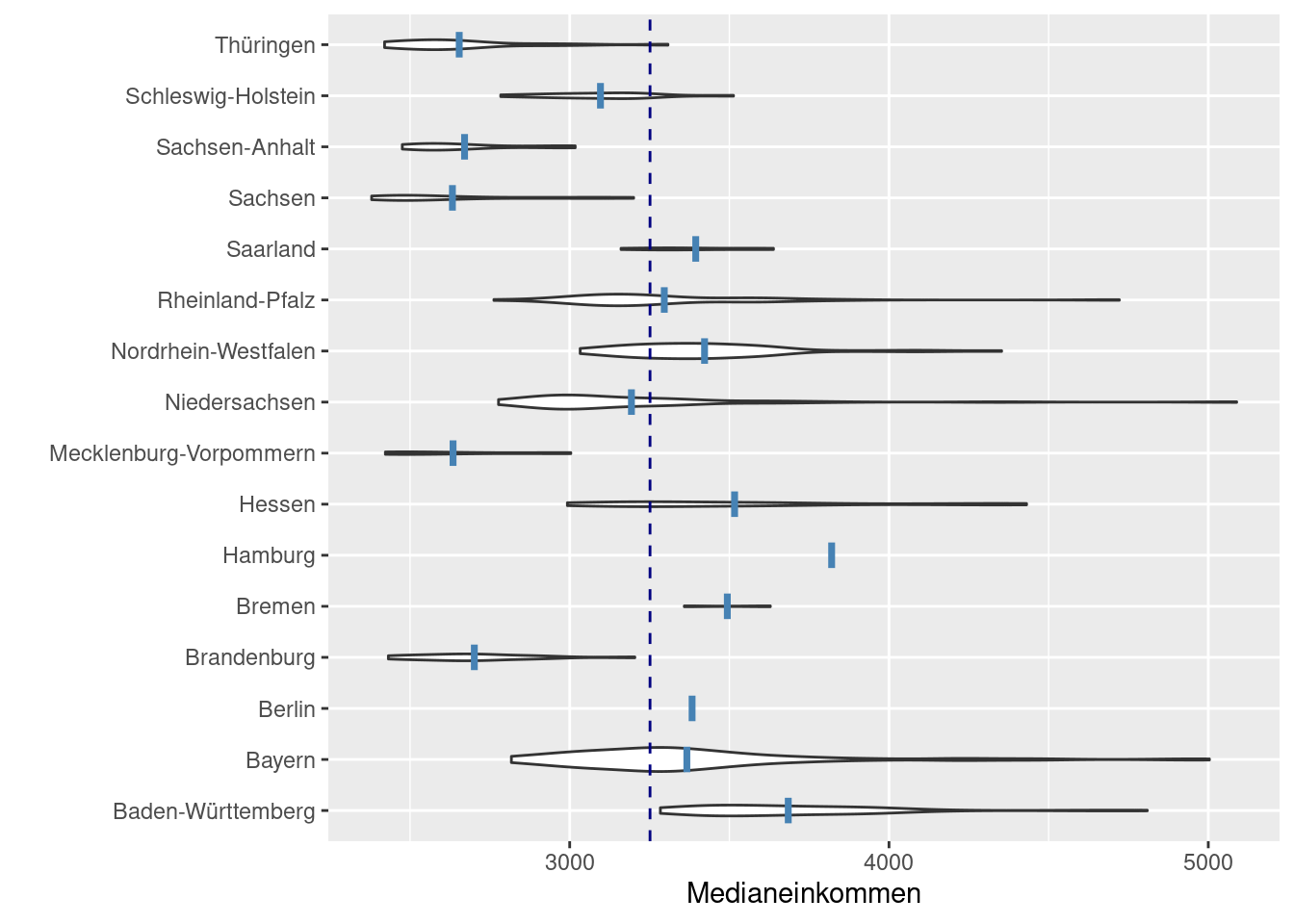
Um zu testen, ob der Gesamteffekt des Prädiktors - also nicht ob einzelne Faktorlevel einen signifikanten Effekt haben, kommt ein F-Test zum Einstatz. Im Fall des Medianeinkommens hat Zugehörigkeit zu einem Bundesland eine Verbesserung der Vorhersage zur Folge. Die Nullhypothese ist, dass die Modellgüte mit und ohne den kategorischen Prädiktor keinen Einfluss auf die Modelgüte (Sum of Squares) hat.
## Analysis of Variance Table
##
## Response: Medianeinkommen
## Df Sum Sq Mean Sq F value Pr(>F)
## GEN_LAN 15 40469734 2697982 23.619 < 2.2e-16 ***
## Residuals 385 43978901 114231
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 117.3 ANCOVA - Einsatz kategorialer und numerischer Variablen in linearen Modellen
Man kann kategoriale und numerische Variablen kombinieren. Dies nennt man klassischerweise ANCOVA (Analysis of Covariance). Auch das lässt sich aber wieder einfach im linearen Modell darstellen.
Schauen wir uns dies am Beispiel der Stimmanteile für die AfD bei der vorletzten Bundestagswahl an. Wir haben die Hypothese, dass dies mit dem Ausländeranteil zusammenhängen könnte, aber vermuten auch einen Unterschied zwischen alten und neuen Bundesländern.
##
## Call:
## lm(formula = Stimmenanteile.AfD ~ ow + Ausländeranteil, data = inkar)
##
## Residuals:
## Min 1Q Median 3Q Max
## -9.4773 -2.1412 -0.2889 2.0010 13.4013
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.98620 0.46787 23.481 <2e-16 ***
## owneue Länder 10.98775 0.48705 22.560 <2e-16 ***
## Ausländeranteil 0.02972 0.03541 0.839 0.402
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.248 on 398 degrees of freedom
## Multiple R-squared: 0.6302, Adjusted R-squared: 0.6284
## F-statistic: 339.2 on 2 and 398 DF, p-value: < 2.2e-16Das Modell zeigt an, dass die Stimmenanteile in den neuen Bundesländern signifikant höher als in den alten Bundesländern sind. Der Ausländeranteil hat allerdings keinen signifikanten Einfluss auf die Stimmenanteile der AfD.
Allerdings sollten wir die Hypothese testen, ob sich der Ausländeranteil unterschiedlich in den neuen und den alten Bundesländern auswirkt. Dies erreichen wir, indem wir eine Interaktion ins Modell mit aufnehmen.
##
## Call:
## lm(formula = Stimmenanteile.AfD ~ ow * Ausländeranteil, data = inkar)
##
## Residuals:
## Min 1Q Median 3Q Max
## -7.7586 -2.0561 -0.1833 2.0229 11.4586
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 10.43556 0.45751 22.810 < 2e-16 ***
## owneue Länder 16.12996 0.97118 16.609 < 2e-16 ***
## Ausländeranteil 0.07488 0.03475 2.155 0.0318 *
## owneue Länder:Ausländeranteil -0.97458 0.16142 -6.038 3.59e-09 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 3.112 on 397 degrees of freedom
## Multiple R-squared: 0.6613, Adjusted R-squared: 0.6588
## F-statistic: 258.4 on 3 and 397 DF, p-value: < 2.2e-16Wie wir sehen ist nun sowohl der Haupteffekt als auch die Interaktion mit der kategorialen Variable signifikant. Schauen wir uns die Koeffizienten einmal etwas genauer an:
- in den Kreisen der fünf neuen Ländern waren die Stimmenanteile im Mittel um 16,13% höher als in den alten Ländern
- der Stimmenanteil der AfD stieg mit jedem Prozentpunkt, den sich der Ausländeranteil erhöhte um 0.075% an.
- in den neuen Bundesländern verreingerte sich dieser Effekt jedoch um -0.97% mit jedem Prozentpunkt, den sich der Ausländeranteil erhöhte (Interaktion)
- in Summe verringerte sich der Stimmanteil der AfD in den neuen Bundesländern um (0.07488 -0.97458) =-0.9% mit jedem Prozentpunkt, den sich der Ausländeranteil erhöhte
Da die Dummy-Variable owneue Länder 0 oder 1 enthält, ist der Effekt der Interaktion für die alten Bundesländer gleich Null (da Null mal irgendwas Null ergibt). Im Fall der neuen Bundesländer ist der Wert 1, deswegen wird dann 1 mit dem Koeffizienten multipliziert.
\[\text{Stimmenanteile.AfD} = \hat{\beta}_0 + \hat{\beta}_1 \cdot \text{`owneue Länder`} + \hat{\beta}_2 \cdot \text{Ausländeranteil} + \hat{\beta}_3 \cdot \text{`owneue Länder`} \cdot \text{Ausländeranteil} \]
Für die alten Bundesländer ergibt sich damit:
\[\text{Stimmenanteile.AfD} = 10.43556 + 16.12996 \cdot 0 + 0.07488 \cdot \text{Ausländeranteil} -0.97458 \cdot 0 \cdot \text{Ausländeranteil} = 10.43556 + 0.07488 \cdot \text{Ausländeranteil}\]
Für die neuen Bundesländer ergibt sich:
\[\text{Stimmenanteile.AfD} = 10.43556 + 16.12996 \cdot 1 + 0.07488 \cdot \text{Ausländeranteil} -0.97458 \cdot 1 \cdot \text{Ausländeranteil} = 26.56552 + 0.07488 \cdot \text{Ausländeranteil} -0.97458 \cdot \text{Ausländeranteil}\]
# erzeugen einer Kombination der Vorhersagewerte
newdat <- expand.grid(Ausländeranteil= seq(min(inkar$Ausländeranteil),
max(inkar$Ausländeranteil), length.out = 10),
ow = levels(inkar$ow))
# Vorhersage auf Basis des Regressionsmodells
thePrediction <- predict(g, newdata = newdat)
# Vorhersagewerte an den data.frame mit den Werte für die
# Vorhersage anfügen
newdat$pred <- thePrediction
# plotten der Regressionslinie und der
# Beobachtungen (liegen als 2 separate data.frames vor)
ggplot(data = newdat, mapping = aes(x= Ausländeranteil, y = pred)) +
geom_line() +
geom_point(data = inkar, alpha =.5,
mapping = aes(x= Ausländeranteil,
y = Stimmenanteile.AfD)) +
facet_wrap(~ow) + ylab("Stimmenanteil AfD")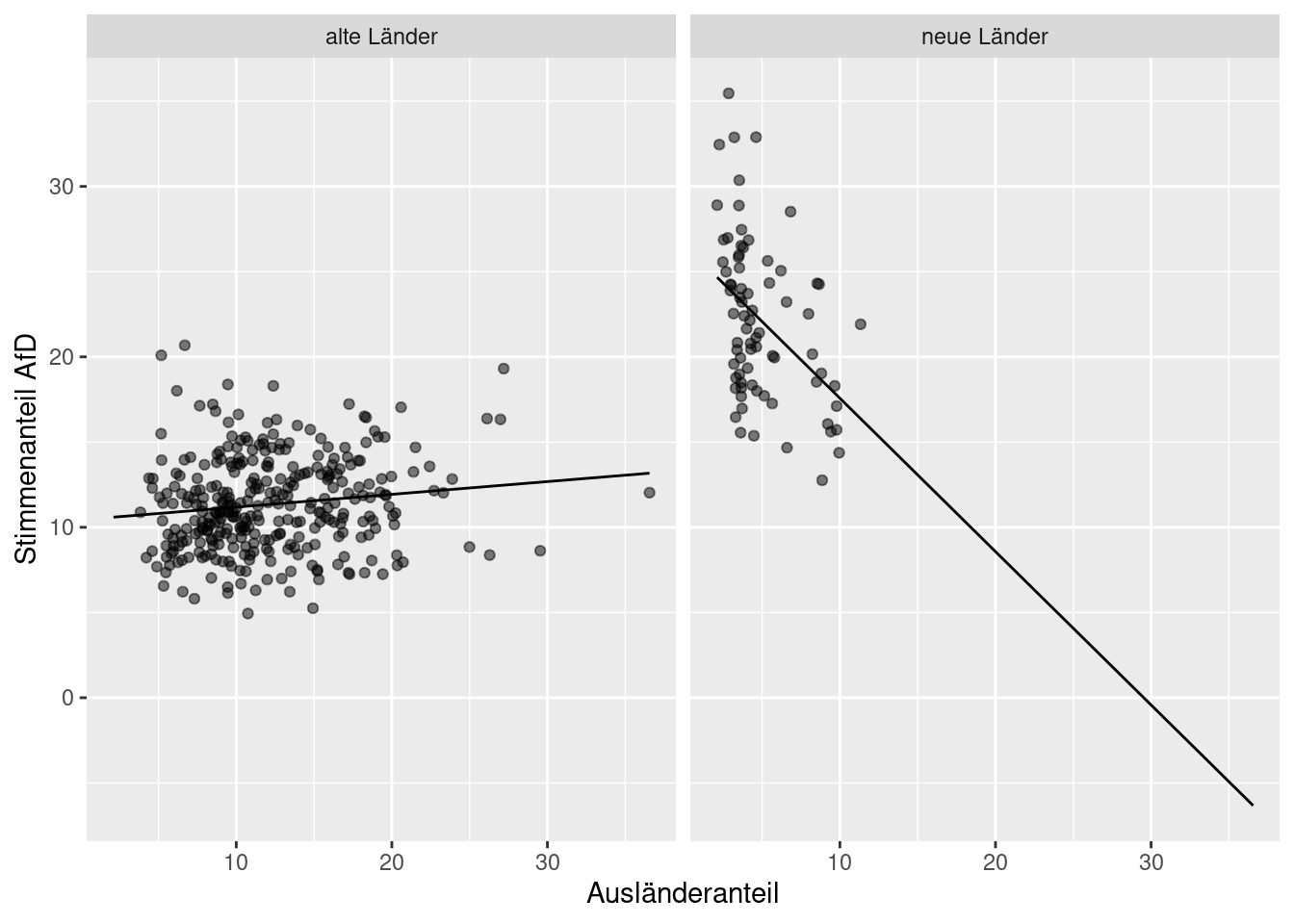
Es gibt neben der ANOVA Typ I, die wir hier betrachten andere Varianten, die für speziellere Situationen z.B. aufgrund des experimentellen Designs angewandt werden müssen. Dann lässt sich das nicht mehr mit einem einfachen linearen Modell darstellen.↩︎
Bei Verwendung der Standard Kontraste.↩︎
Falls man die Kreisstatistik denn als Zufallsstichprobe auffassen möchte.↩︎