Kapitel 6 Beschreibung von Verteilungen

Um empirische Daten miteinander oder mit theoretischen Verteilungen zu vergleichen, verwendet man verschiedene Maße, von denen ich hier die wichtigsten vorstellen möchte. Man setzt diese Maße z.B. ein, um die Mittelwerte zweier Gruppen miteinander zu vergleichen: sind die Covid-19 Inzidenzen im Mittel höher in den neuen oder den alten Bundesländern? Sind die Inzidenzen höher in Großstädten als im ländlichen Raum und in verstädterten Regionen? Haben weibliche Studierende bessere Noten als männliche? …

require(sf)
require(ggplot2)
covidKreise <-st_read("data/health", layer = "covidKreise", quiet = TRUE)

covidKreise$ow <- ifelse(covidKreise$LAN_GEN %in% c( "Brandenburg", "Mecklenburg-Vorpommern", "Sachsen", "Sachsen-Anhalt", "Thüringen"),
       "neue Länder", "alte Länder")

ggplot(data= covidKreise, mapping = aes(x=second_wav / EWZ*10^5 )) +
  geom_histogram() +
  facet_wrap(~ ow, ncol=1, scale = "free_y") +
  xlab("Inzidenz je 100.000 EW") + ylab("Anzahl Kreise") +
  labs("COVID-19, 2. Welle in Dtld.")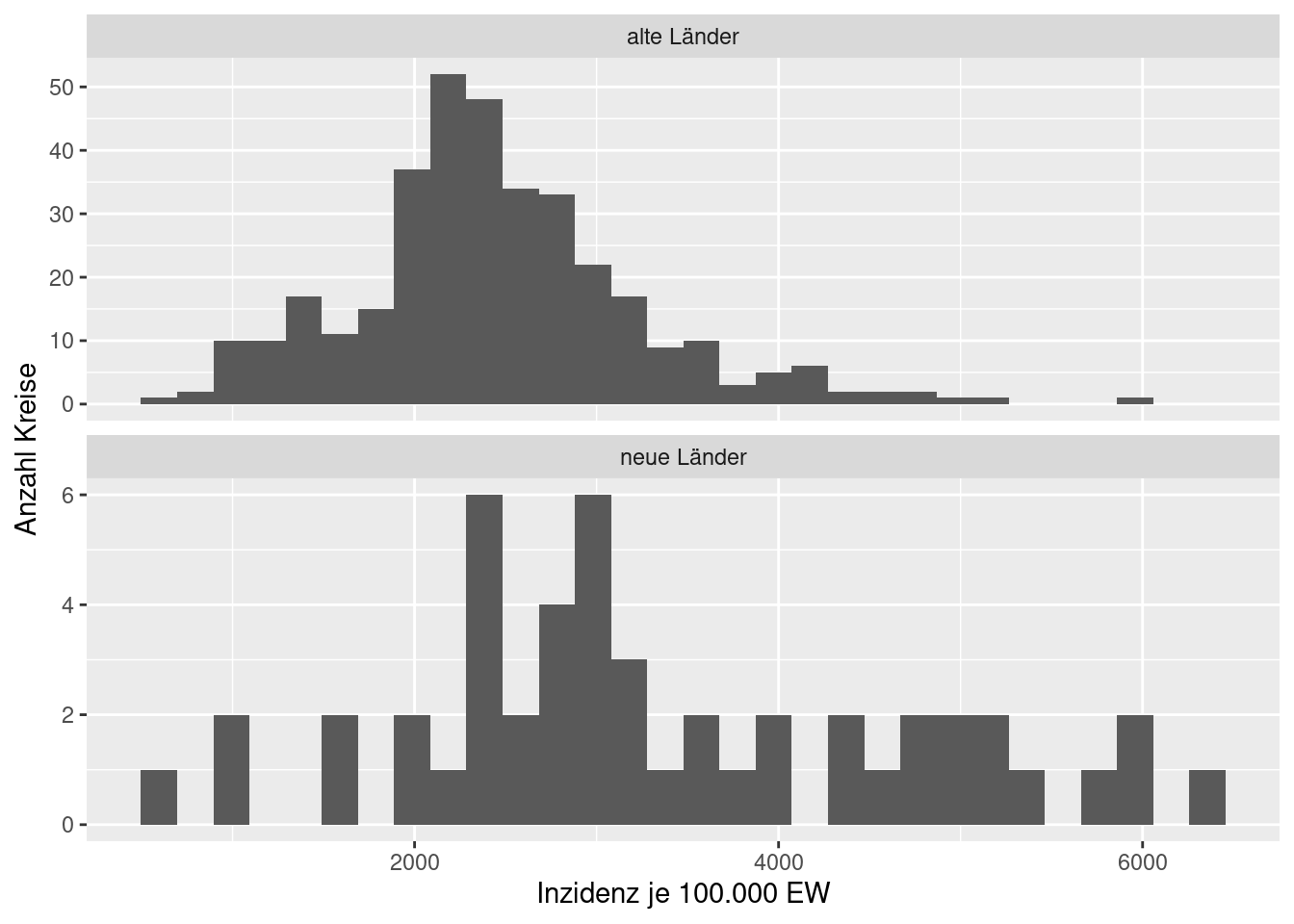

Die statistischen Kennzahlen erlauben es uns, einen schnellen Überblick über einen Datensatz zu erhalten und zu kommunizieren. Anstelle die COVID-19 Inzidenzraten aller Kreise aufzuzählen, können wir sie einfach durch Kennzahlen (wie Mittelwert und Standardabweichung) charakterisieren. Vorab jedoch ein Wort der Warnung: Kennzahlen können auch wichtige Detals verschleiern, insbesondere wenn die Verteilung der Daten schief oder multimodal ist. Deswegen empfiehlt es sich immer, die Daten auch zu plotten, z.B. über ein Histogram, um sicher zu gehen, dass uns kein wichtiges Detail entgeht. Wenn dasnicht der Fall ist, können wir mit den Kennzahlen weiterarbeiten. Falls nicht, sollten wir davon Abstand nehmen, um keine falschen Schlussfolgerungen zu provozieren.

Bei der Berechnung unterscheidet man stets für den Fall, dass man das Maß für eine Stichprobe oder eine Grundgesamtheit berechnen will. Es macht also einen Unterschied, ob man die Standardabweichung für das Alter aller Studierender einer Hochschule berechnet, oder ob man diese für eine Stichprobe aus der Studierendenschaft der Hochschule berechnet. Maße für Grundgesamtheiten sind wahre Werte, während es sich bei den Maßen für Stichproben nur um Schätzungen handeln kann. I.d.R. möchte man aus den Maßen für die Stichprobe auf den wahren Wert der Grundgesamtheit schließen.

Für bestimmte Verteilungen kann es vorkommen, dass einzelne Maße nicht definiert sind, z.B. bei der Cauchy-Verteilung.

6.1 Lagemaße

Lagemaße charakterisieren einen bestimmten Punkt einer Verteilung, z.B. den häufigsten Wert, den Mittelwert oder den Wert, beim dem 25% kleiner und 75% größer sind.

6.1.1 Mittelwert und Erwartungswert

Der Erwartungswert bezieht sich immer auf die Grundgesamtheit. Es ist der Wert, den man erwartet, wenn man sehr oft Werte aus der Verteilung zieht. Er beschreibt die zentrale Lage der Verteilung und wird auch als das erste Moment einer Verteilung definiert. Der Mittelwert dagegen bezieht sich auf die Werte einer Stichprobe.

Je nach Art der Daten sind unterschiedliche Maße sinnvoll.

6.1.1.1 Erwartungswert

Der Erwartungswert einer Zufallsvariablen lässt sich für diskrete Verteilungen als Summe der mit der Eintrittswahrscheinlichkeit multiplizierten zulässigen Werte der Zufallsvariablen berechnen:

\[ E[X] = \sum_{i \epsilon I} x_i p_i = \sum_{i \epsilon I} x_i P(X = x_i) \] \(I\) definiert hierbei den Wertebereich der diskreten Zufallsvariablen.

Beim Würfeln mit zwei sechsseitigen Würfeln ist der Erwartungswert bekanntermaßen:

2*1/36 + 3*2/36 + 4*3/36 + 5*4/36 + 6*5/36 + 7*6/36 + 
  8*5/36 + 9*4/36 + 10*3/36 + 11*2/36 + 12*1/36

## [1] 7

Für diskrete Wahrscheinlichkeitsverteilungen muss man zum Integral übergehen¹⁹:

\[ E[X] = \int_{-\infty}^{\infty} x f(x) dx\]

Der Erwartungswert ist das erste zentrale Moment einer Verteilung.

6.1.1.2 Aritmethisches Mittel

Das arithmetische Mittel, das oft einfach als Mittelwert bezeichnet ist, ist die Summe der Merkmalswerte geteilt durch die Stichprobengröße.

\[ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i \]

In R heißt der zugehörige Befehl mean:

x <- c(3,12,21,0.5, 2.3, 5.4, 6.8)
mean(x)

## [1] 7.285714

6.1.1.3 Gewichtetes arithmetisches Mittel

Hat man keinen Zugriff auf die original Messungen, sondern nur auf die Mittelwerte von Stichproben unterschiedlichen Stichprobenumfanges einer gemeinsamen Grundgesamtheit, dann kann man den Mittelwert über die Stichproben anhand des gewichteten arithmetischen Mittels berechnen.

\[ \bar{x} = \frac{1}{\sum_{i=1}^n w_i} \sum_{i=1}^n w_i \cdot \bar{x}_i \]

Wobei \(\bar{x}_i\) und \(w_i\) der Mittelwert und der Stichprobenumfang (das Gewicht) der jeweiligen Stichprobe sind.

In anderem Kontext taucht das gewichtete arithmetische Mittel z.B. auf, wenn eine Gesamtnote anhand der mündliche und der schriftliche Prüfungsleistung berechnet wird und die Prüfungsleistungen unterschiedlich gewichtet sind.

In R wird der Befehel weighted.mean benutzt, der zwei Vektoren als Argumente benötigt: die Stichprobenmittelwerte und die Gewichte

wt <- c(5,  5,  4,  1)/15
x <- c(3.7,3.3,3.5,2.8)
weighted.mean(x=x, w= wt)

## [1] 3.453333

6.1.1.4 Harmonisches Mittel

Das harmonische Mittel wird verwendet um den Mittelwert von Verhältniszahlen (Quotient zweier Größen) zu berechnen.

\[ \bar{x}_{harm} = \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \] mit \(x_i \neq 0\).

Wenn man unterschiedliche Gewichte verwenden muss, verwendet man das gewichtete harmonische Mittel:

\[ \bar{x}_{harm} = \frac{\sum_{i=1}^n w_i}{\sum_{i=1}^n \frac{w_i}{x_i}} \]

Es wird z.B. eingesetzt, um die mittlere Reisegeschwindigkeit zu berechnen. Im Beispiel sei die Geschwindigkeit eines Fahrzeugs eine Stunde lang 100km/h und zwei weitere Stunden 50km/h, so ist die mittlere Geschwindigkeit 66.66km/h (200km in 3h Fahrtzeit).

Das arithmetische Mittel ist hier korrekt:

mean(x=c(100,50,50))

## [1] 66.66667

Oder:

weighted.mean(x= c(100,50), w= c(1,2))

## [1] 66.66667

Anders sieht es aus, wenn man die Angaben in zurückgelegter Strecke erhält: 100km mit 50km/h und 100km mit 100km/h. Das harmonische Mittel ergibt den korrekten Wert:

(100 + 100) / ((100/50) + 100/100)

## [1] 66.66667

Das gewichtete harmonische Mittel wäre falsch:

weighted.mean(x= c(100,50), w= c(100,100))

## [1] 75

Ähnlich lässt sich mit dem Ansatz die mittlere Geschwindigkeit einer Fahrzeugflotte berechnen, die unterschiedliche Distanzen zurücklegt.

Weitere Beispiele sind die mittlere hydraulische Leitfähigkeit, Populationsgenetik und der F1-score, der uns beim Thema Klassifikation begegnen wird.

Das harmonische Mittel ist stets kleiner gleich dem arithmetischen Mittel und dem geometrischen Mittel.

\[ \bar{x}_{harm} \leq \bar{x}_{geom} \leq \bar{x} \] Es gibt keine Funktion für das harmonische Mittel, dass auch Gewichte berücksichtigt. Es kann aber einfach wie folgt berechnet werden:

x=c(100, 50)
w=c(100,100)
sum(w)/sum(w/x)

## [1] 66.66667

Wir können uns die Funktion auch selbst definieren und dort noch ein paar Spezialfälle abfangen: was soll mit 0-Werten passieren? Wie sollen fehlende Werte behandelt werden? Was passiert, wenn anstelle eines Vektors eine Matrix oder ein data.frame übergeben wird? (Aktuell sollte w ein Vektor sein)

harmonic.mean <- function (x, w, na.rm = TRUE, zero = TRUE) 
{
    if(missing(w))
      w <- rep(1, times= length(x))
    if (!zero) {
        x[x == 0] <- NA
    }
    if (is.null(nrow(x))) {
        harmean <- sum(w)/sum(w/x, na.rm = na.rm)
    }
    else {
        harmean <- sum(w)/(apply(w/x, 2, sum, na.rm = na.rm))
    }
    return(harmean)
}

harmonic.mean(x=c(100, 50), w= c(100, 100))

## [1] 66.66667

6.1.1.5 Geometrisches Mittel

Das geometrische Mittel von n Zufallszahlen ist die n-te Wurzel aus dem Produkt der Zufallszahlen:

\[ \bar{x}_{geom} = \sqrt[n]{\prod_{i=1}^n x_i} \]

Das geometrische Mittel wird verwendet, um den Mittelwert von Raten zu berechnen, z.B. die mittlere Wachstumsrate. Stellen wir uns vor, die \(CO_2\)-Emissionen eines Landes betragen im Jahr 2015 61 MT (etwa Finnland). Die Emissionen wachsen jährlich folgenden Raten:

emissions <- data.frame(
  year = 2016:2021,
  rate= c(1.02, 1.05, 1.14, 1.01, 0.98, 0.99)
)
emissions

##   year rate
## 1 2016 1.02
## 2 2017 1.05
## 3 2018 1.14
## 4 2019 1.01
## 5 2020 0.98
## 6 2021 0.99

Was ist die mittlere Wachstumsrate?

Das arithmetische Mittel ist:

mean(emissions$rate)

## [1] 1.031667

Rechnen wir das mal per Hand aus. Das Produkt der Raten ist:

prodRates <- prod(emissions$rate)
prodRates

## [1] 1.196402

In den sechs Jahren sind die Emissionen als um 19.64% gewachsen.

Wenn wir nun die mittlere Wachstumsrate suchen, suchen wir nach einer Zahl, die sechs mal mit sich selbst multipliziert diesen Wert ergibt. D.h. wir müssen einfach die sechste-Wurzel aus dem Produkt der Raten ziehen (was der Formel des geometrischen Mittels entspricht)

prodRates^(1/6)

## [1] 1.030337

Die mittlere Rate unterscheidet sich hier bei den beiden Rechenarten nur etwas, korrekt ist jedoch das geometrische Mittel.

Wenn wir mit dem arithmetischen Mittel rechnen würden, kämen wir für den gesamten Zeitraum auf eine zu hohe Wachstumsrate der THG-Emissionen.

mean(emissions$rate)^6

## [1] 1.205692

61* (prodRates - mean(emissions$rate)^6)

## [1] -0.5667197

Für die 6 Jahre wären die Emissionen damit 0.57 MT zu hoch, was in etwa der Summe der THG-Emissionen von Fiji und Mikronesien entspricht, also nicht unerheblich ist.

6.1.2 Quantile

Eine andere Möglichkeit, um die Verteilung von Daten einer Stichprobe zu charakterisieren ist es, sie zunächst aufsteigend zu sortieren und dann den Wert anzugeben, der sich bei p (in %) der Daten befindet, z.B. bei 25% (empirisches Quantil). Das p-Quantil ist immer der Wert, bei dem p% kleiner gleich dem angegebenem Wert \(x_p\) sind und (100-p) größer gleich \(x_p\) - sofern keine Werte mehrfach auftreten. Falls Werte mehrfach auftreten, kann es sein dass das Quantil auf einem Wert liegt, der mehrfach vorkommt. Dann ist es so, dass wenigstens p% der Werte kleiner sind als der Quantilwert \(x_p\).

Empirisches Quantil: das p-Quantil einer Zufallsstichprobe (\(x_1, x_2,...x_n\)) \(x_p\) ist definiert als:

• für wenigstens \(p*n\) der Werte gilt \(x_i \leq x_p\)
• für wenigstens \((1-p)*n\) der Werte gilt \(x_i \geq x_p\)

Dies ist der Datenpunkt an Position \(n*p+1\)

Das p-Quantil einer Grundgesamtheit (\(x_p\)) gibt den Wert an, bei dem die Wahrscheinlichkeit, dass ein zufällig gezogener Wert kleiner gleich dem Wert \(x_p\) ist und die Wahrscheinlichkeit, dass ein zufällig gezogener Wert größer gleich \(x_p\) ist (100-p)%.

Für Wahrscheinlichkeitsverteilungen heißt dass, dass eine reele Zahl \(x_p\) ein \(p\)-Quantil der Wahrscheinlichkeitsverteilung \(P\) ist, wenn gilt:

\(P((-\infty,x_p]) \geq p\) und \(P([x_p, \infty) \geq 1-p\).

Für einige gebräuchliche Quantile haben sich spezielle Bezeichnungen etabliert.

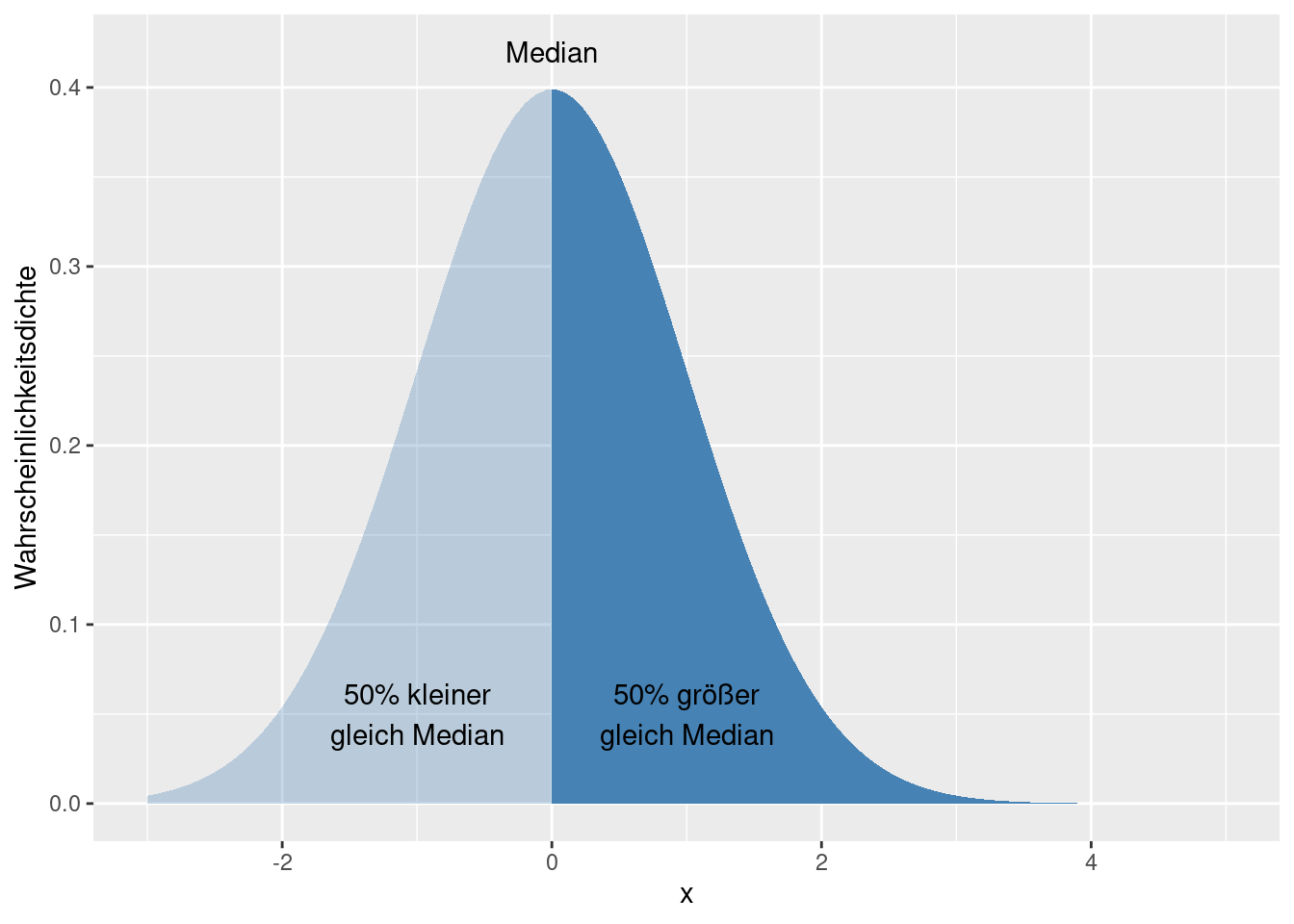
Der Median entspricht dem 50%-Quantil. D.h. wenigstens 50% der Werte sind kleiner gleich diesem Wert und wenigstens 50% der Werte sind größer gleich diesem Wert. Bei einer ungeraden Anzahl von Datenpunkten einer empirischen Stichprobe liegt der Wert also an der Position \(round(n*p+0.5)\) bzw. \(ceiling(n*p)\). round(x,digits) rundet die Zahl x auf digits Nachkommastellen, ceiling(x) liefert den kleinsten Integer- (Ganzzahl-) Wert, der nicht kleiner ist als x.

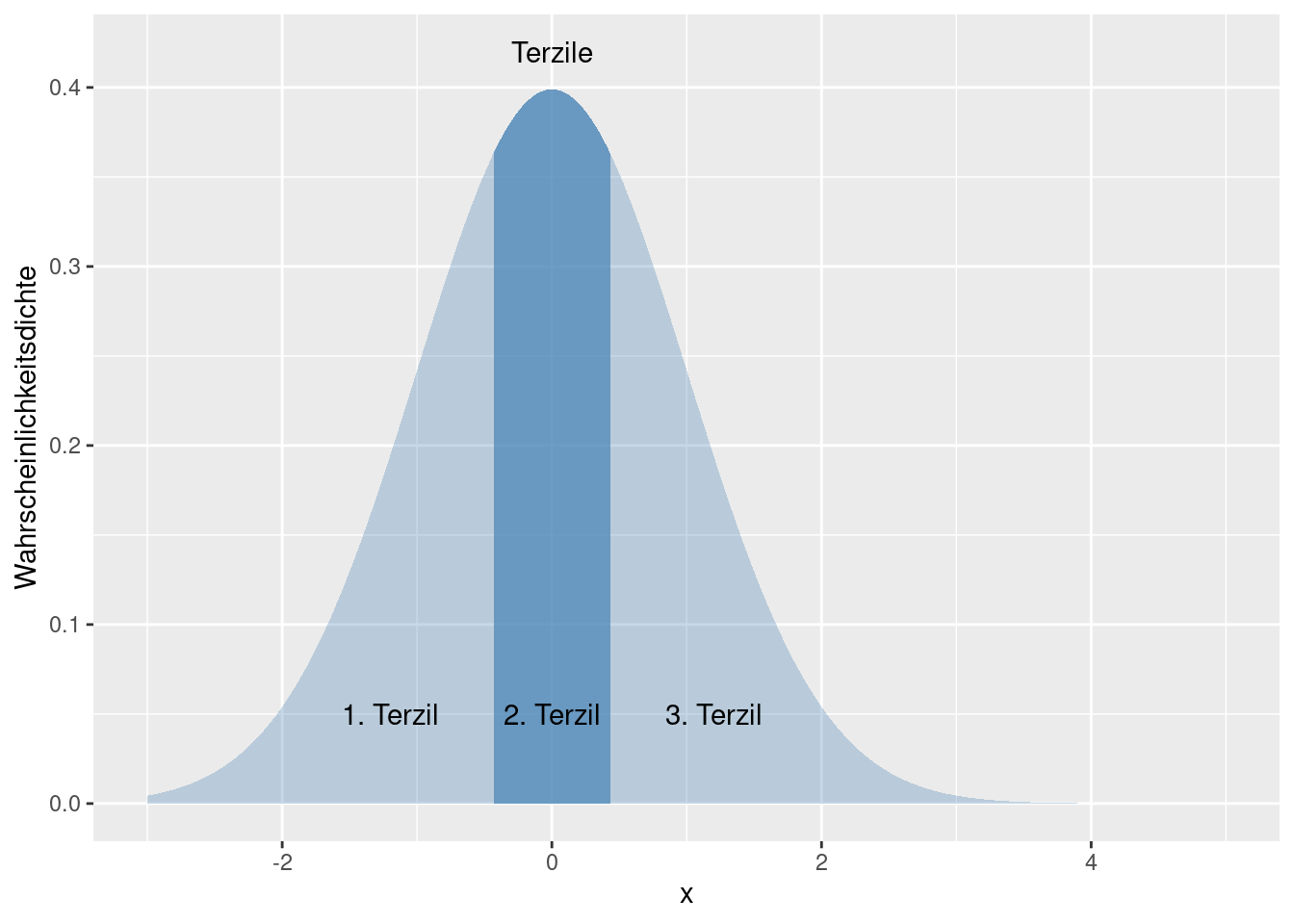
Durch Terzile wird die Stichprobe/Grundgesamtheit/Wahrscheinlichkeitsverteilung in drei gleiche Teile geteilt, beim Quartil in vier, beim Quintil in 5, bei Dezil in 10, beim Perzentil in 100.

Ein Beispiel in R:

theSample <- c( 101, 22, 43, 174, 82, 84.5, 12, 81.5, -12, 23, 11)
median(theSample)

## [1] 43

c wird benutzt, um einen Vektor von Werten zu erzeugen. median berechnet (nicht überraschend) den Median eines Vektors.

Das Ganze noch einmal Schritt für Schritt:

Zunächst sortieren wir die Werte der Reihe nach:

(theSampleSorted <- sort(theSample))

##  [1] -12.0  11.0  12.0  22.0  23.0  43.0  81.5  82.0  84.5 101.0 174.0

Dann ermitteln wir die Anzahl der Datenpunkte:

(n <- length(theSampleSorted))

## [1] 11

Der Median entspricht dem 50-Quantil:

ceiling(n*0.5)

## [1] 6

Der Wert an dieser Position:

theSampleSorted[ceiling(n*0.5)]

## [1] 43

Der eckige Klammeroperator [i] extrahiert aus einem Vektor von Werten das Element an der i-ten Position.

Beim empirischen Quantil tritt die Schwierigkeit auf, dass \(p*n\) nicht ganzzahlig ist, also kein Wert gewählt werden kann. Beim Median wird bei intervallskalierten Daten, so vorgegangen, dass dann der Mittelwert zwischen den beiden nächstgelegenen Datenpunkten verwendet wird. Bei 10 ,Datenpunkten wird dann der Mittelwert aus dem 5 und und dem 6. aufsteigend sortiertem Datenpunkt gebildet wird.

theSample <- c(5, 1, -1, 3)
median(theSample)

## [1] 2

Der Median ist in diesem Fall der Mittelwert des 2. und des 3. Elementes des sortierten Vektors, also: \((1+3)/2 = 2\).

Bei der Berechnung von empirischen Quantilen gibt es eine ganze Reihe von Verfahren, um den Quantilwert zu bestimmen, wenn dieser nicht an einer ganzzahligen Position liegt. Die Funktion quantile(x, probs, type) kennt 9 verschiedene Methoden um diese zu berechnen. Wir müssen uns hier allerdings nicht mit diesen Feinheiten belasten. Wer an Details interessiert ist, sei auf die Hilfeseite ?quantile verwiesen.

quantile(x, probs) liefert für den Vektor x die im Parameter probs definierten empirischen Quantilwert. Standardmäßig sind die das 0-, 25, 50, 75, 100-Quantil.

theSample <- c( 101, 22, 43, 174, 82, 84.5, 12, 81.5, -12, 23, 11, 84, -12.2, 33.33, 0.5, 12.1, 1002, 74, 92, 104.2, 92)
quantile(theSample)

##     0%    25%    50%    75%   100% 
##  -12.2   12.1   74.0   92.0 1002.0

Wünschen wir z.B. das 20- und das 80-Quantile, erhalten wir das wie folgt:

quantile(theSample, probs = c(0.2, 0.8))

## 20% 80% 
##  12  92

6.1.3 Vergleich Median und arithmetisches Mittel

Der Vorteil des arithmetischen Mittels ist, dass es den Abstand zu allen Datenpunkten minimiert. Es ist allerdings sensitiv gegenüber Ausreißern, während der Median robust gegenüber Ausreißern ist.

Gegeben seien die monatlichen Bruttoeinkommen einer Stichprobe:

bEink <- c( 1200, 1800, 2400, 2600, 125000, 2400, 2350, 1800, 5000, 6200, 2400, 2250, 1810)
hist(bEink, breaks = 50, 
     main="Einkommensverteilung Stichprobe",
     xlab = "brutto Einkommen [€]",
     ylab= "Anzahl", las = 1)
abline(v=mean(bEink), lty=3)
text(x= mean(bEink), y= 4, labels = "Mittelwert", pos = 4)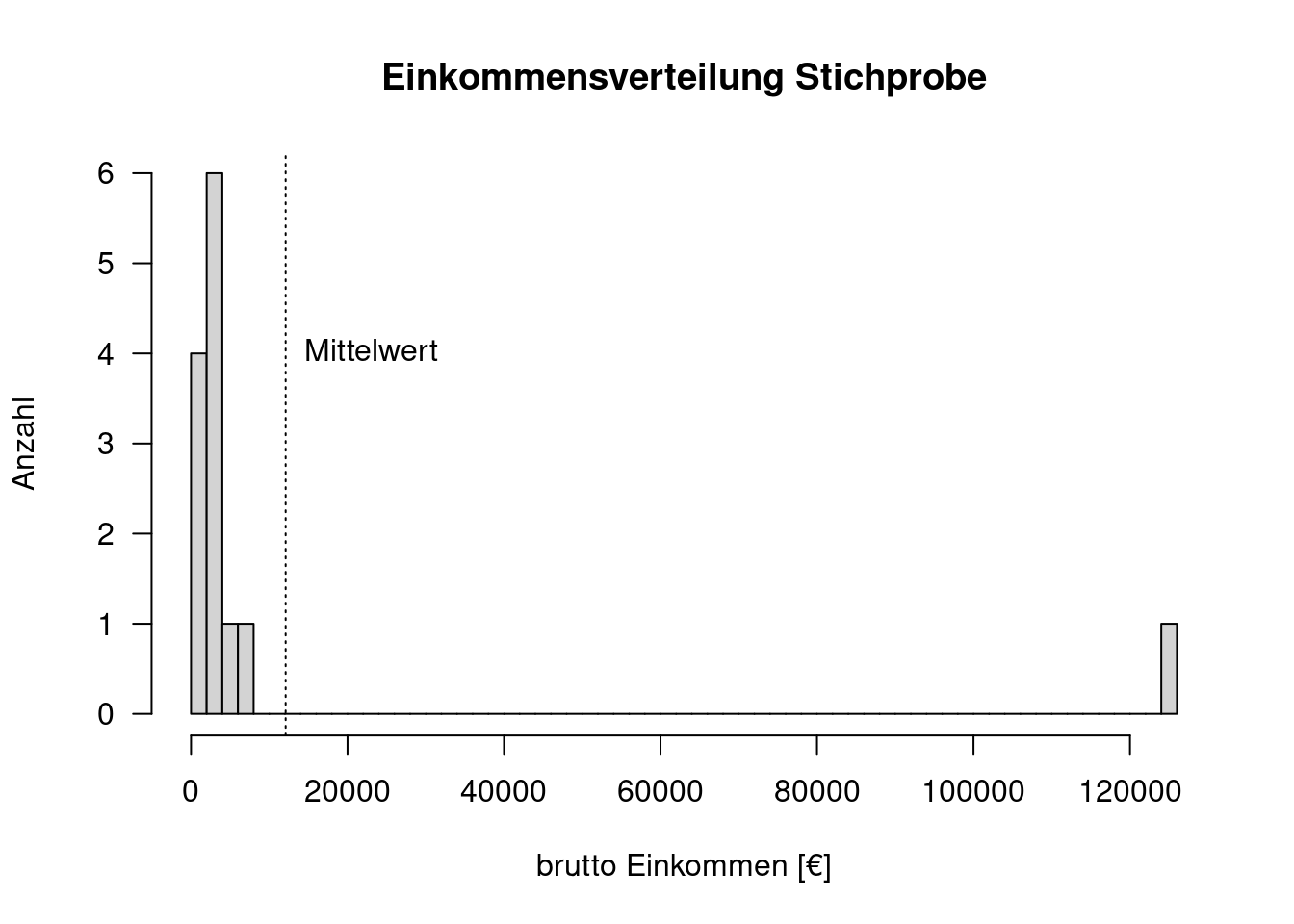

In der Stichprobe hatten wir - zufällig - eine Person mit einem sehr hohen Monatseinkommen. Der Mittelwert (vertikale gestrichelte Linie) ist höher als alle anderen Werte. Wenn wir diesen Wert verwenden, um z.B. die Kaufkraft der Bevölkerung zu charakterisieren, erhalten wir einen vollkommen falschen Eindruck. Der Median wird dagegen von diesem Ausreißer nicht beeinflusst.

hist(bEink, breaks = 50, 
     main="Einkommensverteilung Stichprobe",
     xlab = "brutto Einkommen [€]",
     ylab= "Anzahl", las = 1)
abline(v=mean(bEink), lty=3)
abline(v=median(bEink), lty=3, col= "red")
text(x= mean(bEink), y= 4, labels = "Mittelwert", pos = 4)
text(x= median(bEink), y= 5, labels = "Median", 
     pos = 4, col = "red")

Bei schiefen Verteilungen liegen Mittelwert und Median auseinander

6.1.4 Modus

Der Modus ist einfach der häufigste Wert einer Stichprobe. Er ist sowohl auf ordinal als auch nominal als auch numerisch skalierte Daten anwendbar.

Standardmäßig besitzt R keine Funktion zum Berechnen des Modus. Wir können dies aber leicht nachrüsten.

getmode <- function(x) 
{
   uniqvalues <- unique(x)
   uniqvalues[which.max(tabulate(match(x, uniqvalues)))]
}

theSample <- c("rot", "grün", "blau", "grün")
getmode(theSample)

## [1] "grün"

Details der Funktion müssen uns hier nicht interessieren.

6.2 Verteilungsmaße

Während die Lagemaße auf die Lage eines bestimmten Punktes der - empirischen oder theoretischen - Verteilung abziehlen, beschreiben Verteilungsmaße die Streuung der Daten ausgehend um einen bestimmten Punkt - i.d.R. um den Mittelpunkt bzw. Erwartungswert.

Vereilungsmaße charakterisieren die Unsicherheit des Erwartungswertes. Wenn wir z.B. einen positiven Zusammenhang zwischen Bildungsniveau der Eltern und dem Bildungsniveau in einer Stichprobe feststellen, ist es wichtig zu wissen, wie stark die einzelnen Beobachtungen um diesen mittleren Effekt streuen. Ist die Streuung sehr breit, dann wissen wir, dass der Zusammenhang über die Befragten Teilnehmer sehr stark streut - möglicherweise ist der Effekt sogar bei einer Teilmenge negativ.

6.2.1 Varianz und Standardabweichung

Die Varianz beschreibt die Streuung um den Schwerpunkt (Erwartungswert) der Verteilung. Sie ist definiert als die mittlere quadratische Abweichung einer reellen Zufallsvariablen von ihrem Erwartungswert. Sie ist das zweite zentrale Moment einer Verteilung. Sie wird oft mit \(\sigma^2\) bezeichnet.

\[ Var(X) = E[(X-\mu)^2] \] Bei diskreten Zufallsvariablen ist die Varianz als Summe definiert:

\[ \sigma^2 = \sum_{i=1}^n (x_i - \mu)^2\]

Bei stetigen Zufallsvariablen muss die Varianz als Integral definiert werden:

\[ Var(X) = \int_{-\infty}^{\infty}(x-E[X])^2f(x)dx \] Sofern die Varianz existiert gilt \(Var(X) \geq 0\). ²⁰

Da die Einheit der Varianz die quadrierte Einheit der Werte ist (z.B. falls X Einkommen in € beschreibt, wird die Einheit in \(€^2\) gemessen), wird oft die Standardabweichung (\(Stdev(x) = +\sqrt{Var(x}\)) angegeben, da diese dieselbe Einheit wie die Daten bzw. die Verteilung hat.

## Warning in geom_segment(aes(x = -1, y = 0.1, xend = 1, yend = 0.1), arrow = arrow(length = unit(0.2, : All aesthetics have length 1, but the data has 2 rows.
## ℹ Please consider using `annotate()` or provide this layer with data containing
##   a single row.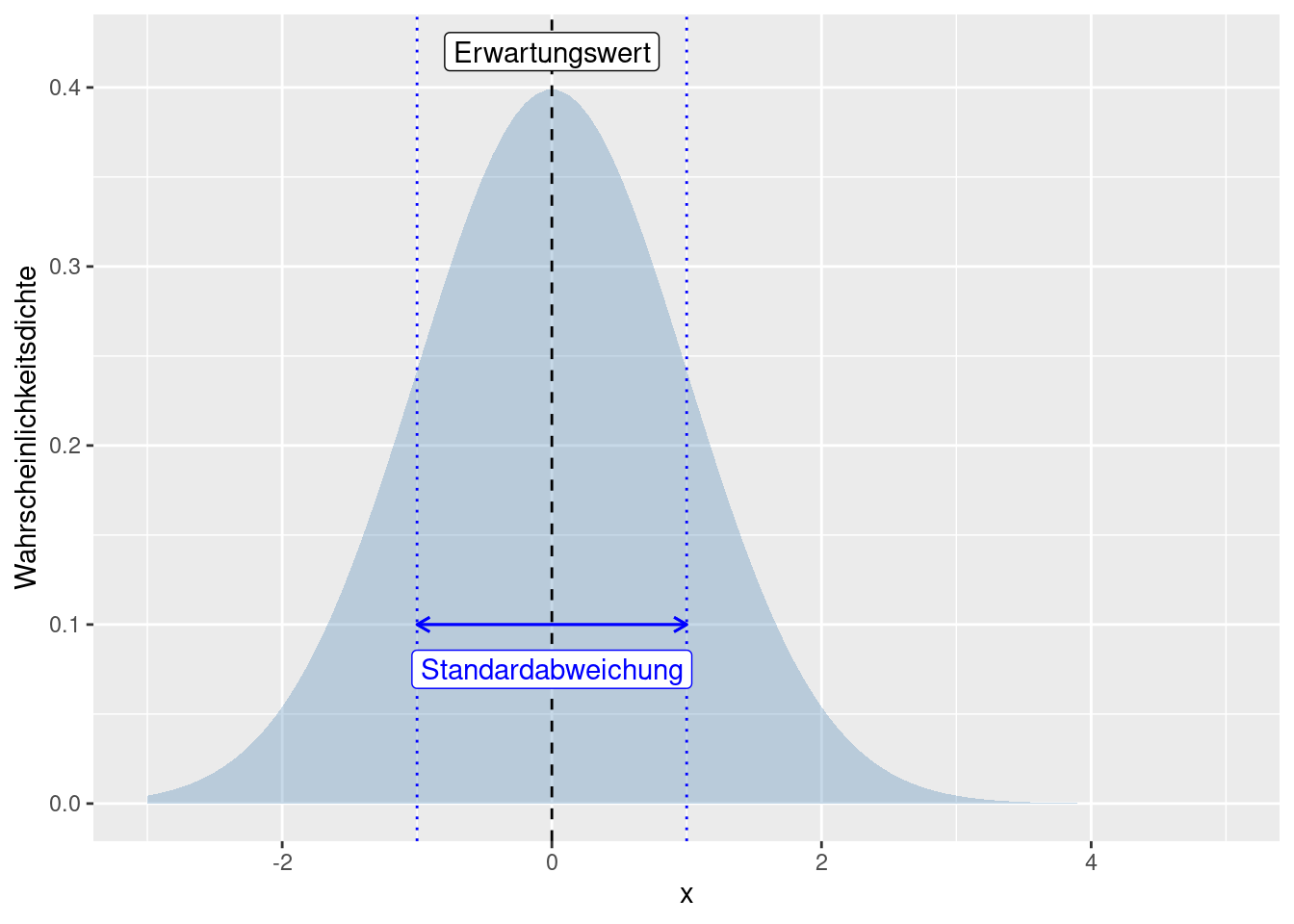

Die Stichprobenvarianz wird wie folgt berechnet:

\[s^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i - \bar{x}^2) \]

Da man für die Berechnung der Stichprobenvarianz den Mittelwert berechnen muss, wird bereits ein Freiheitsgrad verbraucht. Deshalb teilt man durch \(n-1\) und nicht durch \(n\). Durch diese Korrektur (restricted maximum likelihood) erhält man einen erwartungstreuen Schätzer der Varianz der Grundgesamtheit.

In \(R\) wird die Varianz durch var(x) berechnet und die Standardabweichung mit sd(x). Jeweils bezogen auf eine Stichprobe, d.h. \(n-1\) im Nenner.

theSample <- c( 101, 22, 43, 174, 82, 84.5, 12, 81.5, -12, 23, 11, 84, -12.2, 33.33, 0.5, 12.1, 1002, 74, 92, 104.2, 92)
var(theSample)

## [1] 44959.79

sd(theSample)

## [1] 212.0372

mean(theSample)

## [1] 100.1871

6.2.2 Spannbreite

Die Spannbreite (range) gibt die Differenz zwischen dem größten und dem kleinsten Wert einer Stichprobe oder Grundgesamtheit an.

\[ Spannbreite(X) = max(X) - min(X)\] In \(R\) berechnet range(x) die Spannbreite der Werte eines Vektors.

range(theSample)

## [1]  -12.2 1002.0

6.2.3 Interquantile Range / Interquantilabstand

Der Interquantilabstand ist die Differenz zwischen dem 75- und dem 25-Quartil. Sie ist ein robustes Maß und sorgt bei nicht symmetrischen Verteilungen dafür, dass wir keine unsinnigen Werte erhalten.

\[ IQR = \text{75-Quantil} - \text{25-Quantil} \]

IQR(theSample)

## [1] 79.9

quantile(theSample, probs = c(.25, .75))

##  25%  75% 
## 12.1 92.0

6.2.4 Variationskoeffizient

Die Interpretation der Streuungsgrößen sollte immer in Bezug zu den Lagemaßen erfolgen. Was eine große und eine kleiner Streuung ist, hängt immer auch vom Lagemaß ab. Eine Standardabweichung von 500 um einen Mittelwert von einer Million ist von der Interpretation her etwas anderes als die Selbe Standadrdabweichung um einen Mittelwert von 1500.

Wenn es sich bei den Daten um monatlich verfügbares Einkommen je Haushalt handelt, dann bedeutet eine Standarddabweichung von 500€ um einen Mittelwert von 1500€, dass es Haushalte gibt, die Schwierigkeiten haben, zu überleben, während andere recht gut über die Runden kommen. Bei einem Mittelwert von einer Million €, bedeutet eine Standardabweichung von 500€, dass alle Haushalte quasi gleich reich sind.

Ähnliche Effekte treten auf, wenn man sich z.B. anschaut, wie sich die Monatseinkommen in Haushalten verschiedener Länder über die Zeit entwickelt hat oder wenn man untersucht, wie stark verschiedene Nähr- und Schadstoffe in Flussläufen über die Zeit streuen. Da das mittlere Einommen in Mali deutlich geringer als das in den USA ist, kann man die Streuungen nur schlecht direkt vergleichen. Bei der Schadstoffbelastungen liegen gleich mehrere Größenordnungen zwischen den einzelen Stoffklassen (z.B. Phosphat, Nitrat und diversen Pestiziden).

Um die Streuungen vergleichen zu können, normiert man mit dem Mittelwert, was den Variationskoeffizient (coefficient of variation) ergibt.

\[ VarK(X) = \frac{Standardaweichung(X)}{Erwartungswert(X)} \]

bzw. der empirische Variationskoeffizient

\[ VarK(x) = \frac{s}{\bar{x}} \]

Ebenso kann man den Interquantilabstand durch den Median normieren, um einen robusten Schätzer zu erhalten, den sogenanten Quartilsdispersionskoeffizient.

\[ v_r = \frac{x_{0.75} - x_{0.25}}{x_{0.5}} \]

6.3 Schiefe

Die Schiefe einer Verteilung beschreibt, wie stark eine Verteilung asymmetrisch ist. Die Schiefe ist das dritte zentrale Moment einer Verteilung, normiert auf die Standardabweichung.

Die empirische Schiefe:

\[ \gamma = \frac{1}{n} \sum_{i=1}^n ( \frac{x_i- \bar{x}}{s} )^3 \]

Die Schiefe kann jeden reellen Wert annehmen.

• Bei negativer Schiefe, \(\gamma \lt 0\) spricht man von einer linksschiefen oder rechtssteilen Verteilung; sie fällt in typischen Fällen auf der linken Seite flacher ab als auf der rechten.
• Bei positiver Schiefe, \(\gamma \gt 0\), spricht man von einer rechtsschiefen oder linkssteilen Verteilung; sie fällt typischerweise umgekehrt auf der rechten Seite flacher ab als auf der linken.
• Bei symmetrischen Verteilungen ist die Schiefe 0 - umgekehrt sind nicht alle Verteilungen mit einer Schiefe von 0 symmetrisch

Rechtsschiefe Verteilungen haben mehr Wahrscheinlichkeitsmasse im unteren Teil, bzw. bei empirischen Verteilungen viele kleine Werte und wenige Große. Beispiele für Daten, die rehtsschiefe Verteilungen aufweisen sind Flächen (z.B. von Inseln, von Kreisen, von Gemeinden), Einkommen oder Anzahl der Sexualkontakte (relevant für die Modellierung der Ausbreitung sexuell übertragbarer Krankheiten wie HIV oder Affenpocken).

Linksschiefe Verteilungen, bei denen es viele hohe und nur wenige niedrige Werte gibt, treten z.B. bei der Verteilung des Sterbealters auf, sofern die medizinische Versorgung weit genug fortgeschritten ist. In Gesellschaften mit guter Gesundheitsvorsorge sterben die meisten Menschen in hohem Alter, während nur wenige Menschen in jungen Jahren sterben.

6.4 Kurtosis

Die Wölbung, Kyrtosis, Kurtosis oder auch Kurtose misst die Fähigkeit einer Verteilung Ausreißer zu produzieren bzw. die Präsenz von Ausreißern (empirische Kurtosis) (Westfall 2014). Man findet in der Literatur häufig noch die falsche Aussage, die Kurtosis messe die Steilheit bzw. „Spitzigkeit“ einer (eingipfligen) Wahrscheinlichkeitsfunktion, statistischen Dichtefunktion oder Häufigkeitsverteilung.

Sie ist das 4. standardisierte zentrale Moment einer Verteilung. Verteilungen mit geringer Wölbung streuen relativ gleichmäßig; bei Verteilungen mit hoher Wölbung resultiert die Streuung mehr aus extremen, aber seltenen Ereignissen.

Empirische Wölbung:

\[ \omega = \frac{1}{n} \sum_{i=1}^n ( \frac{x_i- \bar{x}}{s} )^4 \]

Der Exzess gibt die Differenz der Wölbung der betrachteten Funktion zur Wölbung der Dichtefunktion einer normalverteilten Zufallsgröße an. Die Normalverteilung hat eine Wölbung von 3.

Man kann Verteilungen anhand ihrer Wölbung wie folgt einteilen:

• Exzess = 0: mesokurtisch.
• Exzess > 0: leptokurtisch, Wird manchmal im Englischen auch super gaussian genannt. Im Vergleich zur Normalverteilung finden sich mehr Ausreißer in der Verteilung. Dies kann daher kommen, dass sich in den Enden einer Wahrscheinlichkeitsverteilung mehr Masse, als bei der Normalverteilung befindet (fat tailed distribution). Eine andere Möglichkeit besteht darin, dass zwar die meiste Wahrscheinlichkeitsmasse im Zentrum der Verteilung befindlich ist, es jedoch gelegentlich extreme Ausreißer gibt.
• Exzess < 0: platykurtisch. Im Vergleich zur Normalverteilung finden sich weniger Ausreißer in der Verteilung. In den Enden einer Wahrscheinlichkeitsverteilung befindet sich weniger Masse, als bei der Normalverteilung.

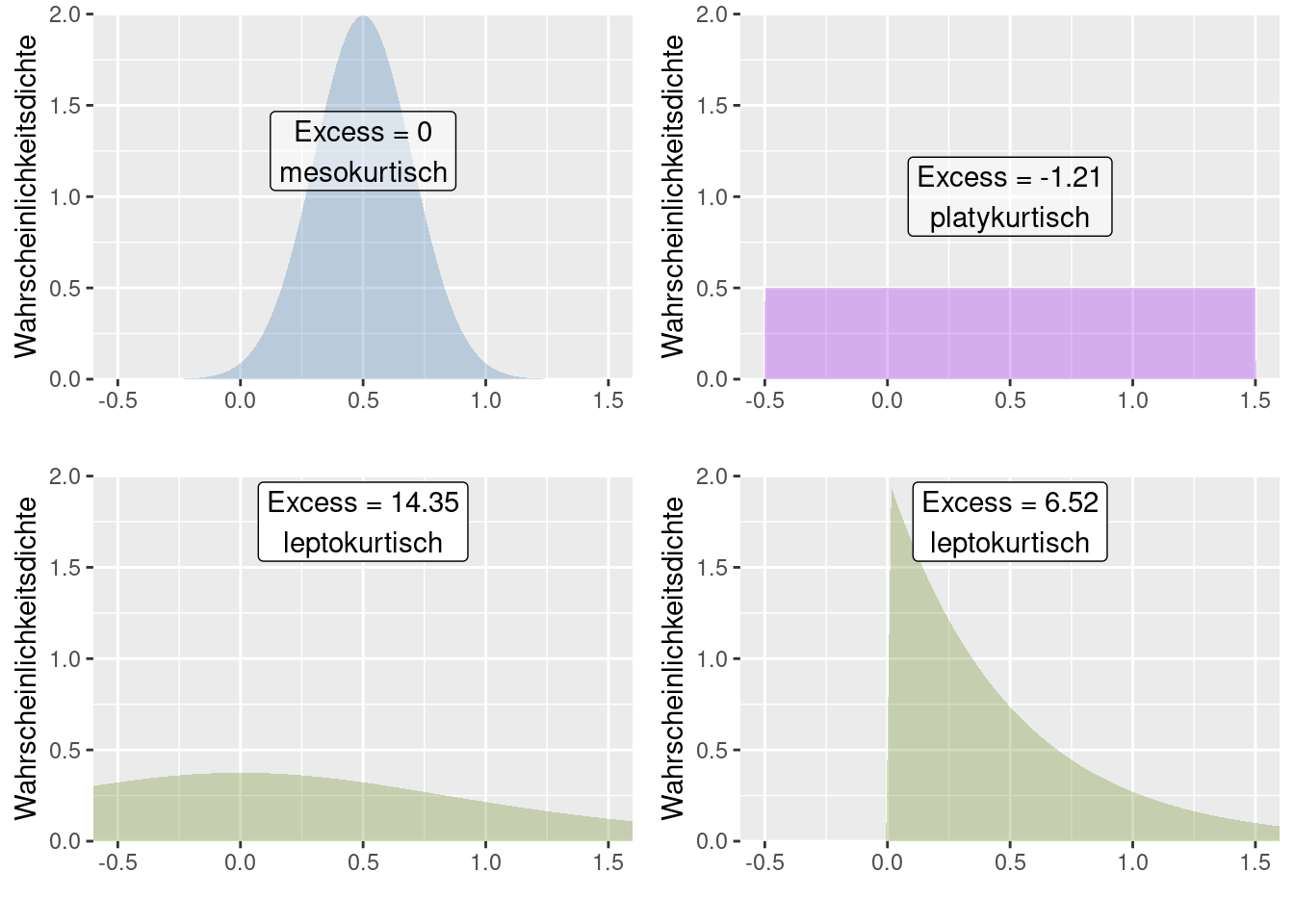
In R kann man die Wölbung mittels moments::kurtosis berechnen.

6.5 Beispiele für die Charakterisierung von empirischen Verteilungen

require(tidyverse)

Schauen wir uns einmal einzelne Indikatoren aus der INKAR Kreisstatistik²¹ für Deutschland an. Ein Teil der auf Kreisebene verfügbaren Indikatoren liegt als CSV Datei vor, die wir mittels read.table einlesen können. Da der in Deutschland gebräuchliche Dezimalseparator (‘,’) verwendet wird, müssen wir dies mittels dec= "," angebeben.

inkar <- read.table("data/Inkar_Kreisstatistik.csv", header = TRUE, sep = ",", dec = ",") 

6.5.1 Gesamtbevölkerung

Fangen wir mit den Einwohnern (2019) je Kreis an:

summary(inkar$Bevölkerung.gesamt)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   34193  103243  154899  207398  241717 3669491

Wieviele Einwohner wohnten im Mittel in einem Kreise?

mean(inkar$Bevölkerung.gesamt)

## [1] 207398.3

Der Median ist kleiner als das arithmetische Mittel, was für eine rechtsschiefe Verteilung spricht. Das sehen wir auch an der Schiefe der Verteilung, die deutlich größer als 0 ist.

moments::skewness(inkar$Bevölkerung.gesamt)

## [1] 8.554332

Die Spannbreite ist mit 3.64 Millionen Einwohnern erheblich. Da die Verteilung rechtsschief ist, kann das auch durch extreme Werte (Berlin, Hamburg,…) verursacht sein.

max(inkar$Bevölkerung.gesamt) - min(inkar$Bevölkerung.gesamt)

## [1] 3635298

Die Streuung um den Mittelwert ist mit einer Standardabweichung von knapp 250 Tausend Einwohnern ebenfalls erheblich.

sd(inkar$Bevölkerung.gesamt)

## [1] 245162.4

Die Standardabweichung ist durch die extrem hohen Werte größer als der Interquantilabstand von etwa 140 Tausend.

IQR(inkar$Bevölkerung.gesamt)

## [1] 138474

Wir erwarten also eine rechtsschiefe Verteilung, bei der 50% der Kreise sich innerhalb des Bereiches ~ einhunderttausend bis etwa 240-tausend Einwohner befinden. Die Einwohnerzahlen der Kreise mit mehr als 240-tausend Einwohnern streuen sehr stark.

Schauen wir uns einmal das zugehörige Histogramm an:

ggplot(inkar, aes(x=Bevölkerung.gesamt)) +
         geom_histogram(bins = 100) + 
  xlab("Bevölkerung gesamt") + 
  ylab("Anzahl Kreise")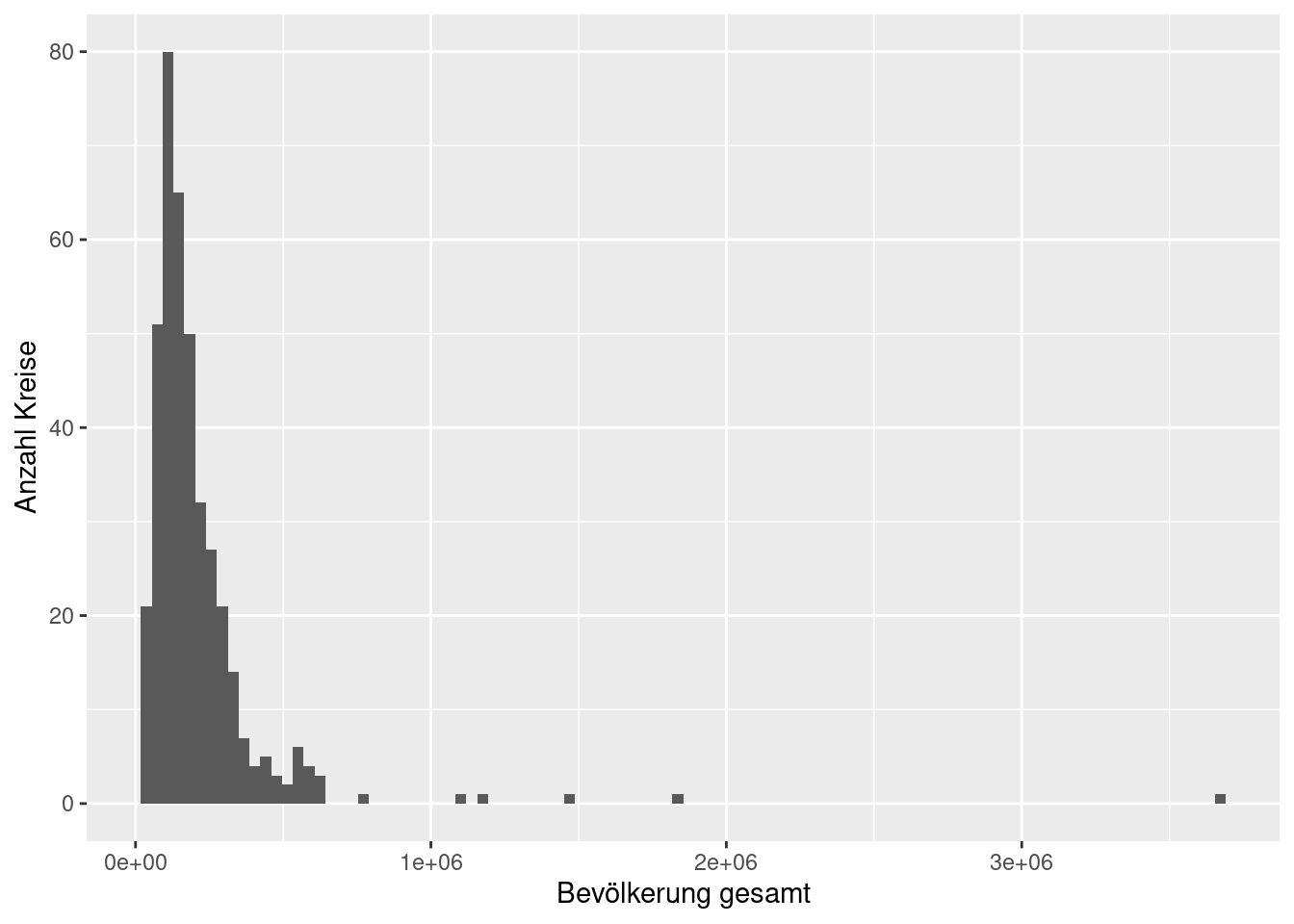

6.5.2 Mietpreise

Es handelt sich hierbei um die Wiedervermietungsmieten inserierter Wohnungen“ (Angebotsmieten) je m², klassifiziert in Stufen unter 4 €, 4 bis unter 5 €, weiter in 1-€ Stufen bis 18 € und mehr

Auch die Mietpreise sind rechtsschief (Median kleiner Mittelwert), allerdings weniger ausgeprägt als bei den Einwohnerzahlen.

summary(inkar$Mietpreise)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##   2.000   4.000   5.000   5.603   7.000  16.000

moments::kurtosis(inkar$Mietpreise)

## [1] 4.561548

Die Spannbreite beträgt 14€/qm - allerdings sind die Werte bei 18 abgeschnitten, so dass Extremwerte nicht auftauchen können.

max(inkar$Mietpreise) - min(inkar$Mietpreise)

## [1] 14

Der Interquantilabstand ist hier größer als die Standardabweichung

sd(inkar$Mietpreise)

## [1] 2.082039

IQR(inkar$Mietpreise)

## [1] 3

ggplot(inkar, aes(x=Mietpreise)) +
         geom_histogram(bins = 100) + 
  xlab("Mietpreis je qm (klassifiziert)") + 
  ylab("Anzahl Kreise")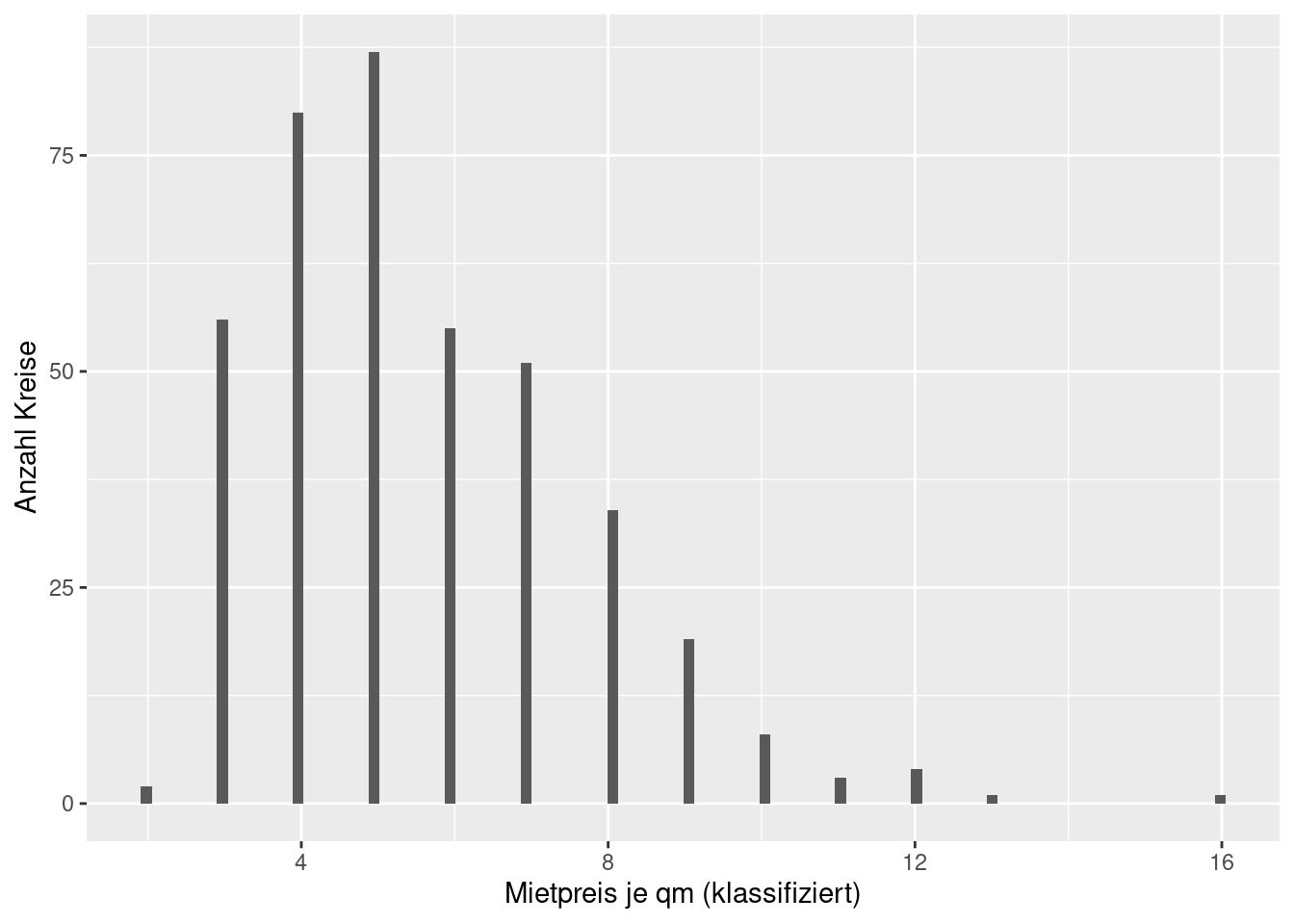

Interessant wäre, welches der beiden Merkmale stärker über die Kreise hinweg streut. Dies können wir mittels des Variationskoeffizienten ermitteln:

sd(inkar$Bevölkerung.gesamt) / mean(inkar$Bevölkerung.gesamt)

## [1] 1.182085

sd(inkar$Mietpreise) / mean(inkar$Mietpreise)

## [1] 0.3715611

Eindeutig streut die Einwohnerzahl stärker als die Mietpreise - auf Basis der Kreise in Deutschland.

Weiterführende/zitierte Literatur

Westfall, Peter H. 2014. “Kurtosis as Peakedness, 1905–2014. R.I.P.” The American Statistician 68 (3): 191–95. https://doi.org/10.1080/00031305.2014.917055.

---

19. Angegebene Formel gilt genaugenommen nur, falls die sogenannte Riemann-Integrierbarkeit vorliegt. Für die meisten Anwendungsfälle ist dies der Fall. Für den allgemeineren Fall, muss man die Dichte bzgl. des Lebesgue-Maßes \(\lambda\) berechnen \[ E[X] = \int_{-\infty}^{\infty} x f(x) d\lambda(x)\]↩︎

20. Sie kann bei manchen Verteilungen \(\infty\) sein. Bei der Cauchy Verteilung ist sie nicht definiert, da der Erwartungswert nicht definiert ist.↩︎

21. https://www.inkar.de/↩︎