Kapitel 7 Hypothesentests - Übersicht

7.1 Generelle Idee

In der Wissenschaft versuchen wir oftmals anhand von Daten Einschätzungen hinsichtlich dem Wahrheitsgehalt von Hypothesen zu erhalten. Beispiele dafür sind:

• die Wahrscheinlichkeit, sich mit COVID-19 zu infizieren sinkt mit dem Tragen einer FFP-2 Maske
  • Maske von Herstellerr X hat eine höhere Schutzwirkung als die Maske von Hersteller Y
• die Wahrscheinlichkeit von Starkregenereignissen hat in Deutschland in den letzten 20 Jahren zugenommen
• Ziel individueller Migration wird maßgeblich durch soziale Netzwerke beeinflusst
• Angsträume im Fahrradverkehr unterscheiden sich sowohl hinsichtlich Geschlecht, als auch hinsichtlich Alter
• es gibt einen negativen Zusammenhang zwischen Kriminalitätsrate und der Präsenz von Nachbarschaftsvereinen
• Ökolandbau benötigt weniger Ressourcen je erzeugter Kalorie als konventioneller Landbau
• …

Um diese Hypothesen überprüfen zu können, benötigen wir Daten, also Beobachtungen der Realität, die uns Informationen über das Phänomen liefern. Anhand dieser wollen wir entscheiden, ob die Hypothese richtig ist oder verworfen werden muss. Wichtig ist, dass wir eine ausreichende Zahl von Informationen haben. Wir wollen sicherlich nicht anhand einer einzigen Beobachtung darauf schließen, dass eine Impfung vor einer Erkrankung schützt und keine gefährlichen Nebenwirkungen hat. Genausowenig können wir anhand eines einzelnen warmen oder kalten Winters in Heidelberg darauf schließen, dass der Klimawandel Realität bzw. Übertreibung ist. Dies ermöglicht es uns genau genommen statistische Hypothesen zu testen, z.B. ob die Anzahl warmer Winter in den letzten 20 Jahren höher war als in den 20 Jahren zuvor. Wieweit die statistische Hypothese mit unserer wissenschaflichen Hypothese (z.B. der Klimawandel führt zu wärmeren Wintern in Dtld.) passt muss kritisch reflektiert werden.

Gehen wir das einmal anhand eines Beispiels durch. Wir wollen wissen, ob Menschen bereit sind höhere Steuern zu zahlen, wenn diese zur Vermeidung des Klimawandels verwendet werden. Dazu formulieren wir die Hypothese, dass diese Bereitschaft bei denjenigen höher ist, die einen Studiengang studieren, der entsprechende Inhalte vermittelt. Es reicht nun nicht aus, jeweils eine Person aus einem entsprechenden Studiengang zu befragen und mit einer anderen Personen aus einem anderen Studiengang zu vergleichen Wir müssen mehrere Personen befragen. Und zwar soviele, dass wir davon ausgehen können, dass unser Ergebnis nicht zufällig zustande gekommen ist.

Wenn wir zudem vermuten, dass es einen Unterschied macht, wie groß das verfügbare Einkommen der Person ist und welches Geschlecht sie hat, müssten wir weiterhin sicher gehen, dass wir ausreichend viele Personen befragen, die sich in diesen Merkmalen unterscheiden. Wir benötigen ein durchdachtes Experimentelles Design, das uns davor schützt zu falschen Schlüssen zu kommen - doch dazu später mehr.

Wenn wir davon ausgehen können, dass die Verteilung der Ergebnisse (z.B. die Bereitschaft einen Betrag X in Form einer zusätzlichen Steuer zu zahlen) einer Verteilung folgen, dann können wir uns anschauen, ob das Ergebniss das wir beobachtet haben zufällig zu erwarten ist oder nicht.

Gehen wir davon aus, wir hätten eine ausreichende Anzahl von Personen entsprechender Studiengänge befragt. Weiterhin hätten wir aus einer anderen Untersuchung eine große Anzahl von Personen unterschiedlichen Hintergrundes zum gleichen Thema befragt. Auf Grundlage der allgemeinen Befragung können wir beschreiben, wie sich der zusätzliche Steuerbetrag verteilt (hellblaue Kurve in nachfolgender Abbildung). Nun berechnen wir den Mittelwert der Befragten aus Studiengängen, die sich explizit mit dem Klimawandel beschäftigen. Dieser betrage 220€ je Jahr. Ist dieser Wert auf Grundlage der gesamten Verteilung zu erwarten oder nicht? Anders herum gefragt: wie wahrscheinlich ist ein solcher (oder ein extremerer) Wert auf Grundlage der angenommenen Verteilung (dunkelblauer Bereich)?

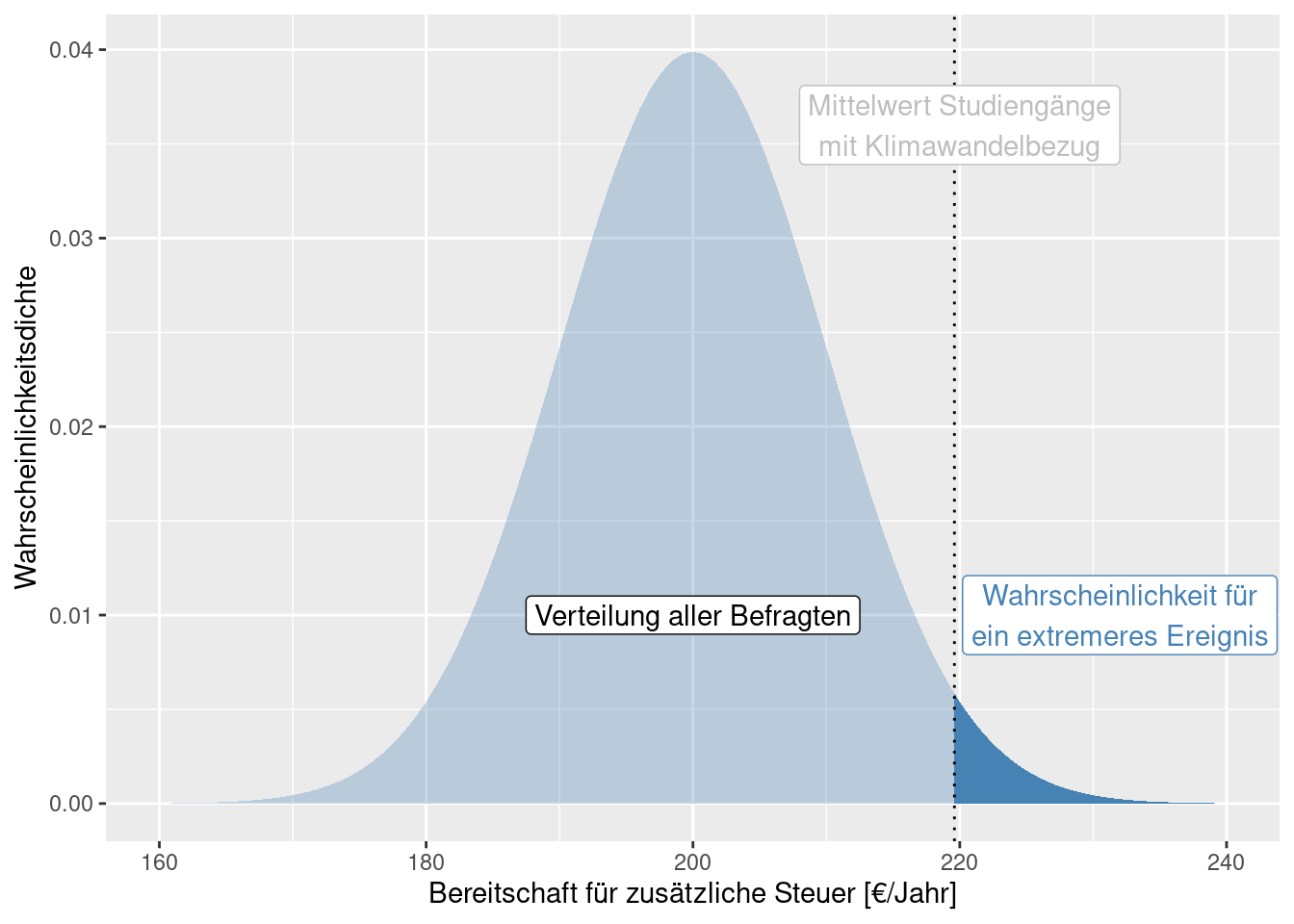
Hier wäre die sogenannte Nullhypothese \(H_0\) das die Zahlungsbereitschaft der untersuchten Gruppe (aus Studiengängen mit Informationen zum Klimawandel) sich nicht von der Allgemeinheit unterscheidet. Die Alternativhypothese \(H_1\) wäre, dass die Zahlungsbereitschaft größer ist (einseitiger Test). Wenn die Wahrscheinlichkeit, einen solchen Wert zufällig zu erreichen, groß wäre, können wir die Nullhypothese nicht verwerfen, sondern müssen davon ausgehen, dass die in den Studiengängen vermittelten Informationen nicht zu einer Erhöhung der Zahlungsbereitschaft beitragen. Falls nicht, könnten wir die Nullhypothese verwerfen und davon ausgehen, dass die Alternativhypothese zutrifft.

7.2 Nullhypothese und Alternativhypothese

Üblicherweise wird die Nullhypothese so formuliert, dass sie die Abwesenheit von Wirkmechanismen unterstellt. Irgendwelchen Unterschiede, z.B. zwischen Gruppen oder aufgrund eines erklärenden Merkmals, wären demnach einfach nur zufällig. Zufall ist also typischerweise der einzig wirksame Faktor, den wir unter der Nullhypothese unterstellen.

Im Gegensatz dazu unterstellen wir unter der Alternativhypothese, dass es einen weiteren Einfluss gibt. So kann die Wintertemperatur sich mit der Zeit verändern, die Zahlungsbereitschaft vom Studiengang abhängen oder die Bodenerosionsrate vom Gefälle und von der Bodenart.

In vielen Fällen wird die Alternativhypothese nicht über die Aussage “Die Nullhypothese gilt nicht.” hinaus spezifiziert. Es kann aber auch eine spezifischer Alternativhypothese formuliert werden. Relativ häufig wird die Richtung eines Unterschiedes spezifiziert, z.B. die Winter werden über die Zeit wärmer wenn die Nullhypothese lautet: “die Wintertemperatur verändert sich nicht systematisch.”. Spezifischere Alternativhypothesen sind im Allgemeinen trennschärfer und leichter mit der zugrundeliegenden wissenschaflichen Hypothese in Übereinstimmung zu bringen.

7.3 Test auf Unterschiede im Mittelwert zweier Gruppen - der Zwei-Stichproben t-Test

In der Realität haben wir oftmals keine ausreichend große Befragung zur gesamten Bevölkerung. Anstelle dessen würden wir z.B. eine experimentelles Design wählen, bei dem wir die Zahlungsbereitschaft von Absolventen verschiedener Studiengänge miteinander vergleichen, z.B. Absolventen aus dem Bereich Maschinenbau im Vergleich mit Studierenden der Geographie. Wir würden uns dann anschauen, wie stark sich die Mittelwerte unterscheiden. Wenn wir davon ausgehen können, dass es keine weiteren relevanten Einflussfaktoren gibt²², dann könnten wir einen t-Test verwenden um festzustellen, ob die Unterschiede der Mittelwerte zwischen den Gruppen zufällig zu erwarten sind oder nicht.

Allerdings müssen wir berücksichtigen, dass wir die Entscheidung ob die Mittelwerte gleich sind oder nicht unter Unsicherheit erfolgt. Wir haben keine vollständige Information über die Grundgesamtheit(en) sondern müssen die Information aufgrund der Stichprobe treffen. Unsere Schlussfolgerung hängt von verschiedenen Faktoren ab:

• wie groß ist der Unterschied zwischen den Mittelwerten? Je größer der Unterschied, desto sicherer können wir (ceteris paribus²³) sein.
• wie groß ist die Streuung innerhalb der Gruppen? Je stärker die Werte innerhalb der Gruppen streuen, desto unsicherer sollten wir sein, dass ein Unterschied der Mittelwerte nicht zufällig ist.
• wie groß ist die Stichprobe? Je größer die Stichprobe ist, desto sicherer können wir sein, dass der Mittelwert der jeweiligen Gruppe dem wahren Wert der Grundgesamtheit entspricht (Gesetz der großen Zahl) und damit, dass Unterschiede nicht zufällig zustande gekommen sind.

Vergleichen wir einmal die nachfolgenden zwei Abbildungen: in beiden Fällen sind die Daten normalverteilt mit gleicher Standardabweichung aber unterschiedlichen Mittelwerten. Im ersten Fall unterscheiden sich die Mittelwerte nicht sehr stark (im Verhältnis zur Standardabweichung). Entsprechend überlappen sich die beiden Verteilungen recht stark - d.h. wir können nicht sehr sicher sein, dass sich die beiden Mittelwerte unterscheiden bzw. dass es sich um zwei getrennte Verteilungen mit unterschiedlichen Mittelwerten handelt. Bei der unteren Abbildung unterscheiden sich die Mittelwerte sehr deutlich, d.h. wir können recht sicher sein, dass der Unterschied der beiden Mittelwerte nicht zufällig ist.

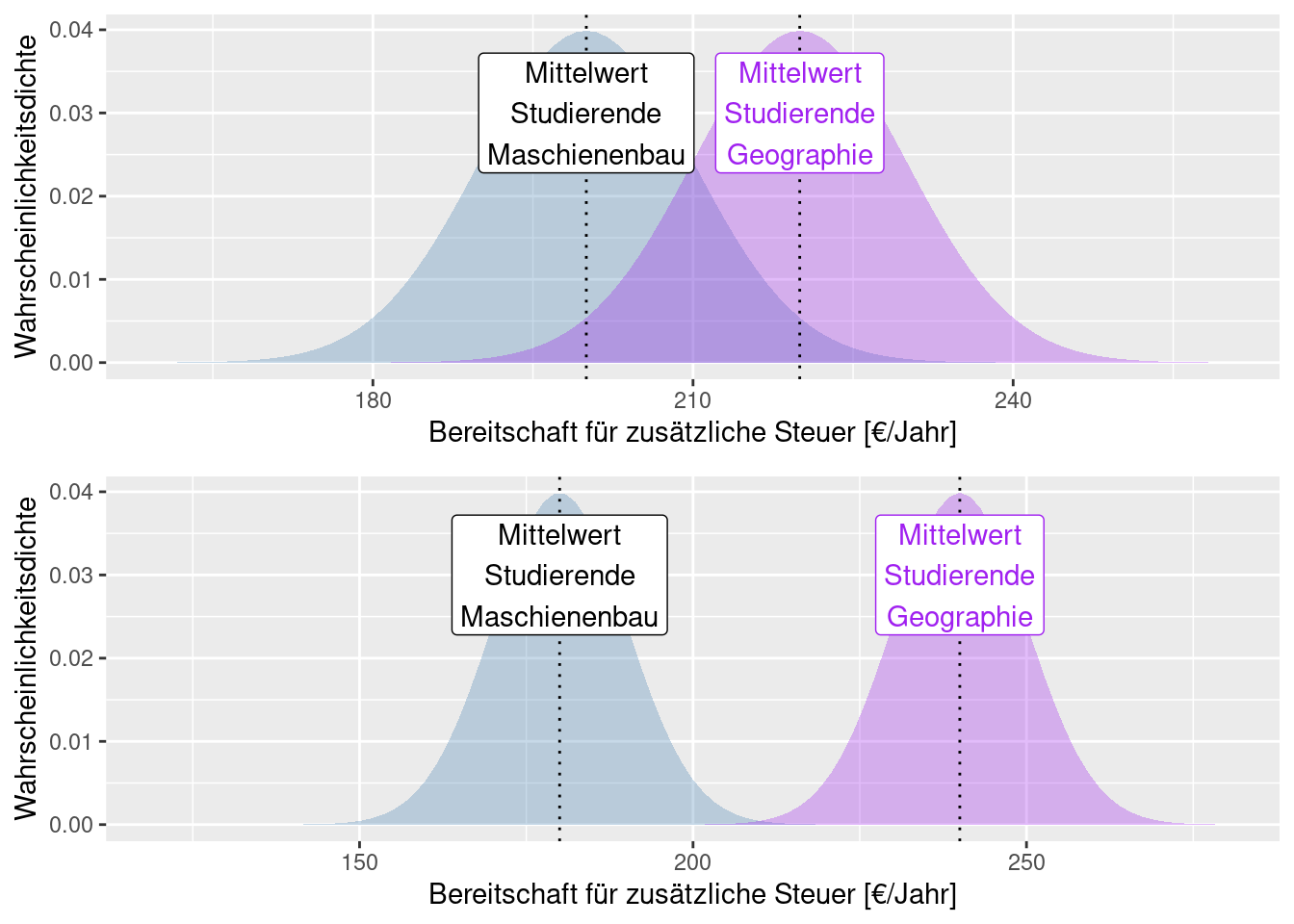
Wie gesagt, ist es wichtig den Unterschied der Mittelwerte ins Verhältnis zur Standardabweichung zu setzen. Die nächsten beiden Abbildungen veranschaulichen dies. Die Mittelwerte der beiden Gruppen sind in beiden Abbildungen gleich. Allerdings ist die Standardabweichung bei der unteren Abbildung deutlich größer. Dies bewirkt wieder eine stärkere Überlagerung der Kurven - d.h. wir können bei der unteren Abbildung wiederum nicht so sicher sein, dass sich die Mittelwerte der Gruppen jeweils unterscheiden.

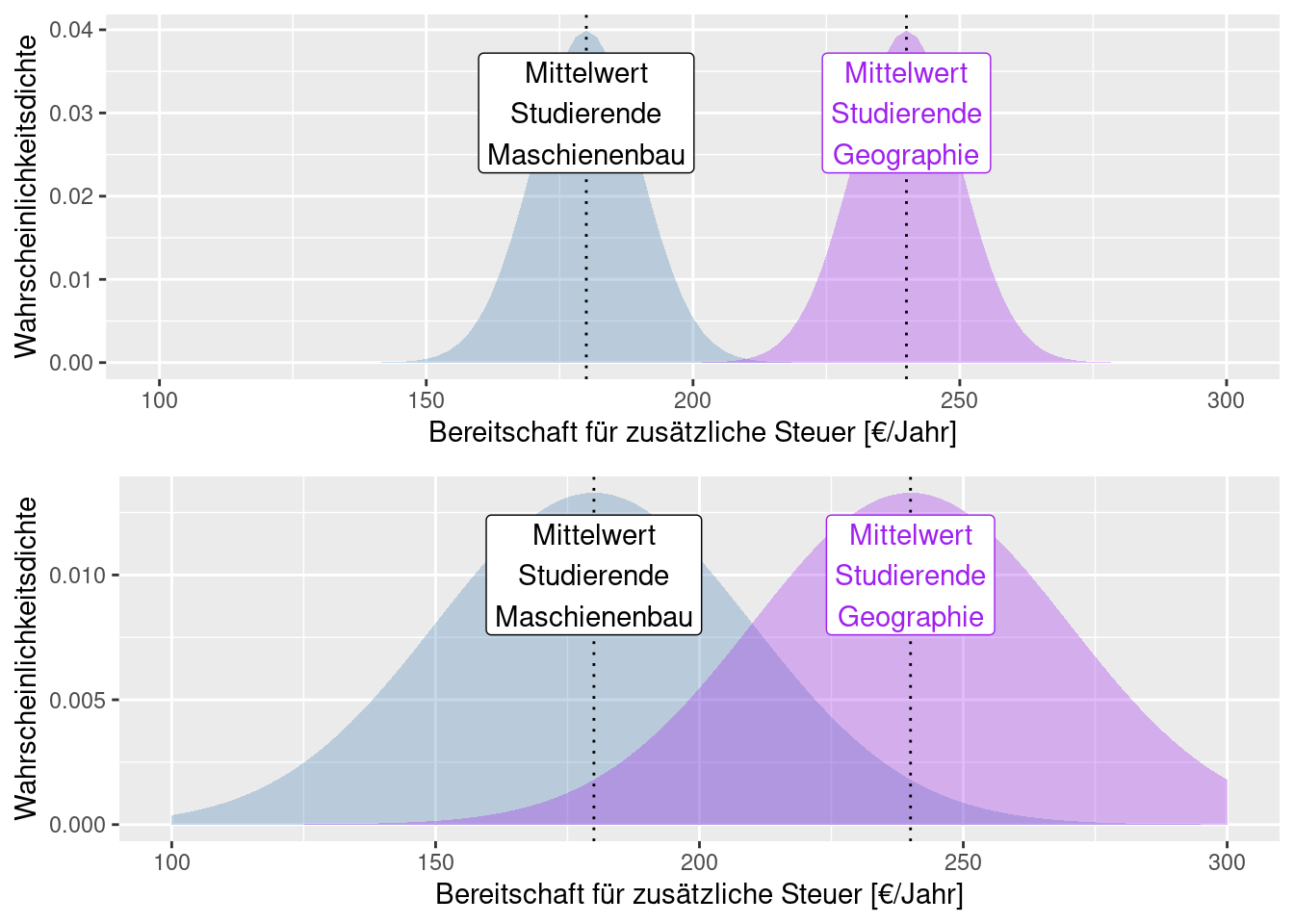
Wir müssen uns nochmals vor Augen führen, dass es sich bei den Verteilungen um Schätzungen aufgrund der Stichprobe handelt. Die Parameter der Verteilungen (bei der Normalverteilung Mittelwert und Standardabweichung) sind aufgrund der Stichproben geschätzt. Je größer die Stichprobe, desto sicherer die Schätzung.

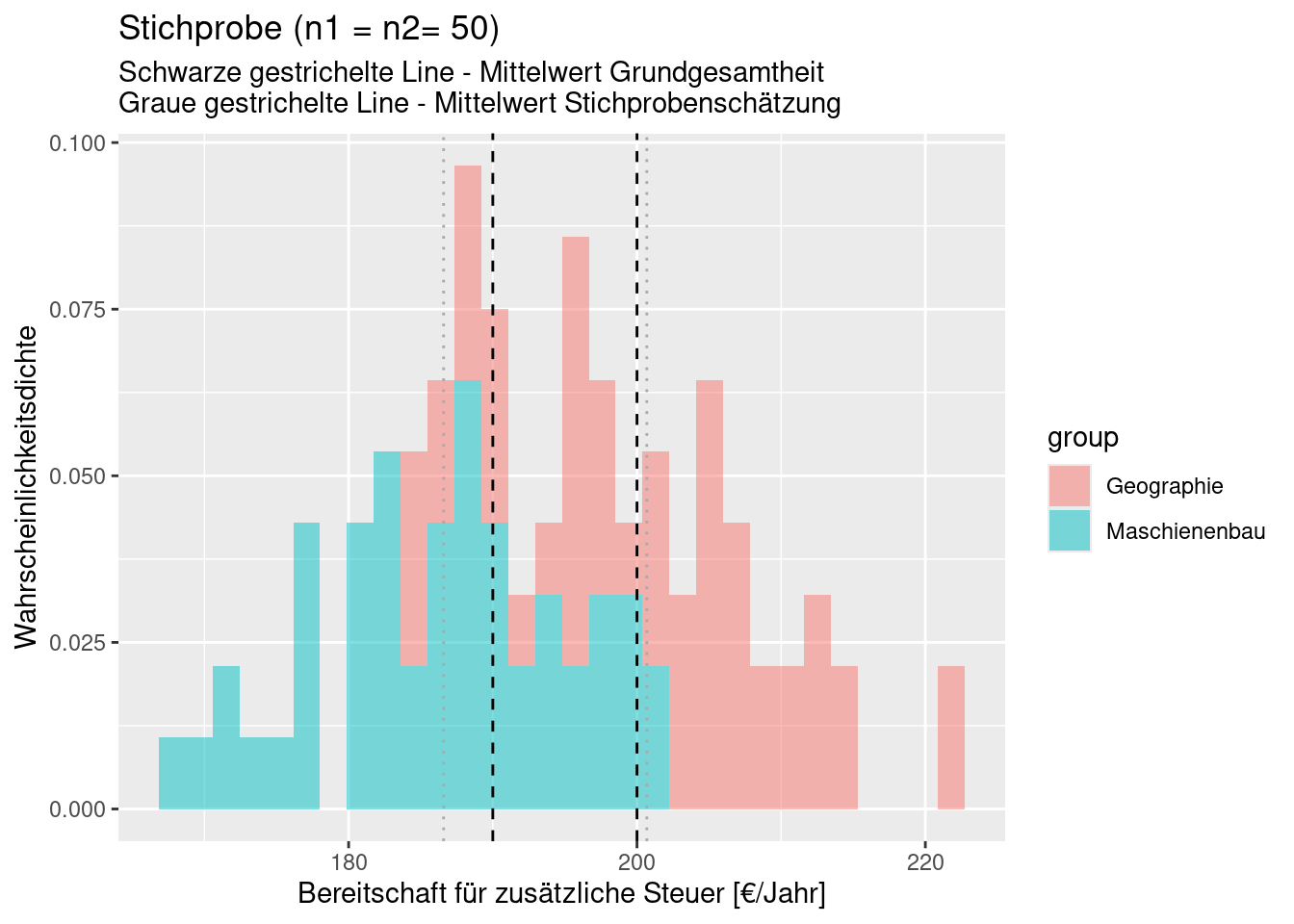
Schauen wir uns wieder ein Beispiel an. Während die aus einer Stichprobe bei n= 20 (jeweils 10 Werte aus jeder Gruppe) abgeleiteten Verteilungen kaum überlappen, überlappen die zugrundeliegenden Grundgesamtheiten (aus denen die Stichprobe gezogen ist) sehr stark. Für diese Realisierung wären wir also viel zu sicher, dass sich beide Verteilungen überlappen (der t-Test berücksichtigt dies jedoch, wie wir noch sehen werden).

## Warning: The dot-dot notation (`..density..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(density)` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.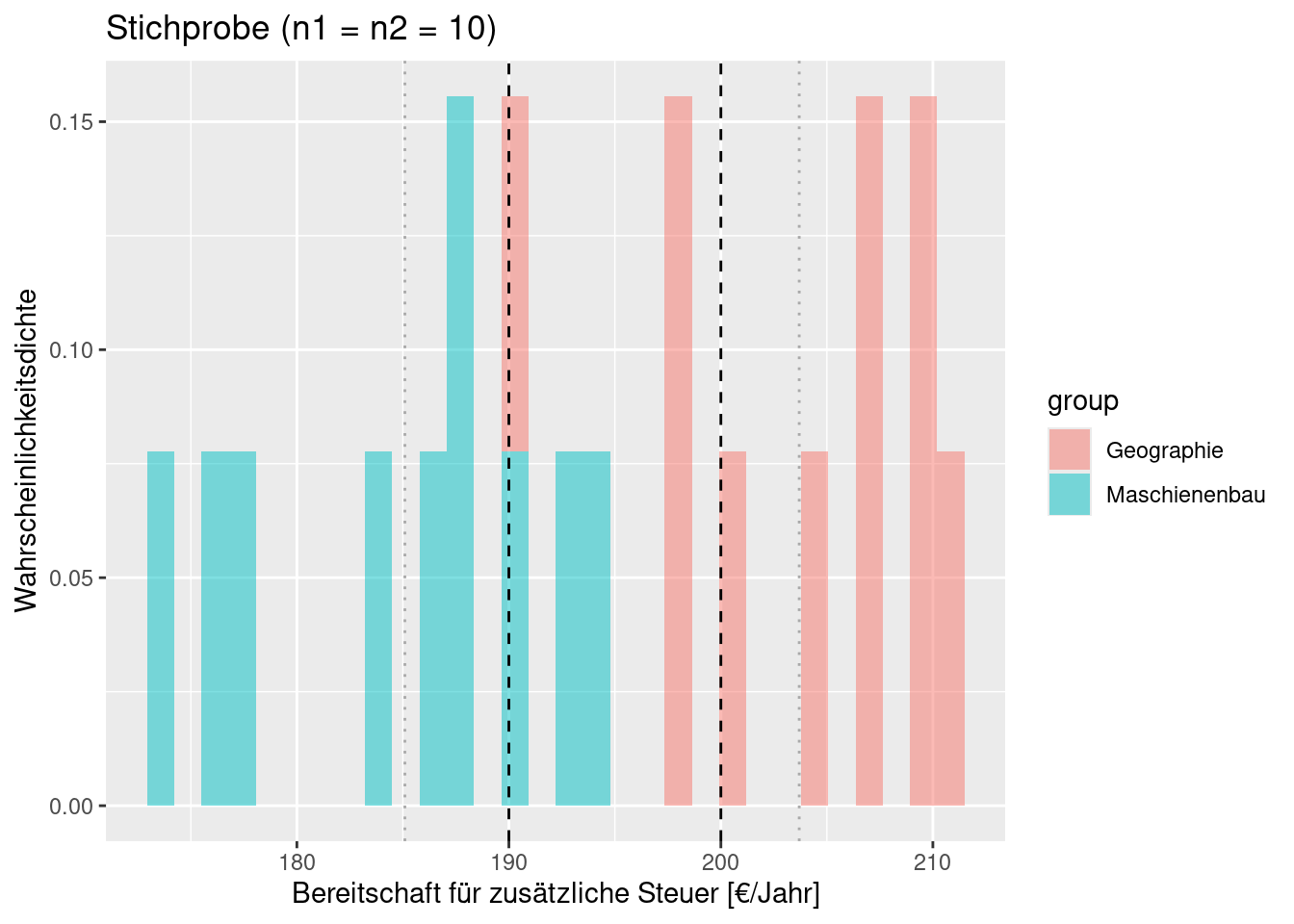

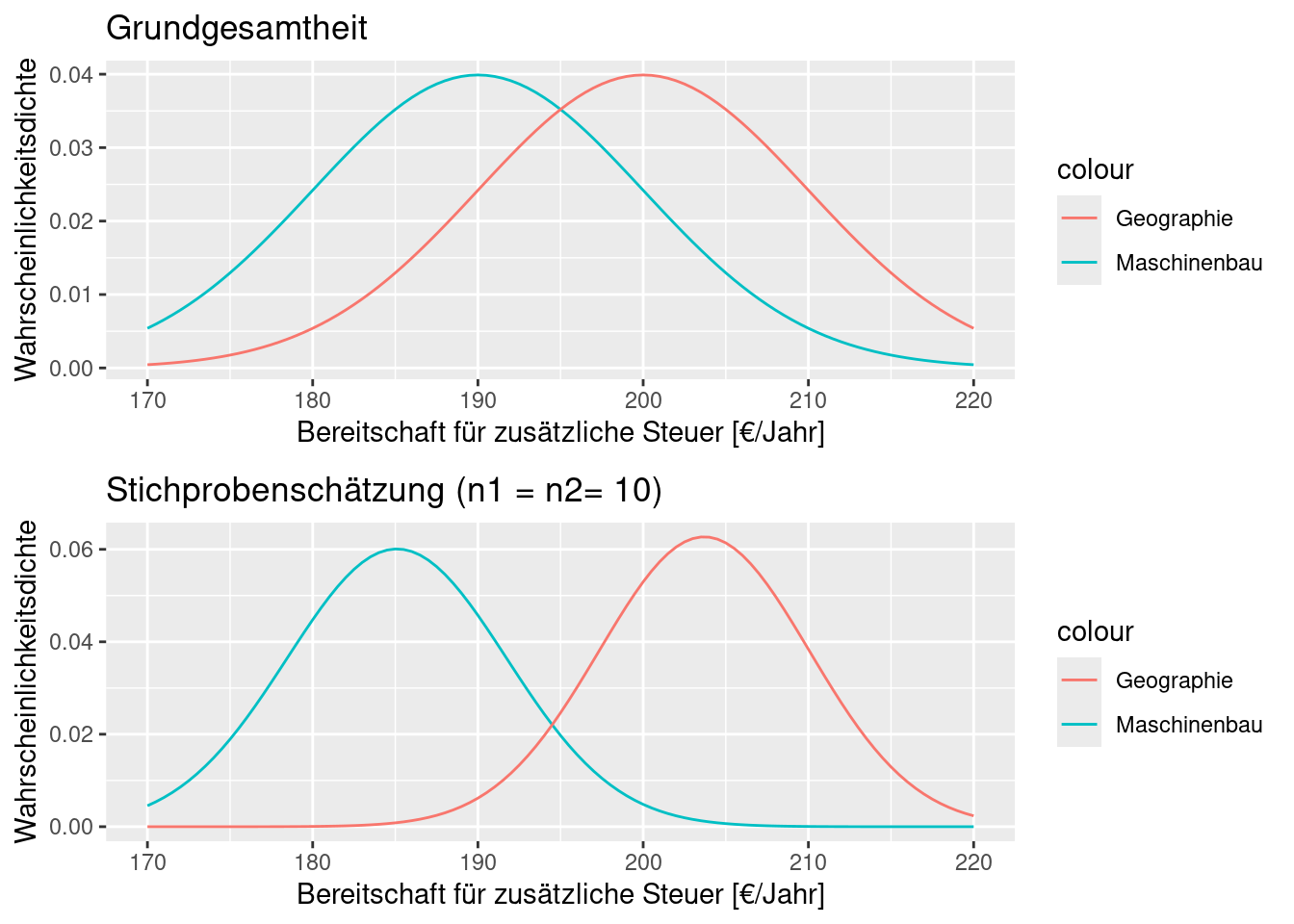
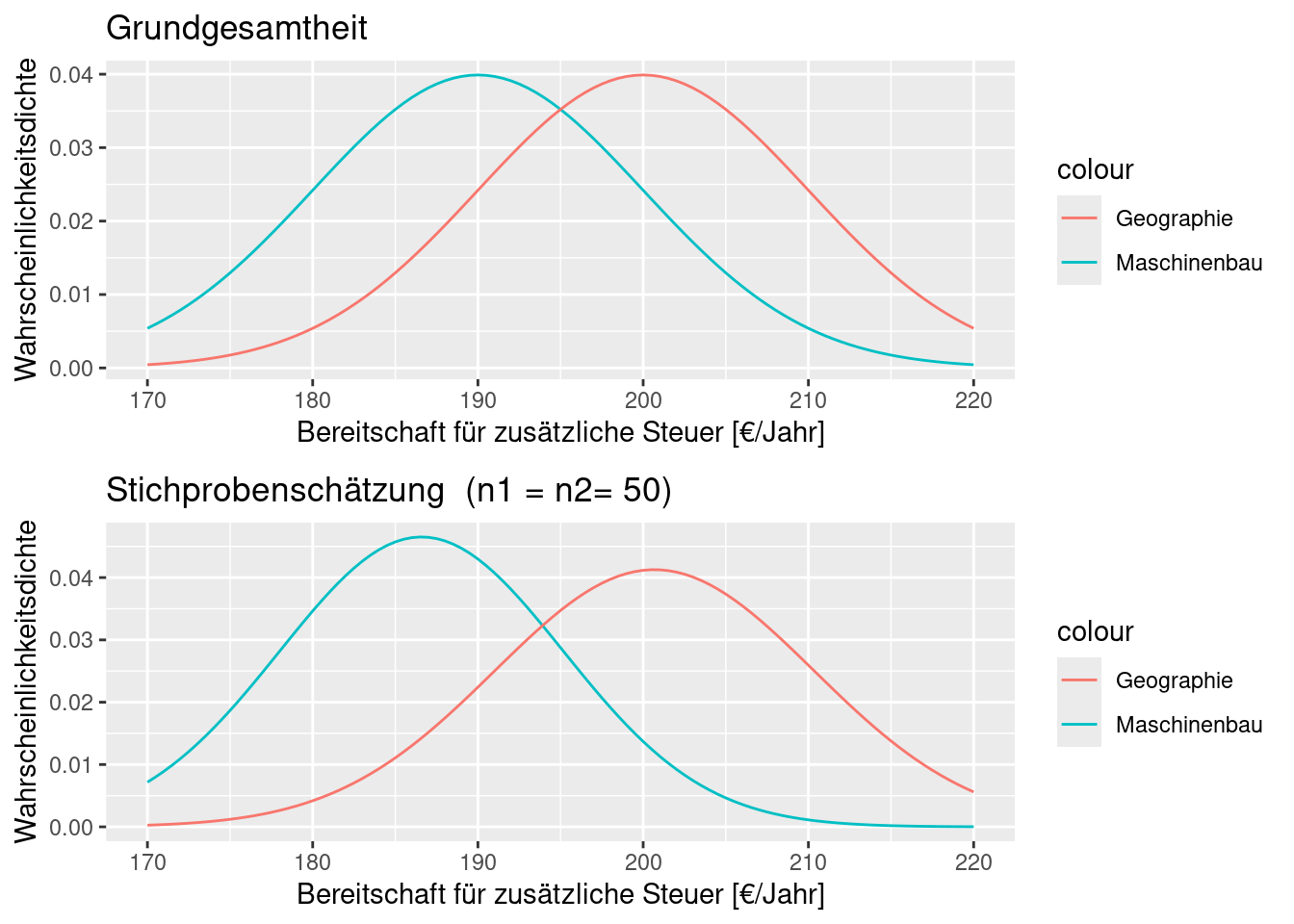
Nun ist 20 eine gefährlich kleine Stichprobengröße für 2 Gruppen. Bei bei n= 100 (jeweils 50 Werte aus jeder Gruppe) repräsentiert die Schätzung schon deutlich besser die Grundgesamtheit.

Der Zwei-Stichproben t-Test formalisiert den Vergleich der Mittelwerte zweier Stichproben. Er setzt voraus, dass beide Stichproben die selbe Varianz bzw. Standardabweichung besitzen. Die Test-Statisik berechnet sich für gleiche Stichprobengröße \(n = n_1 = n_2\) dabei wie folgt:

\[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{ \frac{s^2_{x_1} + s^2_{x_2} }{2}} \sqrt{\frac{2}{n}}} = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{ \frac{s^2_{x_1} + s^2_{x_2} }{n}}}\]

Die Differenz der geschätzten Mittelwerte beider Gruppen wird ins Verhältnis zum Standardfehler dieser Differenz gesetzt, der von der Schätzung der Varianz der Grundgesamtheit und der Stichprobengröße abhängt. Der Betrag der Test-Statistik wird umso größer, je:

• größer die Differenz der Schätzwerte der Mittelwerte der beiden Gruppen
• größer die Stichprobengröße
• kleiner die Summe der Stichprobenvarianz

Diese Schätzgröße ist asymptotisch t-Verteilt mit \(2n -2\) Freiheitsgraden. Für jede der beiden Stichprobe wird der Stichprobenmittelwert geschätzt, deswegen reduziert sich die ANzahl der Freiheitsgrade um 2.

Der Standardfehler beschreibt dabei die Unsicherheit der Schätzung des Parameters (hier Differenz der Mittelwerte) der Grundgesamtheit anhand der Stichprobe - später dazu mehr.

Bei ungleichen Stichprobengrößen und ähnlicher Varianz²⁴ wird die Formel wie folgt modifiziert:

\[ t = \frac{\bar{x}_1 - \bar{x}_2}{\sqrt{ \frac{(n_1 -1) s^2_{x_1} + (n_2 -1) s^2_{x_2} }{2}} \sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}\]

Wenn die Varianzen unterschiedlich sind, kann der sogenannte Welsch-Test angewandt werden. Weiterhin geht der hier definierte Test davon aus, dass es sich um nicht gepaarte Stichproben handelt. Falls z.B. die selbe Person zweimal befragt wird, z.B. vorher und nachdem eine Information bereitgestellt worden ist, wendet man einen gepaarten t-Test an, der eine höhere Trennschärfe hat - aber dazu später mehr.

Bleiben wir beim einfachen Beispiel ähnlicher Varianz und gleicher Stichprobengröße und schauen uns einmal an, wie die Test-Statistik auf Veränderungen der Parameter reagiert. Zunächst definieren ich eine einfache Funktion, die die Test-Statistik berechnet, dann setzen wir ein paar Werte ein.

calcTTeststat <- function(mean1, mean2, sd1, sd2, n)
{
  res <- (mean1 - mean2)/ sqrt((sd1^2 + sd2^2) / n)
  
  return(res)
}

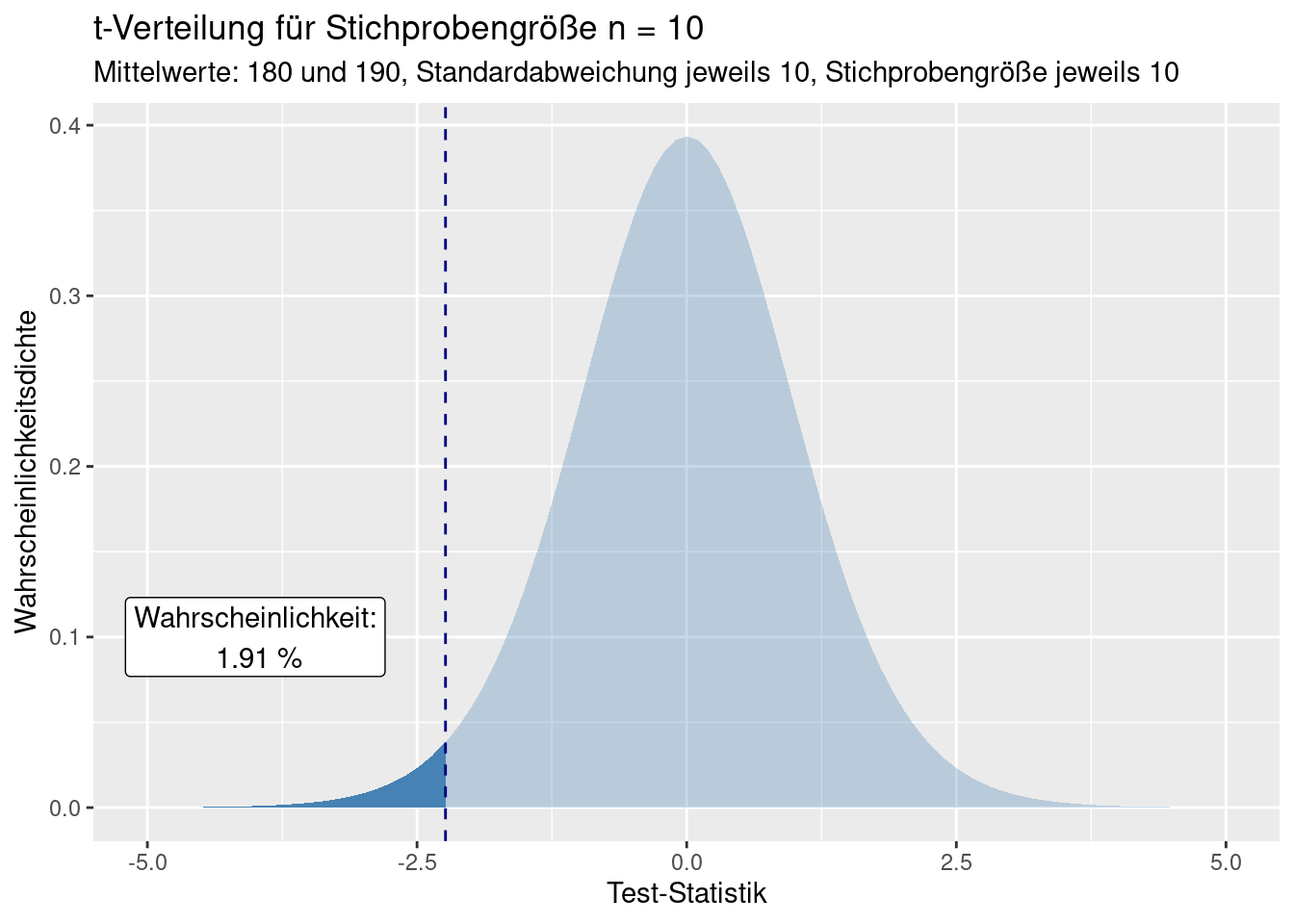
Mittelwerte: 180 und 190, Standardabweichung jeweils 10, Stichprobengröße jeweils 10:

t1 <- calcTTeststat(mean1= 180, mean2 = 190, 
              sd1=10, sd2=10, n = 10)

t1

## [1] -2.236068

Vergrößern wir den Abstand der Mittelwerte: 180 und 200, Standardabweichung jeweils 10, Stichprobengröße jeweils 10:

t2 <- calcTTeststat(mean1= 180, mean2 = 200, 
              sd1=10, sd2=10, n = 10)
t2

## [1] -4.472136

Vergrößern wir die Stichprobengröße: Mittelwerte: 180 und 190, Standardabweichung jeweils 10, Stichprobengröße jeweils 50:

t3 <- calcTTeststat(mean1= 180, mean2 = 190, 
              sd1=10, sd2=10, n = 50)
t3

## [1] -5

Vergrößern wir die Standardabweichung: Mittelwerte: 180 und 190, Standardabweichung jeweils 15, Stichprobengröße jeweils 10:

t4 <- calcTTeststat(mean1= 180, mean2 = 190, 
              sd1=15, sd2=15, n = 50)
t4

## [1] -3.333333

Was sagen uns nun diese Zahlen?

Wir unterstellen, dass die Abstände der Mittelwerte einer t-Verteilung folgen. Wir können uns nun anschauen, wie wahrscheinlich die Test-Statistik Werte sind, wenn wir einen rein zufälligen Prozess unterstellen.

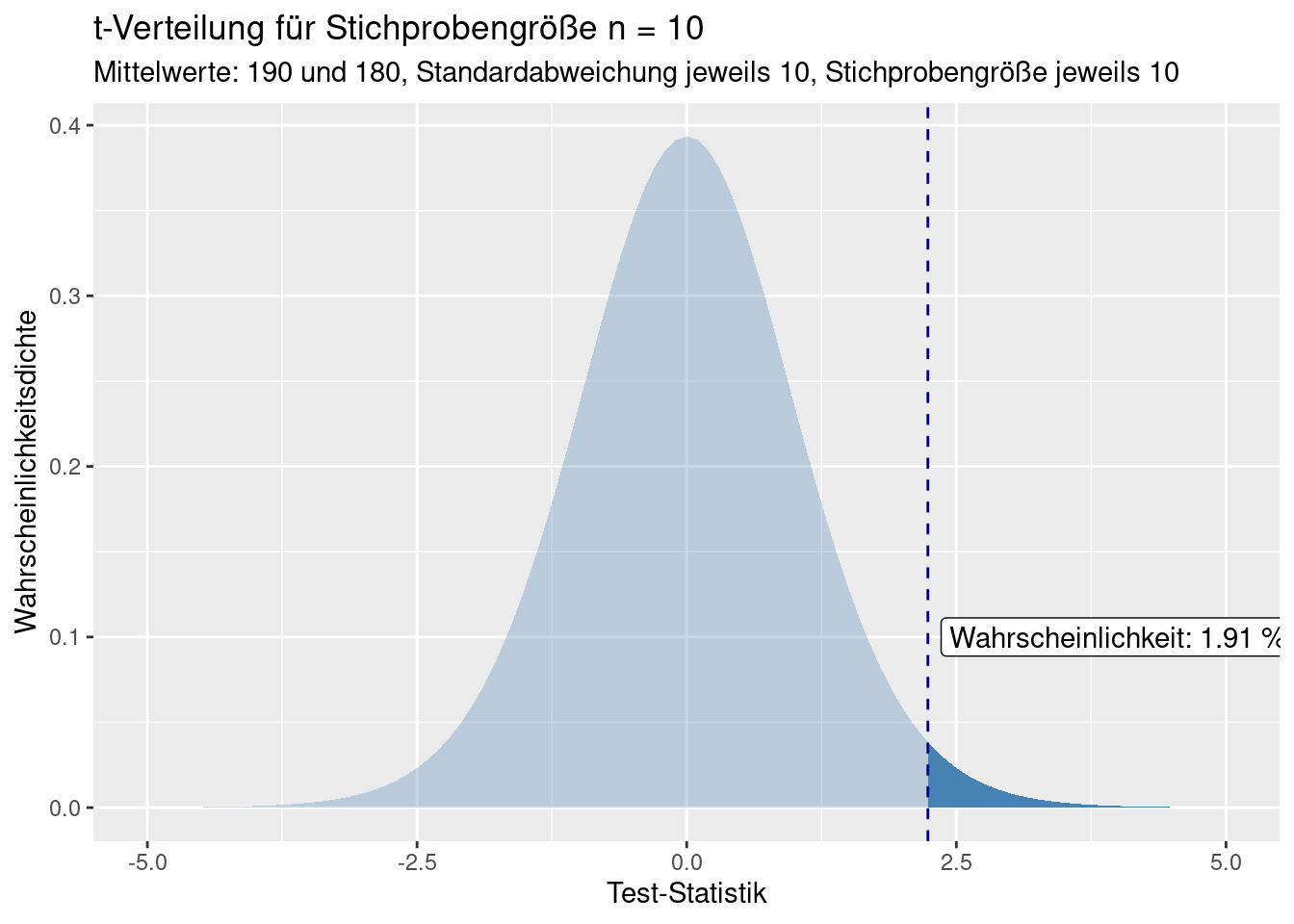
Im folgenden zeichne ich die t-Verteilung für 2*20-2 Freiheitsgrade und trage die Test-Statistiken für die drei Parameterkombinationen t1, t2 und t4 ein. t3 basiert auf einer anderen Stichprobengröße und muss deswegen aufgrund einer anderen Paramterisierung der t-Verteilung betrachtet werden.

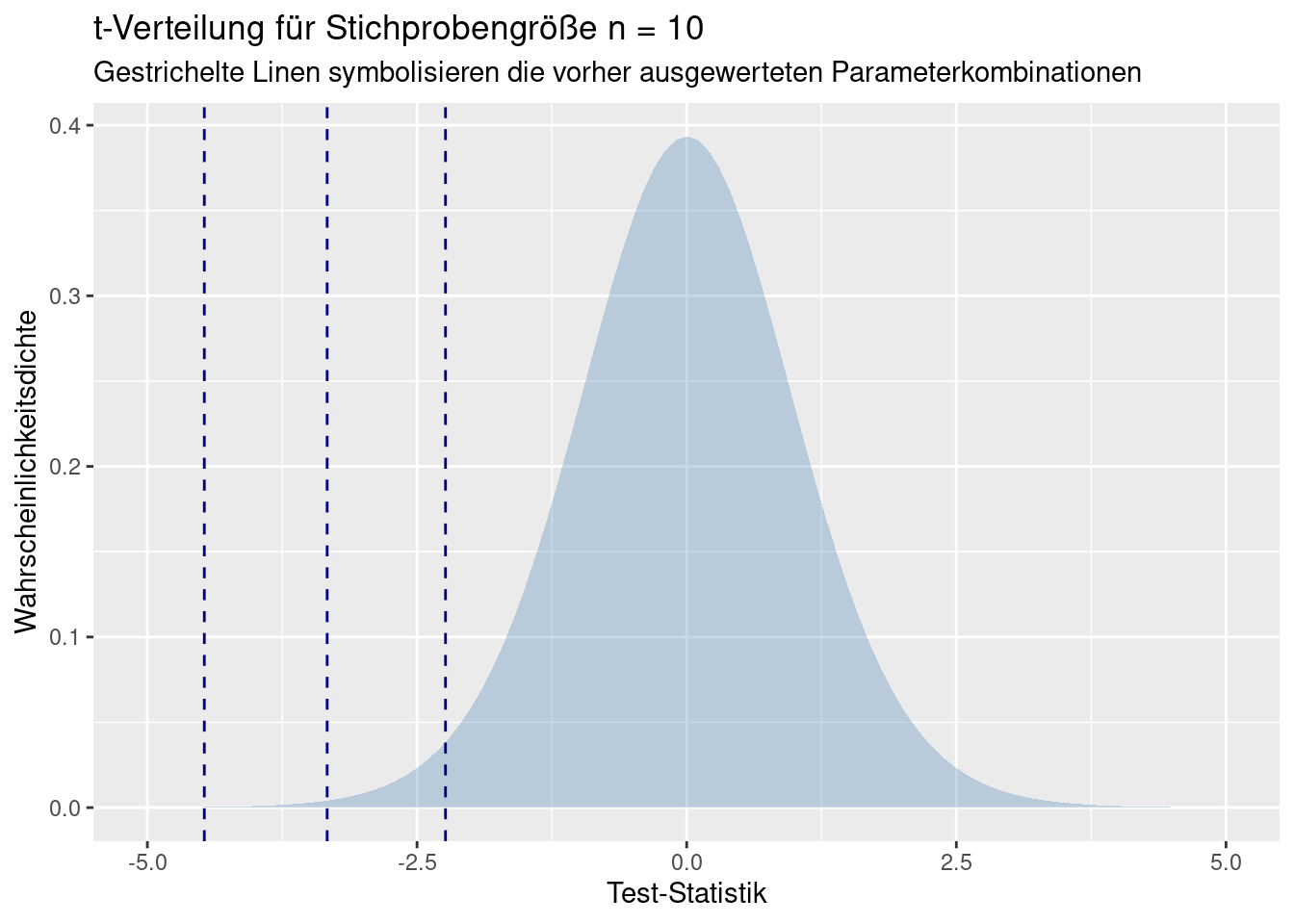
Die Wahrscheinlichkeit für das rein zufällige Auftreten der Test-Statistiken ist die Fläche unter der Kurve, die (in userem Fall) links des beobachteten Wertes liegt. Würden wir die Mittelwerte anderes herum definieren und damit eine positive Differenz bekommen, wären die Test-Statistiken an der y-Achse gespiegelt und wir würde den Teil der Kurve betrachten, der größer als die Test-Statistik ist.

7.3.1 Verteilungswerte abfragen

Die zugehörige Wahrscheinlichkeit für eine bestimmte Test-Statistik lässt sich in Tabellen nachschlagen oder mit R berechnen. Für jede Verteilung gibt es vier Funktionen: zum Nachschlagen der Wahrscheinlichkeit für ein extremeres Ereignis als die Test-Statistik, zum Nachschlagen der Wahrscheinlichkeitsdichte in einem infinitessimal kleinen Intervall, zum Ziehen von einer Zufallsstichprobe von der Verteilung und zur Ausgabe des Wertes der Test-Statistik für ein bestimmtes Quantil. Die Syntax ist immer gleich: pxxx, dxxx, rxx und qxxx - hierbei steht xxx für ein Kürzel der Verteilung. Im Falle der t-Verteilung heißen die Funktionen pt, dt, rt und qt.

Für die Test-Statistik für “Mittelwerte: 180 und 190, Standardabweichung jeweils 10, Stichprobengröße jeweils 10” ergibt sich folgenden Wahrscheinlichkeit für dieses oder ein extremeres Ereignis.

pt(-2.236068, df = 18)

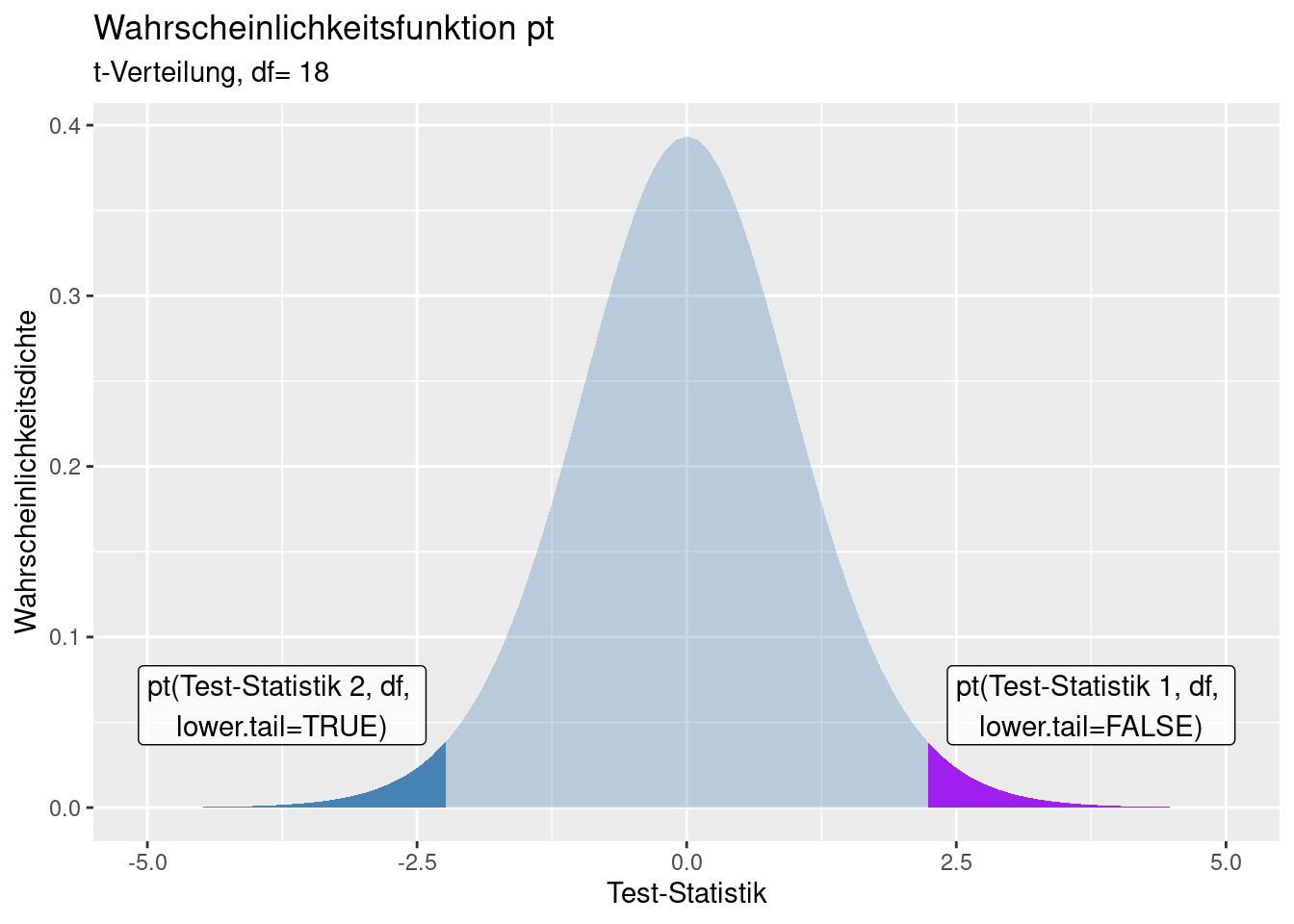
## [1] 0.01912481

Für die vertauschten Mittelwerte kann man die Wahrscheinlichkeit entweder über

1 - pt(2.236068, df = 18)

## [1] 0.01912481

oder über

pt(2.236068, df = 18, lower.tail = FALSE)

## [1] 0.01912481

berechnen.

Sind wir an dem kritischen Wert der Test-Statistik für p = 5% interessiert, können wir das über qt berechnen:

qt(p = 0.05, df= 18)

## [1] -1.734064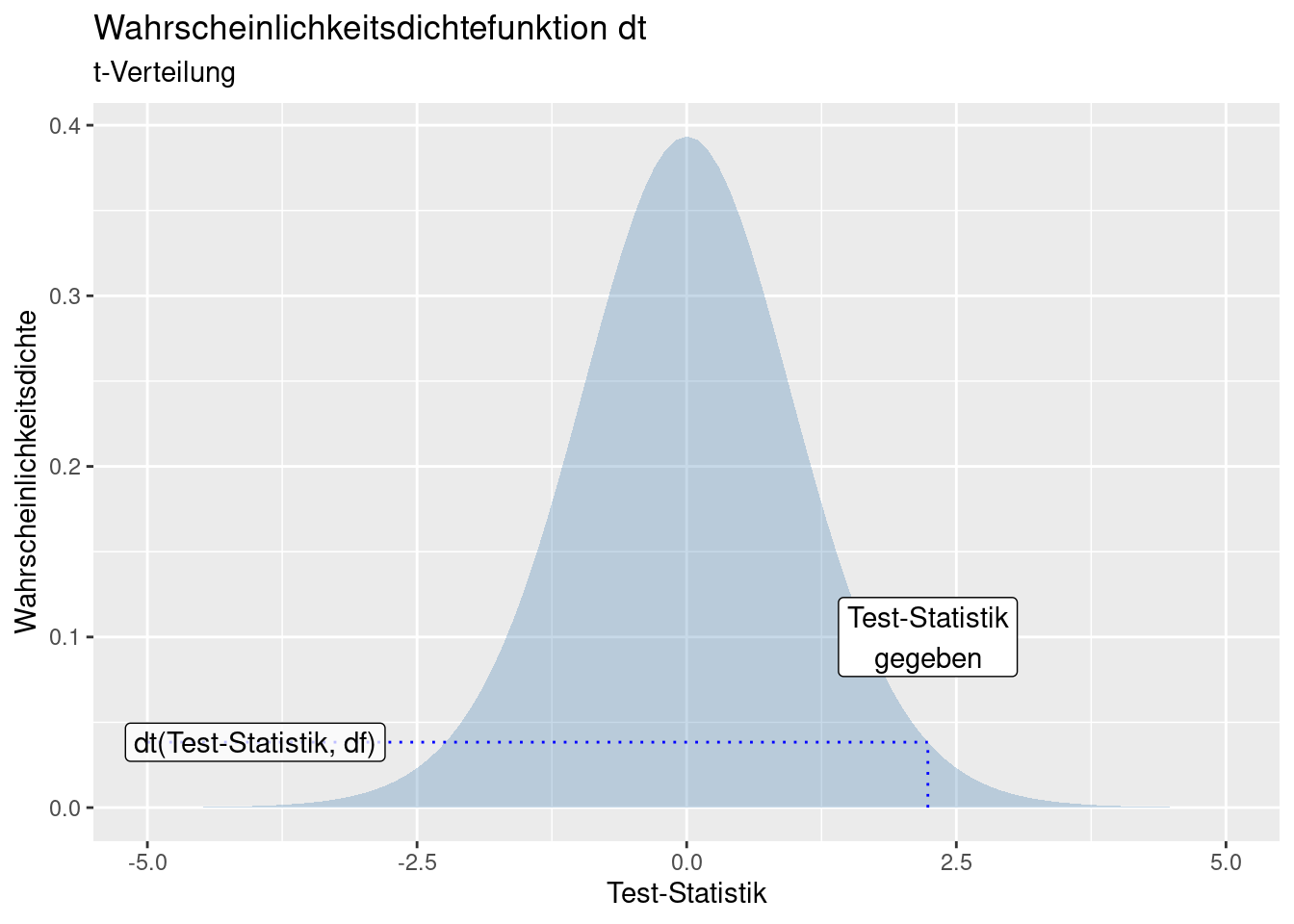

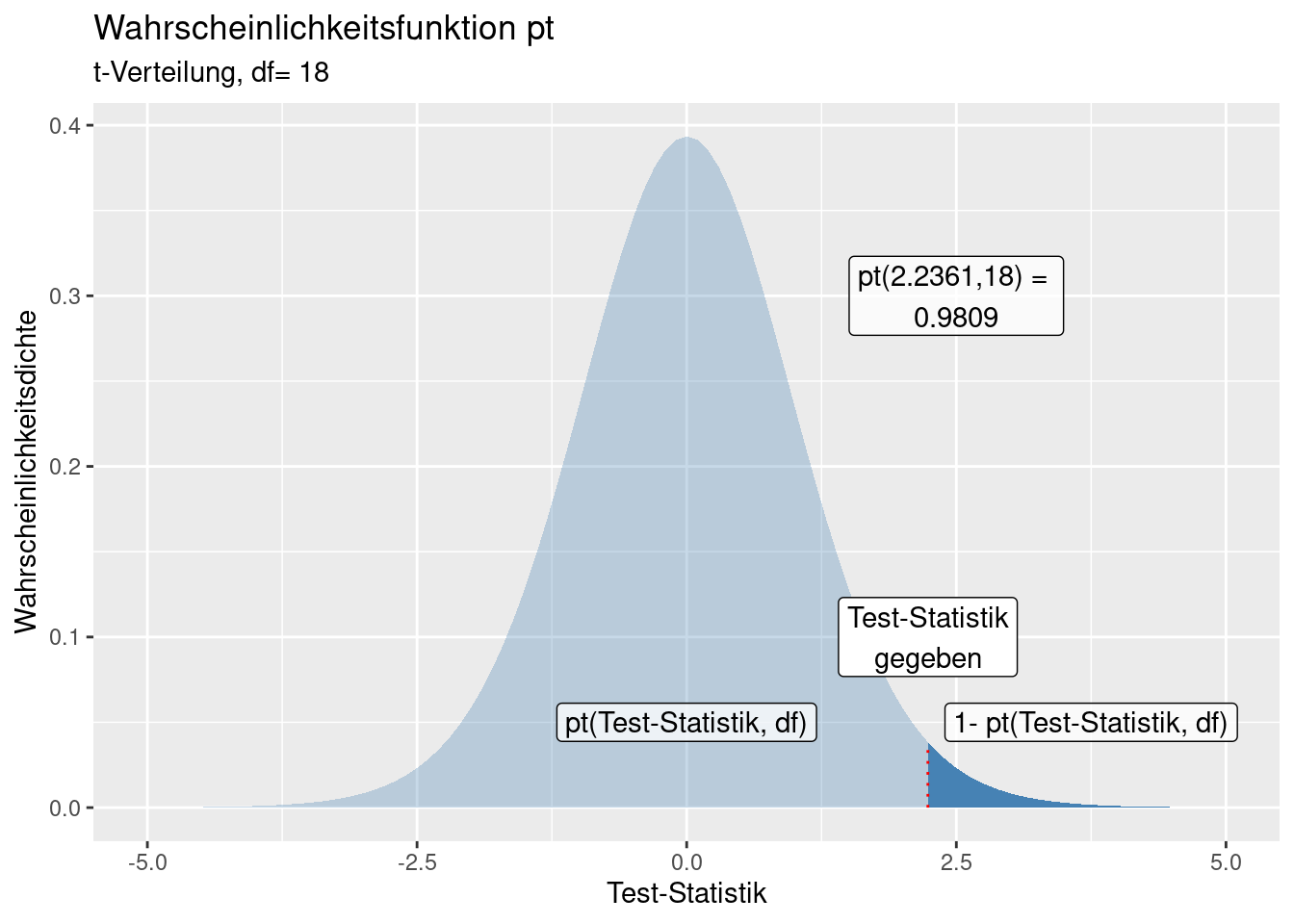
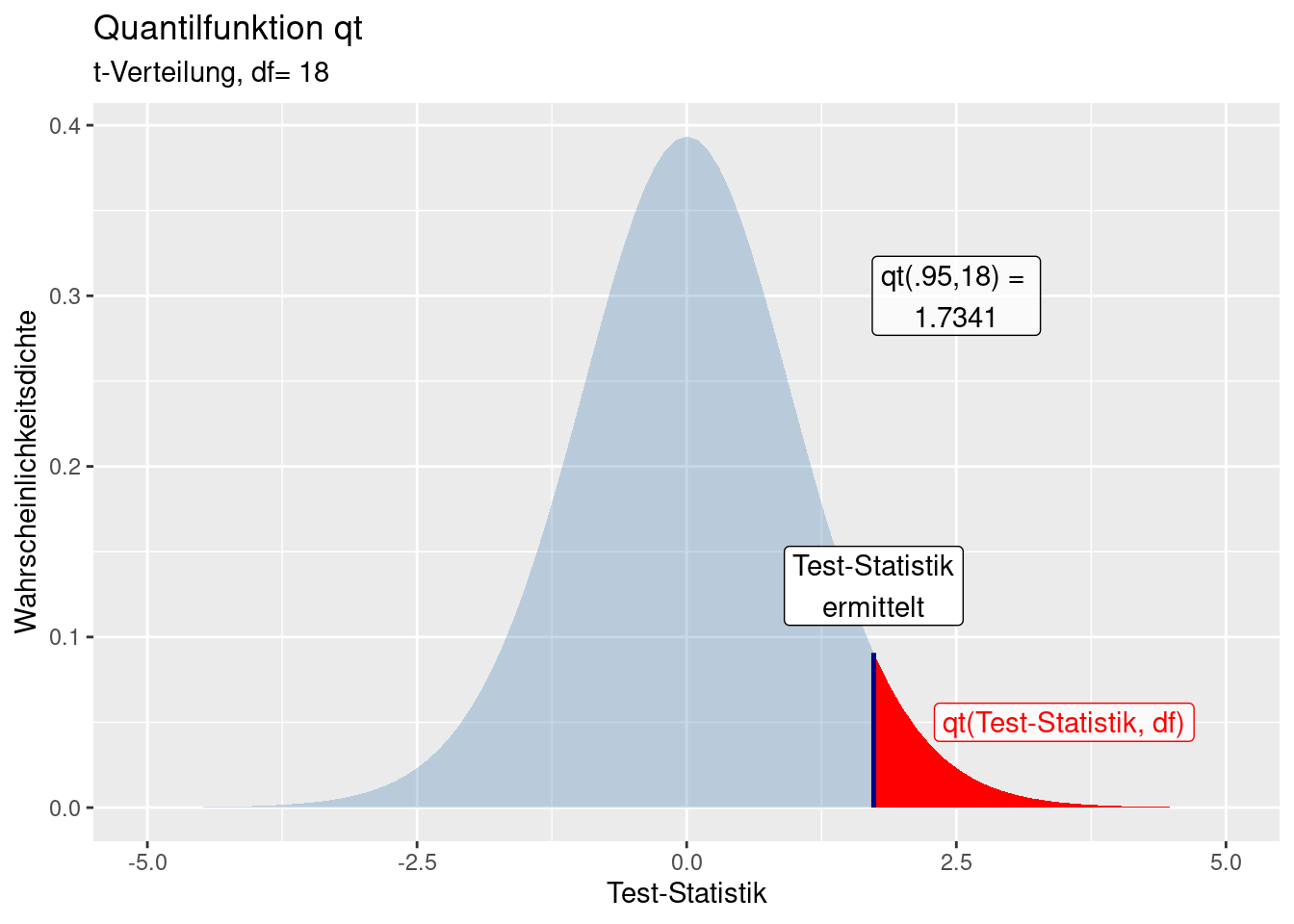
Mit lower.tail=FALSE bzw. lower.tail=TRUE können wir bei pt und qt das oberere bzw. das untere Ende der Verteilung angeben:

• lower.tail=TRUE: \(P[X \leq x]\)
• lower.tail=FALSE: \([X>x]\)

7.3.2 t-Test

Den eigentlichen t-Test in R kann man mittels t.test() durchführen. Die Funktion erwartet zwei Vektoren (Zufallsstichprobe/Beobachtung) der jeweiligen Gruppe und erlaubt weitere Spezifikationen. Hier verwende ich die Alternative “less”, d.h. ich erwarte das der 1. Mittelwert kleiner als der 2. ist. Allgemein würde man alternative="two.sided" verwenden, wenn unklar ist, welcher der beiden Mittelwerte größer ist (allerdings dann mit geringerer Trennschärfe). Da wir eine Zufallsstichprobe ziehen und damit Mittelwerte und Varianz schätzen müssen, kommt dabei natürlich nicht der exakte Test-Statistik-Wert zustande den wir oben berechnet haben.

set.seed(14)
n <- 10
mean1 <- 180
mean2 <- 190
theSd <- 10
x1 <- rnorm(n, mean = mean1, sd= theSd)
x2 <- rnorm(n, mean = mean2, sd= theSd)

t.test(x1, x2, alternative = "less", var.equal = TRUE)

## 
##  Two Sample t-test
## 
## data:  x1 and x2
## t = -2.291, df = 18, p-value = 0.01712
## alternative hypothesis: true difference in means is less than 0
## 95 percent confidence interval:
##       -Inf -2.145298
## sample estimates:
## mean of x mean of y 
##  187.5421  196.3669

Der Test zeigt (für diese Stichprobe) an, dass ein signifikanter Unterschied zu bestehen scheint. Wir sehen weiterhin die anhand der Stichprobe geschätzten Mittelwerte, die Anzahl der Freiheitsgrade (df = 18) sowie weitere Angaben (p-Wert und Konfidenzintervall).

7.4 Fehler 1. und 2. Art

Wären wir im Besitz vollständiger Information (d.h. würden wir die beiden Grundgesamtheiten kennen), könnten wir direkt angeben, ob die beiden Mittelwerte verschieden sind. Da wir jedoch nur die Stichproben kennen, müssen wir die Entscheidung unter Unsicherheit treffen. Dadurch sind folgende Fälle möglich:

.	\(H_0\) beibehalten	\(H_0\) verwerfen
\(H_0\) wahr	Richtige Entscheidung (\(1-\alpha\))	Typ I Fehler (\(\alpha\))
\(H_0\) falsch	Typ II Fehler (\(\beta\))	Richtige Entscheidung (\(1-\beta\))

Wenn wir \(H_0\) beibehalten und \(H_0\) wahr ist, oder wenn \(H_0\) falsch ist und wir \(H_0\) verwerfen, treffen wir die richtige Entscheidung. In diesen beiden Fällen ist alles so, wie es sein sollte. In den beiden anderen Situationen treffen wir allerdings eine falsche Entscheidung. Fall \(H_0\) wahr sein sollte, wir jedoch \(H_0\) verwerfen, begehen wir einen Fehler vom Typ 1, der traditionell mit \(\alpha\) angegeben wird. Dies ist die sogenannte Irrtumswahrscheinlichkeit oder der p-Wert. Falls wir \(H_0\) beibehalten, aber \(H_0\) falsch ist begehen wir einen Fehler Typ II, der traditionell oft mit \(\beta\) angegeben wird.

Man begegnet in diesem Zusammenhang auch den Ausdrücken Spezifität und Sensitivität). Spezifität: die Wahrscheinlichkeit, eine Entscheidung für H0 zu treffen, falls H0 richtig ist. Sensitivität: Wahrscheinlichkeit, eine Entscheidung für H1 zu treffen, falls H1 richtig ist.

Am Beispiel der leider allgemein bekannten Covid-19 Schnelltests sei dies noch einmal verdeutlicht: die Spezifität (\(1-\alpha\)) gibt an, wie häufig der Test bei Gesunden negativ ist. In der Regel wollen wir, das gesunde (nicht mit COVID-19 infizierte) Personen nicht fälschlicherweise als COVID-19 positiv getestet werden. Wir wollen also einen Schnelltest, der einen möglichst hohen \(1-\alpha\) Wert hat, also eine möglichst geringe Irrtumswahrscheinlichkeit \(\alpha\). Die Sensitivität des Tests (\(1-\beta\)) gibt dagegen an, wie häufig der Schnelltest eine Person, die mit COVID-19 infiziert ist auch als positiv identifiziert. Der Fehler II. Art gibt an, wieviele Infizierte im Mittel nicht durch den Test identifiziert werden. Untersuche Schnelltests zeigten eine durchschnittliche Sensitivität von 73% bei Personen mit Symptomen, aber nur 55% für Personen ohne Symptome (Dinnes et al. 2022). D.h. für Personen mit und ohne Symptome hatten wir einen Fehler II. Art von 27% bzw. 45%. Dieser relativ große Fehler II. Art wurde durch einen kleinen Fehler 1. Art “zu haben”aufgewogen”: die Spezifität betrug 99% (Dinnes et al. 2022), d.h. der Fehler I. Art betrug nur 1%. Von 100 nicht infizierten Personen würde demnach im Mittel “nur” eine Person fälschlicherweise als infiziert detektiert (und ggf. in Quarantäne geschickt). Von 100 Infizierten ohne Symptome würden demnach im Mittel 45 Personen fälschlicherweise als nicht infiziert detektiert.

Wir versuchen beide Fehler möglichst gering zu halten. Allerdings ist dies nicht möglich: wenn wir den Fehler Typ I verkleinern, vergrößern wir damit automatisch den Fehler Typ II und umgekehrt. Der Zusammenhang ist nicht-linear und hängt von einer Reihe von Bedingungen ab.

Schauen wir uns das einmal am Beispiel eines Vergleichs des Mittelwertes mit einem Referenzwert an (Abbildung 7.1). In Abhängigkeit von den (geschätzten) Verteilungsparametern (hier Mittelwert und Standardabweichung) können wir die Irrtumswahrscheinlichkeit \(\alpha\) dafür, dass der beobachtet Wert (hier 128) einfach angeben - im Beispiel beträgt dieser Wert 0.0547993. Wir sind also relativ sicher, dass der beobachtete Wert sich von 120 unterscheidet. Um den Fehler II. Art (\(\beta\)) angeben zu können brauchen wir allerdings auch die Verteilung für die Alternativ-Hypothese. Da wir jedoch i.d.R. eine unspezifische Alternativhypothese (\(\mu \neq 120\) bzw. einseitig: \(mu > 120\)) hängt \(\beta\) vom unbekannten Alternativmittelwert ab. Gehen wir von einem wharen Mittelwert der Verteilung von 140 (und einer Standardabweichung von 5) aus, dann beträgt der Fehler II. Art 0.0081975.

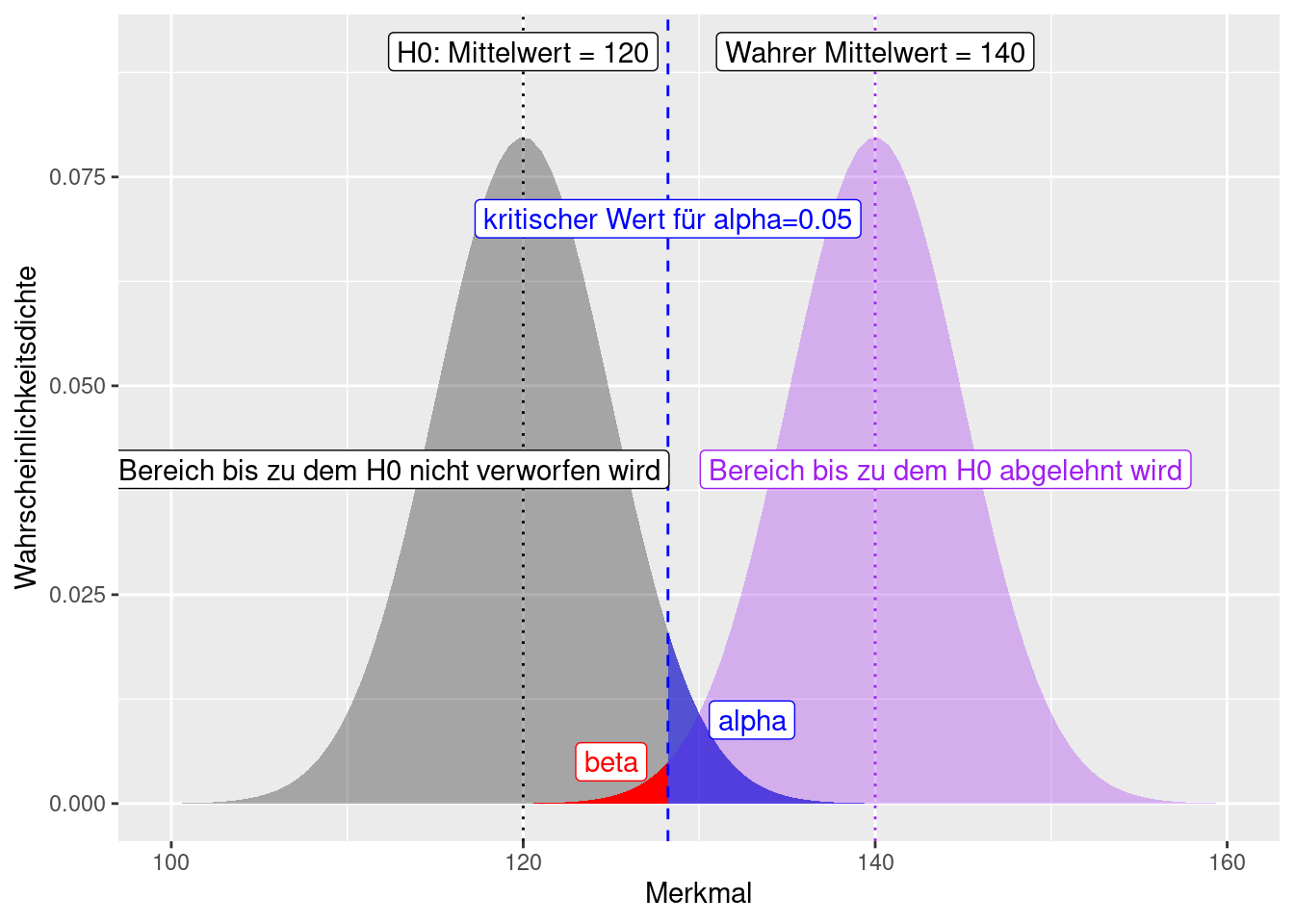
Figure 7.1: Fehler 1. (alpha) und 2. Art (beta) dargestellt am Beispiel. Wir haben einen Wert von 128 beobachtet und fragen uns, ob dieser von einer Verteilung mit einem Mittelwert von 120 und einer Standardabweichung von 5 (graue Verteilung) verschieden ist. Der Fehler I. Art lässt sich direkt aus der Verteilung für H0 ablesen. Um den Fehler II. Art spezifizieren zu können, müssen wir eine Annahme hinsichtlich der Parameter der Alternrativverteilung treffen. Hier nehmen wir einen Mittelwert von 140 und eine Standardabweichung von 5 an.

Paradoxerweise nimmt der Fehler II. Art - bei einer spezifischen Alternativhypothese - zu, je näher der wahre Wert dem in der Nullhypothese behauptetem Wert ist (vergleiche Abbildung 7.2 und 7.3). Allerdings wird der Unterschied damit auch praktisch unrelevanter. Der Fehler I. Art (\(\alpha\)) bleibt dagegen konstant, da er unabhängig von der Lage des wahren Mittelwertes ist.

Wenn der beobachtete Wert von 128 einer Normalverteilung mit Mittelwert 130 und einer Standardabweichung von 5 entstammt, dann beträgt der Fehler II. Art: 0.3445783 (Abbildung 7.2). Falls der beobachtete Wert von 128 einer Normalverteilung mit Mittelwert 125 und einer Standardabweichung von 5 entstammt, dann beträgt der Fehler II. Art: 0.6554217 (Abbildung 7.3).

Wenn der Mittelwert der wahren Verteilung, der der beobachtete Wert entstammt sich nur geringfügig vom Mittelwert der Verteilung der Nullhypothese unterscheidet, besteht einen hohe Wahrscheinlichkeit, dass man sich fälschlicherweise dafür entscheidet \(H_0\) beizubehalten, auch \(H_0\) falsch ist. Das macht intuitiv auch Sinn: wenn der wahre Mittelwert 125 ist, dann fällt es leichter zu glauben, dass der Mittelwert 120 ist, als wenn der wahre Mittelwert 140 ist. Die Konsequenzen einen Fehler II. Art zu machen, unterscheiden sich natürlich auch: wenn ich annehme der Mittelwert ist 120, wenn der wahre Mittelwert 125 ist, ist dies weniger dramatisch, als wenn der wahre Mittelwert 140 beträgt.

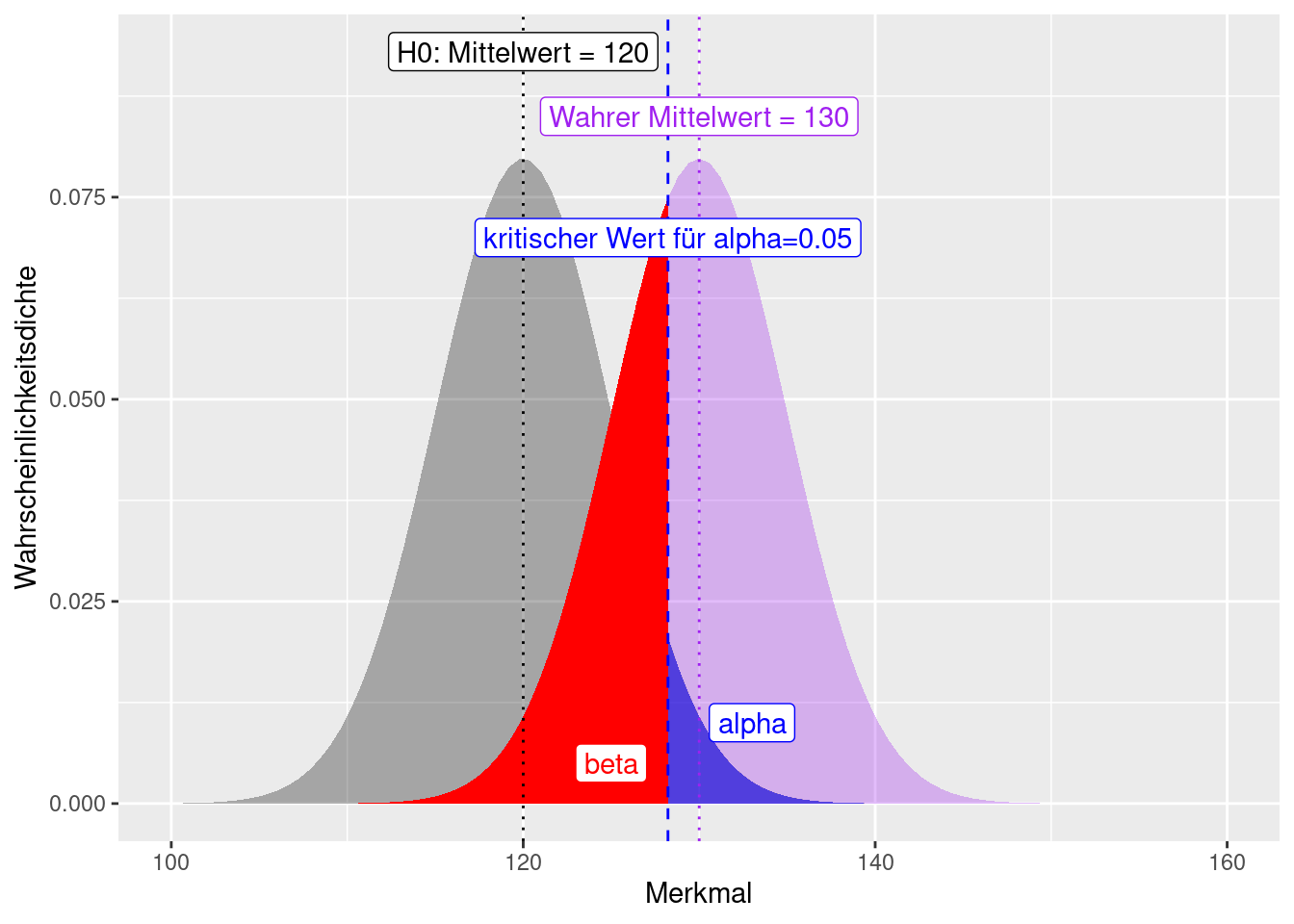
Figure 7.2: Fehler 1. (alpha) und 2. Art (beta) dargestellt am Beispiel. Wir haben einen Wert von 128 beobachtet und fragen uns, ob dieser von einer Verteilung mit einem Mittelwert von 120 und einer Standardabweichung von 5 (graue Verteilung) verschieden ist (spezifische Alternativhypothese). Der Fehler I. Art lässt sich direkt aus der Verteilung für H0 ablesen. Um den Fehler II. Art spezifizieren zu können, müssen wir eine Annahme hinsichtlich der Parameter der Alternrativverteilung treffen. Hier nehmen wir einen Mittelwert von 130 und eine Standardabweichung von 5 an.

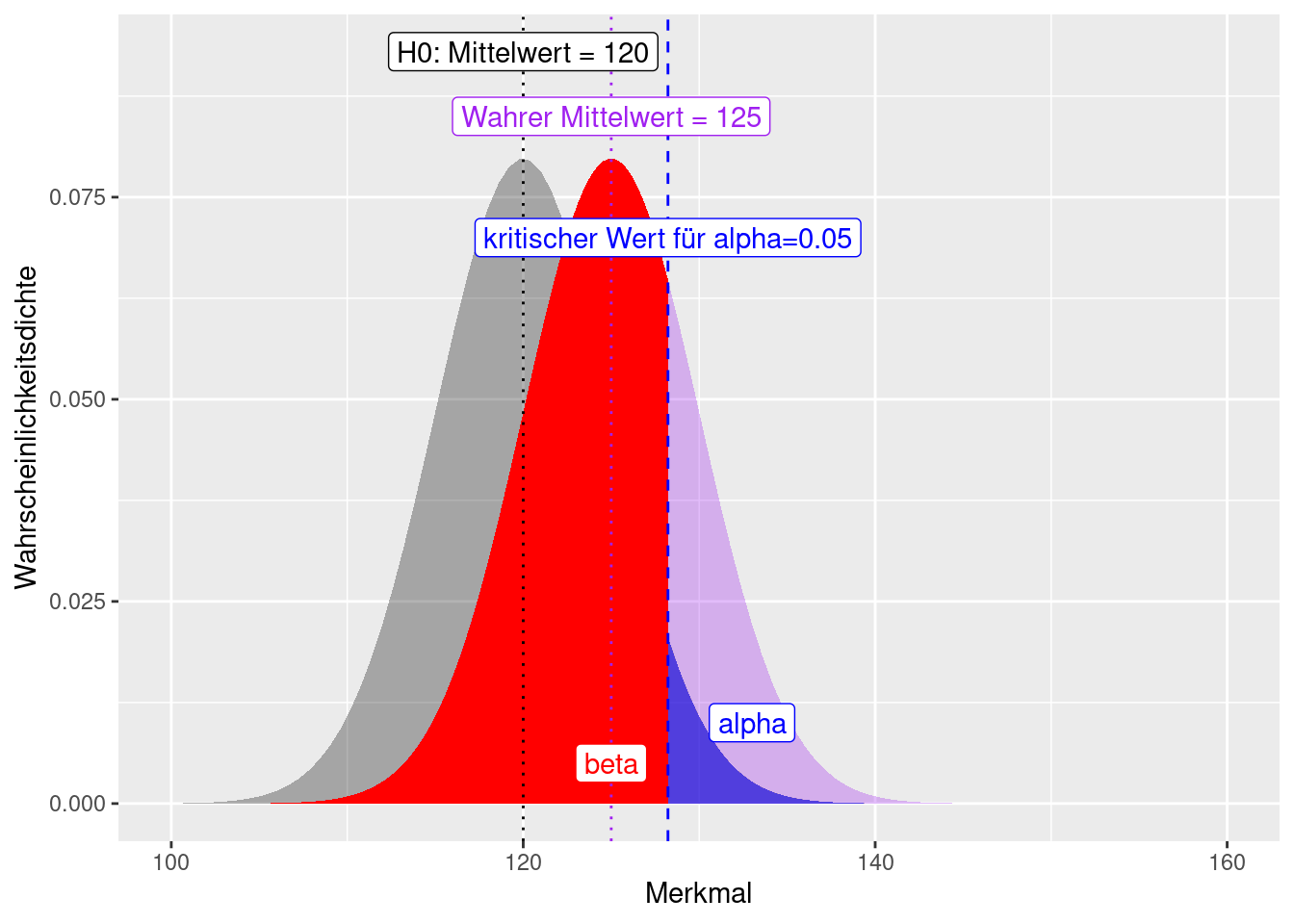
Figure 7.3: Fehler 1. (alpha) und 2. Art (beta) dargestellt am Beispiel. Wir haben einen Wert von 128 beobachtet und fragen uns, ob dieser von einer Verteilung mit einem Mittelwert von 120 und einer Standardabweichung von 5 (graue Verteilung) verschieden ist (spezifische Alternativhypothese). Der Fehler I. Art lässt sich direkt aus der Verteilung für H0 ablesen. Um den Fehler II. Art spezifizieren zu können, müssen wir eine Annahme hinsichtlich der Parameter der Alternrativverteilung treffen. Hier nehmen wir einen Mittelwert von 125 und eine Standardabweichung von 5 an.

Traditionellerweise wurde dem Fehler I. Art mehr Aufmerksamkeit geschenkt. Dafür gibt es verschiedene Gründe. Der wichtigste ist sicherlich, dass wir den Fehler II. Art nur für eine spezifische Alternativhypothese berechnen können. Der üblicherweise gewählte p-Wert von 5% stellt einen Kompromiss zwischen konservativer Irrtumswahrscheinlichkeit für den Fehler I. Art und dem (nicht quantifizierten) Fehler II. Art dar.

Für manche Anwendungsfälle wäre es jedoch günstiger, mehr Wert auf den Fehler II. Art zu legen (oder die Nullhypothese anders herum zu formulieren). So z.B. hinsichtlich der Unbedenklichkeit von neuen Substanzen für Umwelt und menschliche Gesundheit. In der Vergangenheit gingen Umweltbehörden davon aus, dass eine Substanz harmlos war, solange nicht das Gegenteil nachgewiesen war. Vertreter der chemischen Industrie strebten deswegen eine möglichst geringe Irrtumswahrscheinlichkeit hinsichtlich der Nullhypothese das die Substanz harmlos ist (producer’s error) an. Vertreter von Umwelt- und Verbraucherschutzorganisationen wollten dagegen einen möglichst geringen Fehler II. Art (auf Kosten eines höheren Fehlers I. Art) (consumer’s error). Ein Fehler I. Art tritt bei diesem Beispiel dann auf, wenn wir die Nullhypothese - die Substanz ist unschädlich - ablehnen, obwohl die Substanz in Wahrheit unschädlich ist. Der Fehler II. Art liegt in dieser Anwendung vor, wenn wir die Nullhypothese - die Substanz ist unschädlich - beibehalten, obwohl die Substanz in Wahrheit schädlich ist.

7.4.1 Cohen’s d

Cohen’s d hilft bei der Beurteilung der praktischen Relevanz der Mittelwertunterschiede zwischen zwei Stichproben. Der Indikator gibt die Effektstärke für Mittelwertunterschiede zwischen zwei Gruppen mit gleiche Gruppengrößen und gleichen Gruppenvarianzen \(\sigma^2\) an:

\[D = \frac{\mu_1-\mu_2}{\sigma}\]

Bzw. für Stichproben:

\[D = \frac{\bar{x_1}-\bar{x_2}}{s}\]

cohensd <- function(mu1, mu2, sigma)
{
  return((mu1-mu2)/ sigma)
}

In den oben angegebenen Beispielen beträgt Cohens d:

• für \(\mu_1 = 120\) und \(\mu_2 = 140\) und \(\sigma = 5\) ist d = -4
• für \(\mu_1 = 120\) und \(\mu_2 = 130\) und \(\sigma = 5\) ist d = -2
• für \(\mu_1 = 120\) und \(\mu_2 = 125\) und \(\sigma = 5\) ist d = -1.

Daneben existieren Formel zur Berechnung von Cohens d für ungleiche Gruppengrößen und Gruppenvarianzen sowie verwandte Kennzahlen wie Glass \(\Delta\), Hedges g , Cohens \(f^2\), COhens w, Cramers \(\phi\) oder Cramers V, die alle eine Form von Effektstärke quantifizieren.

Für gleiche Gruppengrößen und unterschiedliche Gruppenvarianzen berechnet sich Cohen’s d wie folgt:

\[d = \frac{\bar{x_1}-\bar{x_2}}{\sqrt{(s_1^2 + s_2^2)/2}} \]

7.5 Trennschärfe eines Tests

Die Trennschärfe (statistical power) eines Tests beschreibt die Wahrscheinlichkeit, dass die Nullhypothese verworfen wird, wenn sie falsch ist. Der Power hängt mit dem Tpy II Fehler zusammen: die Wahrscheinlichkeit, die Nullhypothese zu verwerfen, wenn sie wahr ist wird oft mit \(\beta\) angegeben. Die Wahrscheinlichkeit, dass sie verworfen wird, wenn sie falsch ist (Trennschärfe bzw. Power) ist \(1-\beta\). Wie bereits erwähnt gibt es einen Zielkonflikt zwischen dem Typ I und II Fehler: je kleiner der eine, desto größer der andere, wobei der Zusammenhang nichtlinear ist.

Als Faustzahlen haben sich ein \(\alpha\)-Wert von 0.05 und ein \(\beta\)-Wert von 0.2 etabliert. Allerdings sind das nur Faustzahlen und folgen keiner höheren Logik.

Falls man vorher weiß, was man testen möchte - und das sollte man wissen -, kann man mittels Power-Berechnungen vorher abschätzen, wieviele Replikate man benötigt, um einen Effekt auf einem bestimmten Signifikanzniveau zu beobachten. Hierzu sollte man vorab folgende Fragen beantworten:

• Wie groß ist der Effekt, den man beobachten möchte? Ist es sinnvoll, einen 1% Unterschied in der Zahlungsbereitschaft für Umweltschutzmaßnahmen zu testen oder ist dieser Unterschied zu klein, um relevant zu sein? Ist ein Unterschied im Tonanteil von 0.1% zwischen zwei Untersuchungsgebieten relevant? Je kleiner der Unterschied ist, den man feststellen will, desto mehr Replikate (und damit Ressourcen) benötigt man.
• Wie groß ist die Variabilität in den Daten? Je höher die Variabilität, desto größer die Anzahl der benötigten Replikate. In der Regel ist dies nicht vorab bekannt, man kann sich mit vergleichbaren Studien aus der Literatur oder durch Vorstudien behelfen.
• Auf welchem Siginifikanzniveau (p-Wert) soll der Unterschied detektiert werden? Je kleiner, desto mehr Replikate werden benötigt.

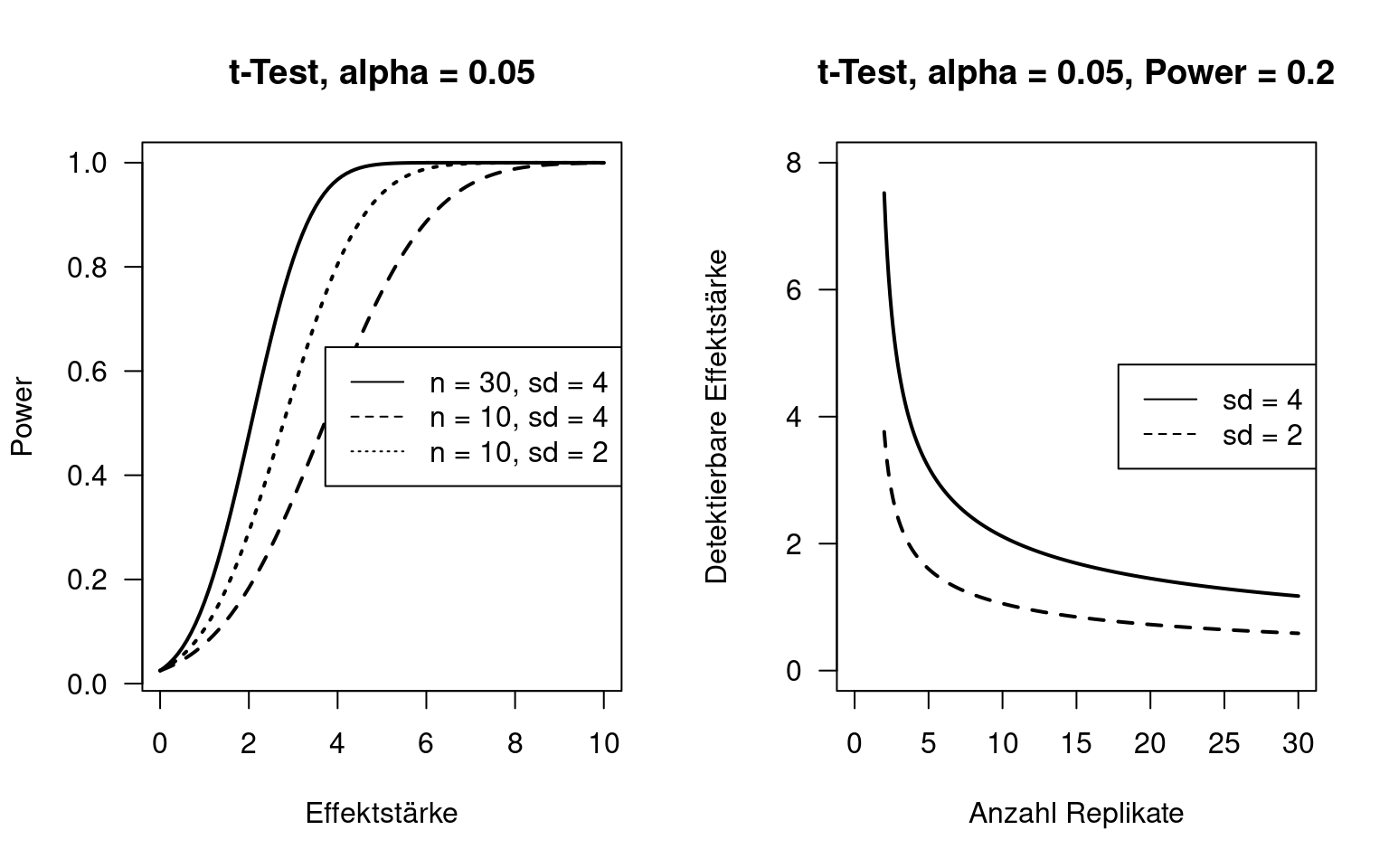
Nachfolgende Abbildung verdeutlicht die Zusammenhänge am Beispiel des ungepaarten, zweiseitigen t-Tests (Unter der Annahme, dass die Daten den Anforderungen entsprechen). Beide Pannel nehmen ein Signifikanzniveau \(\alpha\) von 0.05 an. Das rechte Pannel nimmt einen Powerwert von 0.2 an. Die Effektstärke ist hierbei der Unterschied der Mittelwerte zweier Grundgesamtheiten. Die beobachtbare Effektstärke ist der Unterschied zwischen zwei Grundgesamtheiten, der bei dem gewähltem Power und der gewählten Anzahl von Replikaten noch beim gewähltem \(\alpha\)-Wert unterschieden werden können.

7.5.1 Power Berechnungen in R

In R kann man mittels power.t.test den Power ein- und zweiseitiger t-Tests berechnen. Folgende Parameter können spezifiziert werden - ein Parameter sollte nicht spezifiziert werden, dieser wird dann berechnet:

• n - Anzahl Beobachtungen (Stichprobengröße) je Gruppe
• delta - Wahrer Unterschied der Mittelwerte der beiden Gruppen (auf Grundlage der Grundgesamtheiten)
• sd - Standardabweichung (gleich für beide Gruppen)
• sig.level - Signifikanz-Level \(\alpha\) (Type I Fehlerwahrscheinlichkeit)
• power - Trennschärfe (power) des Tests (1 - Type II Fehlerwahrscheinlichkeit)

Weitere Parameter sind:

• alternative - einseitiger oder zweiseitiger Test ( "two.sided", "one.sided")
• type - Art des t-Tests: "two.sample", "one.sample", "paired"

Wenn man einen Parameter als NULL definiert (z.B. power = NULL, wird dieser Parameter geschätzt. Um z.B. die benötigte Anzahl der Replikate wissen, die man braucht um bei einer Effektstärke von mindestens 2 bei einer Standardabweichung von 4 für beiden Gruppen wissen und verwendet man die üblichen werte für \(\alpha\) und \(1-\beta\), dann hilft folgender Befehl weiter:

(pow <- power.t.test(delta=2, sd=4, power=.8, sig.level=.05))

## 
##      Two-sample t test power calculation 
## 
##               n = 63.76576
##           delta = 2
##              sd = 4
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Wir sehen, dass die benötigte Stichprobengröße 64 je Gruppe beträgt. Wenn man nur die Ressourcen hat, ein Experiment mit 30 Replikaten durchzuführen, sollte man sich fragen, ob man das Experiment wirklich durchführen möchte. Zumindest, wenn die Effektstärke von 2 realistisch ist, kann man davon ausgehen, dass man diesen Unterschied im Experiment nicht nachweisen kann.

(pow_b <- power.t.test(n=30, sd=4, power=.8, sig.level=.05))

## 
##      Two-sample t test power calculation 
## 
##               n = 30
##           delta = 2.942516
##              sd = 4
##       sig.level = 0.05
##           power = 0.8
##     alternative = two.sided
## 
## NOTE: n is number in *each* group

Die minimale Effektstärke, die bei den gewählten Parametern ein signifikantes Ergebnis bringen würde ist 2.94.

Das package pwrenthählt weiter Funktionen für die Berechnung der Trennschärfe verschiedener weitere Tests wie dem \(\chi^2\)-Test oder Korrelations-Tests.

Nicht vergessen sollte man, dass diese Berechnungen der Trennschärfe auf Annahmen beruhen - sollten diese nicht erfüllt sein, sind die Ergebnisse nicht valide. Simulationen oder Ansätze wie der Bootstrap können in solchen Situationen helfen.

7.6 Statistische Freiheitsgrade

Der Begriff der statistischen Freiheitsgrade(degree of freedom, oft mit df abgekürzt) taucht insbesondere bei Testverteilungen auf. Der Begriff gibt an, wieviele Werte in einer Berechnungsformel frei variieren dürfen.

Bei der Berechnung des arithmetischen Mittels können alle Werte frei variieren, d.h. die Anahl der Freiheitsgrade entspricht der Stichprobengröße \(n\). Bei der Berechnung der Stichprobenvarianz \(s^2\) dagegen wird bereits der Mittelwert aus den Daten \((\bar{x})\) geschätzt. Deswegen muss die aNzahl der Freiheitsgrade um 1 reduziert werden auf \(n-1\).

Arithmetisches Mittel:

\[ \bar{x} = \frac{1}{n} \sum_{i=1}^n x_i \]

Stichprobenvarianz:

\[s^2 = \frac{1}{n-1}\sum_{i=1}^n(x_i - \bar{x}^2) \]

Falls der Mittelwert einer Stichprobe bekannt ist, kann man anhand von \(n-1\) Beobachtungen den fehlenden Wert der letzten Beobachtung berechnen. Bei Kenntnis des Mittelwertes ist in der Stichprobe also etwas weniger zusätzliche Information enthalten als wenn der Mittelwert nicht bekannt ist. Dies wird durch die Reduktion der Freiheitsgrade ausgedrückt.

Beispiel: Stichprobe mit folgenden Werten:

theSample <- c(33, 12, 24, 2, 5)

Mittelwert:

mean(theSample)

## [1] 15.2

Wenn ich nun 3 beliebige Werte aus der Stichprobe und den Mittelwert kenne, kann ich den fehlenden Wert berechnen - dieser ist also nicht unhabhängig von den anderen.

\[15.2 = \frac{1}{5} (33 + 12 + 24 + x_4 + 5)\] Umgestellt:

\[x_4 = 15.2*5 -33 - 12 -24 -5\]

15.2*5 -33 - 12 -24 -5

## [1] 2

Der letze Stichprobenwert hat also keine zusätzliche Information, wenn der Stichprobenmittelwert bekannt ist.

Weiterführende/zitierte Literatur

Dinnes, Jacqueline, Pawana Sharma, Sarah Berhane, Susanna S van Wyk, Nicholas Nyaaba, Julie Domen, Melissa Taylor, et al. 2022. “Rapid, Point-of-Care Antigen Tests for Diagnosis of SARS-CoV-2 Infection.” Cochrane Database of Systematic Reviews, no. 7.

---

22. Was nicht der Fall sein dürfte, da z.B. das Einkommen beider Gruppen unterschiedlich sein dürfte. Weiterhin könnte es ggf. auch geschlechterspezifische Unterschiede geben, die allerdings durch die ungleichmäßige Verteilung der Geschlechter über die Studiengänge hinweg schwierig zu erfassen sein dürfte. Aber es handelt sich hier ja auch nur um ein Gedankenexperiment.↩︎

23. Alles andere gleich, d.h. wenn alle anderen Parameter/Eigenschaften bis auf die angesprochene(n) gleich sind.↩︎

24. Ähnlich wird hier als Faustregel so definiert, dass das Verhältnis beider geschätzter Varianzen zwischen 0.5 und 2 liegt.↩︎