Kapitel 12 Lineares Model - univariates lineares Modell

12.1 Theorie

Das lineare Modell ist das einfachste Regressionsmodell. Mir wollen dabei untersuchen, inwiefern ein oder mehrere Prädiktoren (oder erklärende oder unabhängige Variablen) \(X_i\) den Response (oder zu erklärende oder abhängige Variable) \(Y\) erklären. Im Gegensatz zur Korrelation wird ein gerichteter Zusammenhang unterstellt: X wirkt auf Y.

Wir fokussieren zunächst auf den univariaten Fall, d.h. wir betrachten nur einen einzelnen Prädiktor. Wir wollen dennoch gleich die Syntax für das multivariate Modell einführen.

In Matrixschreibweise sieht das Modell wie folgt aus:

\[ Y_i = X_i \hat{\beta} + \epsilon_i \]

wobei \(\epsilon_i \widetilde{~} N(0, \sigma^2)\).

Ohne Matrixschreibweise ist die Schreibweise etwas länglicher:

\(y_i = \hat{\beta}_0 \cdot 1 + \hat{\beta}_1 \cdot x_{1,i} + \hat{\beta}_2 \cdot x_{2,i} + \ldots + \hat{\beta}_p \cdot x_{p,i} + \epsilon_i\)

Der hat-Operator \(\hat{}\) gibt an, dass die Koeffizienten Beta anhand der Stichprobe geschätzt werden.

Beide Formel beschreiben, wie die zu erklärende Variabel \(Y\) andhand einer Reihe von Prädiktoren \(X\) vorhergesagt wird. Der Zusammenhang wird als Linearkombination beschrieben: die Werte der erklärenden Variablen werden mit - anhand der Beobachtungen geschätzten - Koeffizienten \(\beta\) multipliziert und aufaddiert. Zu dem strukturellem Part \(Y= X\hat{\beta}\) kommt noch eine Fehlerkomponente \(\epsilon\), für die wir beim linearen Modell eine Reihe von Annahmen treffen. Dies können in komplexeren Modellen aufgehoben werden. Zunächst müssen wir uns jedoch mit dem linearen Modell als einfachstem Regressionsmodell vertraut machen.

Ein oft gemachter Fehler ist es, davon auszugehen, dass der Zusammenhang zwischen \(Y\) und \(X\) linear sein muss. Dem ist nicht so: der Zusammenhang wird als Linearkombination beschrieben, der Zusammenhang zwischen \(Y\) und \(X\) kann jedoch nicht-linear sein. Nachfolgende Gleichung beschreibt ein lineares Modell:

\[Y = \hat{\beta}_0 + \hat{\beta}_1 \cdot X_1 + \hat{\beta}_2 \cdot X^2_1 + \hat{\beta}_3 \cdot sin(X_3) + \epsilon \] Dagegen handelt es sich z.B. bei der Michaelis-Menten Dynamik nicht um ein lineares, sondern um ein nicht-lineares Modell, da es sich um keine als Linearkombination darstellbare Gleichung handelt:

\[Y= \hat{\beta_1} \frac{X_1}{\hat{\beta}_2+ X_1} + \epsilon\]

Solche Modelle werden in R mittels nls modelliert - das führt hier allerdings zu weit. Der/die interessierte LeserIn sei auf Ritz and Streibig (2008) verwiesen.

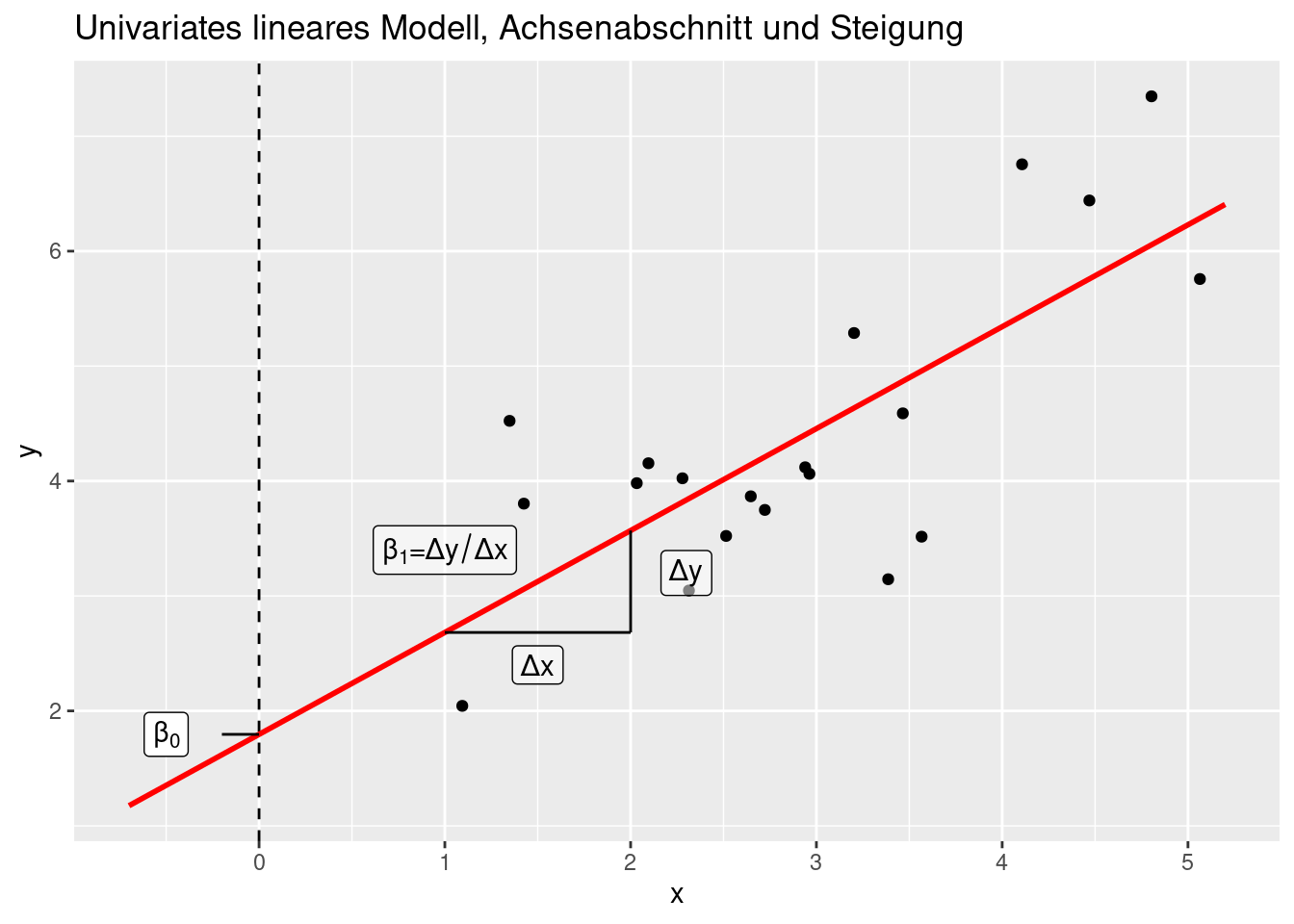
Die Modell- oder Designmatrix \(X\) besteht aus den Prädiktoren als Spaltenvektoren. Zusätzlich wird für den Achsenabschnitt (\(\beta_0\)) noch ein Spaltenvektor vorangestellt, der nur aus 1-en besteht. Die anhand der Beobachtungen geschätzten Koeffizienten \(\beta\) beschreiben, wie stark sich der Response verändert, wenn man einen Prädiktor um eine Einheit verändert (und alle anderen konstant hält).

12.1.1 Matrixmultiplikation

Um die Matrixschreibweise verstehen zu können muss man wissen, wie die Matrixmultiplikation zwischen \(X\) und \(\hat{\beta0}\) definiert ist. Die Matrixmultiplikation zweier Matrizen A und B ist - sofern die Operation zulässig ist - eine Matrix C, deren Elemente wie folgt berechnet werden:

\[ c_{i,k} = \sum_{j=1}^m a_{i,j} \cdot b_{j,k} \]

Die Matrixmultiplikation ist als die komponentenweise Mutliplikation der Einträge der i-ten Zeile von A mit der k-ten Spalte von B und die Summation all dieser Produkte. Die Matrixmultiplikation ist nur für den Fall definiert, dass die Spaltenzahl \(m\) der Matrix \(A\) mit der Zeilenzahl der Matrix \(B\) übereinstimmt. Daraus ergibt sich auch, dass allgemein $ A B B A$ - die Matrixmultiplikation ist also nicht kommutativ.

Dies wird von nachfolgenden Grafik veranschaulicht⁵⁰

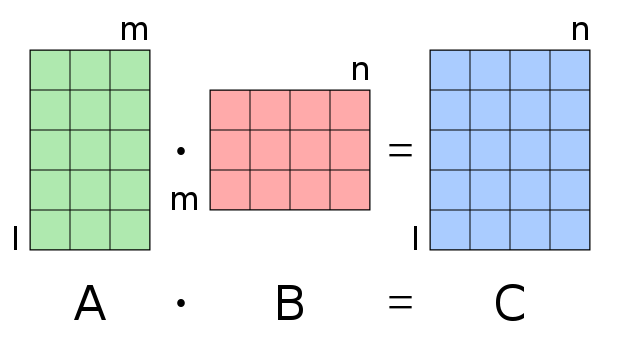
Figure 12.1: Matrixmultiplikation. Die Anzahl der Spalten der Matrix A muss der Anzahl der Zeilen in Matrix B entsprechen, damit die Multiplikation zulässig ist.

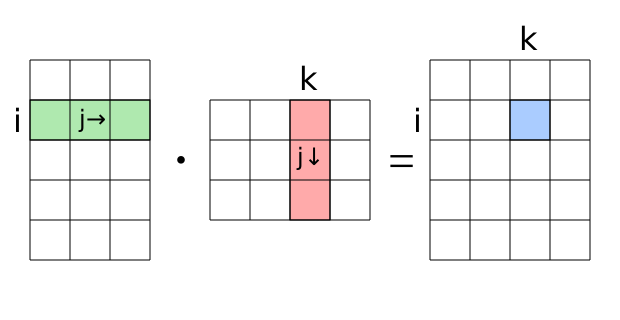
Figure 12.2: Das Element in der i-ten Zeilen und k-ten Spalte der Ergebnismatrix ergibt sich als Summe der elementweisen Produkte der i-ten Zeile in Matrix A mit der k-ten Spalte in Matrix B.

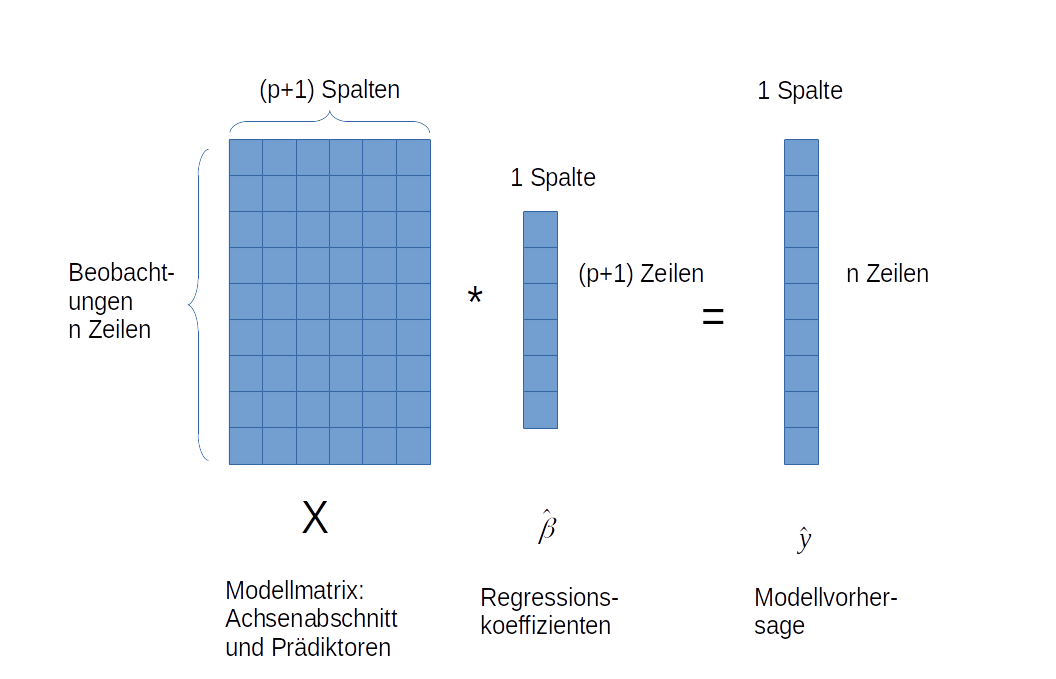
Im Falle des linearen Regressionsmodells ist \(Y\) eine n x 1 Matrix, ebenso wie \(\hat{\beta}\) und \(\epsilon\), während \(X\) eine n x(p+1) Matrix ist. \(n\) ist dabei die Anzahl der Beobachtungen und \(p\) die Anzahl der Prädiktoren.

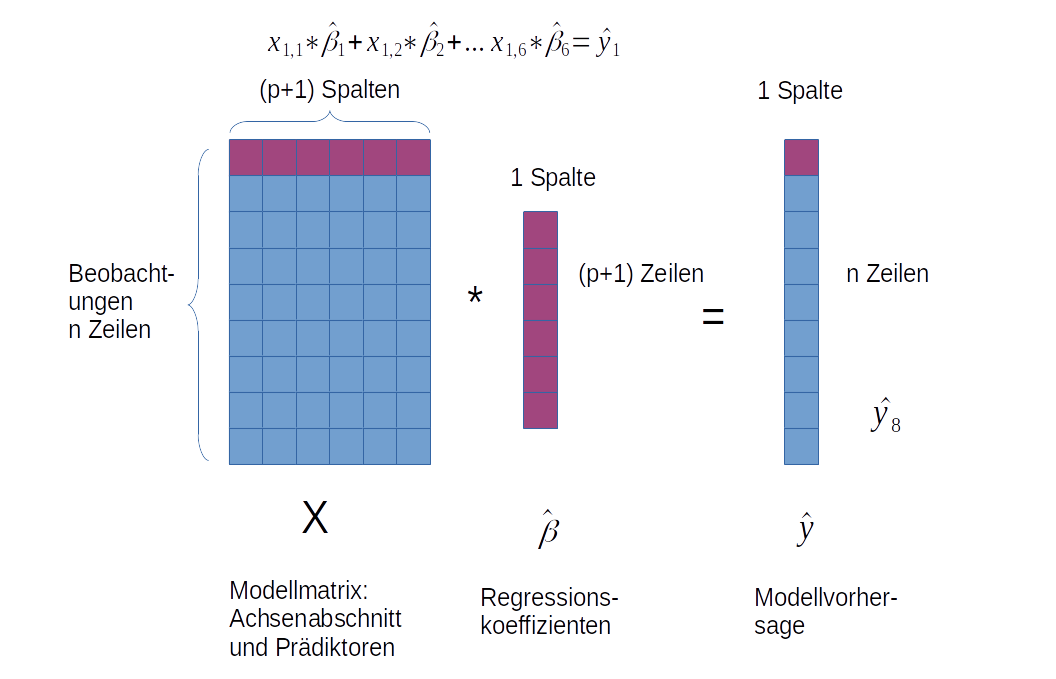
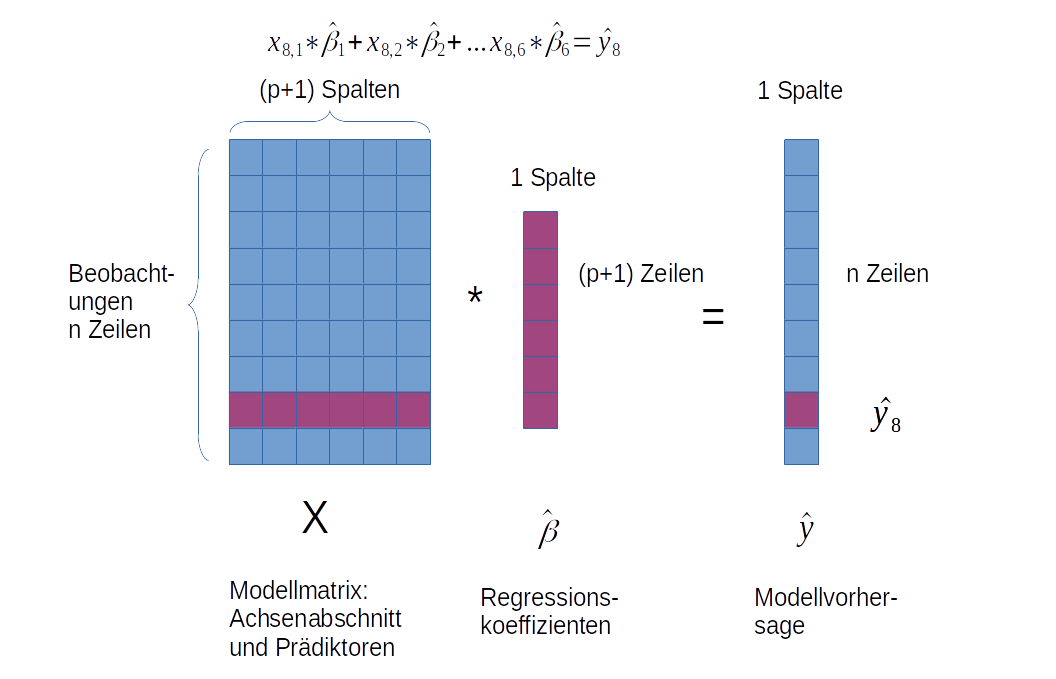
12.1.2 Annahmen

Folgende Annahmen werden bei Verwendung des linearen Modells getroffen:

• Normalverteilung
• Homogenität
• Unabhängigkeit
• Fehlerfrei gemessene Prädiktoren

12.1.2.1 Annahme hinsichtlich des Fehlerterms der unabhängigen Variablen

Die Annahmen der Normalverteilung, der Homogenität und der Unabhängigkeit betreffen den Fehlerterm und nicht die Verteilung der unabhängigen Variablen. Dies ist ein oft gemachter Fehler. Das lineare Modell geht davon aus, dass es einen strukturellen Zusammenhang zwischen Response und Prädiktoren gibt. Um diesen im Mittel korrekten Zusammenhang gibt es nun Schwankungen - z.B. durch Messungenauigkeiten. Die Annahme der Normalität betrifft nur diesen Schwankungsterm. Wir gehen beim linearen Modell davon aus, dass der Fehlerterm durch eine Normalverteilung beschrieben werden kann. Weiterhin gehen wir davon aus, dass die Normalverteilung den Mittelwert 0 (die Fehler mitteln sich aus) und eine konstante Varianz beschrieben werden kann (Annahme der Homogenität). Es macht nach der Annahme also keinen Unterschied hinsichtlich der Größe des erwarteten Fehlers, ob wir diesen für einen sehr kleinen, mittleren oder großen Wert des Response betrachten (s. Abbildung 12.3 und 12.4).

Die Annahme der Homogenität ist also: \(\sigma_1^2 = \sigma_2^2 = \ldots = \sigma^2\), sprich die Varianz ist für jede Beobachtung gleich.

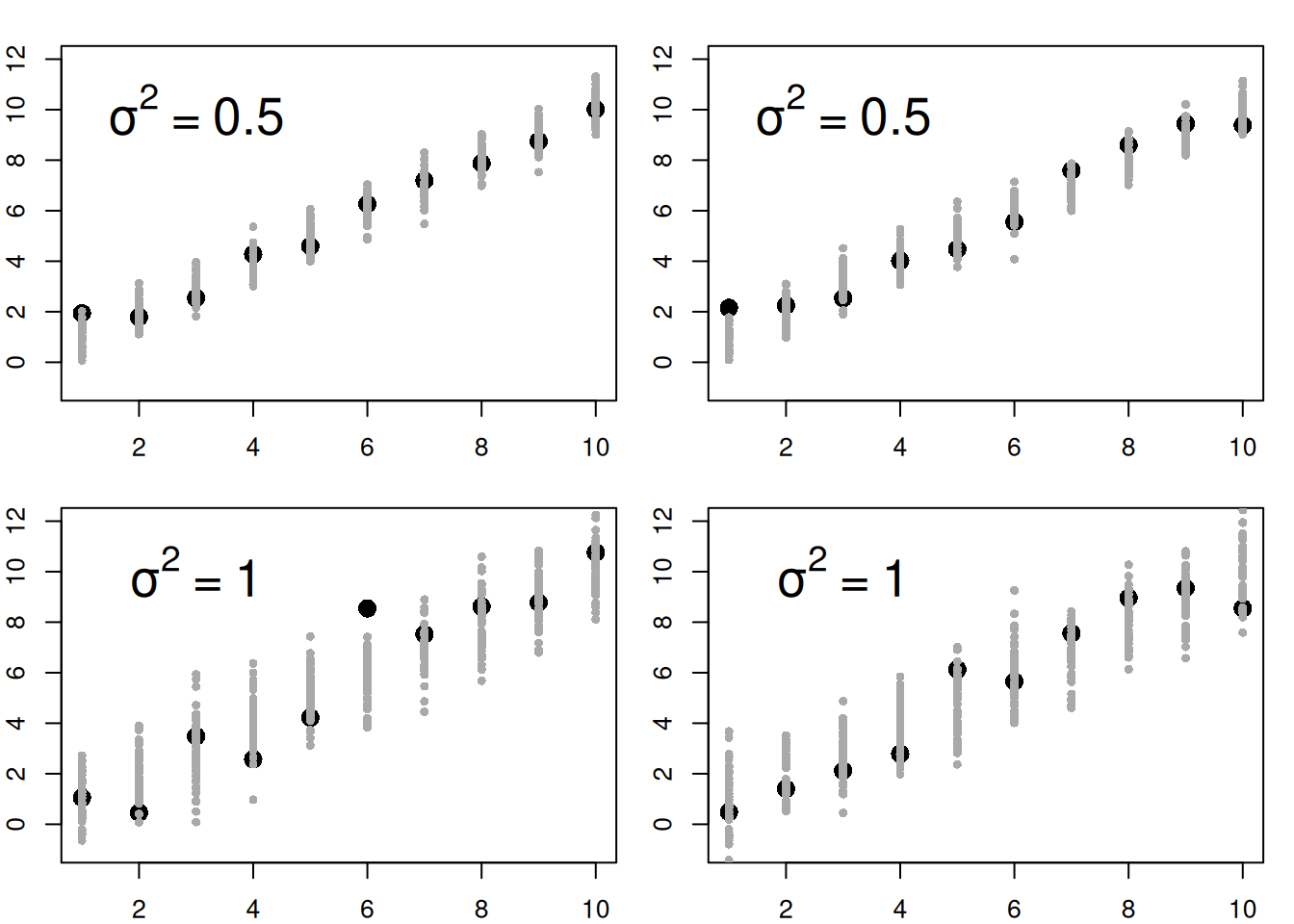
Figure 12.3: Annahme Fehlerterm lineares Model (1).Die Annahme eines normalverteilten Fehlerterms geht davon aus, dass der strukturelle Zusammenhang (hier eine Gerade) von einem weißem Rauschen überlagert wird. Die Wahrscheinlichkeit der Abweichung wird dabei von einer Normalverteilung mit Mittelwert 0 und fixer Varianz beschrieben. Die Abbildung zeigt in schwarz jeweils eine realisierte (beobachtete) Abweichung und in grau weitere mögliche Abweichungen. Linke und rechts werden jeweils verschiedene Realisierungen gezeigt.

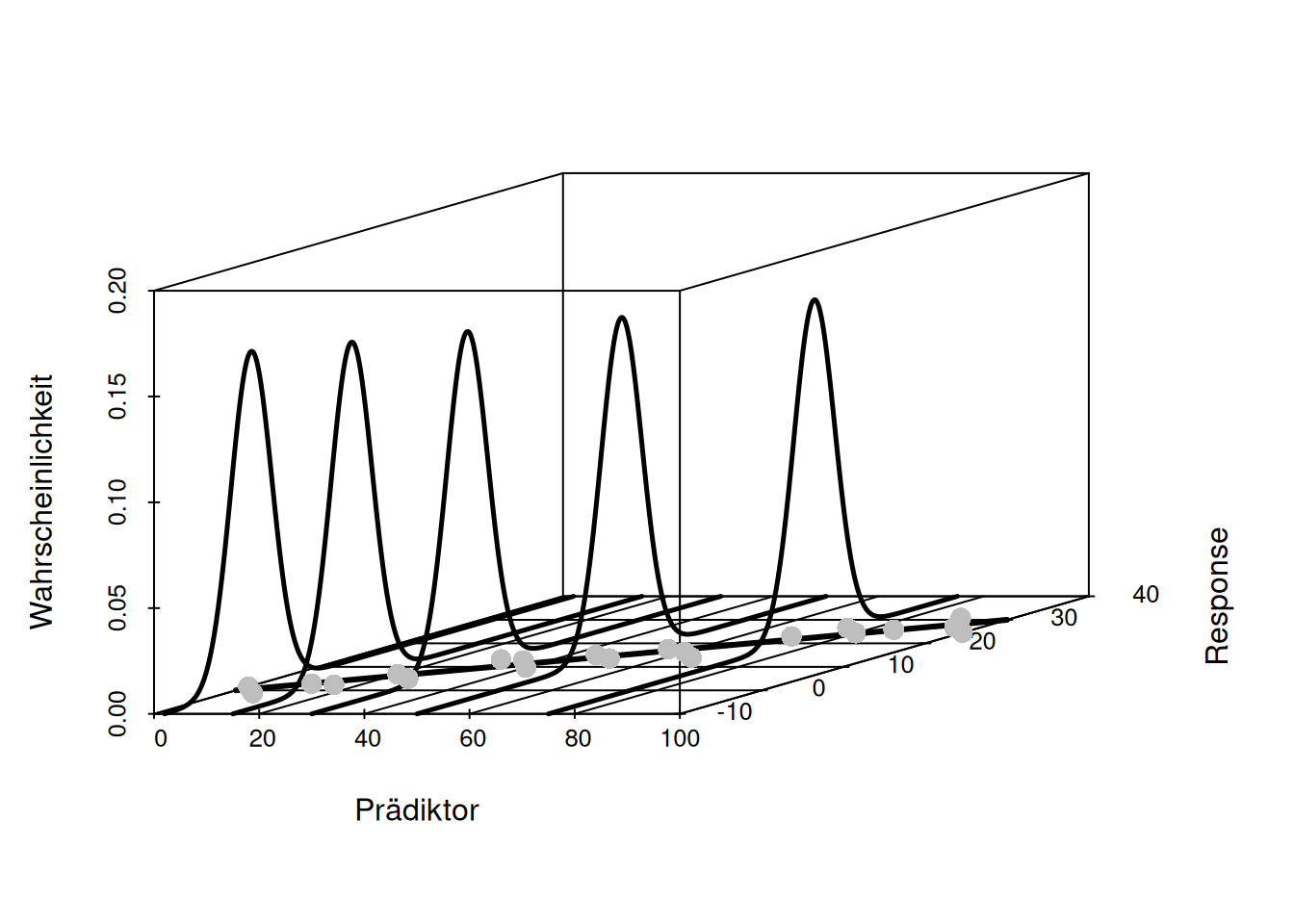
Figure 12.4: Annahme Fehlerterm lineares Model (2). Das lineare Modell unterstellt einen normalverteilten Fehlerterm um den strukturellen Zusammenhang zwischen Response und Prädiktor. Die Annahme der konstanten Varianz führt dazu, dass die Normalverteilung, die den Fehler beschreibt über den gesamten Wertebereich von y gleich ist.

Die Annahme der Unabhängigkeit besagt, dass sich die Fehler einzelner Beobachtungen nicht beeinflussen. Es gibt in der Praxis zahlreiche Fälle, bei denen diese Annahme nicht erfüllt ist. Hierzu zählen zeitlich autokorrelierte Daten, wie sie oft bei Zeitreihen auftreten, räumliche Autokorrelation durch die Beeinflussung der Nachbarn oder hierarchisch strukturierte Daten (z.B. die wiederholte Befragung der gleichen Person).

Es gibt entsprechende Ansätze, um mit Verletzungen der Annahmen umzugehen, z.B.:

• nicht normalverteilter Fehlerterm: generalisierte Lineare Modelle (GLM)
• Heteroskedastizität (nicht konstante Varianz des Fehlerterms): Sandwich Operator, ggf. GLM z.B. bei Zähldaten
• korrelierter Fehlerterm: generalized least squares (GLS, verallgemeinerte Kleinste Quadrate Methode), gemischte (generalisierte) lineare Modelle

12.1.2.2 Fehlerfrei gemessene Prädiktoren

Das lineare Modell geht davon aus, dass nur der Response fehlerbehaftet ist und die Prädiktoren ohne Fehler (bzw. mit vernachlässigbarem Fehler) gemessen wurden. Dies ist z.B. bei der Korrelation anders, bei der Unsicherheit bei allen beteiligten Variablen angenommen wird.

Falls die Annahme verletzt ist, kann man Regressionsmodell vom Typ II anwenden.

Wie in Abbildung 12.5 zu sehen, unterscheidet sich der bei beiden Ansätzen durchaus. Da bei der Typ II Regression auch die Abweichung der Punkte in x-Richtung berücksichtigt wird, ist die Steigung der Ausgleichsgeraden hier geringer als bei der Typ I Regression, bei der nur die Abweichung der Beobachtungen von der Ausgleichsgeraden in y-Richtung berücksichtigt wird.

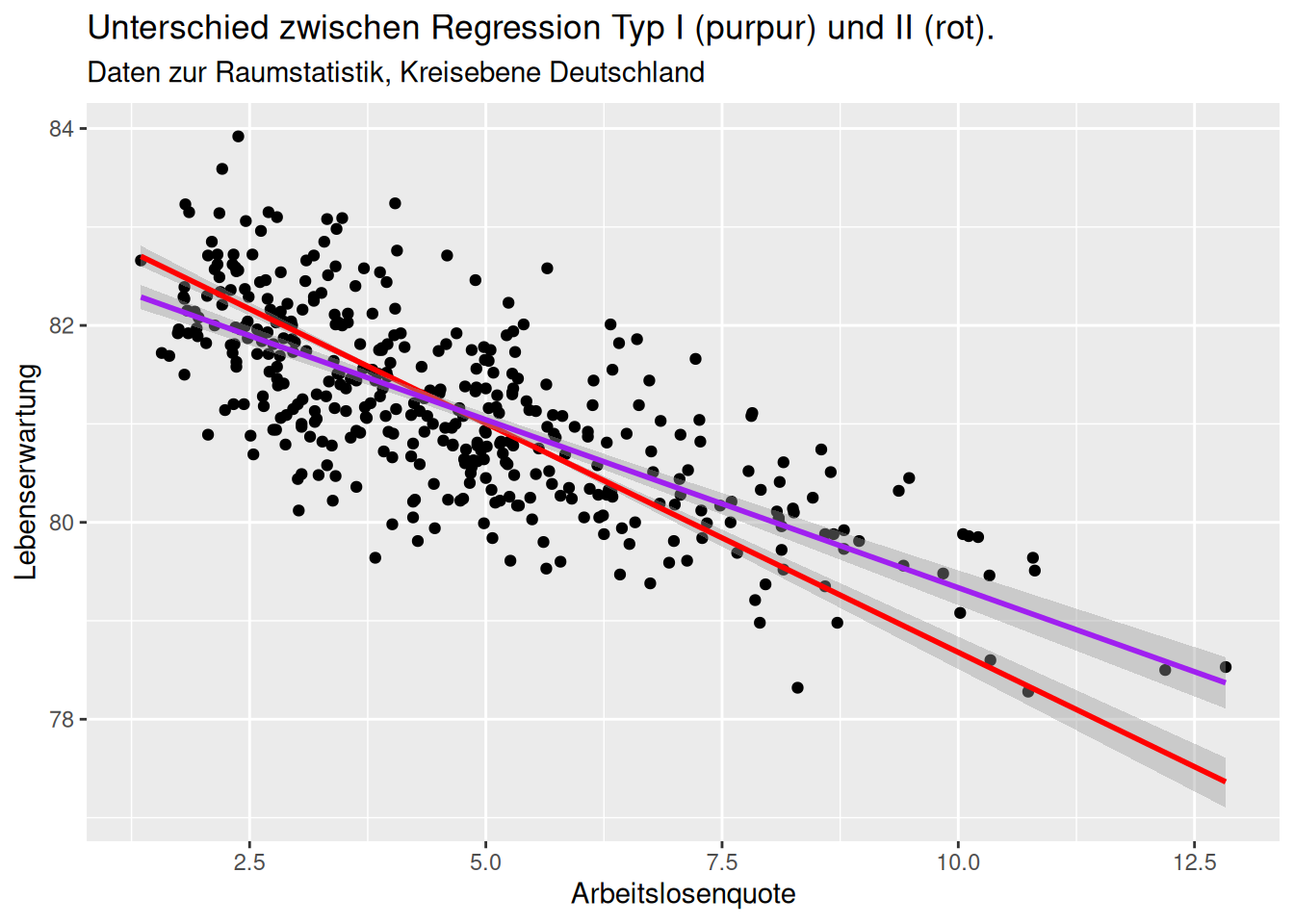
Figure 12.5: Unterschied Regression Typ I und II. Beim Fehler Typ I wird angenommen, dass es nur einen Fehler hinsichtlich der Erfassung von y gibt, nicht hinsichtlich des Prädiktors. Beim Fehler Typ II geht man (wie bei der Korrelation) davon aus, dass sowohl der Response als auch die Prädiktoren mit Fehlern bei der Erfassug behaftet sind.

12.1.3 Weitere Aspekte

Weiterhin lohnt es sich, vor dem Durchführen der Regression folgende Aspekte zu überprüfen:

• Fehlende Werte - gibt es beim Response oder bei den Prädiktoren fehlende Werte?
• Ungewöhnliche Werte - gibt es ungewöhnlich große oder kleine Beobachtungen?
• Sind einzelne Prädiktoren voneinander abhängig / kollinear?
• Treten Nullwerte gehäuft auf? Dies kann auf ein Erfassungsproblem hindeuten.

Die Überprüfung kann mittels summary oder ggplot (Scatterplotmatrix, Histogramme) erfolgen, für die Kollinearität bietet sich cor oder corrplot an.

12.1.4 Maximum-likelihood Schätzung beim linearen Modell

Die folgenden Ausführungen gehen mehr in mathematische Details - diese können ggf. übersprungen werden.

Wir haben uns bereits im Kapitel Verteilungen mit der ML-Schätzung von Verteilungs-Parametern beschäftigt. Dieses Prinzip kommt auch beim Regressionsmodell zur Anwendung. Hier geht es darum, die besten Parameter \(\beta\) zu schätzen, so dass das Modell - bei gegebener Modellstruktur - am besten zu den Daten passt. Wir suchen also die Parameter \(\hat{\beta}\) mit der höchsten Likelihood bei gegebenen Daten. Gegeben ist die strukturelle Modellkomponente (die Prädiktoren) und die oben genannten Annahmen des linearen Modells. Wir verwenden aus numerischen Gründen wieder die log-Likelihood (den Logarithmus aus der Likelihood) \(\mathcal{L}\).

Unter den Annahmen des linearen Modells kann die Verteilung des Response \(y\), gegeben \(X\) (conditional on) wir folgt angegeben werden:

\(y|X \widetilde{~} \mathcal{N}(X\beta, \sigma^2I)\)

Die log-Likelihood für ein lineares Modell für gegebenen Daten berechnet sich wie folgt:

\[ \begin{align} \mathcal{L}(\beta, \sigma^2 | X ) &= ln( \frac{1}{(2\pi)^2 \sqrt{|\sigma^2I|} } e^{(y-X\beta)^T(\sigma^2I)^{-1}(y-X\beta)}) \\ & = -\frac{n}{2}ln(2\pi)- \frac{n}{2}\sigma^2- \frac{1}{2\sigma^2}(y-X\beta)^T(y-X\beta) \end{align} \]

Um die ML Schätzer für die Gleichung zu finden müssen wir die partiellen Ableitungen für\(\beta\) und \(\sigma^2\) bestimmen:

\[ \frac{\delta\mathcal{L}}{\delta\beta^T} = -\frac{1}{2\sigma^2}(-2X^Ty + X^TX\beta) = 0 \implies \hat{\beta}=(X^TX)^{-1}X^Ty\] \[ \frac{\delta\mathcal{L}}{\delta\sigma^2} = - \frac{n}{2\sigma^2}+\frac{1}{2\sigma^4} (y-X\beta)^T(y-X\beta) = 0 \implies \hat{\sigma}^2=\frac{1}{n}(y-X\beta)^T(y-X\beta) \]

Der Operator \(^T\) gibt dabei die transponierte Matrix an, also die Matrix, bei der Zeilen und Spaltenvektoren vertauscht sind.

Dies entspricht exakt dem Ergebnis, wenn wir von der Methode der kleinsten Quadrate (ordinary least square - OLS) her kommen, bei dem die Parameter so geschätzt werden, dass die Summe der Fehlerquadrate minimiert wird.

\[\sum \epsilon_i^2 = \epsilon^T \epsilon = (y-X\beta)^T(y-X\beta)\] Ableiten nach \(\beta\) liefert:

\[\frac{\delta \sum \epsilon_i^2 }{\delta \beta^T} = -2X^T (y-X\beta) = 0 \]

\[ \implies X^TX\hat{\beta} = X^Ty \implies \hat{\beta} = (X^TX)^{-1}X^Ty \]

OLS ist also unter den Annahmen des linearen Modells nichts weiter als die ML-Schätzung der Parameter.⁵¹

12.1.5 Hat-Matrix

Durch Umformen der Gleichung erhalten wir die sogenannte Hat-Matrix oder Projektionsmatrix, die uns im Bereich der Modell-Diagnose noch begegnen wird:

\[ \begin{align} \hat{\beta} &= (X^TX)^{-1}X^Ty \\ X\hat{\beta} &= X(X^TX)^{-1}X^Ty \\ \hat{y} &= Hy \end{align} \] \(X\hat{\beta}\) ergibt die durch das Modell geschätzten Werte für den Response. Dies entspricht der Multiplikation der Hat-Matrix mit den beobachteten Response Werten. Die beobachtenen Werte sind \(Y\), die durch das Modell vorhergesagten Werte \(\hat{Y} = X\hat{\beta}\).

Die Hat Matrix ist die orthogonale Projektion von \(y\) in den Vektorraum, der durch \(X\) aufgespannt wird. Die gefitteten Werte sind: \[\hat{y} = Hy = X\hat{\beta}\] , die Residuen \[\hat{\epsilon} = y - X\hat{\beta} = y - \hat{y} = (I-H)y\]

Die Summe der Quadrate der Residuen (residual sum of squares (RSS)) entspricht \[\hat{\epsilon}^T \hat{\epsilon} = y^T (I-H)^T (I-H)y = y^T (I-H)y\].

Die Varianz von \(\hat{\beta}\) ist \((X^T X)^{-1}\sigma^2\), falls die Annahme \(var (\epsilon) = \sigma^2 I\) erfüllt ist. Der Schätzer der Varianz ist wie folgt definiert:

\[\hat{\sigma}^2= \frac{\hat{\epsilon}^T \hat{\epsilon}}{n-p} = \frac{RSS}{n-p}\]

Wobei \(n-p\) die Freiheitsgrade (degrees of freedom) des Modells angibt. Dabei gibt \(n\) die Anzahl der Datenpunkte an, die für die Schätzung des Modells benutzt wurden und \(p\) gibt die Anzahl der Parameter an, die aus den Daten geschätzt werden.

12.1.6 Modellvorhersagen

Nachdem das Modell gefittet wurde (also die Parameter geschätzt wurden), kann das Modell benutzt werden, um Werte des Response für unbekannte Situationen vorherzusagen, falls die Prädiktoren bekannt sind. Man sollte dabei allerdings stets darauf achten, dass das Modell nur für den Bereich der Prädiktoren in den Trainingsdaten gefittet wurde. Für Wertebereiche außerhalb dieses Bereiches (Extrapolation) sind Vorhersagen nicht zuverlässig.

12.2 Univariates lineares Modell am Beispiel von Temperaturdaten

Wir verwenden wieder die bekannten Temperaturstationen.

Einlesen der Daten:

temp <- read.table("data/temperatur.csv", header=TRUE)

Der Datensatz enthält weltweit Temperaturmeßstationen zusammen mit der Höhe der Meßstation (müNN), der Breiten und Längen der Station (LAT, LON), dem Ländernamen “CNTRY_NAME” sowie dem langjährigen Mittelwert der Jahrestemperatur (YEAR). Alle anderen Werte wollen wir hier ignorieren.

Zunächst erzeugen wir eine Teilmenge (ein subset) der Daten - wir sind zunächst nur an den Stationen interessiert, die in Deutschland liegen.

temp.de <- subset(temp, CNTRY_NAME == "Germany")

Nun wollen wir die Daten zunächst einmal Plotten:

ggplot(temp.de, aes(x= ELEV, y = YEAR)) +
  geom_point() + 
  ylab("Jahresmitteltemperatur [°C]") +
  xlab("Höhe [müNN]")+
  labs(title = "Temperaturstationen in Deutschland")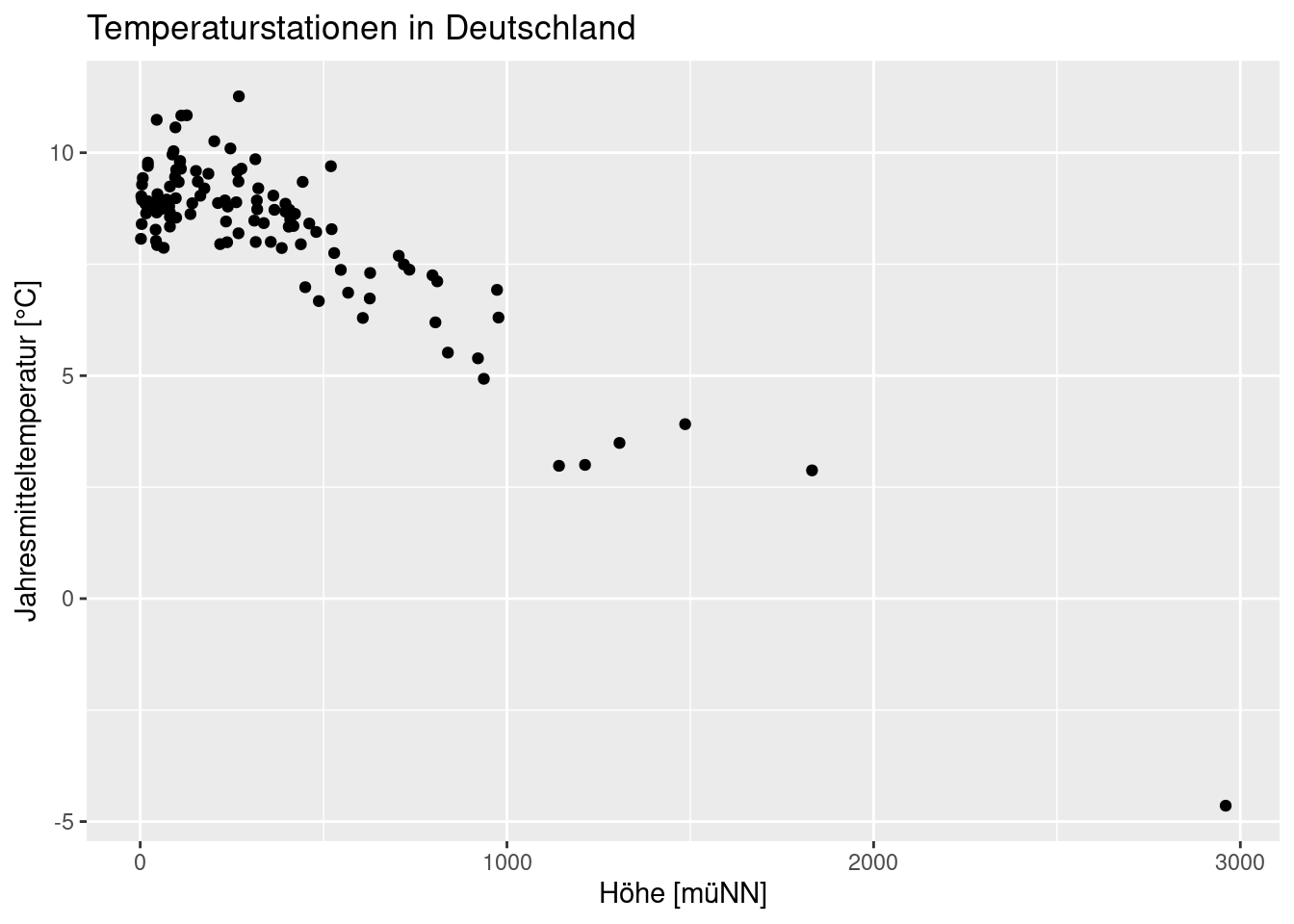

12.2.1 Fitten und Interpretieren eines linearen Modells

Nun fitten wir ein lineares Modell, dass die mittlere Jahrestemperatur in °C durch die Höhe der Station in m üNN erklärt. Das fitten erfolgt mittels lm. Der Befehl erhält eine Formel (formula Objekt), bei dem YEAR durch ELEV erklärt werden soll. Die so benannten Objekte sollen im data.frame temp.de gesucht werden. Wir speichern das Regressionsobjekt in einer Variable g und lassen uns mittels print die Regressionskoeffizienten ausgeben:

g <- lm(YEAR ~ ELEV, data=temp.de)
print(g)

## 
## Call:
## lm(formula = YEAR ~ ELEV, data = temp.de)
## 
## Coefficients:
## (Intercept)         ELEV  
##    9.717838    -0.004194

Was bedeutet dies? Die mittlere Temperatur an einer Station auf Meeresspiegelhöhe beträgt 9,719 °C. Mit zunehmender Höhe fällt die Temperatur um 0,42°C je 100 Höhenmeter.

Wir können uns dies auch graphisch anzeigen lassen, indem wir abline benutzen um die Regressionslinie über den Scatterplot zu legen. Hierzu verwenden wir coefficients um eine Vektor der geschätzten Modellparameter zu extrahieren und geom_abline um über diese Koeffizienten Achsenabschnitt und Steigung der Geraden anzugeben. Diese Art die Regressionsgerade zu zeichnen funktioniert nur bei einem univariaten Modell. Bei mehreren Prädiktoren kann man den Zusammenhang nicht mehr so einfach angeben.

ggplot(temp.de, aes(x= ELEV, y = YEAR)) +
  geom_point() + 
  ylab("Jahresmitteltemperatur [°C]") +
  xlab("Höhe [müNN]")+
  labs(title = "Temperaturstationen in Deutschland") +
  geom_abline(intercept = coefficients(g)[1], 
              slope =coefficients(g)[2] )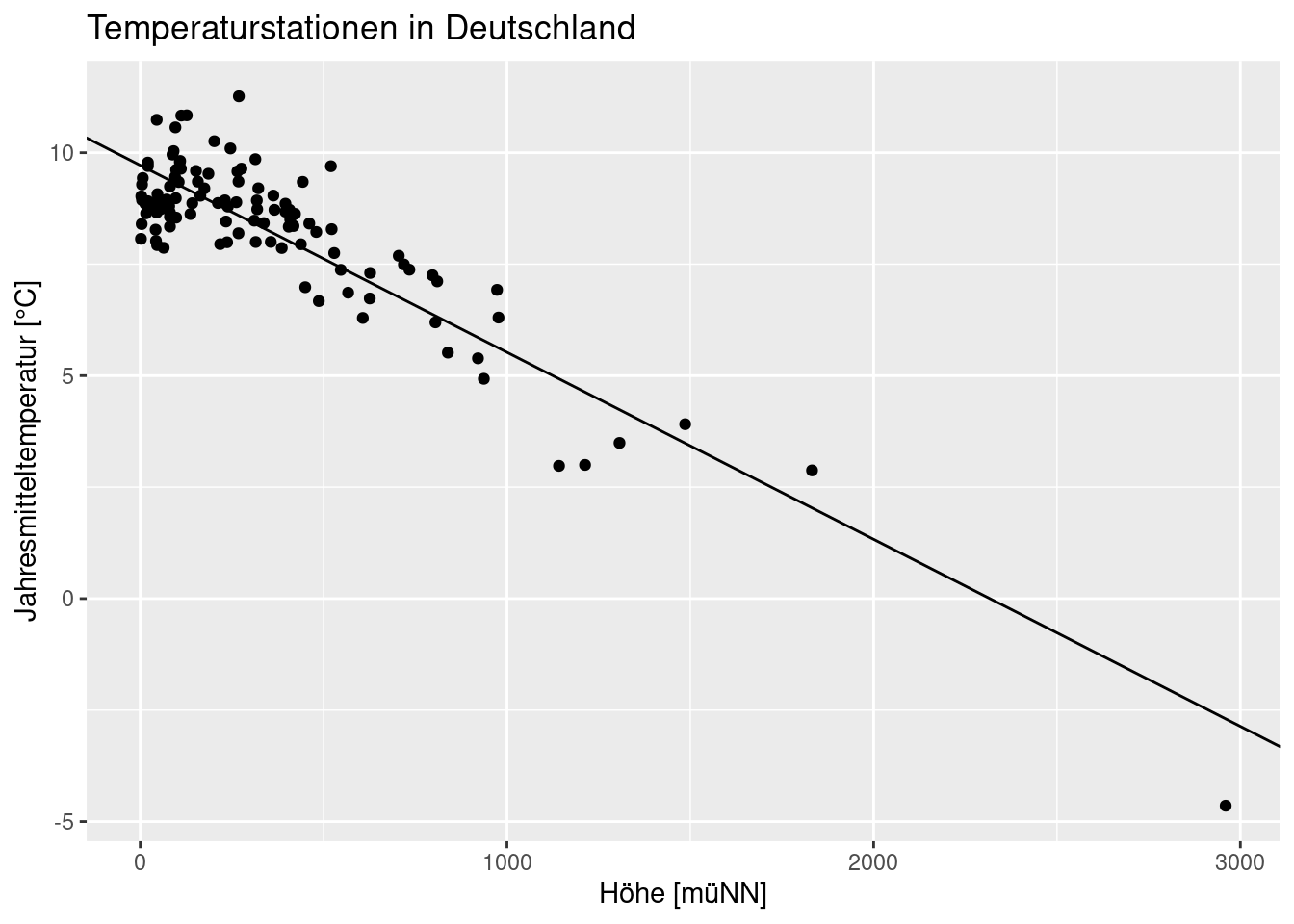

Nun wollen wir uns etwas intensiver mit der Interpretation des Regressionsmodells beschäftigen indem wir summary am Regressionsobjekt aufrufen:

summary(g)

## 
## Call:
## lm(formula = YEAR ~ ELEV, data = temp.de)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.9501 -0.7122  0.0641  0.6232  2.6751 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  9.7178381  0.1066528   91.12   <2e-16 ***
## ELEV        -0.0041944  0.0001965  -21.34   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.8832 on 114 degrees of freedom
## Multiple R-squared:  0.7998, Adjusted R-squared:  0.7981 
## F-statistic: 455.5 on 1 and 114 DF,  p-value: < 2.2e-16

Wir erhalten nun deutlich mehr Informationen. Diese betreffen die Modellgüte, Schätzer, Standardfehler und Signifikanztests der Modellparameter sowie ein Test des Gesamtmodells. Wir wollen uns Schritt für Schritt mit den einzelnen Elementen beschäftigen.

12.2.2 Güte des Modells anhand von \(R^2\)

Auch wenn wir die bestmöglichen Parameter geschätzt haben (bei gegebenen Modellstruktur und gegebenen Annahmen), ist die keine Garantie dafür, dass das Modell die Daten adäquat beschreibt. Wir benötigen also Maße um die Modellgüte zu beschreiben.

Ein beliebtes Maß hierfür ist \(R^2\). Sein Wertebereich reicht von 0 bis 1⁵² - 1 gibt einen perfekten Zusammenhang an, bei 0 ist das Modell nicht besser als das sogenannte Nullmodell.

Als Nullmodell wird das einfachste denkbare Modell verwendet: es wird einfach der Mittelwert des Response verwendet, um neue Werte vorherzusagen. Der Vergleich erfolgt dann anhand des Vergleichs der Summe der Abweichungsquadrate:

\[R^2 = 1 - \frac{RSS}{TSS}\] \(RSS\) (Residual Sums of Squares) ist die Summe der quadrierten Abweichungen zwischen Modellvorhersage und beobachtetem Wert des Response. \(TSS\) sind die Abweichungsquadrate für das Nullmodell.

Die Abweichungen zwischem vorhergesagtem und beobachtetem Wert nennt man auch Residuen \(\epsilon_i\). Wenn die Residuen des mittels ML gefitteten Modells kleiner sind, als die des Nullmodells (Abbildung Residuen ML- und Null-Modell), kann man davon ausgehen, dass das ML Modell besser ist. Der genaue Vergleich erfolgt wie oben angegeben anhand der Abweichungsquadrate - welche sich ja aufgrund der Likelihood als Qualitätkriterium ergeben haben.

## Warning: Use of `temp.de$YEAR` is discouraged.
## ℹ Use `YEAR` instead.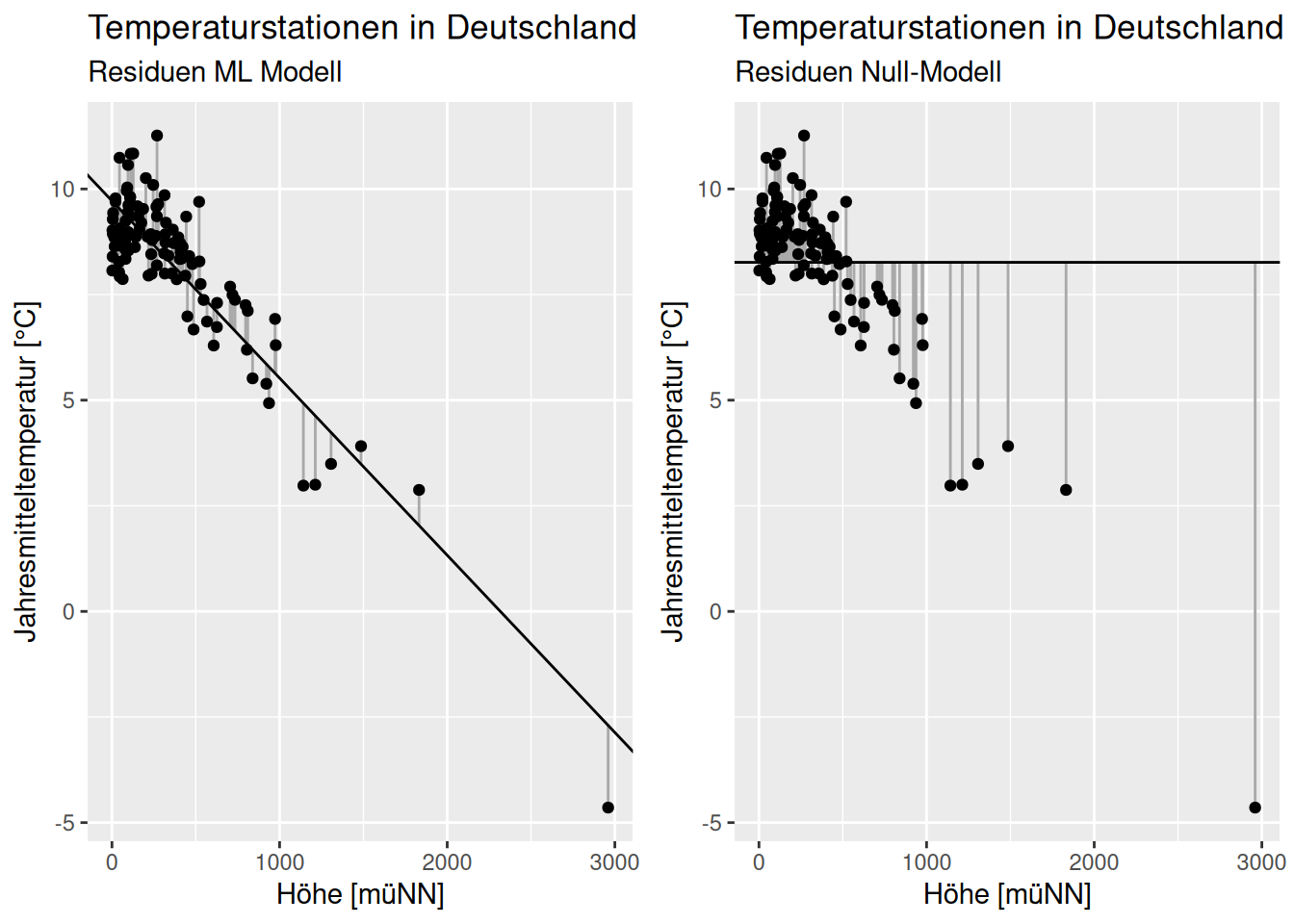

Figure 12.6: Residuen des mittels ML geschätzen Modells und des Nullmodells. Die Abweichungen in y-Richtung werden beim ML fitten im linearen Model jeweils quadriert.

I.d.R. fällt der Vergleich leichter, wenn man die Residuen plottet. Diese lassen sich mittels residuals(model) extrahieren, ebenso wie die gefitteten Werte mittels fitted(model).

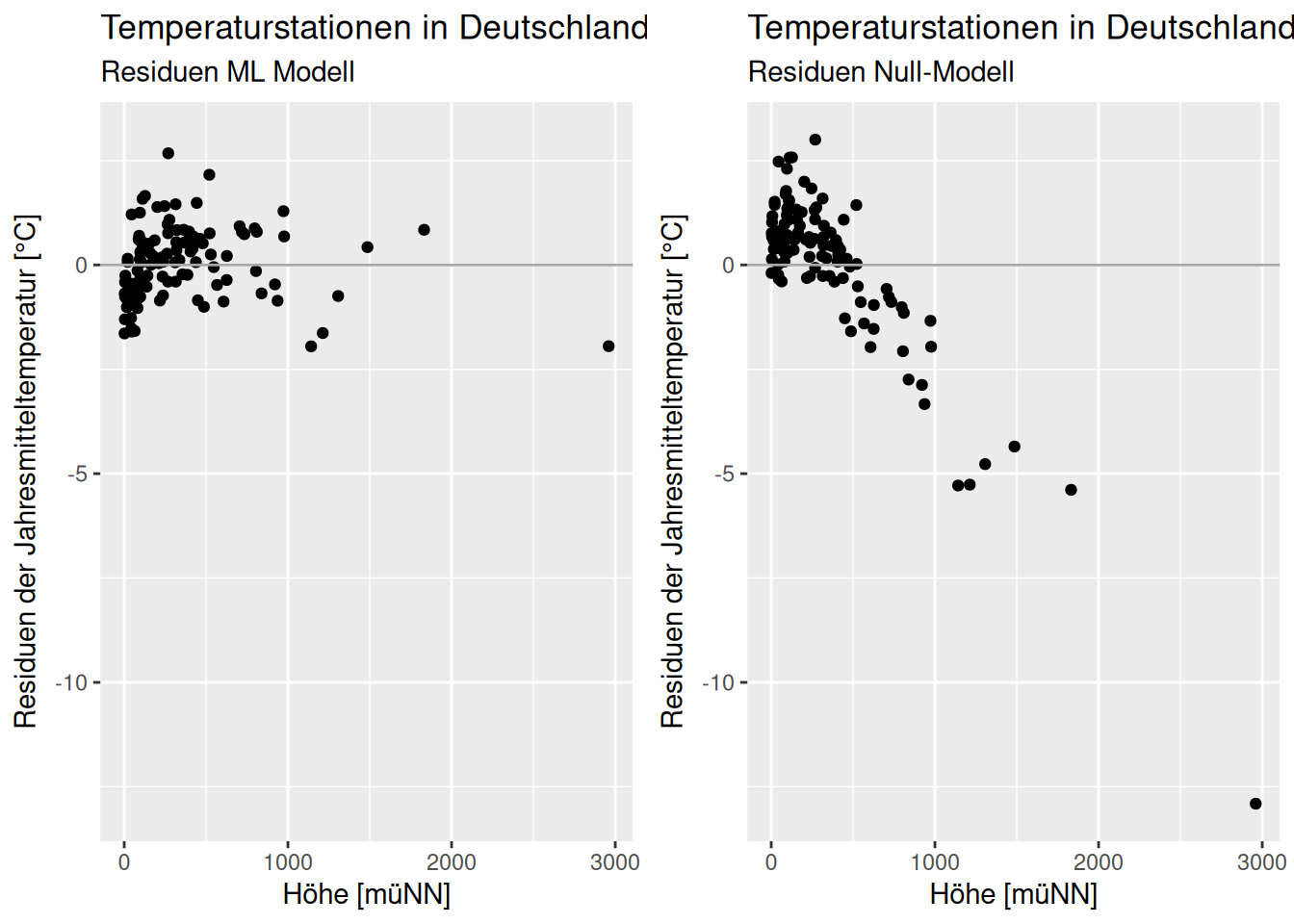
Figure 12.7: Residuen des mittels ML geschätzen Modells und des Nullmodells. Auf der y-Achse werden die Residuen aufgetragen. Der Wertebereich beim ML-Modell ist hier deutlich kleiner als beim Nullmodell.

Man sieht hierbei, dass die Varianz der Residuen beim ML-Modell deutlich kleiner ist, als beim Nullmodell. Dies führt zu einer weiteren Interpretation von \(R^2\) beim linearen Modell: es gibt die erklärte Varianz an. Ein \(R^2\) von 0.8 gibt z.B. an, dass 80% der Varianz im Response durch das Modell erklärt werden und 20% Varianz unerklärt bleiben.

Dies sieht man, wenn man die Varianz der Residuen des ML Modells durch die Residuen des Null Modells teilt:

var(temp.de$residEle)/var(temp.de$residMean)

## [1] 0.2001763

Zurück zu summary.

Wir sehen, dass die Modell Güte mit einem \(R^2\) von 0.8 recht gut ist.

Es werden zwei verschiedene \(R^2\)-Werte angegeben: Multiple R-squared und Adjusted R-squared. Zu den Unterschieden kommen wir, sobald wir uns mit dem Modellvergleich beschäftigen.

12.2.3 Modellkoeffizienten

Weiterhin liefert summary eine Übersicht über die Regressionskoeffizienten. Für jeden Eintrag der Modellmatrix erhalten wir den Schätzer (\(\hat{\beta}\)), den Standardfehler des Schätzers sowie das Ergebnis eines zweiseitigen t-Test mit der Nullhypothese das der Regressionskoeffizient gleich Null ist sowie die zugehörige Test-Statistik.

summary(g)$coef

##                 Estimate   Std. Error   t value      Pr(>|t|)
## (Intercept)  9.717838136 0.1066528214  91.11656 2.439644e-108
## ELEV        -0.004194411 0.0001965295 -21.34240  1.260740e-41

Im Beispiel sind die Regressionskoeffizienten wie folgt zu interpretieren: auf Meeresspiegelniveau wird die mittlere Jahrestemperatur für die Stationen in Deutschland auf 9.72°C geschätzt. Je 100 Höhenmeter fällt dabei die Temperatur um 0.0042°C. Die Koeffizienten definieren - wie oben gezeigt - eine Geradengleichung.

Die Test-Statistik errechnet sich wie beim t-Test für den Vergleich einer Stichprobe mit Referenzwert, angegeben einfach als Schätzer geteilt durch den Standardfehler. Z.B. für Regressionskoeffizienten für Geländehöhe:

-0.0041944 / (0.0001965)

## [1] -21.34555

2 * pt(-21.34555, df= 114)

## [1] 1.243851e-41

Wir sehen für das gefittete Modell, dass der Standardfehler für den Koeffizienten für den Effekt der Höhe deutlich kleiner ist als der Regressionskoeffizient (s. auch Abbildung 12.8). Als Daumenregel gilt: wenn der Koeffizient +/- 2 * den Standardfehler Null nicht einschließt, ist der Koeffizient auf dem 5% Niveau signifikant von Null verschieden.⁵³ Dies können wir auch aus dem p-Wert ablesen, der hier sehr klein ist. Die Wahrscheinlichkeit, dass wir die Nullhypothese, dass der Regressionskoeffizient gleich 0 ist, fälschlicherweise ablehnen ist sehr gering. Der Test auf die Nullhypothese, dass der Regressionskoeffizient gleich 0 ist erfolgt mittels eines t-Tests ((s. hier).

Beim Achsenabschnitt ist der t-Test nur von eingeschränktem Interesse, da der Achsenabschnitt Null sein kann. Für die anderen Regressionskoeffizienten zeigt eine hohe Irrtumswahrscheinlichkeit an, dass der Effekt sowohl negativ als auch positiv sein kann- mit andern Worten ist der Effekt nicht klar spezifiziert, weswegen man in vielen Fällen den Prädiktor aus dem Modell entfernt.

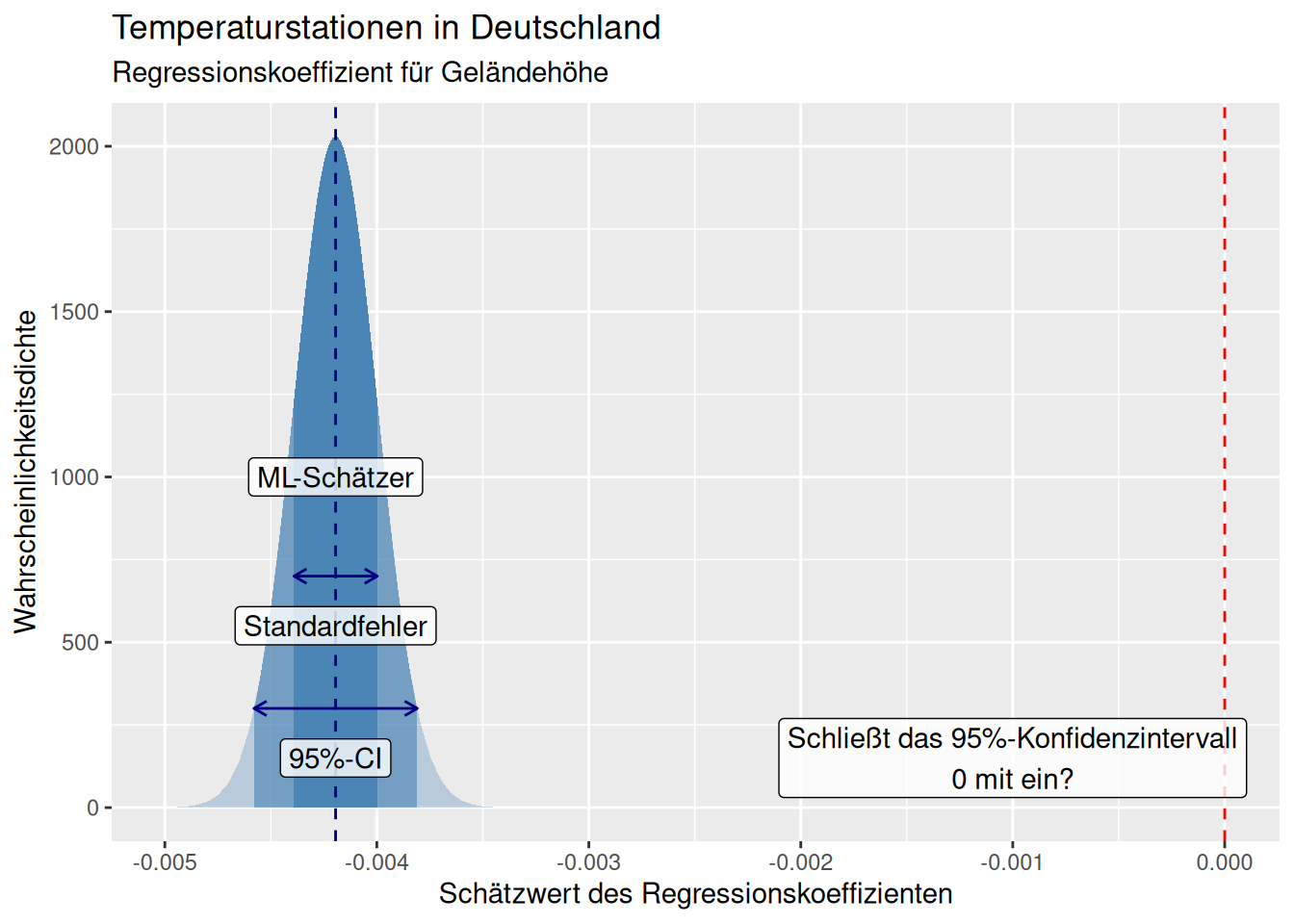
Figure 12.8: Geschätzer Regressionskoeffizient für den Effekt der Geländehöhe auf die Jahresmitteltemperatur für die historischen deutschen Klimastationen. Die Maximum Likelihood Schätzung der Koeffizienten erfolgt unter Unsicherheit. Die Unsicherheit wird unter der Annahme das der zentrale Grenzwertsatz greift durch eine Normalverteilung mit dem Standardfehler als Standardabweichung und dem Schätzwert als Mittelwert beschrieben. Zusätzlich ist das 95%-Konfidenzintervall angegeben, dass sich näherungsweise als ML-Schätzer +/- 1,96 * Standardfehler ergibt. Es ist klar zu sehen, dass dieses 0 nicht mit einschließt und der Schätzer des Regressionskoeffizienten damit signifikant von Null verschieden ist.

Weiterhin erhalten wir Informationen zu den Freiheitsgraden des Modells, hier 114 und zu \(\hat{\sigma}_y\), also der Standardabweichung der Residuen⁵⁴, hier 0.8832387 °C.

Es lohnt sich auch, einen Blick auf die Verteilung der Residuen zu werfen, die in unserem Beispiel einigermaßen symmetrisch um 0 verteilt sind - was ein erstes Indiz ist, dass die Annahme normalverteilter Residuen erfüllt sein könnte.

Der F-Test und die zugehörige Test-Statistik beziehen sich auf den Vergleich der Residuenvarianz des gefitteten Modells mit der Residuenvarianz des Nullmodels (das nur den Achsenabschnitt enthält). Die Nullhypothese ist dabei, dass das Verhältnis 1 ist, also das gefittete Modell nicht überzufällig mehr Varianz im Response erklärt, als das Nullmodell, Als Freiheitsgrade des F-Tests wird einerseits die Anzahl der Parameter und andererseits die Freiheitsgrade des Modells verwendet.

pf(455.5, df1 = 1, df2 = 114, lower.tail = FALSE)

## [1] 1.260491e-41

Wir sehen auch, dass der F-Test auf Modellgüte, der das Modell mit einem Modell, das nur den Achsenabschnitt enthält anzeigt, dass das Modell signifikant besser ist. Der F-Test vergleicht dabei das gesamte Modell mit dem Nullmodell, während die t-Tests testen, ob der individuelle Koeffizient von Null verschieden ist.

12.2.4 Modellvorhersage

Um eine Vorhersage für neue, unbekannte Stationen und Orte vorzunehmen, brauchen wir einen data.frame, der die Werte, für die wir vorhersagen wollen enthält. Die Spalten müssen dabei exakt so benannt sein, wie im Regressionsobjekt. Dieser data.frame kann dann in predict benutzt werden, um mit Hilfe des gefitteten Regressionsmodells den erwarteten Wert für die angegebenen Werte der Prädiktoren zu schätzen.

Wir konstruieren des data.frame so, dass wir 100 gleichmäßig verteilte Werte zwischen 1 und 2500 erzeugen (besser wäre vom kleinsten bis zum größten beobachtetem Wert). Der Befehl seq liefert dabei die bei length.out angegebene Anzahl von Werten zwischen Start- und Endwert.⁵⁵

new.elev <- data.frame(ELEV=seq(from = 1, 
                                to= 2500, length.out = 100))
head(new.elev)

##        ELEV
## 1   1.00000
## 2  26.24242
## 3  51.48485
## 4  76.72727
## 5 101.96970
## 6 127.21212

Diesen data.frame, bei dem wir 100 Werte zwischen 1 und 2500 m erzeugen verwenden wir dann in predict. predict benötigt den data.frame (die Stellen, an denen vorhergesagt werden soll) und das Regressionsobjekt (das Modell, mit dem wir die Vorhersage durchführen wollen.) Anschließend fassen wir das Ergebnis mit den Höhenwerten, für die die Vorhersage gemacht worden ist, in einem neuen data.frame zusammen.

g.pred <- predict(g, newdata = new.elev)
preditionDE <- data.frame(elev = new.elev$ELEV,
                          predTemp = g.pred)

knitr::kable(head(preditionDE))

elev	predTemp
1.00000	9.713644
26.24242	9.607767
51.48485	9.501890
76.72727	9.396012
101.96970	9.290135
127.21212	9.184258

predict wertet hier einfach die Regressionsgleichung aus, in dem es die Werte im bei newdata angegebenen Felder in die Regressionsgleichung einsetzt.

Z.B. für ELEV = 101.96970:

coef(g)

##  (Intercept)         ELEV 
##  9.717838136 -0.004194411

9.717838136 + 101.96970 * -0.004194411

## [1] 9.290135

Wir können die vorhergesagten Werte auch in den Scatterplot eingügen. Hierzu zeichnen wir die original Werte als Punkte und legen die vorhergesagten Werte mittels lines darüber:

plot(YEAR ~ ELEV, data=temp.de, xlab="Höhe [m]", 
     ylab="Jahresmitteltemperatur [°C]", xlim=c(0,5000), las=1)
lines(predTemp~ elev, data=preditionDE,  pch=16, col="grey", cex=1)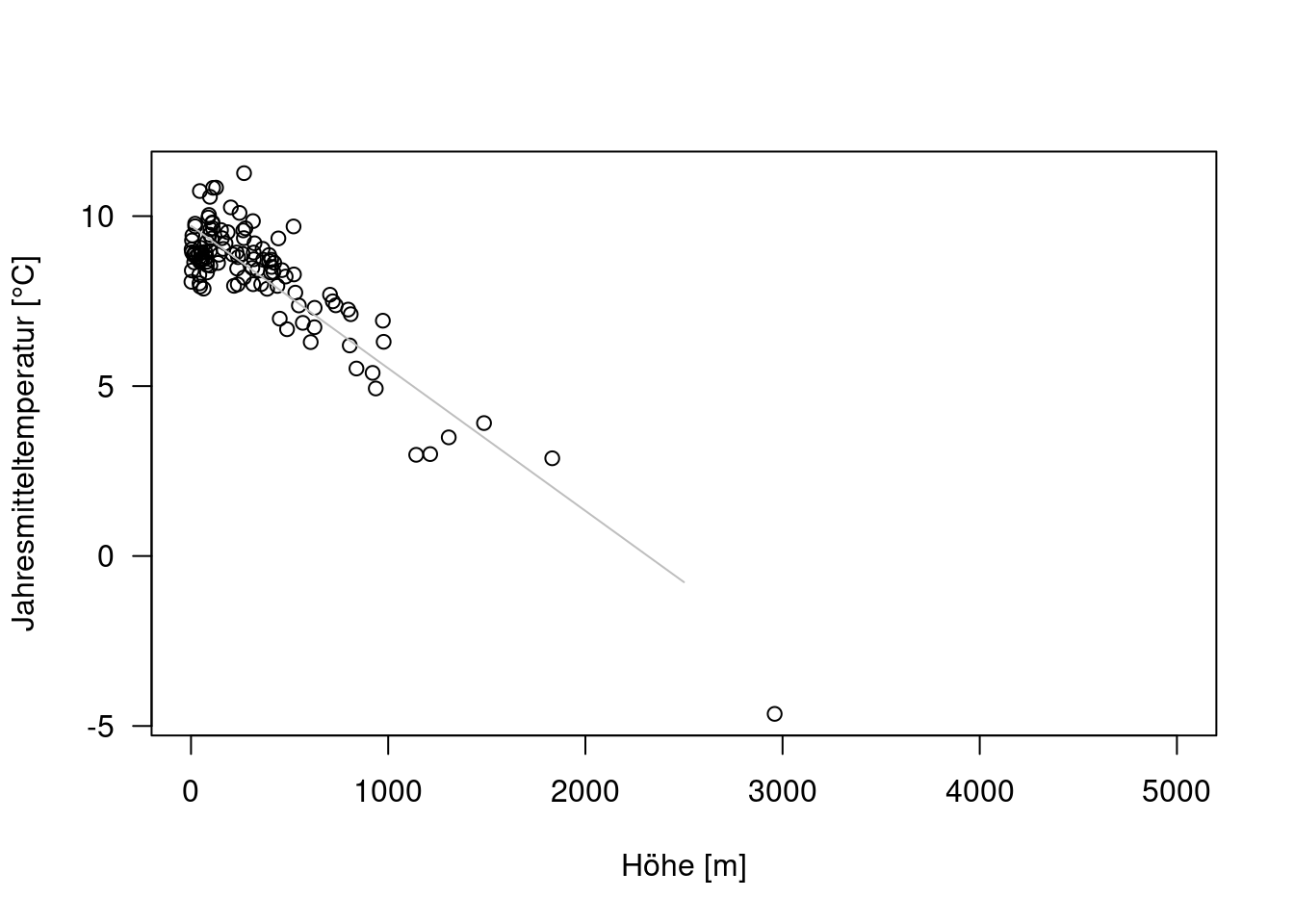

Das Ergebnis ist das gleiche, das wir mittels abline oder geom_abline erhalten hätten (s. oben im Beispiel mit ggplot). Allerdings lässt sich abline bzw. geom_abline nicht mehr sinnvoll verwenden, sobald mir mehr als eine erklärende Variable verwenden.

Abschließend noch einmal der gleiche Plot mittels ggplot. Man sollte sich klar machen, dass wir für insgesamt 100 Punkte Vorhersagen bekommen haben - da diese auf einer Geraden liegen, sehen wir dies nicht wirklich. Um dies zu verdeutlichen lege ich im folgenden noch die Punkte des Linienzuges über den Plot. Wir werden später sehen, dass wir die 100 Punkte benötigen, wenn wir Konfidenz- oder Vorhersageintervalle plotten wollen.

ggplot(temp.de, aes(x= ELEV, y = YEAR)) +
  geom_point() + 
  ylab("Jahresmitteltemperatur [°C]") +
  xlab("Höhe [müNN]")+
  labs(title = "Temperaturstationen in Deutschland") +
  geom_line(mapping = aes(y=predTemp, x=elev), data=preditionDE) +
  geom_point(mapping = aes(y=predTemp, x=elev), data=preditionDE, 
             pch=16, col="red", size = 1) +
  annotate(geom = "label", x = 1500,
           y = 5, label = "Vorhersage",
           color = "red")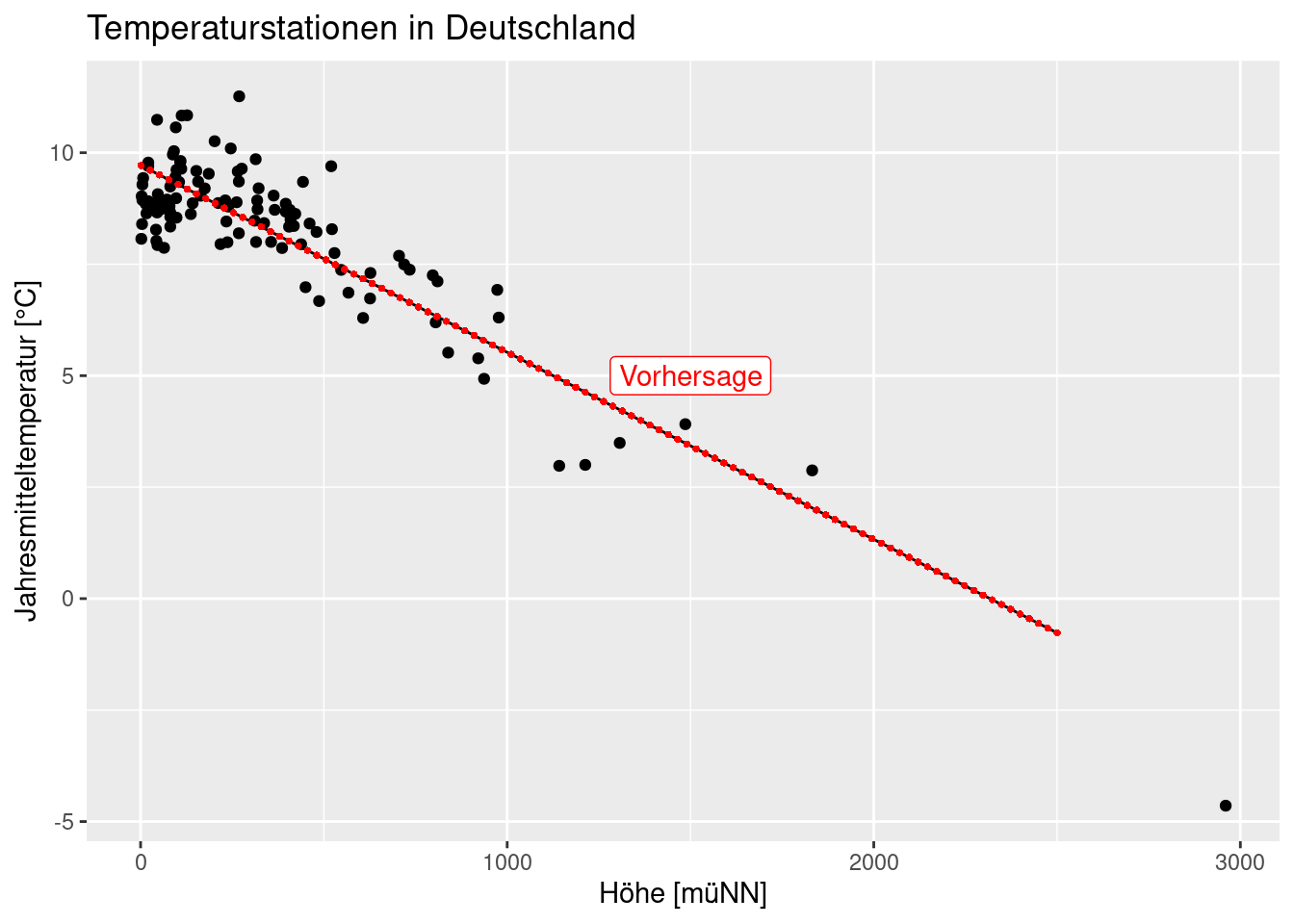

Eine Alternative zur Darstellung ist das package ggeffects, dass eine Darstellung on the fly ermöglicht. Die Funktion ermöglicht es auch bei komplexen Modellen zusammenhänge zu visualisieren, allerdings passiert ziemlich viel hinter den Kulissen, was dem Verständnis dafür, was vor sich geht abträglich ist.

library(ggeffects)

ggpredict(g)

## $ELEV
## # Predicted values of YEAR
## 
## ELEV | Predicted |       95% CI
## -------------------------------
##    0 |      9.72 |  9.51,  9.93
##  400 |      8.04 |  7.88,  8.20
##  800 |      6.36 |  6.12,  6.60
## 1200 |      4.68 |  4.31,  5.05
## 1400 |      3.85 |  3.40,  4.29
## 1800 |      2.17 |  1.58,  2.76
## 2200 |      0.49 | -0.25,  1.23
## 3000 |     -2.87 | -3.91, -1.82

## 
## Not all rows are shown in the output. Use `print(..., n = Inf)` to show
##   all rows.

## 
## attr(,"class")
## [1] "ggalleffects" "list"        
## attr(,"model.name")
## [1] "g"

ggpredict(g, terms="ELEV [0:3000]") %>%
  plot(show_ci=FALSE, show_residuals = TRUE)  + 
  ylab("Jahresmitteltemperatur [°C]") +
  xlab("Höhe [müNN]")+
  labs(title = "Temperaturstationen in Deutschland") 

## Data points may overlap. Use the `jitter` argument to add some amount of
##   random variation to the location of data points and avoid overplotting.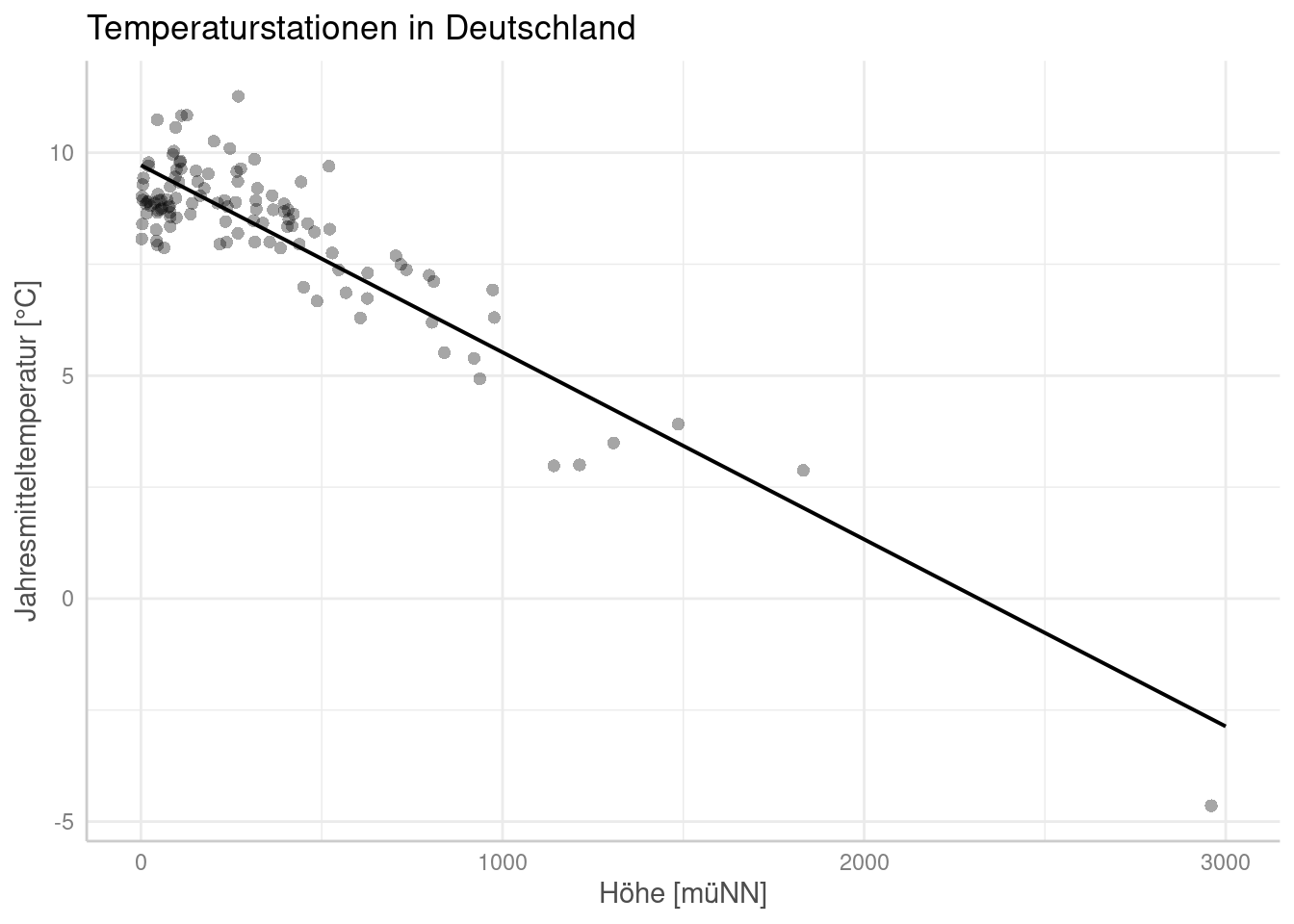

Aufgabe

Bitte führen Sie dieselbe Analyse für Russland (Russia) durch. Können Sie denselben Wirkungszusammenhang feststellen? Falls nicht, an was könnte das liegen?

12.3 Kontrollfragen

• was bedeutet linear im linearen Modell?
• was sind die Vorraussetzungen damit das lineare Modell angewandt werden darf?
• wie interpretiert man die Koeffizienten, Standardfehler und p-Werte des Outputs von summary im linearen Modell?
• was ist die Nullhypothese der t-Tests für die Regressionskoeffizienten
• was ist die Nullhypothese des F-Tests für das lineare Modell?
• wie ist \(R^2\) definiert? Wie kann man es intrpretieren?

Weiterführende/zitierte Literatur

Ritz, Christian, and Jens Carl Streibig. 2008. Nonlinear Regression with r. Springer.

---

50. CC 3.0, https://de.wikipedia.org/wiki/Datei:Matrix_multiplication_qtl1.svg, User:Quartl↩︎

51. Es gibt einen kleinen Unterschied: da Varianzkomponenten mit ML nicht erwartungstreu geschätzt werden, wird bei OLS ein Restricted Maximum Likelihood Ansatz (REML) verwendet um \(\sigma^2\) zu schätzen. Dabei wird hier im Nenner nicht durch \(n\), sondern durch \(n-1\) geteilt.↩︎

52. Unter bestimmten Umständen können auch Werte kleiner 1 auftreten.↩︎

53. Dies kommt daher, dass sich bei der Normalverteilung 95% der Werte innerhalb des Bereiches von ~1.96*\(\sigma\) befinden. Vergleiche den [Abschnitt zur Normalverteilung] normalverteilung. Genauer gesagt wird natürlich eine t-Verteilung verwendet. Wenn die Stichprobengröße groß genug ist, stimmt die Abschätzung aber.↩︎

54. Da es sich dabei um eine Schätzung handelt, ist dies ein Standardfehler.↩︎

55. Eine andere Option ist es, die Schrittweite anzugeben. Für Details s. die Hilfe zu seq.↩︎