Kapitel 16 Lineares Modell - Modelldiagnose
Sind die Annahmen des linearen Modells nicht erfüllt, kann man den Koeffizientenschätzern und den Standardfehlern nicht mehr trauen. Um zu vermeiden, dass man Fehlschlüsse macht, sollte man sich angewöhnen stets die Annahmen zu überprüfen. Man sollte sich klar machen, dass man dies i.d.R. nicht vorab tun kann, sonderns erst anhand des finalen Modells. Hintergrund ist der, dass wir die Annahmen nur anhand der Residuen überprüfen können, diese aber naturgemäß von der Modellstruktur abhängen. Sofern man davon ausgeht, dass zumindestens eine Prädiktor einen Einfluß auf die zu erklärende Variable hat, macht es keinerlei Sinn, zu versuchen die Modellannahmen direkt anhand der zu erklärenden Variablen zu überprüfen. Ebensowenig macht es Sinn, z.B. die Annahme der Normalverteilung an den Prädiktoren zu testen (was man immer wieder sieht).75
Die Annahmen des linearen Modells beziehen sich (mit Ausnahme der fehlerfreien Messung der Prädiktoren, was sich schwerlich nur anhand der Daten prüfen lässt) auf den Fehlerterm.
Neben dem Überprüfen der Modellannahmen lohnt es sich immer, dass Modell auf einflussreiche Beobachtungen und auf Hinweise für fehlende Prädktoren, Interaktionen, polynomiale Terme höherer Ordnung zu untersuchen.
Residuen sind die Abweichung zwischen Beobachtung und Modellvorhersage (s. Abbildung 16.1).
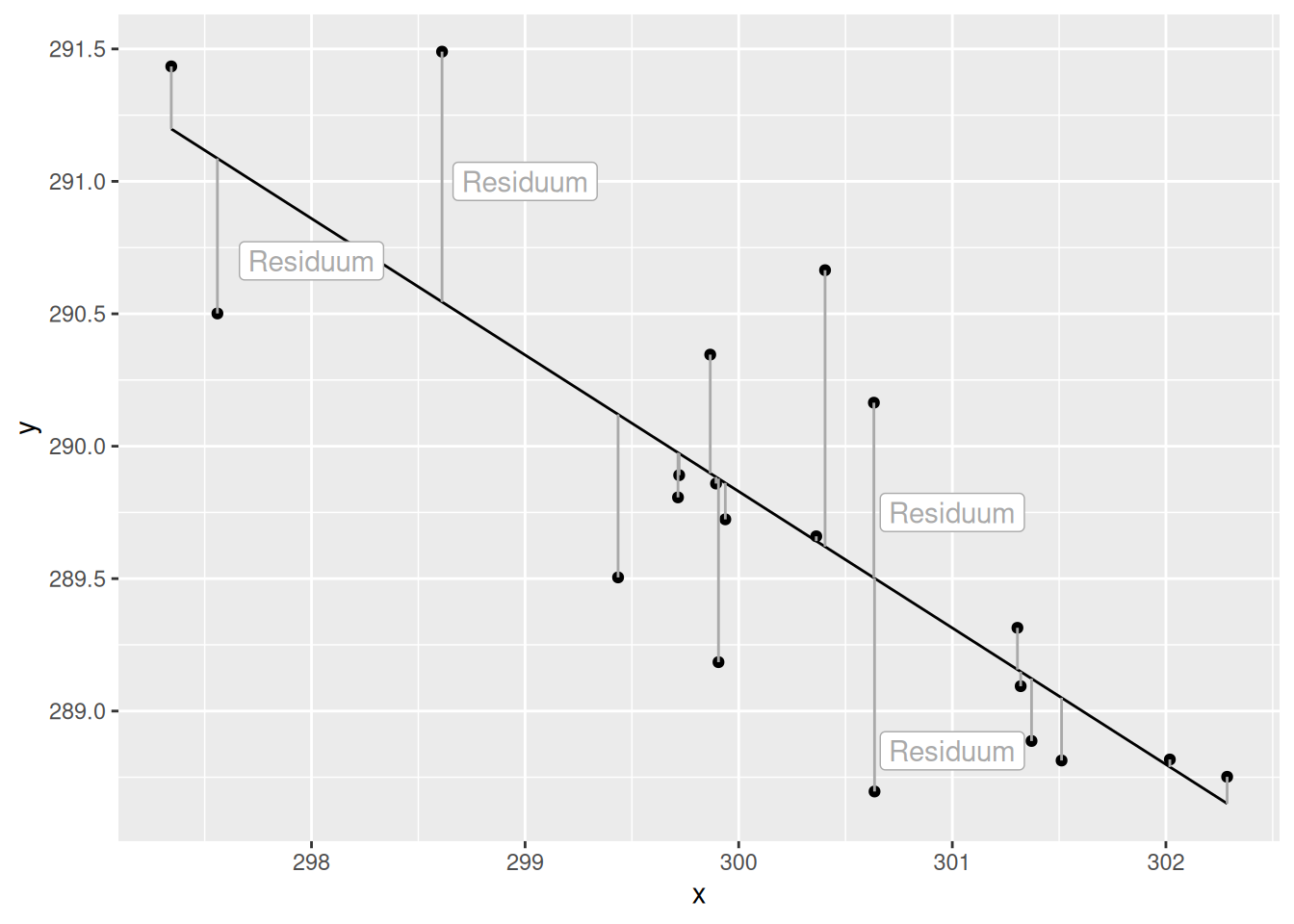
Figure 16.1: Residuen. Die Residuen sind die Abweichung zwischen Beobachteten Werten des Response und der Modellvorhersage für den Response (schwarze Linie). Die Abweichung wird hier durch die dunkelgraue Linie dargestellt. Gemessen werden die Residuen in den Einheiten des Response.
16.1 Struktur in den Residuen?
Zunächst schauen wir uns die Struktur der Residuen an, indem wir Sie zunächst gegen die gefitteten Werte auftragen. Anschließend tragen wir die Residuen gegen alle Prädiktoren im Modell und gegen potentielle Prädiktoren, die aber während der Modellselektion aussortiert worden sind.
Nach was suchen wir? Einerseits nach Heteroskedastizität, d.h. einer Veränderung der Varianz mit dem Mittelwert. Bleibt die Varianz der Residuen über den ganzen Wertebereich annähernd konstant oder nimmt sie zu oder ab? Das lineare Modell geht ja von einer konstanten Varianz des Fehlerterms aus. Weiterhin könne wir anhand der Plots der Residuen Hinweise auf fehlende Prädiktoren, Interaktionen, Terme höherer Ordnung finden. Hierbei halten wir Ausschau nach Mustern in der Beziehung der Residuen zu den einzelnen Prödiktoren - dabei schauen wir sowohl auf Prädiktoren, die im Modell sind, als auch solche, die wir bisher nicht berücksichtigt haben.
Die Residuen und die Vorhergesagten Werte (\(\hat{y}\)) lassen sich mittels residuals(model) und fitted(models) extrahiert werden. Dies können dann einfach mittels plot() oder - falls zuvor an den data,frame angehängt - mittels ggplot() erzeugt werden.
Wir schauen uns das für die bekannten russischen Klimastationen an.
temp <- read.table("data/temperatur.csv", header=TRUE)
temp.ru <- subset(temp, ELEV > -20 & CNTRY_NAME == "Russia")Fitten des Regressionsmodells:
temp.ru$LAT.cent <- temp.ru$LAT - mean(temp.ru$LAT)
temp.ru$LON.cent <- temp.ru$LON - mean(temp.ru$LON)
g <- lm(YEAR ~ ELEV+ LAT.cent + LON.cent, data=temp.ru)Für unsere Fallstudie (s. Abbildung 16.2) zeigen die Plots nichts verdächtiges.
par(mfrow=c(2,2), las=1)
plot(residuals(g) ~ fitted(g),
xlab= "gefittete Werte [°C]",
ylab="Residuen [°C]")
abline(h=0)
plot(residuals(g) ~ temp.ru$ELEV,
xlab= "Geländehöhe [münn]",
ylab="Residuen [°C]")
abline(h=0)
plot(residuals(g) ~ temp.ru$LAT,
xlab= "Geographische Breite [°]",
ylab="Residuen [°C]")
abline(h=0)
plot(residuals(g) ~ temp.ru$LON,
xlab= "Geographische Länge [°]",
ylab="Residuen [°C]")
abline(h=0)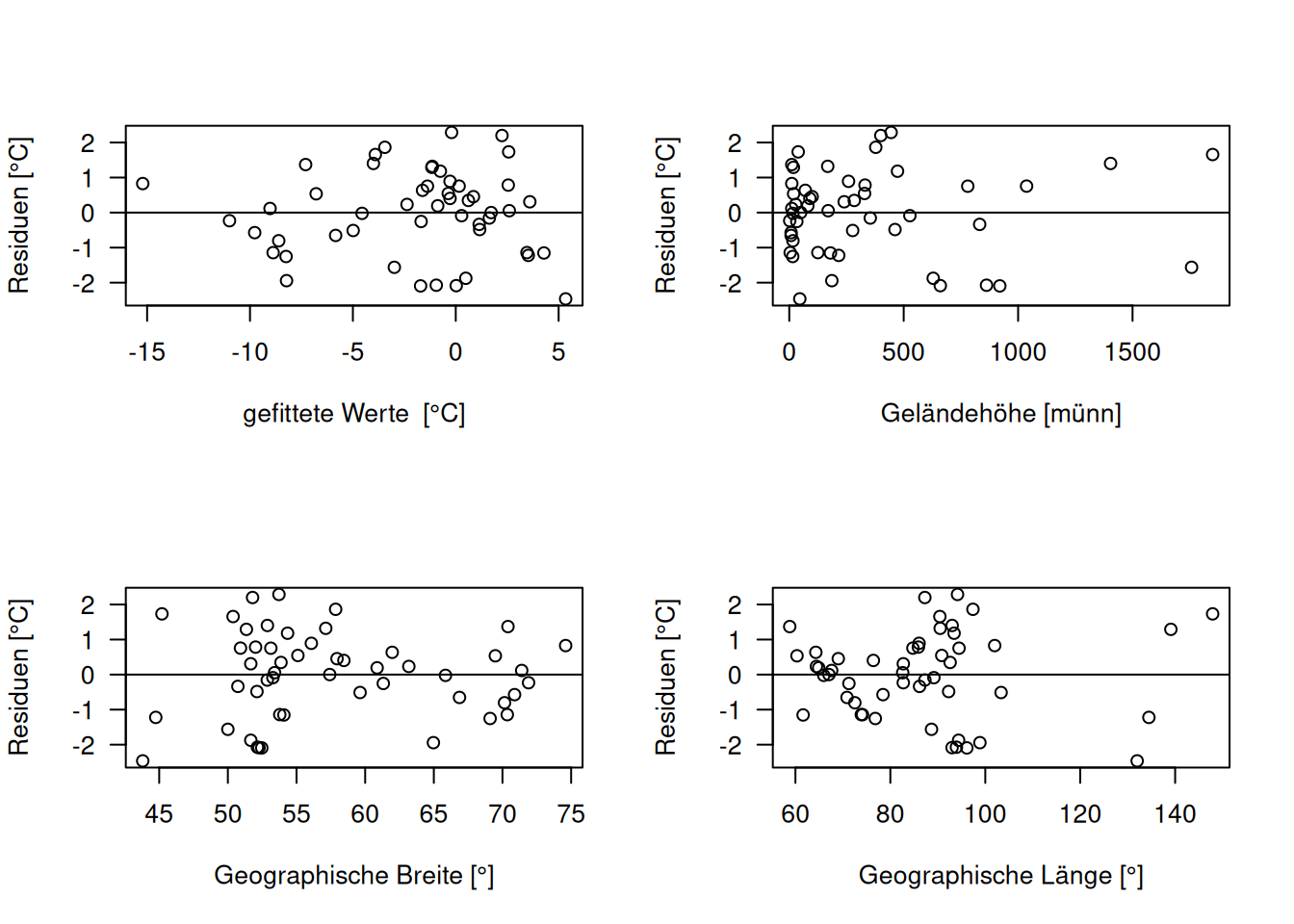
Figure 16.2: Diagnose Plots hinsichtlich der Struktur der Residuen. Wir suchen nach Hinweisen auf Heteroskedastizität oder auf bisher unberücksichtigte Zusammenhänge zwischen Prädiktoren und Response.
Plot Variante mit ggplot hier wurde zusätzlich ein loess Smoother (~gleitender Mittelwert) und ein Generelles Additivies Modell (blau) zum Plot hinzugefügt, der es erleichtert, Strukturen zu erkennen. Die flachen Linien bim GAM dienen als Indikator dafür, dass vermutlich keine Struktur in den Plots vorliegt
temp.ru$resid <- residuals(g)
temp.ru$fit <- fitted(g)
p1 <- ggplot(temp.ru, aes(x=fit, y= resid)) +
geom_point() +
geom_smooth(method="gam") +
geom_smooth(method="loess", col="red") +
geom_hline(yintercept = 0) +
xlab("Vorhergesagte Werte [°C]") +
ylab("Residuen [°C]")
p2 <- ggplot(temp.ru, aes(x=ELEV, y= resid)) +
geom_point() + geom_smooth(method="gam") +
geom_smooth(method="loess", col="red") +
geom_hline(yintercept = 0) +
xlab("Geländehöhe [müNN]") +
ylab("Residuen [°C]")
p3 <- ggplot(temp.ru, aes(x=LAT, y= resid)) +
geom_point() + geom_smooth(method="gam") +
geom_smooth(method="loess", col="red") +
geom_hline(yintercept = 0) +
xlab("Geographische Breite [°]") +
ylab("Residuen [°C]")
p4 <- ggplot(temp.ru, aes(x=LON, y= resid)) +
geom_point() +
geom_smooth(method="gam") +
geom_smooth(method="loess", col="red") +
geom_hline(yintercept = 0) +
xlab("Geographische Länge [°]") +
ylab("Residuen [°C]")
ggpubr::ggarrange(p1,p2,p3,p4)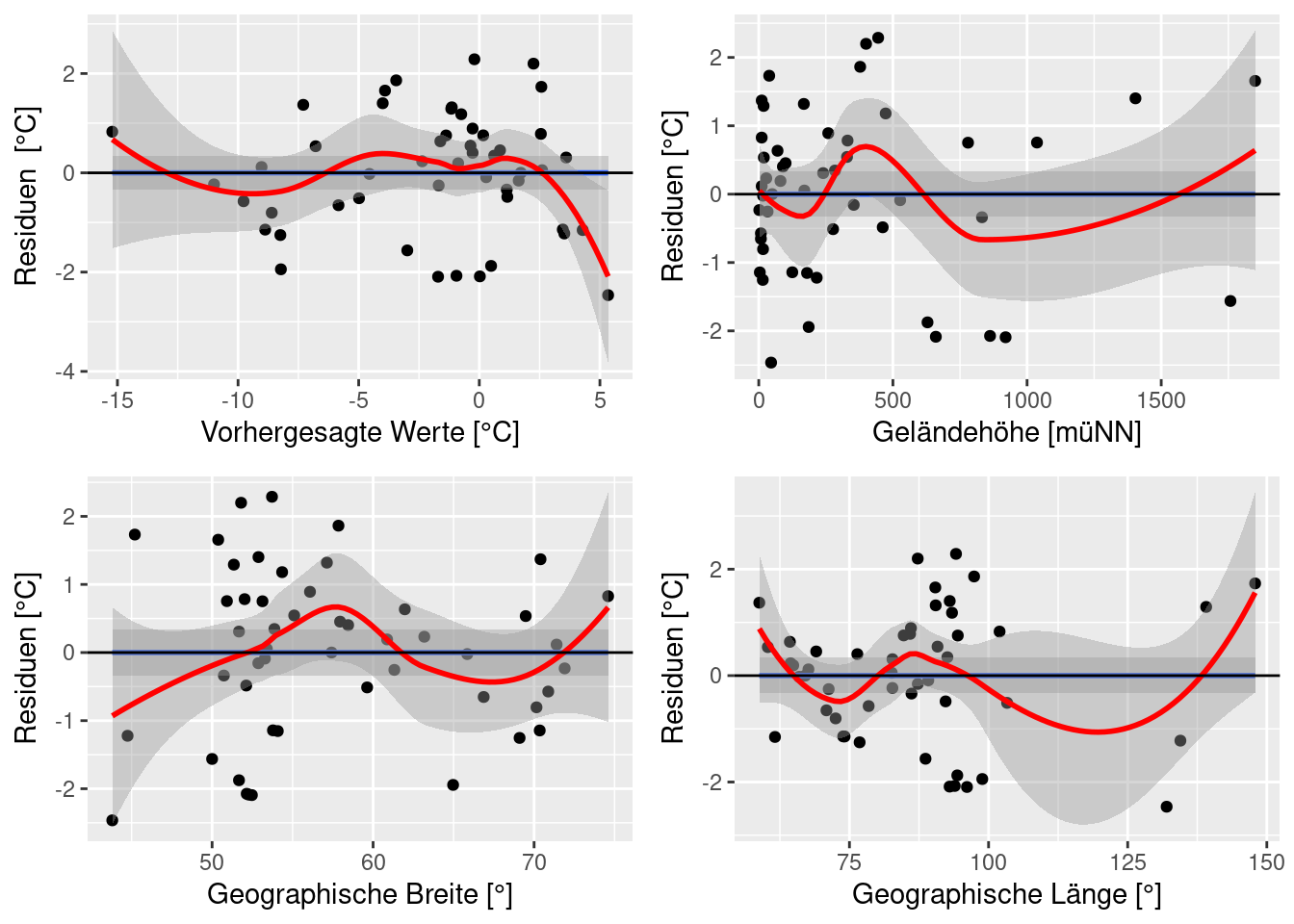
Es macht auch Sinn, den Betrag der Residuen zu plotten, da man darüber ggf. einen Trend mit dem Fit besser detektieren kann (s. Abbildung 16.3). Auch die Plots der Absolutwerte der Residuen sehen für unsere Fallstudie unverdächtig aus.
par(mfrow=c(2,2), las=1)
plot(abs(residuals(g)) ~ fitted(g),
xlab= "gefittete Werte [°C]",
ylab="Absolutwert Residuen [°C]")
plot(abs(residuals(g)) ~ temp.ru$ELEV,
xlab= "Geländehöhe [müNN]",
ylab="Absolutwert Residuen [°C]")
plot(abs(residuals(g)) ~ temp.ru$LAT,
xlab= "Geographische Breite [°]",
ylab="Absolutwert Residuen [°C]")
plot(abs(residuals(g)) ~ temp.ru$LON,
xlab= "Geographische Länge [°]",
ylab="Absolutwert Residuen [°C]")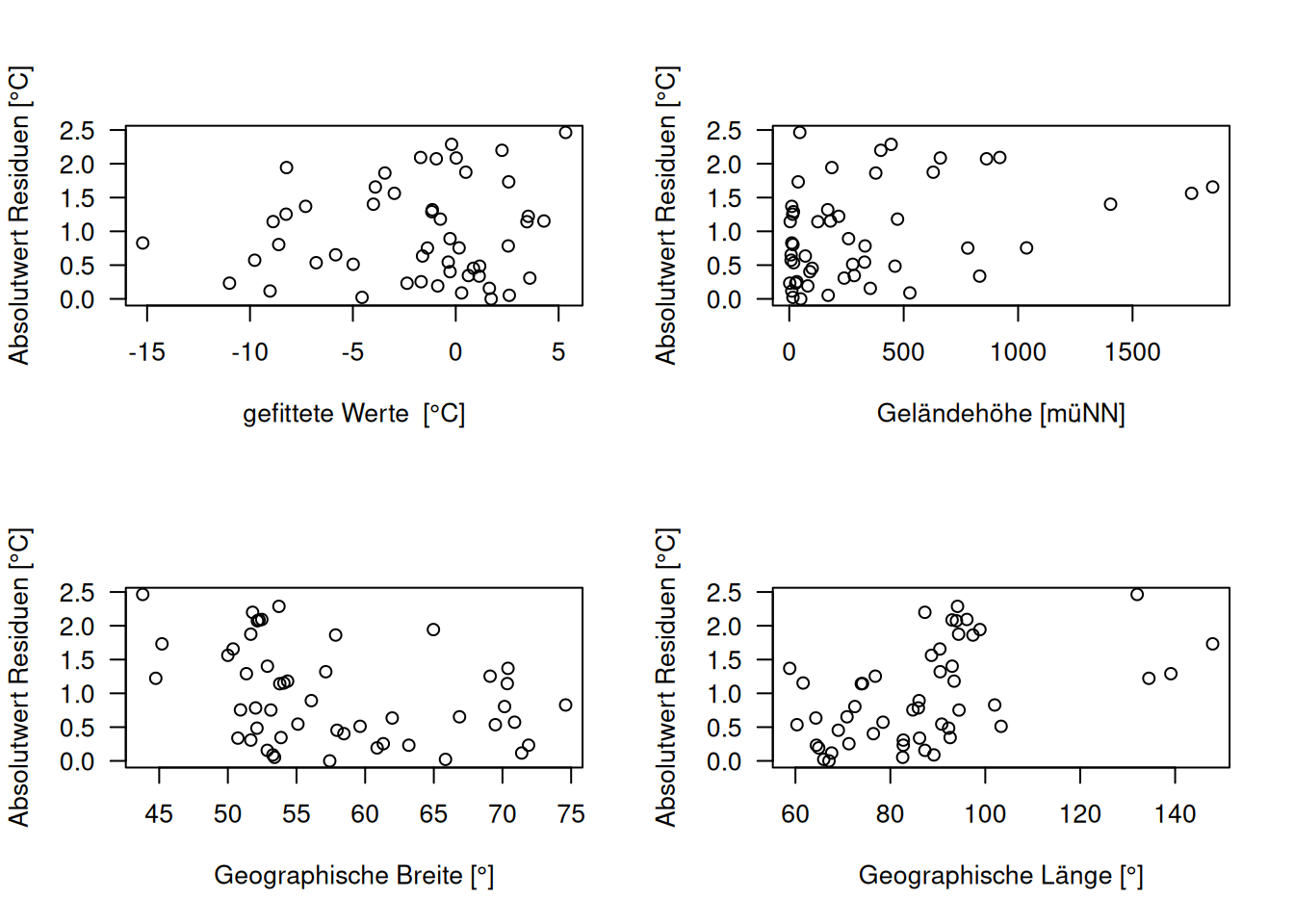
Figure 16.3: Diagnoseplots unter Verwendung des Absolutbetrags der Residuen.
16.1.1 Beispiele für Probleme
Hier möchte ich anhand einiger konstruierter Daten zeigen, wie einige Probleme mit Hilfe der Diagnoseplots identifiziert werden können.
Abbildung 16.4 zeigt ein Beispiel für eine nicht-lineare Struktur in den Residuen. Die Residuen zeigen im Verlauf des Prädiktors x eine Form, die sich mit Hilfe einer nach unten offenen Parabel beschreiben lässt. Also ein Hinweis auf einen fehlenden Quadratischen Effekt in X (mit negativem Vorzeichen).
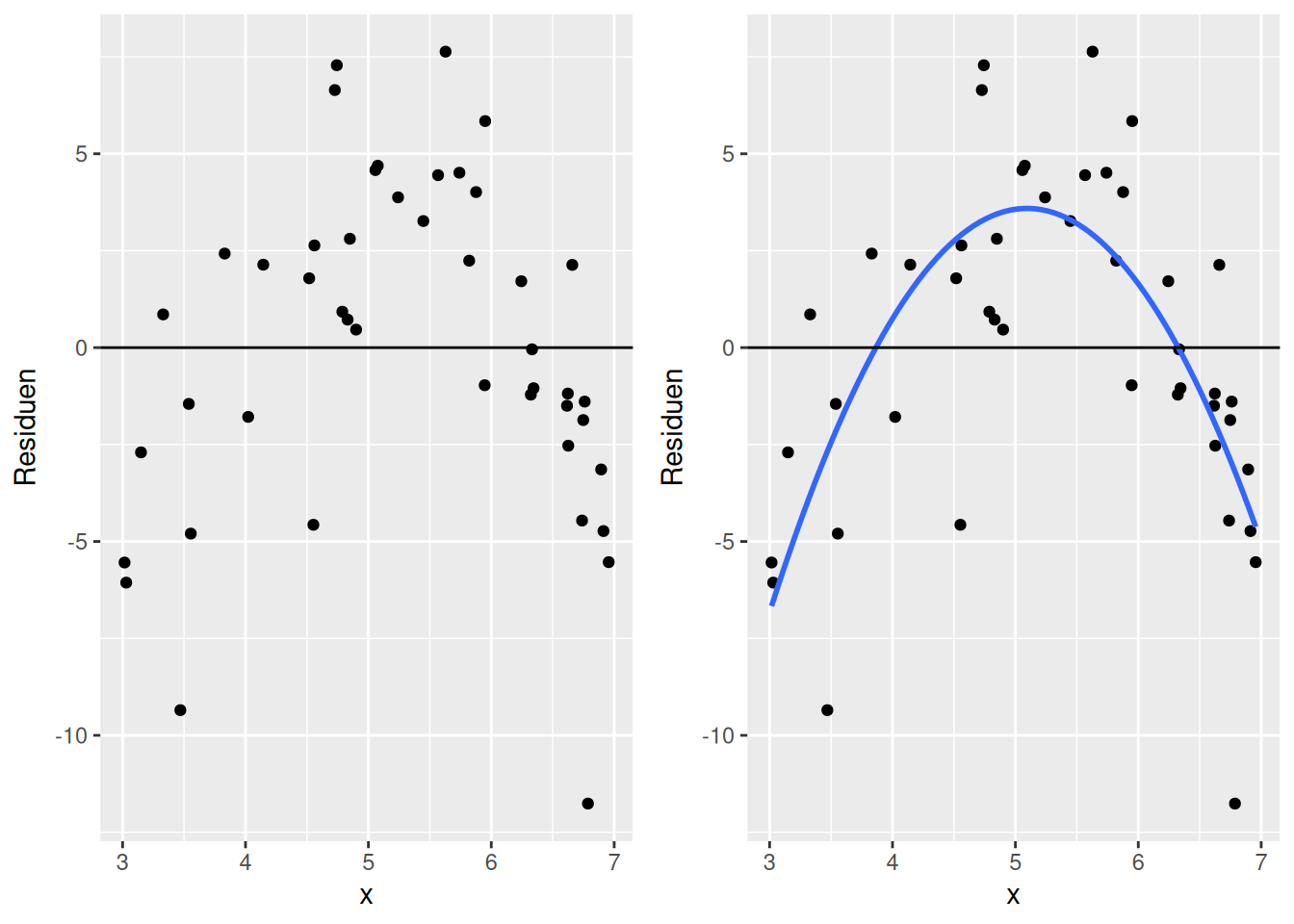
Figure 16.4: Beispiel für nicht-lineare Struktur im Zusammenhang zwischen Residuen und einem Prädiktor (x). Im rechten Plot ist der funktionale Zusammenhang als Hilfslinie eingetragen.
Der Diagnoseplot des korrigierten Modells - welches den Haupteffekt und einen quadratischen Effekt enthält - zeigt - eine schöne gleichmäßige Struktur (Abbildung 16.5).
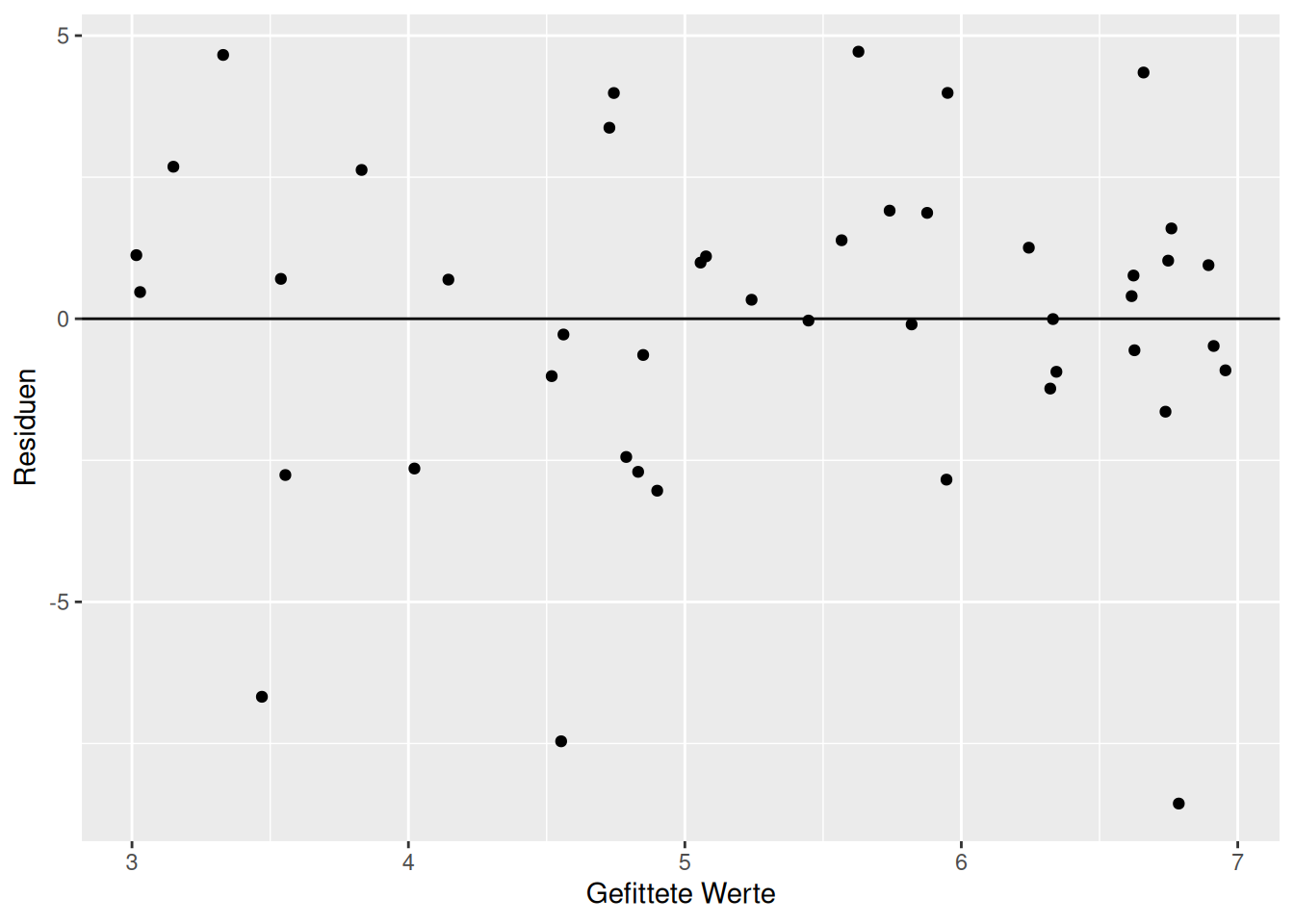
Figure 16.5: Diagnoseplots für das Modell indem der fehlende Quadratische Term integriert wurde.
Abbildung 16.6 zeigt ebenfalls eine nicht-lineare Struktur, die hier einen Hinweise auf ein zyklisches Phänomen - also eine Sinus oder Cosinus Funktion - sein könnte.
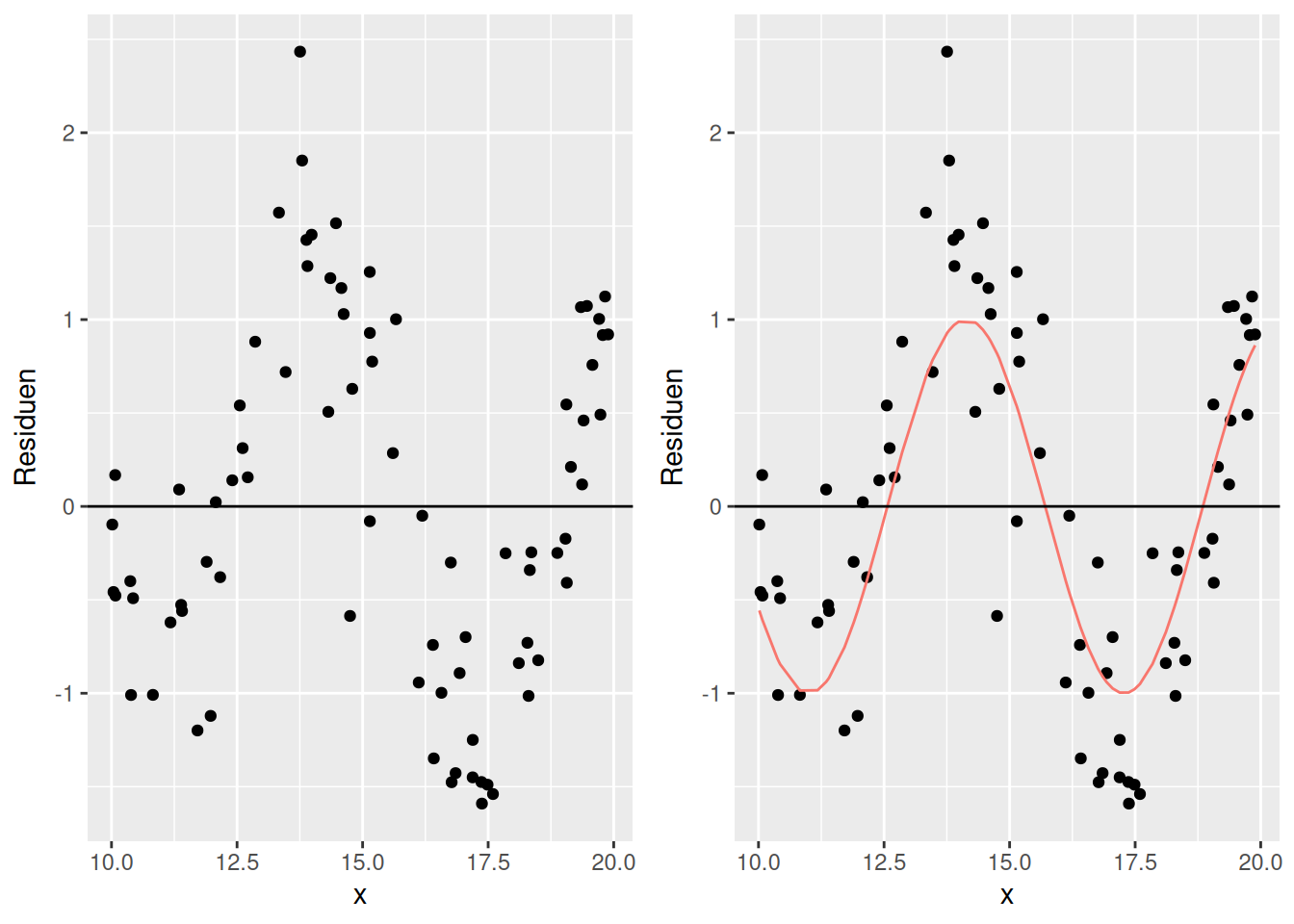
Figure 16.6: Beispiel für nicht-lineare Struktur im Zusammenhang zwischen Residuen und einem Prädiktor (x). Im rechten Plot ist der funktionale Zusammenhang als Hilfslinie eingetragen.
Der Diagnoseplot des korrigierten Modells - welches den Term sin(x) enthält - zeigt - bis auf einen Ausreißer - eine schöne gleichmäßige Struktur (Abbildung 16.7).
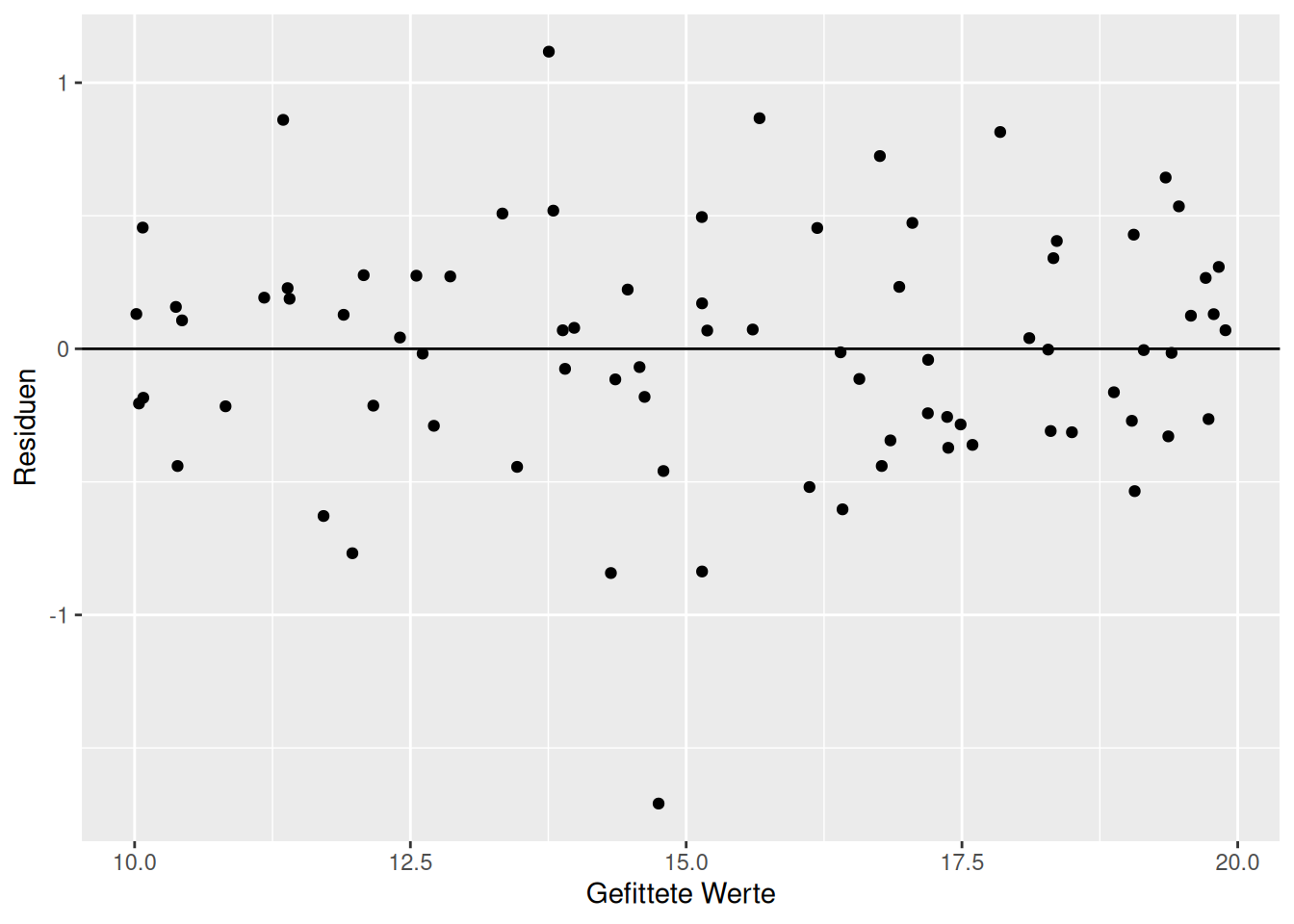
Figure 16.7: Diagnoseplots für das Modell indem der Haupteffekt von x durch sin(x) ersetzt wurde.
Abbildung 16.8 liefert einen klaren Hinweis auf Heteroskedastizität: Die Varianz der Residuen nimmt mit dem vorhergesagtem Wert zu. Dies wird in Abbildung 16.9 nochmal verdeutlicht. Heteroskedastizität ist etwas, das typischerweise bei Zähldaten vorkommt - weswegen das lineare Modell für diese Response Daten oftmals ungeeignet ist. Ggf. ist diese Zunahme der Varianz klarer zu erkennen, wenn man den Absolutwert der Residuen gegen die gefitteten Werte aufträgt.
Hier kann das lineare Modell nicht angewandt werden. Es sollte ein generalisiertes lineares Modell mit Poisson oder negativ-Binomialverteilung angewandt werden.
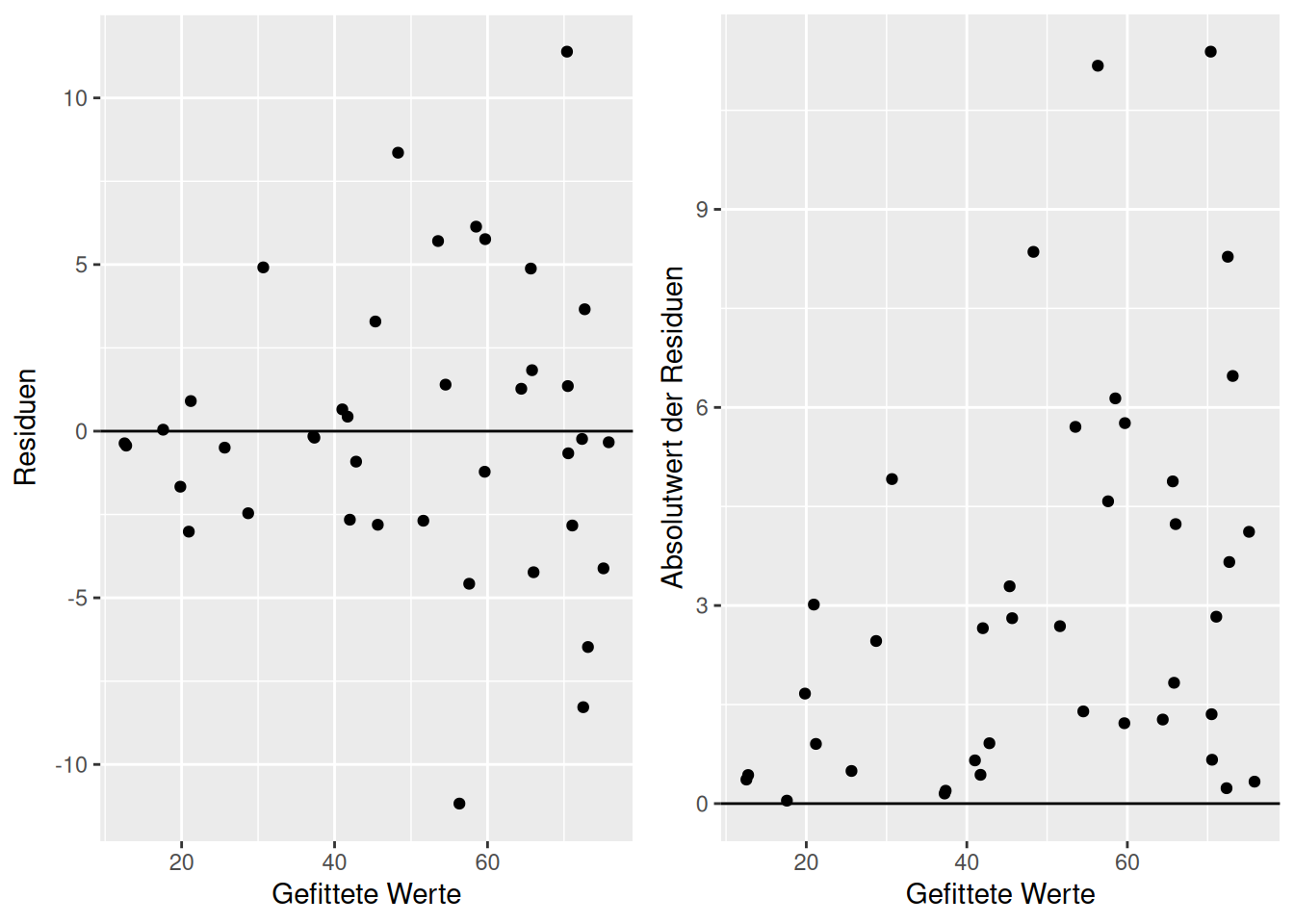
Figure 16.8: Beispiel für Heteroskesastizität der Residuen. Die Varianz der Residuen nimmt mit dem Mittelwert (dem vorhergesagtem/gefittetem Wert) zu.
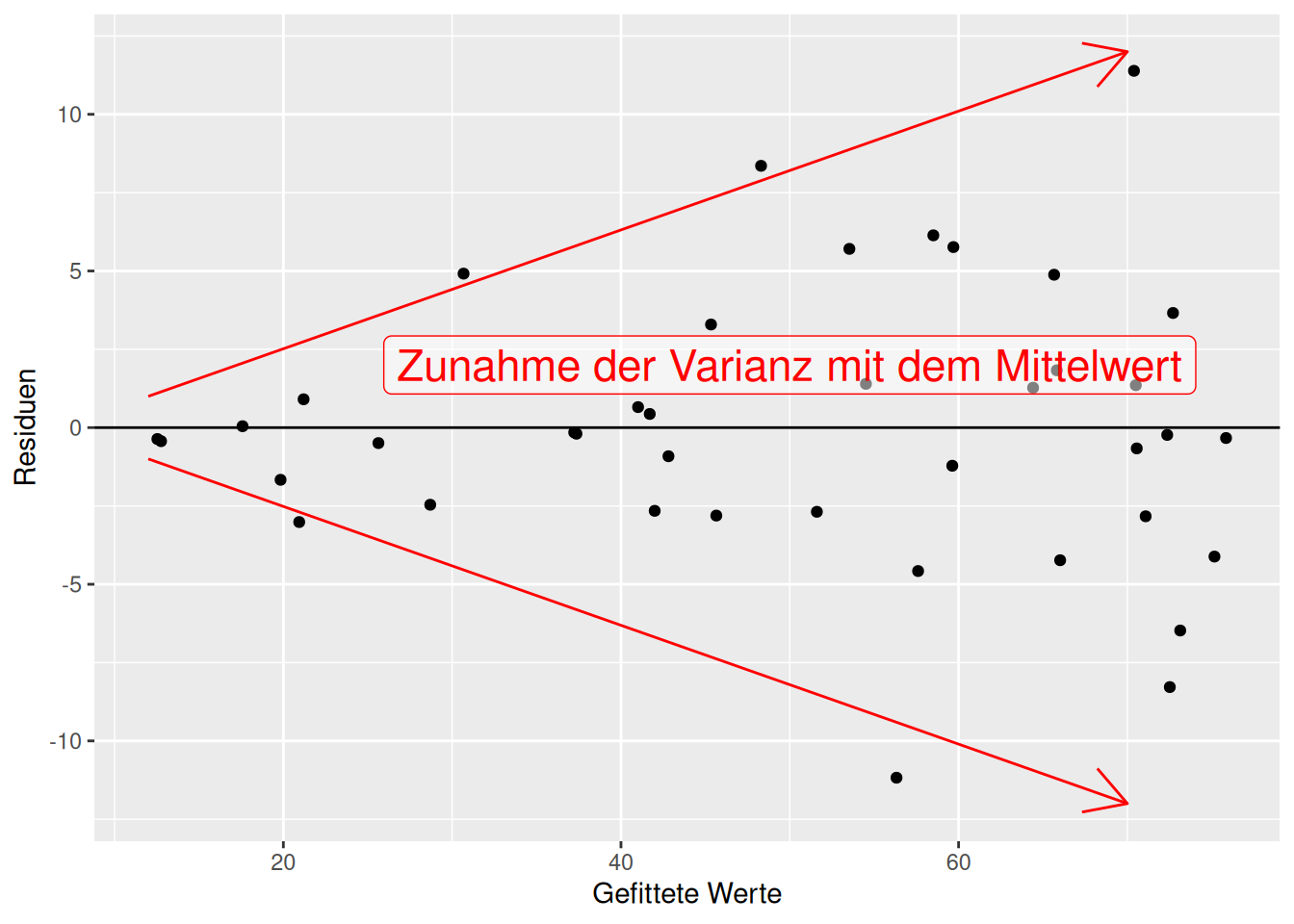
Figure 16.9: Heteroskedastizität in den Residuen. Klar erkennbar ist die Zunahme der Varianz der Residuen mit dem Mittelwert (den vorhergesagten Werten).
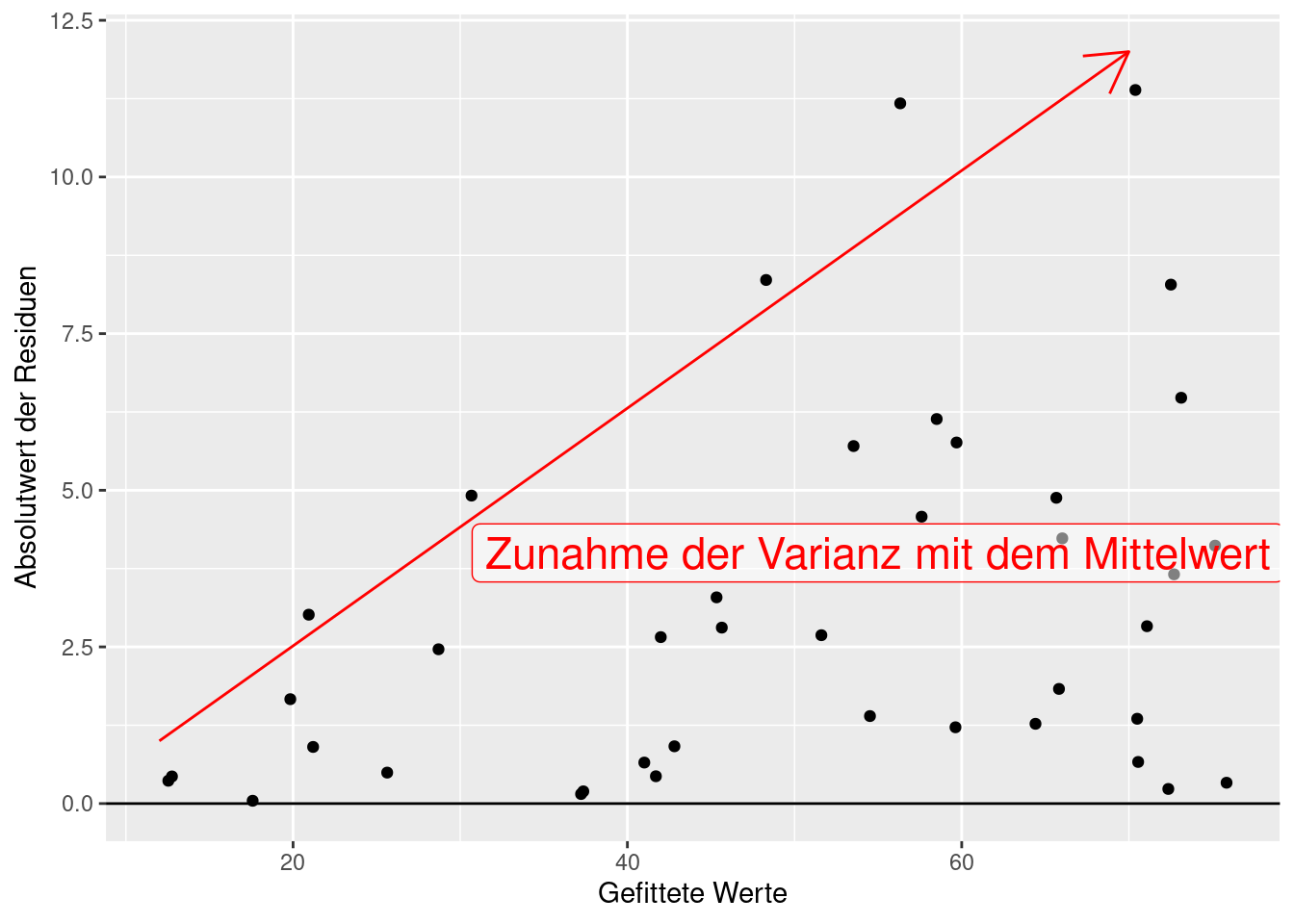
Abbildung 16.10 zeigt auch einen nicht-linearen Zusammenhang. Allerdings ist dessen Ursache vielleicht nicht direkt ersichtlich. Sowohl bei großen als auch bei kleinen vorhergesagten Werten sind dir Residuen groß - die Residuen scheinen einen quadratischen Zusammenhang mit den vorhergesagten Werten aufzuweisen. Plottet man die beiden Prädiktoren im Modell gegen die Residuen sieht man jeweils eine Zunahme der Varianz wenn man von einem mittleren Wert abweicht. Allerdings ist der Zusammenhang nicht quadratisch.
Die Ursache ist eine Interaktion zwischen beiden Prädiktoren, die nicht im Modell berücksichtigt war.
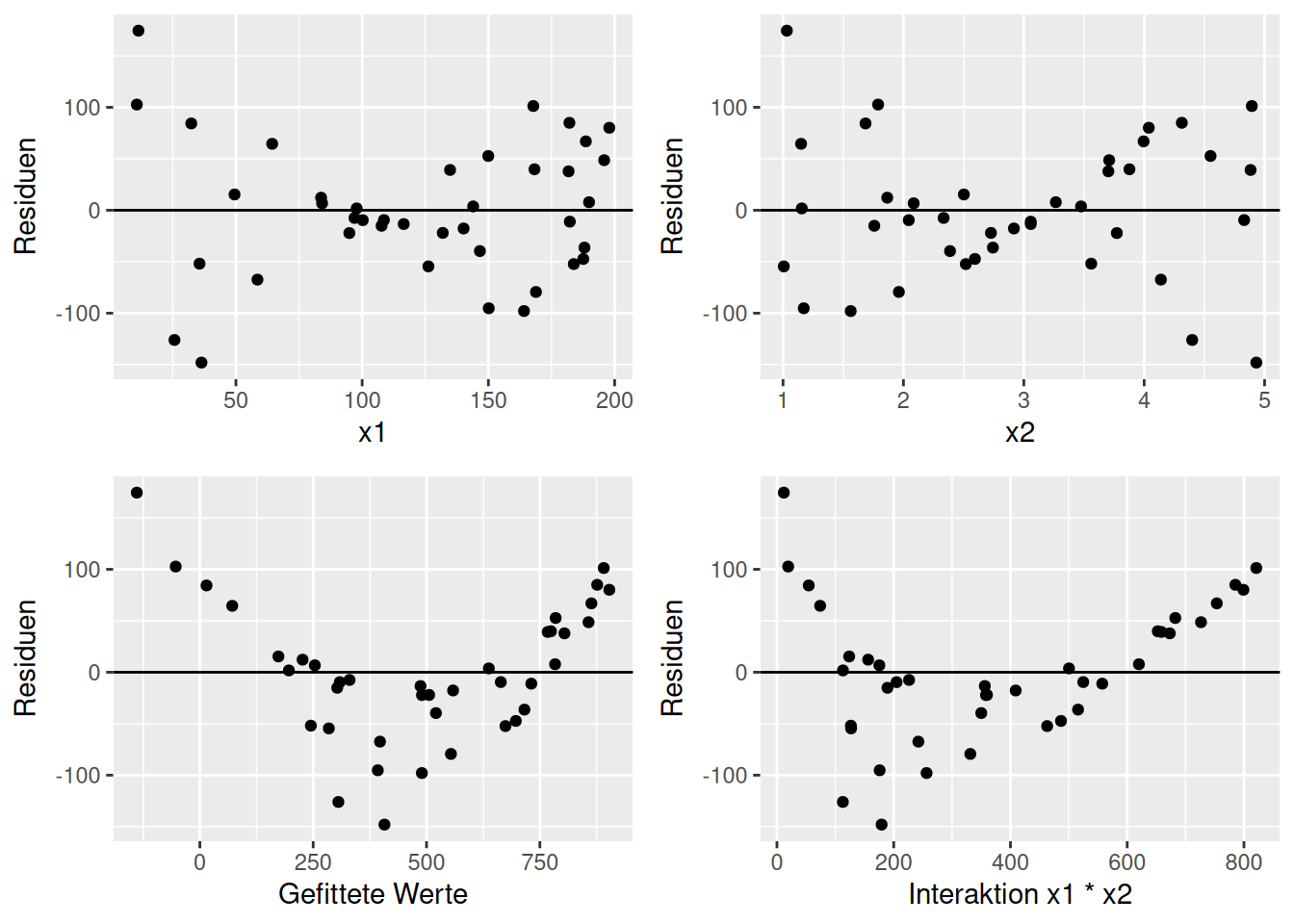
Figure 16.10: Beispiel für nicht-lineare Struktur im Zusammenhang zwischen Residuen und einem Prädiktor (x).
Der Diagnoseplot des korrigierten Modells - welches die Interaktion enthält - zeigt - bis auf einen Ausreißer - eine schöne gleichmäßige Struktur (Abbildung 16.11).
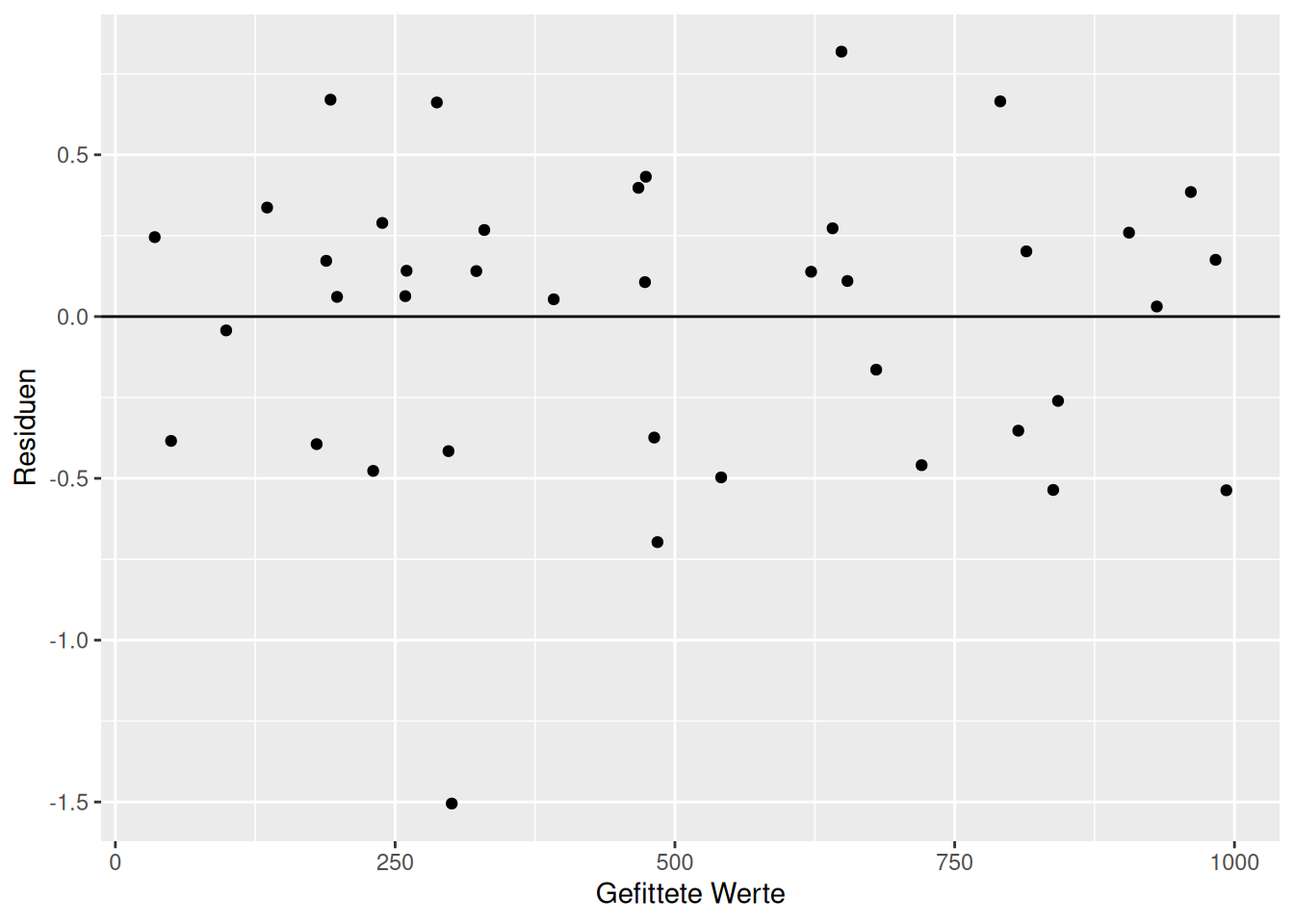
Figure 16.11: Diagnoseplots für das Modell indem die fehlende Interaktion integriert wurde.
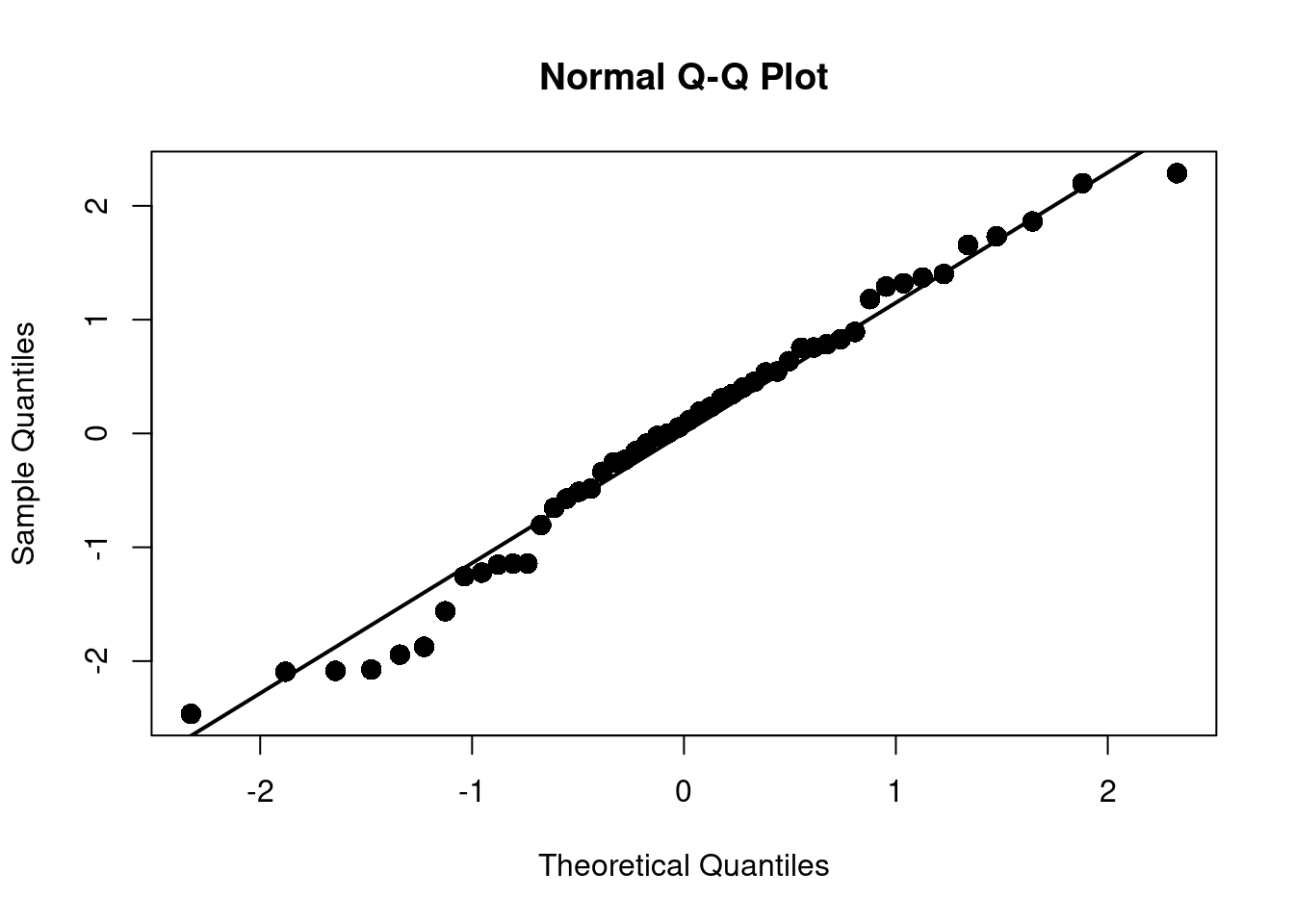
16.2 Verteilung der Residuen: QQ-Plot
Um zu ermitteln, ob die Residuen einer Normalverteilung folgen plotten wir in einem QQ-Plot die Quantile der Verteilung der Residuen gegen die theoretische Verteilung. Wir suchen dabei nach Abweichungen von der Verteilung. Insbesondere die Enden der Verteilung (engl. tails) sind von Interesse.
Etwas schöner geht das noch im Packet car, das bei qqPlot angewandt auf ein lineares Regressions-Objekt die studentized Residuals gegen die Quantile einer t-Verteilung plottet und auch die über einen parametrischen Bootstrap-Ansatz ermittelten Konfidenzintervalle angibt. car ist mit R bereits installiert und muss nicht separat installiert werden.
Studentized Residuen sind dabei Residuen, die durch die Standardabweichung und der Quadratwurzel aus dem 1-Leverage (Diagonalelement der Hat-Matrix, s. unten) geteilt wird:
\[ \hat{\epsilon}_{i,stud} = \frac{\hat{\epsilon_i}}{\hat{\sigma}\sqrt{1-h_{ii}}} \]
Die Residuen sind damit um den Effekt unterschiedlicher Varianz (bei Normalverteilung sollte die ja überall gleich sein) und den Leverage (s. unten) bereinigt. Damit kann man besser erkennen, welche Punkte hervorstechen. Standardmäßig werden die beiden extremsten Punkte gelabelled - dies heißt nicht, dass diese Punkte notwendigerweiße auffällig sind. Die Funktion liefert weiterhin die Label der identifizierten Punkte zurück, die dann ggf. weiterverwendet werden können.
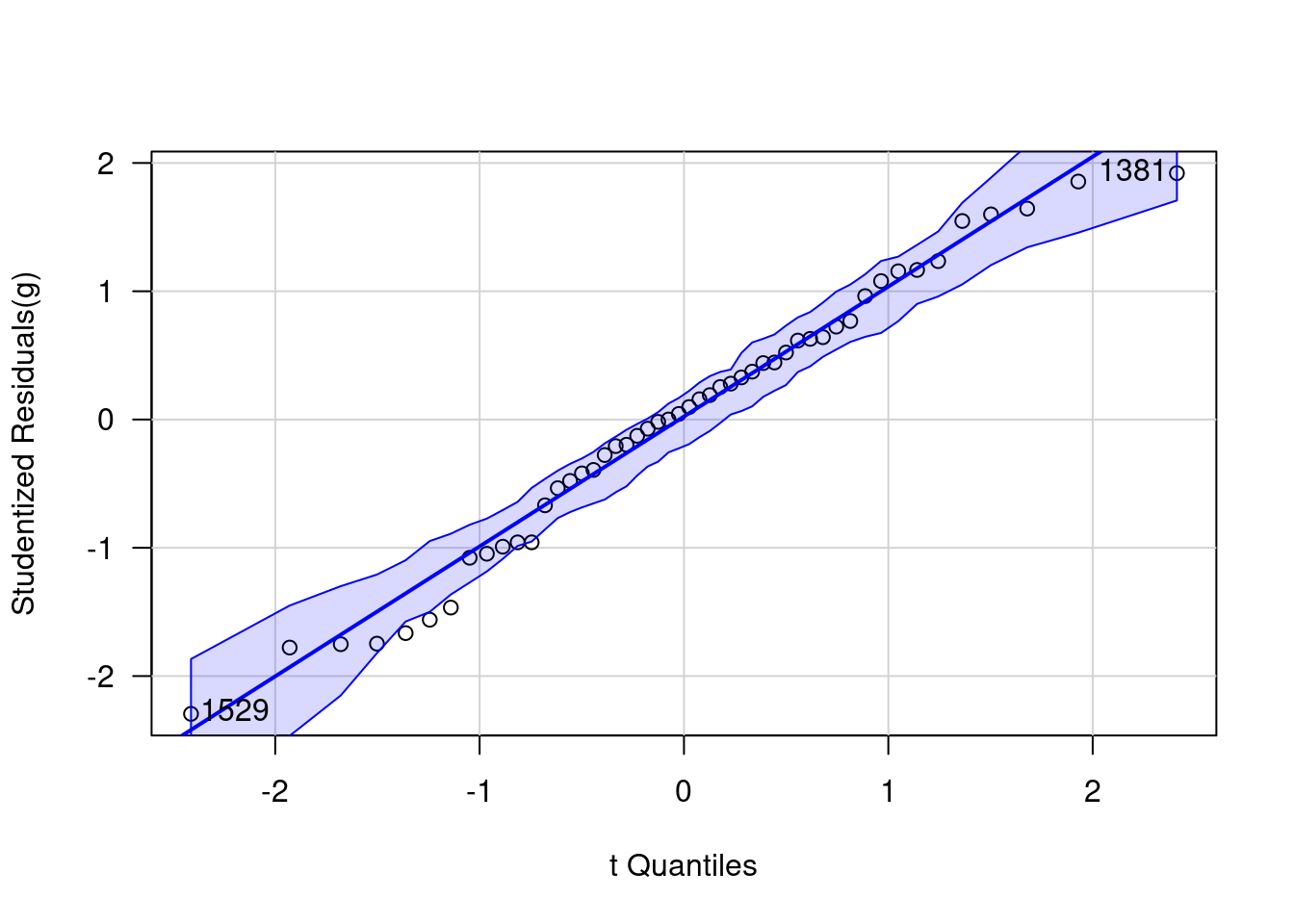
Wie man sieht, gibt es keinen Grund zur Annahme, dass die Residuen nicht normalverteilt sein könnten.
16.2.1 Beispiele für Probleme
Hier möchte wieder ich anhand einiger konstruierter Daten zeigen, wie einige Probleme mit Hilfe des QQplots identifiziert werden können.
Nachfolgend zeige ich die QQ-Plots der studentized Residuen für jeweils neun Zufallsstichproben von 4 Verteilungen: Cauchy-, t- Weibull- und Gaussverteilung (Abbildung 16.12). Für die Cauchy-Verteilung (Abbildung 16.13) sieht man, dass es insbesondere die Ausreißer sind, die dazu führen, dass es zu Abweichungen von der angenommenen Verteilung kommt. Eine der Zufallssatichproben würde anhand des QQ-Plots sogar als normalverteilt durchgehen. Bei der t-Verteilung mit 3 Freiheitsgraden sind es ebenfalls die Ausreißer, die manche Zufallssstichproben als abweichend von den Annahmen erkenntlich machen. Im Gegensatz zur Cauchy-Verteilung ist die Tendenz zu extremen Ausreißern bekanntermaßen geringer. Deswegen kommt es auch seltener zu klar erkennbaren Abweichungen von der angenommenen Verteilung. Bei der gewählten Parametrisierung der Weibull-Verteilung fällt es deutlich schwerer, Abweichungen von der angenommenen Verteilung zu erkennen (Abbildung 16.15): nur bei wenigen Zufallsstichproben kann man klar eine Abweichung erkennen. Bei den normalverteilten Daten liegen - nicht unerwartet - alle Punkte innerhalb des Konfidenzbandes (Abbildung 16.16).
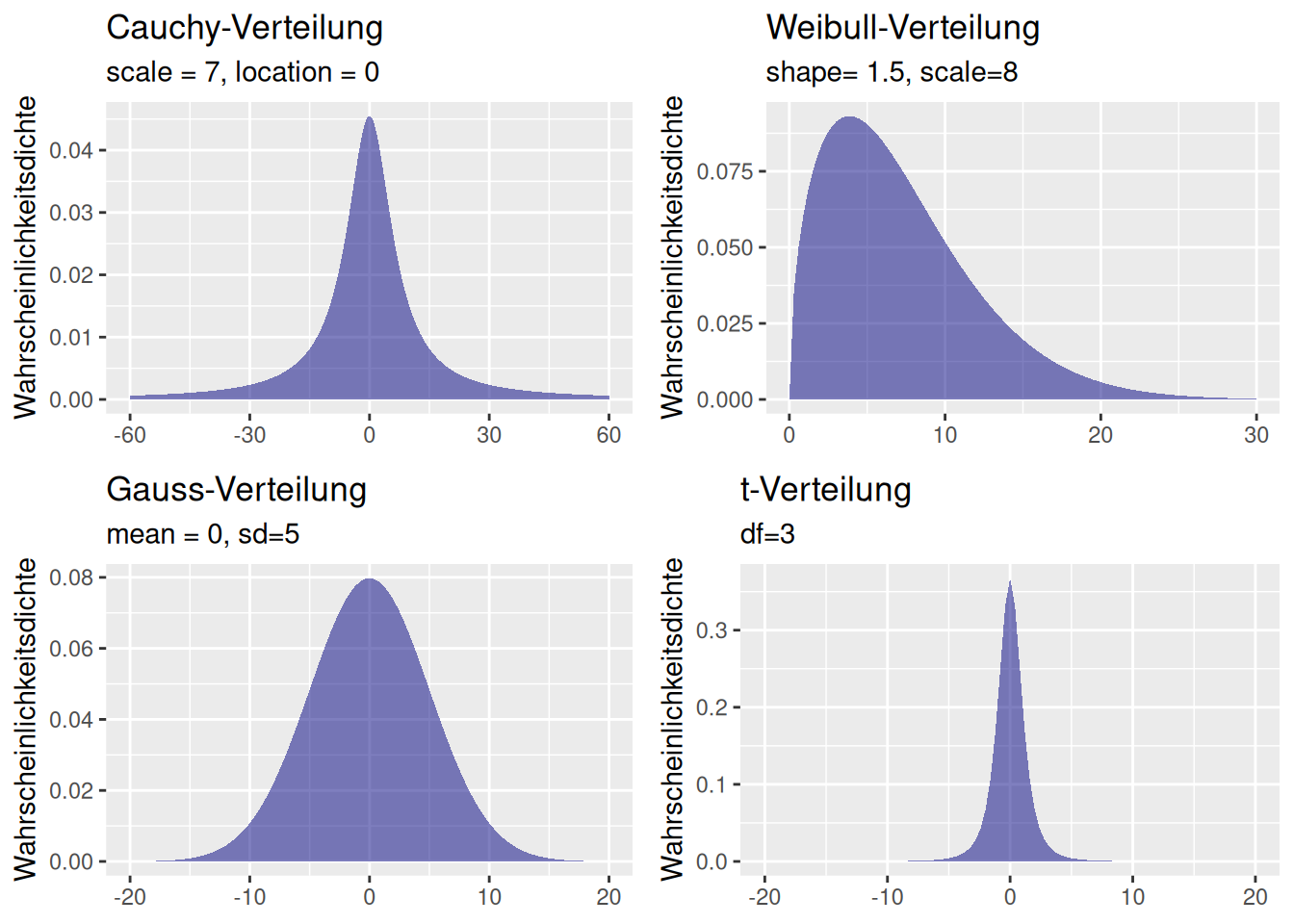
Figure 16.12: Die für dieQQ-Plots verwendete Cauchy, t-, Weibull- und Gauss-Verteilung.
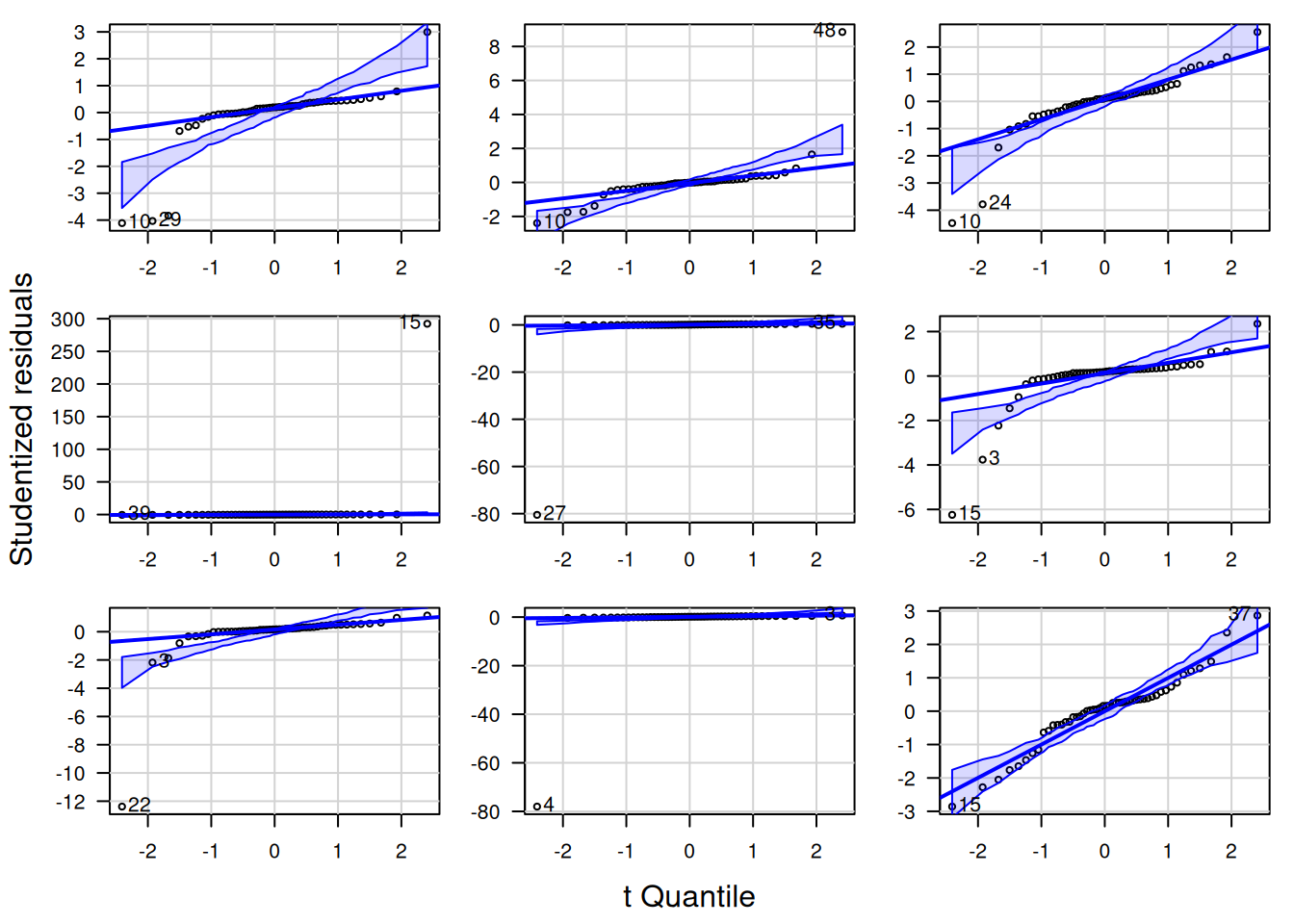
Figure 16.13: QQ-Plot für Cauchy-verteilte Residuen (scale = 7, location = 0). Die neun Plots zeigen die Variabilität für unterschiedliche Zufallsstichproben.
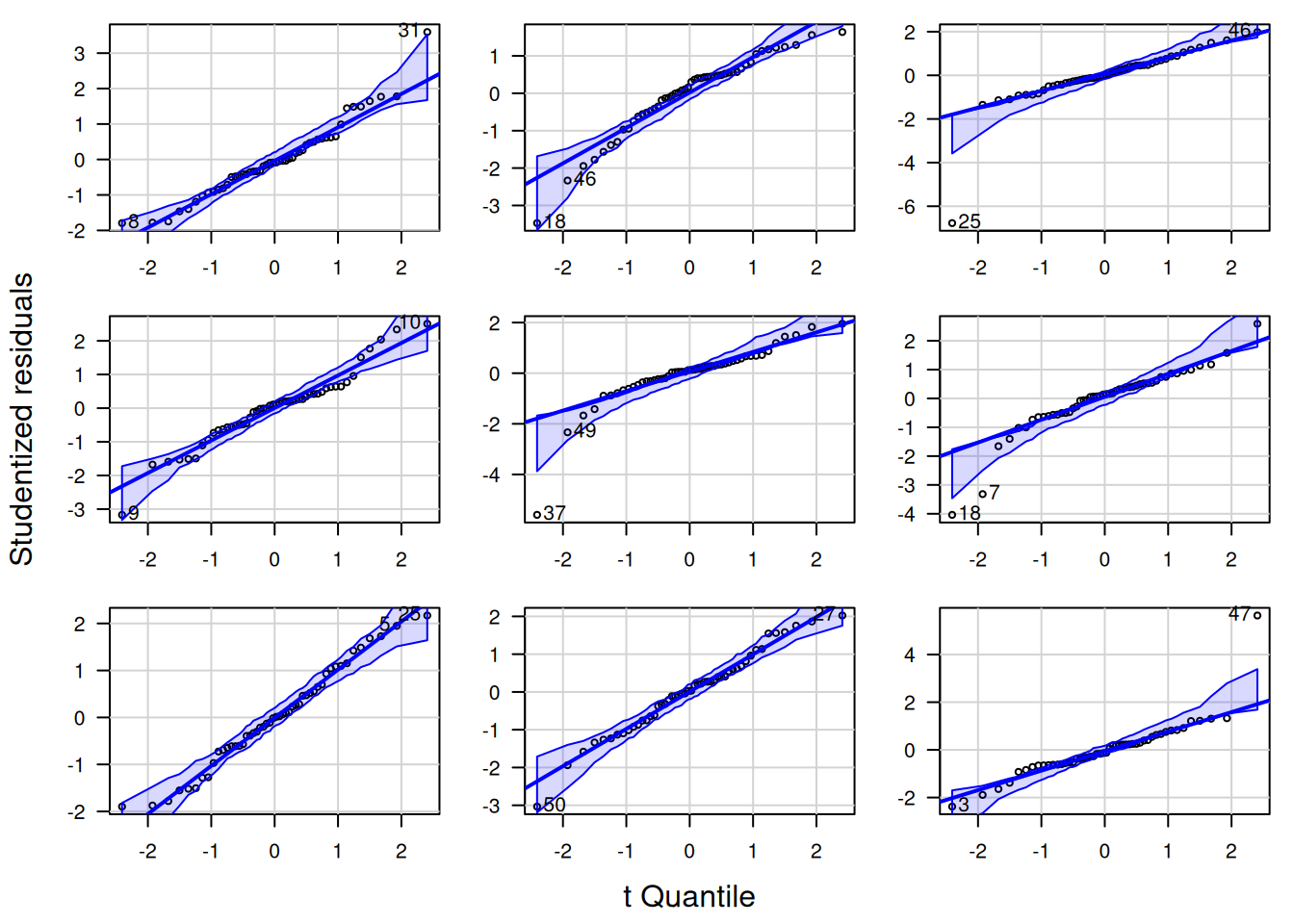
Figure 16.14: QQ-Plot für t-verteilte Residuen (df=3). Die neun Plots zeigen die Variabilität für unterschiedliche Zufallsstichproben.
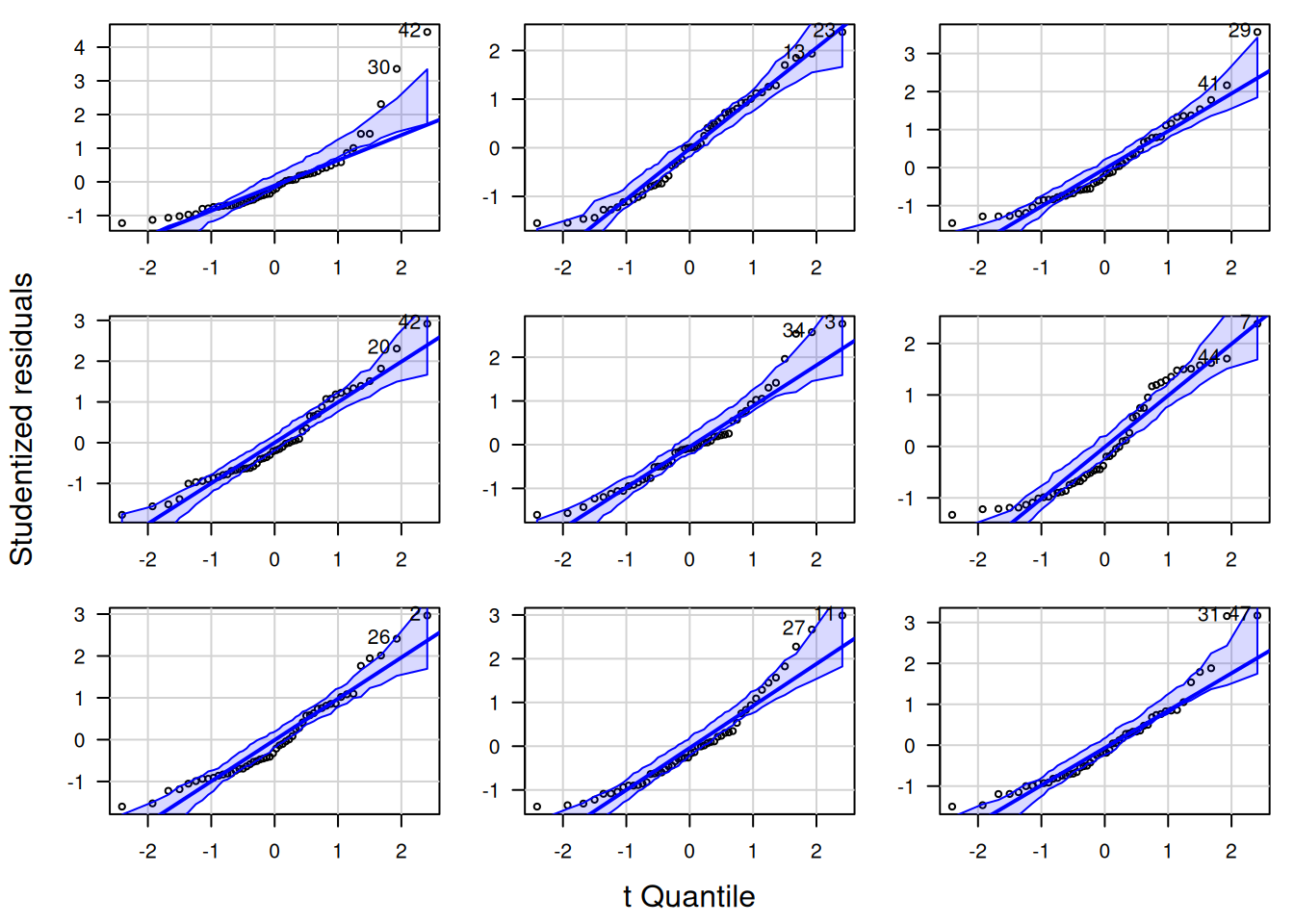
Figure 16.15: QQ-Plot für Weibull-verteilte Residuen (shape = 1.5, scale=8). Die neun Plots zeigen die Variabilität für unterschiedliche Zufallsstichproben.
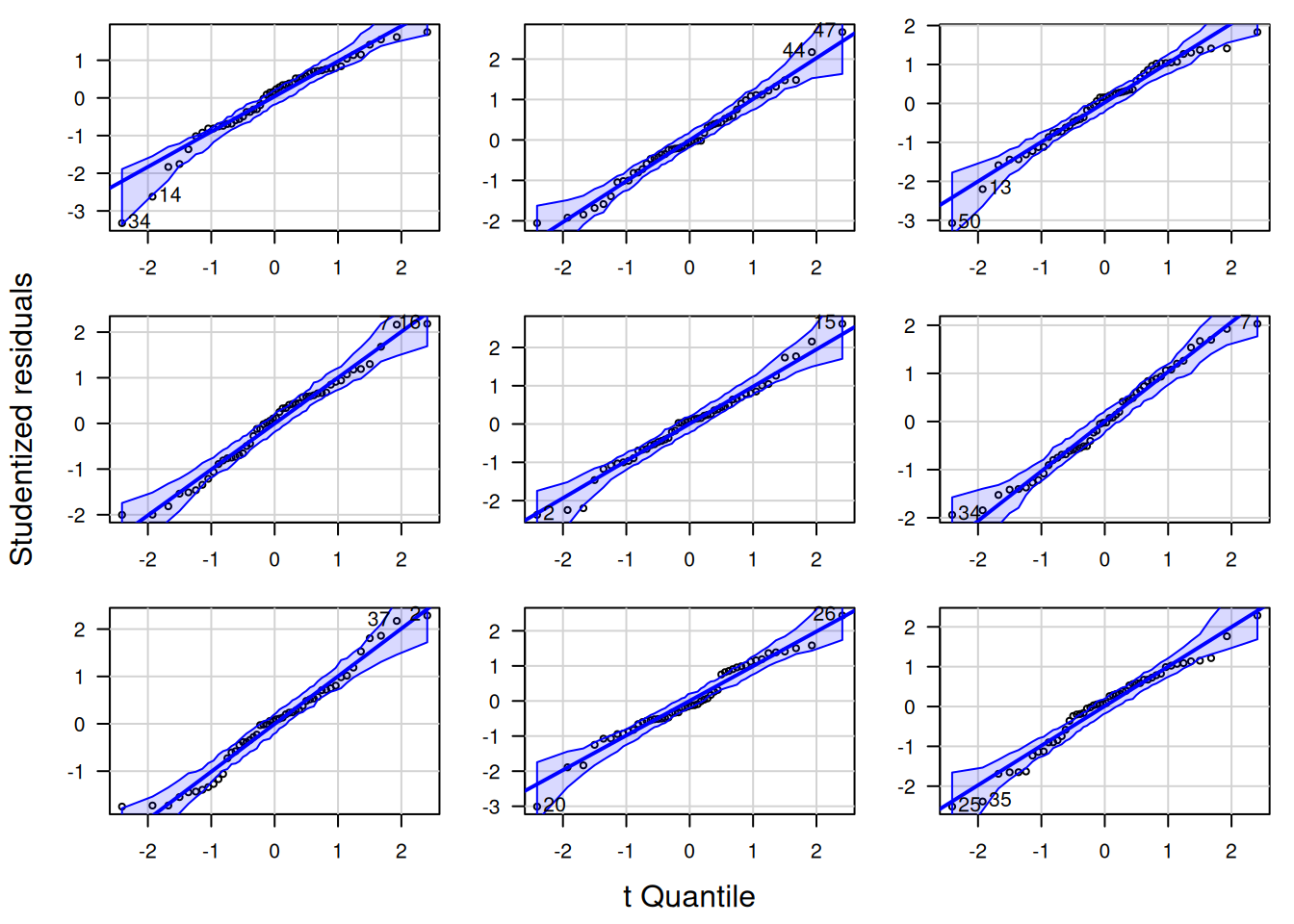
Figure 16.16: QQ-Plot für normalverteilte Residuen (mean = 0, sd=5). Die neun Plots zeigen die Variabilität für unterschiedliche Zufallsstichproben. Für die gezeigten Beispiele liegen alle Punkte innerhalb der 95%-Konfidenzbänder.
Die Entsprechung des Plottens des Absolutwertes der Residuen anstelle der Residuen selbst für den QQPlot ist der Plot gegen die am Mittelwert gefaltete Verteilung, z.B. die Halbnormalverteilung.
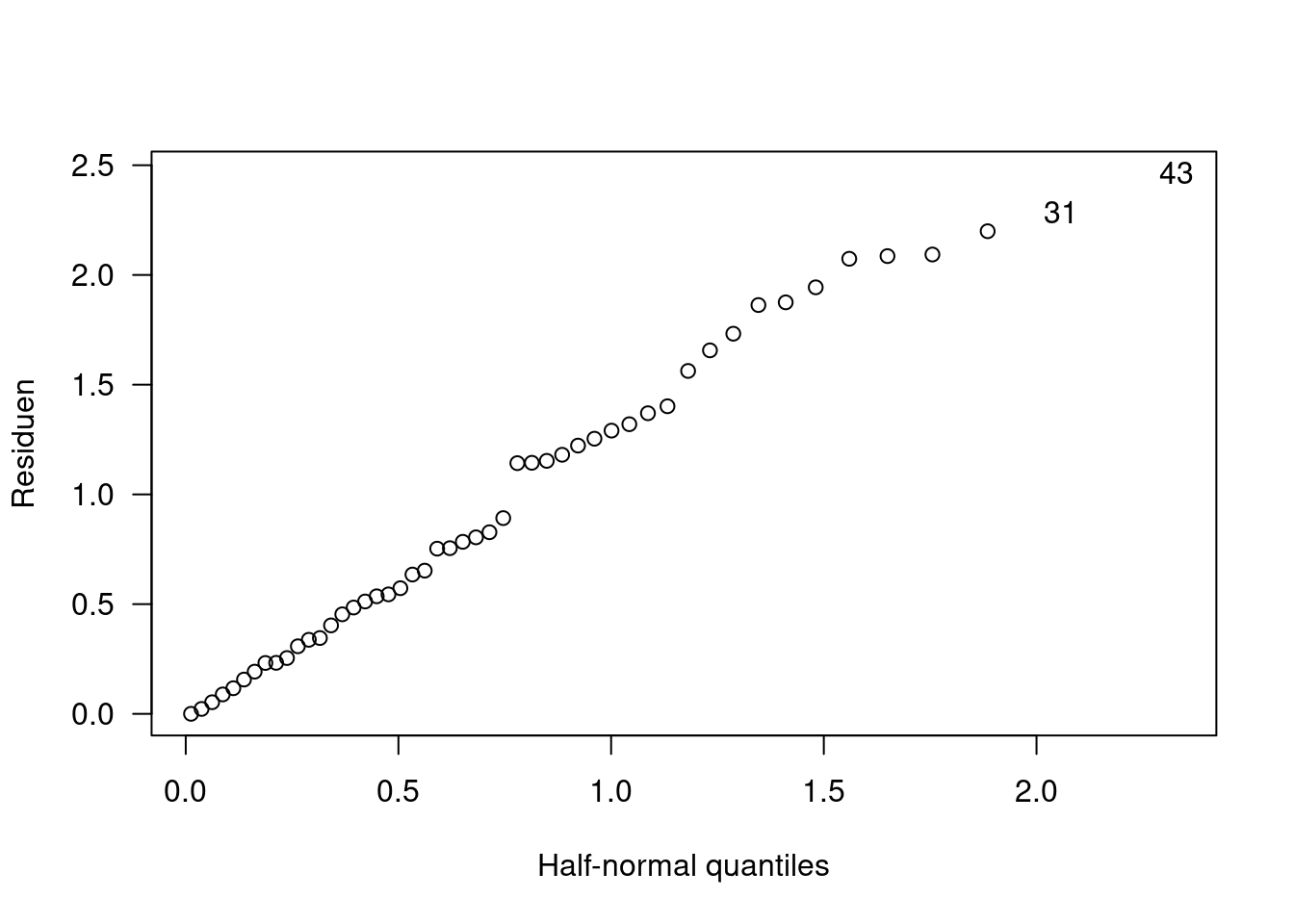
Im package hnp werden zur die halfnorm Plots zudem wie bei car::qqPlot zudem über einen Bootstrap-Ansatz mit Unsicherheitsbändern versehen.
## Gaussian model (lm object)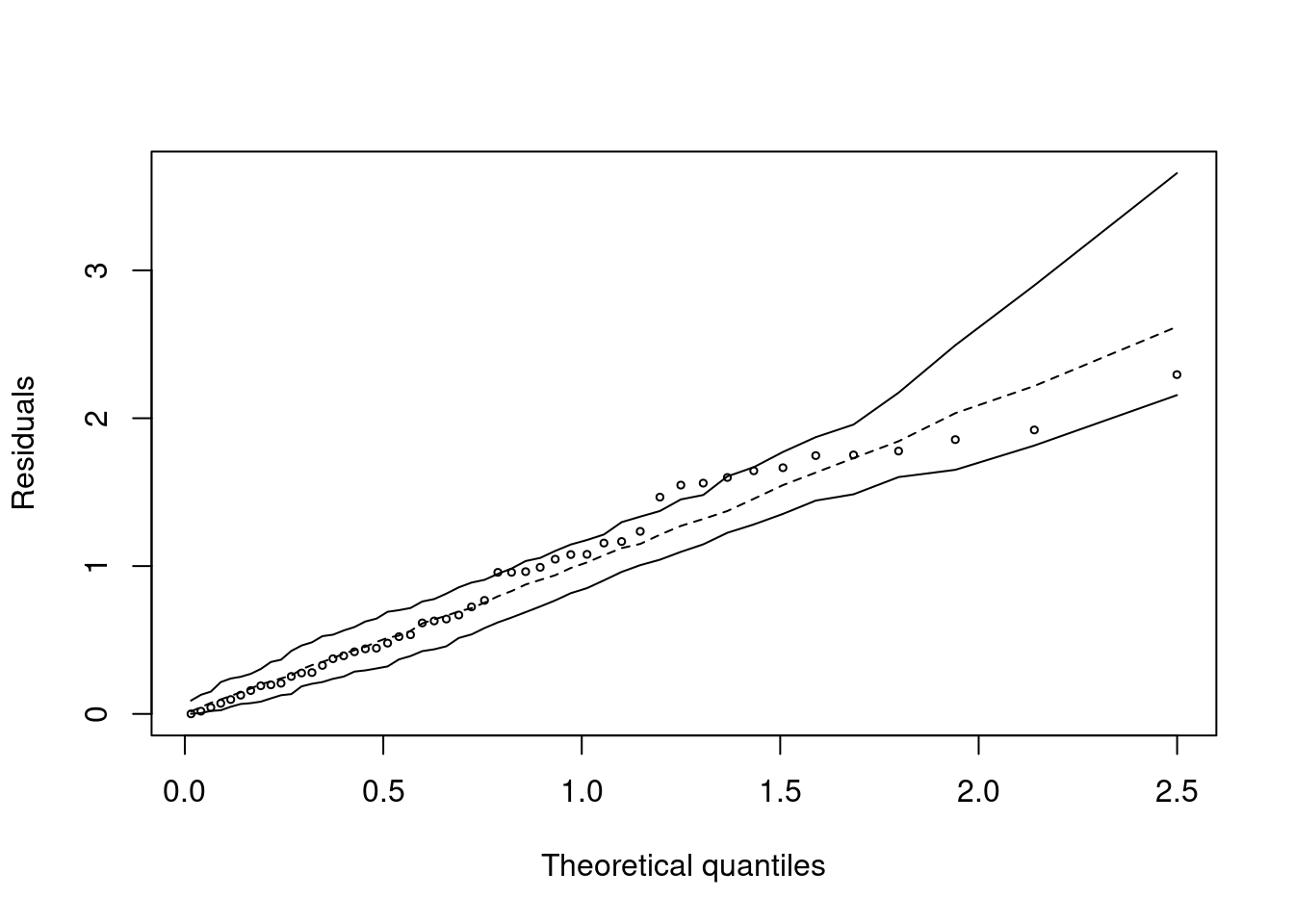
16.3 Einflußreiche Punkte: Leverage Points und Cook’s Distance
16.3.1 Leverage (#leverage)
Der Leverage (deutsch: Hebel) eines Punktes gibt an, wie weit außerhalb des Zentrums der Beobachtungen \(\overline X\) ein Punkt liegt. Je weiter außerhalb ein Punkt liegt, desto stärker ist üblicherweise sein Hebel, d.h. desto stärker zieht der Punkt die Regressionsgerade potentiell in seine Richtung.
Formal werden die Leverages mit der sogennanten Hat-Matrix berechnet:
\[ H = X(X^T X)^{-1}X^T\]
Die Hat-Matrix projiziert geometrisch gesprochen die beobachteten Werte (den Response) auf den Modell-Fit. Daher auch der Name Hat-Matrix: die Matrix, die den Hat (das Symbol ^, welches angibt, das der Wert anhand der Daten geschätzt ist) zum Response (\(y\)) dazufügt.
\[ \hat{y} = X\beta = X(X^T X)^{-1}X^T y = H y\] \(H\) enthält die Gewichte aller Beobachtungen für den geschätzten (gefitteten) Wert:
\[\hat{y}_i = \sum_{j=1}^n h_{ij} \cdot y_j\]
Die Diagonal-Elemente der Hat Matrix \(h_{ii}\) geben an, wie stark \(y_i\) auf \(\hat{y_i}\) wirkt und damit auch wie stark sich die Beobachtung \(i\) auf den Fit des Modells auswirkt. Sie werden als Leverage oder auch Levarage Scores bezeichnet.
Ausgehend von von der Tatsache, dass die Summe aller Leverages der Anzahl der Modellparameter p entspricht kann man ableiten, dass ein Punkt i im Mittel ein Leverage von \(h_i = p/n\) haben sollte. Als Faustregel sollten alle Punkte unsere Aufmerksamkeit erregen, bei denen \(h_i > 2p/n\) ist - es ist aber auch die Faustregel \(h_i > 3p/n\) im Gebrauch. Diese Punkte weißen nicht notendigerweise große Residuen auf: wenn die Regressionslinie zu dem Punkt gezogen wird, verläuft die Regressionslinie möglicherweise nahe am Punkt vorbei (d.h. kleines Residuum).
Aufmerksamkeit heißt nicht aus dem Modell entfernen! Hier können wir ggf. etwas über das Modell lernen.
Die Leverage Werte eines Modells bekommen wir über lm.influence(model)$hat. Nachfolgende wird gezeigt, wie man diese plottet und die Werte oberhalb des kritischen Leverages auswählt und labelt.
hat.vals <- lm.influence(g)$hat
par(mar = c(4.5,4.5,0.5,0.5), cex.lab = 1.5, cex.axis = 1.5)
plot(hat.vals,
xlab = "Sample index", ylab = "Hat values", cex.axis = .8, type="h", las=1)
n <- nrow(g$model)
p <- length(coef(g))-1 # ohne Achsenabschnitt
crit.val <- 2*p/n # kritischer Wert
abline(h= crit.val, lty=2) # den zeichnen wir in den Graph ein
idx <- which( hat.vals > crit.val) # Indizes der Punkte, deren Leverage oberhalb des kritischen Wertes liegt
text(x=idx, y = jitter(hat.vals[idx] + 0.005), labels= temp.ru$NAME[idx], xpd=TRUE, cex=.7) # für diese tragen wir den Stationsnamen ein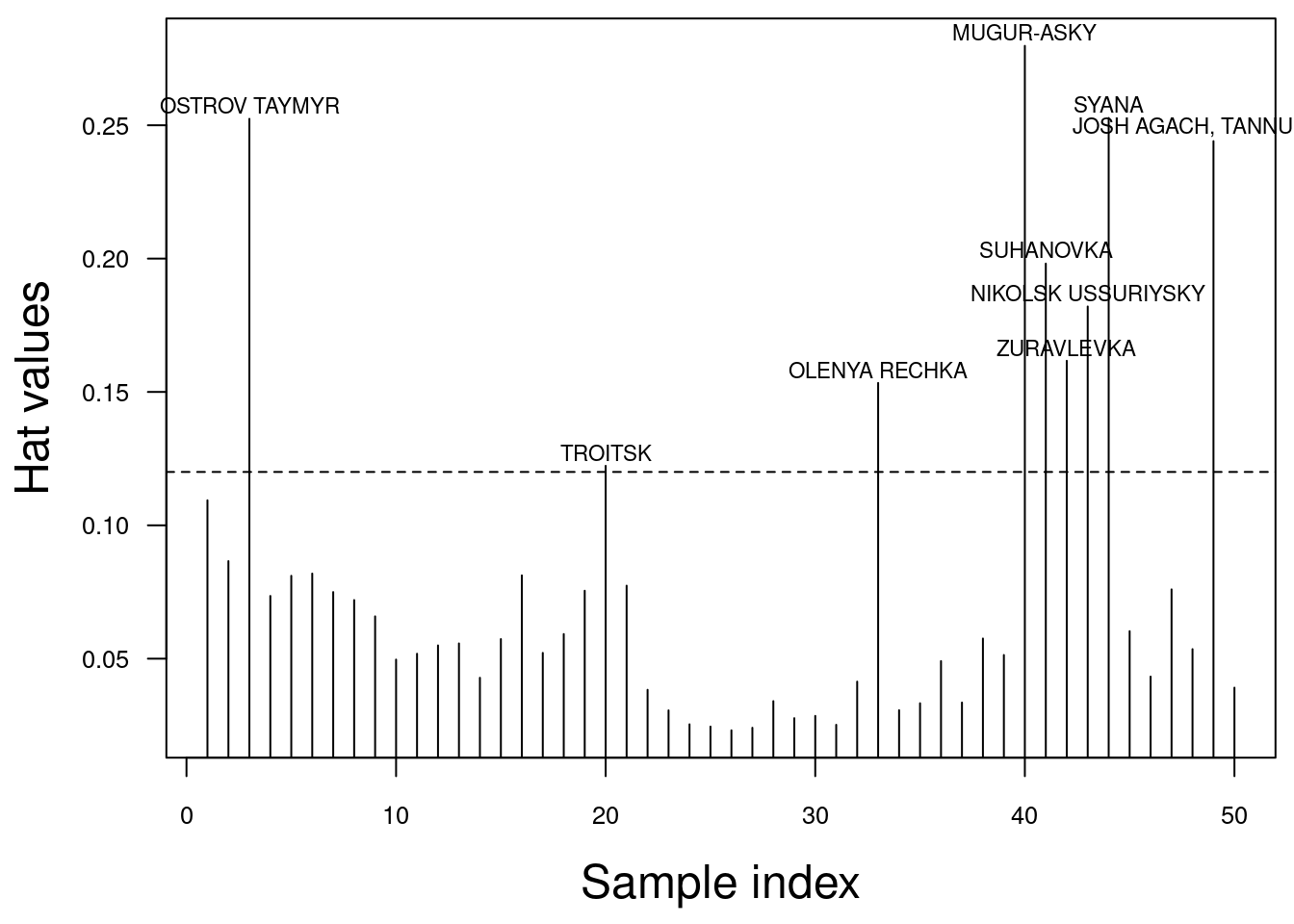
Für die deutschen Klimastationen ist die Analyse etwas einfacher, da wir die Gegebenheiten besser kennen:
temp.de <- subset(temp, CNTRY_NAME == "Germany")
g.de <- lm(YEAR ~ ELEV + LAT + LON, data=temp.de)
hat.vals <- lm.influence(g.de)$hatpar(mar = c(4.5,4.5,0.5,0.5), cex.lab = 1.5, cex.axis = 1.5)
plot(hat.vals, las = 1,
xlab = "Sample index", ylab = "Hat values",
cex.axis = .9, type="h")
n <- nrow(g.de$model)
p <- length(coef(g))-1 # ohne Achsenabschnitt
crit.val <- 2*p/n # kritischer Wert
abline(h= crit.val, lty=2)
idx <- which( hat.vals > crit.val)
text(x=idx, y = jitter(hat.vals[idx] + 0.005), labels= temp.de$NAME[idx], xpd=TRUE, cex=.7)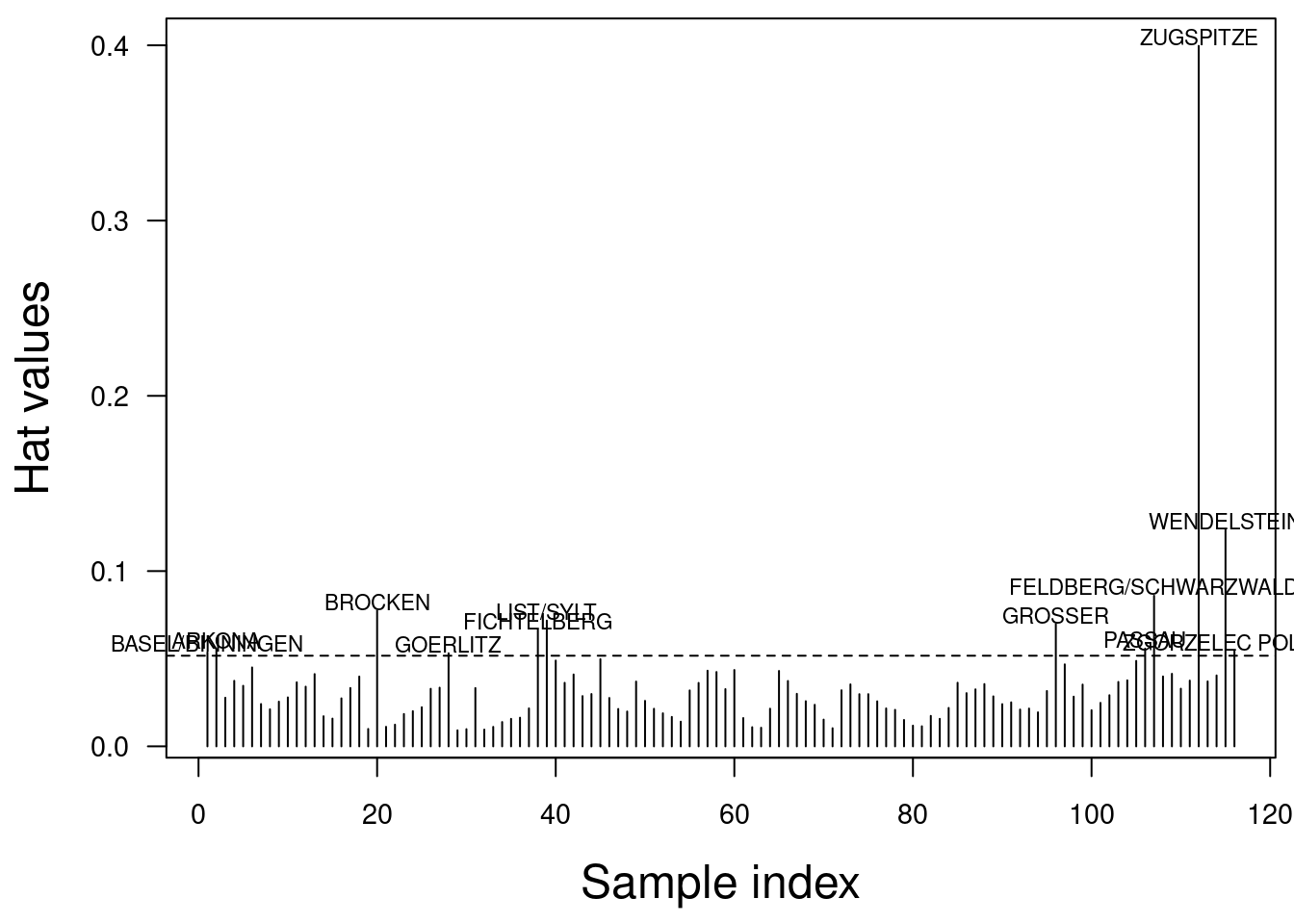
Vor allem die Zugspitze sticht heraus.
Welche Punkte sind das im Scatterplot?
newDat.de <- data.frame(ELEV=seq(min(temp.de$ELEV), max(temp.de$ELEV), length.out=100), LAT=mean(temp.de$LAT), LON=mean(temp.de$LON))
pred.de <- as.data.frame(predict(g.de, newdata = newDat.de, interval="confidence"))
# identify points in the scatterplot as well
temp.de$hat.vals <- hat.vals
plot(YEAR ~ ELEV, data=temp.de, pch=16, cex=sqrt(hat.vals)*5, col=ifelse(hat.vals > crit.val, "red", "grey"), main="Temperaturstationen in Deutschland", ylab="Jahresmitteltemperatur [°C]", xlab="Höhe [m]")
lines(pred.de$fit ~ newDat.de$ELEV, col="grey")
lines(pred.de$lwr ~ newDat.de$ELEV, lty=2, col="grey")
lines(pred.de$upr ~ newDat.de$ELEV, lty=2, col="grey")
legend(x="topright", pch=16, col="red", legend="Hoher \nLeverage\nWert ", bty = "n")
text(x=temp.de$ELEV[idx], y =temp.de$YEAR[idx] , labels= temp.de$NAME[idx], xpd=TRUE, cex=.6, col="red", offset = 1, pos = 1:4)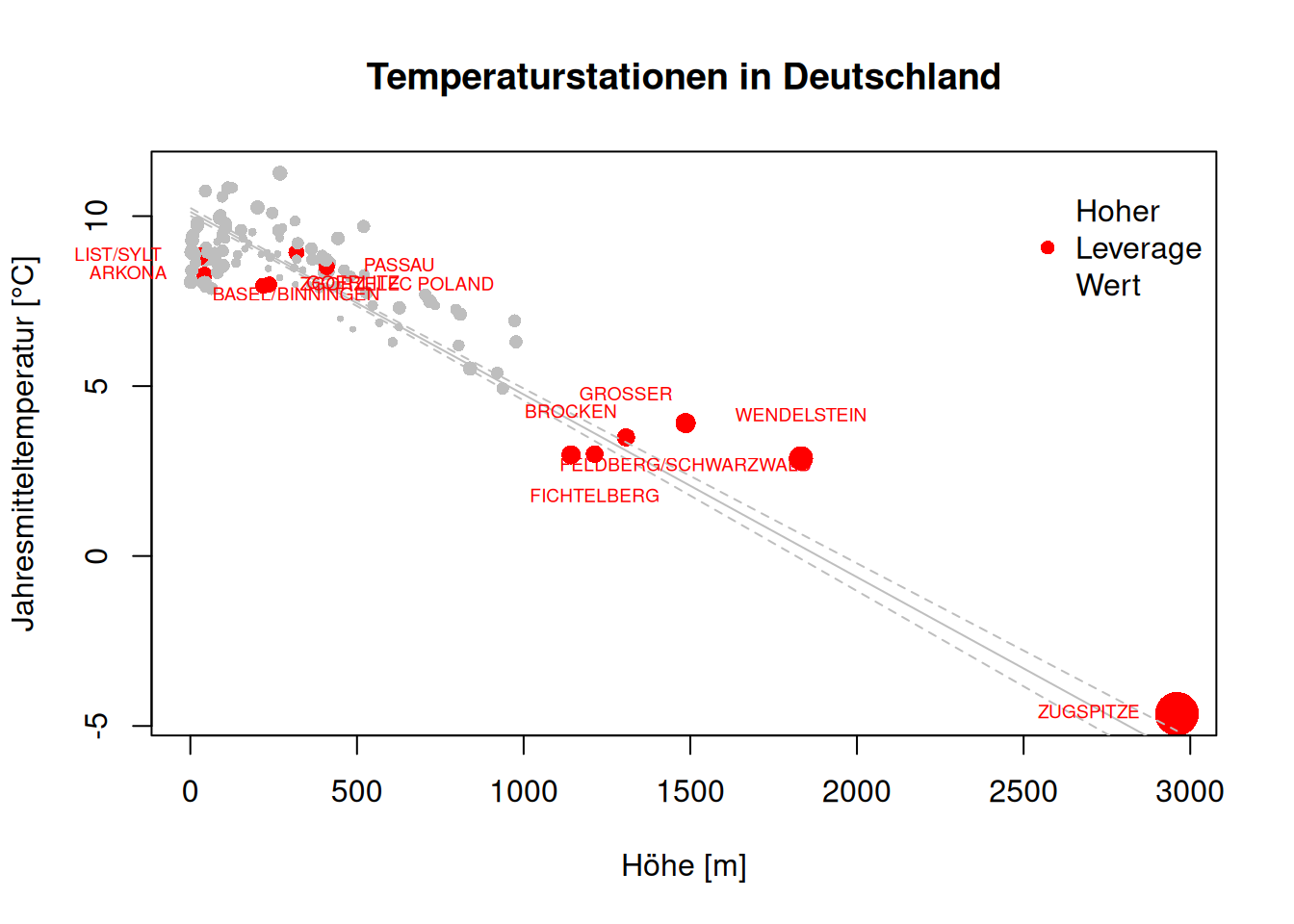
Figure 16.17: Verdeutlichung des Leverages einzelner Punkte anhand des deutschen Klimastationen Datensatzes. Gezeigt wird der Zusammenhang zwischen Geländehöhe und Jahresmitteltemperatur. Als graphische Variable wird Größe benutzt, über die der Leverage Score dargestellt wird. Bedeutende Punkte sind zudem eingefärbt und gelabelt.
Wie wir sehen (Abbildung 16.17), besitzt Zugspitze einen hohen Leverage Score, aber auch die Werte im mittleren Höhenbereich und einige Punkte im niedrigen Höhenbereich.
Eine andere Möglichkeit, die Leverages darzustellen ist der sogennante halfnorm Plot im Packet faraway. Der Plot ist ähnlich wie der QQ-Plot, nur plottet er die Werte gegen die Quantile der Halbnormalverteilung. Die Interpretation ist ähnlich wie beim QQ-Plot, allerdings sollten wir keine gerade Linie erwarten. Interessant sind große Abweichungen vom allgemeinen Verlauf, also Sprünge.
Bei den deutschen Klimastationen sehen wir auch im halfnorm Plot (Abbildung 16.18), dass die Klimastationen Zugspitze und deutlich schwächer Wendelstein eine starke Wirkung auf die Regressionsline haben.
## Loading required package: faraway##
## Attaching package: 'faraway'## The following objects are masked from 'package:car':
##
## logit, vifhalfnorm(lm.influence(g.de)$hat, labs=temp.de$NAME,
ylab="Leverages", xlim=c(0,3),
las = 1)
abline(h=crit.val, lty=3,
col="grey")
text(x=2.75, y= crit.val +-0.013,
labels = "Schwellwert 2*p/n ",
col="grey")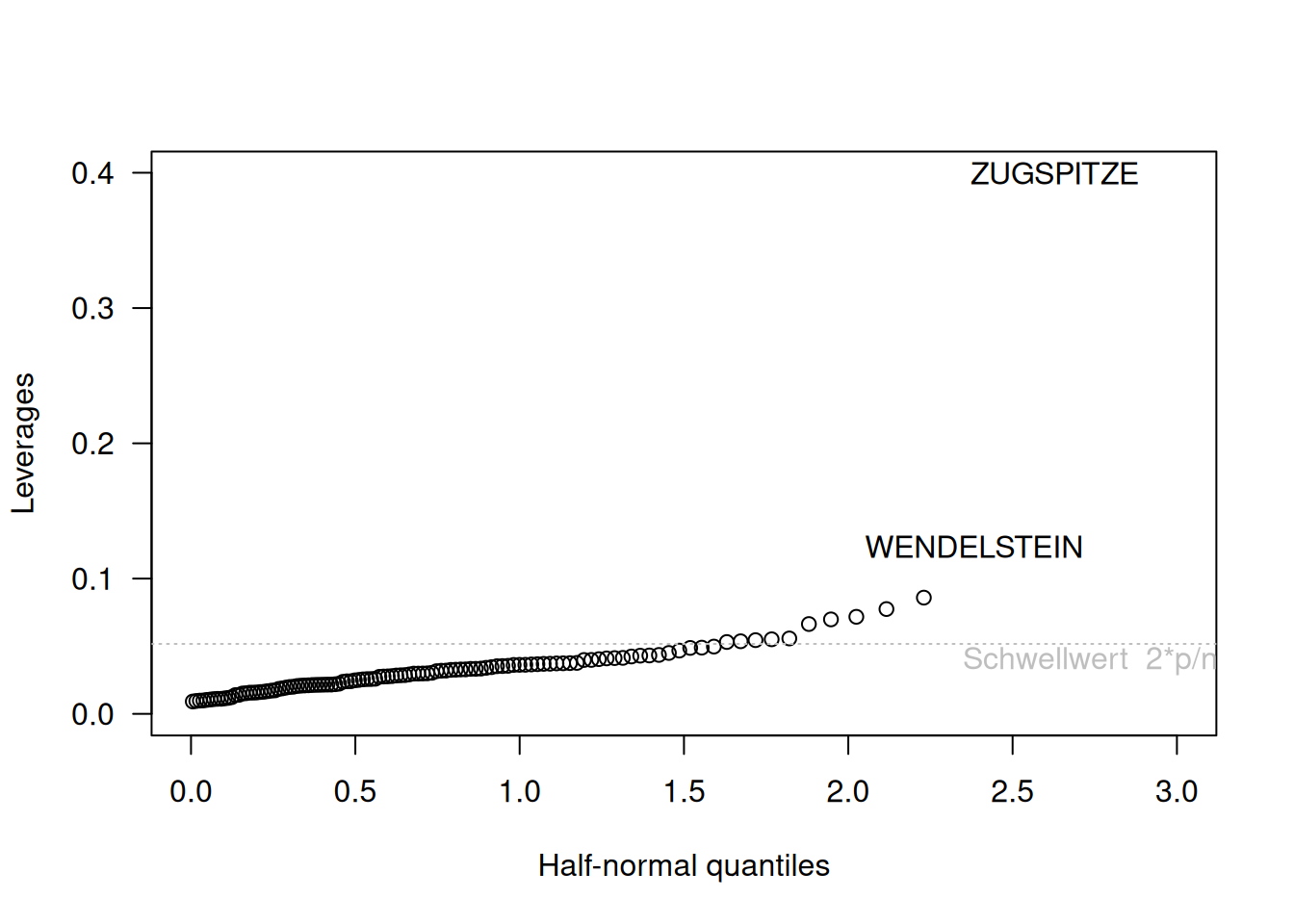
Figure 16.18: Halfnormplot für die deutschen Klimastationen. Die Beobachtungen sind anhand ihrer Leveragewerte sortiert und werden gegen die Quantile des positiven Teils der Standardnormalverteilung geplottet. Werte die deutlich neben dem Verlauf der anderen Beobachtungen liegen sind auffällig.
Andere interessante Einflussmerkmale, die wir über lm.influence(model) erhalten sind neben hat sind insbesondere die Regressionskoeffizienten, die wir erhalten würden, wenn wir die Regression ohne die betreffende Beobachtung fitten würden.
Wie wir sehen, sind die Stationen Wendelstein und Zugspitze einflußreich im Hinblick auf den Regressionskoeffizienten für Geländehöhe (Abbildung 16.19). Für den Breitengrad sind es Freiburg, München (Stadt) und Basel/Binningen Abbildung 16.20). Für den Regressionskoeffizienten von Längengrad ist es vor allem Wahnsdorf Abbildung 16.21).
g.de_dfbetas <- lm.influence(g.de)$coefficients %>% as.data.frame()
g.de_dfbetas$Name <- temp.de$NAME
g.de_dfbetas$index <- 1:nrow(temp.de)
ggplot(g.de_dfbetas, aes(y=ELEV, x=index)) +
geom_point() +
geom_text(data= subset(g.de_dfbetas, (ELEV > 2*10^-5) | (ELEV < -5*10^-5)),
mapping=aes(label= Name),
hjust= "inward",
vjust="inward") +
ylab("beta für Geländehöhe ohne die Station") +
xlab("Index der Station")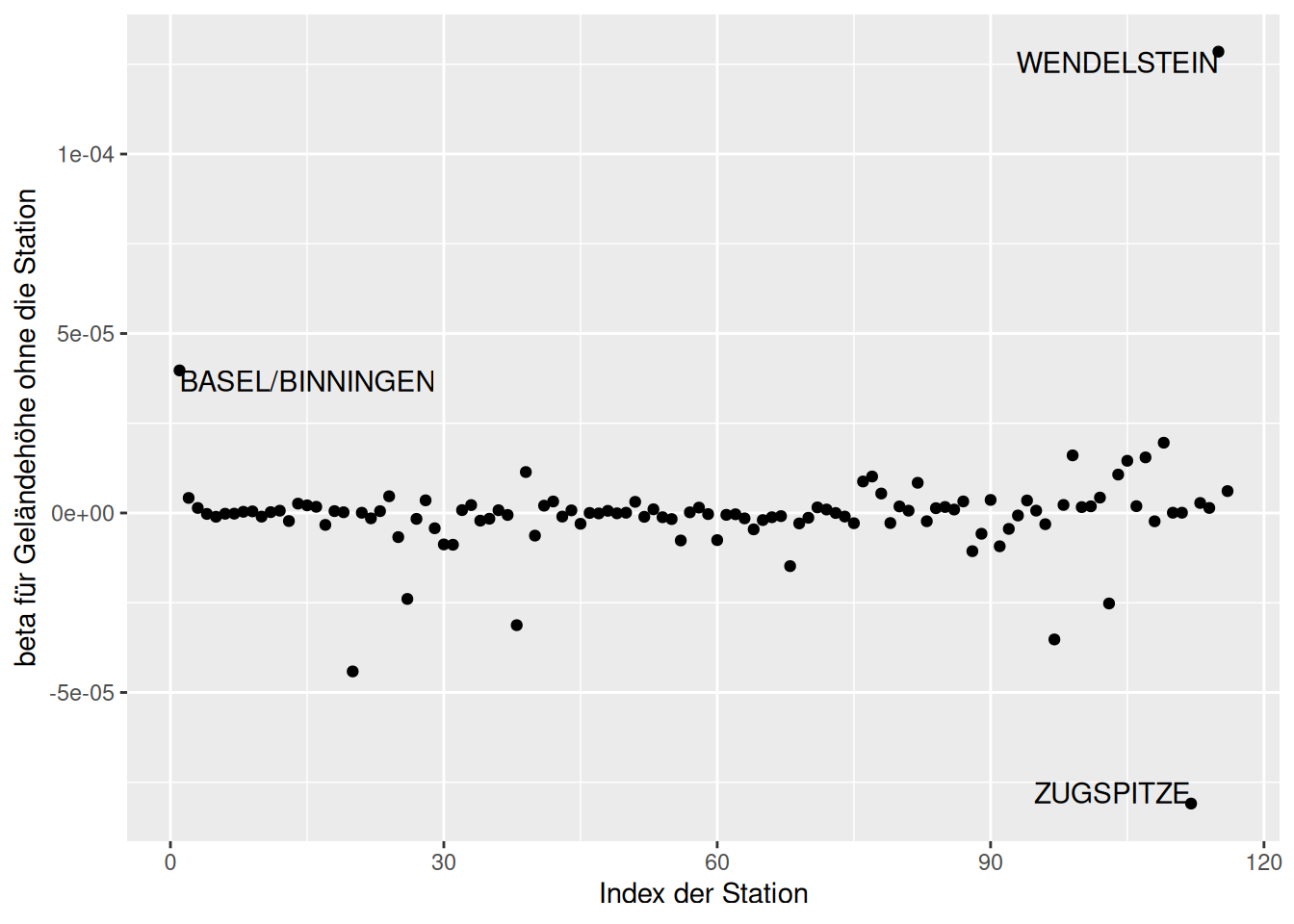
Figure 16.19: Veränderung der Regressionskoeffizienten wenn eine Station weggelassen würde. Dargestellt für die deutschen Klimastationen und den Effekt auf Geländehöhe.
ggplot(g.de_dfbetas, aes(y=LAT, x=index)) +
geom_point() +
geom_text(data= subset(g.de_dfbetas, (LAT > .01 ) | (LAT < -0.01)),
mapping=aes(label= Name),
hjust= "inward",
vjust="inward")+
ylab("beta für Breitengrad ohne die Station") +
xlab("Index der Station")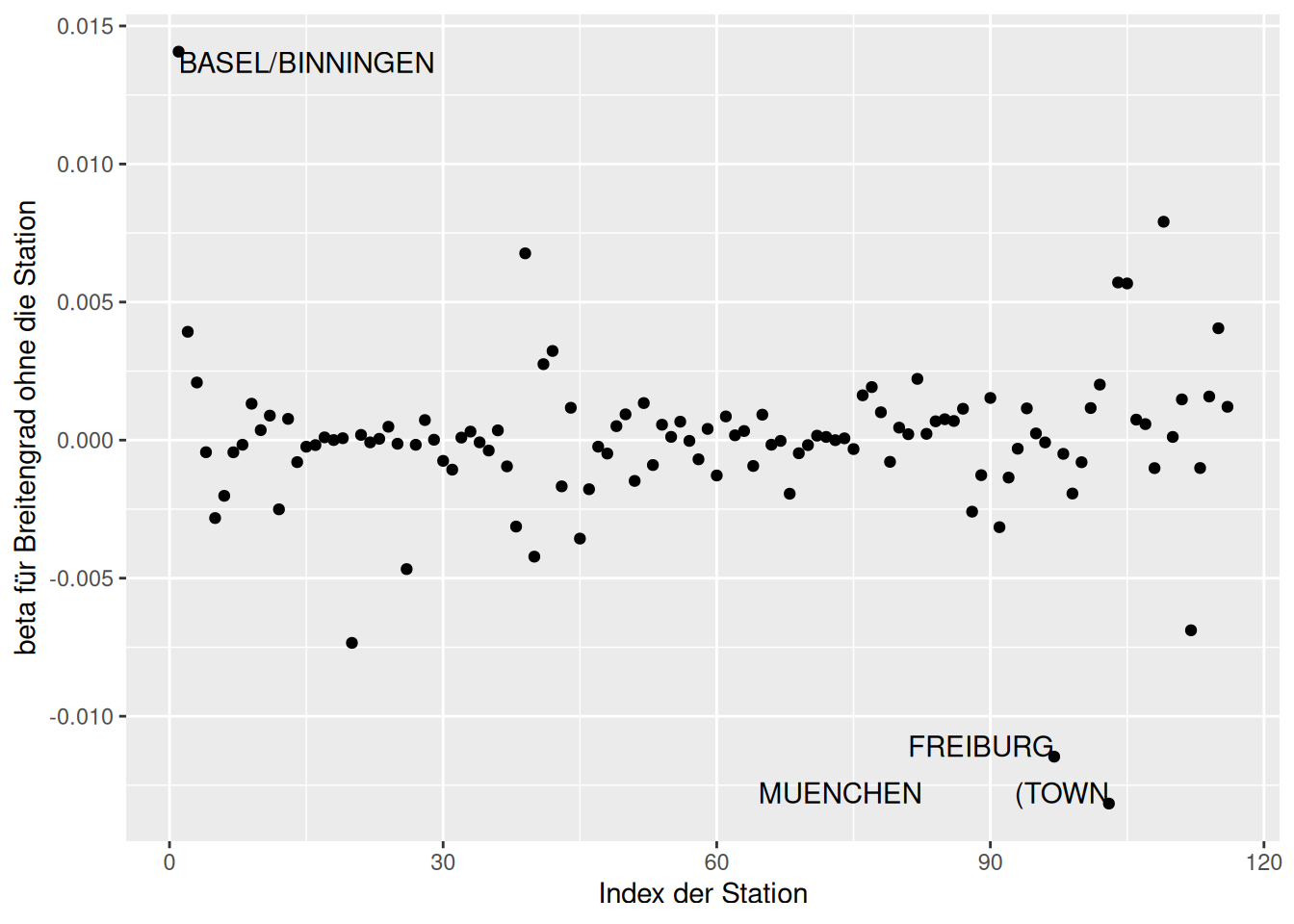
Figure 16.20: Veränderung der Regressionskoeffizienten wenn eine Station weggelassen würde. Dargestellt für die deutschen Klimastationen und den Effekt auf Breitengrad.
ggplot(g.de_dfbetas, aes(y=LON, x=index)) +
geom_point() +
geom_text(data= subset(g.de_dfbetas, (LON > .01 ) | (LON < -0.005)),
mapping=aes(label= Name),
hjust= "inward",
vjust="inward") +
ylab("beta für Längengrad ohne die Station") +
xlab("Index der Station")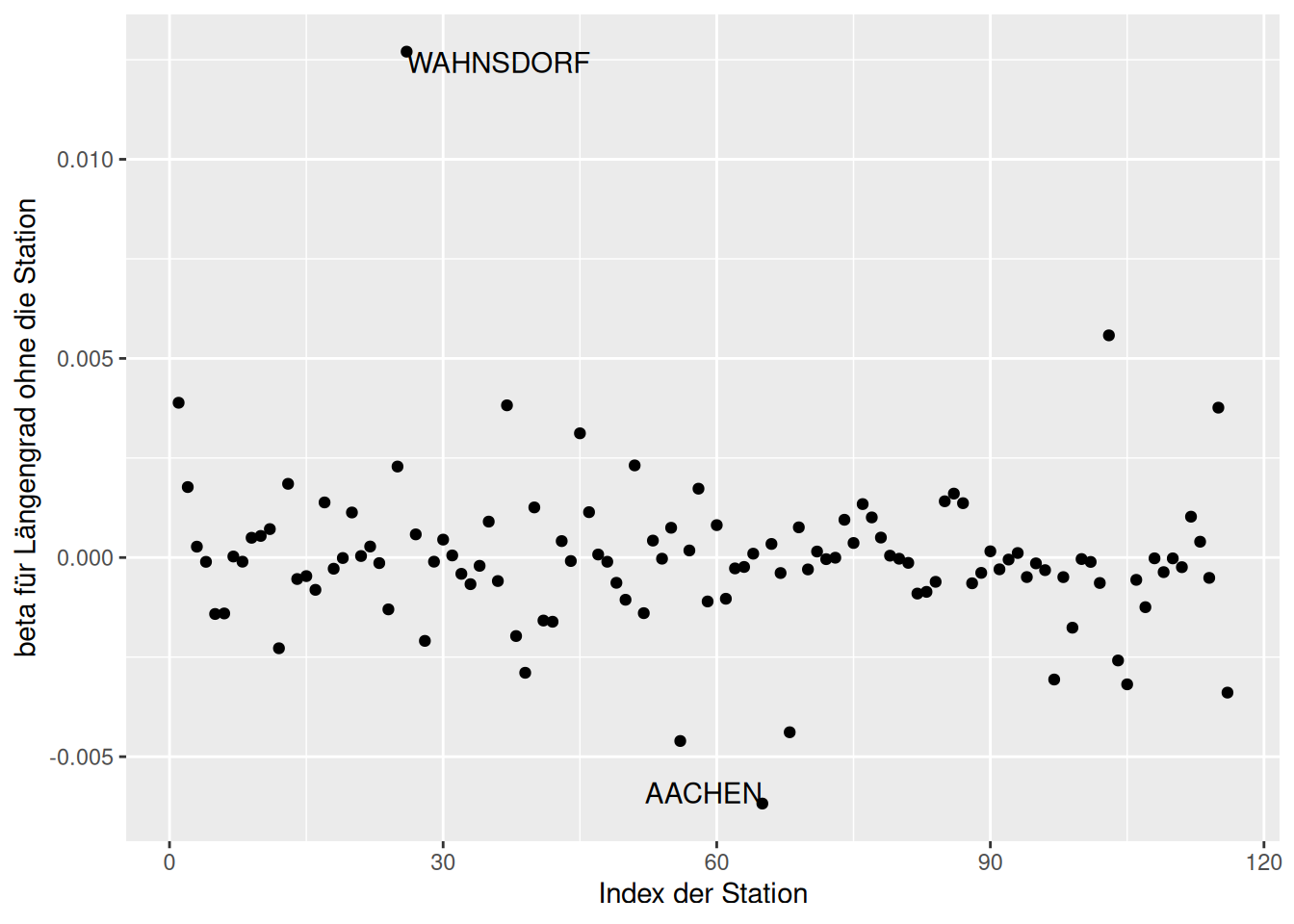
Figure 16.21: Veränderung der Regressionskoeffizienten wenn eine Station weggelassen würde. Dargestellt für die deutschen Klimastationen und den Effekt auf geographische Länge.
16.4 Cook’s Distance (#cooksdistance)
Zusätzlich interessant ist die sogenannte Cook’s Distance, die misst, wie stark sich die Regressionsline verändert, wenn die Regression ohne den Punkt gefittet wird (Cook 1977). Der Indikatorwert berücksichtigt sowohl die Residuen als auch den Leverage. Dem Ansatz liegt folgende Überlegung zugrunde: ein einflußreicher Punkt kann ein Ausreißer sein oder auch nicht und er kann einen hohen Leverage besitzen oder auch nicht. Ein Punkt, der einen hohen Leverage Score oder ein hohes Residuum besitzt ist i.d.R. jedoch als einflußreich zu charakterisieren.
Die Werte werden wie folgt berechnet:
\[ D_i = \frac{(\hat{y} - \hat{y}_{(i)})(\hat{y} - \hat{y}_{(i)})}{p\hat{\sigma}^2} = \frac{1}{p}r_i^2\frac{h_i}{1-h_i} \]
\(\hat{y}_{(i)}\) ist dabei der geschätzte Wert, wenn das Modell ohne den Datenpunkt i gefittet wird, während \(\hat{y}\) den geschätzten Wert beim Modell, das mit allen Datenpunkten gefittet wurde beschreibt. \(h_i\) ist der Leverage Wert für die Beobachtung, \(r_i\) ist das Residuum, \(p\) die Anzahl Parameter im Modell und \(\sigma^2\) die Residualvarianz des Modells.
Cook’s distance für einen Datenpunkt i ergibt sich somit anhand der Anzahl der Modellparameter p, des Residums \(r_i\) und des Verhätnisses von Leverage \(h_i\) zu 1- Leverage.
Als Fausregel sind Beobachtungen mit einer Cook’s Distance größer 1 auffällig.
Interessanterweise ist es nun nicht mehr die Zugspitze, die auffällig ist, sondern die Klimastationen Wendelstein und Wahnsdorf. Vom absoluten Wert her sind die Beobachtungen allerdings nicht beorgniserregend, da Cook’s Distance stets kleiner als 1 ist.
cook.de <- cooks.distance(g.de)
halfnorm(cook.de, labs=temp.de$NAME,
ylab="Cook's Distance", xlim=c(0,3),
las = 1)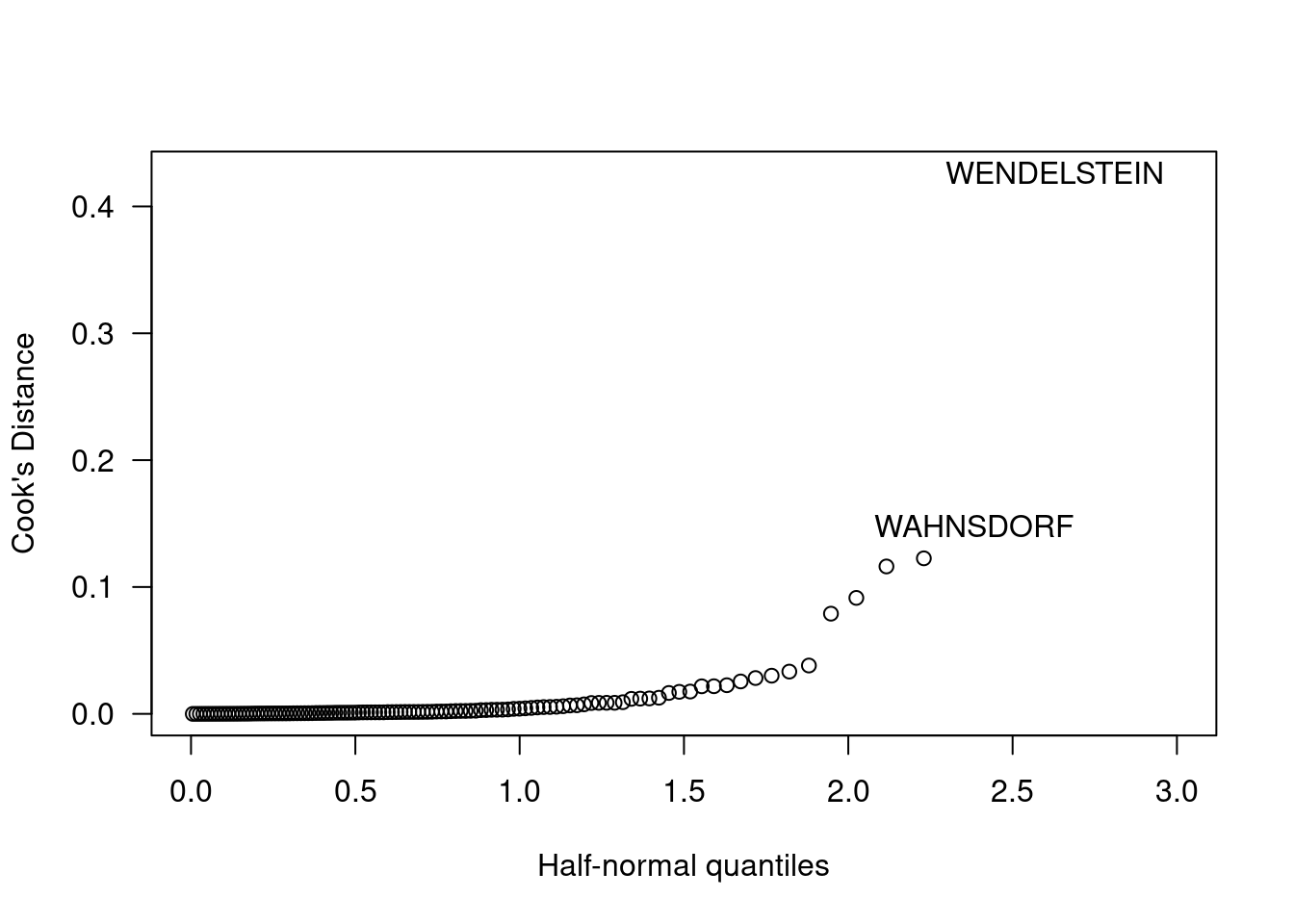
Welche Punkte sind das im Scatterplot?
temp.de$cooksd <- cook.de
plot(YEAR ~ ELEV, data=temp.de, pch=16, cex=sqrt(cooksd)*5, col=ifelse(cooksd > .1, "red", "grey"), main="Klimastationen in Deutschland", ylab="Temp [°C]", xlab="Geländehöhe [müNN]")
lines(pred.de$fit ~ newDat.de$ELEV, col="grey")
lines(pred.de$lwr ~ newDat.de$ELEV, lty=2, col="grey")
lines(pred.de$upr ~ newDat.de$ELEV, lty=2, col="grey")
legend(x="topright", bty="o", pch=16, col="red", legend="Hohe \nCook's Distanz")
idx <- which(temp.de$cooksd > .1)
text(x=temp.de$ELEV[idx], y =temp.de$YEAR[idx] , labels= temp.de$NAME[idx], xpd=TRUE, cex=.6, col="red", offset = 1, pos = 1:4)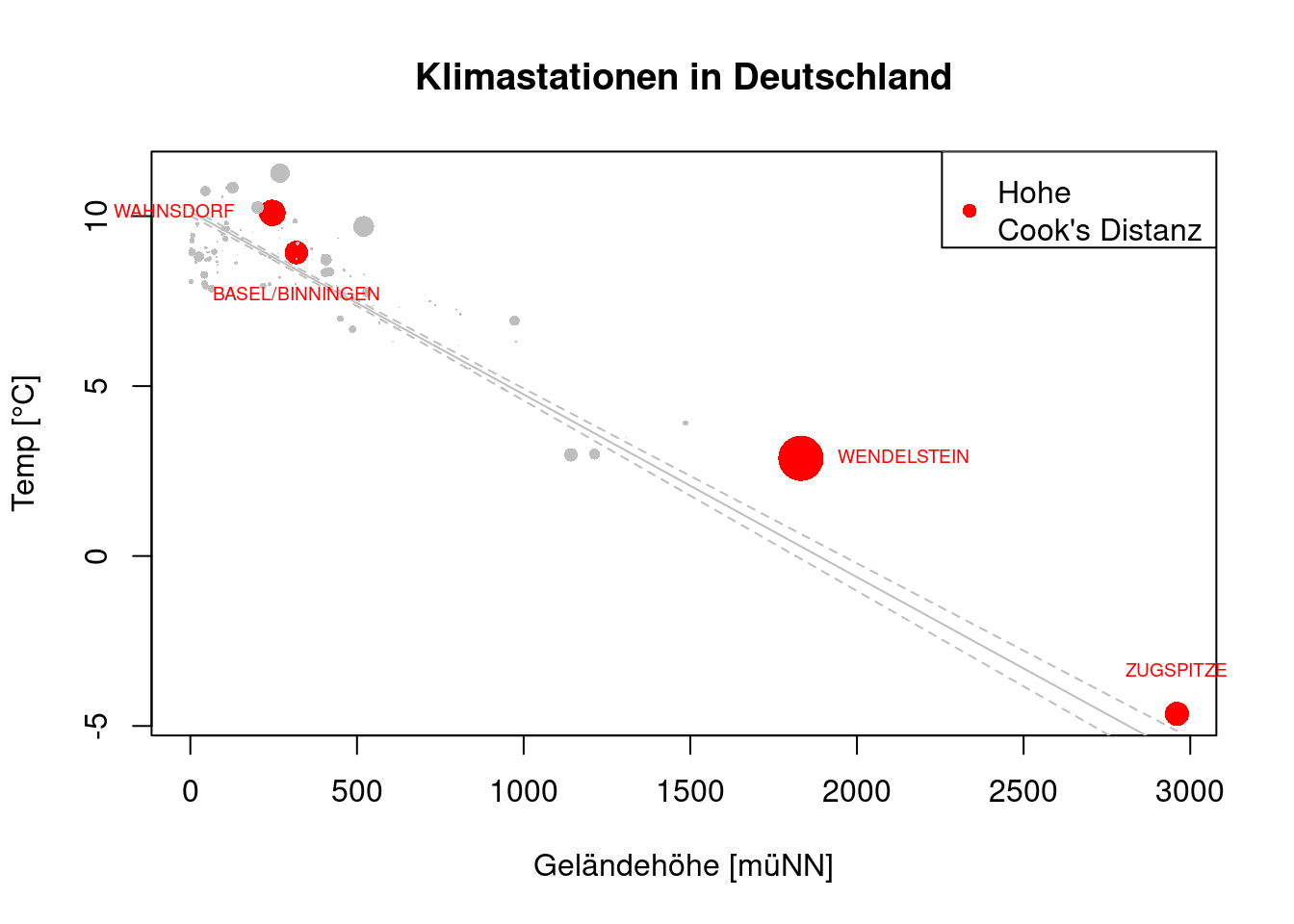
Weiterführend Informationen zu einflussreichen Punkten und Maßen um diese zu identifizieren finden sich in (Chatterjee and Hadi 1986).
R bietet eine einfache Möglichkeit, oft benutzte Diagnoseplots zu erzeugen, indem wir einfach das Regressionsobjekt plotten. Da wir standardmäßig 4 (hier 6) Plots zurück bekommen, empfiehlt es sich ggf. mittels par(mfrow=c(2,2)) bzw. par(mfrow=c(3,2)) den Plotbereich in 2 bzw. 3 Zeilen und 2 Spalten auszuteilen (Abbildung @ref{fig:standardDiagnosticPlots}).
Neben den bereits behandelten Plots wird die Quadratwurzel der standardisierten Residuen gegen die vorhergesagten Werte geplottet (Plot 3) sowie die Residuen gegen den Leverage (Plot 5) und der Leverage geteilt durch (1-Leverage) gegen Cook’s Distance (Plot 6), wobei Cook’s Distance bzw. die standardisierten Residuen in Form von Isolinien als dritte Komponente dem Plot überlagert werden. Die Hilfe für die Funktion findet man unter ?plot.lm.
# use the default diagnostics plot for regression models
par(mfrow=c(3,2))
plot(g.de, which=1:6, labels.id=temp.de$NAME)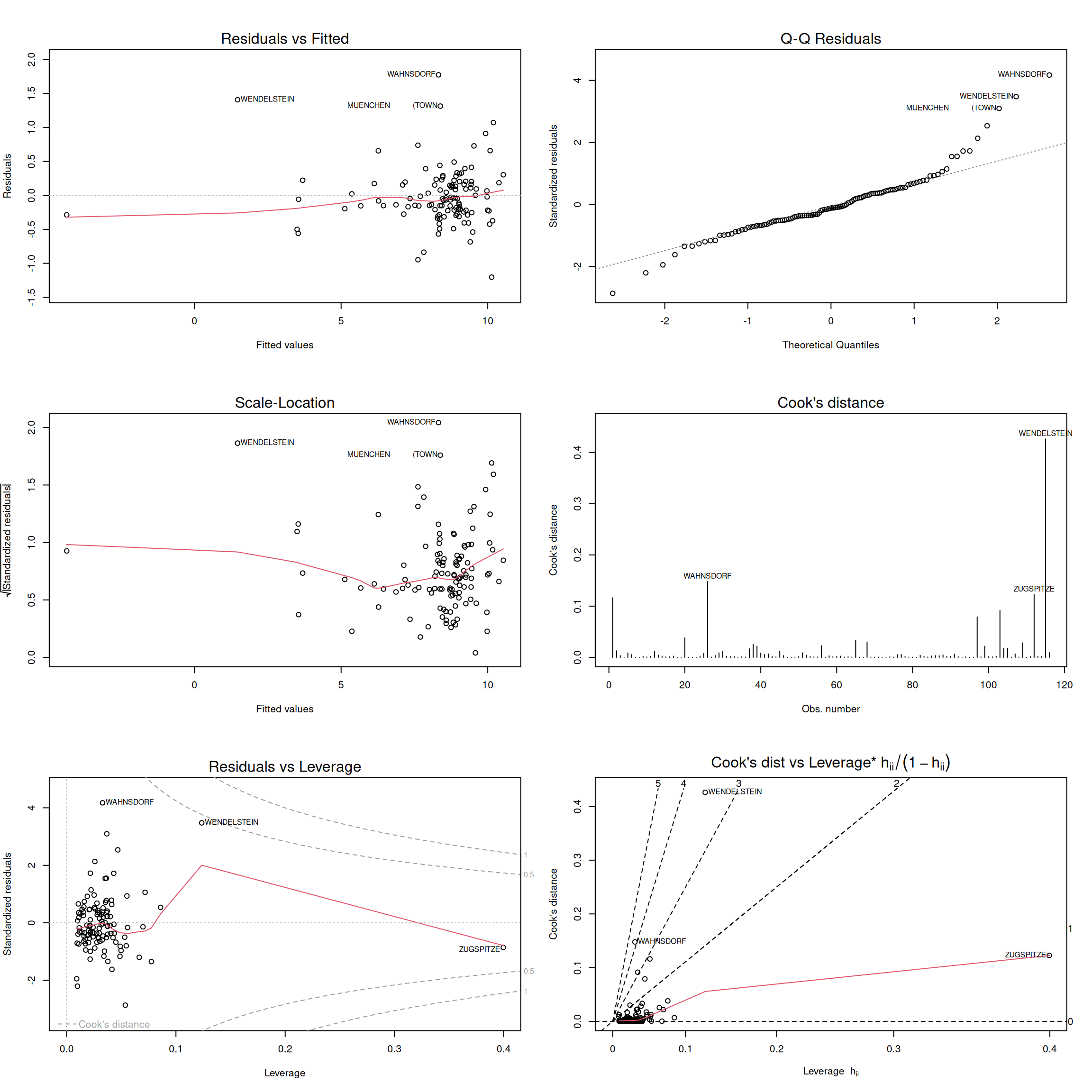
Figure 16.22: Die sechs Standard Diagnostik-Plots die R für lm Objekte anbietet.
Weiterführende/zitierte Literatur
Wenn wir uns eine Verteilung für die Prädiktoren wünschen dürften, sollten diese i.d.R. möglichst gleichverteilt und nicht normalverteilt sein.↩︎