Kapitel 22 Forschungsdesign

Bisher habe wir uns weitgehend darauf fokussiert, wie man Daten analysiert und nicht damit, wie man Daten erhebt. Im Bereich der Assoziations-Tests hatte ich angedeutet, dass das Design der Studie relevant sein kann um zu entscheiden, welcher Test angewandt werden kann (G-Test, \(\chi^2\)-Anpassungstest und Fishers exakter Test). Nun wollen wir uns etwas intensiver mit der Materie beschäftigen, da es a) relevant ist, wenn man selbst in die Verlegenheit kommt Daten erfassen zu müssen und b) die Art und Weise des Stichproben oder experimentelles Designs nicht unerhebliche Konsequenzen für die statistische Auswertung haben kann.

22.1 Abgrenzung verschiedener Forschungsdesigns

Die Erhebung von Daten erfolgt unter unterschiedlichen Randbedingungen. Welche Art der Datenerhebung durchführbar ist hängt von einer Vielzahl von Faktoren ab, die z.B. die verfügbaren Ressourcen (Zeit und Geld) aber auch ethische und moralische Fragen umfassen.

22.1.1 Randomisierte kontrollierte Studie

Vielfach gilt eine randomisierte kontrollierte Studie (randomized controlled experiment) als Goldstandard. Dabei werden die Auswirkungen einer oder mehrerer Intervention(en) auf Studienobjekte durch Vergleich mit einer Kontrollgruppe untersucht. Die eine Versuchsgruppe erhält z.B. Informationen zu den möglichen Auswirkungen des Klimawandels, die Kontrollgruppe nicht. Dann wird untersucht, ob sich z.B. die Zahlungsbereitschaft für Klimaschutzprogramme unterscheidet. Im Bereich der physischen Geographie untersucht man z.B. Bodenerosion auf Parzellen am Hang, wobei ein Teil der Parzellen konventionell bearbeitet wird, während andere z.B. mit einer Zwischensaat oder hangparallelem Pflügen bewirtschaftet werden.

Die Zuordnung zu einer Gruppe (Versuchsgruppe oder Kontrollgruppe) erfolgt dabei zufällig. D.h. es wird sowohl ein self-selection bias (z.B. Studienteilnehmer wählen selbst eine Gruppe) als auch ein (unbewusster) Bias durch die Wissenschaftler (Auswahl sympathischerer oder jüngerer oder weiblicher oder interessierter erscheiender oder … Personen für die Versuchsgruppe) vermieden.

Zuletzt zeichnet sich eine radomisierte kontrollierte Studie dadurch aus, dass die Intervention unter der Kontrolle der Wissenschaftler ist. Die Intervention erfolgt also ausschließlich aufgrund der Zuordnung zu einer der Gruppen. Man nennt solche Studien auch manipulative Experimente, da die Intervention nicht zufällig, sondern kontrolliert erfolgt.

Ziel ist es, die Auswirkung der Intervention auf eine Ergebnissgröße zu untersuchen. Eventuelle Stör- oder Einflussgrößen (confounding factors) müssen mit erfasst werden, um dafür - z.B. in Regressionsmodellen - korrigieren zu können. Durch das Forschungsdesign werden eine Reihe von Problemen ausgeschaltet. Trotzdem kann natürlich einiges schief gehen bzw. die Studie nicht aussagekräftig sein. Relevante Faktoren sind (wie bei anderen Forschungsdesign auch) die Anzahl der Teilnehmer bzw. Subjekte bzw. Objekte (die Anzahl der Replikate), die Genauigkeit der Messung, die Variabilität der Reaktion auf die Intervention, eine günstige Erfassung der confounding factors und einiges mehr. Da das Experiment kontrolliert erfolgt, können die Forschenden allerdings auf solche Faktoren eingehen - vorausgesetzt die benötigten Ressourcen sind verfügbar.

Wichtig ist beispielsweise, dass Nebenwirkungen der Intervention mit kontrolliert werden. So wurden in einem Experiment zusammen mit dem psychologischen Institut die Auswirkungen von Karten zu hochaufgelösten \(CO_2\)-Emissionen auf die Zahlungsbereitschaft untersucht. Um auszuschließen, dass alleine das zeigen einer Karte einen Einfluss hat, wurde auch den Teilnehmern der Kontrollstudie eine Karte anderen Inhalts gezeigt. Wenn man den Effekt des Ausschlusses von Beweidung auf die Vegetationsdecke untersuchen will, sollte man sicherstellen, dass es durch den Zaun oder die Mauer nicht zu anderen Effekten (Verschattung, Mikroklimatische Änderungen durch Verwirbelung,…) kommt.

In vielen Fällen sind randomisierte kontrollierte Studien allerdings nicht durchführbar. So wäre es sicher aus wissenschaftlicher Sicht von Vorteil gewesen, die Auswirkung der Viruslast von SARS-CoV-2 in Abhängigkeit vom Alter und von Vorerkrankungen auf die Überlebenswahrscheinlichkeit zu untersuchen. Aus ethischer und moralischer Perspektive verbietet sich das aber aus naheliegenden Gründen. Weiterhin kann man aus Ressourcengründen in der Regel solche Studien nur mit relativ kleinen Anzahl von Replikaten und nur für wenige (kontrollierte) Einflussgrößen möglich.

.	Versuchs- und Kontrollgruppe	Randomisierung	Intervention kontrolliert durch Forschenden	Replikation
Randomisierte kontrollierte Studie	ja	ja	ja	ja
Natürliches Experiment	ja (durch natürliche Manipulation)	ja (ggf. nach Datenmanipulation)	nein	nein
Quasi-Experiment	ja	nein	nein	nein
Beobachtungsstudie	nein	nein	nein	nein

22.1.2 Natürliche Experimente

Im Fall sogenannter natürlicher Experimente (natural experiments) erfolgt die Zuordnung in Versuchs- und Kontrollgruppe nicht durch den/die StudienleiterIn, sondern aufgrund eines externen Prozesses. Die Grundgesamtheit kann also in verschiedene Gruppen eingeteilt werden und diese dann für die Untersuchung des Effekts der Intervention genutzt werden. Im Fall der natürlichen Experimente wird die Intervention nicht durch den/die Forschende(n) kontrolliert, sondern ergibt sich durch den natürlichen oder auch sozio-ökonomischen Prozess. Wichtig ist dabei, dass die Einteilung zufällig oder “so wie zufällig” (as-if at random) erfolgt, damit man keinem Bias aufsitzt.

So analysieren (Bursztyn and Cantoni 2016) die Auswirkungen der Verfügbarkeit von Westfernsehen in der ehemaligen DDR vor dem Mauerfall auf das Konsumverhalten nach dem Mauerfall. Da die Westsender in Abhängigkeit von der Entfernung zur Grenze der BRD bzw. West-Berlins und der Topographie schlechter oder gar nicht zu empfangen waren, waren die Einwohner diesem Einfluss unterschiedlich stark ausgesetzt (Abbildung 22.1). Wenn man davon ausgeht, dass a) es keinen self-selection bias gab (also nicht Menschen die Westfernsehen sehen wollten in Gebiete zogen, in denen es möglich war), b) diejenigen, die Westfernsehen empfangen konnten, dieses auch taten und 3) die Unterschiede im Konsumverhalten auf Nachfrage- und nicht auf Angebotseffekte zurückzuführen sind, dann kann man davon ausgehen, dass dieses Setting ein natürliches Experiment darstellt. Die Bevölkerung der DDR wurde “so wie zufällig” in Gruppen mit und ohne Westfernsehen eingeteilt, so dass man von einer de facto Randomisierung in Versuchs- und Kontrollgruppe ausgehen kann.

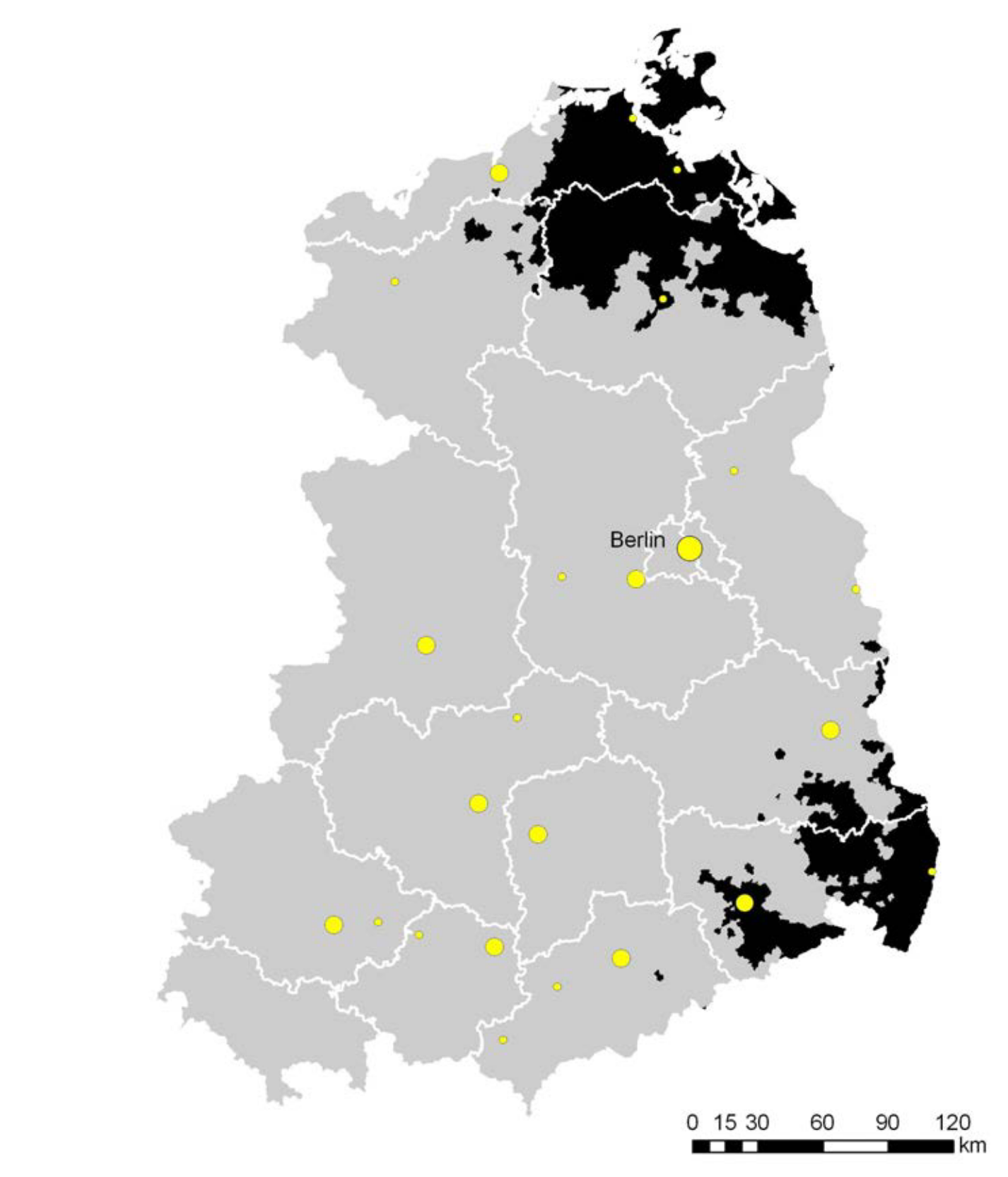
Figure 22.1: Westfernsehempfang ausreichender Stärke (grau) als Beispiel für ein natürliches Experiment. Quelle: Bursztyn & Cantoni (2016).

Ein anderes Beispiel ist die Arbeit von (Kuemmerle et al. 2008). Die Arbeit untersucht, wie sich die unterschiedlichen politischen Rahmenbedingungen nach dem Fall des Eisernen Vorhangs auf Landnutzungsveränderungen in den Kaparthen ausgewirkt haben. Da die naturräumlichen Unterschiede gering sind, sind es die politischen Grenzen, die die Zuordnung zu den verschiedenen Gruppen bedingen (Abbildung 22.2 und 22.3). In diesem Fall ist es allerdings schwierig, eine Kontrollgruppe zu definieren - anstelle dessen muss man sich auf die Unterschiede zwischen den verschiedenen Ländern konzentrieren.

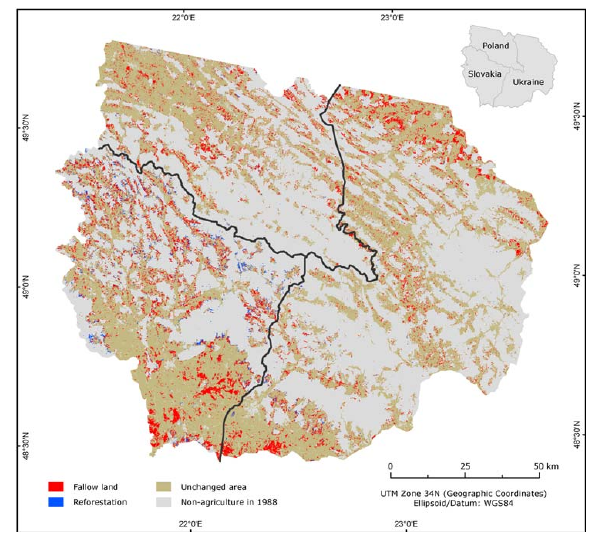
Figure 22.2: Veränderungen des politischen Systems nach dem Fall des Eisernen Vorhangs als natürliches Experiment für Landnutzungswandel. Quelle: Kümmerle et al. (2008).

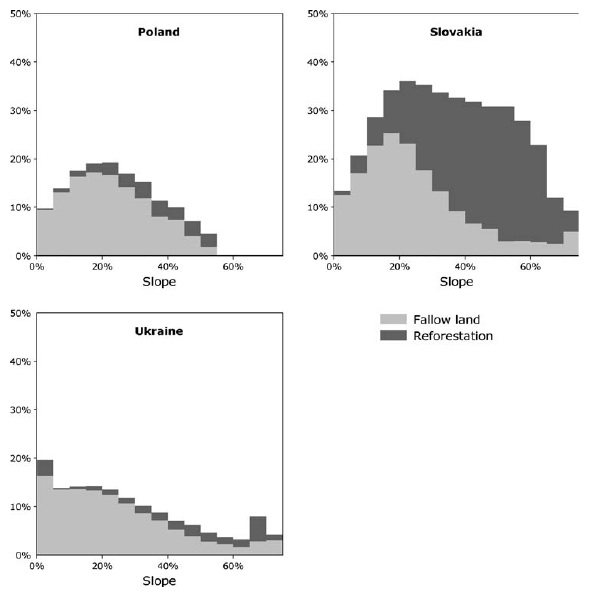
Figure 22.3: Unterschiedliche Auswirkung von Hangneigung auf die Aufgabe von Ackerland in den Karpathen nach dem Fall des Eisernen Vorhangs je nach politischen Rahmenbedingungen der 3 Länder. Quelle: Kümmerle et al. (2008).

In vielen Fällen muss man allerdings davon ausgehen, dass die räumliche Trennung durch sogenannte spill-over Effekte verwässert wird und die Regionen nicht wirklich homogen sind. Damit stellen natürliche Experimente größere Herausforderungen an die statistische Analyse dar. Der große Vorteil ist, dass sich damit großräumige Vergleiche durchführen lassen, was mit manipulativen Experimenten nicht möglich ist.

Weitere Beispiele finden sich z.B. in (Dunning 2008).

22.1.3 Quasi-Experimente

Im Fall von Quasi-Experimenten erfolgt die Intervention nicht unter Kontrolle des/der Forschenden und es gibt keine Randomisierung. Im Gegensatz zum natürlichen Experiment findet keine “so wie zufällig” Einteilung statt. Bei der Mehrheit der Quasi-Experimente handelt es sich um vorher-nachher Studien, bei denen ein “Differenz in Differenzen” Ansatz zur Anwendung kommt. Die Beobachtungsgruppe wird vor und nach der Intervention erfasst und die Unterschiede dann der Intervention zugeordnet. Da man nicht weiß, welche Veränderungen ohne die Intervention aufgetreten wären, ist die Zuordnung zur Intervention konzeptionell schwierig. Man sollte nicht versuchen, Kausalbeziehungen aufzudecken, sondern sich auf die Analyse von Assoziationen beschränken.

(Campbell and Ross 1968) z.B. untersuchen die Auswirkungen von Geschwindigkeitsbegrenzungen auf Verkehrstote in Conneticticut in ein vorher-nachherSetting. Da das Gesetz zu einem Zeitpunkt in Kraft trat, als die Verkehrstoten auf einem historischen Höchststand waren, stellt sich die Frage, inwiefern man die Reduktion allein auf das Gesetz zurück führen kann, oder ob es sich bei dem Peak einfach um eine statistische Schwankung handelte.

Ähnliche Fragestellungen, die üblicherweise durch Quasi-Experimente untersucht werden sind z.B. die Untersuchung der Auswirkungen des Klimawandels auf die Häufigkeit des Auftretens von meterologischen Extremereigenissen. Bei diesem Beispiel wird klar, dass man keine kontrolliertes Experiment durchführen kann und Replikate schwierig sind, da wir nur eine Erde haben. Da Veränderungen weltweit auftreten wird es naturgemäß schwierig eine Kontrollgruppe zu finden.

22.1.4 Beobachtungsstudien

Bei Beobachtungsstudien (non experimental observational studies) wird eine Grundgesamtheit durch Stichproben beprobt, um Assoziationen zwischen Variablen zu ermitteln. Diese Studien weisen keine Randomisierung auf, die Intervention wird nicht von den Forschenden kontrolliert, es gibt keine Versuchs- und Kontrollgruppe und auch keine Replikate. Eine Vielazhl von Co-Variaten muss als potentielle Einflussfaktoren kontrolliert werden. All dies erschwert die Untersuchung von Kausalbeziehungen massiv (geringe interne Validität). Ebenso ist die Übertragbarkeit der Ergebnisse auf z.B. andere Regionen i.d.R. unklar bis zweifelhaft (geringe externe Validität).

Dennoch sind solche Beobachtungsstudien nicht ohne Wert. Ihr großer Vorteil ist, dass sie das Phänomen von Interesse unter realistischen (und damit komplexen) Bedingungen untersuchen. Weiterhin sind Beobachtungsstudien mit deutlich geringerem Aufwand durchführbar als experimentelle Studien. Ggf. wird auf Grundlage der Ergebnisse von Beobachtungsstudien aufwendigere und fokussierte experimentelle Studien durchgeführt.

Auch Beobachtungsstudien können weiter differnziert werden. So unterscheidet man insbesondere in der medizinischen Forschung zwischen Kohortenstudien, Fall-Kontroll-Studien und Querschnittsstudien.

Bei Fall-Kontroll-Studien in der Epidemiologie werden z.B. erkrankte Probanden mit gesunden Probanden in einer Kontrollgruppe verglichen. Bei dieser retrospektiven Studie wird rückblickend nach der Krankheitsursache gesucht und ermittelt, ob in der Vergangenheit eine Exposition gegenüber potenziellen Risikofaktoren vorlag. Ein signifikanter Unterschied zwischen beiden Gruppen bedeutet eine Korrelation zwischen Risikofaktor und Erkrankung, auf Kausalwirkungen kann jedoch nicht geschlossen werden.

Kohortenstudie beobachten eine Gruppe exponierter und eine Gruppe nicht exponierter Personen über einen bestimmten Zeitraum hinsichtlich des Auftretens bestimmter Krankheiten oder deren Sterblichkeit beobachtet. Ziel ist es, einen Zusammenhang zwischen einer oder mehreren Expositionen und dem Auftreten einer Krankheit aufzudecken. Sie ist eine spezielle Form der Paneluntersuchung, bei der alle Personen einer Stichprobe derselben Kohorte angehören. Unter einer Kohorte versteht man eine Gruppe von Personen, in deren Lebensläufen ein bestimmtes biographisches Ereignis annähernd zum selben Zeitpunkt aufgetreten ist (z.B. Geburtskohorten, Einschulungskohorten, Scheidungskohorten). Angewandt werden solche Studien oft, wenn das Auftreten des Ereignisses eher langfristig auftritt. Beispiele sind Leukämiefälle im Umkreis von Atomkraftwerken, Lungenkrebs bei Raucher, Herz-Kreislauferkrankungen in Folge von Luftverschmutzung. Am Ende der Untersuchung wird die Anzahl von Neuerkrankungen (Inzidenz) bei Exponierten und Nichtexponierten gemessen und verglichen um daraus das relative Risiko für die Erkrankung abzuleiten. Im Bereich der empirischen Sozialforschung kann man mit solchen Studien z.B. die Auswirkungen des Einkommens der Eltern auf den beruflichen Erfolg der Kinder untersuchen.

Querschnittsstudien erfassen den Zustand des Systems anhand einer einmaligen Stichprobe. Im Gegensatz dazu erfassen Längsschnittstudien den Zustand zu mehreren Zeitpunkten. Bei Panelstudien werden dabei immer dieselben Personen befragt (Kohortenstudien sind ein Spezialfall der Panelstudie), bei Trendstudien wird immer eine neue Stichprobe gezogen (ungepaarte Daten).

22.2 Stichprobendesign für Beobachtungsstudien

Wollen wir anhand einer Stichprobe die zugrundeliegende Grundgesamtheit charackterisieren, sollten wir uns Gedanken darüber machen, wie wir die Stichprobe erheben wollen - das sogenannte Stichprobendesign. Die Ziele des Stichprobendesigns sind die Selben wie bei manipulativen Experimente: Unabhängigkeit, Durchmischung und Replikation. Unabhänigkeit der Daten ist eine Grundvorraussetzung für statistische Auswertung. Durchmischung ist wichtig um systematische Fehler durch übersehene Einflussgrößen zu kontrollieren. Befragen wir Personen indem wir an verschiedenen Punkten in der Stadt Befrager platzieren und geraten dabei zufällig in die Nähe eines Parteitages einer extremeren Partei oder einer Demonstration, müssen wir davon ausgehen, dass die Befragungsergebnisse um diesen Punkt eine gewisse Tendenz aufweisen. Haben wir nur wenige Befragungsorte, kann dies unsere Ergebnisse verfälschen. Wenn wir den Tongehalt im Oberboden in einem Gebiet ermitteln, sollten wir sicher sein, dass wir alle relevanten Gradienten (Relief, Ausgangsgestein, aktuelle und historische Landnutzung,…) mit erfassen oder eben durchmischen (randomisieren). Replikate sind notwendig, um auch die Variabilität zu erfassen und darüber z.B. den Standardfehler ermitteln zu können und die Irrtumswahrscheinlichkeit berechnen zu können.

Es gibt eine Reihe unterschiedlicher Stichprobendesigns, die sich hinsichtlich ihrer Sampling-Effizienz (wie hoch ist mein Aufwand um eine repräsentative Stichprobe zu bekommen) und der Komplexität der Berechnungen unterscheiden. Der Trade-off ist leider so, dass höhere Sampling-Effizienz mit einer größeren Komplexität der Auswertung erkauft werden muss. Unterscheiden kann man die unterschiedlichen Stichprobendesigns dahingehend, ob alle Untersuchungseinheit die gleiche Wahrscheinlichkeit haben beprobt zu werden (simple random sampling versus z.B. stratified sampling) und ob pro Untersuchungseinheit ein oder mehrer Werte gezogen werden.

Man kann weiterhin zwei Hauptrichtungen hinsichtlich der Auswertung der Stichprobendesigns unterscheiden (Carsten F. Dormann 2013): survey-Statistik und gemischte Modelle. Erstere sind in der Forstwissenschaft, der Fischerei aber auch den Sozialwissenschaften weit verbreitet. Hier gibt es je Stichprobendesing spezielle Formeln, um die relevanten statistischen Kennzahlen zu ermitteln (s. z.B. Thompson (2012), Quatember (2019) oder Lumley (2010)). Die gemischten Modelle (mixed models) sind Regressionsmodelle, die zusätzlich zu den fixed effects - mit denen wir uns bisher beschäftigt haben - Zufallseffekte (random effects) mit berücksichtigen. Solche random effects können aufgrund individueller Variabilität z.B. bei Panelstudien, auftreten, bei räumlicher Clusterung der Messwerte, übersehenen Gradienten, die sich in räumlichen Blockeffekten nierderschlagen und einiges mehr. Diese gemischten Modelle führen hier etwas zu weit, der interessierte Leser sei auf die weiterführende Literatur verwiesen: Faraway (2006), Pinheiro and Bates (2006), Zuur et al. (2009).

In der Praxis haben wir es i.d.R. immer mit dem Ziehen ohne Zurücklegen zu tun. Entsprechend beziehen sich alle Formeln auf diesen Fall.

22.2.1 Einstufige Stichprobenverfahren - einfache Zufallsstichprobe

Bei der einfachen Zufallsstichprobe (simple random sampling, SRS) werden zufällig \(n\) Einheiten (z.B. Addressangaben, Waldparzellen, Planquadrate an einem Hang, Telefonnummern) aus der Grundgesamtheit \(N\) zufällig ausgewählt. Eine Variante davon ist es, ein systematisches Sampling zu verwenden (z.B. immer 10 Planquadrate weiter zu gehen und dann erneut zu beproben), allerdings den Startpunkt zufällig zu wählen (s. Abbilung 22.4.

Figure 22.4: Zufällige, eingeschränkt zufällige und zufällig-systematische Auswahl von 16 Beprobungspunkten in quadratischem Untersuchungsgebiet, z.B. für Bodenproben. Das Gitternetz bei der eingeschränkt zufälligen Auswahl stellt einen Mindestabstand zwischen den Probenahmestellen sicher, Beim zufällig-systematischem Verfahren wird nur der Startpunkt zufällig gewählt.

Alle \(n\) Einheiten haben dabei die gleiche Wahrscheinlichkeit \(n/N\) ausgewählt und beprobt zu werden (equal probability sampling). Diese Auswahlwahrscheinlichkeit wird oft mit \(\pi\) bezeichnet. Beim SRS ist \(\pi = n/N\). Wenn es in einer Stadt 50.000 Haushalte gibt und wir 200 auswählen, ist die Wahrscheinlichkeit je Haushalt ausgewählt zu werden 200/ 50.000. Wenn wir wissen wollen, wie groß die Zahlungsbereitschaft für Klimaschutzmaßnahmen insgesamt in der Stadt ist und je Haushalt die Zahlungsbereitschaft im Mittel 50,3€/Jahr beträgt, ist der Schätzer für die gesamte Zahlungsbereitschaft 50.000 * 50,3€/Jahr.

Eine andere Möglichkeit den Wert zu bestimmen ist, dass die 200 Haushalte zusammen \(\hat{\tau}_y = 1006\) € Zahlungsbereitschaft haben. Damit ergibt sich die gesamte Zahlungsbereitschaft als:

\(\frac{\hat{\tau}_y}{\pi} = \frac{1006}{200/5000} = 251500\)€/Jahr.

Diese Berechnungsformel nenn man den Horvitz-Thompson Schätzer.

Für den Mittelwert der Grundgesamtheit berechnet sich der Horvitz-Thompson Schätzer als:

\[\hat{y}_{HT} = \frac{1}{N} \sum_{i=1}^n \frac{y_i}{\pi_i}\]

Für die Summe der Grundgesamtheit berechnet sich der Horvitz-Thompson Schätzer als:

\[\hat{\tau}_{HT} = N \hat{y}_{HT} = \sum_{i=1}^n \frac{y_i}{\pi_i}\]

Da beim SRS \(\pi\) für alle Einheiten gleich ist, kann der Index i entfallen. Bei anderen Sampling-Verfahren unterscheiden sich allerdings die Auswahlwahrscheinlichkeiten.

Die Varianz des Mittelwertes (quadrierter Standardfehler) bzw. des Gesamtwertes berechnet sich als:

\[var(\hat{\tau})= N^2 var(\hat{y}) = N^2(1-\frac{n}{N})\frac{s_y^2}{n} \]

wobei sich die Standardabweichung\(s_y\) berechnet als: \(s_y = \frac{1}{n-1}\sum_{i=1}^n (y_i - \bar{y})^2\)

Der Term \((1-\frac{n}{N})\) stellt einen Korrekturfaktor für fast-vollständige Beprobung dar. Wenn wir einen nicht unerheblichen Teil der Grundgesamtheit beproben (als Schwellwert wird 5% angegeben), dann müssen wir die Unsicherheit der Schätzung korrigieren, da wir den Standardfehler sonst überschätzen (finite population correction).

22.3 Mehrstufige Stichprobenverfahren

Bei den mehrstufigen Stichprobenverfahren erfolgt vor der eigentlichen Bebrobung eine Gruppierung der Stichproben.⁶⁸

22.3.1 Stratifizierte Stichprobe

Beim SRS beproben wir nicht unbedingt effektiv. Wenn wir z.B. die Bodenerosionsrate in einer Region ermitteln wollen, davon ausgehen das u.a. der Bodentyp relevant ist und die Bodentypen sehr ungleich im Gebiet verteilt sind (z.B. 85% Braunerde, 10% Parabraunerde, 4% Podsol, 1% Pararendzina), dann müssen wir beim SRS recht viele Beprobungsorte auswählen, damit wir eine ausreichende Anzahl von Proben im Bereich der selten im Gebiet vorkommenden Bodentypen erhalten. Wir werden die Varianz im Beispiel für Erosion auf Braunerde sehr genau schätzen können, die für Pararendzina deutlich weniger genau, es sei denn wir treiben einen enormen Aufwand (und haben enorme finanzielle Ressourcen).

Ein naheligender Gedanke ist es, je Bodenart eine Mindestanzahl von Probenorten zu ziehen oder die Probeorte gleichmäßg über die 4 Bodentypen zu verteilen (25% der Probepunkt für Braunerde, 25% für Parabraunerde, 25% für Podsol und 25% für Pararendzina). Dies ist die Idee hinter dem stratifiziertem Stichprobenverfahren (stratified sampling): Die Grundgesamtheit wird anhand eines oder mehrere Merkmale (Bodentyp, Hangneigung, Bewirtschaftungsform,…) unterteilt und jede Teilmenge (jedes Strata) getrennt beprobt (z.B. Abbildung 22.5). Ebenso würde man be einer Befragung, bei der Ethinizität eine relevante Einflussgröße darstellt sichergehen wollen, dass alle relevanten ethnischen Gruppen in der Befragung auftauchen oder man bei einer Befragung sicher geht, dass alle Stadtteile oder Stadtteile mit verschiedenen vorherrschenden sozio-ökonomischen Gruppen in der Befragung angemessen repräsentiert sind. Repräsentative Umfragen folgen ebenfalls diesem Konzept. Es soll damit sichergestellt werden, dass in jeder relevanten Bevölkerungsgruppe (Altersgruppe, ökonomischer Status, Bildung, Religion, Gender,…) ausreichend Personen befragt werden.

Figure 22.5: Stratifizieres Stichprobendesign. Im Beispiel wurden innerhalb jedes Stratas (farbcodiert) 4 Probenorte zufällig platziert.

Zur Aufteilung der Stichprobenelemente auf die Strata sind drei Verfahren gebräuchlich: (1) Gleiche Anzahl je Strata, (2) Proportional zu einer Strataeigenschaft, (3) Varianz-optimal.

Gleiche Anzahl Stichprobenelemente: in jedem Strata wird die gleiche Anzahl von Stichprobenelementen gezogen.

\[n_i = n/k\]

• \(n\) - Anzahl Stichprobenelemente insgesamt
• \(n_i\) - Stichprobenelemente in Strata \(i\)
• \(k\) - Anzahl Strata

Anzahl proportional zu einer Eigenschaft \(A\) der Strata wie Fläche, Größe der Wohnbevölkerung, Anzahl der Twitternutzer, Zeitdauer,… “Große” Strata erhalten mehr Stichprobenpunkte.

\[n_i = n \frac{A_i}{\sum_{i=1}^n A_i} \]

Varianz-optimal (“Neyman Zuordnung”): Die Anzahl der Messungen je Strata ist proportional zur Varianz innerhalb der Strata (\(s_i\) - Standardabweichung im Strata \(i\)). Dafür müssen wir natürlich vorab die Varianz je Stata kennen bzw. abschätzen können - z.B. aus Pilotstudien oder aus der Literatur.

\[n_i = n \frac{A_i \cdot s_i}{\sum_{i=1}^n A_i \cdot s_i} \]

Im Gegensatz zum SRS ist die Wahrscheinlichkeit, dass ein Ort oder ein Individum ausgewählt wird nicht mehr über alle Untersuchungseinheiten gleich, sondern variiert je Strata. Die Grundform der Horvitz-Thompson Schätzer bleibt gleich:

Mittelwert der Grundgesamtheit:

\[\hat{y}_{HT} = \frac{1}{N} \sum_{i=1}^n \frac{y_i}{\pi_i}\]

Für die Summe der Grundgesamtheit:

\[\hat{\tau}_{HT} = N \hat{y}_{HT} = \sum_{i=1}^n \frac{y_i}{\pi_i}\]

Der Gesamtwert aller Strata ist natürlich einfach die Summe der Gesamtwerte der Strata: \(\hat{\tau}_G = \hat{\tau}_1 + \hat{\tau}_2 + \cdots \hat{\tau}_k = \sum_{h=1}^k \hat{\tau}_h\).

Die Varianz des Gesamtwertes einer stratifizierten Stichprobe berechnet sich als Summe der Varianzen der Gesamtwerde je Stratum - d.h. die Unsicherheiten addieren sich auf:

\[var(\hat{\tau}_g) = \sum_{h=1}^kvar(\hat{\tau}_h)\]

22.3.1.1 Beispiel

Wir wollen uns die Rechenschritte anhand eine fiktiven Beispiels anschauen. Es seien in einer Stadt mit 100.000 Einwonern insgesamt 1000 Personen zur Zahlungsbereitschaft für Klimaschutzmaßnahmen [€/Jahr] befragt worden. Die Befragung sei anhand der Sinus-Leitmileus⁶⁹ stratifiziert worden.

Sinus-Leitmileu	Prozenanteil Gesamteinwohner	Befragte	mittlere Zahlungsbereitschaft	Varianz Zahlungsbereitschaft
Leitmilieus (LM)	32,5%	325	100	484
Zukunftsmilieus (ZM)	18,5%	185	240	100
Moderner Mainstream (MM)	29%	290	110	1156
Traditioneller Mainstream (TM)	21%	210	60	441

Summe Zahlungsbereitschaft:

\[\hat{\tau}_G = \sum_{i=1}^4 N_i \hat{y}_i = 32.500 * 100 + 18.500 * 240 + 29.000 * 100 + 21.000 * 60 = 11.850.000\] Die Varianz der Gesamtzahlungsbereitschaft berechnet sich als Summe der Varianz der einzelnen Strata. Zunächt berechnen wir die Varianz je Strata.

\[var(\hat{\tau}_{LM}) = N_{LM}^2(1-\frac{n_{LM}}{N_{LM}})\frac{s_{y_{LM}}^2}{n_{LM}} = 32.500^2 (1- \frac{325}{32500})\frac{484}{325} = 1.415.700.000 \]

\[var(\hat{\tau}_{ZM}) = N_{ZM}^2(1-\frac{n_{ZM}}{N_{ZM}})\frac{s_{y_{ZM}}^2}{n_{ZM}} = 18.500^2 \cdot 0.9 \cdot\frac{100}{185} = 166.500.000 \]

\[var(\hat{\tau}_{MM}) = N_{MM}^2(1-\frac{n_{MM}}{N_{MM}})\frac{s_{y_{MM}}^2}{n_{MM}} = 29.000^2 \cdot 0.9 \cdot\frac{110}{290} = 287.100.000 \]

\[var(\hat{\tau}_{TM}) = N_{TM}^2(1-\frac{n_{TM}}{N_{TM}})\frac{s_{y_{TM}}^2}{n_{TM}} = 21.000^2 \cdot 0.9 \cdot\frac{60}{210} = 113.400.000 \] \[var(\hat{\tau}_G)= 1.415.700.000 + 166.500.000 287.100.000 + 113.400.000 = 1.982.700.000\]

D.h. wir erwarten eine Zahlungsbereitschaft der gesamten Stadtbevölkerung von 11,85 Millionen €/Jahr bei einem Standardfehler von 44.527,52 €/Jahr (s. Abbildung 22.6).

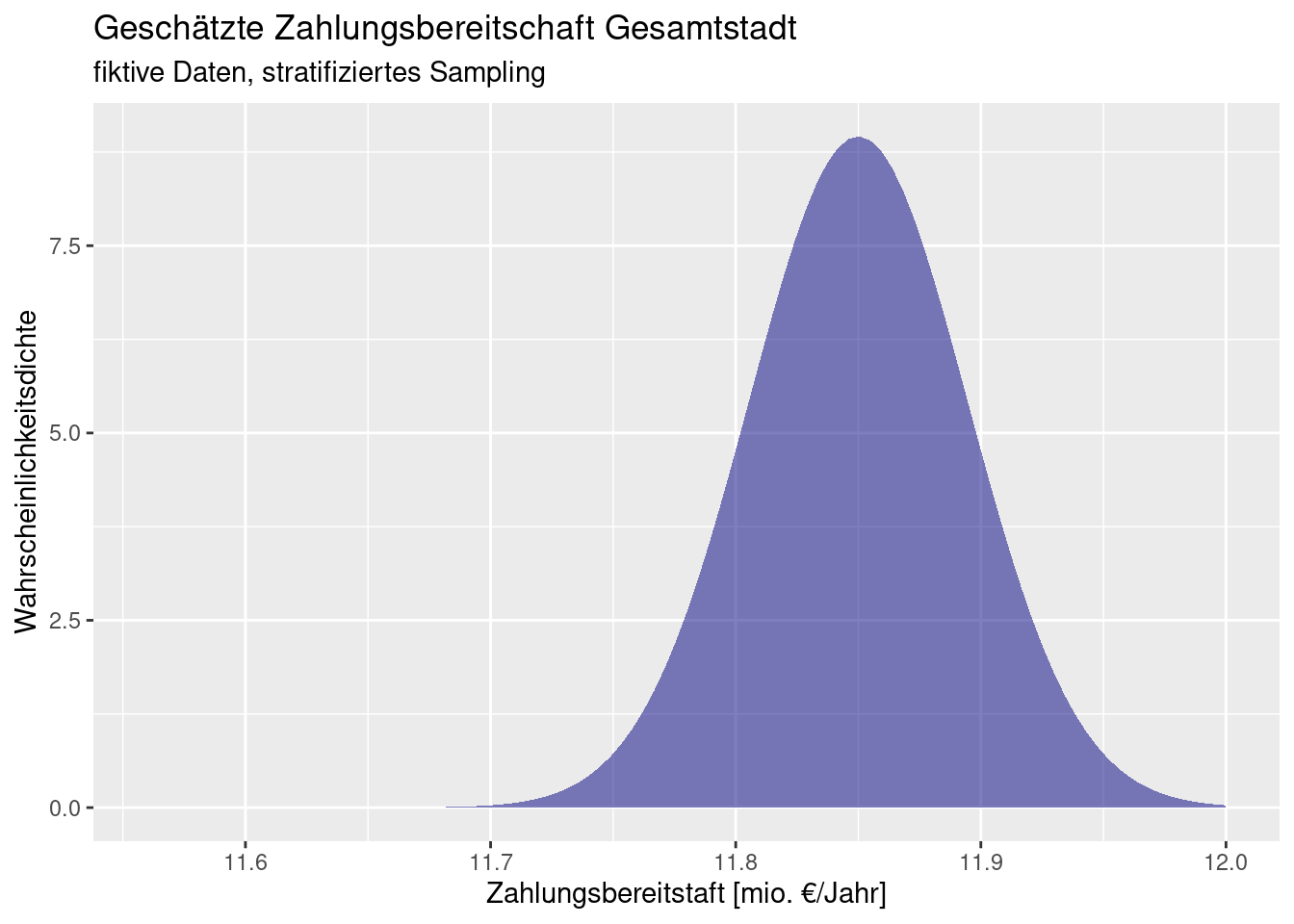
Figure 22.6: Geschätzte Zahlungsbereitschaft Gesamtstadt anhand fiktiver Daten. Der im Text ermittelte Wert für die Gesamtzahlungsbereitschaft wird zusammen mit der Unsicherheit (Standardfehler der Schätzung) dargestellt. Es wird angenommen, dass der zentrale Grenzwertsatz greift, weswegen für die Darstellung der Unsicherheit eine Normalverteilung verwendet wird.-

22.3.2 Geclustertes Stichprobendesign (cluster sampling)

Der Grundgedanke des cluster sampling (auch geklumptes Stichprobendesign) ist es, den logistischen Aufwand für die Probenerhebung zu minimieren. Oftmals ist die Anfahrt oder der Fussweg zu einer Probenahmestelle aufwendig, insbesondere wenn Messinstrumente abseits von Wegen transportiert werden müssen. Aber auch bei Befragungen steigt der Aufwand, wenn z.B. eine Vielzahl von Haushalten in einem Landkreis besucht werden muss.

Beim cluster sampling werden am Ort einer Probenahme gleich mehrere (geclusterte) Proben entnommen (z.B: Bodenproben oder Haushaltsbefragung). Damit sind die einzelnen Proben innerhalb eines Clusters nicht unabhängig, da sich z.B. die Topographie, die sozio-ökonomischen Bedingungen etc. in der Nähe vermutlich ähneln (Toblers erstes “Gesetz” der Geographie). Deswegen können die Werte nur auf Ebene der Cluster und nicht auf Ebene der einzelnen Datenpunkte ausgewertet werden.⁷⁰

Ob das cluster sampling effizient ist, hängt von der Variabilität der Daten ab. Wenn die Daten innerhalb der Cluster stark variieren, dann kann man bereits mit wenigen Clustern eine gute Abschätzung der Variabilität der Messung erzielen. Falls die Variabilität innerhalb der Cluster gering ist, enthalten die Messungen innerhalb der Cluster nicht wirklich viel Information. Da wir in diesem Fall hauptsächlich die Variabilität zwischen Clustern beproben ist das Stichprobendesign in diesem Fall auch nicht wirklich effizient.

Formal lässt sich die anhand des Designeffektes beschreiben. Der Designeffekt \(d_\text{eff}\) beschreibt das Verhältnis der Varianz einer Schätzfunktion bei gegebenem Stichprobendesign zur Varianz der Schätzfunktion bei einfacher Zufallsauswahl (und demselben Stichprobenumfang). Er beschreibt damit die statistische Verzerrung, die durch ein Auswahlverfahren einer Stichprobe (Schichtung, Klumpung, Mehrstufige Ziehung) im Vergleich zur reinen Zufallsauswahl (simple random sample) entstanden ist. Ein kleiner Designeffekt ist also erstrebenswert.

\[D_\text{eff}= 1 + (m-1) \rho\] mit

• \(\rho\) - Korrelation der Responsewerte oder der Residuen innerhalb des Clusters
• \(m\) - Anzahl der Proben je Cluster (hier Annahme, dass diese Zahl über alle Cluster konstant ist)

Falls \(\rho = 0.1\), dann beträgt der Designeffekt bei 10 Proben je Cluster 1,9 (d.h. der Standardfehler ist gegenüber dem SRS etwa 1,4 mal so groß), falls \(\rho = 0.5\), dann beträgt der Designeffekt bei 10 Proben je Cluster bereits 5,5, die Varianz der Schätzgröße ist damit 5,5 mal so groß, d.h. der Standardfehler ist etwa 2,3 mal so groß.

Insbesondere bei stark geklumpten Daten sind geklumpte Stichprobendesigns von Vorteil, da wir bei zufälligem oder systematischem Sampling die relevanten Objekte nur sehr selten antreffen.

Figure 22.7: Geklumptes Stichprobendesign. Alle relevanten Objekte (rote Punkte) innerhalb des selektierten Planquadrates werden untersucht.

Für jeden Cluster \(i\) berechnet sich der Gesamtwert als Summe der Probenwerte innerhalb des Clusters:

\[\tau_i = \sum_{i=1}^n y_i = N_i \bar{y}_i\]

Der Gesamtwert über alle Cluster hinweg ist deren Summe, gewichtet mit der Wahrscheinlichkeit, cluster \(i\) in der Stichprobe zu haben:

\[\hat{\tau}_G = \sum_{k=1}^K \frac{\bar{y}_k}{\pi_k}\]

Die Formel entsoricht dem HT-Schätzer für ein SRS, allerdings auf Ebene der Cluster, nicht der einzelnen Proben.

Die Formeln zur Ermittlung der Varianz sind nicht unterkomplex, da die Wahrscheinlichkeit, dass ein Ort bzw. Subjekt innerhalb eines Clusters ausgewählt wird mit der Wahrscheinlichkeit kombiniert werden muss, dass der Cluster gewählt wird. Generell teilt sich die Varianz in einen Teil zwischen den Clustern und einen Teil innerhalb der Cluster auf.

22.3.3 Mehrstufiges Stichprobendesign (multi-stage sampling)

Beim mehrstufigem Stichprobendesign wird auf mehreren Ebenen zufällig ausgewählt: zunächst die oberste Ebene, dann innerhalb des gewählten Objektes eine Teilmenge und so weiter. Das geklumpte Stichprobendesign ist ein zweistufiges Stichprobendesign, es sind allerdings Stichprobendesign mit mehr Stufen im Einsatz. So werden beispielsweise bei den amerikanischen National Health and Nutrition Examination Surveys (NHANES) Gesundheitsdaten in Form von Interviews in Kombination mit einer physischen Untersuchung und mit Blutproben kombiniert. Da der logistische Aufwand erheblich ist (die Befragung und die Probenahme erfolgen in separaten.mobilen Einrichtungen), erfolgt die Beprobung der Bevölkerung in Form, eines vier-stufigen Stichprobendesigns (s. Abbildung 22.8).

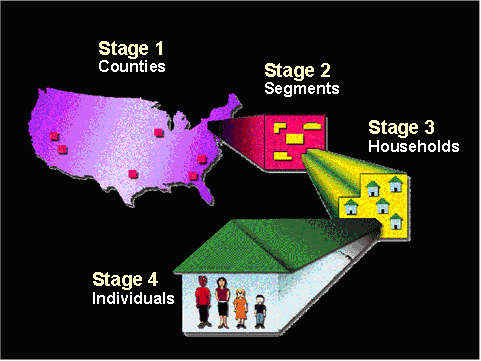
Figure 22.8: Mehrstufiges Stichprobendesign am Beispiel des amerikanischen National Health and Nutrition Examination Surveys (NHANES). Quelle: https://wwwn.cdc.gov/nchs/nhanes/tutorials/SampleDesign.aspx

Man kann die Auswahl der nächsten Ebene abhängig von Co-Variaten machen, um z.B. nur Teileinheiten zu beproben, die überhaupt in Frage kommen. Wenn wir z.B. zunächst Städte zufällig auswählen und dann Nachbarschaften innerhalb der Städte und wir nur an Mehrfamilienhäusern interessiert sind, lassen wir alle andern Gebäude bei der Auswahl auf dieser Ebene aus. Dies verkompliziert natürlich die Formeln für die Berechnung der Varianz nicht unerheblich. Dafür ist das Verfahren sehr effizient - wir beproben nur, was neue Erkenntnisse liefert.

Das mehrstufige Stichprobendesign ist besonders geeignet, wenn die zu erfassenden Objekte stark geclustert vorliegen. Dann kann man die Effizienz weiter steigern, wenn man große Cluster (viele Bäume in einem Waldstück, viele Bewohner in einem Haus) intensiver beprobt als kleine Cluster.

22.4 Experimentelles Design

Im Bereich manipulativer Experimente spricht man vom experimentellen Design, wenn es um die konzeptionelle Gestaltung des Versuchsaufbaus geht. Auch hier sind Unabhängigkeit, Durchmischung und Replikation die relevanten Faktoren für die Auswertung des Versuches. Wird beim Design des Versuchs auf diese Faktoren nicht geachtet, ist es schwierig bis unmöglich, diesen Fehler bei der statistischen Auswertung der Ergebnisse zu korrigieren.

Die wichtigsten Grundlagen nochmal in aller Kürze:

• Ohne Kontrollgruppe kein Effekt! Wir würden gerne wissen, wie sich die Intervention ausgewirkt hat. Dazu sollten wir abschätzen können, was ohne Intervention passiert wäre. Deswegen brauchen wir die Kontrollgruppe.
• Randomisierung schützt uns vor den Einflüssen unbekannter oder unbedachter Einflussgrößen.
• Replikate sind notwendig für die Varianzschätzung und damit für die Beurteilung, ob ein Effekt auch zufällig zustande gekommen sein könnte.

Eine ausführliche Diskussion über Fehlerquellen im Versuchsaufbau und wie man diesen vorbeugen kann findet sich bei Hurlbert (1984). Auch wenn Hurlbert ökologische Experimente im Fokus hat, sollte der Text zumindestens auch für die Durchführung von physisch-geographischen Experimenten hilfreich sein.

Ähnlich wie bei Beobachtungsstudien gibt es wieder einen Zielkonflikt zwischen Komplexität der Auswertung und Effizienz der Beprobung. Bei Carsten F. Dormann (2013) findet sich eine lesenswerte Übersicht der wichtigsten experimentellen Design zuzüglich Hinweisen zur Auswertung.

Weiterführende/zitierte Literatur

Bursztyn, Leonardo, and Davide Cantoni. 2016. “A Tear in the Iron Curtain: The Impact of Western Television on Consumption Behavior.” Review of Economics and Statistics 98 (1): 25–41.

Campbell, Donald T, and H Laurence Ross. 1968. “The Connecticut Crackdown on Speeding: Time-Series Data in Quasi-Experimental Analysis.” Law and Society Review, 33–53.

Dormann, Carsten F. 2013. Parametrische Statistik. Springer.

Dunning, Thad. 2008. “Improving Causal Inference: Strengths and Limitations of Natural Experiments.” Political Research Quarterly 61 (2): 282–93.

———. 2006. Extending the Linear Model with R - Generalized Linear, Mixed Effects and Nonparametric Regression Models. Edited by Chapman & Hall/CRC. Chapman & Hall/CRC.

Hurlbert, Stuart H. 1984. “Pseudoreplication and the Design of Ecological Experiments.” Ecological Monographs 54 (2): 187–211.

Kuemmerle, Tobias, Patrick Hostert, Volker C. Radeloff, Sebastian Linden, Kajetan Perzanowski, and Ivan Kruhlov. 2008. “Cross-Border Comparison of Post- Socialist Farmland Abandonment in the Carpathians.” Ecosystems 11 (4): 614–28. https://doi.org/10.1007/s10021-008-9146-z.

Lumley, Thomas. 2010. Complex Surveys - A Guide to Analysis Using R. Wiley.

Pinheiro, José, and Douglas Bates. 2006. Mixed-Effects Models in S and S-PLUS. Springer science & business media.

Quatember, Andreas. 2019. Datenqualität in Stichprobenerhebungen: Eine Verständnisorientierte Einführung in Die Survey-Statistik. Berlin, Heidelberg: Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-662-60274-4.

Thompson, Steven K. 2012. Sampling. 3rd ed. Wiley Series in Probability and Statistics. Hoboken, N.J: Wiley.

Zuur, Alain F, Elena Ieno, Neil J Walker, Anatoly A Saveliev, and Graham M Smithe. 2009. Mixed Effect Models and Extensions in Ecology with R. Springer. https://doi.org/10.1017/CBO9781107415324.004.

---

68. Bei den Post-hoc Stratifizierungsverfahren auch danach.↩︎

69. Besser nach den Sinus-Mileus aber das wäre hier zuviel Rechenarbeit. Zur Abgrenzung der Milieus s. https://de.wikipedia.org/wiki/Sinus-Milieus.↩︎

70. Oder mit gemischten (oder sonstigen hierarchischen) Modellen, die solche hierarchischen Beziehungen abbilden können.↩︎