Kapitel 11 Assoziation zwischen Variablen
Nachdem wir uns bisher überwiegend mit der Verteilung einzelner Variablen beschäftigt haben, wollen wir uns nun mit der Frage beschäftigen, ob es Zusammenhänge zwischen Variablen gibt. Ist das Einkommen eines Haushaltes positiv mit dem Bildungsabschluss verknüpft? Wählen Wahlkreise mit einem hohen Anteil von Wahlberechtigten, die der Katholischen Kirche zugehörig sind vermehrt CDU/CSU? Findet sich in Staulagen ein höherer Tongehalt im Oberboden? Ist die Bodenerosion auf Böden mit höherem Sandanteil höher?
Wir werden uns hier mit ungerichteten Zusammenhängen beschäftigen, d.h. ohne eine Wirkungsbeziehung anzunehmen. Mit gerichteten Zusammenhängen werden wir uns im Abschnitt Regression beschäftigen.
Wichtig ist sich klar zu machen, dass eine positive oder negative Assoziation keinen Kausalzusammenhang beweist. Wir können einen Zusammenhang als Hypothese formulieren und diesen dann durch die Kovarianz oder Korrelation testen. Allerdings sagt das eben nur etwas über Stärke und Richtung des Zusammenhanges aus und nicht über einen Kausalzusammenhang. Oftmals haben wir es mit (ggf. nicht gemessenen) latenten Variablen zu tun, die den Zusammenhang herstellen. Ein bekanntes Beispiel ist der positive Zusammenhang zwischen der Anzahl Störche und der Geburtenrate - sprich weniger Störche führen zu weniger Geburten. Man knnte dies naiv für die Bestätigung des Kausalzusammenhanges “Der Storch bringt die Kinder, gibt es weniger Störche, gibt es weniger Kinder” halten. Wie sicherlich bekannt ist, ist dies jedoch nur ein scheinbarer Zusammenhang. Beide Größen wurden durch die fortschreitende Industrialisierung beeinflusst (latente Variable). Die Veränderungen der Baustruktur sowie die größere Luftverschmutzung und der Verlust an Habitat führten zu einem Rückgang der Storchpopulation. Auf der anderen Seite führten die vielfältigen sozialen Veränderungen in Folge der Industrialisierung dazu, dass die Kinderanzahl sank.
11.1 Kovarianz
Die Kovarianz ist ein unskaliertes Maß dafür, wie stark eine Variation in einer Zufallsvariablen \(X\) mit einer Variation einer zweiten Zufallsvariable \(Y\) einhergeht. Dies wird über das Produkt der Abweichungen vom Ewratungswert der jeweiligen Zufallsgröße ausgedrückt.
\[ COV(X,Y) = E(X- E(X)) \cdot E(Y-E(Y)) \]
Einfacher ist es, wenn man sich die empirische Kovarianz anschaut. Hier gehen wir von \(n\) Messpunkten (z.B. Klimastationen) aus, an denen jeweils zwei Eigenschaften (z.B. Temperatur und Geländehöhe) gemessen wurden. Die Frage ist nun, wie stark positive Abweichungen vom Mittelwert der einen Größe (Temperatur) mit positiven Abweichungen vom Mittelwert der 2. Variablen (Geländehöhe) auftreten oder ob es umgehert so ist, dass positive Abweichungen der einen Variable gehäuft mit negativen Abweichungen der zweiten Variable auftreten. Oder, als 3. Alternative, ob es kein Muster gibt.
\[COV(X_j, X_k) = \frac{1}{n-1} \sum_{i=1}^n(x_{i,j} - \bar{x_j}) (x_{i,k} - \bar{x_k}) \]
Wir betrachten also nacheinander jede Beobachtung (im Beispiel Klimastation, Index \(i\) in der Formel) und berechnen das Produkt der jeweiligen Abweichung vom Mittelwert. Zunächst berechnen wir jeweils den Mittelwert der beiden Variablen (die \(j\)-te und die \(k\)-te Spalte unserer Datenmatrix), also im Beispiel den Mittelwert der Temperatur und den Mittelwert der Geländehöhe über alle Klimastationen. Dann berechnen wir für jede Beobachtung/Datenpunkt die Abweichung der Ausprägung der Variablen \(j\) (Temperatur) vom Mittelwert (mittlere Temperatur über die Stationen) sowie die Abweichung der zwei (Geländehöhe) vom Mittelwert (mittlere Geländehöhe über alle Stationen) und multiplizieren die beiden Abweichungen. Dieses Produkt berechnen wir für alle Beobachtungen und summieren die Produkte auf. Anschließend teilen wir durch (\(n-1\))47
Wenn positive Abweichungen der einen Variablen mit positiven Abweichungen der anderen Variablen einhergehen, dann ist das Produkt positiv. Das gleiche gilt, wenn negative Abweichungen mit negativen Abweichungen einher gehen. Wenn positive Abweichungen der einen mit negativen Abweichungen der anderen einhergehen, dann ist das Produkt negativ. Die Größe des Produktes hängt von der Größe der beiden Abweichungen ab - hohe Abweichungen spielen also in der Summe eine größere Rolle, als kleinere Abweichungen. Wenn die Abweichungen zufällig verteilt sind - also es keinen Zusammenhang zwischen beiden ariablen gibt -, dann sollte die Summe in etwa Null sein. Wenn viele große positive Terme auftreten, dann erhalten wir einen positive Summe und wenn viele negative Produktterme auftreten eine negative. Entsprechend gilt:
- Kovarianz > 0: positiver Zusammenhang (wenn \(X_j\) hoch ist, ist im Mittel auch \(X_k\) hoch, wenn \(X_j\) niedrig ist, ist im Mittel auch \(X_k\) niedrig)
- Kovarianz < 0: negativer Zusammenhang (wenn \(X_j\) hoch ist, ist im Mittel \(X_k\) niedrig, wenn \(X_j\) niedrig ist, ist im Mittel \(X_k\) hoch)
- Kovarianz = 0: kein Zusammenhang
11.1.1 Fallbeispiel langjährige Jahresmitteltemperatur und Geländehöhe
11.1.1.1 Preprocessing und explorative Analyse
Einlesen der Daten
Der Befehl ‘read.table’ dient zum Einlesen von Textdatein. Der Befehl benötigt den Dateinamen (hier relativ zum aktuellen Arbeitsverzeichnis, Sie müssen den Pfad ggf. anpassen). Dazu kann angegeben werden,
- ob die erste Zeile die Spaltennamen enthält (header=TRUE)
- was das Trennzeichen ist (z.B. sep=“;”, der default ist Whitespace, d.h. Leerzeichen und Tabulatoren)
- was das Dezimaltrennzeichen ist (dec=“.”, bei Werten die aus dem deutschen Sprachraum stammen, muss man ggf. auf “,” umstellen)
- auslassen von den ersten zeichen
- Kommentarzeichen
- Zeichen, die Strings kennzeichnen
- …
Wie immer hilft ?read.table weiter, wenn man an den Details interessiert ist.
Wichtig ist, dass wir den Rückgabewert der Funktion (hier ein data.frame) einer Variable zuweisen - sonst können wir damit nicht weiterarbeiten.
## [1] "TEMP_STA_1" "FID_1" "AREA" "PERIMETER" "TEMP_STATI"
## [6] "COUNTRY_ID" "NAME" "LAT" "LON" "ELEV"
## [11] "FIRST" "LAST" "MISSING" "DISC" "FID_2"
## [16] "ISO_3DIGIT" "ISO_NUM" "CNTRY_NAME" "LONG_NAME" "SQKM"
## [21] "SQMI" "centerX" "centerY" "JAN" "FEB"
## [26] "MAR" "APR" "MAI" "JUN" "JUL"
## [31] "AUG" "SEP" "OCT" "NOV" "DEC"
## [36] "YEAR"Der Datensatz enthält weltweit Temperaturmeßstationen zusammen mit der Höhe der Meßstation (müNN), der Breiten und Längen der Station (LAT, LON), dem Ländernamen “CNTRY_NAME” sowie dem langjährigen Mittelwert der Jahrestemperatur (YEAR). Alle anderen Werte wollen wir hier ignorieren.
Zunächst erzeugen wir eine Teilmenge (ein subset) der Daten - wir sind nur an den Stationen interessiert, die in Deutschland liegen.
Da wir nach dem CNTRY_NAME Attribut abfragen, sollten wir wissen, welche Einträge es gibt. Mit levels können wir die Faktorlevel einer Variablen abfragen. Aus Platzgründen zeige ich hier nur die ersten 6 Namen. Für den vollen Output verwenden Siie den Befehl ohne head.
## [1] NA "Norway" "Svalbard" "Sweden"
## [5] "Finland" "United Kingdom"Wir verwenden nun den Befehl subset um eine logische Bedingung zu formulieren. Wichtig ist das doppelte Gleicheitszeichen. Während ein einfaches Gleichheitszeichen eine Zuweisung bedeutet, bedeutet ein doppletes Gleichheitszeichen einen logischen Vergleich. Subset liefert eine Teilmenge des data.frames zurück, die wir in einer neuen Variable speichern.
Mittels dim schauen wir uns an, wieviele Stationen wir damit erhalten haben.
## [1] 6039 36## [1] 116 36Nun wollen wir die Daten zunächst einmal Plotten:
ggplot(temp.de, aes(y=YEAR, x= ELEV)) +
geom_point() +
ylab("Jahresmitteltemperatur [°C]") +
xlab("Höhe [m]") +
labs(title = "Temperaturstationen Deutschland") +
geom_vline(xintercept = mean(temp.de$ELEV), lty=2, color="red") +
geom_hline(yintercept = mean(temp.de$YEAR), lty=2, color="red")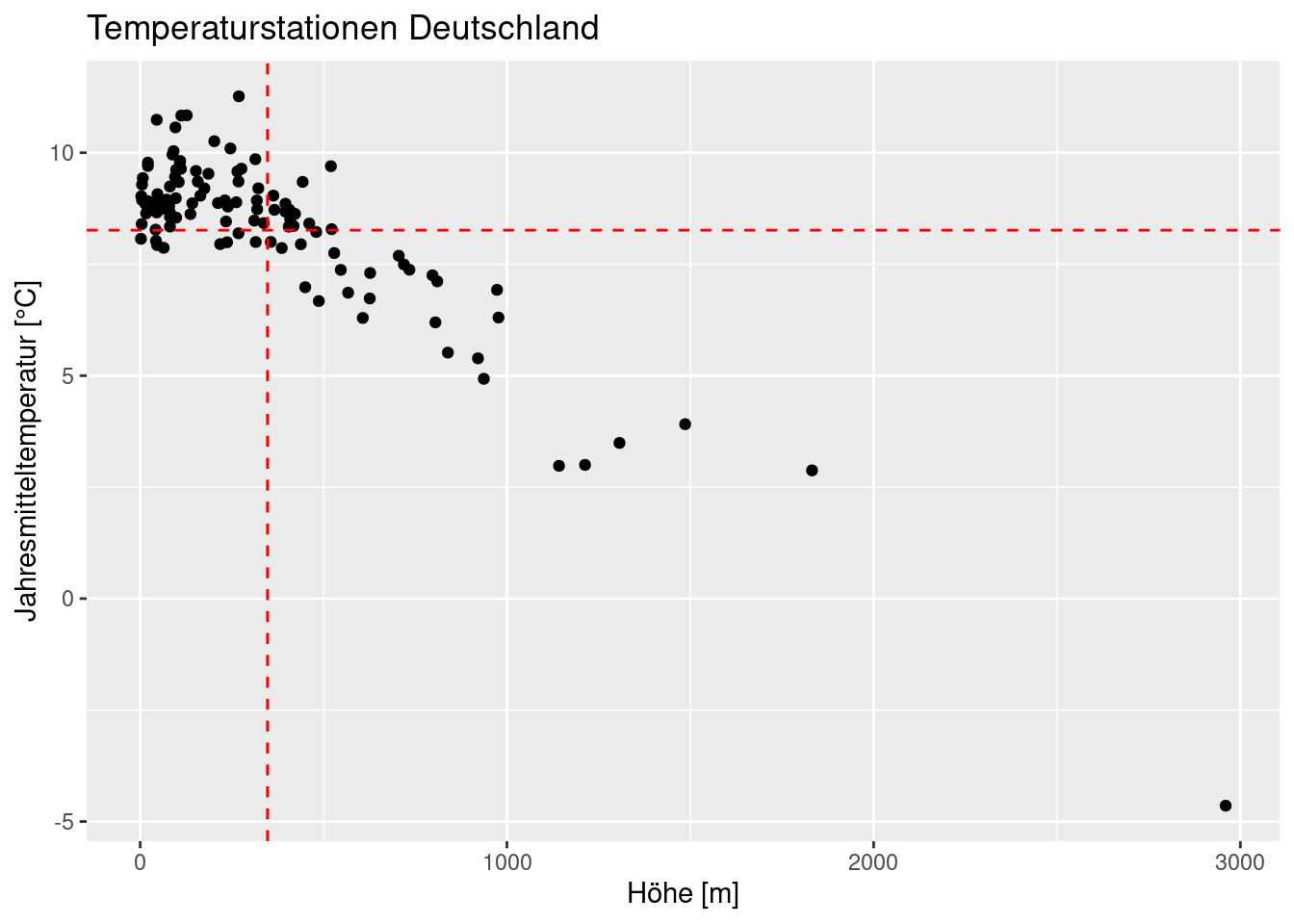
Es scheint einen negative Zusammenhang zu geben: große Geländehöhen sind mit niedrigen Jahresmitteltemperaturen assoziert und umgekehrt.
Zentrieren wir nun die beiden Variablen (d.h. wir ziehen den Mittelwert davon ab) und plotten diese dann:
temp.de$YEAR_cent <- temp.de$YEAR - mean(temp.de$YEAR)
temp.de$ELEV_cent <- temp.de$ELEV - mean(temp.de$ELEV)temp.de$YEAR_cent <- temp.de$YEAR - mean(temp.de$YEAR)
temp.de$ELEV_cent <- temp.de$ELEV - mean(temp.de$ELEV)
ggplot(temp.de, aes(y=YEAR_cent, x= ELEV_cent)) +
geom_point() +
ylab("Jahresmitteltemperatur [°C], zentriert") +
xlab("Höhe [m], zentriert") +
labs(title = "Temperaturstationen Deutschland") +
geom_vline(xintercept = mean(temp.de$ELEV_cent), lty=2, color="red") +
geom_hline(yintercept = mean(temp.de$YEAR_cent), lty=2, color="red")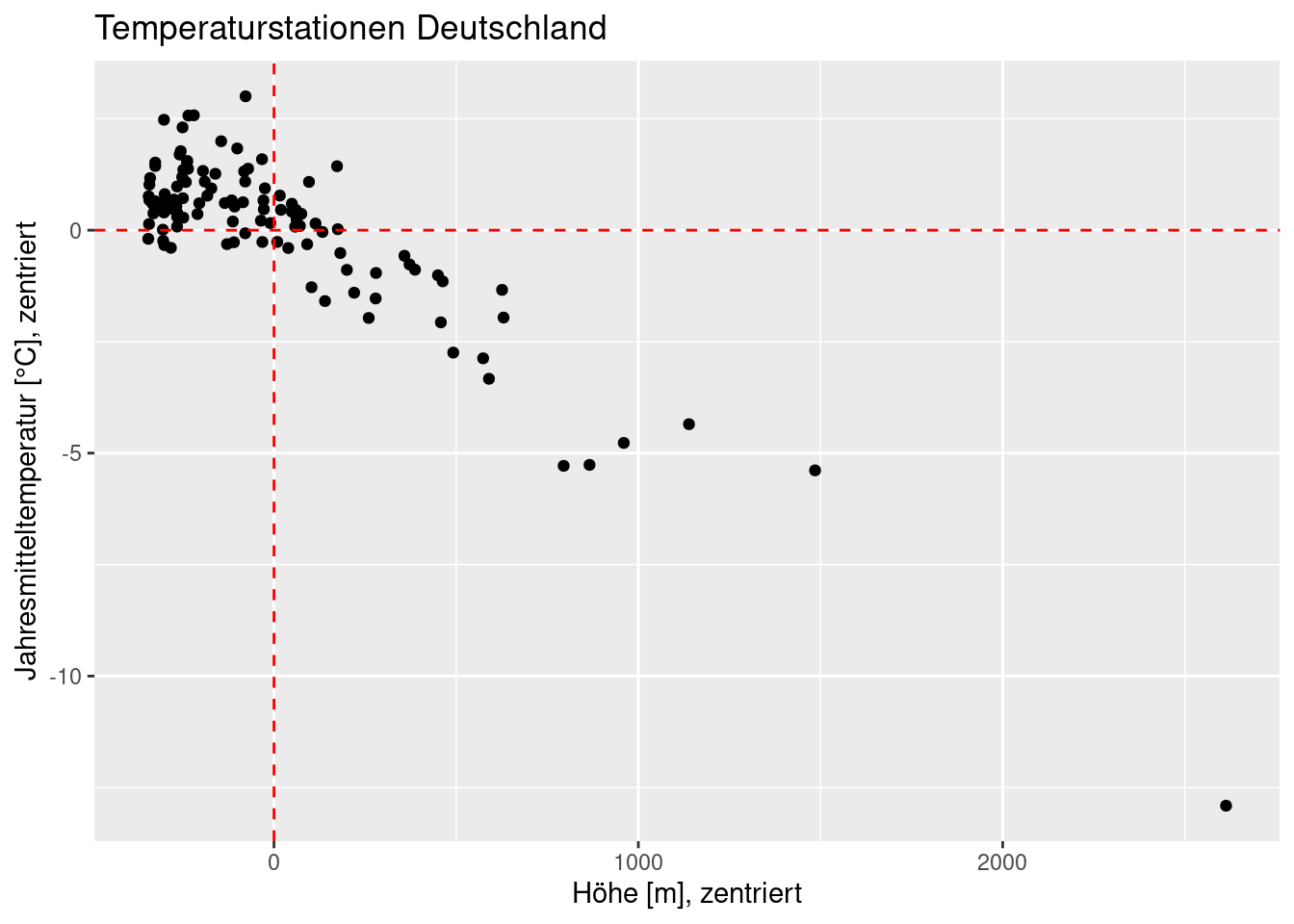
Nun können wir diese Werte miteinander multiplizieren:
## [1] -19.302556 -3.424079 -143.279477 -47.064389 100.580341
## [6] 66.844741 -119.897751 -211.599785 -105.449412 -187.766921
## [11] -21.516014 112.012534 -137.570754 -134.302889 -145.030376
## [16] -79.828954 -242.266478 -70.058339 -2.377806 -4201.576165
## [21] -21.988485 -141.397171 -123.811011 -75.792882 -261.358511
## [26] -185.047354 -179.199719 29.756915 -131.783395 -222.622934
## [31] -1966.497748 8.471573 5.463801 -427.394952 -7.689707
## [36] -15.627543 6.699103 -4558.461045 -175.265711 72.934168
## [41] -397.524317 -349.823118 -124.932122 -196.775215 -230.877252
## [46] -261.261677 -140.376065 -210.510661 -469.164698 -300.483432
## [51] -188.735715 -336.864725 -196.467994 -260.528586 -199.257257
## [56] -747.629708 -439.264499 -493.967414 -259.056095 -1350.975262
## [61] -206.915715 -77.482100 -161.184614 -511.904466 -289.217479
## [66] -268.769323 -453.693186 -566.648277 -178.085147 -203.698282
## [71] -82.123515 -1649.741948 -107.967255 -5.313695 -946.959838
## [76] -365.951257 -325.115120 -369.257699 -86.169364 -53.207765
## [81] -1.580110 -57.192331 -308.510841 -28.723404 12.441119
## [86] 20.405590 -23.444063 -603.997133 -578.570322 29.084694
## [91] -52.466525 -97.907417 27.460952 -13.115206 8.692054
## [96] -4580.662681 -234.058545 -455.332397 -837.961079 -343.017919
## [101] 3.934383 17.007988 248.170858 -93.356792 4.525399
## [106] 15.083545 -4955.588487 104.003209 27.359380 -205.580622
## [111] -531.379410 -33725.631885 -1234.724090 -285.887012 -7999.661332
## [116] 40.326517Und aufaddieren und durch n-1 teilen
## [1] -736.6715Oder einfacher:
## YEAR ELEV
## YEAR 3.86323 -736.6715
## ELEV -736.67150 175631.7031cov berechnet uns sowohl die Kovarianz als auch die Varianzen. Wie wir sehen ist die Kovarianz negativ, also sind hohe Temperaturen mit niedrigen Geländehöhen (und umgekehrt) assoziert. Ein Zusammenhang, der sich mit unseren Erwartungen decken dürfte (im Gebirge ist es kälter als im Flachland).
Die Kovarianz hat das Problem, dass sie nicht standardisiert ist, d.h. wir können Werte hinsichtlich ihrer Größe nicht über Variablen und/oder Datensätze hinweg vergleichen. Wir wissen, dass eine negative Kovarianz auf einen negativen Zusammenhang hindeutet, ob -736 ein starker oder ein schwacher Zusammenhang ist, können wir nicht generell sagen.
Um dies zu verdeutlichen, überlegen wir einmal in welcher Einheit die Kovarinz vorliegt. Es sind im Beispiel °C * müNN. Was würde passieren, wenn wir die Geländehöhe nicht in münn sondern in kmünn ausdrücken würden?
## [1] -0.7366715Die Kovarianz verändert sich dramatisch, auch wenn der Zusammenhang doch derselbe geblieben ist. Auch wenn wir die Jahresmitteltemperatur °Fahrenheit ausdrücken würde ändert sich die Kovarianz. Wenn wir nur eine Additive Konstante dazu addieren, wie z.B: bei der Umrechnung in in °K ändert sich die Kovarianz nicht.
Kovarianz für Temperatur in °K:
## [1] -736.6715Kovarianz für Temperatur in °F?
## [1] -1326.009Um dieses Problem zu umgehen, verwendet man die Korrelation um die Stärke von Zusammenhängen anzugeben.
11.2 Korrelation
Im Gegensatz zur Kovarianz handelt es sich bei der Korrelation um ein normiertes Maß um zu beschreiben, wie stark zwei Zufallsvariablen oder zwei Realisierungen von Zufallsvariablen zusammenhängen. Wir werden uns verschiedene Korrelationskoeffizienten anschauen. Diese unterscheiden sich u.a. dahingehend, für welches Skalennivaeu (nominal, ordinal, numerisch)48 sie angewendet werden können.
11.2.1 Pearsons r
Der Pearson Korrelationskoeffizient \(r\) basiert auf der Kovarianz. Die Kovarianz wird dabei durch die Quadratwurzel aus dem Produkt der Abweichungsquadrate vom jeweiligem Mittelwert normiert. Dadurch entfällt die Normierung auf \(n-1\), da die Summe der Abweichungsquadrate über alle Beobachungen geht.
\[ cor(X_j, X_k) = r = \frac{ \sum_{i=1}^n(x_{i,j} - \bar{x_j}) (x_{i,k} - \bar{x_k})}{\sqrt{\sum_{i=1}^n(x_{i,j} -\bar{x_j})^2 \sum_{i=1}^n(x_{i,k} -\bar{x_k})^2}} \]
Der Korrelationskoeffizient ist auch als Bravis-Pearson Korrelationskoeffizient oder Produkt-Moment Korrelationskoeffizient bekannt. Er quantifiziert den linearen Zusammenhang zwischen zwei Zufallsvariablen bzw. deren Realisierungen. Der Wertebereich umfasst das Intervall[-1, 1]. Je höher der Betrag von \(r\), desto stärker der lineare Zusammenhang. Ist das Vorzeichen positiv, treten hohe Werte der einen Variablen zusammen mit hohen Werten der andern Variablen auf, und niedrige zusammen mit niedrigen. Ist das Vorzeichen negativ, treten hohe Werte zusammen mit niedrigen Werten und niedrige Werte zusammen mit hohen Werten auf.
In der Fallstudie der Klimamessstationen in Deutschland beträgt der Korrelationskoeffizient -0.89, also ein starker Zusammenhang.
## [1] -0.8943286Dieser Wert ist unabhängig von den Einheiten die wir verwenden:
## [1] -0.8943286Schauen wir uns einmal ein Beispiel - anhand von simulierten Daten - an, wie Beobachtungen für unterschiedliche Korrelationskoeffizienten aussehen können.
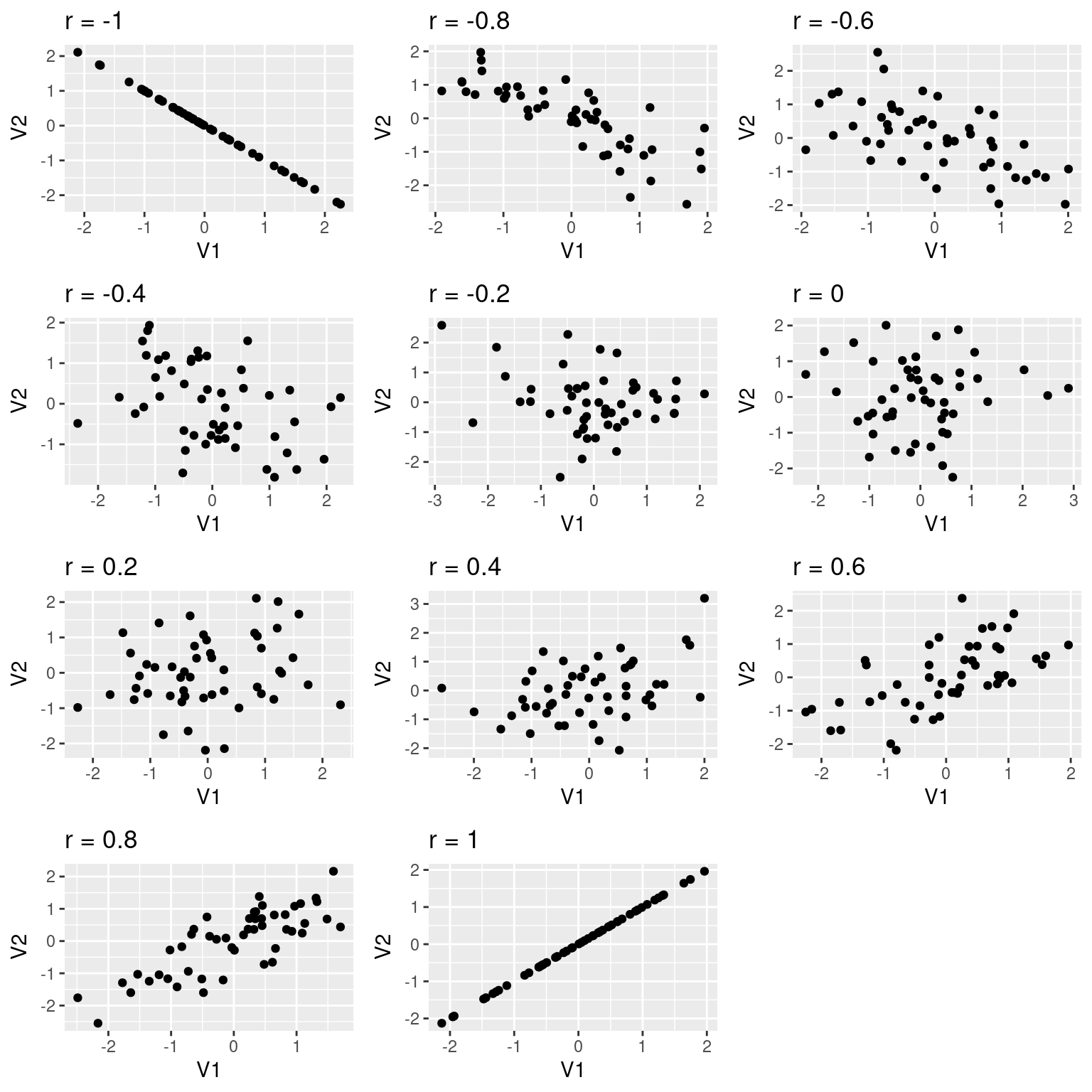
Wie wir sehen, kann man bei Korrelationskoeffizienten von \(|0.2|\) einen Zusammenhang mit bloßem Auge nur schwer erahnen. Wichtig ist sich klar zu machen, dass die obige Abbildung nur eine von vielen möglichen Realisierungen ist. Schauen wir uns einmal an, wie stark die Streuung für unterschiedliche Realisierungen sein kann.
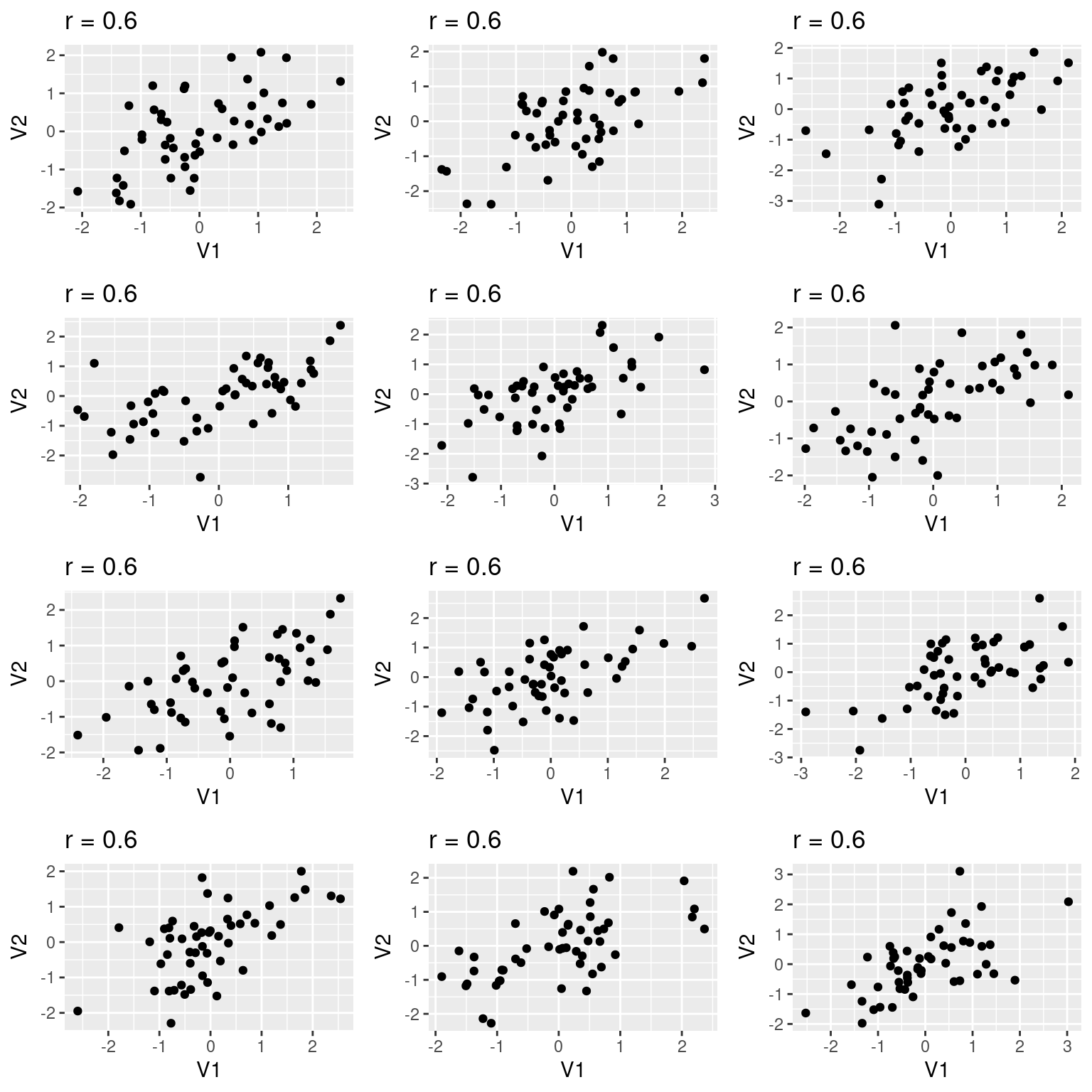
11.2.1.1 Anscombes Quartett
Das schöne an einer statistischen Kennzahl ist, dass sie die Information in einer Kennzahl aggregieren. Allerdings muss man aufpassen mit der Interpretation. Wir schauen uns einen speziell preparierten Zusammenhang an, der uns die Schwächen eines blinden Vertrauens auf Kennzahlen aufzeigt.
Der Datensatz enthält 4 Paare von Spalten: x1-y1, x2-y2, x3-y3 und x4-y4. Für diese wollen wir uns die Zusammenhänge anschauen. Berechnen wir zunächst Pearson’s r:
## [1] 0.8164205## [1] 0.8162365## [1] 0.8162867## [1] 0.8165214Alle positive korreliert, mit exakt dem gleichen Korrelationskoeffizient. Wir würden also vermuten, dass die Daten im Scatterplot alle ähnlich aussehen. Weit gefehlt!
p1 <- ggplot(anscombe, aes(x=x1, y = y1)) + geom_point()
p2 <- ggplot(anscombe, aes(x=x2, y = y2)) + geom_point()
p3 <- ggplot(anscombe, aes(x=x3, y = y3)) + geom_point()
p4 <- ggplot(anscombe, aes(x=x4, y = y4)) + geom_point()
ggpubr::ggarrange(p1,p2,p3,p4, ncol = 2, nrow=2)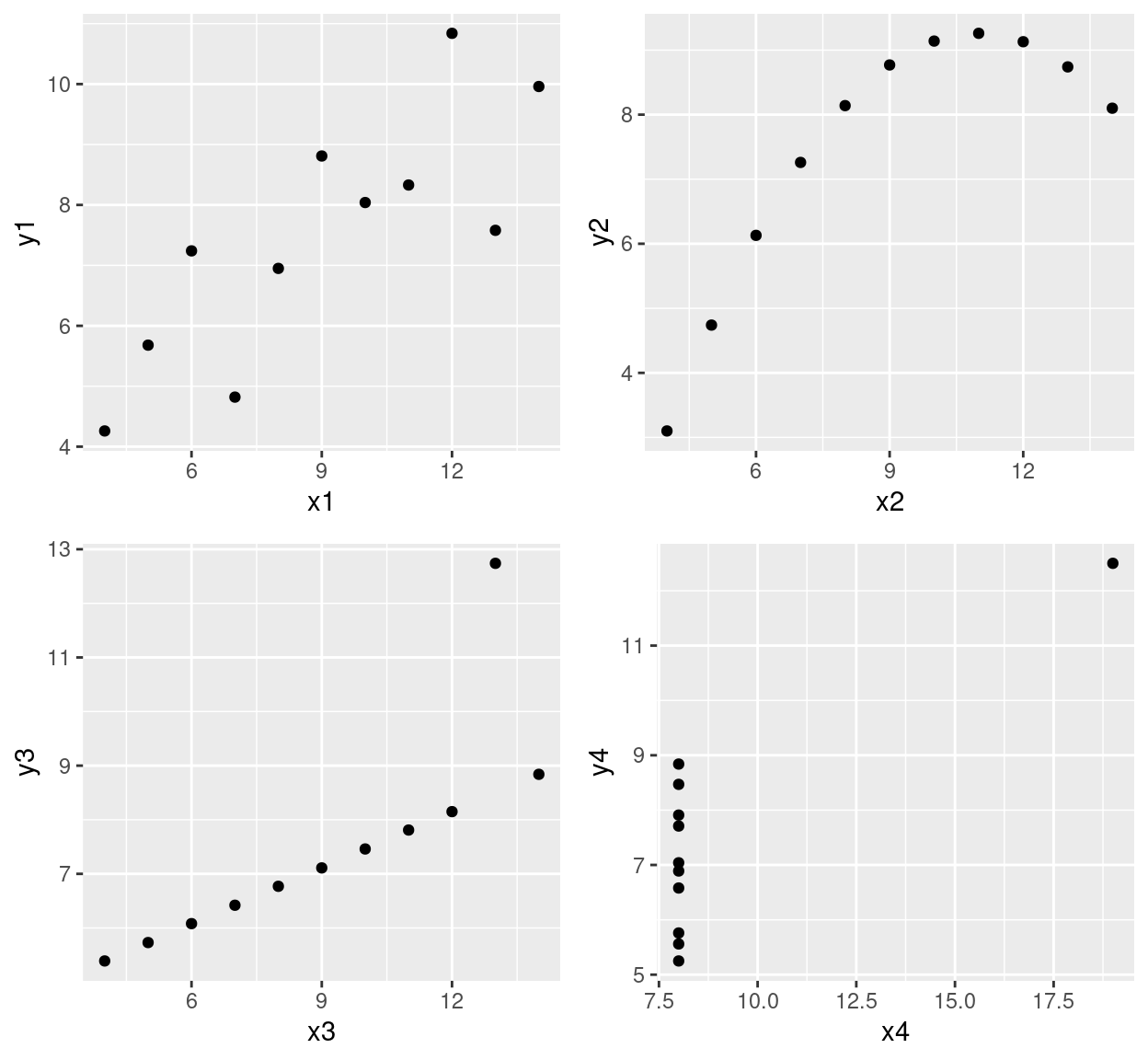
Wie wir sehen, sind die Zusammenhänge doch sehr unterschiedlich. Der Zusammenhang zwischen x1 und x2 ist so, wie wir das erwartet hätten: ein klarer linearer Zusammenhang, mit etwas Streuung. Der Zusammenhang zwischen x2 und y2 folgt perfekt einer Parabel, die durch einen linearen Zusammenhang allerings nur teilweise erfasst wird. Für x3 gegen y3 sehen wir einen perfekten Zusammenhang, allerdings mit einem Ausreißer. Diesen sollten wir unbedingt noch einmal untersuchen und am besten noch einmal nachmessen - falls sich dies bewerkstelligen lässt. Der Zusammenhang zwischen x4 und y4 ist mit den vorhandenen Daten nur schwer zu beurteilen. Es sieht so aus, als hätten wir bei x4 = 8 eine große Streuung. Bei x4 = 19 haben wir nur einmal gemessen und können die Streuung gar nicht beurteilen. In diesem Fall sollten wir unbedingt mehr Messungen entlang x4 durchführen und auf mehrere Messungen von y4 für denselben Wert von x4 achten.
Wir sehen, dass die Interpretation und das weitere Vorgehen in diesem Fall fundamental unterschiedlich wären. Dies zeigt die Wichtigkeit, Daten zu plotten und nicht nur auf Kennzahlen zu vertrauen, auch wenn Kennzahlen hilfreich und wichtig sind.
11.2.1.2 Standardfehler und Signifikanztest
Der Standardfehler von Pearsons r beträgt \(se_r = \sqrt{\frac{1-r^2}{n-2}}\).
Um die Signifikanz des Zusammenhanges zu testen verwenden wir das Verhältnis aus \(r\) und \(se_r\). Dieses ist näherungsweise t-verteilt, mit \(n-2\) Freiheitsgraden.
Schauen wir uns das einmal für den deutschen Klimadatensatz an:
## [1] 0.04190385## [1] -21.3424Irrtumswahrscheinlichkeit p:
## [1] 6.303698e-42Der Korrelationskoeffizient ist also mit an Sicherheit grenzender Wahrscheinlichkeit von Null verschieden, d.h. wir können davon ausgehen, dass der gefundene negative Zusammenhang zwischen Jahresmitteltemperatur und Geländehöhe nicht zufällig ist.
Einfacher geht es über cor.test.
##
## Pearson's product-moment correlation
##
## data: temp.de$YEAR and temp.de$ELEV
## t = -21.342, df = 114, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## -0.9257077 -0.8507233
## sample estimates:
## cor
## -0.894328611.2.2 Spearmans rho
Pearsons r ist anfällig gegenüber Ausreißern und gegenüber nicht linearen Zusammenhängen. Der t-Test mit \(H_0: r = 0\) beruht weiterhin auf der Annahme einer bivariaten Normalverteilung. Ist diese Annahme verletzt, kann das Testergebnis irreführend sein. Aus diesem Grund wurden robuste Alternativen entwickelt. Die bekannteste ist Spearmans \(\rho\), bei dem einfach Pearsons r auf die rangtransformierten Werte angewendet wird. Rangtransformiert heißt dabei einfach, dass der Wert durch seinen Rang (von groß nach klein) ersetzt wird. Die Werte beider Zufallsvariablen werden also getrennt voneinander sortiert. Dann wird jeweils der Größte Wert mit 1 ersetzt, der zweitgrößte mit 2,… Dann wird auf diesen rangtransformierten Werten Pearsons r berechnet.
Sei \(rank(x_j)\) die rangtransformierteVariable \(x_j\) und \(\overline{rank(x_j})\) der Mittelwert dieser rangtransformierten Variablen. Dann lässt sich Spearmans Rangkorrelationskoeffizient \(\rho\) wie folgt ausdrücken:
\[ cor_{spearman}(X_j, X_k) = \rho = \frac{ \sum_{i=1}^n(rank(x_{j})_i - \overline{ rank(x_j}) ) (rank(x_{k})_i - \overline{rank(x_k}))}{\sqrt{\sum_{i=1}^n(rank(x_{j})_i -\overline{rank(x_j}))^2 \sum_{i=1}^n(rank(x_{k})_i -\overline{rank(x_k}))^2}} = cor_{pearson}(rank(X_j), rank(X_k))\]
Die Rangtransformation führt dazu, dass nun nicht mehr nur ein linearer Zusammenhang, sondern ein streng monotoner Zusammenhang bewertet wird. Schauen wir uns ein Beispiel für einen streng monotonen Zusammenhang an:
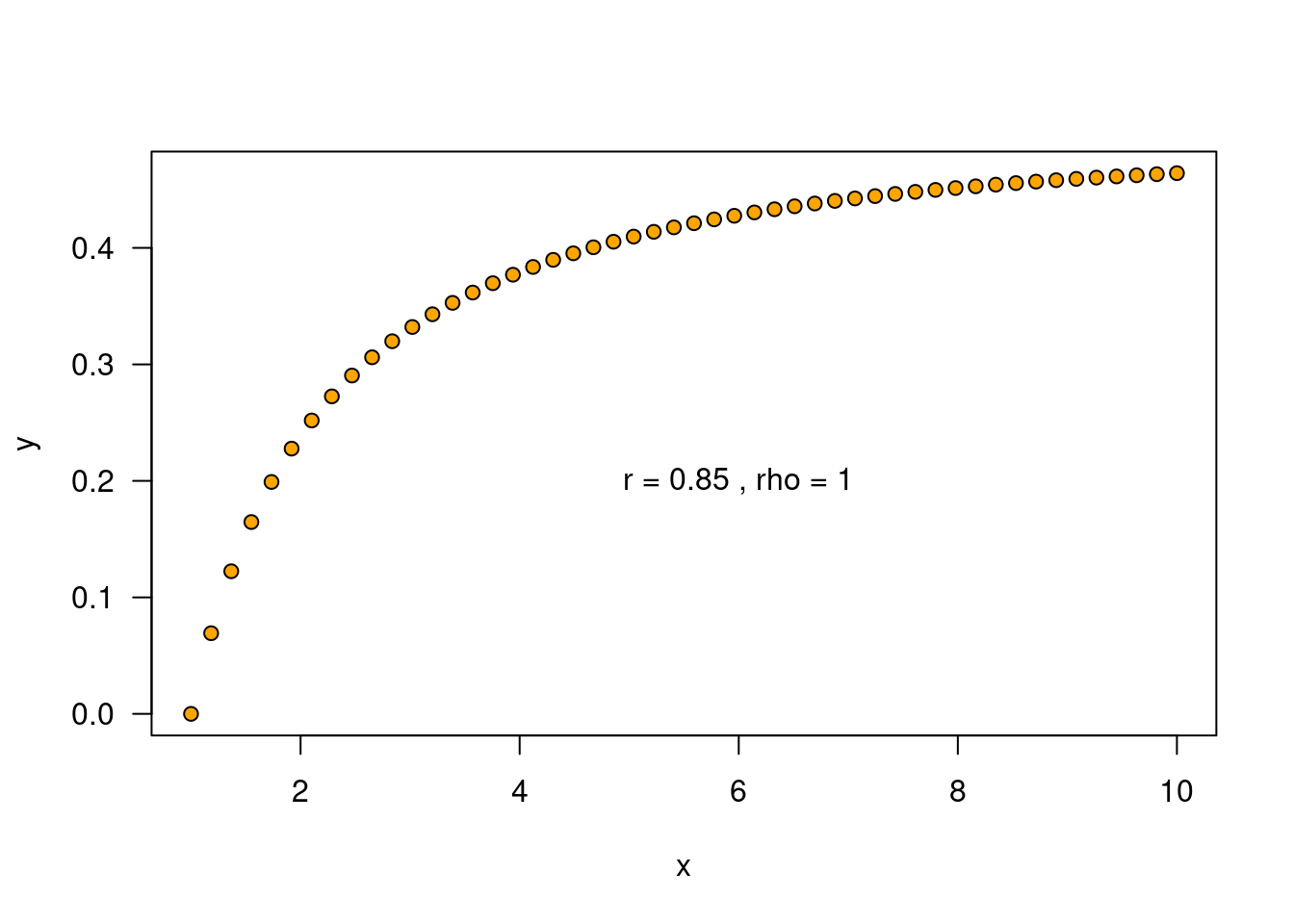
Da der Zusammenhang nicht linear ist, zeigt Pearsons r mit 0.85 keinen perfekten Zusammenhang an. Die vorgeschaltete Rangtransformation ergibt dann den klaren perfekten Zusammenhang.
x_ranked <- rank(x)
y_ranked <- rank(y)
r_ranked <- cor(x_ranked,y_ranked, method="pearson") %>% round(2)
rho_ranked <- cor(x_ranked,y_ranked, method="spearman") %>% round(2)
plot(y_ranked~x_ranked, type="p", pch=21, bg="orange ",
las=1, xlab= "x, rangtransformiert", ylab = "y, rangtransformiert")
text(x = 15, y=40, labels = paste("r =", r_ranked, "\nrho =", rho_ranked))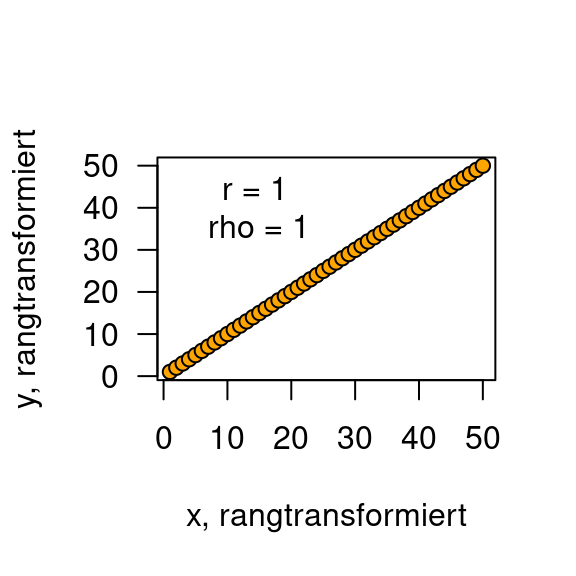
11.2.3 Kendals tau
Spearmans \(\rho\) ist der üblicherweise benutzt Rangkorrelationskoeffizient. Kendalls \(\tau\) führt dagegen eher ein Nischendasein - auch wenn Kendalls \(\tau\) Spearmans \(\rho\) in einiger Hinsicht überlegen ist. Der wichtigste Aspekt ist die Interpretation. Wenn sich \(\rho\) von 0.2 auf 0.4 erhöht, bedeutet das nicht, dass die Korrelation doppelt so stark ist - man kann nur sagen, dass sie ist nun stärker ist. Wenn sich dagegen \(\tau\) verdoppelt, dann ist die Korrelation tatsächlich doppelt so stark.
Kendalls \(\tau\) für zwei gemeinsam für alle Datenpunkte gemessenen Variablen \(x_j\) und \(x_k\) beruht darauf, dass man sich für jede Beobachtung anschaut, wieviele der anderen Beobachtungen koncordant oder discordant sind. Ein Datenpaar \(a\) ist mit einem anderen Datenpaar \(b\) konkordant, wenn entweder \(x_a > x_b\) und \(y_a > y_b\) oder \(x_a < x_b\) und \(y_a < y_b\) gilt. Die Datenpaare sind entsprechend discordant, wenn entweder \(x_a > x_b\) und \(y_a < y_b\) oder \(x_a > x_b\) und \(y_a < y_b\) gilt. Datenbindungen (ties), d.h. gleiche Werte innerhalb einer Variablen werden nicht gezählt.
Die nachfolgende Abbildung zeigt für ein ausgewähltes Datenpaar konkordante und dicordante Datenpaare. Alle Datenpaare innerhalb der dunkelgrauen Flächen sind konkordant zum ausgewählten Datenpaar. Die Datenpaare außerhalb sind discordant.
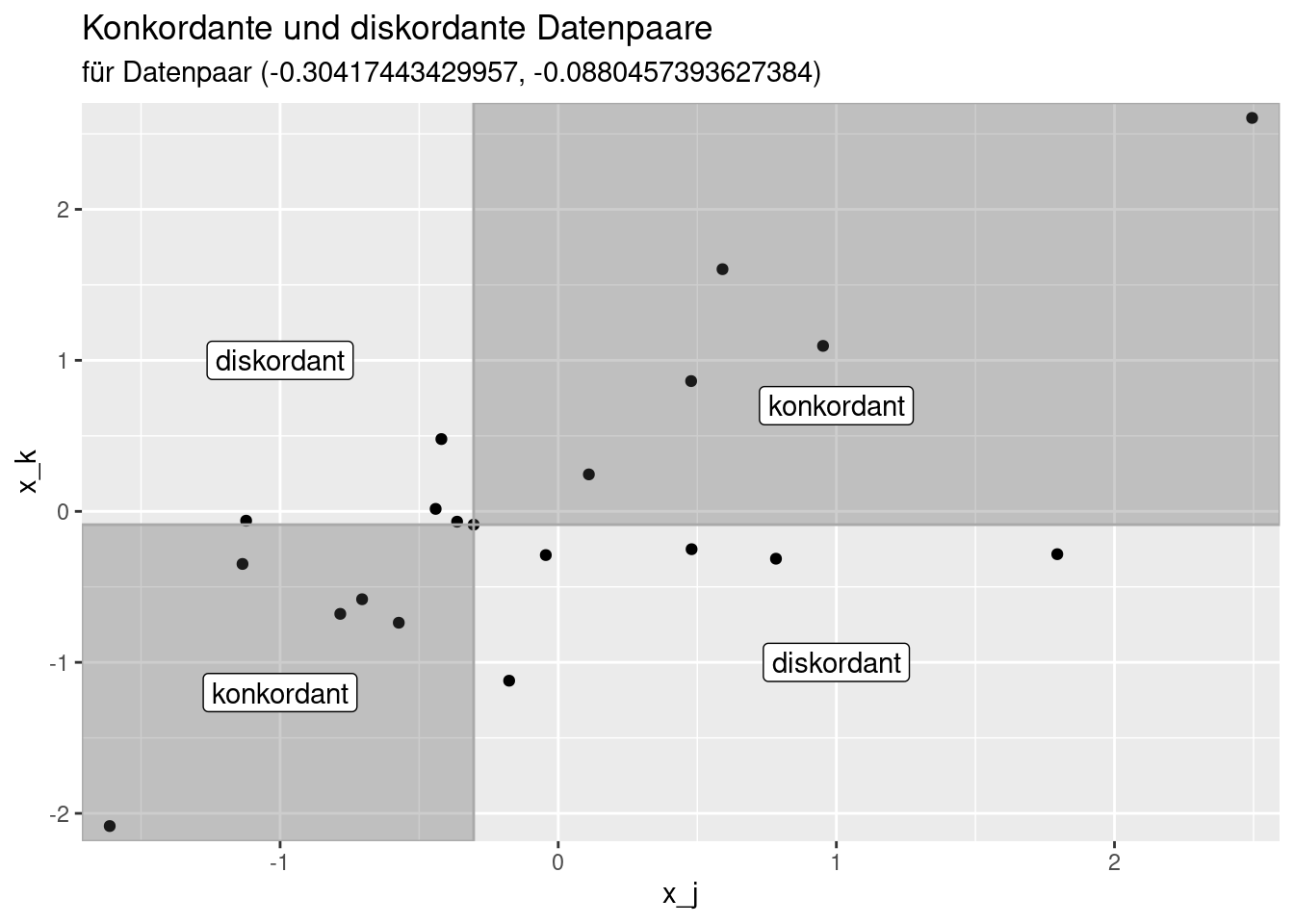
Die konkordanten und diskordanten Datenpaare werden nun gezählt. Anschließend wird für das nächste Datenpaar die Anzahl der konkordanten und diskordanten Datenpaare ermittelt und aufaddiert.
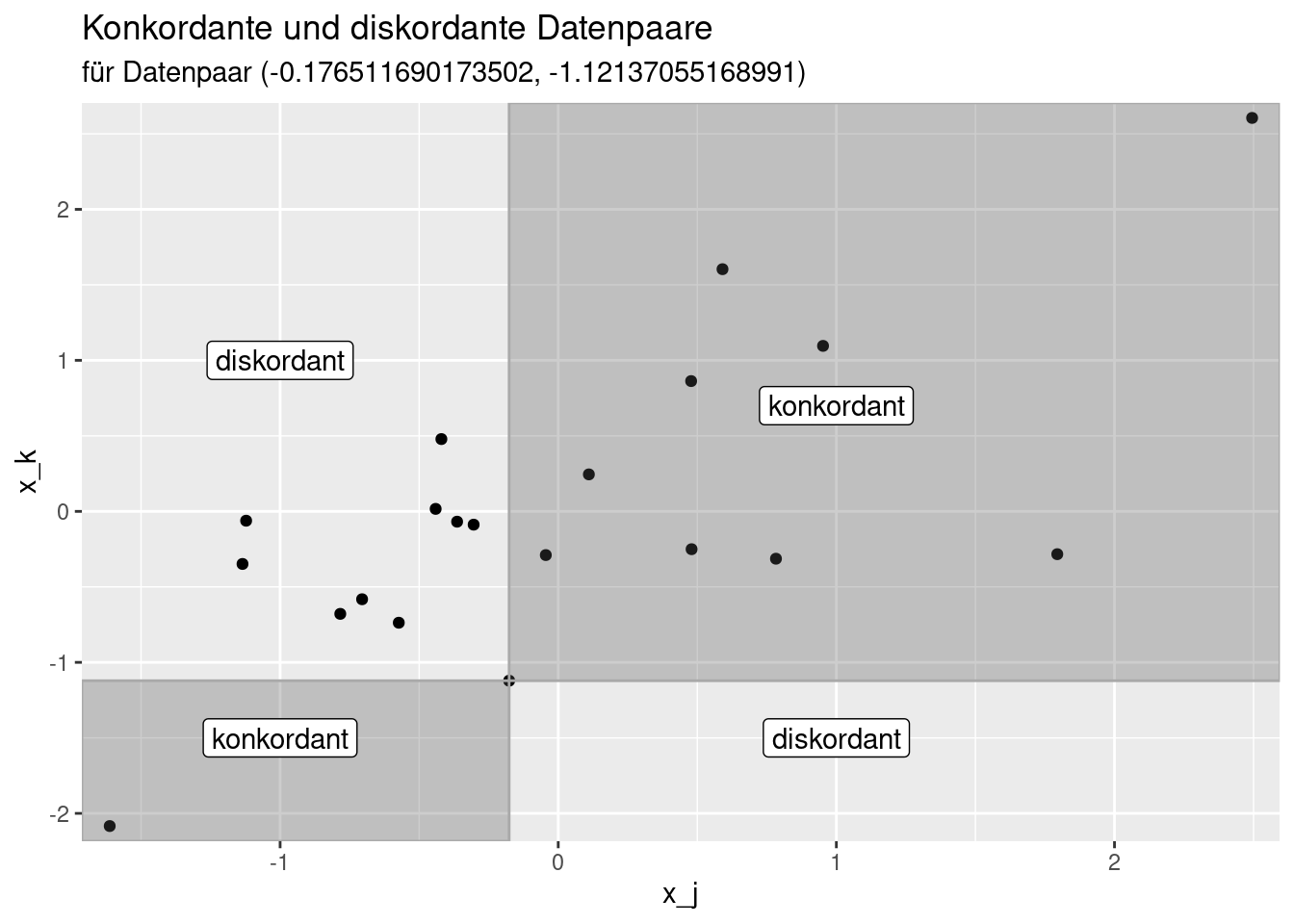
Auf der Grundlage der so ermittleten Zahlen kann Kendalls \(\tau\) berechnet werden:
\[ \tau = \frac{\text{Anzahl konkordanter Paare} - \text{Anzahl diskordanter Paare}}{\text{Anzahl Paare}} = 1 - \frac{2\cdot \text{Anzahl diskordanter Paare}}{\binom{n}{2}}\]
Wobei \(\binom{n}{2} = \frac{n(n-1)}{2}\) der aus der Schule bekannte Binomialkoeffizient ist, der angibt wieviele Möglichkeiten bestehen, zwei Beobachtungen aus einer Menge von \(n\) Beobachtungen zu wählen.
Man kann \(\tau\) auch explizit definieren:
\[ \tau = \binom{n}{2}\sum_{i=1}^n\sum_{j=i+1}^n sign(x_{i,k} - x_{j,k})sign(y_{i,k} - y_{j,k}) \] Die Funktion \(sign(a)\) liefert dabei das Vorzeichen von \(a\) zurück, also -1, 0 oder 1, je nachdem ob \(a\) kleiner, gleich oder größer 0 ist. Die explizite Definition beruht also drauf zu schauen, ob die Unterschiede der Datenpaare in \(x_j\) und \(x_k\) gleichsinning sind oder nicht.
Großer Vorteil von Kendalls \(\tau\) ist wie bereits erwähnt die besser Interpretierbarkeit. Bei sehr großen Datensätzen steigt die Rechenzeit stark an, da wir eine doppelte Summe berechnen müssen, weswegen die Laufzeit quadratisch mit der Anzahl der Datenpunkte ansteigt.49
Schauen wir uns einmal die drei Korrelationskoeffizienten, die wir kennengelernt haben für Anscombes Quartett an:
calc3CorString <- function(x,y)
{
r <- cor(x,y) %>% round(2)
rho <- cor(x,y, method = "spearman") %>% round(2)
tau <- cor(x,y, method = "kendall") %>% round(2)
res <- paste("r=", r, ", rho=", rho, ", tau=", tau)
return(res)
}
p1 <- ggplot(anscombe, aes(x=x1, y = y1)) + geom_point() +
labs(title = calc3CorString(anscombe$x1,anscombe$y1) )
p2 <- ggplot(anscombe, aes(x=x2, y = y2)) + geom_point()+
labs(title = calc3CorString(anscombe$x2,anscombe$y2) )
p3 <- ggplot(anscombe, aes(x=x3, y = y3)) + geom_point()+
labs(title = calc3CorString(anscombe$x3,anscombe$y3) )
p4 <- ggplot(anscombe, aes(x=x4, y = y4)) + geom_point()+
labs(title = calc3CorString(anscombe$x4,anscombe$y4) )
ggpubr::ggarrange(p1,p2,p3,p4, ncol = 2, nrow=2)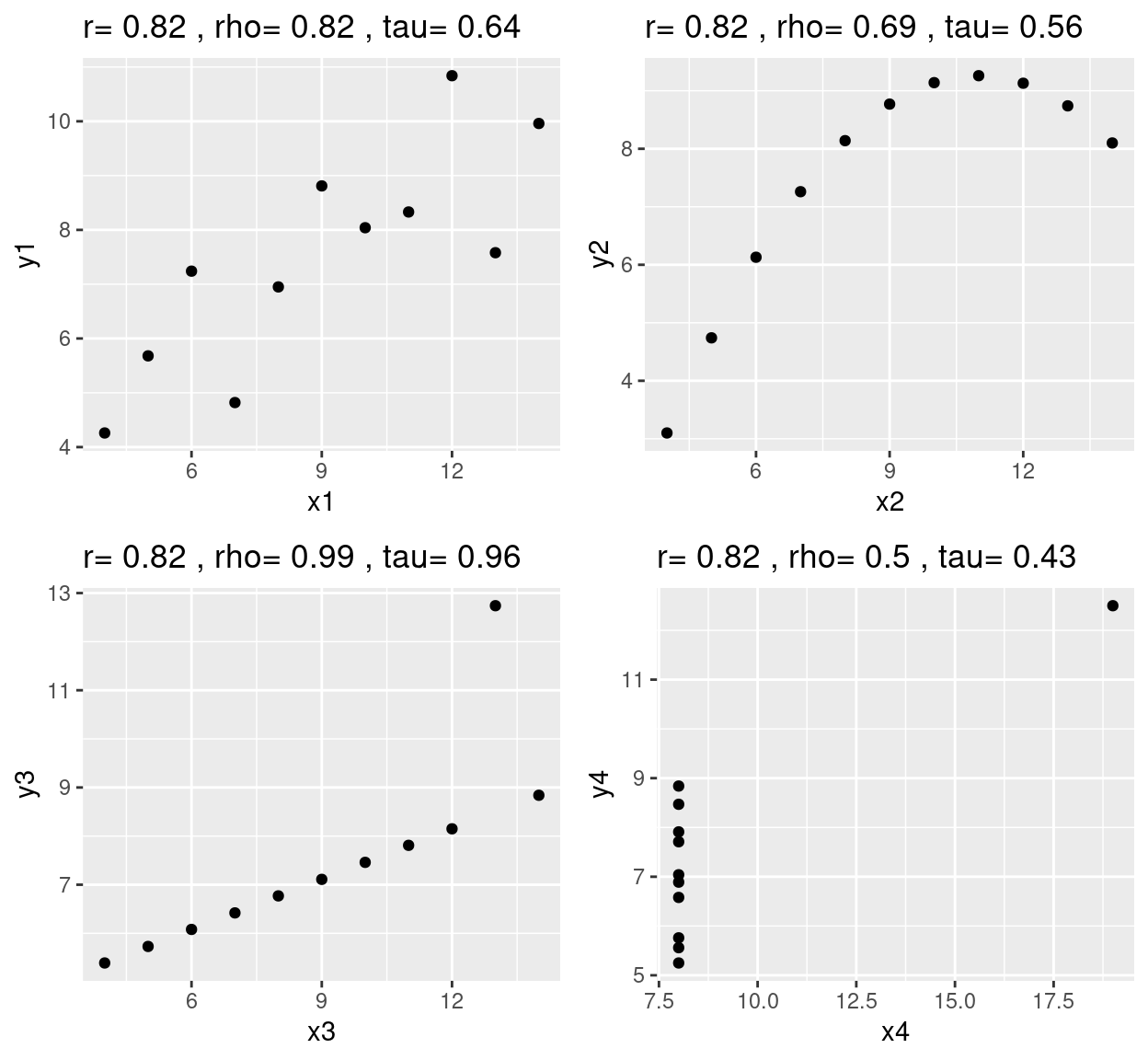
Auffällig ist, dass:
- \(\rho\) und \(\tau\) robust gegenüber Ausreißern zu sein scheinen (y3~x3), was vielleicht nicht in jedem Fall gut ist
- \(\rho\) und \(\tau\) für den 4. Fall den Zusammenhang deutlich schwächer einschätzen, als \(r\)
- der nicht-monotone parabelförmige Zusammenhang (y2~x2) durch die Rangtransformation als noch schwächer eingeschätzt wird
- \(\tau\) den Zusammenhang für y1~x1 deutlich schwächer einschätzt als \(r\) und \(\rho\).
Die wichtige Botschaft sollte in jedem Fall sein, dass es sich lohnt, die Daten zu plotten und nicht blindlings auf statistische Kennzahlen zu vertrauen.
11.3 Tests auf Assoziation für kategorische Variablen
Daten zweier kategorischer Variablen werden üblicherweise in sogenannten Kontigenztabellen (contigency table, auch Kreuztabelle) zusammengefasst. Oftmals handelt es sich dabei um 2x2 Tabellen. Die hier vorgestellten Tests sind jedoch auch für Kreuztabellen mit mehreren Kategorien je kategorialer Variable geeignet. Der Grundgedanke ist stets, zu testen ob die Anzahl der Einträge (z.B. die Anzahl der Studienteilnehmer) im jeweiligen Feld zufällig zu erwarten ist, oder durch das Zusammenspiel der beiden Faktoren bedingt ist.
Dazu benötigen wir den Erwartungswert. Wen wir unterstellen, dass die einzelnen Ausprägungen der kategorischen Variablen keinen Einfluss auf die Anzahl der Einträge haben (Nullhypothese), können wir dies einfach anhand der relativen Häufigkeit der einzelnen Kategorien in der Stichprobe berechnen: \[ \text{Erwartete Anzahl in Kategorie i,j} = \frac{\text{Anzahl in Kategorie i}}{\text{Gesamtanzahl}} \cdot \frac{\text{Anzahl in Kategorie j}}{\text{Gesamtanzahl}} \cdot \text{Gesamtanzahl}\]
Leichter nachvollziehbar wird es, wenn wir uns ein Beispiel anschauen: In einer Umfrage in Norwich (Flowerdew and Martin 2005, 209) sollte ermittelt werden, ob es Unterschiede zwischen dem Wohnort und praktizierter Mülltrennung gibt.
recycling <- matrix(data = c(64, 152, 16, 85, 42, 58), ncol=2, nrow=3, byrow = TRUE)
colnames(recycling) <- c("No-recycling", "Recycling")
rownames(recycling) <- c("Costessy", "South Park", "Woodcock")
knitr::kable(recycling)| No-recycling | Recycling | |
|---|---|---|
| Costessy | 64 | 152 |
| South Park | 16 | 85 |
| Woodcock | 42 | 58 |
Um die Tabelle zu visualisieren bietet sich ein sogenannter Mosaic-Plot an.
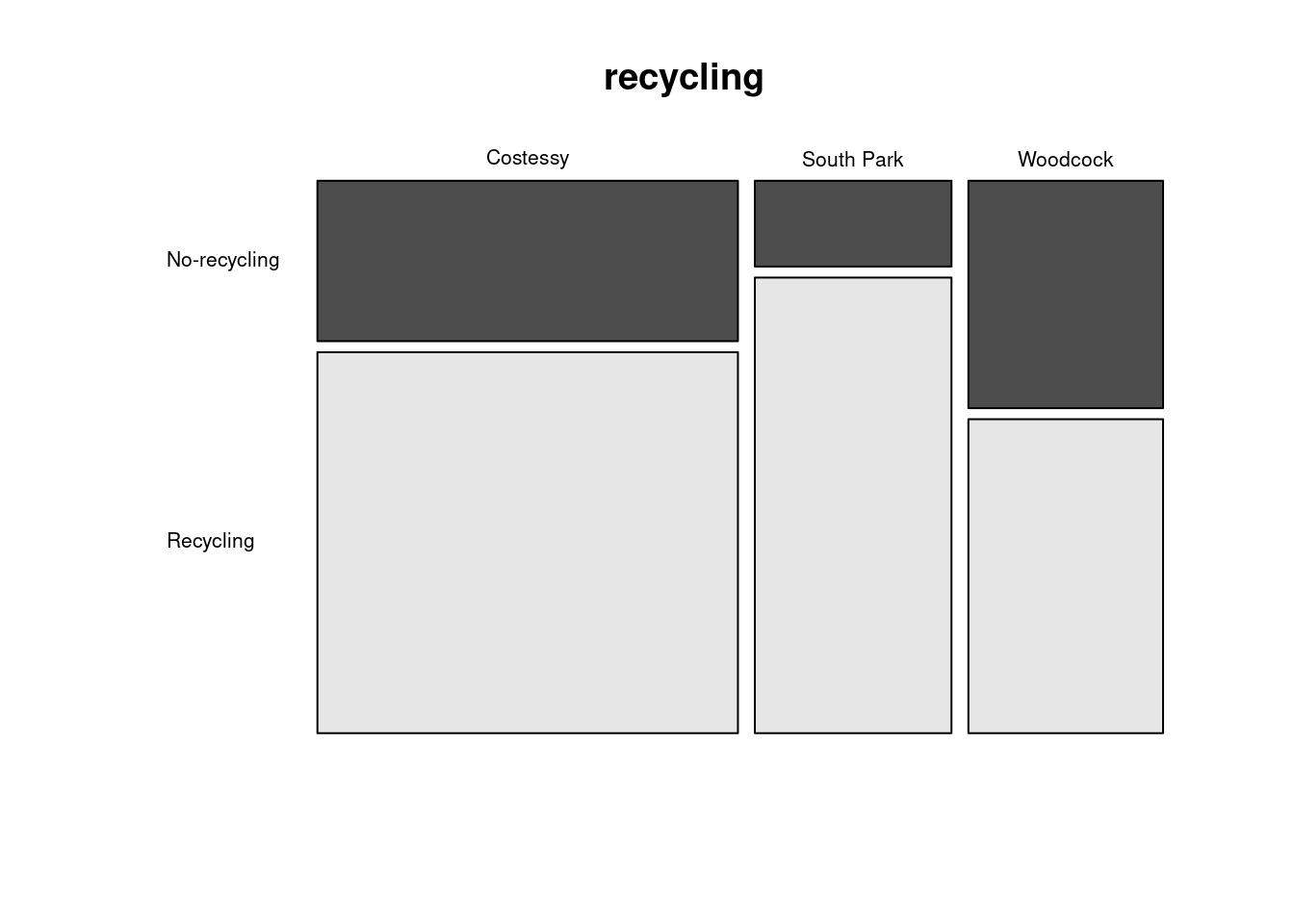
Über addmarginskönnen wir bequem die Randsummen hinzufügen
| No-recycling | Recycling | Sum | |
|---|---|---|---|
| Costessy | 64 | 152 | 216 |
| South Park | 16 | 85 | 101 |
| Woodcock | 42 | 58 | 100 |
| Sum | 122 | 295 | 417 |
Die Frage ist nun, welche Werte wir erwarten würden, wenn wir davon ausgehen, dass sich das Recyclingverhalten der Haushalte nicht zwischen den Wohnorten unterscheidet.
Wenn wir davon ausgehen, dass Wohnort Und Mülltrennungsverhalten unabhängig voneinander sind würden wir erwarten, dass sich die Einträge in der Kreuztabelle einfach aus dem Produkt der Wahrscheinlichkeit in einem Ort zu wohnen und der Wahrscheinlichkeit Müll zu trennen ergibt - jeweils anhand der Stichprobe geschätzt.
Von den 417 Teilnehmern der Befragung lebten 216 / 417 = 51.8% in Costessy, 101/417 = 24.22% in South Park und 100/417 = 23.98% in Woodcock.
Mülltrennung praktizierten 295 / 417 = 70.74%.
Wir würden also erwarten, dass in Costessy 216 / 417 * 295/417 * 417 = 152.8057554 der Befragten Mülltrennung praktizieren, was ziemlich genau dem in der Befragung ermittelten Wert entspricht. Für South Park erwarten wir, dass (unter der Annahme der Unabhängigkeit) 101 / 417 * 295/417 * 417 = 71.4508393 Teilnehmer Mülltrennung praktizieren. Hier sind es in der Befragung mehr gewesen (nämlich 85). Für Woodcock würden wir erwarten, dass 100 / 417 * 295/417 * 417 = 70.7434053 Teilnehmer Mülltrennung praktizieren. Hier sind es in der Befragung weniger gewesen (nämlich 58).
Die Berechnung ergibt sich daraus, dass wir je Zelle die Schnittmenge der Wahrscheinlichkeiten berechnen. Dadurch, dass wir unterstellen, dass die beiden Merkmale keinen Einfluss auf die Wahrscheinlichkeiten haben, diese also unabhängig voneinander sind (das ist ja die Nullhypothese, die wir testen), lässt sich die Schnittmenge einfach als Produkt der Wahrscheinlichkeiten zu einer der beiden Klassen zu gehören ausdrücken.
Wir können diese Zahlen in R einfach erhalten, wenn wir auf die Matrix die Funktion chisq.test anwenden und dann den slot expected anzeigen lassen. Das ergibt die Absolutwerte - wenn wir die relativen Werte angezeigt habe möchten, müssen wir nur durch die Gesamtanzahl dividieren.
## No-recycling Recycling
## Costessy 63.19424 152.80576
## South Park 29.54916 71.45084
## Woodcock 29.25659 70.74341Relative Werte (mit 100 multiplizieren, um % Werte zu erhalten.)
## No-recycling Recycling
## Costessy 0.1515450 0.3664407
## South Park 0.0708613 0.1713449
## Woodcock 0.0701597 0.169648511.3.1 \(\chi^2\)-Test
Nun interessiert uns, ob die beobachteten Abweichungen zufällig zustande gekommen sein können, oder ob wir davon ausgehen müssen, dass es zwischen den Gemeinden deutliche Unterschiede im Verhalten gibt.
Man testet dabei die Summe der quadrierten Abweichungen zwischen errwarteter (\(E\)) und beobachter (\(O\)) Anzahl je Feld der Kreuztabelle und teilt dass durch die Gesamtzahl:
\[ \text{Teststatistik} = \sum_{i=1}^r \sum_{j=1}^s \frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}}\]
Asymptotisch sollte die Verteilung der Teststatistik einer \(\chi^2\)-Verteilung folgen. Die Anzahl der Freiheitsgrade ergibt sich dabei als \[df = (\text{Anzahl Spalten der Kreuztabelle}-1) \cdot (\text{Anzahl Zeilen der Kreuztabelle}-1)\] , in unserem Fall als \(df = 2\).
##
## Pearson's Chi-squared test
##
## data: recycling
## X-squared = 16.643, df = 2, p-value = 0.0002433Der \(\chi^2\)-Test zeigt deutlich, dass der die Verteilung der Werte nicht zufällig zu erwarten ist. Die Irrtumswahrscheinlichkeit ist gering. Wir haben also einen deutlichen Hinweise darauf, dass die Müllltrennung unterschiedlich in den Gemeinden praktiziert wird. Diese Unterschiede könnten sich z.B. mit unterschiedlichem Bildungsstand oder politischer Zugehörigkeit erklären lassen, mit dem verfügbaren Einkommen oder damit, dass es in manchen Gemeiden Initiativen zur Mülltrennung gab. Dies zu klären, ist die Aufgabe weiterführender Analysen, für die zusätzliche Daten benötigt werden würden.
EIne Möglichkeit, zu visualisieren, welche Kategorien besonders stark vom Erwartungswert abweiche ist der Assoziationsplot.
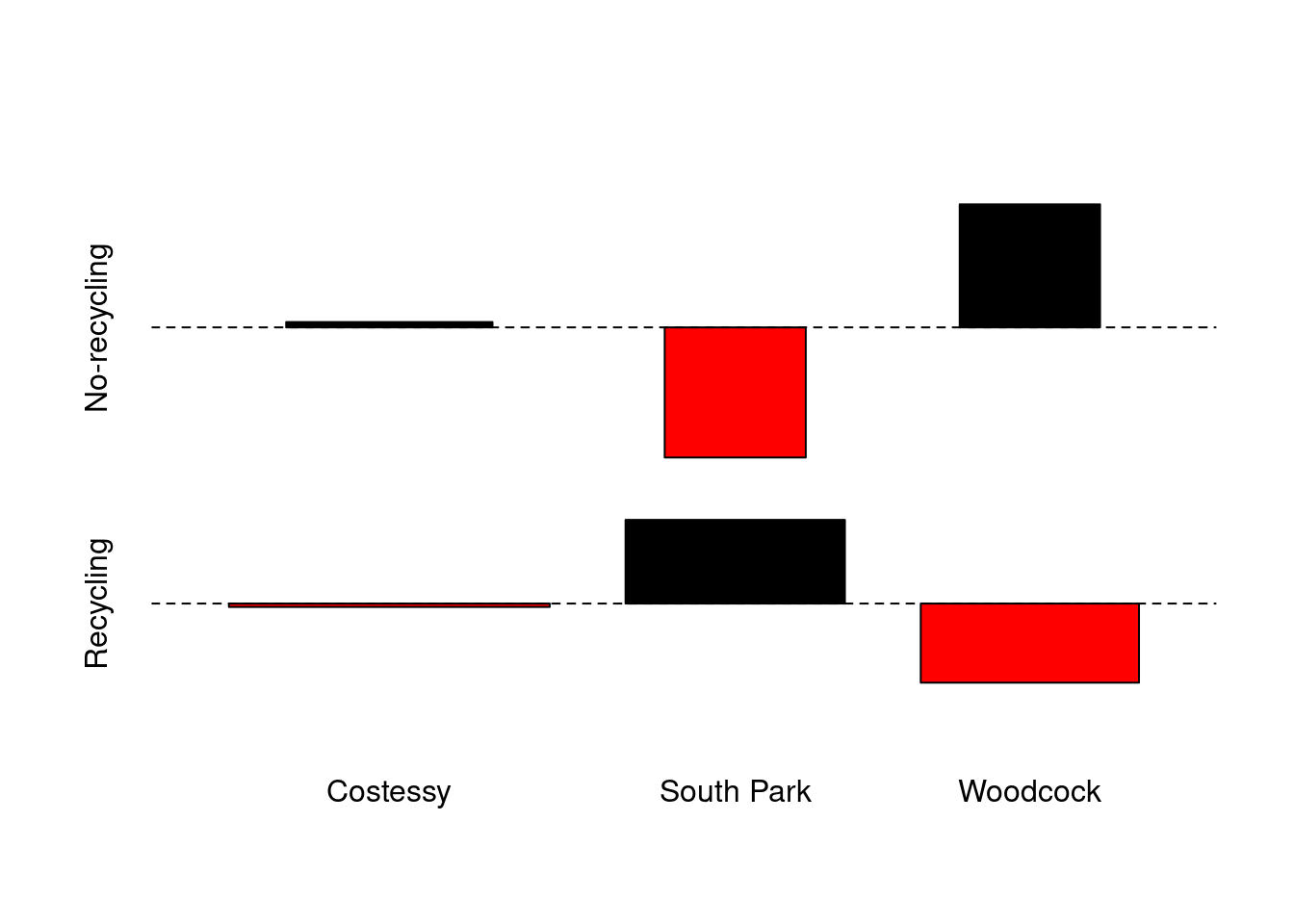
Je Kategorie wird die Differenz vom Erwartungswert angezeigt: \(d_{ij} =(f_{ij} −e_{ij} )/\sqrt{e_{ij}}\), wobei \(f_{ij}\) die beobachten Werte und \(e_{ij}\) die Erwartungswerte sind. Jede Zelle der Kreuzmatrix wird durch ein Rechteck mit der Höhe proportional zu \(d_{ij}\) und der Breite proportional zu \(\sqrt{e_{ij}}\) dargestellt.
Wir sehen, dass die Zahlen in Cotessy nicht wirklich vom Erwartungswert abweichen, während in South Park deutlich weniger Haushalte Mülltrennung betreiben als zu erwarten. Für Woodcock dagegen betreiben mehr Haushalte Mülltrennung als zu erwarten.
11.3.1.1 Einfluss der Stichprobengröße auf die Irrtumswahrscheinlichkeit
Hinsichtlich der Berechnung der Freiheitsgrade besteht ein deutlicher Unterschied zur Regressionsanalyse, bei der die Freiheitsgrade u.a. von der Stichprobengröße abhängen. Die Stichprobengröße spielt trotzdem eine wichtige Rolle für die Irrtumswahrscheinlichkeit. Dies liegt daran, dass die Abweichung quadriert wird. Wenn wir also bei gleichen relativen Abweichungen vom Erwartungswert eine größere absolute Anzahl haben, wird die quadrierte Abweichung gegenüber dem Erwartungswert deutlich größer und damit die Irrtumswahrscheinlichkeit kleiner.
Schauen wir uns dass einmal an einem hypothetischen Beispiel an, bei dem wir unterstellen, dass wir die gleichen relativen Angaben bei einer zehnmal so großen Stichprobe erhalten hätten.
## No-recycling Recycling
## Costessy 640 1520
## South Park 160 850
## Woodcock 420 580Die Erwartungswerte, unter der Nullhypothese der Unabhängigkeit beider Merkmale, sind auch einfach zehnmal so groß.
## No-recycling Recycling
## Costessy 631.9424 1528.0576
## South Park 295.4916 714.5084
## Woodcock 292.5659 707.4341## No-recycling Recycling
## Costessy 63.19424 152.80576
## South Park 29.54916 71.45084
## Woodcock 29.25659 70.74341Die Irrtumswahrscheinlichkeit ist bei der zehnmal größeren Stichprobe deutlich geringer:
##
## Pearson's Chi-squared test
##
## data: recycling10
## X-squared = 166.43, df = 2, p-value < 2.2e-16##
## Pearson's Chi-squared test
##
## data: recycling
## X-squared = 16.643, df = 2, p-value = 0.0002433Schauen wir uns doch einmal genauer an, wie das zustande kommt. Für South Park erwarten wir bei der Originalstichprobe 71.45 Befragte, die ihren Müll trennen. Beobachtet wurden 85. Der Beitrag dieses Feldes zur Teststatistik ist wie folgt:
## [1] 2.569315Für den hypothetischen Fall der zehnmal größeren Stichprobe ist der Beitrag zur Teststatistik zehnmal so groß:
## [1] 25.69315Dies lässt sich mathematisch einfach nachvollziehen:
\[ \frac{(E*10 - O*10)^2} {E*10} = \frac{(10*(E - O))^2} {E*10} = \frac{10^2(E - O)^2} {E*10} = 10*\frac{(E - O)^2} {E}\]
Wenn wir bei gleichen relativen Werten eine \(x\)-mal größere Stichprobe hätten, würde sich der Beitrag jeder Zelle zur Teststatistik um den Faktor \(x\) erhöhen. In Summe ist die Teststatistik damit zehnmal so groß und damit das zufällige Auftreten dieses Wertes unwahrscheinlicher. Um wieviel sich die Irrtumswahrscheinlichkeit verringert wird durch die \(\chi^2\)-Verteilung mit dem entsprechenden Freiheitsgrad angegeben.
In unserem Beispiel:
## [1] 0.0002432307## [1] 7.247441e-37Dies unterstreicht nachdrücklich, dass es wichtig ist, die Rohdaten und nicht die Raten (relative Werte) zu verwenden. Leider ist dies ein oft gemachter Fehler - auch im Regressionskontext -, mit den einfachen Raten (crude rates) zu rechnen, anstelle die Rohdaten zu verwenden. Die dadurch verursachten Fehler und dadurch bedingten Fehlschlüsse können dramatisch sein.
11.3.1.2 Der Kontingenz-Koeffizient
Der Kontingenzkoeffizient ist ein Maß für die Stärke des Zusammenhanges. Der \(\chi^2\)-Test sagt ja nur etwas über die Irrtumswahrscheinlichkeit aus, nicht über die Stärke des Zusammenhangs. Wir wir gesehen haben, wird der p-Wert von der Stichprobengröße beeinflusst. Dies gilt aber nicht für die Stärke des Zusammenhanges.
Diese wird durch den Pearsonschen Kontigenzkoeffizienten quantifiziert:
\[ CC = \sqrt{\frac{\chi^2}{n + \chi^2}} \]
Der Kontigenzkoeffizient nutzt aus, dass die Größe der Schätzgröße mit der Stichprobengröße zusammenhängt (s. den vorherigen Abschnitt). Man könnte also durchaus die Teststatistik zweier Stichproben vergleichen, wenn die Stichprobengröße exakt gleich ist. Oder man normiert eben wie angegeben. Der Kontigenzkoeffizient liegt zwischen 0 und 1, was für Vergleiche schonmal gut ist. Allerdings hängt die maximale Größe des Kontigenzkoeffizienten auch von der Klassenanzahl ab. Der Zusammenhang ist wie folgt bestimmt:
\[ CC_{max} = \sqrt{\frac{min(r,s)-1}{min(r,s)}}\]
Dabei ist \(r\) die Anzahl Zeilen, \(s\) die Anzahl Spalten und \(min(r,s)\) der kleinere der beiden Werte. Damit kann ein korrigierte Kontingenzkoeffizient berechnet werden:
\[ CC_{korr} = \frac{CC}{Cc_{max}} = \sqrt{\frac{min(r,s) \cdot \chi^2}{(min(r,s)-1)\cdot(n + \chi^2)}}\]
In R kann der (korrigierte) Kontingenzkoeffizient mittels DescTools::ContCoef(x, correct = TRUE) berechnet werden.50 Wie wir sehen, ist der Kontingenzkoeffizient unabhängig von der Stichprobengröße.
## [1] 0.2770522## [1] 0.2770522Der Zusammenhang ist somit nicht wirklich sehr stark.
11.3.1.3 Voraussetzungen für die Anwendung des \(\chi^2\)-Tests
Der \(\chi^2\)-Test hat die Voraussetzung, dass für jedes Feld der Kontingenztabelle die erwartete Anzahl mindestens 5 beträgt. Sonst sollte der Test nicht angewandt werden.
In einem solche Fall kann man entweder versuchen, einzelne Kategorien zusammenzulegen - falls dies sinnvoll erscheint - oder Fishers exakten Test anwenden - falls dieser zulässig ist.
11.3.2 Fishers exakter Test
Dieser Test nutzt für 2x2 Kreuztabellen die Tatsache aus, dass für feste Randsummenwerte die erwartete Anzahl der Einträge eines Feldes einer Hypergeometrischen Verteilung folgt - falls die Randsummen der Spalten und Zeilen vorab fixiert waren. Die Wahrscheinlichkeit lässt sich anhand der Wahrscheinlichkeit für das Auftreten des beobachteten und extremerer Werte berechnen, wenn die Randsummen fixiert sind. Die Nullhypothese ist wie bisher, dass die Zeilen- und Spaltenvariablen unabhängig sind.
Die Wahrscheinlichkeit für das Auftreten des beobachteten Wertes lässt sich - bei fixierten Randsummen - einfach aus der Anzahl der Permutationen, die zu diese Lösung führen berechnen. Dieser Wert wird dann in Beziehung zu dem auf Grundlage der Multininominalverteilung berechneten Möglichkeiten, die Feldwerte zu erhalten.
Anzahl der Permutationen, die - bei fixierten Randsummen - zu dieser Lösung führen können:
\[ \binom{N}{Y_{1,1} + Y_{1,2}} \binom{N}{Y_{1,1} + Y_{2,1}} = \frac{N!}{(Y_{1,1} + Y_{1,2})!(Y_{2,1} + Y_{2,2})!} \cdot \frac{N!}{(Y_{1,1} + Y_{2,1})!(Y_{1,2} + Y_{2,2})!} \]
Anzahl der Möglichkeiten, exakt diese Verteilung zu erhalten auf Grundlage der Multinomial-Verteilung:
\[ \frac{N!}{Y_{1,1}! \cdot Y_{1,2}! \cdot Y_{2,1}! \cdot Y_{2,2}!} \]
Teilt man die zweite Gleichung durch die erste51, so erhält man die Wahrscheinlichkeit für das Eintreten der beobachteten Fallzahl:
\[ P_{obs} = \frac{Y_{1,1}! \cdot Y_{1,2}! \cdot Y_{2,1}! \cdot Y_{2,2}!}{ (Y_{1,1} + Y_{1,2})! \cdot (Y_{2,1} + Y_{2,2})! \cdot (Y_{1,1} + Y_{2,1})! \cdot (Y_{1,2} + Y_{2,2})! } \]
Um auch noch die Wahrscheinlichkeit für das Auftreten extremerer Werte zu berechnen, muss man je möglichen extremeren Wert (es sind ja nur ganzzahlige Werte möglich) die Eintrittswahrscheinlichkeit berechnen. Summiert man all diese Eintrittswahrscheinlichkeiten auf, erhält man den gewünschten p-Wert (die Irrtumswahrscheinlichkeit).
Der Test kann auch für mehr Faktorlevel je Kategorie (sogenannte RxC-Kreuztabellen) übertragen werden - die mathematische Herleitung wird dann etwas komplexer, letztendlich folgt das Vorgehen dem bei der 2x2 Kreuztabelle.
Fishers exakten Test bestätigt hier den Zusammenhang zwischen Wohnort und Verhalten (Mülltrennung) hier noch einmal.
##
## Fisher's Exact Test for Count Data
##
## data: recycling
## p-value = 0.0001908
## alternative hypothesis: two.sidedMan könnte sich nun fragen, warum wir nicht einfach immer Fishers exakten Test verwenden. Der Grund dafür liegt darin, dass Fishers exakter Test konservativer ist, d.h. der Test benötigt größere Unterschiede, um einen signifikanten Effekt anzuzeigen. Mit anderen Worten, wenn wir stets Fischers exakten Test anwenden, entgehen uns vermutlich Zusammenhänge zwischen kategorialen Variablen, die wir mit dem \(\chi^2\)-Test erkannt hätten. Außerdem gibt es die wichtige Einschränkung, dass das experimentelle Design so war, dass die Randsummen von vorneherein festgelegt waren. In unserem Anwendungsbeispiel ist es nicht wahrscheinlich, dass die Randsummen von vorneherein fixiert waren, weswegen wir Fishers exakten Test nicht anwenden sollten.
11.3.3 G-Test
Als dritten gebräuchlichen Test für Assoziationen anhand von Kreuztabellen gibt es den G-Test, der die erwarteten Werte anhand einer Multinominal Verteilung ermittelt.52 Auch der G-Test stellt Anforderungen an die minimale Anzahl der Einträge je Feld in der Kreuztabelle. Wenn der Erwartungswert einer Zelle der Kreuztabelle kleiner 5 ist, sollte der Test nicht angewandt werden.53
Es gibt zwei äquivalente Varianten, die Teststatistik zu formulieren. Die einfachere verwendet die Erwartungswerte, wie sie bereits beim \(\chi^2\)-Test verwendet wurden.
\[ G = 2 \cdot \sum_{i=1}^r\sum_{j=1}^s(O_{i,j}\cdot ln(\frac{O_{i,j}}{E_{i,j}})) \] G ist wiederum asymptotisch \(\chi^2\)-verteilt, mit \((r-1)\cdot(s-1)\) Freiheitsgraden.
Wir verwenden hier die Implementierung im package AMR, da diese der Syntax von chisquare,test und fisher.test gleicht.
##
## G-test of independence
##
## data: recycling
## X-squared = 17.235, p-value = 0.00018111.3.4 Anmerkungen zur Auswahl des Test
Welchen der 3 Tests sollen wir verwenden? Verlockend, aber falsch wäre es, immer aller drei Tests durchzuführen und dann einfach den Test zu verwenden, der das beste Ergebnis liefert.
Wir sollten uns klar machen, dass verschiedene experimentell Design zu einer Kreuztabelle geführt haben können und das die relevant für die Auswahl des Tests ist (Gotelli and Ellison 2004, 363f):
- Model I Design: es wurde von vorneherein eine fixe Stichprobengröße definiert. So kann z.B. die Wahl getroffen worden sein insgesamt 500 Personen befragen zu wollen, ohne Randbedingungen - wie die benötigte Anzahl von Antworten einer Kategorie - festzulegen.
- Modell II Design: die Anzahl der Elemente für die Kategorien einer (aber nicht beider) kategorialen Variablen (die Spalten- oder Zeilenrandsummen) wird vorab festgelegt. Man will z.B. 100 Teilnehmer je Gemeinde befragen oder 50 weibliche und 50 männliche Versuchspersonen einbeziehen. -Model III Design: die Spalten- und Zeilenrandsummen sind vorab festgelegt. Wir wollen z.B. 100 Personen über 65 und 100 Personen zwischen 16 und 25 befragen und wollen jeweils 100 Raucher und 100 Nichtraucher befragen.
Design Modell I triff vor allem bei beobachtenden Studien auf, II und III treten bei experimentellen Studien auf.
Fishers exakter Test sollte nur für Modell III Designs angewandt werden. Der G-Test nur für Modell Design I oder II Studien, während der \(\chi^2\)-Test für alle drei Modell Designs angewendet werden kann (solange der Erwartungswert für alle Felder groß genug ist). Im Beispiel der Befragung zur Mülltrennung hätten wir damit vermutlich Fishers exakten Test nicht anwenden dürfen.
11.3.5 Erzeugen von Kreuztabellen
Einen Schritt, den wir bisher ignoriert haben, ist das Erzeugen von Kreuztabellen aus den Rohdaten. Dem wollen wir uns hier widmen. Laden wir zunächst die Daten.
## recycling location
## 1 No-recycling Costessy
## 2 No-recycling Costessy
## 3 No-recycling Costessy
## 4 No-recycling Costessy
## 5 No-recycling Costessy
## 6 No-recycling CostessyEs gibt zwei Felder, die jeweils Verhalten (Mülltrennung ja/nein) und die Gemeinde enthalten. Um daraus eine Kreuztabelle zu erzeugen verwenden wir xtabs(). Über ein formula-Objekt legen wir fest, was wir aufaddieren wollen - wenn auf der linken Seite der Tilde nichts steht, werden einfach die Anzahl der Zeilen, die in die Kategorie fallen aufaddiert. Falls wir ein Attribut hätten, dass wir je Kategorie aufaddieren wollten, dann würden wir dessen Namen auf der linken Seite des formula-Objektes angeben. Auf der rechten Seite des formula-Objektes definieren wir die Felder, aus denen wir die Kategorien ableiten wollen. Über data können wir den data.frame definieren, in dem nach den Spaltennamen gesucht werden soll.
## recycling
## No-recycling Recycling
## 122 295## location
## Costessy South Park Woodcock
## 216 101 100## recycling
## location No-recycling Recycling
## Costessy 64 152
## South Park 16 85
## Woodcock 42 58Auch wenn das Objekt, dass von xtabs zurückgegeben wird von der Klasse xtabs ist, können wir es direkt in chisq.test verwenden. Falls nötig. können wir es über as.data.frame() oder as.matrix() umwandeln.
## [1] "xtabs" "table"##
## Pearson's Chi-squared test
##
## data: recyclingXtab
## X-squared = 16.643, df = 2, p-value = 0.0002433## recycling
## location No-recycling Recycling
## Costessy 64 152
## South Park 16 85
## Woodcock 42 58## location recycling Freq
## 1 Costessy No-recycling 64
## 2 South Park No-recycling 16
## 3 Woodcock No-recycling 42
## 4 Costessy Recycling 152
## 5 South Park Recycling 85
## 6 Woodcock Recycling 5811.4 Korrelation zwischen kategorialen und numerisch skalierten Variablen
Falls wir die Assoziation zwischen einer numerischen und einen kategorialen Variable ermitteln wollen, dürfen wir nicht die Korrelationskoeffizienten für numerische Variablen verwenden. Wir könnten die Werte der numerischen Variable klassifiziern um den Kontingenzkoeffizienten zu ermitteln allerdings würden wir dabei viel Information wegwerfen.54
11.4.1 Punktbi-/polyseriale Korrelation
Für diesen Anwendungsfall kommen spezialisierte Korrelationskoeffizienten ins Spiel. Die einfachsten sind die punktbi- und punktpolyserialen Korrelationskoeffizienten.
Der punktbiseriale Korrelationskoeffizient ist für die Grundgesamtheit definiert als:
\[r_{pb}= \frac{M_1-M_2}{s_n}\sqrt{\frac{n_1 n_2}{n^2}} \] Und für eine Stichprobe als \[r_{pb}= \frac{M_1-M_2}{s_{n-1}}\sqrt{\frac{n_1 n_2}{n(n-1)}}\]
Wobei \(M_1\) und \(M_2\) die Mittelwerte der numerische Variablen je Kategorie der kategorialen Variable sind, \(n_1\) und \(n_2\) die Gruppengröße, \(n=n_1 + n_2\) und \(s_n\) ist die Standardabweichung der Grundgesamtheit (d.h. \(n\) im Nenner), \(s_n\) entsprechend die Standardabweichung der Stichprobe (d.h. \(n-1\) im Nenner).
Schauen wir uns das anhand des Beispiels der Überlebenswahrscheinlichkeit von Passagieren den Titanic in Abhängigkeit vom Alter an.
## Loading required package: carData# macht die im package enthaltenen Daten im aktuellem Workspace verfügbar
data(TitanicSurvival)
ggplot(TitanicSurvival, aes(x=survived, y=age)) +
geom_violin (draw_quantiles = c(.25,.5,.75)) +
xlab("Überleben") + ylab("Alter des Passagiers")## Warning: Removed 263 rows containing non-finite outside the scale range
## (`stat_ydensity()`).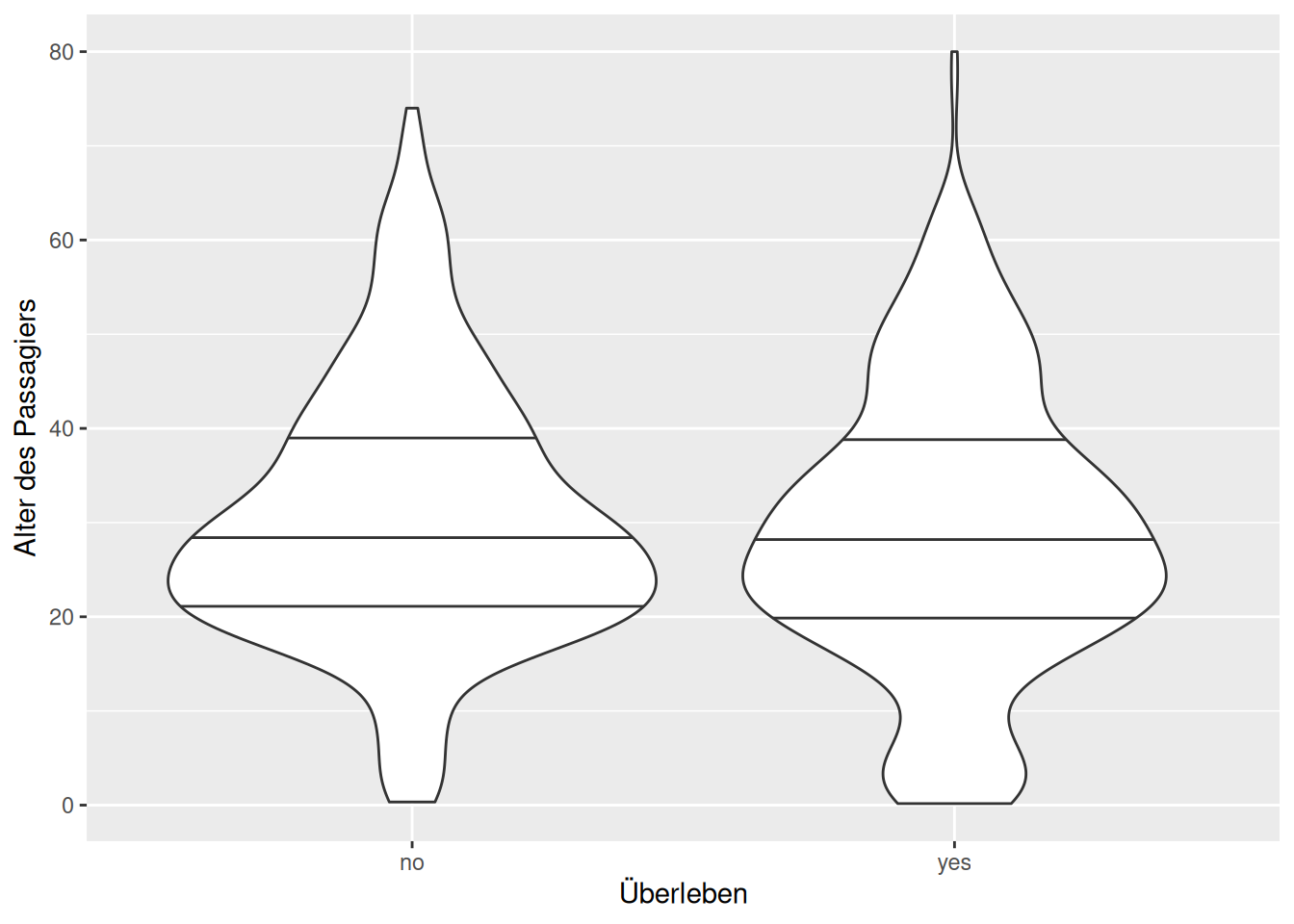
Wie wir anhand der Violinplots - diese stellen gedrehte Histogramme dar, je breiter die Form, desto mehr Passagiere in einer Altersklasse - sehen, gibt es Unterschiede in der Alterszusammensetzung der verstorbenen und der überlebenden Passagiere: die Altersklasse 20-30 ist bei den Überlebenden deutlich schwächer vertreten, als bei den Verstorbenen. Allerdings sind der Median und das 25 und 75-Quantil (die horizontalen Linien) jeweils gleich.
Schauen wir uns den punktbiserialen Korrelationskoeffizienten an. Zunächst berechnen wir je Kategorie (Überlebt ja/nein) den Mittelwert und die Anzahl. Da es bei einigen Passagieren keine Altersinformation gibt (NA-Werte), müssen wir diese vorab rausfiltern.
TitanicSurvival %>% filter(!(is.na(age))) %>%
group_by(survived) %>%
summarize(avg=mean(age, na.rm = TRUE), n=n())## # A tibble: 2 × 3
## survived avg n
## <fct> <dbl> <int>
## 1 no 30.5 619
## 2 yes 28.9 427Weiterhin benötigen wir nach der Formel die Gesamtstandardabweichung
## [1] 14.4135Damit können wir den punktbiserialen Korrelationskoeffizienten berechnen:
\[r_{pb} = \frac{30.55-28.92}{14,41}\sqrt{\frac{619 \cdot 427}{1046^2}} = 0,06\]
Also ein sehr schwacher (vermutlich nicht signifikanter), positiver Zusammenhang: das Durchschnittsalter bei den Überlebenden (Kategorie 2) ist leicht höher als bei den Verstorbenen (Kategorie 1).
11.4.2 Bi-/polyseriale sowie bi-/polychorische Korrelation
Anstelle der Mittelwerte kann man auch versuchen, bessere Repräsentanten für die Klassen zu schätzen. Dies erfolgt auf Basis einer Verteilungsannahme - typischerweise auf Grundlage einer Normalverteilung um zu schätzen, wo die Umbrüche wohl erfolgt sein könnten. Im Gegensatz zum punktbi- oder punktpolyseriale Ansatz - welcher die Klassenmittelwerte verwendet - nennt man diesen Ansatz biseriale oder polyseriale Olsson, Drasgow, and Dorans (1982). Wenn beide Variablen katgegorial sind und man die Klassenrepräsentanten auf Grundlage einer Verteilungsannahme schätzt, spricht man von einer bi- oder polychorischen Korrelation (Cox 1974). Da das Verfahren zum Schätzen eine gewisse Komplexität aufweist, steigen wir hier zunächst nicht in die Details ein. Bi- steht hierbei immer für den Fall, dass man zwei Klassen betrachtet, beim poly- betrachtet man mehrere Klassen zugleich. Die bi-/polyserialen und bi-/polychorischen Ansätze gehen von der Annahme aus, dass es sich bei den kategorialen Variablen um ungenau gemessene kontinuierliche Variablen handelt, also z.B. Düngestufe hoch, da die Ausbringng des Düngers nicht genau erfasst werden konnte. Formaler ausgedrückt geht man von einer kontinuierlichen latenten (nicht beobachteten aber einflussreichen) Variable aus, welche die kategoriale Variable bestimmt. Bei den bi-/polychorischen Korrelationskoeffizienten geht man davon aus, dass die latente Variable normalverteilt ist, bei den bi-/polychorischen Korrelationskoeffizienten davon, dass beide latente Variablen normalverteilt sind.
Im R package polycorfindet sich die Funktion hetcor, die in Abhängigkeit von der Klasse der Variablen automatisch die punkt- oder polyseriale oder die normale Pearson Korrelationskoeffizienten berechnet. Weiterhin gibt es eine Funktion polyserial() zum Berechen der punktpolyserialen Korrelation sowie polychor() zum berechnen der polychorischen Korrelation.
Wir wollen uns das einmal anhand der Daten zum Untergang der Titanic anschauen. Der Datensatz TitanicSurvival, der im package carData enthalten ist, enthält Informationen zu den Passagieren der Titanic: haben sie überlebt, wie alt waren sie, welchen Geschlechts waren Sie, welche Passagierklasse hatten sie gebucht.
require(carData)
data(TitanicSurvival) # macht die im package enthaltenen Daten im aktuellem Workspace verfügbar
summary(TitanicSurvival)## survived sex age passengerClass
## no :809 female:466 Min. : 0.1667 1st:323
## yes:500 male :843 1st Qu.:21.0000 2nd:277
## Median :28.0000 3rd:709
## Mean :29.8811
## 3rd Qu.:39.0000
## Max. :80.0000
## NA's :263Wie sieht es mit dem Zusammenhang zwischen Alter der Passagiere und dem Überleben aus?
polycor::polyserial(x= TitanicSurvival$age, y = TitanicSurvival$survived,
ML = TRUE, std.err = TRUE)##
## Polyserial Correlation, ML est. = -0.06988 (0.03896)
## Test of bivariate normality: Chisquare = 21.83, df = 5, p = 0.0005644
##
## 1
## Threshold 0.23210
## Std.Err. 0.03907Der polyseriale (eigentlich biseriale, da nur 2 Klassen) Korrelationskoeffizient zeigt, dass es keinen signifikanten Zusammenhang zu geben scheint: der Schätzwert plus minus zweimal den Standardfehler schließt Null ein. Der Test auf bivariate Normalität zeigt an, dass die Annahme nicht erfüllt ist. Die Nullhypothese bei diesem Test ist das die Verteilung der beiden Merkmale vor der Klassifikation durch eine bivariate Normalverteilung beschrieben werden kann. Diese kann hier mit geringer Irrtumswahrscheinlichkeit verworfen werden.
In diesem Fall sind sich der punktseriale (s. oben) und der polyseriale Korrelationskoeffizient sehr ähnlich.
Schauen wir uns die Ergebnisse des \(\chi^2\)-Tests für den Einfluss von Geschlecht und Passagierklasse - als Proxy für den ökonomischen Status der Person - zusammen mit dem korrigierten Kontingenzkoeffizienten an. Da beide Variablen ebenso wie die Überleben Variable kategorial sind und wir Erwartungswerte haben, die für alle Klassen höher als 5 sind können wir den Test anwenden.
##
## Pearson's Chi-squared test with Yates' continuity correction
##
## data: TitanicSurvival$sex and TitanicSurvival$survived
## X-squared = 363.62, df = 1, p-value < 2.2e-16## [1] 0.6609912##
## Pearson's Chi-squared test
##
## data: TitanicSurvival$passengerClass and TitanicSurvival$survived
## X-squared = 127.86, df = 2, p-value < 2.2e-16## [1] 0.4218653In beiden Fällen finden wir einen signifikanten Zusammenhang von relevanter Größe (Kontingenzkoeffizient). Über die Richtung des Effektes können wir - anhand des Testergebnisses und des korrigierten Kontingenzkoeffizienten alleine - leider nichts aussagen.
Wir können die Korrelationskoeffizienten auch mittels hetcor berechnen . Da wir für einzelne Passagiere fehlende Werte haben benutzen wir use = "pairwise.complete.obs".
##
## Two-Step Estimates
##
## Correlations/Type of Correlation:
## survived sex age passengerClass
## survived 1 Polychoric Polyserial Polychoric
## sex -0.7453 1 Polyserial Polychoric
## age -0.07005 0.08149 1 Polyserial
## passengerClass -0.4438 0.1853 -0.4533 1
##
## Standard Errors/Numbers of Observations:
## survived sex age passengerClass
## survived 1309 1309 1046 1309
## sex 0.0252 1309 1046 1309
## age 0.03896 0.03939 1046 1046
## passengerClass 0.0347 0.04045 0.02715 1309
##
## P-values for Tests of Bivariate Normality:
## survived sex age
## survived
## sex <NA>
## age 0.0005623 0.0007213
## passengerClass 0.6122 0.9433 0.0008194Das Ergebnis besteht aus drei Teilen. Der erste Teil gibt in der unteren Diagonalen die Korrelationskoeffizienten an, zusammen mit der Information, welcher Korrelationskoeffizient verwendet wurde (obere Diagonale). Der zweite Teil gibt die Standardfehler (untere Diagonale) und die Anzahl Datenpunkte (obere Diagonale) an. Im dritten Teil wird die Irrtumswahrscheinlichkeit (p-Wert) für den Test angegeben, ob die Annahmen der polyserialen Korrelation (bivariate Normalität) erfüllt sind. Werte die hier nicht signifikant sind, sind vertrauenswürdig. Bei survived vs. sexsteht NA, da es sich hier nicht um einen polyseriale sondern um einen polychorische Korrelationskoeffizienten handelt - beide Variablen sind ja kategorisch.
Wir entnehmen der Korrelationsanalyse folgendes:
- die Überlebenswahrscheinlichkeit von Männern war deutlich geringer als bei Frauen (Frauen (und Kinder) zuerst in die Rettungsboote?). Das Faktorlevel
femaleist hier die Vergleichsklasse beisexundnobeisurvived. Wenn nicht anders angegeben, geht R beim ordnen der Faktorlevel alphabetisch vor. - die Überlebenswahrscheinlichkeit nahm mit dem ökonomischem Status ab (Passagierklasse) - hier ist die Reihung
1st-2nd-3rd. - das Alter der Passagiere hatte keinen Einfluss auf die Überlebenswahrscheinlichkeit (s. Standardfehler und Schätzwert sowie p-Wert) - das kann auch damit zusammenhängen, dass das Alter sehr ungleich über die Passagierklassen verteilt ist.
Schauen wir uns die Daten auch noch einmal an:
par(mfrow= c(2,3))
mosaicplot(sex ~ survived, data=TitanicSurvival,
las=1, color = TRUE)
mosaicplot(passengerClass ~ survived, data=TitanicSurvival,
las=1, color = TRUE)
boxplot(age ~survived, data= TitanicSurvival, las = 1,
notch=TRUE, varwidth=TRUE)
boxplot(age ~sex, data= TitanicSurvival, las = 1,
notch=TRUE, varwidth=TRUE)
boxplot(age ~passengerClass, data= TitanicSurvival, las = 1,
notch=TRUE, varwidth=TRUE)
mosaicplot(passengerClass ~ sex, data=TitanicSurvival,
las=1, color = TRUE)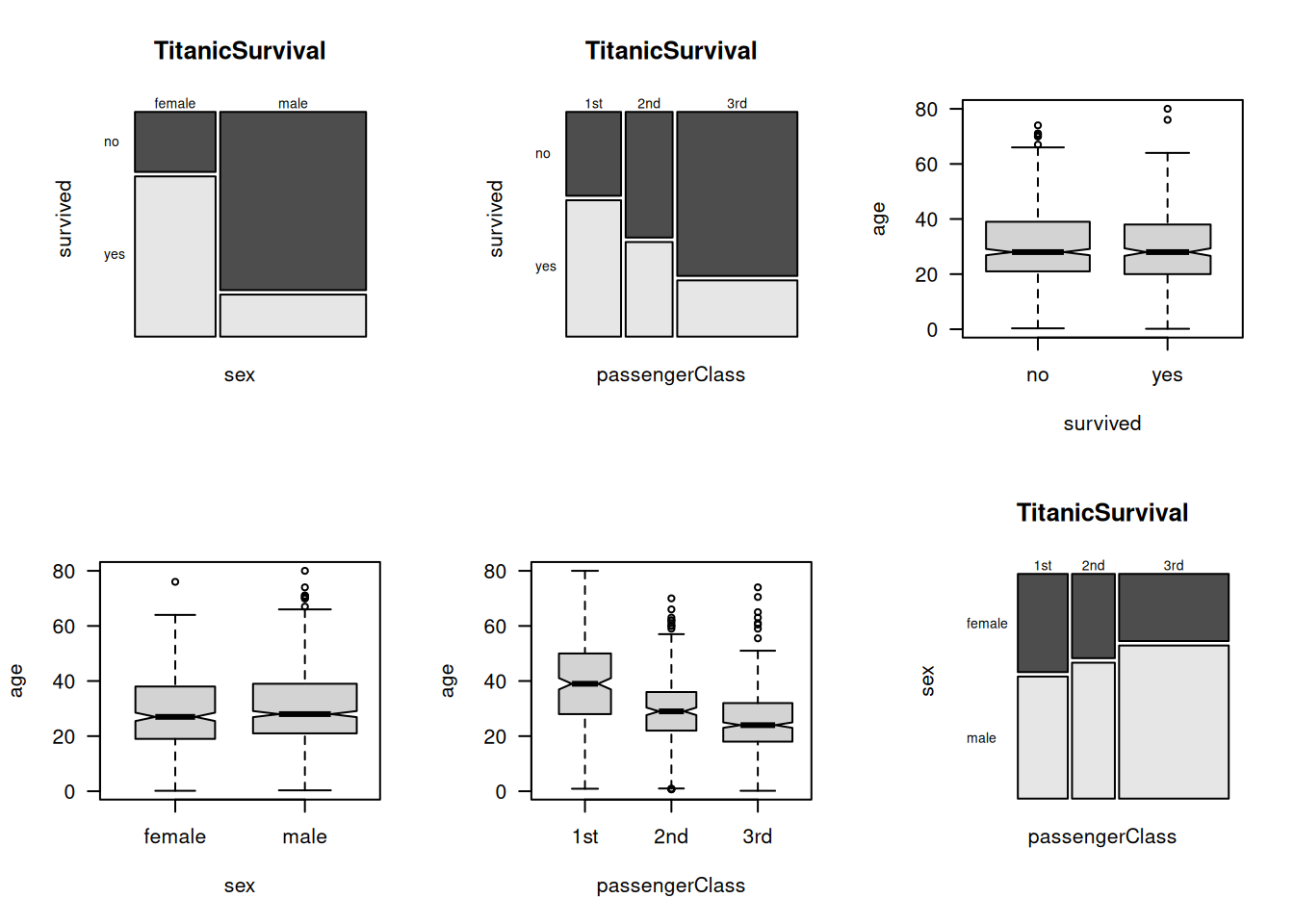
Hierbei verwenden wir mosaicplot für die Darstellung kategorialer gegen kategorialer Daten und boxplot für die Darstellung numerischer gegen kategorialer Daten.
11.4.3 Details zur polyserialen Korrelation
Die polyseriale Korrelation wird dann angewandt, wenn man davon ausgeht, dass das kategoriale Merkmal (bzw. die latente Variable) in Wirklichkeit kontinuierlich verteilt ist, aber aufgrund von z.B. Messungenauigkeiten nur in Katgegorien aufgezeichnet wurde.
## Loading required package: polycor## Loading required package: mvtnorm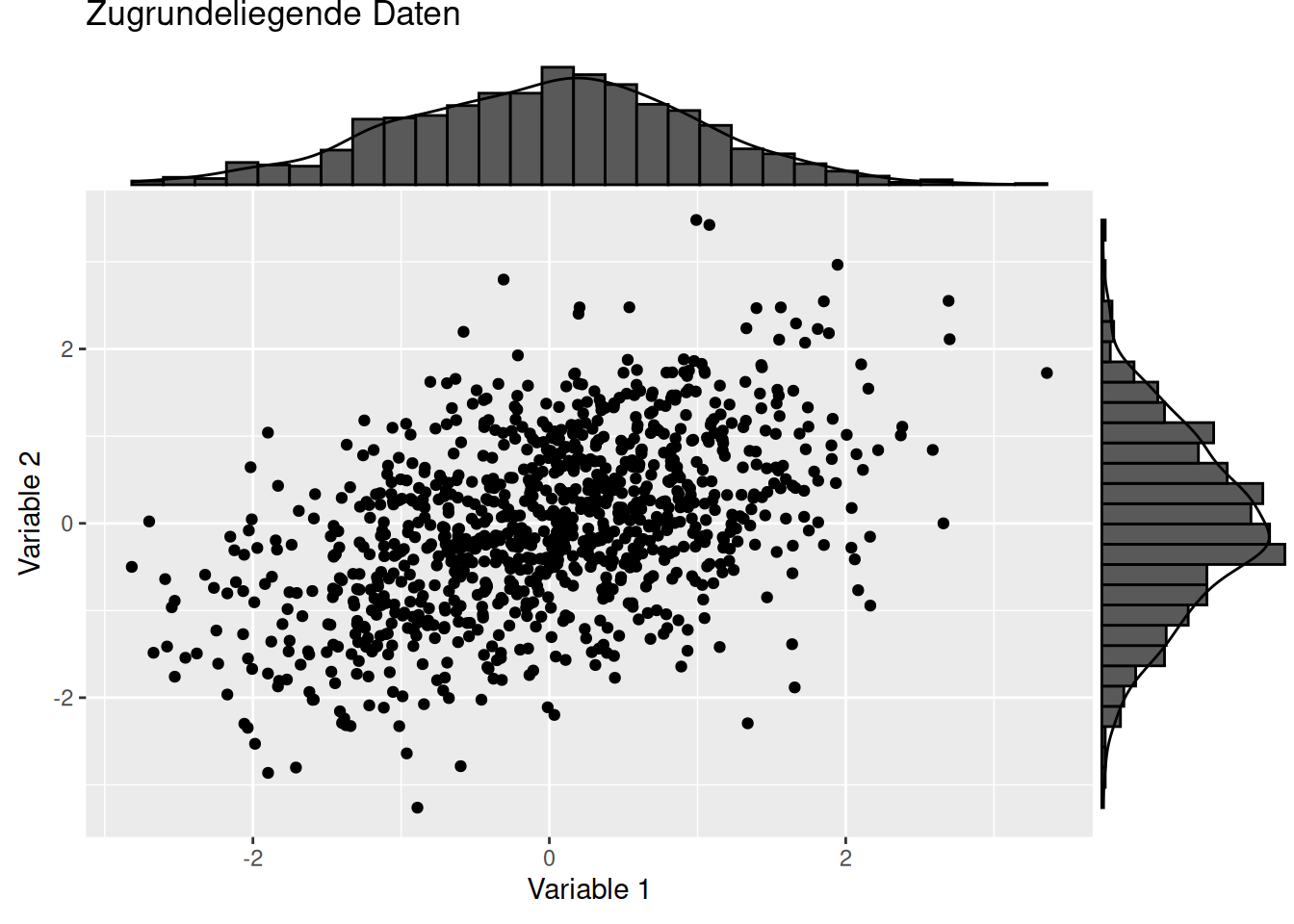
Der wahre (i.d.R. unbekannte) Korrelationskoeffizient zwischen den beiden kontinuierlichen (latenten) Variablen ist:
##
## Pearson's product-moment correlation
##
## data: dat$V1 and dat$V2
## t = 17.326, df = 998, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.4317545 0.5271546
## sample estimates:
## cor
## 0.4808765Der polyseriale Korrelationskoeffizient zwischen V1 und der nur kategorisiert vorliegenden Variable V2 lautet:
##
## Polyserial Correlation, ML est. = 0.4899 (0.02624)
## Test of bivariate normality: Chisquare = 17.58, df = 8, p = 0.02462
##
## 1 2
## Threshold -0.54060 0.78060
## Std.Err. 0.03888 0.04106Der Unterschied ist nur marginal. Als (wahre) Schwellwerte zur Kategorisierung wurden von V2 wurde -0.5 und 0.75 verwendet. Die Schätzung der Schwellwerte (Treshold) klappt sehr gut. Der \(\chi^2\) Test hinsichtlich bivariater Normalverteilung zeigt an, dass die Nullhypothese des Vorliegens einer bivariaten Normalverteilung nicht abgelehnt werden kann. 55
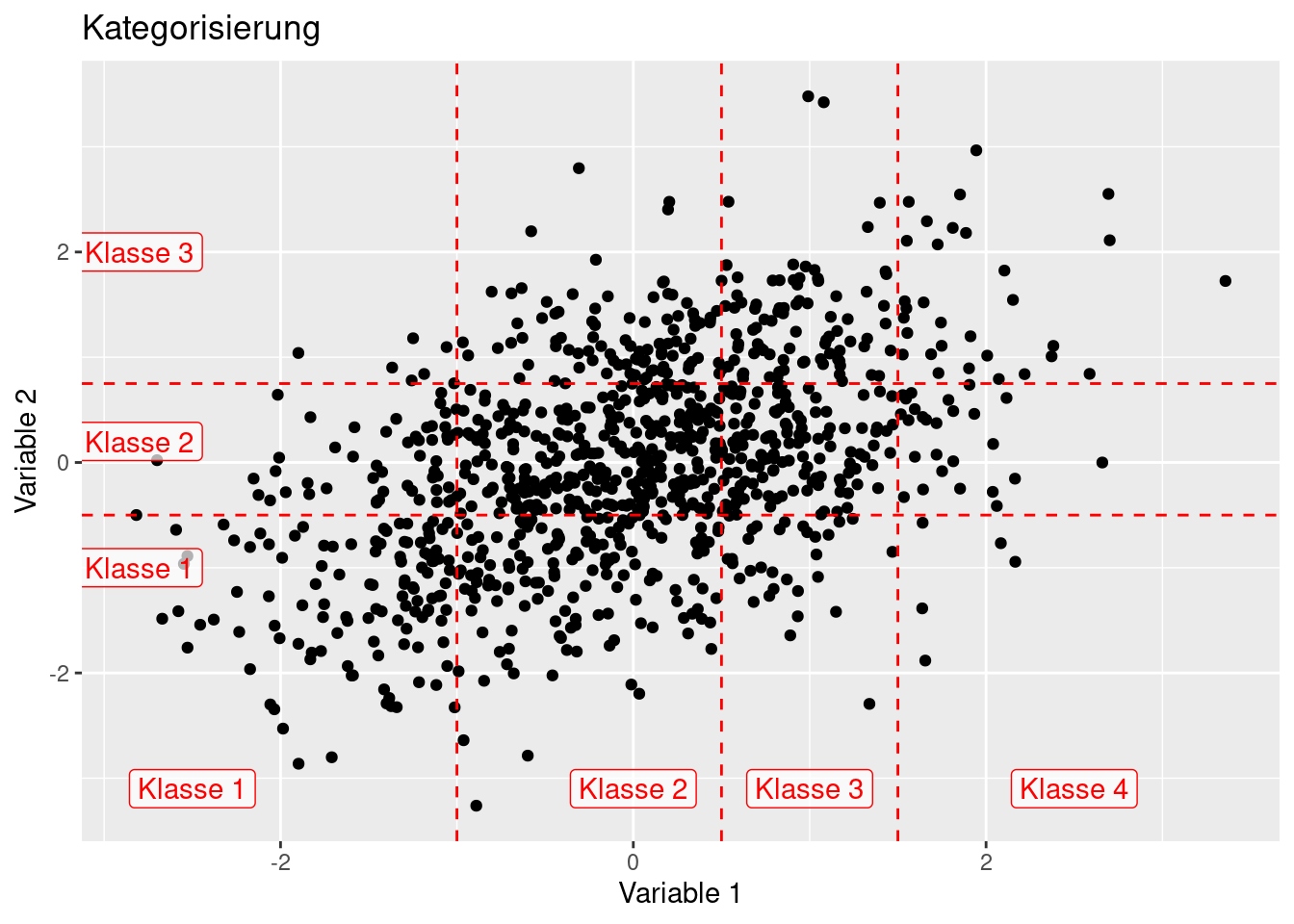
Wenn wir beide Variablen klassifizieren, kommen wir in den Anwendungsbereich der polychorische Korrelationskoeffizienten.
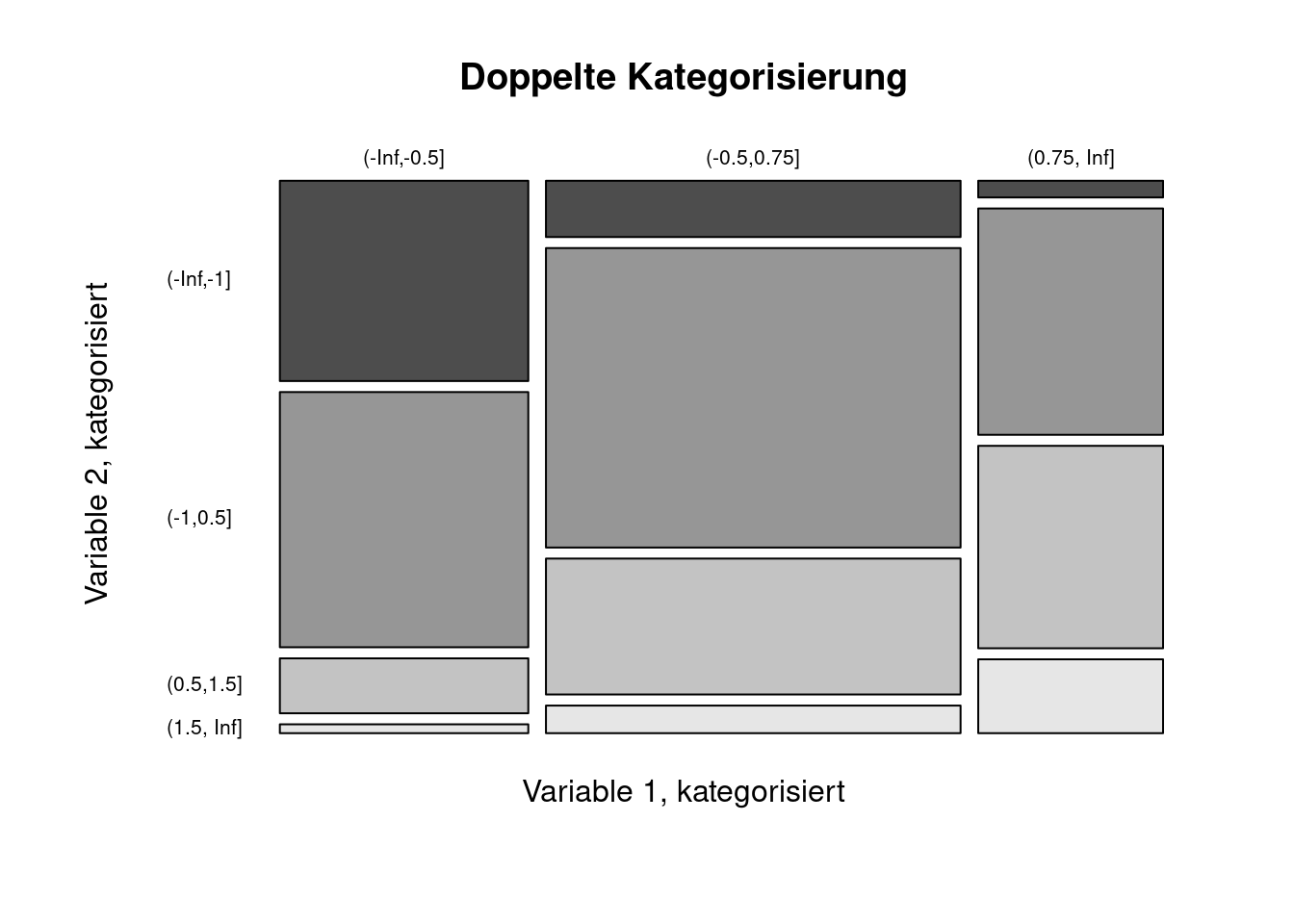
mosaicplot(V2cat ~ V1cat, data=dat,
las=1, color = TRUE,
main = "Doppelte Kategorisierung",
xlab = "Variable 1, kategorisiert",
ylab = "Variable 2, kategorisiert")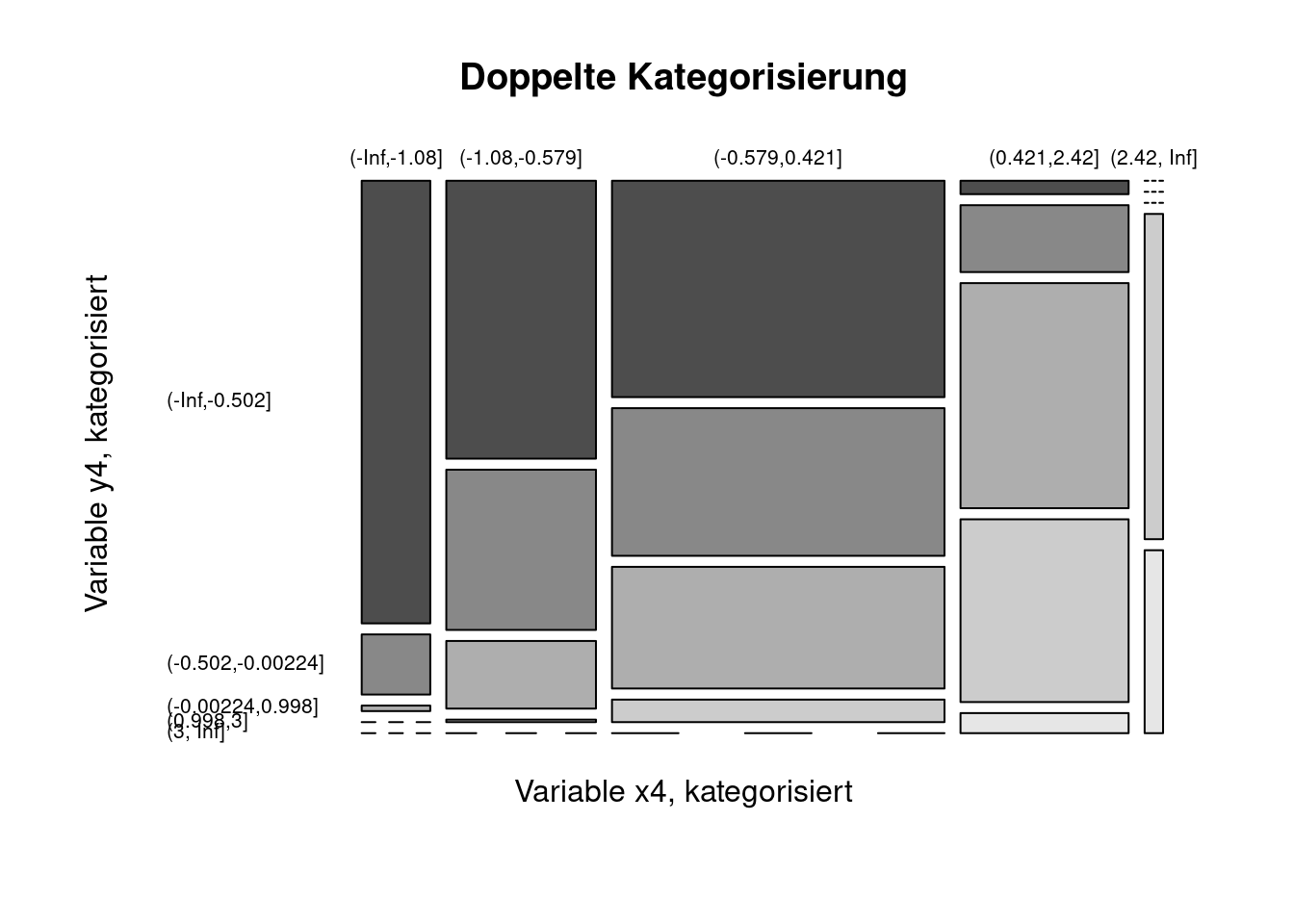
##
## Polychoric Correlation, ML est. = 0.491 (0.0305)
## Test of bivariate normality: Chisquare = 9.072, df = 5, p = 0.1062
##
## Row Thresholds
## Threshold Std.Err.
## 1 -0.9433 0.04703
## 2 0.5143 0.04131
## 3 1.5270 0.06174
##
##
## Column Thresholds
## Threshold Std.Err.
## 1 -0.5398 0.04197
## 2 0.7815 0.04412Auch hier ist der polychorische Korrelationskoeffizient eine gute Schätzung für Pearsons r auf Grundlage der latente Variablen. Die Klassengrenzen der 2. Variablen (-1, 0.2, 2) werden einigermaßen gut geschätzt, der Test auf bivariate Normalverteilung zeigt, dass man diese Annahme nicht verwerfen kann.
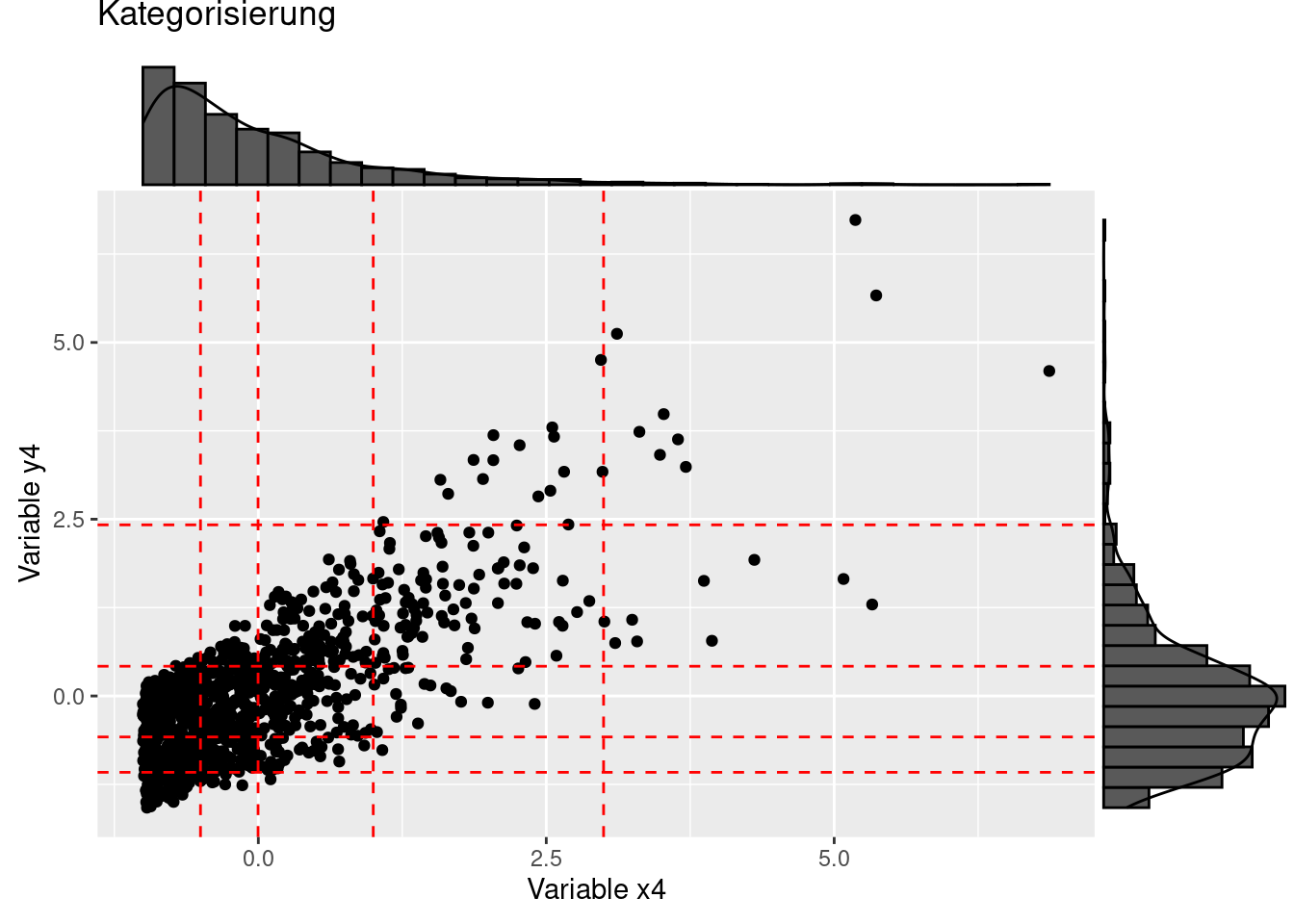
Schauen wir uns die Performance der polyserialen und polychorischen Korrelation für eine schwierigeren Fall an:
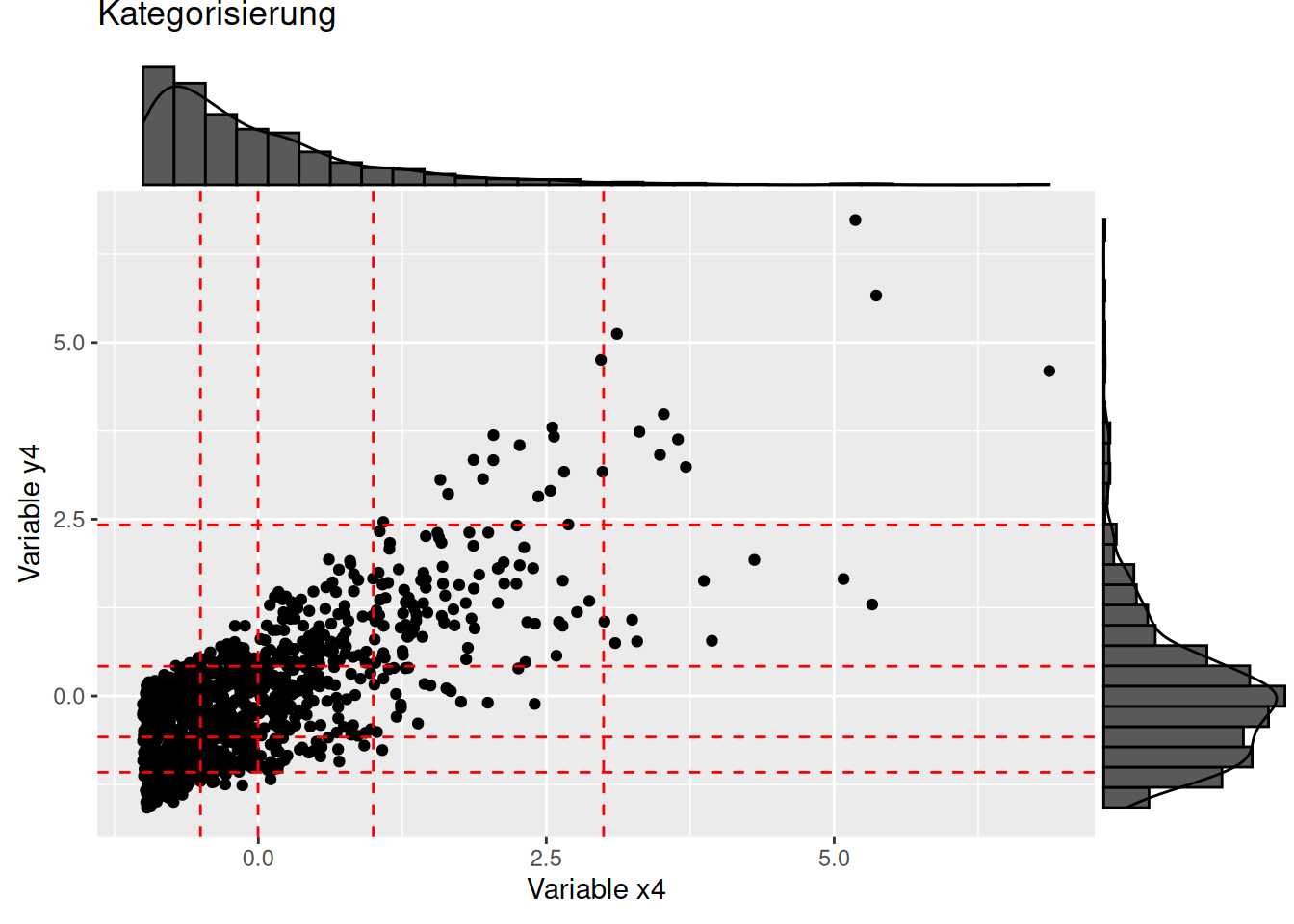
mosaicplot(y4cat ~ x4cat, data=dat2,
las=1, color = TRUE,
main = "Doppelte Kategorisierung",
xlab = "Variable x4, kategorisiert",
ylab = "Variable y4, kategorisiert")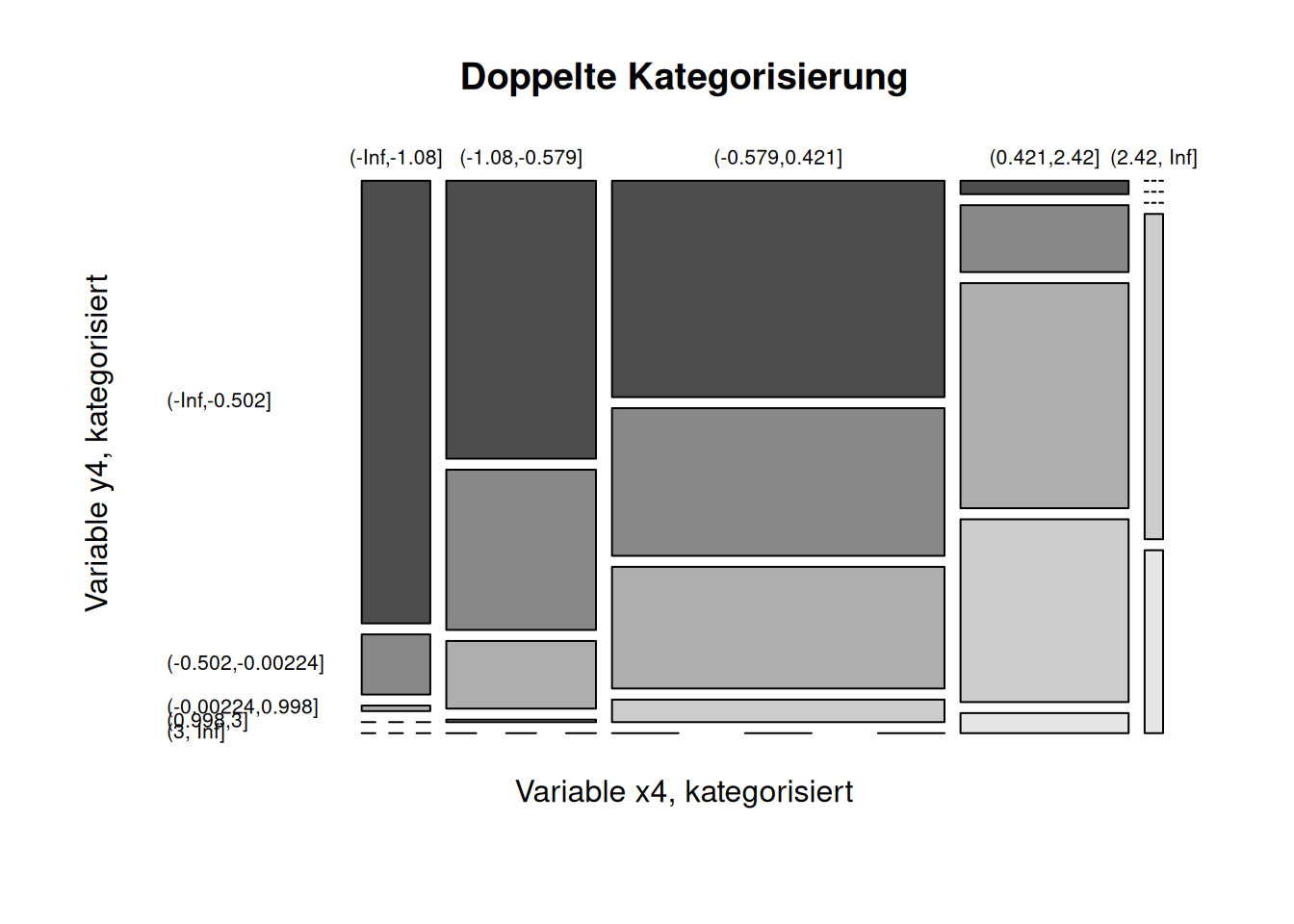
##
## Pearson's product-moment correlation
##
## data: dat2$x4 and dat2$y4
## t = 36.674, df = 998, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
## 0.7299560 0.7828843
## sample estimates:
## cor
## 0.7576632##
## Polyserial Correlation, ML est. = 0.7474 (0.01614)
## Test of bivariate normality: Chisquare = 156.4, df = 14, p = 3.751e-26
##
## 1 2 3 4
## Threshold -1.18600 -0.56240 0.54620 2.32800
## Std.Err. 0.04287 0.03048 0.03674 0.09871##
## Polychoric Correlation, ML est. = 0.7325 (0.01901)
## Test of bivariate normality: Chisquare = 65.31, df = 15, p = 3.018e-08
##
## Row Thresholds
## Threshold Std.Err.
## 1 -0.2968 0.03938
## 2 0.2891 0.04005
## 3 1.1050 0.05029
## 4 2.1820 0.09591
##
##
## Column Thresholds
## Threshold Std.Err.
## 1 -1.2760 0.05426
## 2 -0.5369 0.04075
## 3 0.6541 0.04355
## 4 2.0410 0.08603Auch hier stimmen der polyseriale bzw. polychorische Korrelationskoeffizient als Schätzer gut mit Pearson’s \(r\) für die latenten Variablen überein. Die Nichtnormalität der Daten wird bei beiden \(\chi^2\)-Tests angezeigt. Auch wenn man in diesem Fall davon ausgehen muss, dass die Klassenschätzung nicht wirklich gut funktioniert, hat das für diesen Testfall hier diesmal gut funktioniert.
Wahre Schwellwerte x4: -0.5022438, -0.0022438, 0.9977562, 2.9977562
Wahre Schwellwerte y4: -1.0793783, -0.5793783, 0.4206217, 2.4206217
11.5 Visualisierung von Assoziationen
In vielen realen Anwendungen hat man es mit einer Vielzahl von potentiell erklärenden Variablen zu tun. Oftmals sind diese Variablen nicht nur mit der zu erklärenden Variablen, sondern auch untereinander korreliert. Diese Abhängigkeit sind insbesondere für Regressionsanalysen bei der Modellselektion problematisch. Es ist deswegen wichtig und hilfreich, sich zunächst einmal einen Überblick über Zusammenhänge zwischen den Daten zu verschaffen.
Um mit dem Problem der Kollinearität (collinearity) im Rahmen von Regressionsanalysen umzugehen gibt es eine Reihe von Ansätzen (Carsten F. Dormann et al. 2013).
11.5.1 Mittels corrplot
Das package corrplot bietet vielfältige Optionen, um Korrelationsmatrizen ansprechend darzustellen. Als Input benötigt es eine Korrelationsmatrix, wie man sie mit cor erzeugt. Wir schauen uns dies einmal anhand eines Datensatzes an, der die Pflanzenarten-Diversität in Wäldern in Abhängigkeit von Bodeneigenschaften darstellt. Der Datensatz wurde in den südlichen Appalachen erhoben (Bondell, Reich, and Carolina 2008).
## Loading required package: corrplot## corrplot 0.95 loadedNeben der Pflanzenarten-Diversität (Diversity) haben wir Informationen zum ph-Wert, zur Bodendichte, dem Gehalt an Huminstoffen sowie relevanten Bodenbestandteilen, der Kationenaustauschkapazität (cation exchange capacity CECbuffer), austauschbare oder potentielle Azidität (exchangeable acidity ExchAc) sowie zur Basensättigung (BaseSat [%]) und der Summe der Kationen (SumCation). Einige Größen fassen andere zusammen, z.B. die Kationenaustauschkapazität, die Summe der Kationen oder die Kationenaustauschkapazität. Diese Zusammenhänge erkennen wir, wenn wir die Korrelationsmatrix plotten. Ohne weitere Optionen werden Größe und Farbe als graphische Variablen verwendet.
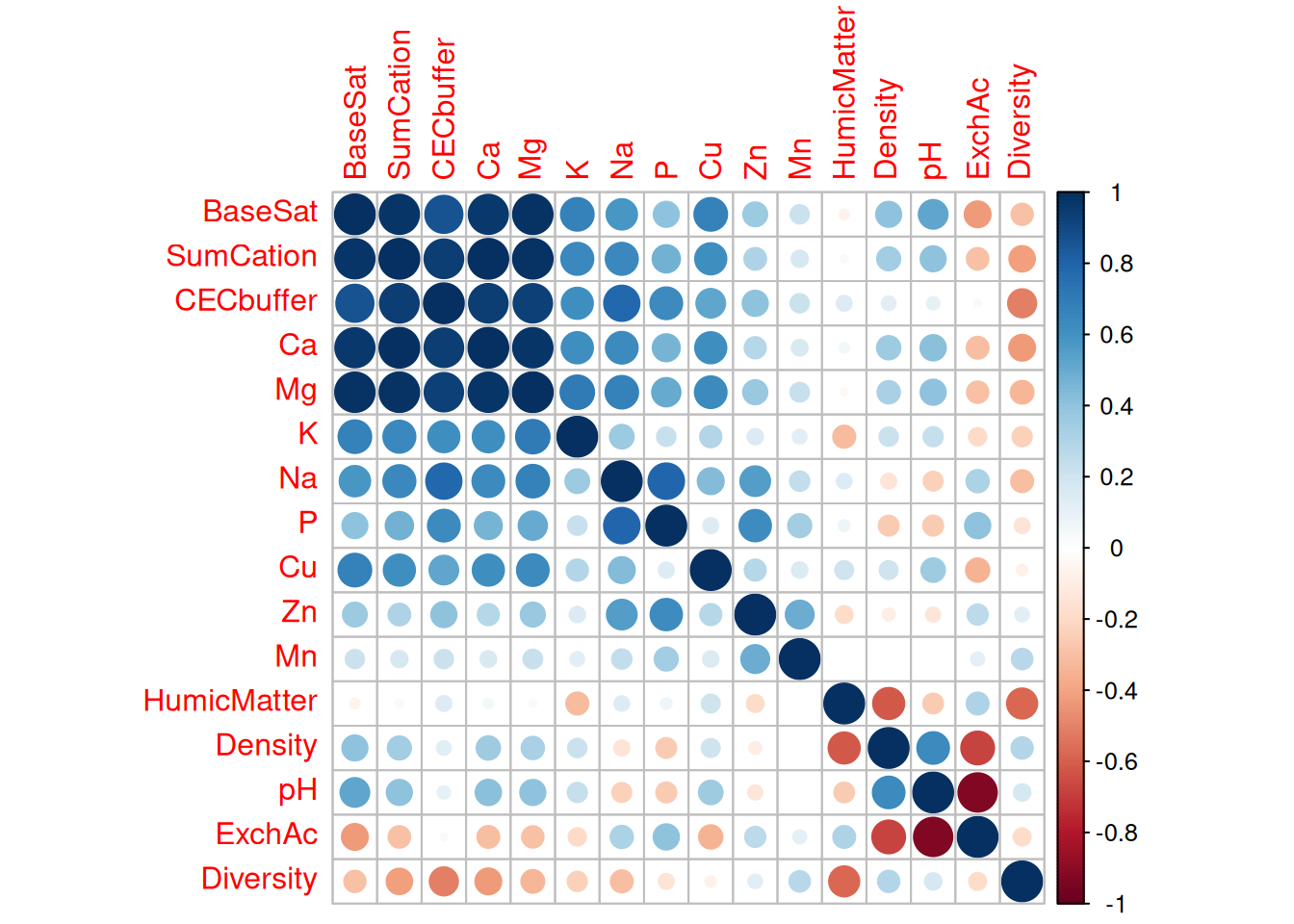
Die Hauptdiagonale ist natürlich immer perfekt korreliert (Korrelation der Variablen mit sich selbst). ANsosnten sehen wir einen Cluster extrem stark korrelierter Variablen: Basensättigung, Summe der Kationen, Kationenaustauschkapazität , Calcium- und Magnesiumanteil sind extrem hoch miteinander korreliert. Der ph-Wert und die austauschbare Azidität sind (wie sich aus deren Definition ergibt) extrem stark negativ korreliert. Die zu erklärende Variable Pflanzendiversität ist nur mässig stark mit einzelnen erklärenden Variablen korreliert, der Zusammenhang zwischen Diversität der Waldpflanzen und Bodeneigenschaften ist also nicht unmittelbar.
Die Matrixdarstellung ist natürlich entlang der Hauptdiagonalen gespiegelt. Dies kann man ausnutzen, um nur die obere (oder die untere) Dreicksmatrix zu plotten. Weiter Optionen der Darstellung mittels corrplot umfassen die Darstellungsoption (method=) und eine automatische Sortierung, um Cluster leichter erkennen zu können (order=).
corrplot(corM,
method = 'number',
number.digits= 2,
number.cex = 0.5,
order = 'AOE',
type = 'upper')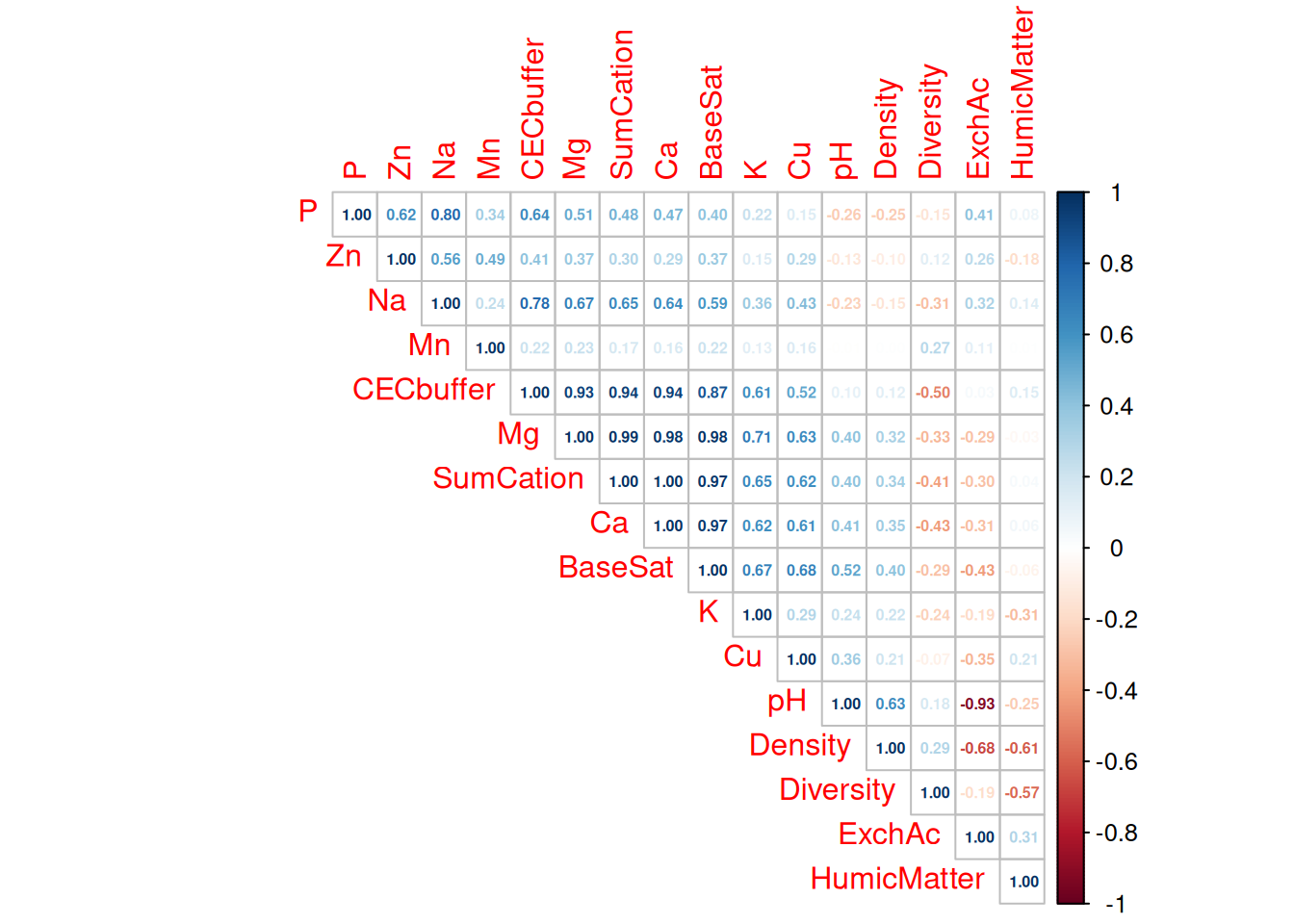
11.5.2 Mittels pairs
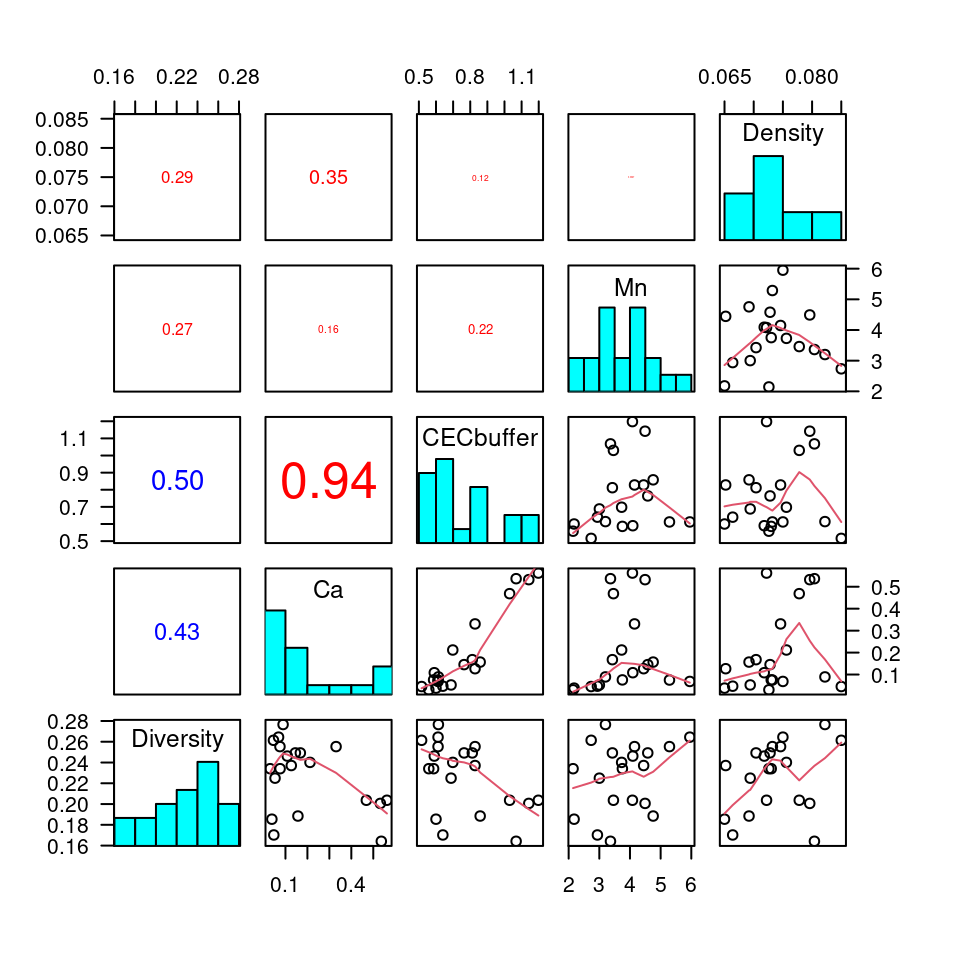
Um den Zusammenhang zwischen Variablen besser verstehen zu können empfiehlt es sich, die Zusammenhänge mittels Scaterplots (oder Boxplots oder Mosaicplots) darzustellen. Für eine überschaubare Anzahl von Variablen kann z.B. pairs eingesetzt werden, um eine sogenannte Scatterplotmatrix zu erstellen.
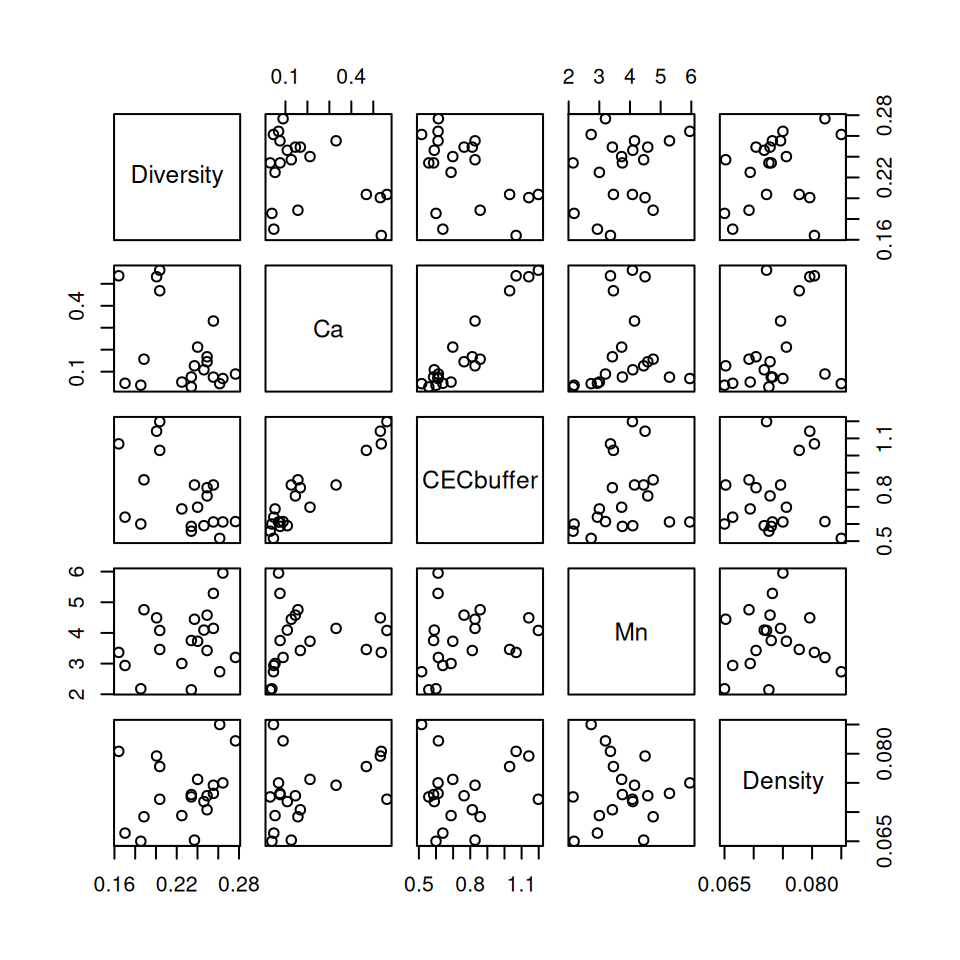
Noch schöner wird die Darstellung, wenn man sogenannte pannel-functions definiert und verwendet, um darüber Zusatzinformationen darzustellen.
## put histograms on the diagonal
panel.hist <- function(x, ...)
{
usr <- par("usr")
par(usr = c(usr[1:2], 0, 1.5) )
h <- hist(x, plot = FALSE)
breaks <- h$breaks; nB <- length(breaks)
y <- h$counts; y <- y/max(y)
rect(breaks[-nB], 0, breaks[-1], y, col = "cyan", ...)
}
## put (absolute) correlations on the upper panels,
## with size proportional to the correlations.
panel.cor <- function(x, y, digits = 2, prefix = "", cex.cor, ...)
{
#usr <- par("usr"); on.exit(par(usr))
par(usr = c(0, 1, 0, 1))
r.sign <- sign(cor(x, y, use = "pairwise.complete.obs"))
r <- abs(cor(x, y, use = "pairwise.complete.obs"))
txt <- format(c(r, 0.123456789), digits = digits)[1]
txt <- paste0(prefix, txt)
if(missing(cex.cor)) cex.cor <- 0.8/strwidth(txt)
text(0.5, 0.5, txt, cex = cex.cor * r + 0.1, col=ifelse(r.sign < 0, "blue", "red"))
}pairs(soilSub, lower.panel = panel.smooth, upper.panel = panel.cor,
row1attop=FALSE, diag.panel = panel.hist, las=1)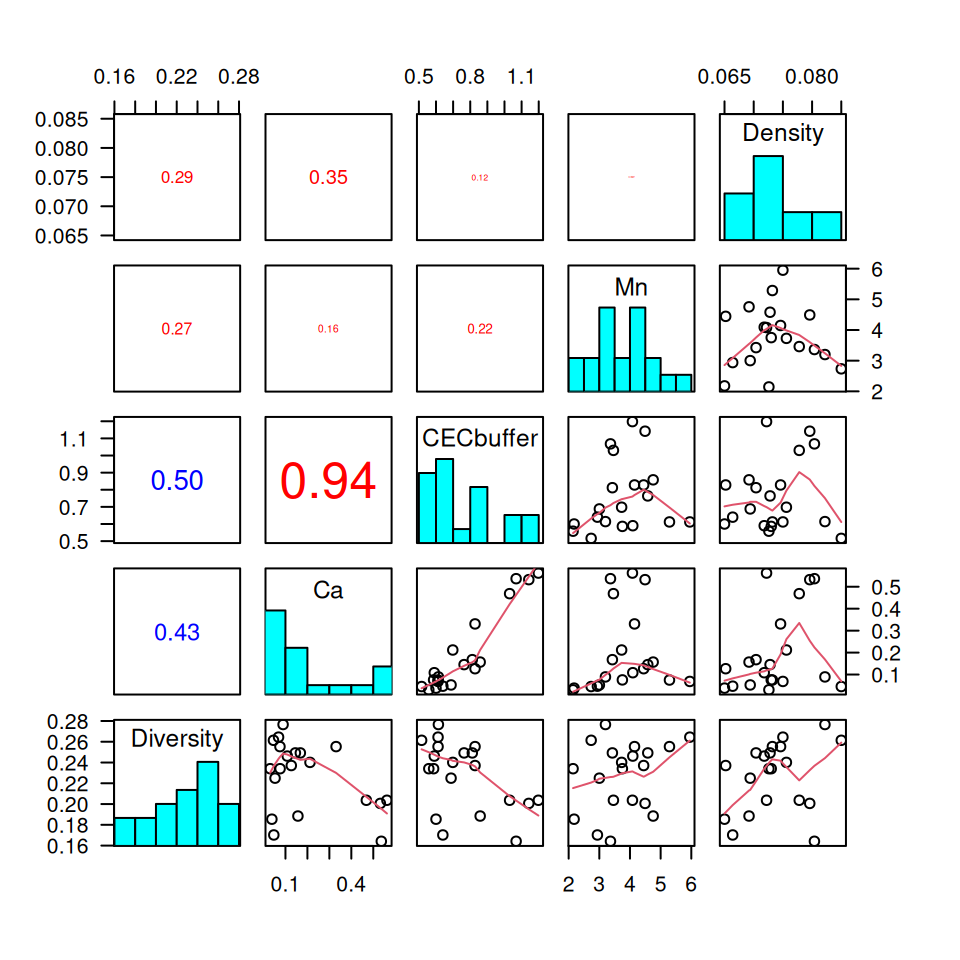
Die pannel functions sorgen dafür, dass jeweils das Histogram der Variablen auf der Hauptdiagonalen gezeichnet wird, der Korrelationskoeffizient mit Größe und Farbe (Vorzeichen) als graphischen Variablen in der Dreiecksmatrix und auf der unteren Dreiecksmatrix ein Scatterplot mit einem lowess Smoother (einer Art gleitendem Mittelwert) dargestellt wird.
11.6 Relevante Funktionen in R
Die wichtigsten Funktionen:
covzum Berechnen der Kovarianz zweier Vektoren oder einer Matrix- auch für die Kovarianz kann eine Berechnung auf Grundlage einer Rangtransformation durchgeführt werden. Entsprechend der Möglichkeiten bei
cornur wird der Wert nicht standardisiert.
- auch für die Kovarianz kann eine Berechnung auf Grundlage einer Rangtransformation durchgeführt werden. Entsprechend der Möglichkeiten bei
corzum Berechnen der Kovarianz zweier Vektoren oder einer Matrix- über den Parameter
methodkann der zu berechnende Korrelationskoeffizient ausgewählt werden:"pearson","kendall"oder"spearman"
- über den Parameter
rank- Rangtransformation eines numerischen Vektorschisquare.test- \(\chi^2\)-Testfisher.test- Fishers exakter TestAMR:g.test- G-Testpolycor::hetcor- für die Berechnung einer heterogenen Korrelationsmatrix, die bei Bedarf polyseriale oder polychorische Korrelationskoeffizienten berechnetpolycor::polyserial- für die Berechnung eines polyserialen Korrelationskoeffizientenpolycor::polychor- für die Berechnung eines polychorischen Korrelationskoeffizientencorrplot::corrplot- zum Plotten einer Korrelationsmatrixpairs- zum Plotten einer Scatterplotmatrix
11.7 Kontrollfragen
- was ist der Unterschied zwischen Korrelation und Korrelation?
- wie hängt Pearson’s \(r\) mit Spearmann’s \(\rho\) zusammen?
- wie wird Kendall’s \(\tau\) berechnet?
- für welche experimentellen Designs kann der \(\chi^2\)-Assoziationstest angewandt werden? Wann Fisher’s exakter Test?
- welche weiteren Voraussetzungen müssen beim \(\chi^2\)-Assoziationstest erfüllt sein?
- wie kann man bei Experimenten mit zwei kategorialen Variablen die Stärke des Zusammenhanges bestimmen?
- beschreiben Sie das Grundprinzip des polyserialen Korrelationsanalyse
Weiterführende/zitierte Literatur
Da wir den Erwartungswert anhand der Daten schätzen verlieren wir einen Freiheitsgrad, deswegen \(n-1\) und nicht \(n\).↩︎
Die Skalenniveau sind in der Vorlesung Kartographie behandelt worden.↩︎
Es gibt effiziente Implementierungen, deren Laufzeit (im sogenannten O-Kalkül) nur mit n*log(n) ansteigt.↩︎
Das package
DescToolskann benutzt werden um weitere Assoziationsmaße zu berechnen. Je an Anwendungsfeld sind verschiedene Maße gebräuchlich. Ich werde diese hier aus Zeitgründen nicht weiter behandeln.↩︎Dies entspricht dem Verhältnis der erfolgreiche Versuche durch die Anzahl der Versuche↩︎
S. hierzu auch http://www.biostathandbook.com/gtestgof.html.↩︎
Mehr Details zu dieser Faustregel und auch dazu, wie man mit solchen Situationen umngehen kann, z.B: durch Korrekturfaktoren findet sich unter http://www.biostathandbook.com/small.html .↩︎
Generell ist es keine gute Idee, numerische Variablen für statistische Verfahren zu klassifizieren. In der Kartographie ist dies üblich und sinnvoll, da man die Darstellung im Kartenblatt nicht überfrachten möchte und eine einfache Zuordnung von Symboleigenschaften (z.B: Farbhelligkeit bei der Choroplethenkarte, Größe bei abgestuften Symbolgrößenkarten) zum Merkmalswert ermöglichen möchte. Dies darf man jedoch nicht auf statistische Analysen übertragen.↩︎
Dies ist in unserem Beispiel nicht verwunderlich, da die Daten von einer bivariaten Normalverteilung generiert wurden.↩︎