Kapitel 20 Generalisierte lineare Modelle für Zähldaten

## Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
## logical.return = TRUE, : there is no package called 'AICcmodavg'

20.1 Einführendes Beispiel

Wir werden uns hier mit einem Datensatz aus Portugal beschäftigen. Wie versuchen zu ergründen, welche treibenden Kräfte hinter den unterschiedlichen Zahlen überfahrener Amphibien bestehen. Diese dient als Proxy für die Anzahl lebender Amphibien in der Umgebung des Fundortes. Es geht uns also in Wirklichkeit um die Abundanz von Amphibien in der Region. Wenn wir verstehen, von welche Umweltfaktoren die Abundanz ausgeht, können wir den Schutz der Amphibien verbessern. Zunächst werden wir uns nur mit der Distanz zum Nationalpark beschäftigen. Die Hypothese ist, dass mit zunehmender Distanz zum Schutzgebiet die Abundanz abnimmt. Dieser Prädiktor ist jedoch mit vielen andern Umweltfaktoren kollinear.

rk <- read.table("data/RoadKills.txt", header=TRUE)
names(rk)

##  [1] "Sector"       "X"            "Y"            "BufoCalamita" "TOT.N"       
##  [6] "S.RICH"       "OPEN.L"       "OLIVE"        "MONT.S"       "MONT"        
## [11] "POLIC"        "SHRUB"        "URBAN"        "WAT.RES"      "L.WAT.C"     
## [16] "L.D.ROAD"     "L.P.ROAD"     "D.WAT.RES"    "D.WAT.COUR"   "D.PARK"      
## [21] "N.PATCH"      "P.EDGE"       "L.SDI"

Folgendes müssen Sie über den Datensatz wissen:

TOT.N - ist die Response-Variable. Sie enthält die Anzahl überfahrener Amphibien im Straßenabschnitt. Diese dient als Proxy für die Anzahl lebender Amphibien in der Umgebung des Fundortes
D.Park - beschreibt die Entfernung zu einem nahegelegenen Nationalpark in Metern.
X und Y enthalten die Koordinaten in einem projizierten Koordinatensystem - gelegentlich werde ich sie zum Plotten verwenden

Alle anderen Variablen sind hier zunächst nicht von Interesse.

20.1.1 Können wir ein lineares Modell verwenden?

Aus Platz- und Zeitgründen verzichten wir auf eine explorative Analyse sondern fitten gleich ein lineares Modell.

g.lm <- lm(TOT.N ~ D.PARK , data=rk)
summary(g.lm)

## 
## Call:
## lm(formula = TOT.N ~ D.PARK, data = rk)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -41.470  -9.316  -1.511   6.269  53.441 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 57.3049305  4.5478538  12.600  < 2e-16 ***
## D.PARK      -0.0024763  0.0003113  -7.955 1.95e-10 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 16.29 on 50 degrees of freedom
## Multiple R-squared:  0.5586, Adjusted R-squared:  0.5498 
## F-statistic: 63.28 on 1 and 50 DF,  p-value: 1.952e-10

Das Modell sieht erstmal nicht schlecht aus. Schauen wir uns einmal an, wie das graphisch aussieht:

plot(TOT.N ~ D.PARK , data=rk, pch=16, col="darkgrey",   cex=1.5, xlab="Distanz zum Nationalpark [m]", ylab="Überfahrene Amphibien", las=1)
newDat <- data.frame(D.PARK= seq(0, 25000, by=1000))
pred.lm <- predict(g.lm, newDat, se=TRUE )
lines(newDat$D.PARK, pred.lm$fit,  col="navy", lwd=3)
lines(newDat$D.PARK, pred.lm$fit + 1.96* pred.lm$se, lty=2,  col="navy", lwd=3)
lines(newDat$D.PARK, pred.lm$fit - 1.96* pred.lm$se, lty=2,  col="navy", lwd=3)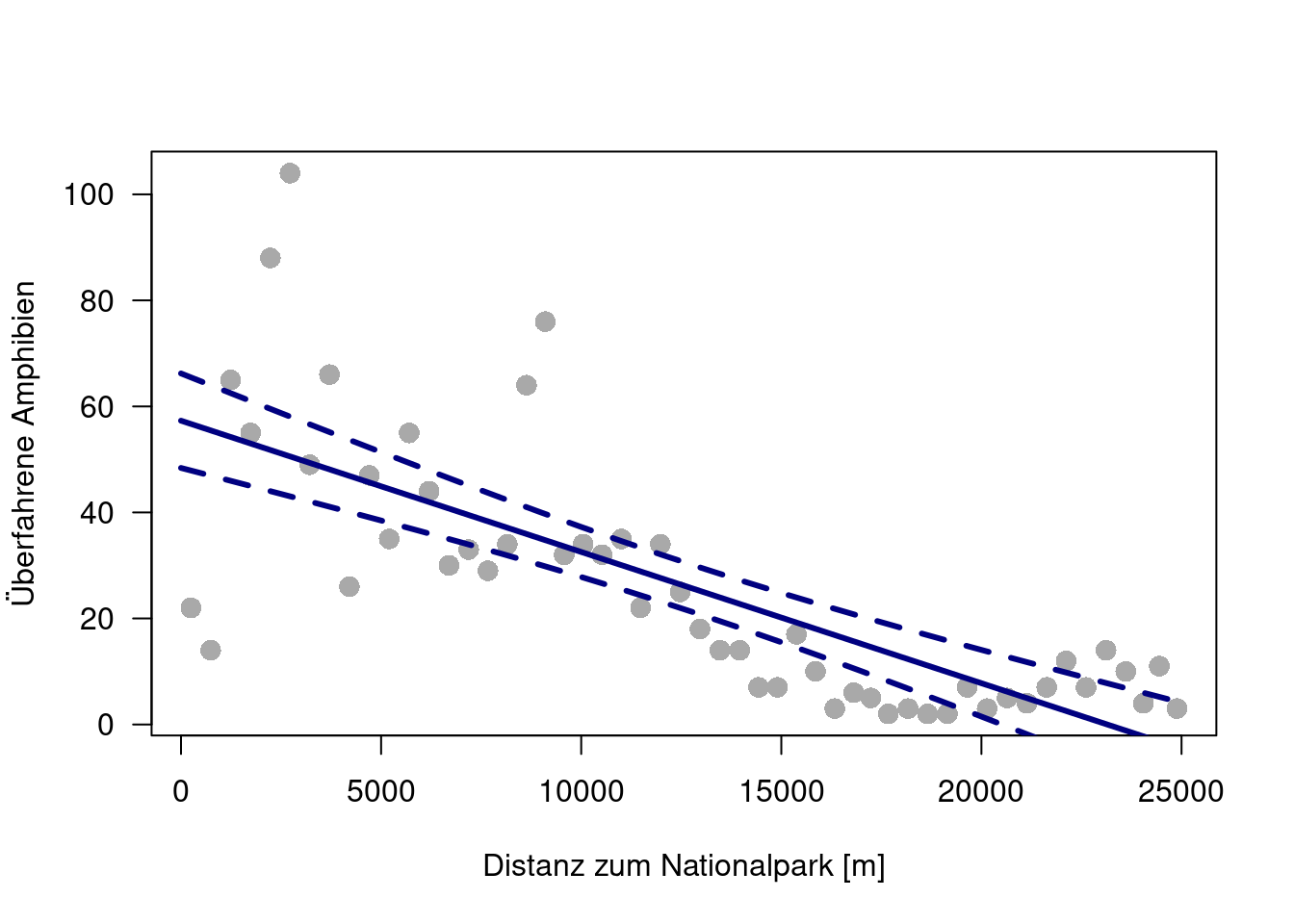

Die Vorhersage einer negativen Anzahl überfahrene Amphibien ab etwa 24km Entfernung zum Nationalpark sollten uns am Sinn des Modells zweifeln lassen…

Schauen wir uns auch noch ein paar Diagonseplots an:

par(mfrow=c(2,2), mar=c(4,4,1,1))
plot(residuals(g.lm) ~ fitted(g.lm), xlab="Fit", ylab="Residuen", pch=16, col="darkgrey", cex=1.2)
abline(h=0)
plot(residuals(g.lm) ~ rk$D.PARK, ylab="Residuen", xlab="Distanz zum Nationalpark", pch=16, col="darkgrey", cex=1.2)
abline(h=0)
plot(sqrt(abs(residuals(g.lm))) ~ fitted(g.lm), xlab="Fit", ylab=expression(sqrt(abs(Residuals))), pch=16, col="darkgrey", cex=1.2)
qqnorm(residuals(g.lm), main="", cex=1.2, pch=16, col="grey")
qqline(residuals(g.lm))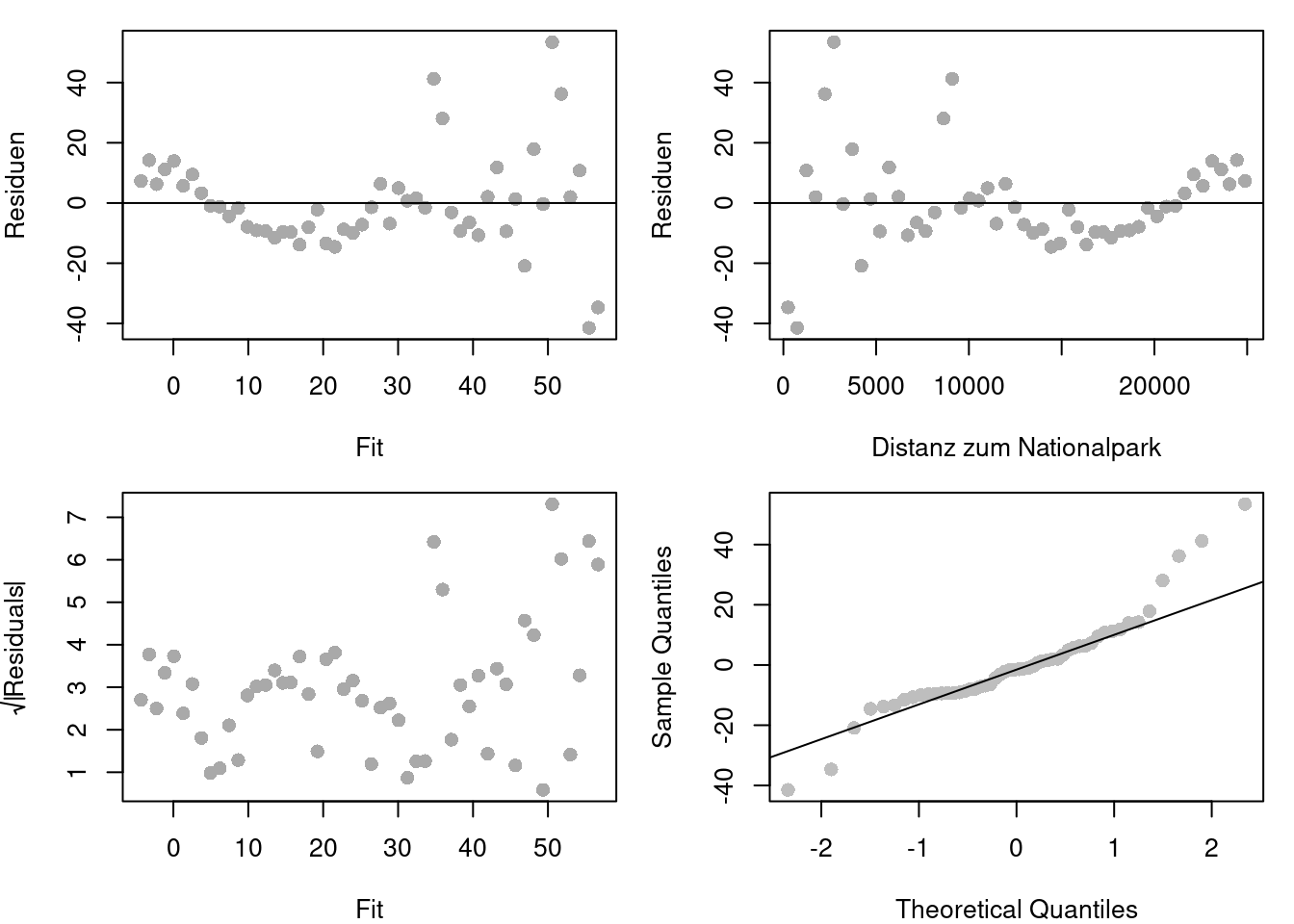

Hhmm…so richtig normalverteilt sieht das nicht aus.

20.2 GLM mit Poissonverteilung

Zähldaten sind i.d.R. nicht normalverteilt, nur bei hohen Zahlen ähnelt die Poisonverteilung in ihrer Wahrscheinlichkeitsdichteverteilung der Normalverteilung - wobei sie immer noch nur ganzzahlige Werte enthält!

Also fitten wir ein GLM mit einer Poissonverteilung. Der Aufruf erscheint uns doch sehr vertraut: anstelle von lm schreiben wir glm und zusätzlich müssen wir mit dem family argument angeben, welche Famile benutzt werden soll. Der default ist gaussian, d.h. ein lm (wobei das Fitten im GLM anders erfolgt als beim LM, wir merken uns nur, dass wir lineare Modelle immer mit lm fitten und beim GLM immer die Verteilungsfamile spezifizieren müssen).

g.po <- glm(TOT.N ~D.PARK, data=rk, family=poisson)
summary(g.po)

## 
## Call:
## glm(formula = TOT.N ~ D.PARK, family = poisson, data = rk)
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.316e+00  4.322e-02   99.87   <2e-16 ***
## D.PARK      -1.059e-04  4.387e-06  -24.13   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 1071.4  on 51  degrees of freedom
## Residual deviance:  390.9  on 50  degrees of freedom
## AIC: 634.29
## 
## Number of Fisher Scoring iterations: 4

Auch die Ausgabe von summary wirkt vertraut: Regressionskoeffizienten, Standardfehler, p-Wert, … aber kein $R^2$, dass ist nur für lineare Modelle definiert. Immerhin erhalten wir einen AIC Wert.

Aber können wir die Regressionskoeffizienten einfach wie bisher interpretieren?

Fangen wir doch einmal mit dem Achsenabschnitt an. Im linearen Modell beträgt er:

coef(g.lm)[1]

## (Intercept) 
##    57.30493

Im Poisson GLM sieht er etwas anders aus..

coef(g.po)[1]

## (Intercept) 
##    4.316485

Wie kann das sein?

Erinnern wir uns nochmal, wie ein GLM funktioniert: es gibt eine Linkfunktion, nennen wir sie einmal g(), die den Zusammenhang linearisiert. Beim Poissonmodell ist die sogenannte kanonische Linkfunktion (die gebräuchlichste oder die am direktesten abzuleitende, aber nicht zwangsläufig die einzige oder die für alle Fälle anzuwendende) der Logarithmus, d.h.:

\[ Y = g(X \beta) \] \[ g(x) = log(x) \] \[ Y = e^{X\beta} = e^{\beta_0 + \beta_1 * x_1 + ...} \]

Die Regressionskoeffizienten beziehen sich also auf die Linkskala. Damit wir sie auf der Responseskala interpretieren können, müssen wir Sie rücktransformieren.

exp(coef(g.po)[1])

## (Intercept) 
##     74.9248

Das passt von der Größenordnung schon eher.

Was aber ist mit dem Regressionskoeffizenten für die Distanz zum Nationalpark?

(xx <- exp(coef(g.po)[2]))

##    D.PARK 
## 0.9998942

Was fangen wir mit 0.9998942 an? Hierfür müssen wir uns nocheinmal mit der Link Funktion auseinandersetzen und unsere Schulmathematik bzgl. des Rechnens mit Logarithmen bemühen.

\[ TOT.N = e^{X\beta} = e^{ 4.3164849800 -0.0001058506 * D.PARK} \]

In einer Distanz von 0m zum Nationalpark erwarten wir:

\[ e^{ 4.3164849800} \] überfahrene Amphibien

exp(4.3164849800)

## [1] 74.9248

In einer Entfernung von 1m erwarten wir: \[ e^{ 4.3164849800 -0.0001058506 \cdot 1} = e^{4.3164849800} \cdot e^{-0.0001058506 \cdot 1} = 74.9248027 \cdot 0.9998942 \] überfahrene Amphibien. Hierfür müssen wir uns erinnern, dass :

\[ z^{a+b} = z^a * z^b \] und \[ z^{a-b} = z^a / z^b = z^a * z^{-b} \]

exp(4.3164849800)* exp(-0.0001058506)

## [1] 74.91687

In einer Entfernung von 2m erwarten wir: \[ e^{ 4.3164849800 -0.0001058506 \cdot 2} = e^{4.3164849800} \cdot e^{-1 \cdot(0.0001058506 + 0.0001058506)} = \] \[ e^{4.3164849800} \cdot e^{-0.0001058506 } \cdot e^{-0.0001058506} = 74.9248027 \cdot 0.9998942^2\]

überfahrene Amphibien.

exp(4.3164849800)* exp(-0.0001058506)^2

## [1] 74.90894

Entsprechend in 1km:

exp(4.3164849800)* exp(-0.0001058506)^1000

## [1] 67.39928

Wir können natürlich auch predict nutzen. Wir können bei predict.glm, also predict, das an einem GLM Objekt aufgerufen wird angeben, ob die Ergebnisse auf der link oder der response Skala zurückgegeben werden. Siehe: ?predict

Erstmal ist es komfortabler, wenn wir die Ergebnisse auf der response Skala bekommen.

pred.po <- predict(g.po, newDat, se=TRUE, type="response" )
head(cbind(newDat, pred.po))

##   D.PARK      fit   se.fit residual.scale
## 1      0 74.92480 3.238249              1
## 2   1000 67.39928 2.689930              1
## 3   2000 60.62963 2.232786              1
## 4   3000 54.53993 1.856008              1
## 5   4000 49.06189 1.550239              1
## 6   5000 44.13406 1.307183              1

Allerdings gibt es keine Option, sich Konfidenzintervalle bei GLMs mit predict ausgeben zu lassen. Wir müssen diese anhand der Standardfehler selbst konstruieren - und zwar auf der link Skala. Auf dieser können wir die Konfidenzintervalle als -näherungsweise - 1.96*Standardfehler abschätzen.

pred.po <- predict(g.po, newDat, se=TRUE, type="link" )
head(cbind(newDat, pred.po))

##   D.PARK      fit     se.fit residual.scale
## 1      0 4.316485 0.04321998              1
## 2   1000 4.210634 0.03991037              1
## 3   2000 4.104784 0.03682664              1
## 4   3000 3.998933 0.03403027              1
## 5   4000 3.893083 0.03159762              1
## 6   5000 3.787232 0.02961847              1

Beim Plotten müssen wir daran denken, dass wir die vorhergesagten Werte zurück auf die Response Skala transformieren müssen.

###################################################
### plot the Poisson regression together with
### the estimated 95% confidence band
###################################################
plot(TOT.N ~D.PARK, data=rk, xlab="Distanz zum Nationalpark [m]", ylab="Überfahrene Amphibien", las=1, pch=16, col="orange")
lines(newDat$D.PARK, exp(pred.po$fit),  col="green", lwd=3)
lines(newDat$D.PARK, exp(pred.po$fit + 1.96* pred.po$se), lty=2, col="green", lwd=3)
lines(newDat$D.PARK, exp(pred.po$fit - 1.96 *pred.po$se), lty=2, col="green", lwd=3)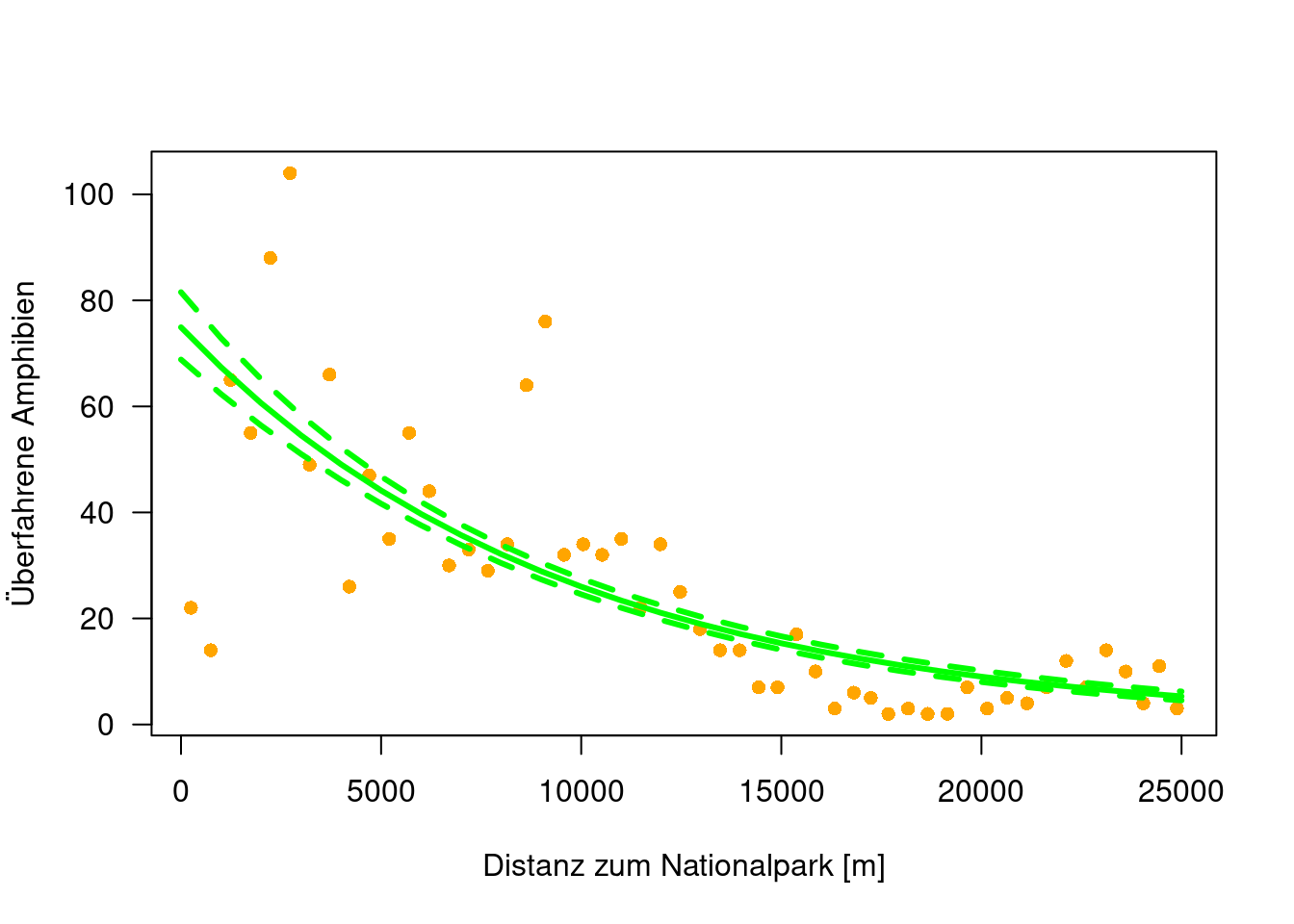

Auch bei den Konfidenzintervallen der Regressionskoeffizienten ist die Welt etwas komplizierter geworden: anders als im linearen Modell können wir die Konfidenzintervalle nicht mehr exakt berechnen, sondern müssen Sie näherungsweise iterativ schätzen. confint in {MASS} erledigt das für uns. Auch hier dürfen wir nicht vergessen, die Werte rückzutransformieren.

require(MASS)
conf.po <-confint(g.po)

## Waiting for profiling to be done...

conf.po

##                     2.5 %        97.5 %
## (Intercept)  4.2310250582  4.400462e+00
## D.PARK      -0.0001145178 -9.731733e-05

exp(conf.po)

##                  2.5 %     97.5 %
## (Intercept) 68.7877074 81.4885282
## D.PARK       0.9998855  0.9999027

Wie gesagt gibt es kein $R^2$ mehr. Allerdings existieren eine Reihe von sogenannten Pseudo$R^2$-ten, die einzelne Aspekte des $R^2$ im linearen Modell näherungsweise abbilden. Für unseren Fall reicht es, wenn wir uns die explained deviance anschauen, die angibt wieviel Deviance durch das Modell erklärt wird. Die Deviance gibt die Abweichung an, im linearen Fall entspricht sie den Abweichungsquadraten.

Während die erklärte Varianz im linearen Modell wie folgt berechnet wird:

\[R^2= 1- \frac{RSS}{TSS}\]

ist es beim GLM:

\[explained.deviance = 1 - \frac{residual.deviance}{null.deviance}\]

Die null deviance gibt dabei die deviance beim Modell an, das nur aus dem Intercept besteht (analog zum linearen Modell).

1-g.po$deviance/ g.po$null.deviance

## [1] 0.6351681

Wie wir sehen, ist unser Modell gar nicht so schlecht.

Die deviance leitet sich aus der Differenz der log-Likelihoods des tatsächlichen und des gesättigten (oder maximalen) Modells her:

\[ D(y) = -2( log(p(y |\hat{\theta}_m)) - log(p(y|\hat{\theta}_s))) \]

Wobei $D(y)$ die deviance für den response y und das Modell m. $\hat{\theta}_m)$ sind die gefitteten Modellparameter des Modells m, während $\hat{\theta}_s)$ die Modellparameter des maximalen Modells angibt.

Wenn man die log-Likelihood Definition der Poisson-Verteilung einsetzt, erhält man die Formeln für die deviance der Poissonverteilung:

\[D(y, \hat{y}) = 2 \sum (y log(\frac{y}{\hat{y}}) -(y-\hat{y}))\]

Nun können wir die deviance auch von Hand berechnen:

y <- rk$TOT.N
yhat <- fitted(g.po)

2*sum(y * log(y/yhat) - (y - yhat))

## [1] 390.8969

Vergleichen wir das mit dem Modelloutput:

g.po$deviance

## [1] 390.8969

Derselbe Wert - wobei die Deviance aus glm nur bis zu einer additiven Konstante korrekt ist (wir haben den Faktor 2 in der Berechnung weggelassen), die sich beim Modellvergleich aber wegmittelt.

Schauen wir uns doch einmal Schritt für Schritt an, was in der Deviance passiert:

Die Differenz zwischen beobachtetem und vorhergesagtem Wert:

plot(y-yhat, type="h")

Das Verhältnis von beobachtetem und vorhergesagtem Wert:

plot(log(y/yhat)~y, type="h")

Wenn der vorhergesagte Wert nahe beim beobachteten Wert liegt, geht das Verhältnis gegen 1, der Logarithmus davon ist bekanntermaßen 0.

Das Verhältnis multipliziert mit dem beobachtetem Wert (wir erwarten ja, dass die Varianz mit dem Mittelwert zunimmt):

plot(y*log(y/yhat)~y, type="h")

Und nun die Differenz mit der Differenz von beobachtetem und vorhergesagtem Wert:

plot(y*log(y/yhat) -(y-yhat) ~y, type="h")

20.2.1 Modellselektion

Wie vergleichen wie Modelle? Wie bisher:

AIC bzw. AICc
BIC
Likelihood-ratio test
Signifikanz der Koeffizienten (nun kein t-Test sondern ein Wald-Test)

20.2.2 Modell-Diagnose

20.2.3 Residuen

Wie vielleicht schon erwartet, sind auch die Residuen nicht mehr so einfach zu handhaben wie im linearen Modell. Wir gehen ja davon aus, dass die Varianz mit dem Mittelwert zunimmt, d.h. wir erwarten dort auch größere Abweichungen. Entsprechend ist es nicht sinnvoll, die reine Abweichung $y-\hat{y}$ zu plotten (die sogenannten response residuals). Das Muster würde uns nur vom wesentlichen ablenken. Anstelle der raw residuals verwendet man nun die pearson Residuen, die deviance Residuen oder auch die studentized residuals. Sie entfernen jeweils ein anderes zu erwartendes Muster aus den response Residuen.

Pearson Residuen $r_P$:

Hier werden die response Residuen jeweils durch die Standardabweichung der Vorhersage geteilt um den Effekt der Veränderung des Mittelwertes auf die Varianz zu berücksichtigen.

\[r_P = \frac{y-\hat{y}}{\sqrt{var(\hat{y})}} \]

Die Pearson Residuen sind dabei so konstruiert, das die Summe der Variablen $\chi^2$ verteilt ist (mit df= Anzahl der Modellparameter), womit sich der Fit der Daten auch absolut vergleichen lässt - dies wollen wir hier jedoch nicht vertiefen.

Deviance Residuen $r_D$:

Hier werden die Residuen so skaliert, dass ihre Summe die Deviance ergibt. Auch hier wird der unerwünschte (weil bekannte) Effekt des Mittelwertes auf die absolute Abweichung der Residuen vom Mittelwert unterdrückt. Typischerweise unterscheiden sich Pearson und Deviance Residuen nicht sehr stark.

\[ r_D= sign(y-\hat{y}) \sqrt(d) \]

Wobei d der Vektor der deviance ist. Die Funktion sign gibt nur das Vorzeichen zurück.

Studentized Residuen oder standardisierte deviance Residuen $r_{SD}$:

Hierbei wird zusätzlich der Leverage der Datenpunkte $h_i$ und die Dispersion $\hat{\phi}$ (s. unten) mit einbezogen.

\[r_p = \frac{r_D}{\sqrt{\hat{\phi}(1-h_i)}} \]

Während die Pearson und die Deviance Residuen zumeist relativ ähnlich sind, unterscheiden sich die studentized Residuen typischerweise deutlich davon. Die einfachen Response Residuen sind für GLMs (außer mit Gaussverteilung) nicht hilfreich.

Schauen wir uns die vier verschiedenen Residuen doch einmal an. Wichtig ist, dass wir die Residuen auf der link-Skala plotten um Muster erkennen zu können. Wir sollten nicht erwarten, hier normalverteilte Residuen zu Gesicht zu bekommen.

muhat <- predict(g.po, type="link") # der gefittete Wert auf der link-skala
resResp <- residuals(g.po, type="response")
resDevi <- residuals(g.po, type="deviance")
resPear <- residuals(g.po, type="pearson")
resStud <- rstudent(g.po)

par(mfrow=c(2,2), mar=c(4,4,1,1))

plot(resResp ~ muhat, ylab="Response Residuen", xlab=expression(hat(mu)), las=1, pch=21, bg="blue")
abline(h=0)
plot(resDevi ~ muhat, ylab="Deviance Residuen", xlab=expression(hat(mu)), las=1, pch=21, bg="blue")
abline(h=0)
plot(resPear ~ muhat, ylab="Pearson Residuen", xlab=expression(hat(mu)), las=1, pch=21, bg="blue")
abline(h=0)
plot(resStud ~ muhat, ylab="Studentized Residuen", xlab=expression(hat(mu)), las=1, pch=21, bg="blue")
abline(h=0)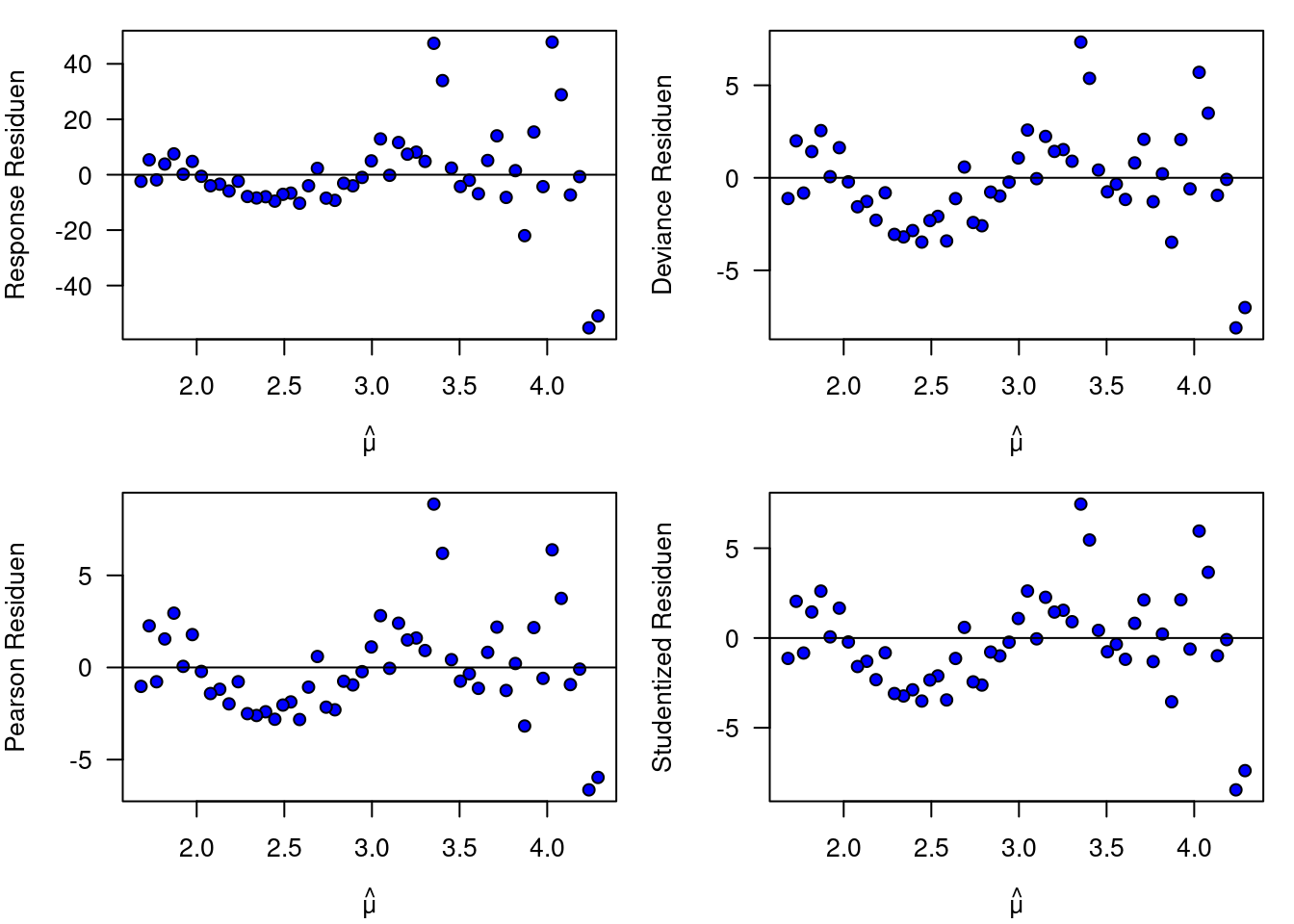

Figure 20.1: Plot der 4 Residuentypen gegen den vorhergesagten Wert für das Poisson GLM für die Roadkill Daten.

In diesem Beispiel (Abbildung 20.1) sehen wir keine deutlichen Unterschiede zwischen den Pearson, den Deviance und den studentized Residuen. Alle Residuen zeigen eine Zunahme der Varianz mit dem Mittelwert, was darauf hindeutet, dass die Varinaz stärker als der Mittelwert ansteigt. Die response Residuen zeigen dies deutlicher (vergleiche Achsenbeschriftung), was ja zu erwarten ist, da keine Korrektur für die Zunahme der Varianz mit dem Mittelwert erfolgt. Dies wird noch deutlicher, wenn wir die Achsen alle gleich skalieren (Abbildung 20.2). Was wir auch sehen, ist eine unschöne zyklische Struktur, die entweder das fehlen weiterer erklärender Variablen aufzeigt oder auf Autokorrelation der Residuen hinweisen könnte.

par(mfrow=c(2,2), mar=c(4,4,1,1))

plot(resResp ~ muhat, ylab="Response Residuen", 
     xlab=expression(hat(mu)), las=1, pch=21, bg="blue",
     ylim=c(-40,40))
abline(h=0)
plot(resDevi ~ muhat, ylab="Deviance Residuen", 
     xlab=expression(hat(mu)), las=1, pch=21, bg="blue",
     ylim=c(-40,40))
abline(h=0)
plot(resPear ~ muhat, ylab="Pearson Residuen", 
     xlab=expression(hat(mu)), las=1, pch=21, bg="blue",
     ylim=c(-40,40))
abline(h=0)
plot(resStud ~ muhat, ylab="Studentized Residuen", 
     xlab=expression(hat(mu)), las=1, pch=21, bg="blue",
     ylim=c(-40,40))
abline(h=0)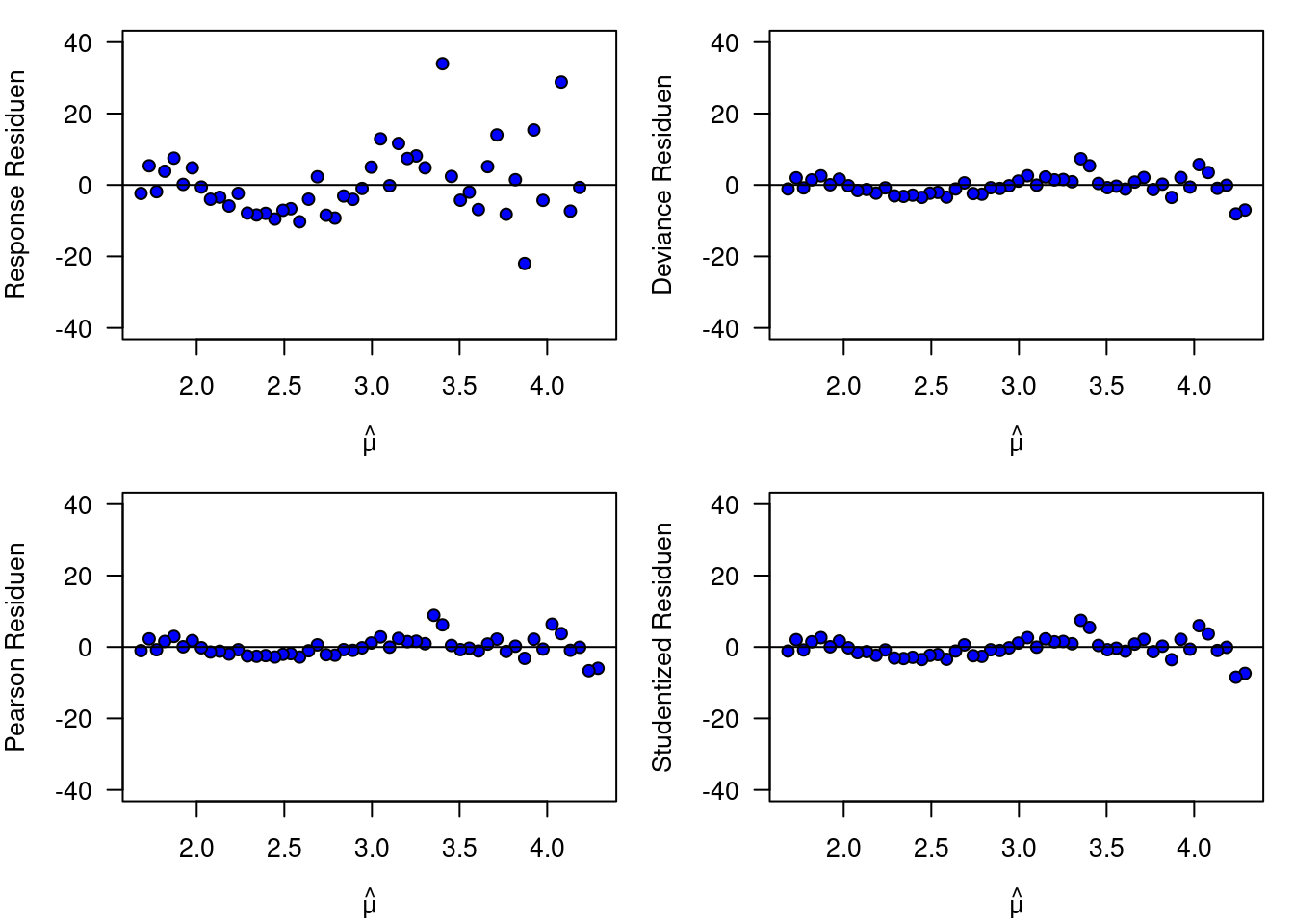

Plot der 4 Residuentypen gegen den vorhergesagten Wert für das Poisson GLM für die Roadkill Daten. Die y-Achse wurde für alle 4 Plots gleich skaliert.

Figure 20.2: Plot der 4 Residuentypen gegen den vorhergesagten Wert für das Poisson GLM für die Roadkill Daten. Die y-Achse wurde für alle 4 Plots gleich skaliert.

Da die Daten raumbezogen sind, lohnt es sich stets auch zu schauen, ob die Residuen Anzeichen räumlicher Autokorrelation aufweisen.

###################################################
### check if we can spot signs
### for a spatial autocorrelation of the errors
###################################################

rk$p.resid <-  residuals(g.po,type="pearson")
plot(rk$Y ~ rk$X, col=c("blue", "red")[sign(rk$p.resid)/2+1.5], pch=19, cex=1+abs(rk$p.resid)/max(rk$p.resid)*2, xlab="geographische X-Koordinaten", ylab="geographische y-Koordinaten")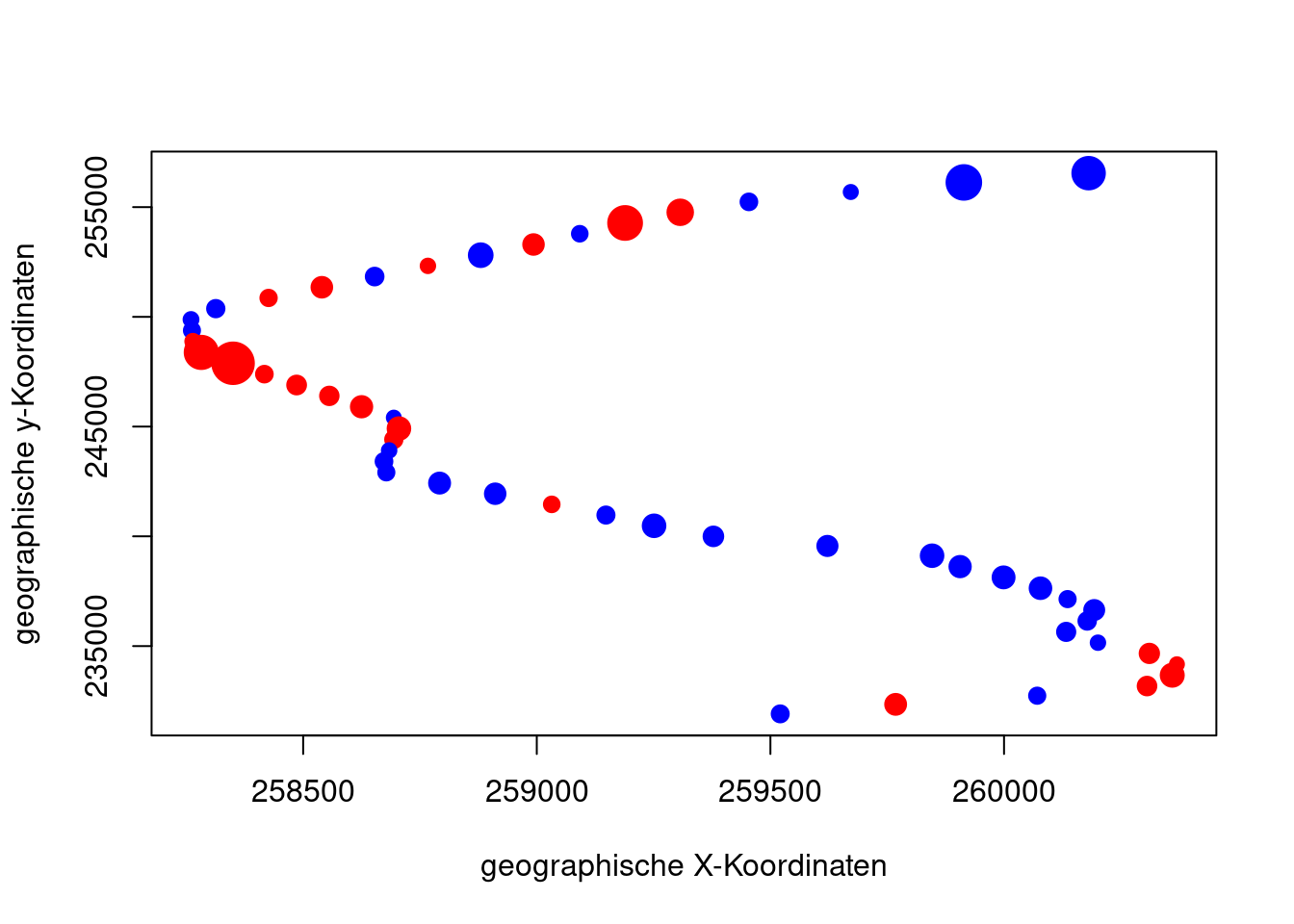

20.3 Overdispersion

Soweit, so gut. Nun erinnern wir uns, dass bei der Poisson die Varianz mit dem Mittelwert zunimmt:

\[ Varianz = Mittelwert \]

Das muss natürlich nicht der Fall, sein, weswegen wir als nächstes überprüfen, ob die Varianz schneller (overdispersed) oder langsamer (underdispered) als der Mittelwert zunimmt. Während underdispersion unkritisch ist, stellt overdispersion unser Modell in Frage.

Ein schneller Test ist, die residual deviance durch die residual degrees of freedom zu teilen. Wenn die Varianz mit dem Mittelwert steigt, sollte das Ergebniss nahe 1 liegen. Die Deviance lässt sich als Varianz im Modell deuten und wenn es ein Poisson Prozess wäre, sollte die Varianz dem Mittelwert entsprechen.

sum.po <- summary(g.po)
(phi <- sum.po$deviance/sum.po$df.residual)  # overdispersed

## [1] 7.817937

Wie wir sehen, liegt der Wert bei 7.8 und zeigt an, dass die Residuen overdispersed sind. Was bedeuted das? Nun, es sagt das wir zu optimistisch hinsichtlich unserer Standardfehler waren. Die Standardfehler sind in Wirklichkeit $\sqrt(\phi)$-mal so groß. Das heißt, dass eine ggf. vorangegangene Modellselektion fehlerbehaftet war und wir möglicherweise einen Modell mit nicht signifikant von Null verschiedenen Koeffizienten aufgesessen sind.

Wir können den Effekt berechnen, wenn wir den Dispersionsfaktor bei summary mit angeben:

summary(g.po, dispersion=phi)

## 
## Call:
## glm(formula = TOT.N ~ D.PARK, family = poisson, data = rk)
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.316e+00  1.208e-01  35.719   <2e-16 ***
## D.PARK      -1.058e-04  1.227e-05  -8.629   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 7.817937)
## 
##     Null deviance: 1071.4  on 51  degrees of freedom
## Residual deviance:  390.9  on 50  degrees of freedom
## AIC: 634.29
## 
## Number of Fisher Scoring iterations: 4

Was bedeuted dies? Wir unterstellen im Poisson GLM zwingend, das die Varianz gleich dem Mittelwert ist. Plotten wir den Mittelwert auf der Link-Skala gegen die Residuen, sollten diese um eine 1:1 Linie liegen. Das tun sie jedoch offensichtlich nicht! Die Steigung der Residuen ist viel stärker, geschätzt liegt sie bei 7.82.

Wir plotten hierfür einmal die Varianz-Mittelwert Beziehung (s. Abbildung 20.3). Wir teilen hierfür die beobachtete Anzahl überfahrener Amphibien in 10 Gruppen ein und berechnen hierfür jeweils Mittelwert und Varianz und tragen diese gegeneinander auf.

Die Gruppeneinteilung nehmen wir nicht anhand der Quantile der beobachteten überfahrenen Amphibien vor, sondern anhand der vorhergesagten Werte - wir sind ja an den Werten ohne den Fehler interessiert, die beste Schätzung dafür ist unser Regressionsmodell. Ich habe hier 10 Gruppen gewählt, damit wir wenigstens 5 Werte in jeder Gruppe haben. Bei mehr Beobachtungen würde ich Gruppen wählen, die mehr Werte enthalten, damit die Schätzungen des Mittelwertes und insbesondere der Varianz verläßlicher sind.

xb <- predict(g.po, type="response") # um Klassen zu bilden 
groups <- cut(xb,breaks=quantile(xb,seq(0,100,by = 10)/100))

mittelwert <- tapply(rk$TOT.N, groups, mean)

varianz <- tapply(rk$TOT.N, groups, var)

plot(varianz~mittelwert, xlab="Mittelwert", ylab="Varianz", 
     main="Mittelwert-Varianz Beziehung", 
     pch=21, bg="orange",
     las=1)

x <- seq(0,80,1)

lines(x, x*phi, lty=2)


lines(x,x, lty=4)

legend("topleft", lty=c(2,4), legend=c("Q. Poisson", "Poisson"), inset=0.05)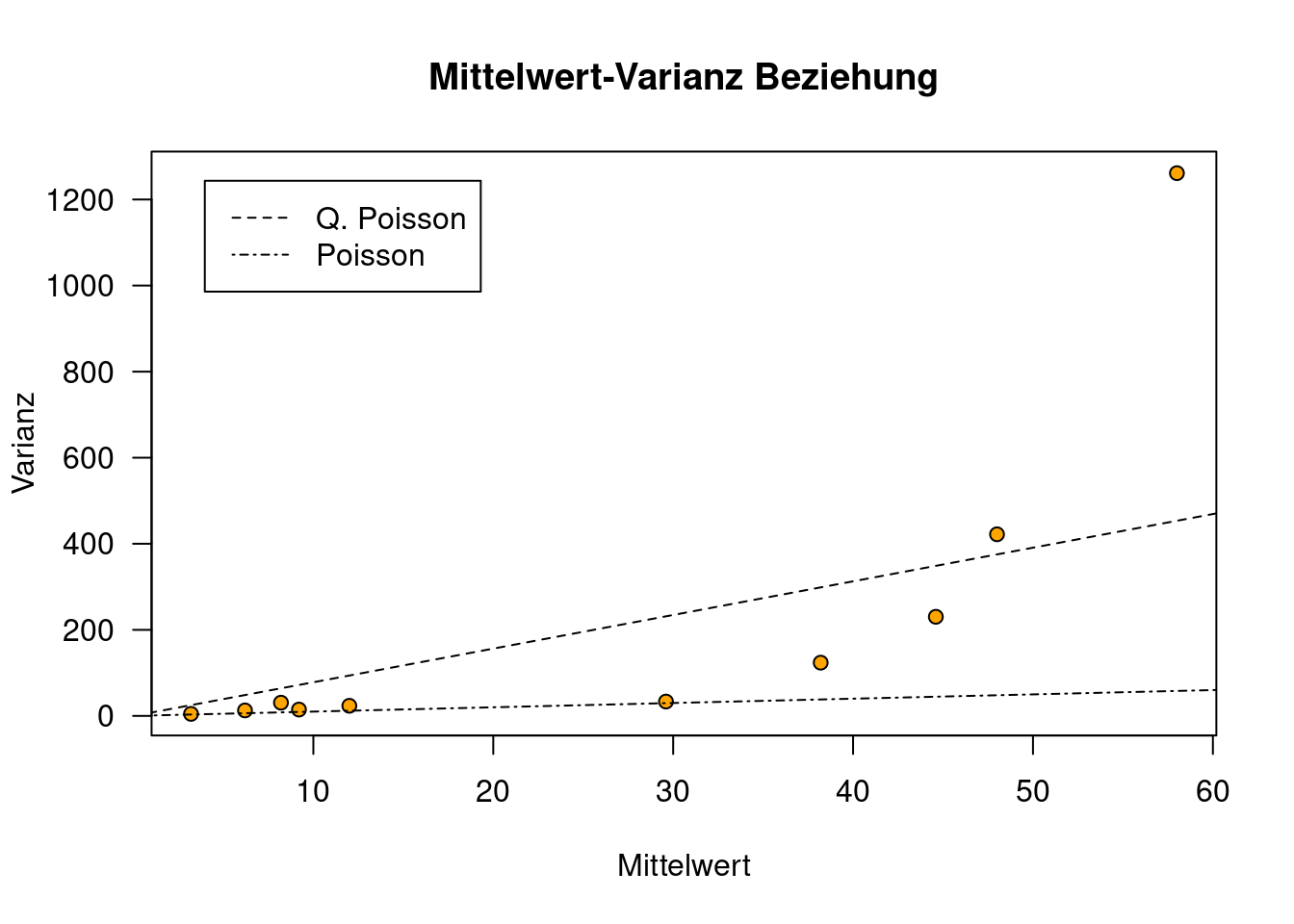

Plot der für den Roadkill Datensatz beobachteten Varianz gegen den Mittelwert der Beobachtungen. Hierfür wurde die Beobachtungen der Größe nach sortiert und in Gruppen je 5 Straßenabschnitte eingeteilt. Die im Poisson GLM unterstellte Steigung von 1 ist zu gering. Wenn wir einen linearen Zusammenhang unterstellen, wäre die Steigung durch den Overdispersion-Faltor angegeben (Quasipoisson Modell).

Figure 20.3: Plot der für den Roadkill Datensatz beobachteten Varianz gegen den Mittelwert der Beobachtungen. Hierfür wurde die Beobachtungen der Größe nach sortiert und in Gruppen je 5 Straßenabschnitte eingeteilt. Die im Poisson GLM unterstellte Steigung von 1 ist zu gering. Wenn wir einen linearen Zusammenhang unterstellen, wäre die Steigung durch den Overdispersion-Faltor angegeben (Quasipoisson Modell).

Wie wir sehen, steigt die Varianz innerhalb der beobachteten Werte mit dem Mittelwert der beobachteten Werte an. Allerdings deutlich stärker, als im Poisson Modell angenommen (Varianz = Mittelwert). Das Quasispoisson Modell verwendet die Overdispersion 7.82 um die Steigung anzupassen.

Was können wir tun?

Es gibt 2 Strategien: entweder wir fitten ein Quasi-Poisson Modell, dass die Vergrößerung der Standardfehler mit einbezieht oder ein negativ-binomial verteiltes Modell, dass overdispersion über einen quadratischen Term mit einbeziehen kann. Beide Wege sind gangbar.

20.3.1 Quasi-Poisson GLM

Wir müssen einfach nur das family argument von poisson auf quasipoisson setzen und das Modell erneut fitten.

g.qpo <- glm(formula = TOT.N ~ D.PARK, family = quasipoisson, data = rk)
summary(g.qpo)

## 
## Call:
## glm(formula = TOT.N ~ D.PARK, family = quasipoisson, data = rk)
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  4.316e+00  1.194e-01  36.156  < 2e-16 ***
## D.PARK      -1.058e-04  1.212e-05  -8.735 1.24e-11 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for quasipoisson family taken to be 7.630148)
## 
##     Null deviance: 1071.4  on 51  degrees of freedom
## Residual deviance:  390.9  on 50  degrees of freedom
## AIC: NA
## 
## Number of Fisher Scoring iterations: 4

coef(g.po)

##   (Intercept)        D.PARK 
##  4.3164849800 -0.0001058506

coef(g.qpo)

##   (Intercept)        D.PARK 
##  4.3164849800 -0.0001058506

Die Regressionskoeffizienten sind exakt gleich geblieben, allerdings haben sich die Standardfehler deutlich erhöht.

Wenn wir das näherungsweise ausrechnen, sehen wir, dass sich - wie bereits angekündigt - die Standardfehler um $\sqrt(\phi)$ erhöht haben.

sqrt(phi)

## [1] 2.796057

Plotten wir doch einmal beide Modelle inklusive der geschätzten Konfidenzbänder:

pred.qpo <- predict(g.qpo, newDat, se=TRUE, type="link" )

plot(TOT.N ~D.PARK, data=rk, xlab="Distanz zum Park [m]", ylab="Überfahrene Amphibien", las=1)
lines(newDat$D.PARK, exp(pred.qpo$fit),  col="green", lwd=3)
lines(newDat$D.PARK, exp(pred.qpo$fit + 1.96*pred.qpo$se), lty=2, col="green", lwd=3)
lines(newDat$D.PARK, exp(pred.qpo$fit - 1.96*pred.qpo$se), lty=2, col="green", lwd=3)

lines(newDat$D.PARK, exp(pred.po$fit),  col="navy", lwd=1)
lines(newDat$D.PARK, exp(pred.po$fit + 1.96*pred.po$se), lty=2, col="navy", lwd=1)
lines(newDat$D.PARK, exp(pred.po$fit - 1.96*pred.po$se), lty=2, col="navy", lwd=1)
legend(x="topright", legend=c("Quasipoisson","Poisson"), col=c("green", "navy"), lwd=c(3,1))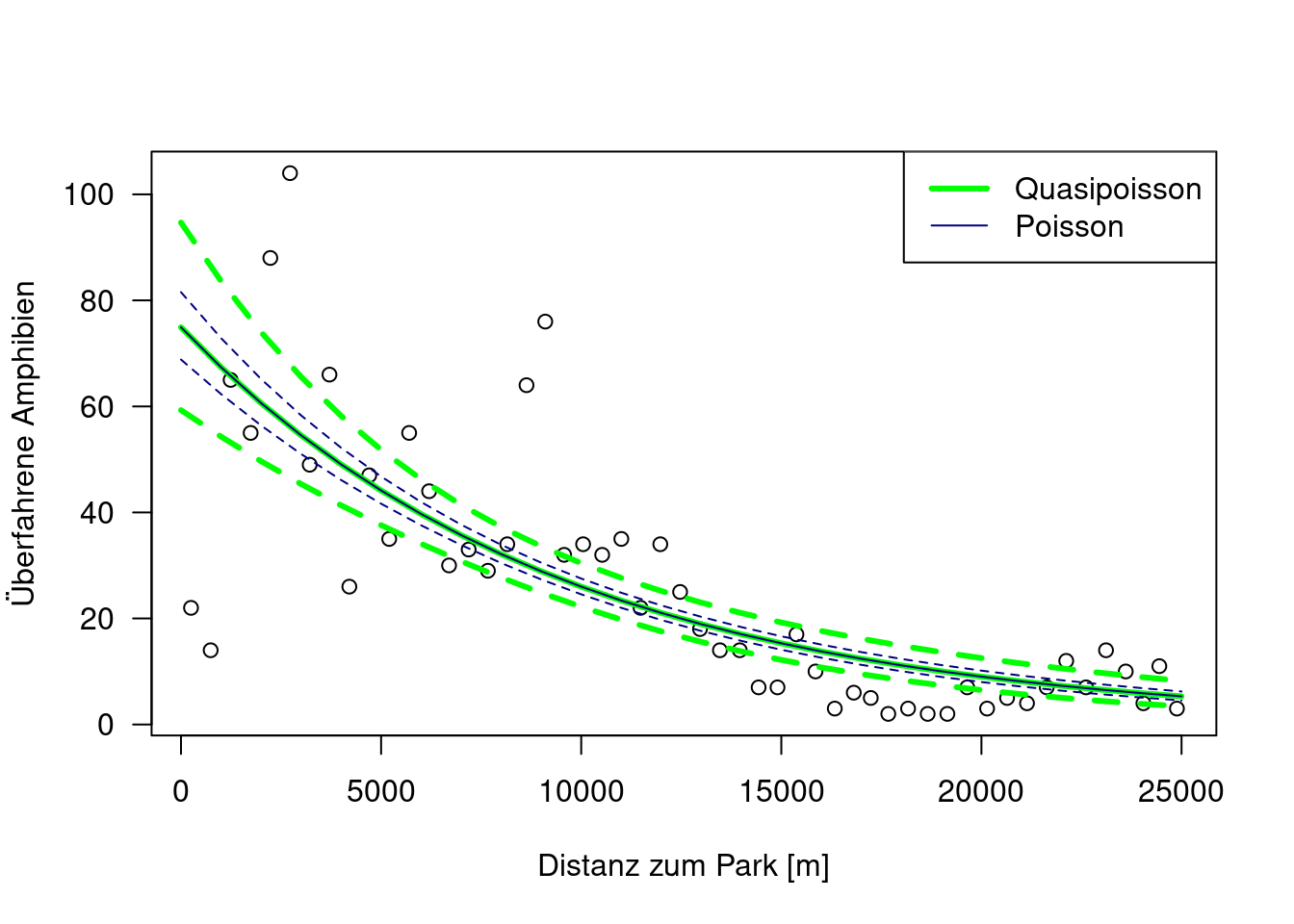

Wie erwartet liegt der vorhergesagte Mittelwert exakt übereinander, während die Unsicherheit deutlich zugenommen hat.

Das gleiche hätten wir erreicht, wenn wir die Standardfehler manuell erhöht hätten:

# we would have gotten the same thing if we would have scaled the standard errors by the dispersion factor
plot(TOT.N ~D.PARK, data=rk,  xlab="Distanz zum Park [m]", ylab="Überfahrene Amphibien", las=1)
lines(newDat$D.PARK, exp(pred.qpo$fit),  col="darkgreen", lwd=3)
lines(newDat$D.PARK, exp(pred.qpo$fit + 1.96*pred.qpo$se), lty=4, col="darkgreen", lwd=3)
lines(newDat$D.PARK, exp(pred.qpo$fit - 1.96*pred.qpo$se), lty=4, col="darkgreen", lwd=3)


lines(newDat$D.PARK, exp(pred.qpo$fit + 1.96*pred.po$se* sqrt(7.630148)), lty=2, col="purple", lwd=3)
lines(newDat$D.PARK, exp(pred.qpo$fit - 1.96*pred.po$se*sqrt(7.630148)), lty=2, col="purple", lwd=3)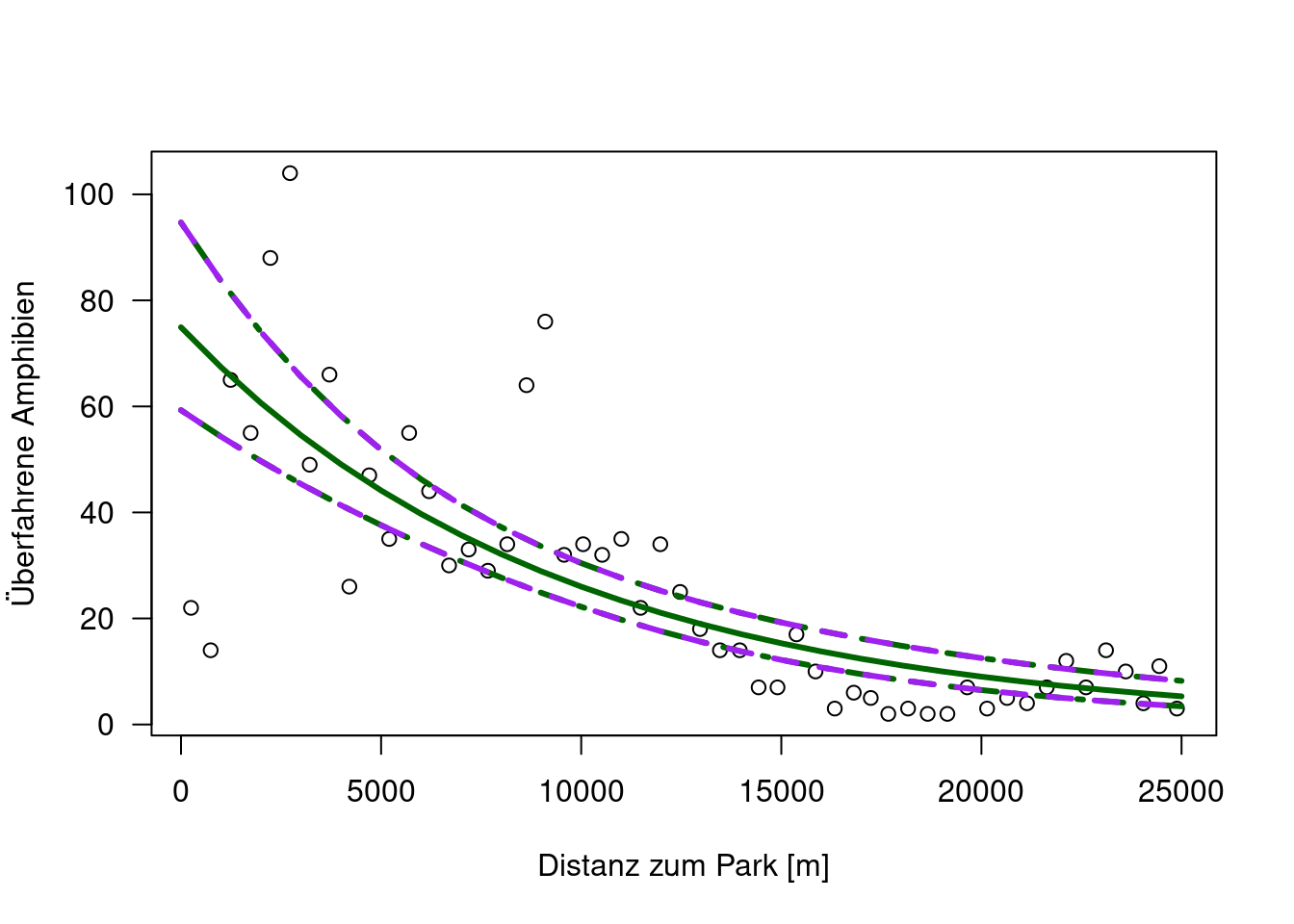

Wichtig ist, dass nicht das Quasi-Poisson GLM unsicherer ist als das Poisson GLM, es stellt die Unsicherheit nur richtig da. Wir müssen von einer deutlich größeren Unsicherheit bei kleinen Distanzen ausgehen, was dazu führt, das die Unsicherheit der Schätzung der Regressionslinie entsprechend unsicher ist.

Schauen wir uns einmal die Residuen beider Modelle an:

muhat <- predict(g.qpo, type="link") # der gefittete Wert auf der link-skala, identisch für qpo und po
resD.qpo <- residuals(g.qpo, type="deviance")
resD.po <- residuals(g.po, type="deviance")

op <- par(mfrow=c(1,2))

plot(resD.qpo ~ muhat, ylab="Deviance Residuen", xlab=expression(hat(mu)), main="Quasi-Poisson", las=2)
abline(h=0)
plot(resD.po ~ muhat, ylab="Deviance Residuen", xlab=expression(hat(mu)), main="Poisson", las=1)
abline(h=0)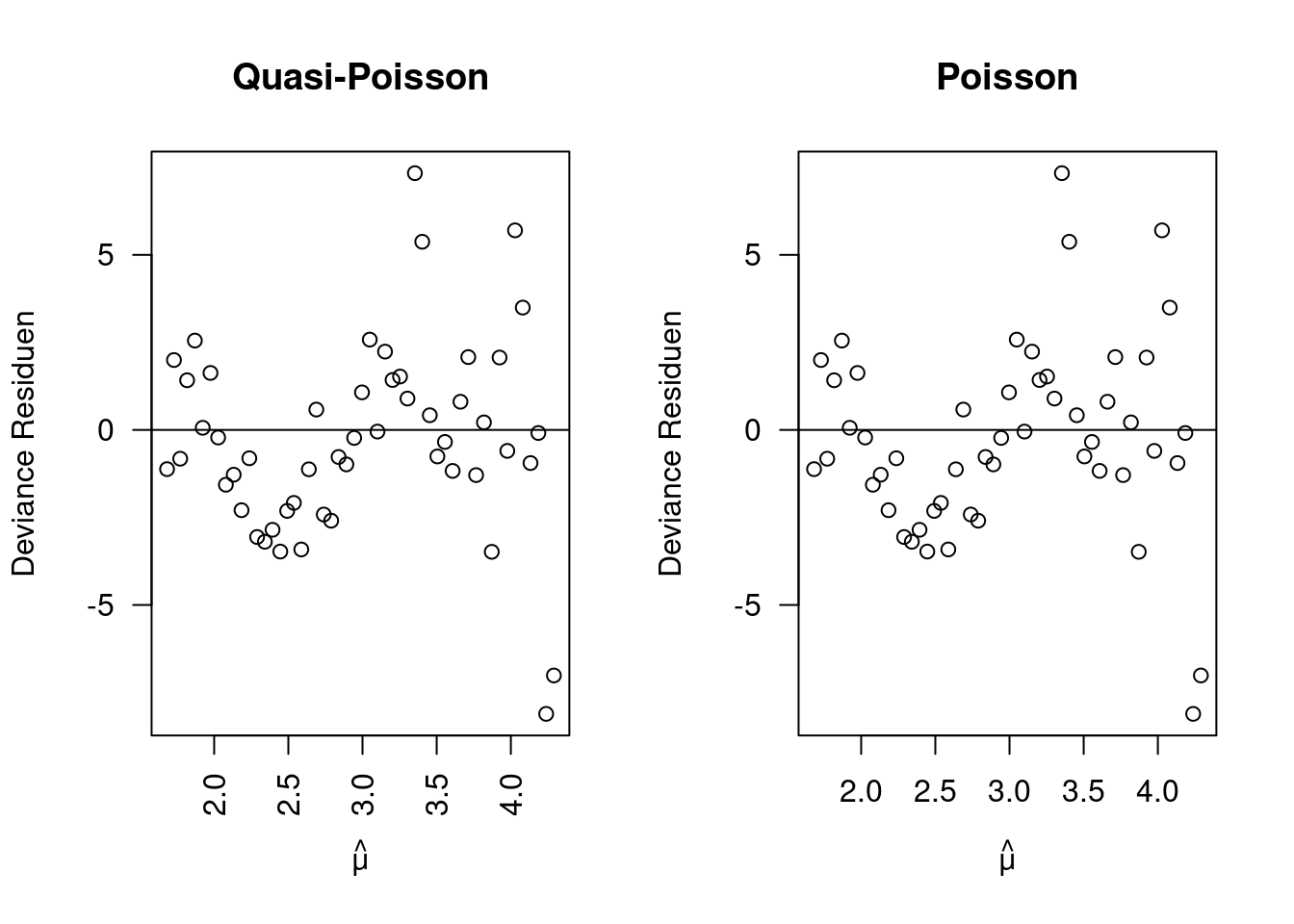

par(op)

summary(lm(resD.qpo ~ resD.po))

## Warning in summary.lm(lm(resD.qpo ~ resD.po)): essentially perfect fit: summary
## may be unreliable

## 
## Call:
## lm(formula = resD.qpo ~ resD.po)
## 
## Residuals:
##        Min         1Q     Median         3Q        Max 
## -3.851e-15 -7.110e-17  1.111e-16  2.061e-16  1.248e-15 
## 
## Coefficients:
##              Estimate Std. Error   t value Pr(>|t|)    
## (Intercept) 6.402e-17  8.612e-17 7.430e-01    0.461    
## resD.po     1.000e+00  3.141e-17 3.184e+16   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 6.176e-16 on 50 degrees of freedom
## Multiple R-squared:      1,  Adjusted R-squared:      1 
## F-statistic: 1.014e+33 on 1 and 50 DF,  p-value: < 2.2e-16

Wie nicht anders zu erwarten stimmen die Residuen exakt überein.

Auch die Pearson Residuen stimmen perfekt überein, bei den studentized Residuen gibt es gewissen Veränderungen, die aber praktisch nicht relevant sind.

20.3.1.1 Modellselektion im Quasipoisson GLM

Unschön ist, dass es keine Likelihood gibt, was gleichbedeutend damit ist, dass wir AIC, AICc, BIC und Konsorten nicht zum Modellvergleich heranziehen können. Uns bleibt nur ein Test bei genesteten Modellen, den wir mittels drop1(model, test=“F”) aufrufen können.

Hierbei wird das größere Modell $M_1$ mit dem darin genesteten Modell $M_2$ anhand foldender Teststatistik verglichen:

\[ \frac{D_2 - D_1} {\phi(p_1 - p_2)} ~ F_{p_1-p_2, n-p_1} \]

Wobei D jeweils die Deviance angibt und p die Anzahl der Paramter im jeweiligem Modell. $\phi$ ist der Overdispersion-Faktor. Der F-Test vergleicht dabei die Reduktion der Deviance zwischen den Modellen. Kleine p-Werte zeigen an, dass das größere Modell besser als das genestete ist.

g.qpo.2 <- update(g.qpo, ~. + URBAN + OLIVE)

drop1(g.qpo.2, test="F")

## Single term deletions
## 
## Model:
## TOT.N ~ D.PARK + URBAN + OLIVE
##        Df Deviance  F value    Pr(>F)    
## <none>      341.24                       
## D.PARK  1  1060.66 101.1945 2.085e-13 ***
## URBAN   1   344.16   0.4107   0.52464    
## OLIVE   1   364.84   3.3196   0.07469 .  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

g.qpo.2 <- update(g.qpo.2, ~. - URBAN)
drop1(g.qpo.2, test="F")

## Single term deletions
## 
## Model:
## TOT.N ~ D.PARK + OLIVE
##        Df Deviance  F value    Pr(>F)    
## <none>      344.16                       
## D.PARK  1  1060.80 102.0303 1.441e-13 ***
## OLIVE   1   390.90   6.6537   0.01295 *  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Der Test zeigt in diesem Beispiel an, dass wir URBAN aus dem Modell entfernen sollten, OLIVE sollten wir dagegen im Modell behalten - falls wir den üblichen magischen p-Wert von 5% verwenden wollen.

20.3.2 Negativ-binomial-verteiltes GLM

Bei der negative Binomialverteilung wächst die Varianz als Polynom zweiten Grades mit dem Mittelwert:

\[ Varianz = \mu + \frac{\mu^2}{k} \]

Der Klumpungsparameter k muss dabei ebenfalls aus den Daten geschätzt werden. Dieses Schätzen erledigt freundlicherweise die Funktion glm.nb in {MASS} für uns.

require(MASS)
g.nb <- glm.nb(TOT.N ~ D.PARK, data = rk, link = "log")
summary(g.nb)

## 
## Call:
## glm.nb(formula = TOT.N ~ D.PARK, data = rk, link = "log", init.theta = 3.681040094)
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept)  4.411e+00  1.548e-01   28.50   <2e-16 ***
## D.PARK      -1.161e-04  1.137e-05  -10.21   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for Negative Binomial(3.681) family taken to be 1)
## 
##     Null deviance: 155.445  on 51  degrees of freedom
## Residual deviance:  54.742  on 50  degrees of freedom
## AIC: 393.09
## 
## Number of Fisher Scoring iterations: 1
## 
## 
##               Theta:  3.681 
##           Std. Err.:  0.891 
## 
##  2 x log-likelihood:  -387.093

Wie wir sehen, haben wir hier eine likelihood und damit den AIC, AICc, BIC im Angebot.

Überprüfen wir nocheinmal die Overdispersion:

sum.nb <- summary(g.nb)
(phi.nb <- sum.nb$deviance/sum.nb$df.residual)

## [1] 1.094839

Nahe 1, sprich das negative binomiale GLM hat das Problem der Overdispersion beseitigt.

Plotten wir nun die Vorhersage inklusive der Konfidenzbänder.

pred.nb <- as.data.frame(predict(g.nb, newDat, se=TRUE ))
plot(TOT.N ~D.PARK, data=rk,  xlab="Distanz zum Park [m]", ylab="Überfahrene Amphibien", las=1)
lines(newDat$D.PARK, exp(pred.nb$fit),  col="tomato", lwd=3)
lines(newDat$D.PARK, exp(pred.nb$fit + 1.96*pred.nb$se),  col="tomato", lwd=3, lty=2)
lines(newDat$D.PARK, exp(pred.nb$fit - 1.96*pred.nb$se),  col="tomato", lwd=3, lty=2)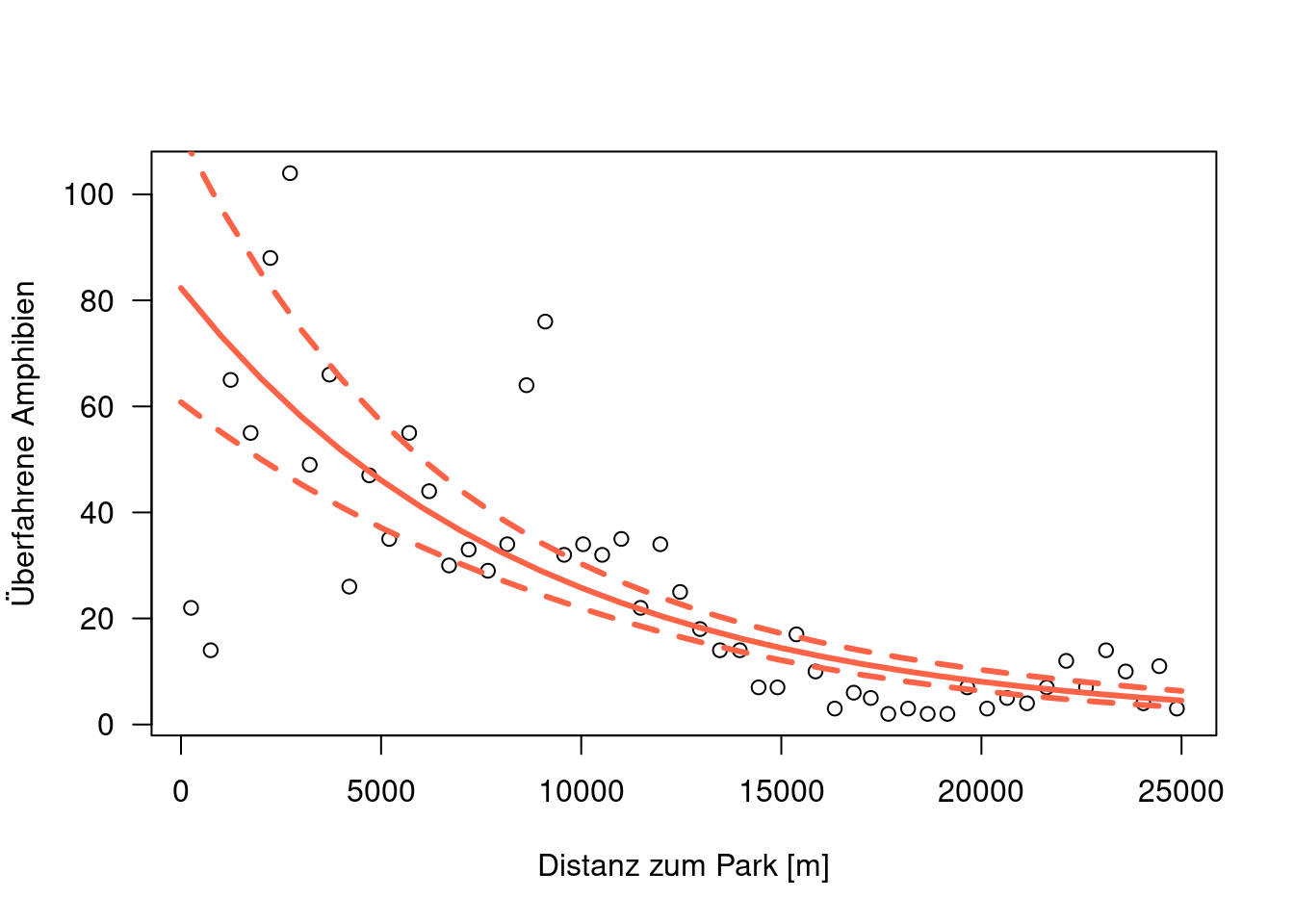

Wie sieht es mit den Residuen aus? Auffällig ist hier (Abbildung 20.4), dass die im Poisson (und auch Quasipoisson) GLM immer noch erkennbare Heteroskadastizität in den Deviance, Pearson und Studentized Residuen nun verschwunden ist. Was bleibt ist die bereits angesprochene zyklische Struktur. In den (unkorrigierten) Response Residuen ist die Heteroskedastizität (erwartungsgemäß) klar zu erkennen - hier durch die gepunkteten Linien angedeutet.

par(mfrow=c(2,2), mar=c(4,4,1,2))
plot(residuals(g.nb, type="deviance") ~ predict(g.nb, type = "link"), xlab=expression(hat(mu)), 
     ylab="Deviance Resideun", pch=16, col="darkgrey", cex=1.4, las=1)
abline(h=0)
plot(residuals(g.nb, type="pearson") ~ predict(g.nb, type = "link"), xlab=expression(hat(mu)), 
     ylab="Pearson Residuen", pch=16, col="darkgrey", cex=1.4, las=1)
abline(h=0)

plot(rstudent(g.nb) ~ predict(g.nb, type = "link"), xlab=expression(hat(mu)), 
     ylab="studentized Residuen", pch=16, col="darkgrey", cex=1.4, las=1)
abline(h=0)

plot(residuals(g.nb, type="response") ~ predict(g.nb, type = "link"), xlab=expression(hat(mu)), 
     ylab="Response Residuen", pch=16, col="darkgrey", cex=1.4, las=1)
abline(h=0)
gResidResp <- lm(abs(residuals(g.nb, type="response")) ~ predict(g.nb, type = "link"))
gResidRespNeg <- lm(-1*abs(residuals(g.nb, type="response")) ~ predict(g.nb, type = "link"))
abline(gResidResp, lty=3, col="navy")
abline(gResidRespNeg, lty=3, col="navy")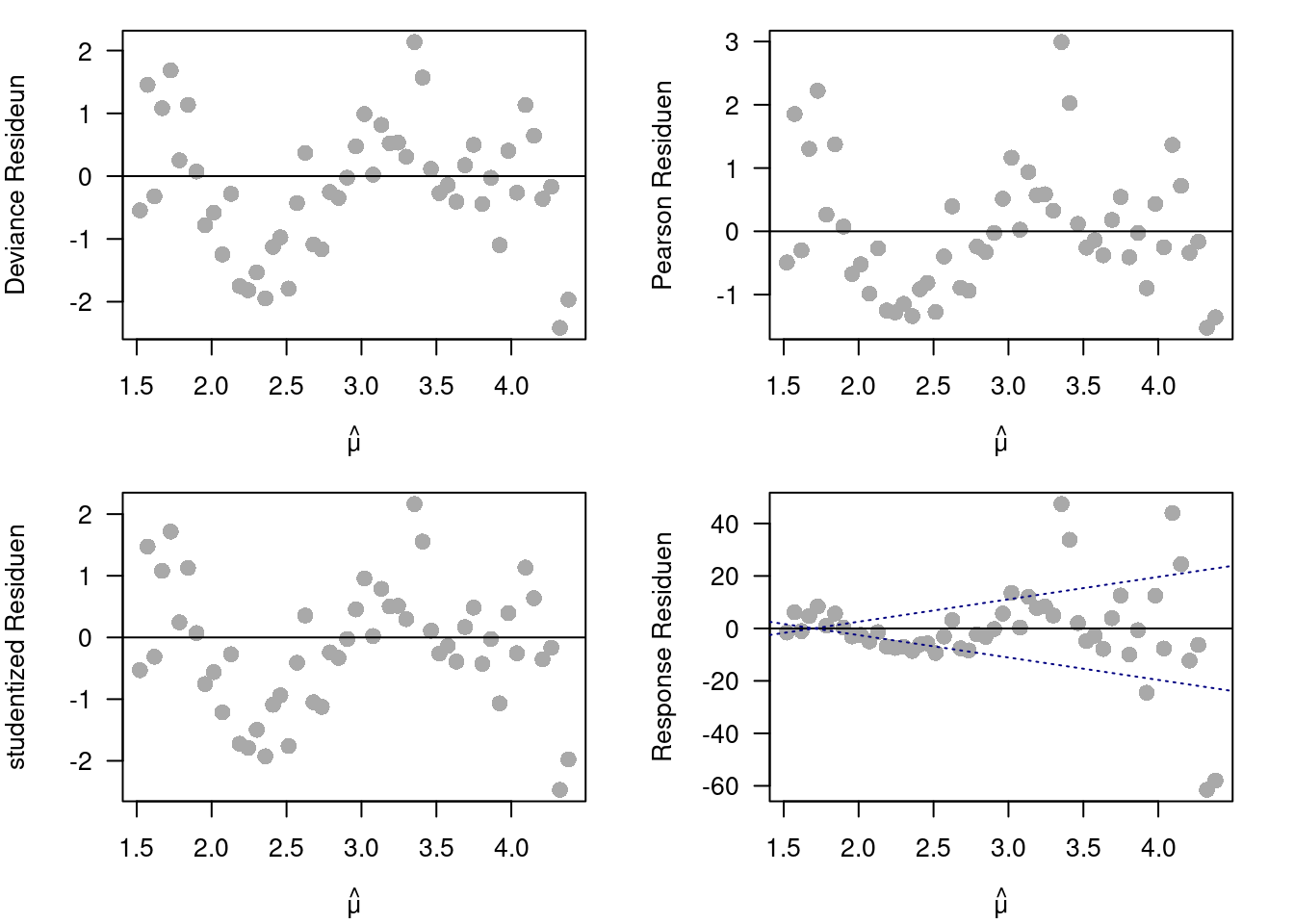

Residuen gegen vorhergesagte Werte Plots für die 4 unterschiedlichen Residuenarten. Für die (ungeeigneten) Response Residuen ist die Heteroskedastizität durch die gepunkteten Linien angedeutet.

Figure 20.4: Residuen gegen vorhergesagte Werte Plots für die 4 unterschiedlichen Residuenarten. Für die (ungeeigneten) Response Residuen ist die Heteroskedastizität durch die gepunkteten Linien angedeutet.

Was ist mit einflußreichen Punkten?

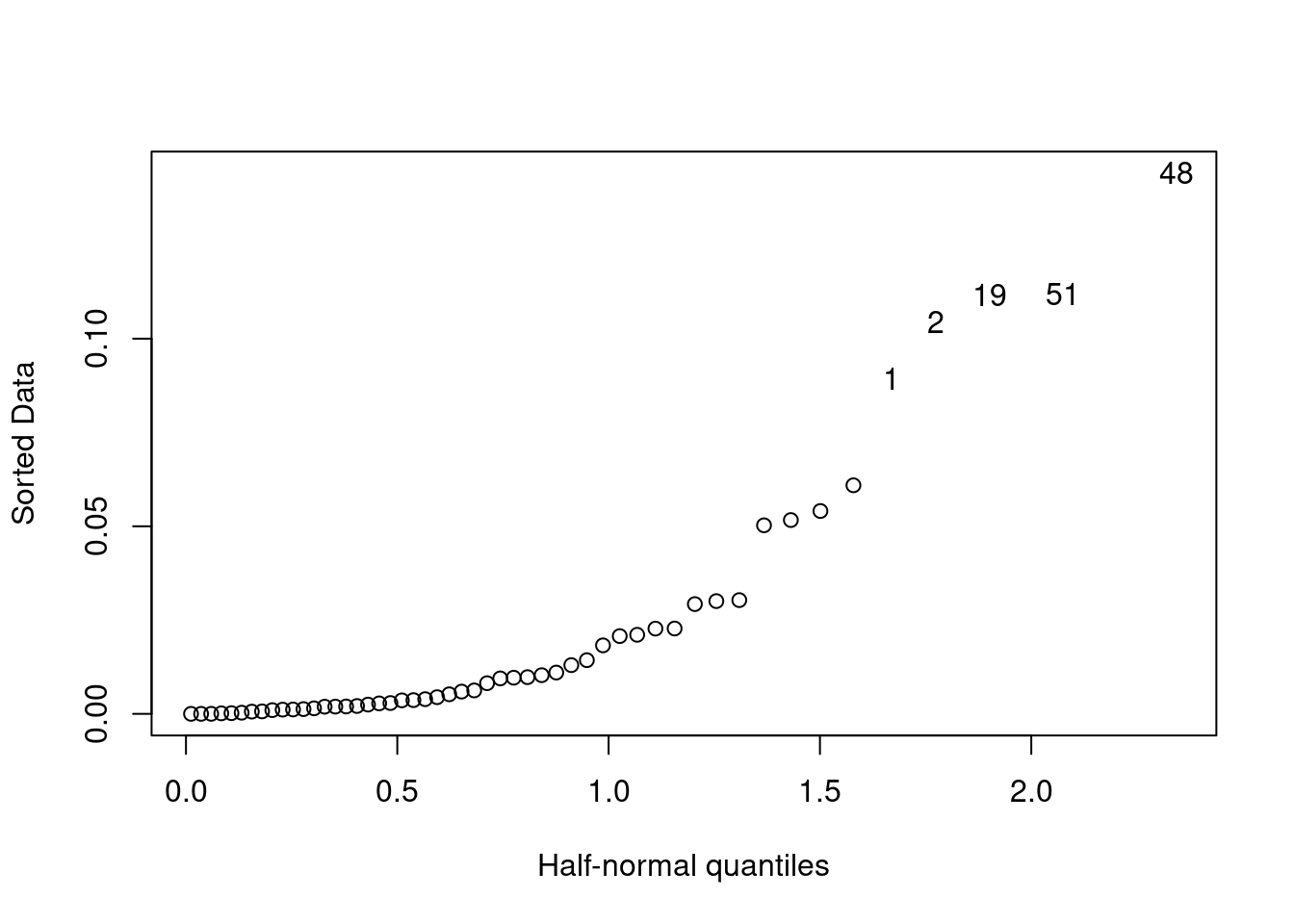
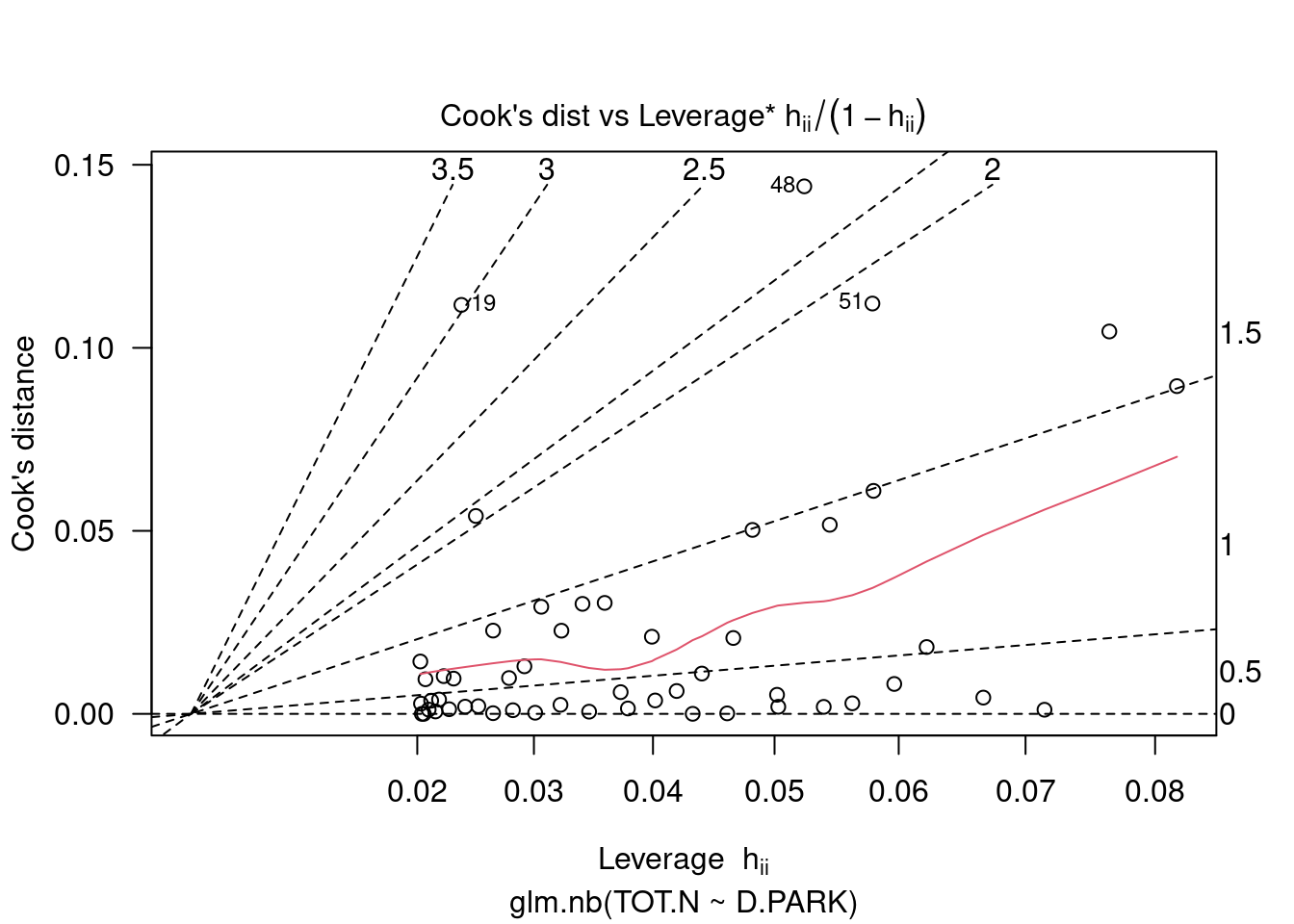
faraway::halfnorm(cooks.distance(g.nb), nlab = 5)

plot(g.nb, which=6, las=1)

Die Punkte 48, 51, 19, 2 und 1 könnten interessant sein (die Zahlen kommen von row.names(rk), wenn nichts anderes angegeben wird:

rk[c(1,2, 19,48, 51),]

##    Sector      X      Y BufoCalamita TOT.N S.RICH OPEN.L  OLIVE MONT.S   MONT
## 1       1 260181 256546            5    22      3 22.684 60.333  0.000  0.653
## 2       2 259914 256124            1    14      4 24.657 40.832  0.000  0.161
## 19     19 258350 247885            8    76      7 39.460  0.462  5.235 45.817
## 48     48 260360 233672            3    14      5 16.478  6.362  1.376 69.984
## 51     51 259768 232345            0    11      4 33.511 20.406  0.000 20.496
##    POLIC SHRUB  URBAN WAT.RES L.WAT.C L.D.ROAD L.P.ROAD D.WAT.RES D.WAT.COUR
## 1  4.811 0.406  7.787   0.043   0.583 3330.189    1.975   252.113    735.000
## 2  2.224 0.735 27.150   0.182   1.419 2587.498    1.761   139.573    134.052
## 19 1.700 0.702  1.003   0.000   2.721 1272.977    2.290   668.000    256.812
## 48 0.000 0.214  0.033   0.000   3.934 2242.183    0.953  1405.000     24.313
## 51 1.861 0.000 17.523   0.000   1.290 4255.414    2.960  1300.000    111.764
##       D.PARK N.PATCH  P.EDGE L.SDI   p.resid
## 1    250.214     122 553.936 1.801 -5.966543
## 2    741.179      96 457.142 1.886 -6.640840
## 19  9101.411      36 383.130 1.939  8.866346
## 48 23113.450      36 304.567 1.750  2.949342
## 51 24444.874      69 482.146 1.838  2.260135

Allerdings sind die Werte hinsichtlich der Cook’s Distance deutlich unterhalb des Schwellwertes von 1 und deswegen nicht wirklich auffällig.

Räumliche Autokorrelation? Die Residuen zeigen klaren Anzeichen für eine räumliche Struktur. Positive und negative Residuen treten gehäuft zusammen auf. Dies könnte allerdings auch der Effekt im Modell fehlender Prädiktoren sein.

rk$nb.resid <-  residuals(g.po,type="pearson")
plot(rk$Y ~ rk$X, col=c("blue", "red")[sign(rk$nb.resid)/2+1.5], 
     pch=19, cex=1+abs(rk$nb.resid)/max(rk$nb.resid)*2, 
     xlab="geographische x-Koordinaten", 
     ylab="geographische y-Koordinaten")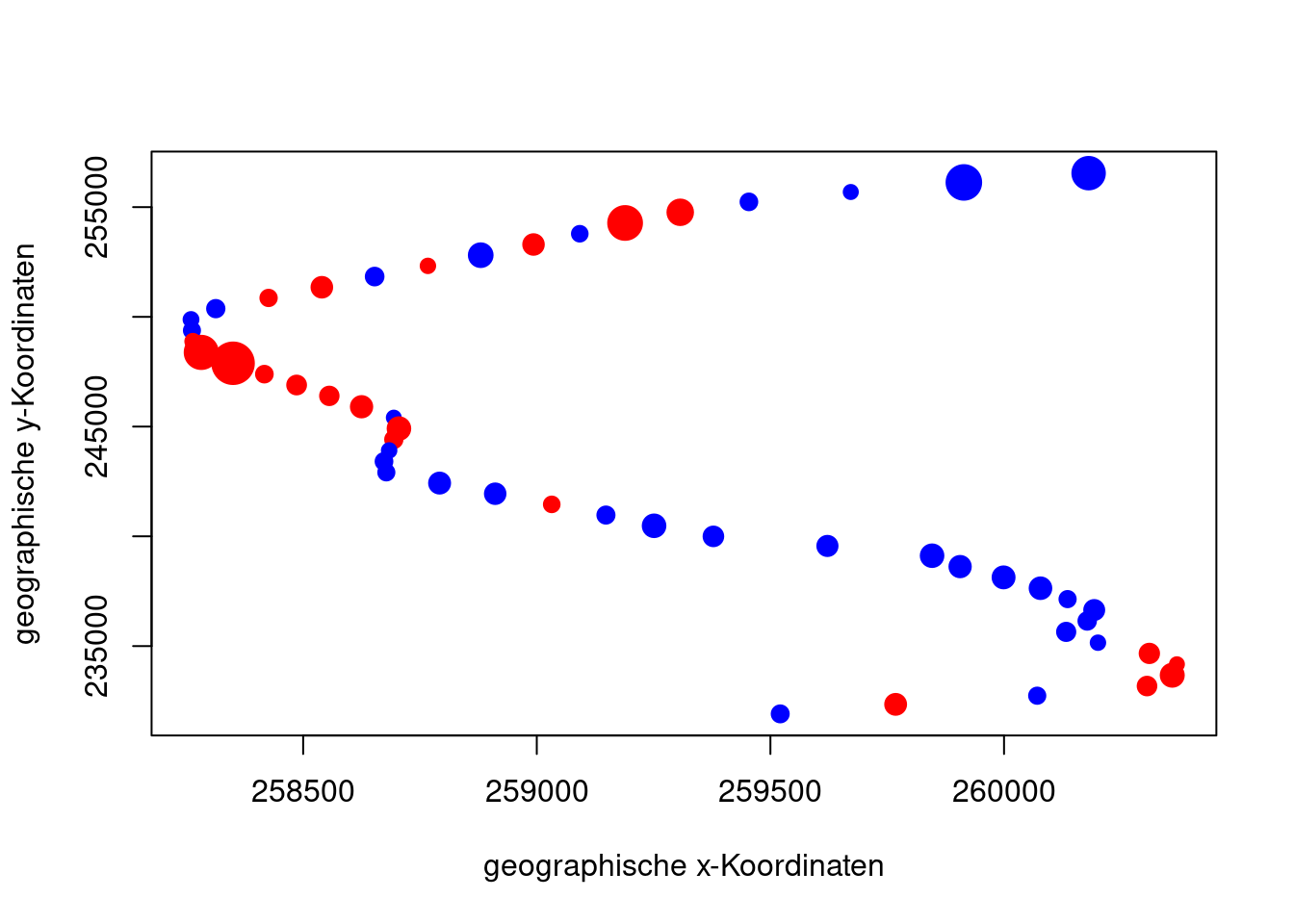

Das Poisson GLM und das negative Binomiale GLM können wir direkt über den AIC oder (wie hier) dem BIC vergleichen:

BIC(g.nb, g.po)

##      df      BIC
## g.nb  3 398.9467
## g.po  2 638.1893

Das negativ Binomiale Modell g.nb ist also deutlich besser als das Poisson Modell g.po.

Beim Vergleich mit dem Quasi-Poisson Modell sind wir schlecht gerüstet, da es keinen geeigneten Vergleich gibt.

Wir können aber zumindestens die vorhergesagten Werte miteinander vergleichen.

plot(TOT.N ~ D.PARK, data=rk)
points(fitted(g.nb) ~ rk$D.PARK, pch=16, col=rgb(1, 165/255,0,.5))
points(fitted(g.qpo) ~ rk$D.PARK, pch=16, col=rgb(160/255,32/255,240/255,.5))
legend(x="topright", legend=c("quasi-poisson", "neg. Binomial"), pch=16, col=c(rgb(160/255,32/255,240/255,.5), rgb(1, 165/255,0,.5)), bty = "n")
abline(h=0)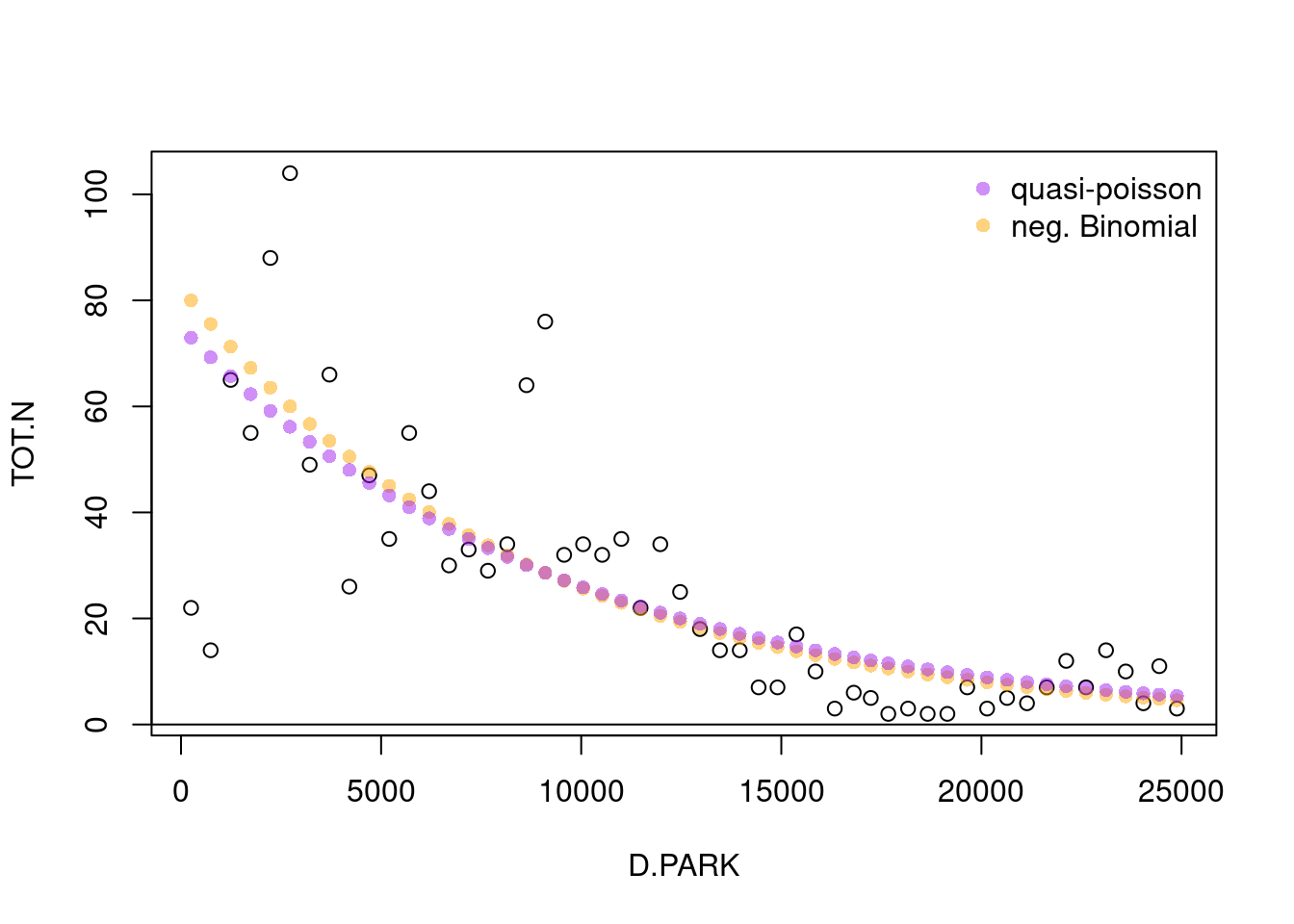

Was ist mit der explained deviance?

1- g.nb$deviance / g.nb$null.deviance

## [1] 0.6478371

1- g.qpo$deviance / g.qpo$null.deviance

## [1] 0.6351681

1- g.po$deviance / g.po$null.deviance

## [1] 0.6351681

Die deviance für das quasipoisson GLM stammt aus dem Poisson Modell (es gibt ja keine Likelihood für die quasifamilen). Generell ist es schwer, zwischen Modell basierend aus den beiden Ansätzen mit overdispersion umzugehen zu unterscheiden.

Was wir tun können, ist die Varianz gegen Mittelwert Plots zu analysieren.

xb <- predict(g.qpo, type="response") # um Klassen zu bilden 
groups <- cut(xb,breaks=quantile(xb,seq(0,100,10)/100)) # die Gruppeneinteilung muss anhand der Anzahl Datenpunkte angepasst werden

# pro Gruppe Mittelwert, Anzahl und Varianz berechnen
mittelwert <- tapply(rk$TOT.N, groups, mean)

varianz <- tapply(rk$TOT.N, groups, var)

count <- tapply(rk$TOT.N, groups, length)

# Plot Gruppenmittelwert gegen Gruppenvarianz  
plot(varianz~mittelwert, 
     xlab="Mittelwert", ylab="Varianz", 
     main="Mittelwert-Varianz Beziehung", 
     pch=21, bg="orange", las=1)

# Nun plotten wir die Verläufe für...
x <- seq(0,80,1)
# Quasipoisson (varianz = mean * phi)
lines(x, x*phi, lty=2)
# negative binimoal (varianz = mean + mean^2/k)
lines(x, x*(1+x/g.nb$theta), lty=3)
# Poisson (mean=varianz)
lines(x,x, lty=4)

legend("topleft", lty=2:4, legend=c("Q. Poisson","Neg. Binom.", "Poisson"), inset=0.05)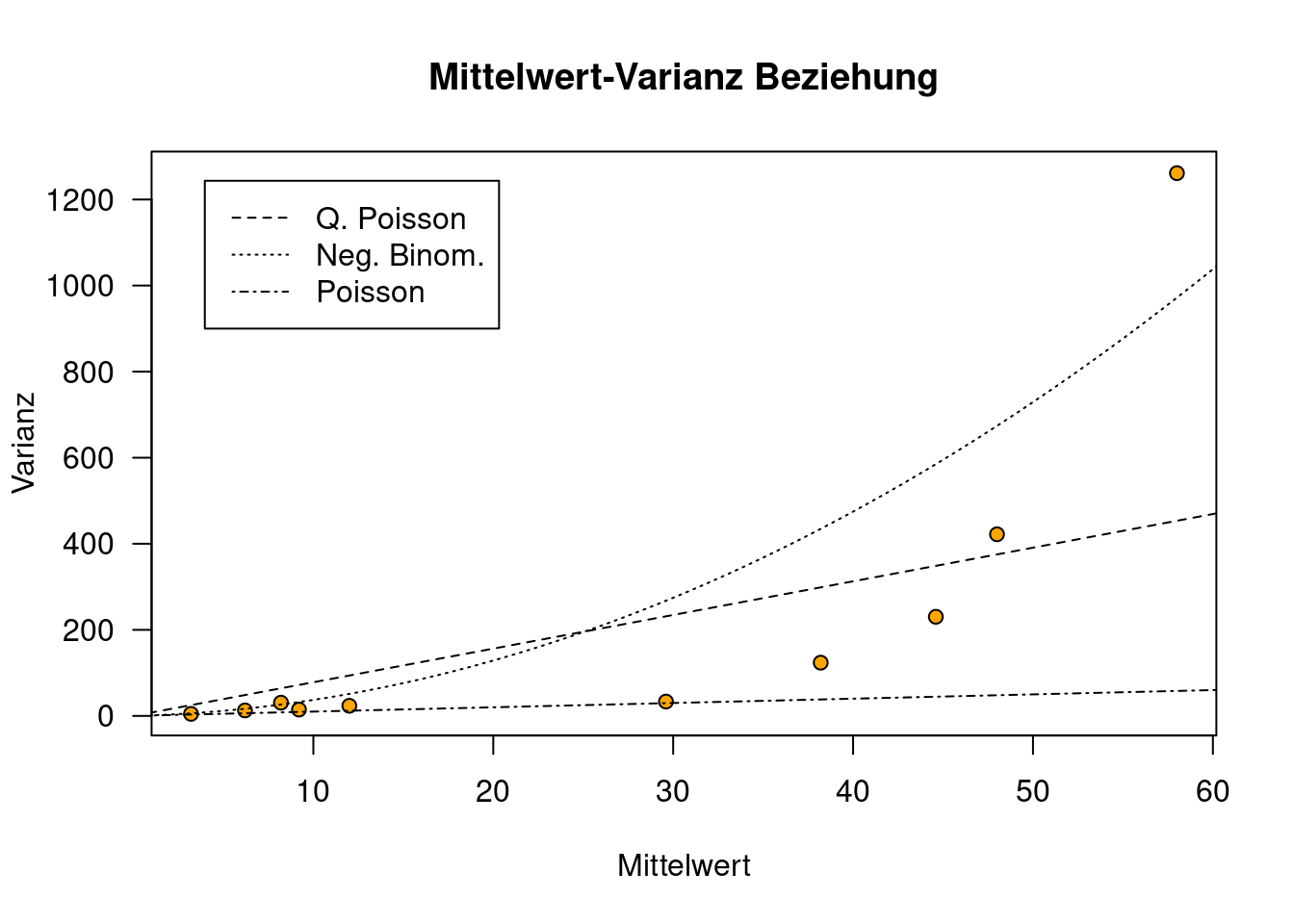

Wie wir sehen, liegen in diesem Fall das negativ-binomial-verteilte GLM besser, da es die Varianz-Mittelwert Beziehung besser modelliert.

Eine andere Option, die Varianz-Mittelwertbeziehung darzustellen, ist rollierende Funktionen für Mittelwert und Varianz zu berechnen. Der Vorteil des Verfahrens ist, dass wir Varianz und Mittelwert stets für eine ausreichnd große Anzahl von Beobachtungen berechnen. Die Anzahl der Punkte, die wir ein die jeweilige Berechnung einbeziehen (rollwidth) wirkt sich allerdings sehr stark auf den Plot aus.

rollwidth <- 30
rollBy <- 2
sortedVal <- sort(rk$TOT.N)
rollVar <- zoo::rollapply(sortedVal, width=rollwidth, FUN=var, by=rollBy)
rollMean <- zoo::rollapply(sortedVal, width=rollwidth, FUN=mean, by=rollBy)

plot(rollVar ~ rollMean, type="p", 
     xlab="Mittelwert", ylab="Varianz", 
     main="Mittelwert-Varianz Beziehung", 
     pch=21, bg="orange", las=1)
# Nun plotten wir die Verläufe für...
x <- seq(0,80,1)
# Quasipoisson (varianz = mean * phi)
lines(x, x*phi, lty=2)
# negative binimoal (varianz = mean + mean^2/k)
lines(x, x*(1+x/g.nb$theta), lty=3)
# Poisson (mean=varianz)
lines(x,x, lty=4)

legend("topleft", lty=2:4, legend=c("Q. Poisson","Neg. Binom.", "Poisson"), inset=0.05)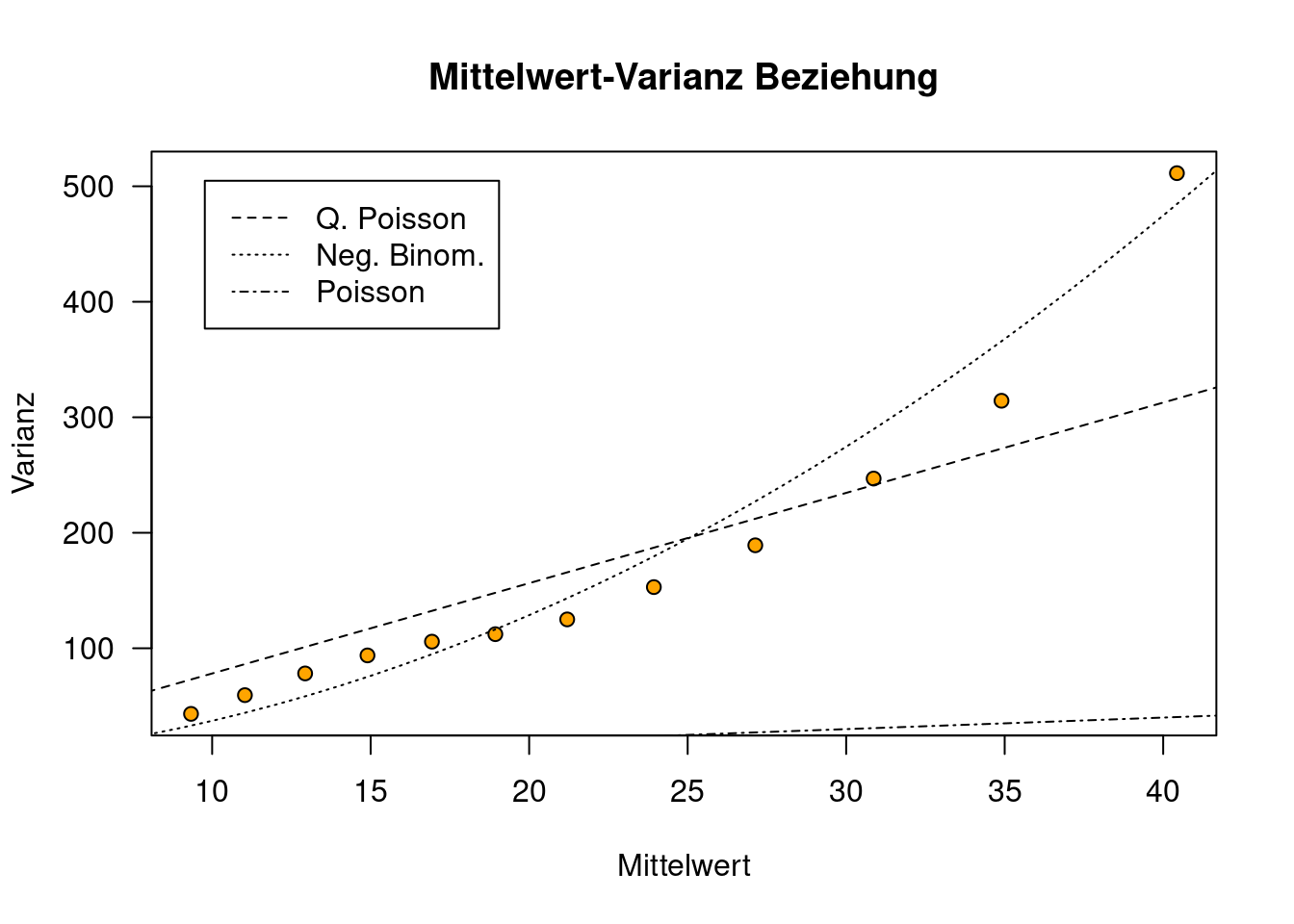

20.4 Aufgabe

Fitten Sie ein Poisson Modell für den gala Datensatz. Müssen Sie dabei von vorne beginnen? Leider ja, die Modellselektion muss erneut durchlaufen werden.
Berechnen Sie die explained deviance und schätzen Sie die Overdispersion ab.
Wenn notwendig verwenden Sie ein negativ binomial verteiltes GLM und ein Quasi-Poisson GLM um die overdispersion zu korrigieren
Erzeugen Sie Vorhersageplots für das Poissonmodell und das neg.bin. GLM und das Quasi-Poisson GLM einschließlich der Konfidenzbänder.
Suchen Sie nach einflussreichen Punkten und Strukturen in den Residuen (nicht die response Residuen verwenden).

20.4.1 Workflow

Fitten Sie das Modell mit glm anstelle von lm, vergessen Sie nicht das family Argument
Führen Sie die Modellselektion mittels AICc oder BIC durch
Schauen Sie sich die Koeffizienten an - denken Sie bei der Interpretation daran, dass die Koeffizienten auf der Link-Skala sind
Berechnen Sie die explained deviance als Maß für die Modellgüte
Berechnen Sie die Dispersion im Modell mittels summary(g)$deviance/summary(g)$df.residual
Ist der Faktor deutlich größer als 1? Falls ja, dann
- Verwenden Sie ein Quasi Poisson Modell (glm, family=quasipoisson) und eine negative binoniaml modell (glm.nb)
- Führen Sie jeweils die Modellselektion durch
- (Entscheiden Sie sich anhand des Mittelwert-Varianz Plots für eines der beiden Modelle)
- Beschreiben Sie das Modellverhalten mittels predict - denken Sie dabei daran, dass Sie auf der Link-Skala vorhersagen müssen und die Konfidenzintervalle anhand des Standardfehlers berechnen müssen. Bevor Sie Fit und Konfidenzbänder plotten, müssen Sie mittels exp auf die Response-Skala rücktransformieren
- Schauen Sie sich die Deviance oder Pearson Residuen an
- Suchen Sie nach einflußreichen Punkten mittels der Cook’s Distance
- (Überprüfen Sie auf Kollineare Prädiktoren mittels vif)

20.5 Ergänzende Literatur

Zur Vertiefung empfohlen:

(O’Hara and Kotze 2010)
(Lindén and Mäntyniemi 2011)
(Ver Hoef and Boveng 2007)

Weiterführende/zitierte Literatur

Lindén, Andreas, and Samu Mäntyniemi. 2011. “Using the Negative Binomial Distribution to Model Overdispersion in Ecological Count Data.” Ecology 92 (7): 1414–21.

O’Hara, R., and J. Kotze. 2010. “Do Not Log-Transform Count Data.” Nature Precedings. https://doi.org/10.1038/npre.2010.4136.1.

Ver Hoef, Jay M, and Peter L Boveng. 2007. “Quasi-Poisson Vs. Negative Binomial Regression: How Should We Model Overdispersed Count Data?” Ecology 88 (11): 2766–72.