Kapitel 8 Verteilungen
Wenn wir annehmen können, dass Zufallsereignisse einer gewissen Verteilung folgen, können wir auf dieser Grundlage die Wahrscheinlichkeit einer bestimmten Realisierung angeben. Wenn wir annehmen, dass der Messfehler eines Temperatursensors normalverteilt um den Mittelwert mit eine Standardabweichung von X °C auftritt, dann können wir angeben, wie wahrscheinlich eine Abweichung um Y °C rein zufällig ist. Ist dies unwahrscheinlich, dann können wir davon ausgehen, dass es irgendeine Art von Ereignis gegeben hat, dass diese Abweichung ausgelöst hat.
Je nachdem, welches Ereignis wir betrachten, kommen andere Verteilungen in Frage, um die Wahrscheinlichkeit für das Auftreten bestimmter Werte zu beschreiben. Aus der Schule sollten manche Verteilungen wie die Binomial- oder die Normalverteilung bekannt sein. Wir werden im folgenden noch eine ganze Reihe weiterer Verteilungen kennenlernen.
Zudem werden die Verteilungen jeweils durch Parameter beschrieben. Diese müssen in den meisten Fällen anhand der Daten geschätzt werden.
Die Summe kontinuierlicher und das Integral kontinuierlicher Verteilungen müssen stets 1 ergeben (Gesetz der totalen Wahrscheinlichkeit).
8.1 Kontinuierliche Verteilungen
8.1.1 Normalverteilung
Bei der Normal- oder Gaussverteilung handelt es sich um eine Verteilung, die symmetrisch um den Mittelwert ist. Die Breite der Verteilung hängt von der Standardabweichung ab.
Die Normalverteilung wird benutzt um sogenanntes weißes Rauschen zu beschreiben, wie es z.B. bei Messfehlern vieler Sensoren angenommen werden kann - zumindestens für einen gewissen Messbereich. Unter der Annahme der Normalverteilung vereinfachen sich viele mathematische Beschreibungen, weswegen sie auch so beliebt ist.
Die Normalverteilung wird durch zwei Parameter beschrieben: den Mittelwert \(\mu\) und die Standardabweichung \(\sigma\) (bzw. der Varianz \(\sigma^2\)).31 Eine Veränderung des Mittelwertes führt zu einer Verschiebung der Kurve entlang der x-Achse (s. Abb. 8.1). Eine Erhöhung der Standardabweichung führt zu einer breiteren Verteilung, d.h. stärkere Abweichungen werden wahrscheinlicher. Umgekehrt führt eine Verringerung der Standardabweichung dazu, dass mehr Wahrscheinlichkeitsmasse um den Mittelwert zentriert wird und stärkere Abweichungen unwahrscheinlicher werden.
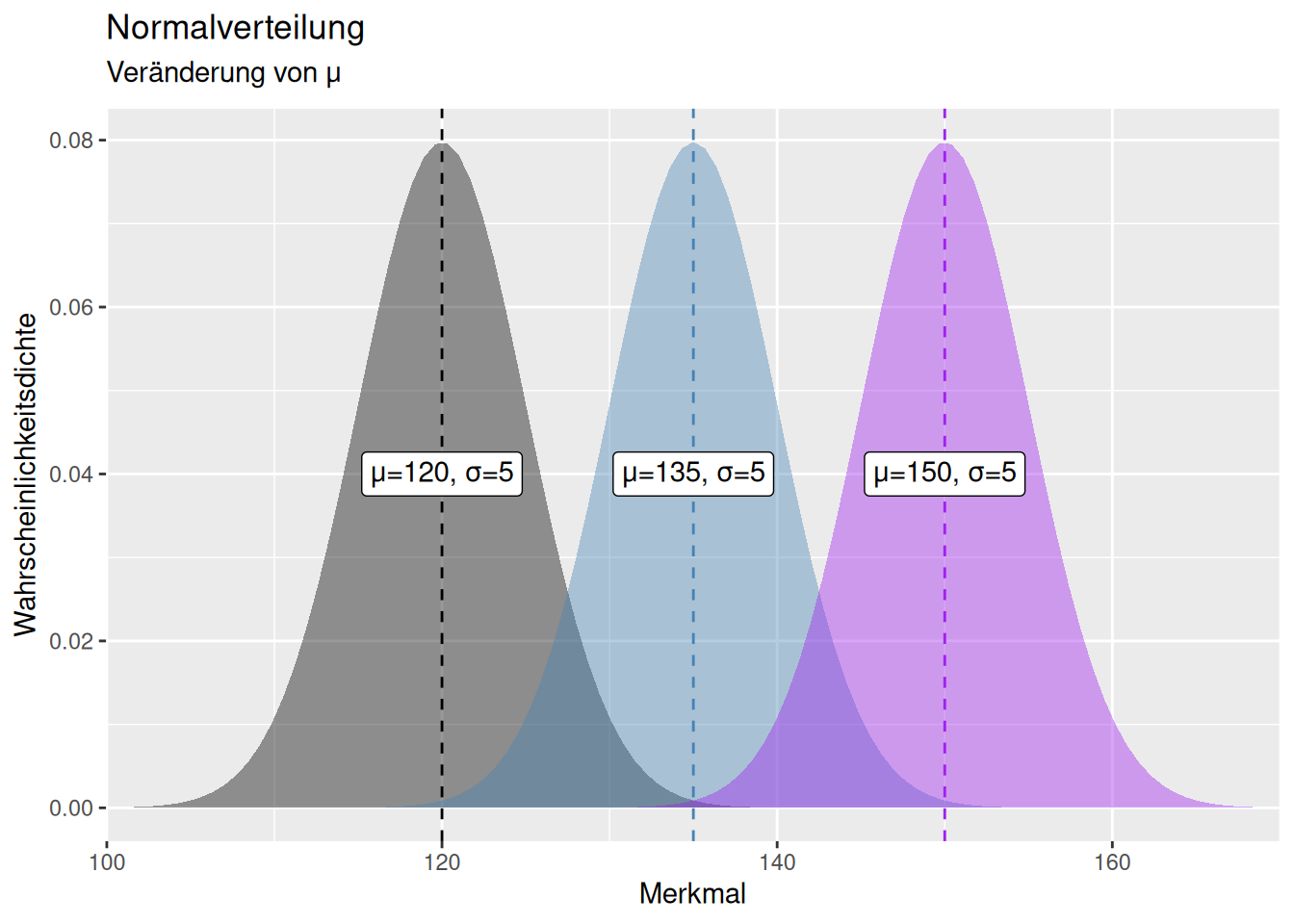
Figure 8.1: Effekt einer Veränderung des Parameters \(\mu\) auf die Form und Lage der Normalverteilung. Während sich die Lage der Normalverteilung mit \(\mu\) verändert, bleibt die Form der Normalverteilung (insbesondere die Streuung um den Mittelwert) identisch.
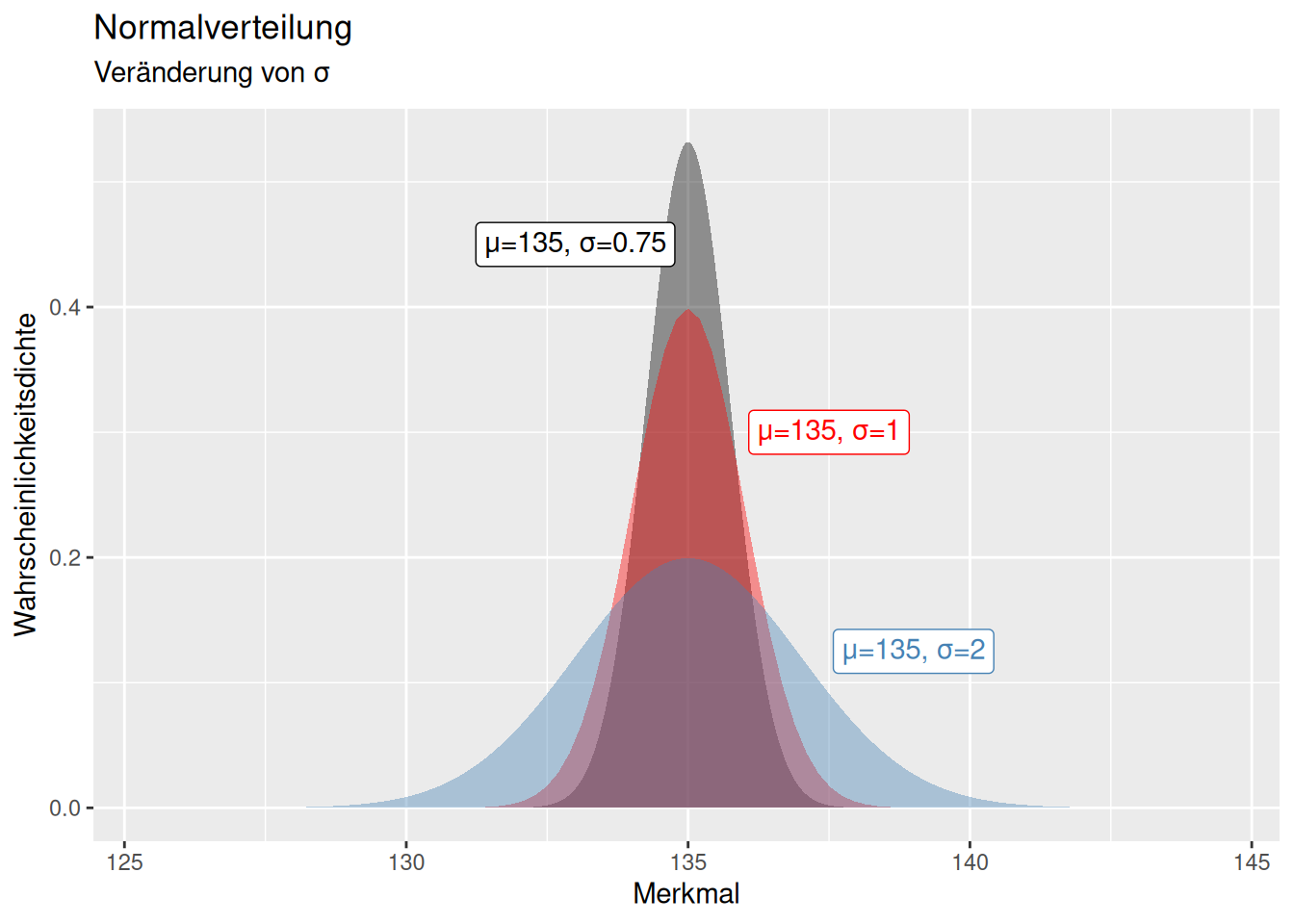
Figure 8.2: Effekt einer Veränderung des Parameters \(\sigma\) auf die Form und Lage der Normalverteilung. Während sich die Lage der Normalverteilung mit \(\sigma\) nicht ändert, verändert sich die Breite der Normalverteilung (Streuung um den Mittelwert) mit dem Parameter \(\sigma\). Je höher \(\sigma\)$, desto breiter die Streuung um \(\mu\).
Wichtig ist, dass die Normalverteilung nicht begrenzt ist. Auch wenn die Wahrscheinlichkeit mit zunehmender Distanz zum Mittelwert zunehmend stark abnimmt, geht ihr Wertebereich von \(-\infty\) bis \(\infty\). Wenn der Mittelwert recht nahe bei Null liegt, kann das dazu führen, dass unsinnige Werte eine gewisse Wahrscheinlichkeit haben und auftreten. So sollten z.B. Konzentrationen, Artenzahlen, Artabundanzen, Inzidenzen,… stets größer Null sein.
Ein Anwendungsfall, für den die Normalverteilung gut geeignet ist, um eine Verteilung zu beschreiben ist die Meßungenauigkeit aufgrund einer Unschärfe des Sensors, z.B. eines Temperatursensors. Wir gehen davon aus, dass die Temperatur im Mittel richtig gemessen wird, es aber zufällige Ungenauigkeiten der Messung gibt. Wenn wir davon ausgehen können, dass die Messungenauigkeit nicht von der gemessenen Temperatur abhängt, können wir Messungen wie in Abb. 8.3 modellieren: wir gehen vom einem normalverteilten Fehler aus, welcher jeweils den wahren Temperaturwert als \(\mu\) hat und eine über den gesamten Wertebereich konstante Streuung um \(\sigma\). In der Realität müssen wir natürlich davon ausgehen, dass der Sensor nur innerhalb eines bestimmten Wertebereiches genau mißt und das der Fehler außerhalb dieses Bereiches deutlich größer wird. Ein handelsübliches Thermometer wird Temperaturen von 1000°C oder -200°C nicht sehr genau erfassen können. Außerdem ist die Temperaturskala natürlich durch den absoluten Nullpunkt von 0°K beschränkt. Unser Modell gilt also nur für einen Ausschnitt der Realität. Werden die Annahmen verletzt sollten wir ein anderes Modell verwenden.
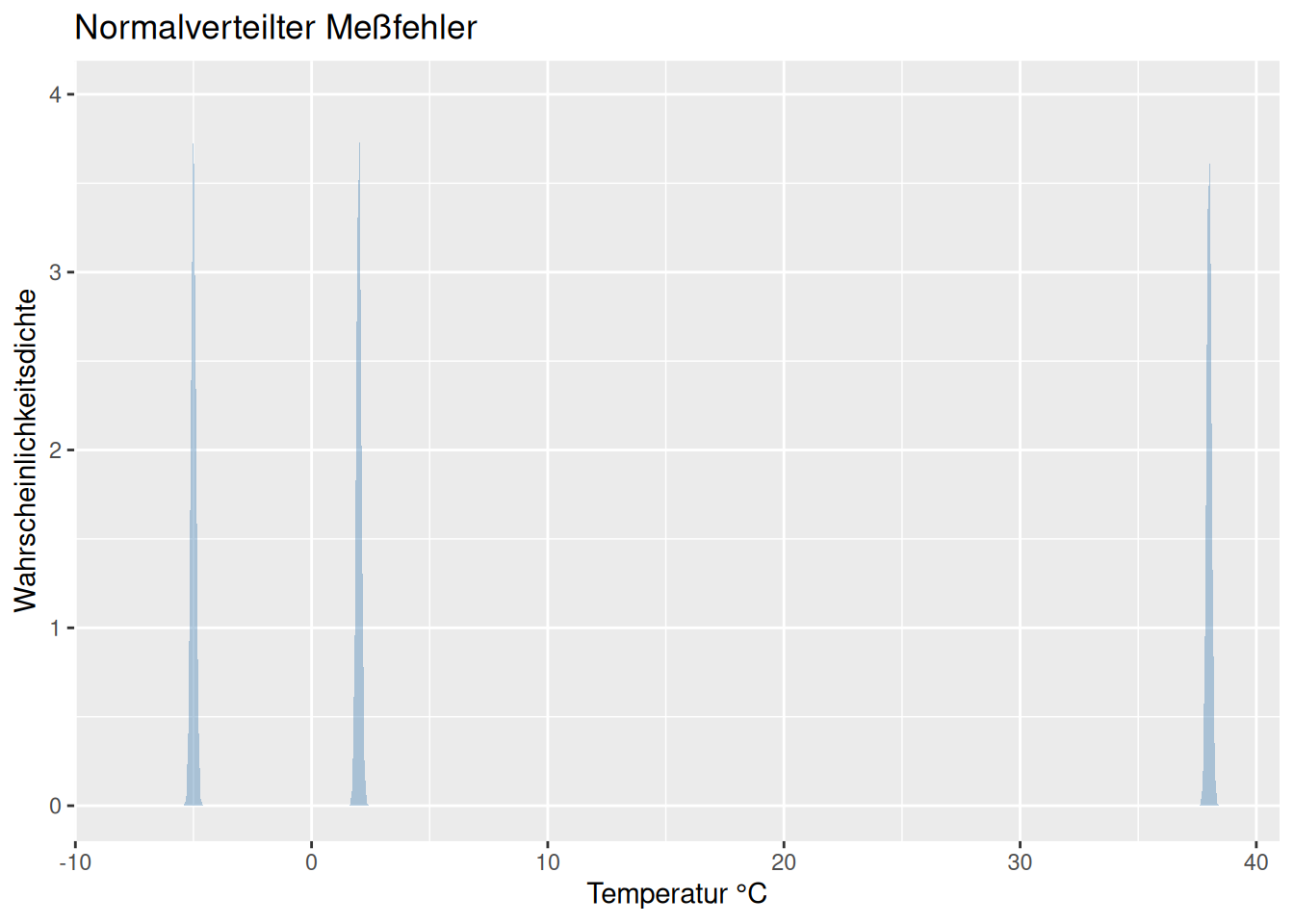
Figure 8.3: Anwendungsbeispiel normalverteilter Meßfehler bei Temperaturmessung. Wir gehen davon aus, dass der Meßfehler über den dargestellten Wertebereich konstant ist. Da der Meßfehler klein ist, sind die Gaussverteilungen sehr schmal (was zu Darstellungproblemen führt).
Verteilungsfunktion :
\[ N(x) = P(X=x|\mu, \sigma) = \frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x-\mu)^2}{2 \sigma^2}} \]
Wenn man vom ersten Term absieht, der einfach zur Normierung des Integrals auf 1 dient, dann haben wir es mit einer symmetrischen Funktion zu tun, die mit zunehmender Distanz zum Mittelwert \(\mu\) quadratisch abnimmt.32 Der Abfall ist schwächer, je größer die Varianz \(\sigma^2\) ist.
Der Mittelwert und die Varianz der Normalverteilung sind (nicht wirklich überraschend) \(\mu\) und \(\sigma^2\). Die Schiefe beträgt 0 und die Wölbung 3.
Trägt man die kumulative Häufigkeitsverteilung auf, kann man ablesen, wieviel Wahrscheinlichkeitsmasse in einem bestimmten Wertebereich liegt. In Abb. 8.4 ist dies für drei Parametrisierungen der Normalverteilung dargestellt. Der Erwartungswert wurde hier jeweils als 0 gewählt. Beim Merkmalswert 0 sind bei den drei Beispielen jeweils 50% der kumulierten Wahrscheinlichkeitsmasse erreicht, d.h. im Intervall \([-infty, 0]\) befinden sich 50% der Wahrscheinlichkeitsmasse. Anders ausgedrückt: die Wahrscheinlichkeit, dass ein zufällig von der Verteilung gezogener Wert \(\le 0\) ist beträgt 50% (\(P(x \le 0)= 50%\)).
Für andere Merksmalswerte unterscheiden sich die kumulierten Wahrscheinlichkeitsmassen der drei Parametrisierungen: während die kumulierte Wahrscheinlichkeit für den Merkmalswert -1 für \(N(\mu=0, \sigma=0.5)\) 2.28% beträgt, sind es für \(N(\mu=0, \sigma=1)\) 15.87% und für \(N(\mu=0, \sigma=2)\) 30.85%.
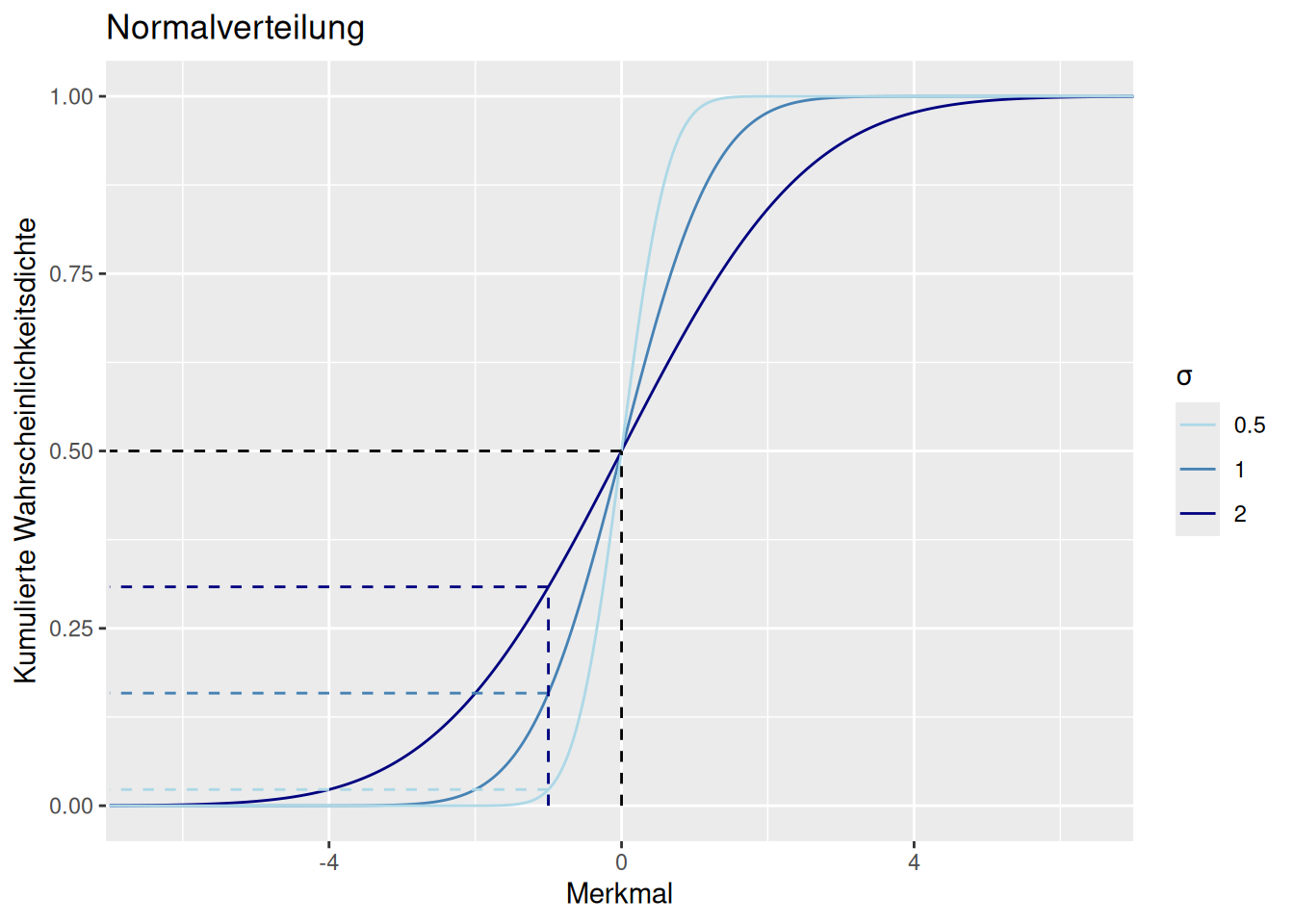
Figure 8.4: Kumulierte Wahrscheinlichkeitsdichtefunktion für die Normalverteilung bei unterschiedlichen Werten für \(\sigma\). Je geringer \(\sigma\), desto steiler die s-förmige Kurve. \(\mu\) wurde für alle drei Verteilungen als 0 gewählt. Die gestrichelten Linien geben jeweils an, wieviel Wahrscheinlichkeitsmasse der Verteilung sich von \(-\infty\) bis zum Merkmalswert befindet.
Verschiebt man die Normalverteilung, in dem man den Erwartungswert \(\mu\) verändert um einen Wert \(\Delta x\), so verändert sich der Merkmalswert, an dem (für gewählten Parameter \(\sigma\)) ein kumulierter Wahrscheinlichkeitswert liegt ebenfalls um \(\Delta x\).
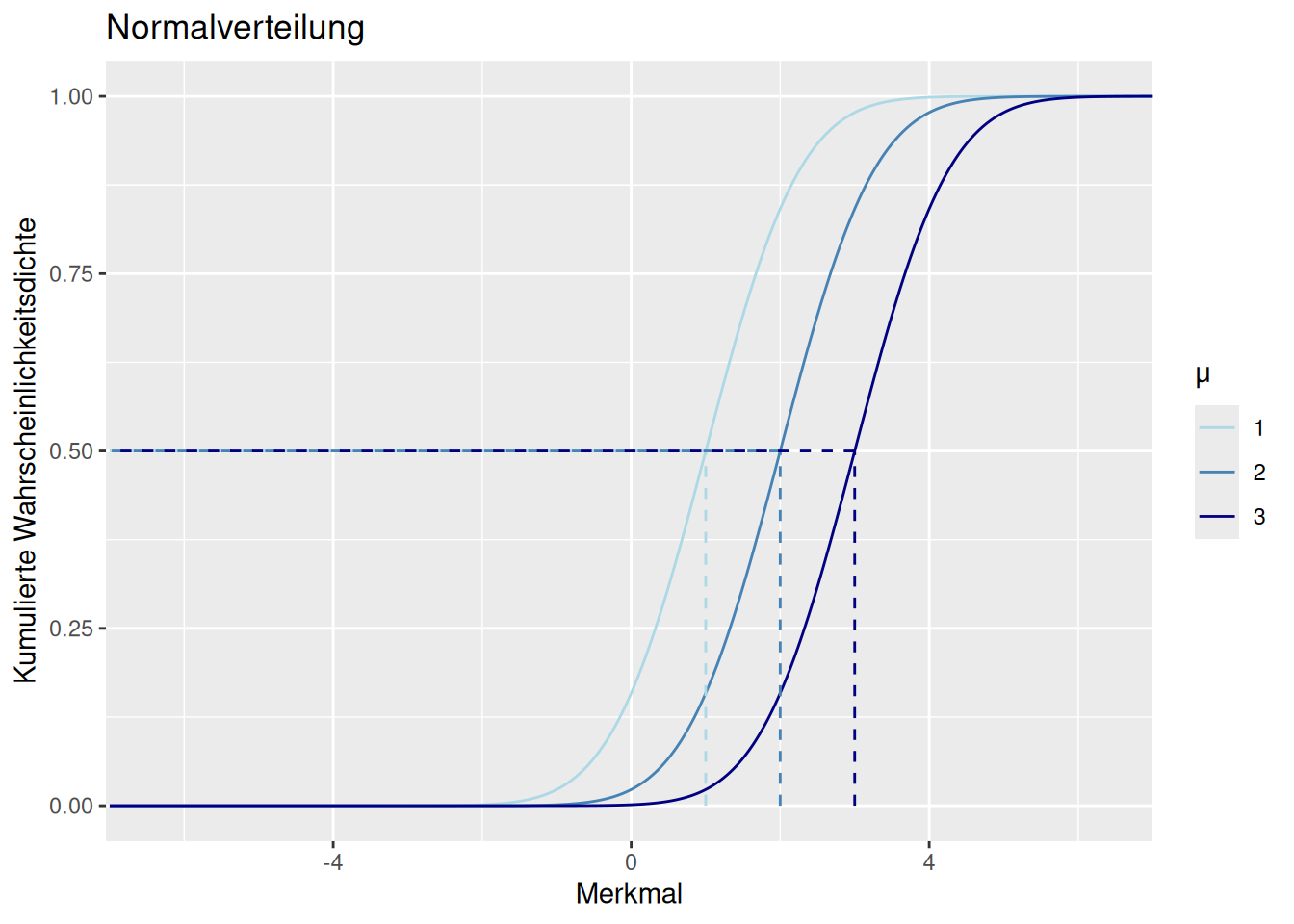
Figure 8.5: Kumulierte Wahrscheinlichkeitsdichtefunktion für die Normalverteilung bei unterschiedlichen Werten für \(\mu\) und konstantem \(\sigma\). Die gestrichelten Linien geben jeweils an, wieviel Wahrscheinlichkeitsmasse der Verteilung sich von \(-\infty\) bis zum Merkmalswert befindet. Für den Merkmalswert \(x=\mu\) erhält man stets die kumulierte Wahrscheinlichkeit von 50%.
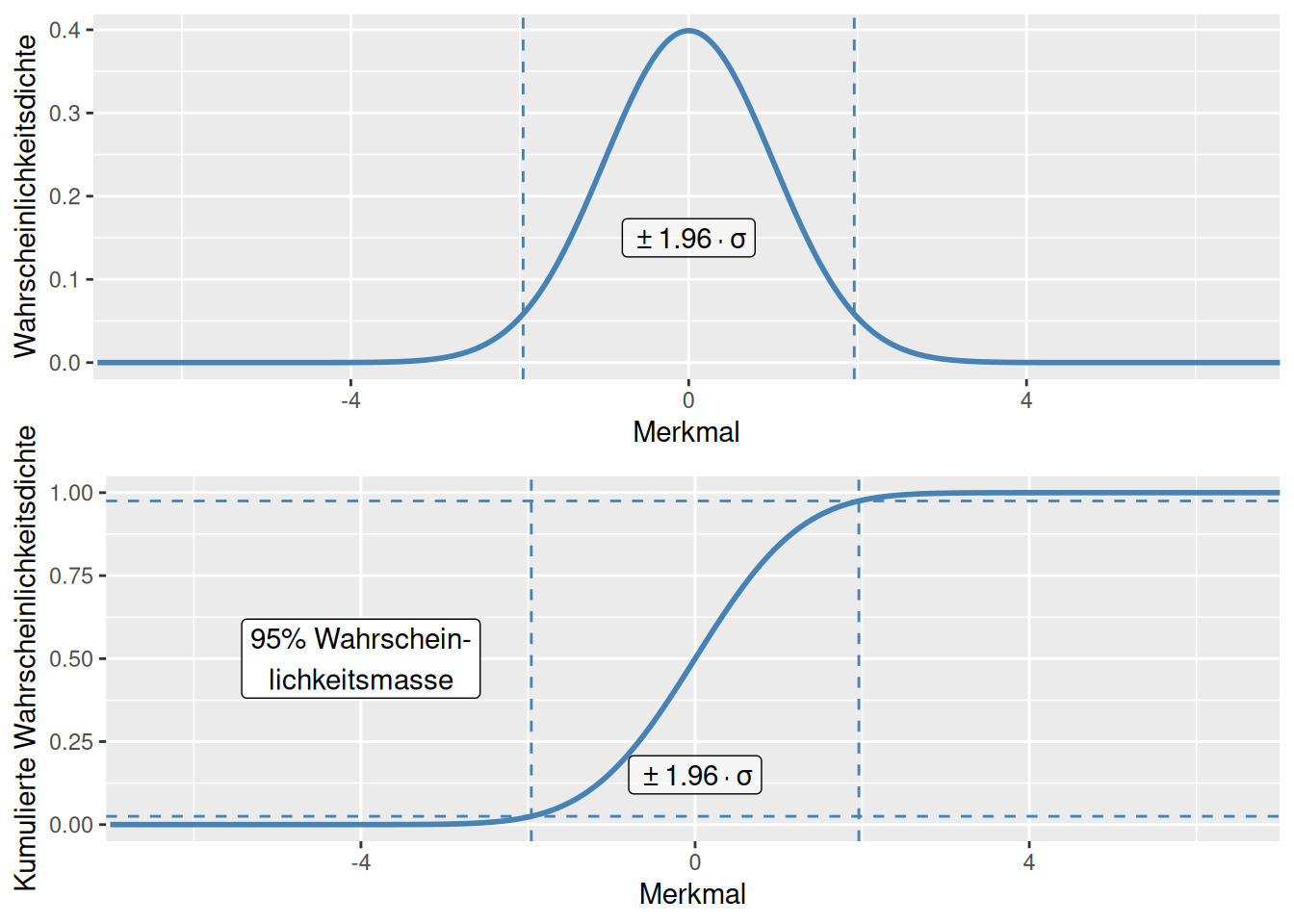
Figure 8.6: Kumulierte Wahrscheinlichkeitsdichtefunktion und Wahrscheinlichkeitsdichtefunktion für die Normalverteilung. Die gestrichelten Linien geben auf der y-Achse den Bereich an, in dem 95% der Wahrscheinlichkeitsmasse liegen. Auf der x-Achse geben die gestrichelten Linien den Bereich an, der um 1,96 Standardabweichungen um den Erwartungswert 0 liegt.
Man kann näherungsweise angeben, wieviel Prozent der Werte sich innerhalb eines wieviel-fachen der Standardabweichung befinden: - Im Intervall der Abweichung $ $ vom Erwartungswert sind 68,27 % aller Messwerte zu finden, - Im Intervall der Abweichung $ $ vom Erwartungswert sind 95,45 % aller Messwerte zu finden, - Im Intervall der Abweichung $ $ vom Erwartungswert sind 99,73 % aller Messwerte zu finden.
Und ebenso lassen sich umgekehrt für gegebene Wahrscheinlichkeiten die maximalen Abweichungen vom Erwartungswert finden (s. Abb. 8.6:
- 50 % aller Messwerte haben eine Abweichung von höchstens \(0,675 \sigma\) vom Erwartungswert,
- 90 % aller Messwerte haben eine Abweichung von höchstens \(1,645 \sigma\) vom Erwartungswert,
- 95 % aller Messwerte haben eine Abweichung von höchstens \(1,960 \sigma\) vom Erwartungswert,
- 99 % aller Messwerte haben eine Abweichung von höchstens \(2,576 \sigma\) vom Erwartungswert.
Man kann diese kritischen Werte in Tabellenwerken nachschlagen oder einfacher mir R berechnen. Für jede Verteilung in R gibt es vier Funktionen:
- qverteilungsname um Quantile zu einer Wahrscheinlichkeit anzugeben
- pverteilungsname um die Wahrscheinlichkeit anzugeben, diesen Wert oder einen kleineren zu erhalten (p-Wert, kumulierte Wahrscheinlichkeitsdichte)
- dverteilungsname um die Wahrscheinlichkeitsdichte für einen Wert zu berechnen
- rverteilungsname um eine Zufallsstichprobe zu ziehen
Möchte man wissen, für welchen Wert 97,5 % der gesamten Wahrscheinlichkeitsmasse bei einer Standardnormalverteilung (\(\mu = 0\), \(\sigma = 1\)) links davon liegen, kann man die Quantilfunktion verwenden
## [1] 1.959964Möchte man wissen, wie wahrscheinlich es ist, bei einer Standardnormalverteilung eine Beobachtung von kleiner gleich -1 zu machen, kann man dies über die Wahrscheinlichkeitsfunktion herausfinden.
## [1] 0.1586553Die Wahrscheinlichkeitsdichte für einen bestimmten Wert erhält man mittels dnorm. Man erhält die Wahrscheinlichkeitsdichte an der Stelle x+dx, d.h. für den angegebenen Wert und ein bischen mehr. An der Stelle x selbst muss die Wahrscheinlichkeitsdichte 0 sein, da man bei kontinuierlichen Verteilungen unendlich viele Werte hat und die Summe einer unendlichen Zahl von Werten größer Null unendlich ergibt, während das Integral doch auf 1 beschränkt ist.
## [1] 0.3989423Zehn Zufallszahlen von einer Standardnormalverteilung erhält man mittels rnorm(10):
## [1] 0.1983903 -2.0396511 -1.7596117 -0.8016100 -0.4650483 -0.6323969
## [7] 0.4972991 -0.5398677 0.2388589 0.10562528.1.1.1 Standardnormalverteilung
Als Standardnormalverteilung bezeichnet man eine Normalverteilung mit \(\mu = 0\) und \(\sigma^2 = 1\). Jede normalverteilte Zufallsvariable X mit \(X ~ N(\mu, \sigma^2)\) lässt sich durch folgende Transformation in eine Standardnormalverteilung überführen. Dies wird als z-score bezeichnet.
\[ z = \frac{X - \mu} {\sigma}\]
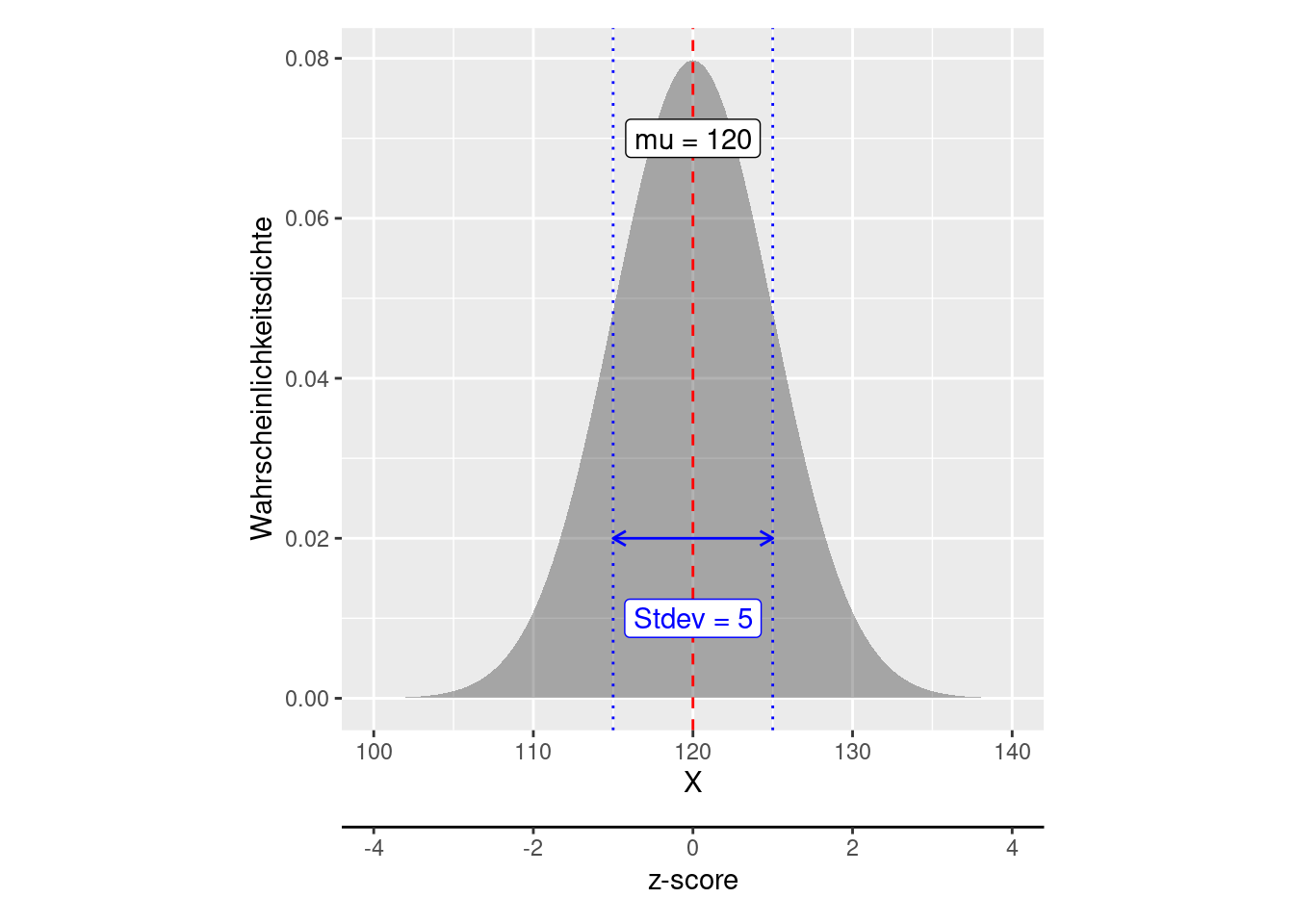
Figure 8.7: Jede Normalverteilung kann durch entsprechende Standardisierung (z-score) in eine Standradnormalvertilung überführt werden. Im Beispiel wird eine Normalverteilung mit Mittelwert 120 und Standardabweichung 5 dargestllt. Über die z-score Transformation kann diese in eine Standradnormalverteilung überführt werden. Die zweite Achse (z-score) zeigt die x-Koordinaten für die Standardnormalverteilung. Die y-Achse bleibt dabei vollkommen unverändert.
Damit lassen sich Aussagen für die Standardnormalverteilung auf z-transformierte Normalverteilungen übertragen.
8.1.2 Halbnormalverteilung
Bei der Halbnormalverteilung handelt es sich um eine um 0 gefaltete Normalverteilung mit Mittelwert 0 (Abbildung 8.8). Wenn \(X\) durch eine Normalverteilung \(N(0, \sigma^2)\) beschrieben wird, dann folgt \(Y=|X|\) einer Normalverteilung.
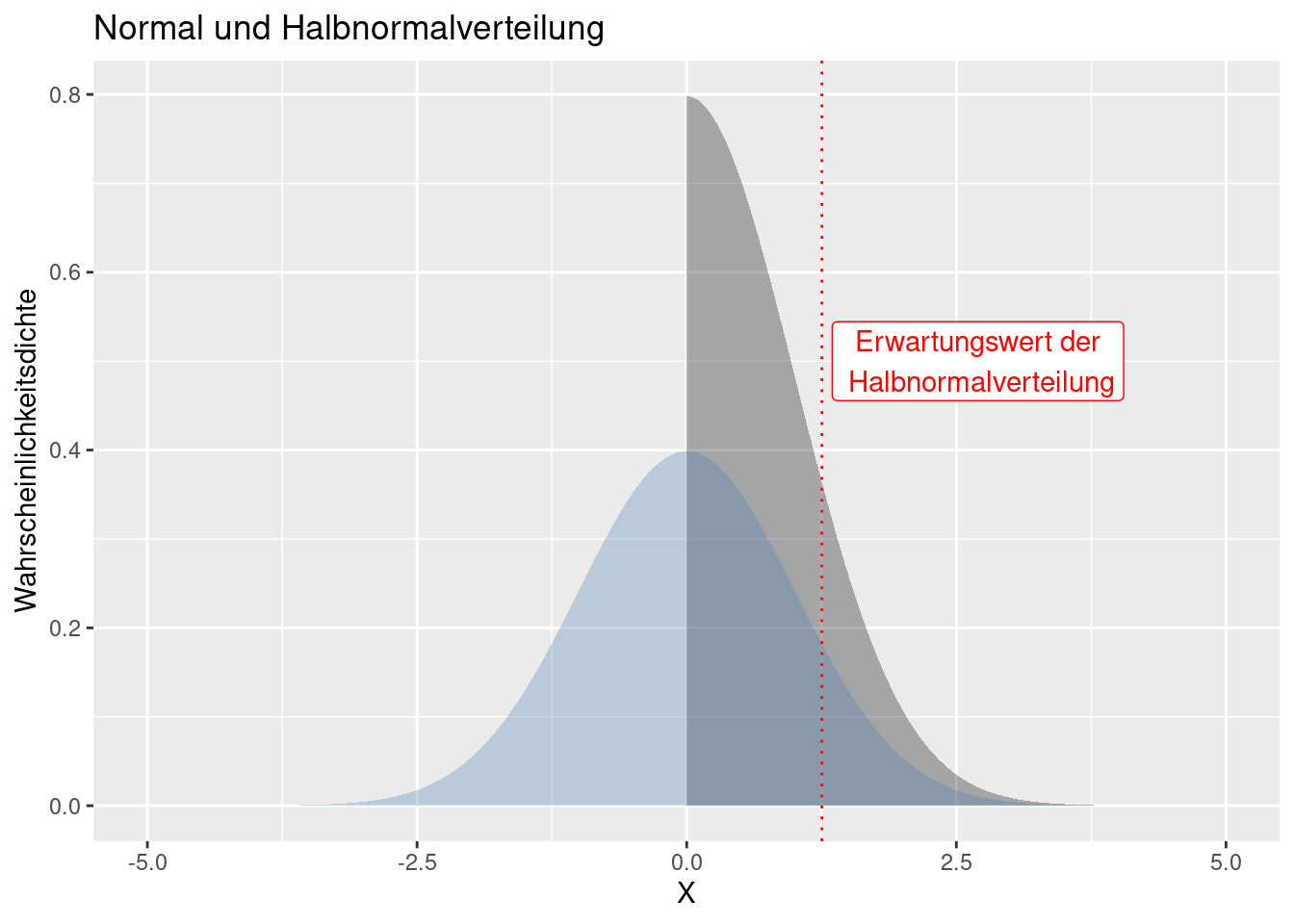
Figure 8.8: Die Halbnormalverteilung (in grau) ist eine um 0 gefaltete Normalverteilung mit Mittelwert 0 (in blau dargestellt).
Verteilungsfunktion :
\[ N(x) = P(X=x|\mu, \sigma) = \frac{\sqrt{2}}{\sqrt{\pi \sigma^2}} e^{- \frac{x^2}{2 \sigma^2}}\]
für \(y \geq 0\).
Eine alternative Parametrisierungsform - wie sie z.B. im package fdrtoolverwendet wird, in dem dhalfnormetc. definiert sind - verwendet anstelle von \(\sigma\) die Präzison (precision), dass Inverse der Varianz ($):
\[\theta=\frac{\sqrt{\pi}}{\sigma \sqrt{2}}\]
\[ N(x) = P(X=x|\mu, \sigma) = \frac{\theta}{\pi} e^{- \frac{x^2\theta^2}{\pi}}\]
Erwartungswert:
\[E[X] = \frac{\sigma\sqrt{2}}{\sqrt{\pi}} \]
bzw.:
\[E[X]= \frac{1}{\theta}\]
Die Verteilung wird z.B. bei Diagnoseplots eingesetzt um anhand der Leverage oder Cook’s Distance Werte Beobachtungen mit großer Bedeutung für die Lage der Regressionsgeraden aufzuspüren. Hierfür kommt z.B. die Funktion faraway::halfnorm zum Einsatz.
8.1.3 Testverteilungen
Die nachfolgend bechriebenen studentsche t-, die \(\chi^2\)- und die F-Verteilung werden benutzt um Aussagen über Stichproben zu treffen. Hierbei hängt die Unsicherheit von der Stichprobengröße ab. Entsprechend werden die Verteilungen anhand der Freiheitsgrade beschrieben, die ja abhängig von der Stichprobengröße sind. - bei der F-Verteilung vergleicht man 2 Stichproben, entsprechend gibt es 2 Parameter für die Verteilung
8.1.4 Studentsche t-Verteilung
Im Gegensatz zu einer Normalverteilung, die eine Grundgesamtheit beschriebt, beschreibt die studentsche t-Verteilung (auch t-Verteilung genannt) eine Stichprobe. Wird der Mittelwert einer Stichprobe, bei unbekannter Varianz, geschätzt, so ist der Schätzer nicht normal- sondern t-verteilt. Bei steigendem Stichprobenumfang geht die t-Verteilung allerdings schnell in eine Normalverteilung über.
Verwendet wird die studentsche t-Verteilung vor allem bei der Durchführung von statistischen Tests, so um die Differenz zwischen zwei Mittelwerten zu beurteilen, bei der Konstruktion von Konfidenzintervallen oder beim Testen von Regressionskoeffizienten (\(\hat{\beta} = 0\)) im linearen Modell. Die t-Verteilung erlaubt weiterhin – insbesondere für kleine Stichprobenumfänge – die Berechnung der Verteilung der Differenz vom Mittelwert der Stichprobe zum wahren Mittelwert der Grundgesamtheit.
Die Verteilung geht auf William Sealy Gosset zurück. Gosset arbeitete in der Dubliner Guinness-Brauerei. Diese gestattete die Veröffentlichung nicht, weswegen Gosset sie unter dem Pseudonym Student veröffentlichte.
Die t-Verteilung wird durch einen einzigen Parameter beschrieben, die Freiheitsgrade (degree of freedon), der dem Stichprobenumfang entspricht.
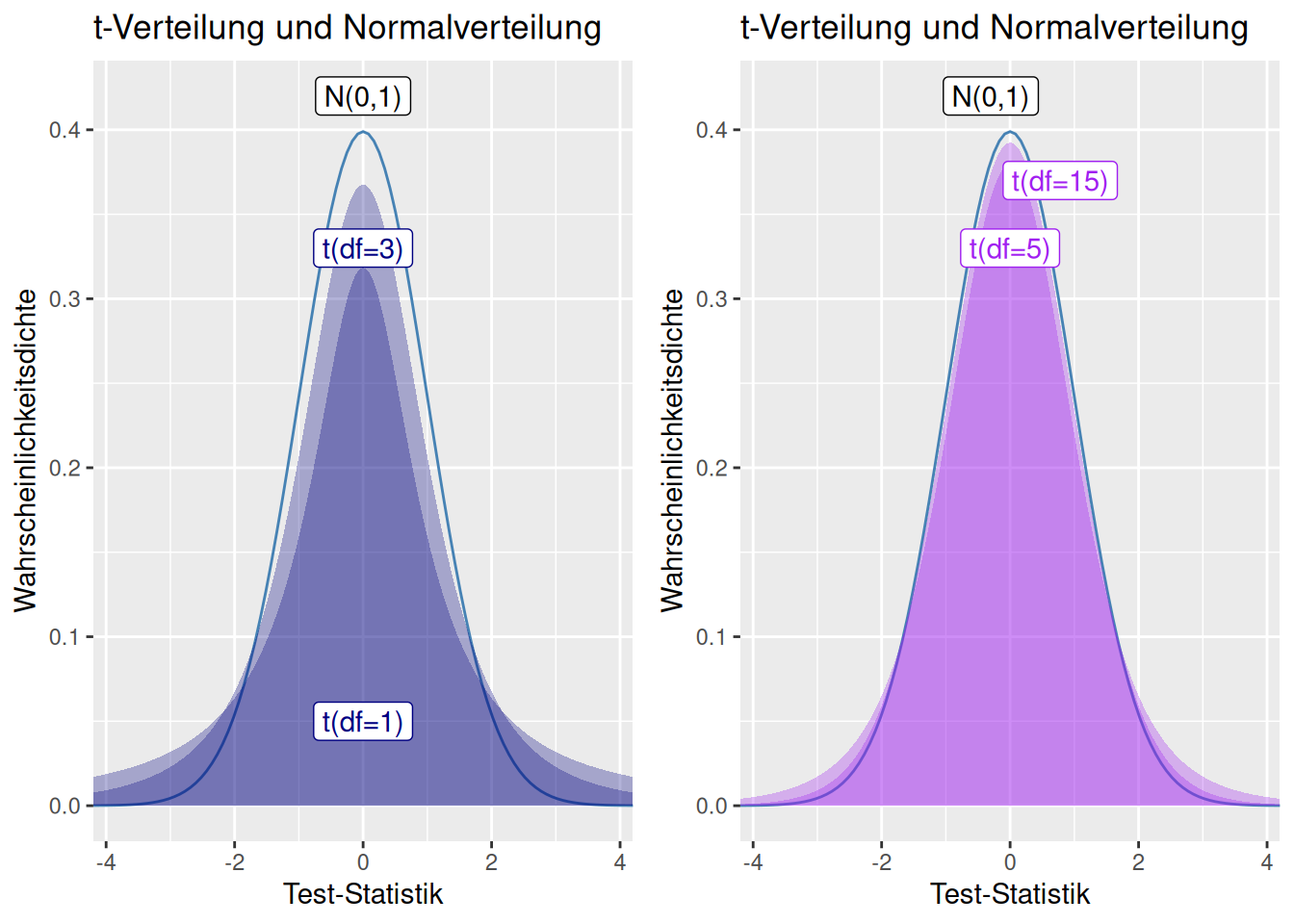
Figure 8.9: Einfluss des Parameters df auf die Form der t-Verteilung. Man sieht das sich mit wachsender Anzahl Freiheitsgrade die t-Verteilung der Standardnormalverteilung annähert.
Wie in Abbildung 8.9 deutlich zu erkennen ist, hat die t-Verteilung im Vergleich zur Standardnormalverteilung - insbesondere für geringe Freiheitsgrade - deutlich mehr Wahrscheinlichkeitsmasse in den Rändern der Verteilung (heavy tails), d.h. extreme Abweichungen vom Mittelwert sind wahrscheinlicher:
- 95% der Werte der Standardnormalverteilung liegen zwischen \(\pm 1.96\)
- bei der t-Verteilung mit 2 Freiheitsgraden liegen 95% der Werte innerhalb von \(\pm 4.30\)
- bei der t-Verteilung mit 4 Freiheitsgraden liegen 95% der Werte innerhalb von \(\pm 2.78\)
- bei der t-Verteilung mit 8 Freiheitsgraden liegen 95% der Werte innerhalb von \(\pm 2.31\)
- bei der t-Verteilung mit 16 Freiheitsgraden liegen 95% der Werte innerhalb von \(\pm 2.12\).
Dies können wir wieder mit den Verteilungsfunktionen in R nachrechnen:
- 95% der Werte der Standardnormalverteilung liegen im Intervall:
## [1] -1.959964 1.959964- 95% der Werte der t-Verteilung mit 2 Freiheitsgraden liegen im Intervall von:
## [1] -4.302653 4.302653- 95% der Werte der t-Verteilung mit 4 Freiheitsgraden liegen im Intervall von:
## [1] -2.776445 2.776445- 95% der Werte der t-Verteilung mit 8 Freiheitsgraden liegen im Intervall von:
## [1] -2.306004 2.306004- 95% der Werte der t-Verteilung mit 16 Freiheitsgraden liegen im Intervall von:
## [1] -2.119905 2.119905- 95% der Werte der t-Verteilung mit 100 Freiheitsgraden liegen im Intervall von:
## [1] -1.983972 1.983972- 95% der Werte der t-Verteilung mit 1000 Freiheitsgraden liegen im Intervall von:
## [1] -1.962339 1.962339Dies lässt sich auch beim Vergleich der kumulierten Wahrscheinlichkeitsdichtefunktionen sehen (Abb. 8.10): die Absolutwerte der Teststatistik, innerhalb derer 95% der Wahrscheinlichkeitsmasse liegen sind bei der t-Verteilung mit einem und fünf Freiheitsgraden deutlich größer.
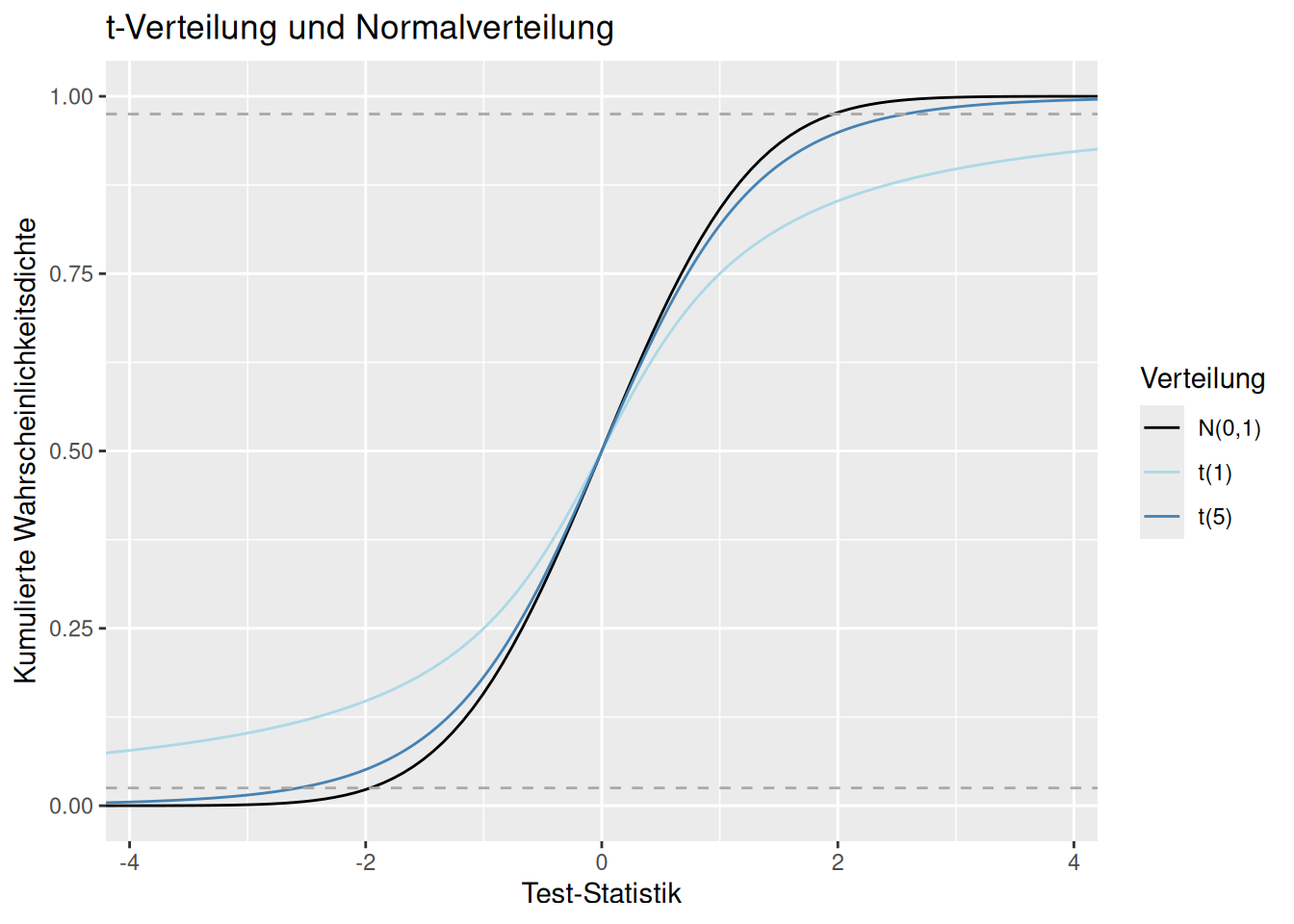
Figure 8.10: Kumulierte Wahrscheinlichkeitsmasse für verschiedene Freiheitsgrade der t-Verteilung und der Standardnormalverteilung. Die gestrichelten Linien geben den Bereich an, in dem 95% der Wahrscheinlichkeitsmasse um das Zentrum der Verteilung liegen.
Momente der Verteilung:
- Für n > 1 ist der Erwartungswert = 0 (für n=1 ist E[X] nicht definiert.)
- Für n > 2 gilt \(Var(X) = \frac{n}{n-2}\) (mit steigender Stichprobengröße \(n\) konvergiert die Varianz der t-Verteilung gegen die Varianz der Standradnormalverteilung (\(\sigma^2 = 1\)))
- Für n> 3 ist die Schiefe = 0 (d.h. symmetrisch um den Erwartungswert 0)
- Für n> 4 ist die Wölbung = \(\frac{3n -6}{n-4}\) (d.h. die Neigung Extremwerte zu erzeugen, nimmt mit steigender Stichprobengröße \(n\) ab und konvergiert gegen die Wölbung der Normalverteilung von 3).
8.1.5 Chi-Quadrat Verteilung
Die \(\chi^2\)-Verteilung lässt sich aus der Normalverteilung ableiten: Hat man \(n\) Zufallsvariablen \(Z_i\), die unabhängig und standardnormalverteilt sind, so ist die Chi-Quadrat-Verteilung mit \(n\) Freiheitsgraden definiert als die Verteilung der Summe der quadrierten Zufallsvariablen \(Z_1^2 + \dotsb + Z_n^2\). Solche Summen quadrierter Zufallsvariablen treten u.a. bei der Schätzung der Varianz einer Stichprobe auf. Die \(\chi^2\)-Verteilung ermöglicht dadurch eine Beurteilung der Güte eines vermuteten funktionalen Zusammenhangs mit Messergebnissen (\(\chi^2\)-Anpassungstest).
Die \(\chi^2\) Verteilung wird insbesondere in folgenden Tests verwendet:
- Verteilungstest (auch Anpassungstest): sind vorliegende Daten auf eine bestimmte Weise verteilt ?
- Unabhängigkeitstest: sind zwei Merkmale stochastisch unabhängig?
- Homogenitätstest: entstammen zwei oder mehr Stichproben derselben Verteilung bzw. einer homogenen Grundgesamtheit?
Als Summe quadrierter Zufallsvariablen kann die \(\chi^2\)-Verteilung nur positive Werte annehmen. Wenn \(n > 1\), kann die Verteilung auch 0 annehmen.
Der Erwartungswert der \(\chi^2\)-Verteilung entspricht der Anzahl der Freiheitsgrade (der Anzahl der Zufallsvariablen):
\[ E(\chi_n^2) = n \] Die Varianz entspricht zweimal der Anzahl der Freiheitsgrade:
\[ Var(\chi_n^2) = 2n \] Die \(\chi^2\)-Verteilung ist rechtsschief. Je höher die Anzahl der Freiheitsgrade, desto geringer die Schiefe.
\[ \gamma(\chi_n^2) = \frac{2\sqrt{2}}{\sqrt{n}} \]
Die Wölbung der Verteilung ähnelt mit zunehmender Anzahl der Freiheitsgrade der Normalverteilung:
\[ Kurtosis(\chi_n^2) = 3 + \frac{12}{n} \]
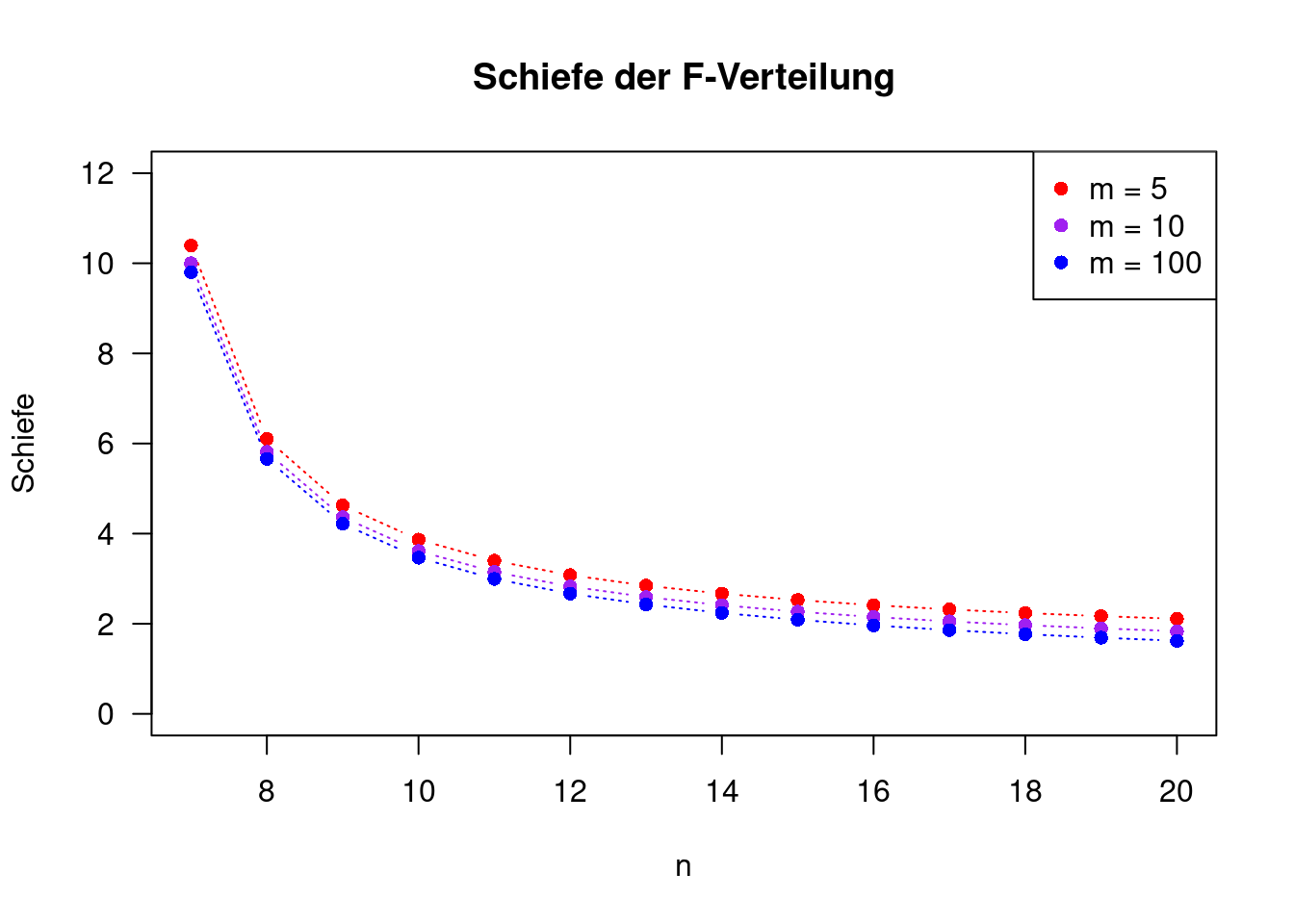
8.1.6 F-Verteilung
Die F-Verteilung ergibt sich als Quotient zweier (unabhängiger) jeweils durch die zugehörige Anzahl von Freiheitsgraden (\(m\) und \(n\)) geteilter Chi-Quadrat-verteilter Zufallsvariablen. Die Verteilung besitzt damit zwei unabhängige Freiheitsgrade als Parameter.
\[ F_{m,n} = \frac{ \frac{\chi^2_m}{m}}{\frac{\chi^2_n}{n}} \]
Die F-Verteilung wird ebenfalls oft für Hypothesentests eingesetzt, z.B. um festzustellen, ob der Unterschied zweier Stichprobenvarianzen auf statistischer Schwankung beruht oder ob er auf unterschiedliche Grundgesamtheiten hinweist. Sie wird auch im Rahmen der Varianzanalyse, zum Test auf signifikante Unterschiede zwischen Grundgesamtheiten (Gruppen) verwendet. Dies beruht darauf, dass man alternativ die F-Verteilung auch über das Verhältnis der Summe der Abweichungsquadrate oder der Stichprobenvarianzen (\(S_{X_1}, S_{X_2}\)) geteilt durch die Varianz der Grundgesamtheit, zweier unabhängiger, normalverteilter Zufallsvariablen \(X_1\) und \(X_2\) beschreiben kann.
\[ X_1 \sim N(\mu_1, \sigma_1^2) \] \[ X_2 \sim N(\mu_2, \sigma_2^2) \] \[ \frac{S_{X_1}^2}{\sigma_1^2} \sim \frac{\chi^2_{m-1}}{m-1} \] \[ \frac{S_{X_2}^2}{\sigma_2^2} \sim \frac{\chi^2_{n-1}}{n-1} \]
\[ \frac{\frac{S_{X_1}^2}{\sigma_1^2}} {\frac{S_{X_2}^2}{\sigma_2^2}} \sim F_{m-1, n-1}\]
F-verteilte Zufallsvariablen können nur Werte \(x \geq 0\) annehmen. Für \(m=1\) ist der Wertebereich auf \((0, \infty)\) begrenzt
Der Erwartungswert einer F-verteilten Zufallsvariablen \(X\) hängt nur von den Freiheitsgraden der zweiten (im Nenner befindlichen) Verteilung ab. Der Erwartungswert ist nur für \(n > 2\) definiert.
\[ E[X] = \frac{n}{n -2}\]
Die Varianz ist nur für \(n > 4\) definiert und hängt von beiden Stichprobenumfängen (Freiheitsgrade) ab.
\[ Var(X) = \frac{2n^2(m+n-2)}{m(n-2)^2(n-4)} \]
Je größer beide Stichprobengrößen, desto kleiner die Varianz von \(X\). Der Einfluss von \(n\) ist dabei größer als der von \(m\), allerdings gibt es eine deutliche Interaktion zwischen beiden Stichprobenumfängen.
Die Schiefe von X ist nur für \(n > 6\) definiert und stets positiv.
\[ \gamma = \frac{(2m + n-2)\sqrt{8(n-4)}}{(n-6)\sqrt{m(m+n-2)}} \]
Die Schiefe nimmt mit zunehmender Stichprobengrößen ab, der Einfluss von \(n\) ist größer als der von \(m\), allerdings mit deutlicher Interaktion. Die Schiefe bleibt stets größer als Null (konvergiert mit zunehmenden Stichprobengrößen gegen Null). Die F-Verteilung ist somit für Stichprobengrößen bis zu mehreren hundert rechtsschief.
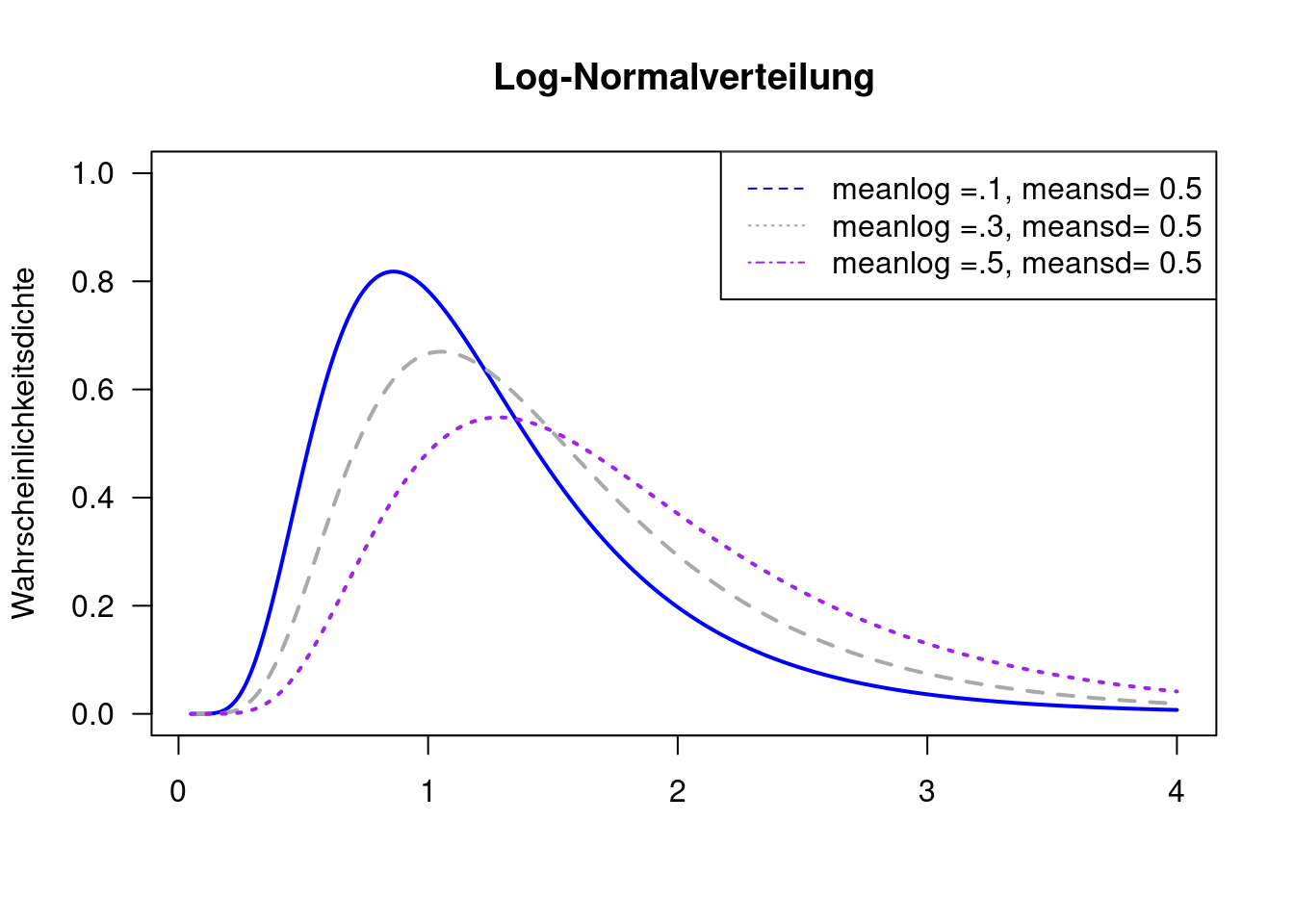
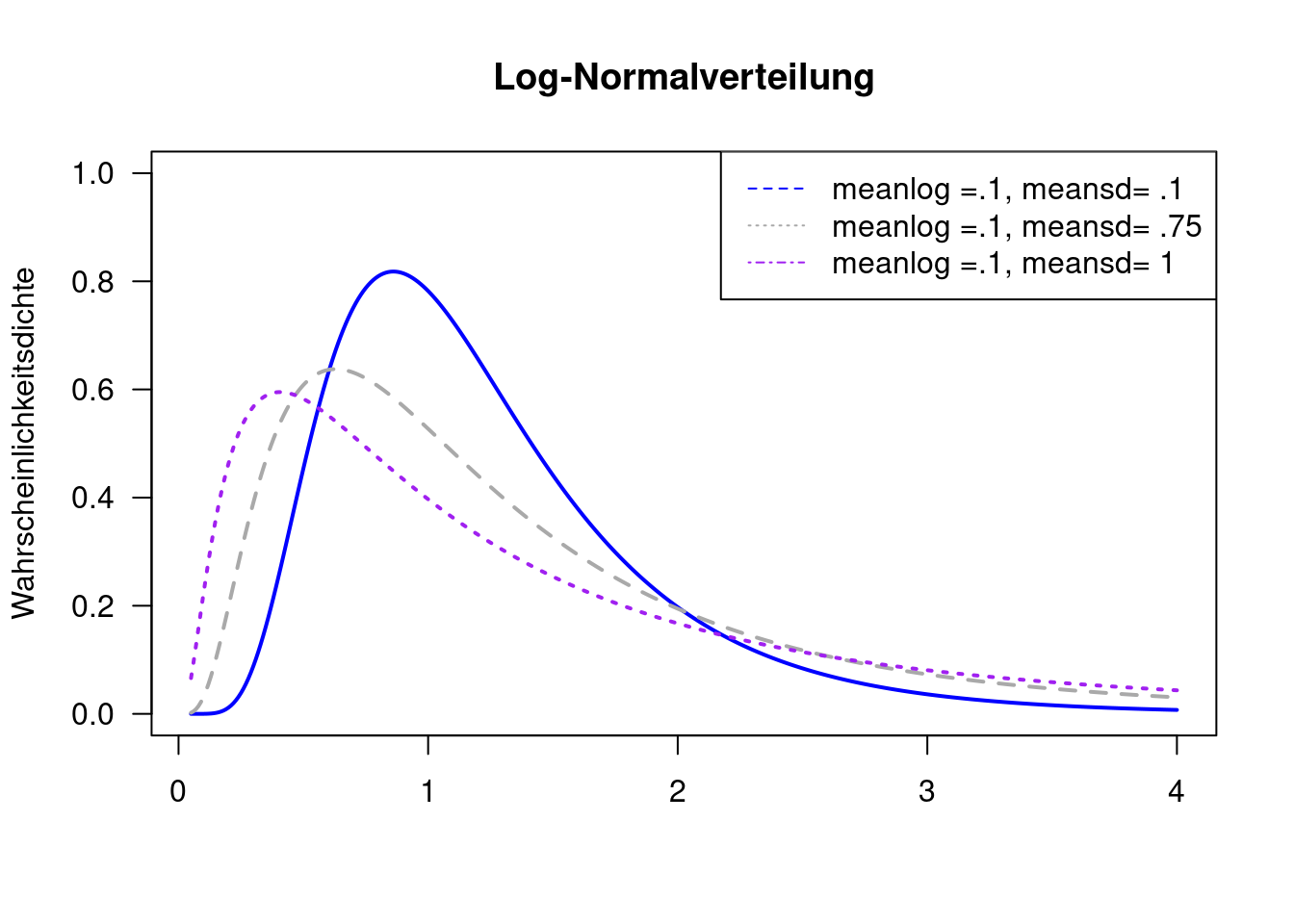
8.1.7 Log-Normalverteilung
Die Log-Normalverteilung kann nur positive Werte annehmen. Sie beschreibt die Verteilung einer Zufallsvariablen \(X\), wenn die logarithmierte Zufallsvariable \(Y = log(X)\) normalverteilt ist.33 Wenn \(Z\) eine Standardnormalverteilte Zufallsvariable ist, dann ist \(X = e^{\mu + \sigma Z}\) Log-Normalverteilt. Die Verteilungsparameter \(\mu\) und \(\sigma\) sind der Erwartungswert und die Standardabweichung der Logarithmus der Zufallsvariablen und nicht der Zufallsvariablen selbst.
Da die Realisierungen nur positive Werte umfassen eignet sich die Verteilung für Größen, die einen positiven Wertebereich haben wie z.B. Konzentrationen. Die Verteilung ist rechsschief und hat einen positiven Exzess und eignet sich damit um Phänomene zu beschreiben, bei denen hohe Werte gelegentlich auftreten. So kann die Verteilung z.B. eingesetzt werden, um Abflusswerte in Flüssen zu beschreiben. Andere Anwendungsbeispiele aus der Geographie sind die Einkommensverteilung 34 oder die Verteilung von Stadtgrößen.
In R kann die Dichte, die Verteilungsfunktion, … der Verteilung mit dlnorm, plnorm,… abgefragt werden. Mittelwert und Standardabweichung werden auf der Log-Skala definiert (mittels meanlog und meansd).
Im Gegensatz zur Normalverteilung wird die Log-Normalverteilung nicht nur translatiert (verschoben), wenn man den Verteilungsparameter \(\mu\) verändert. Es ändert sich auch die Varianz.
Verändert man den Verteilungsparameter \(\sigma\) (der sich ja auf den Logarithmus der Zufallsvariable bezieht), dann ändert sich auch der Mittelwert der Verteilung.
Der Erwartungswert der Log-Normalverteilung ist \(E(X) = e^{\mu + \frac{\sigma^2}{2}}\) und nicht wie oftmals fälschlicherweise angenommen \(E(X) = e ^{\mu}\). Tatsächlich ist der Median als $ median(X) = e^{}$ definiert.
Die Varianz der Log-Normalverteilung ist gegeben durch \(Var(X) = e^{2\mu}+\sigma^2(e^{\sigma^2}-1)\)
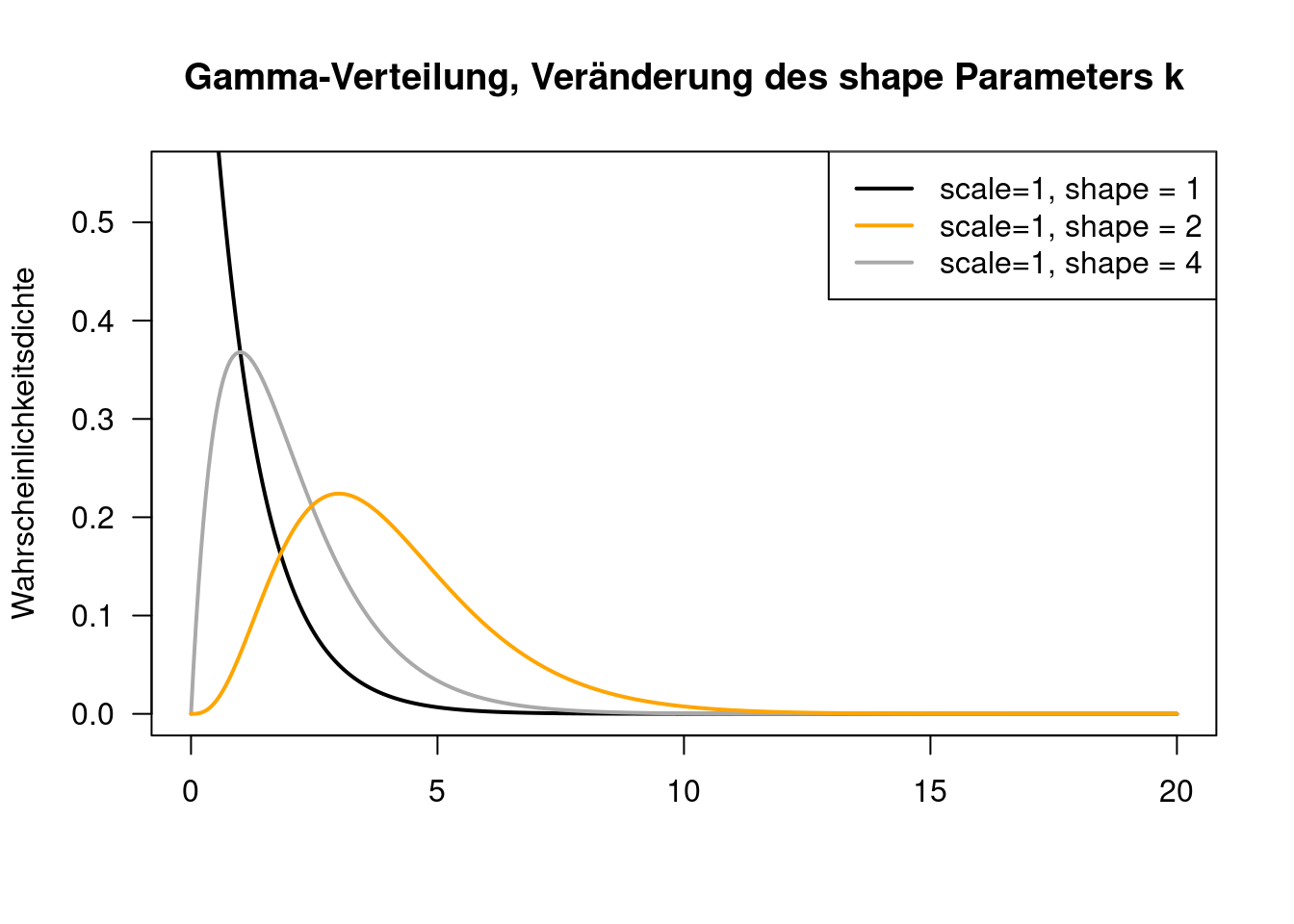
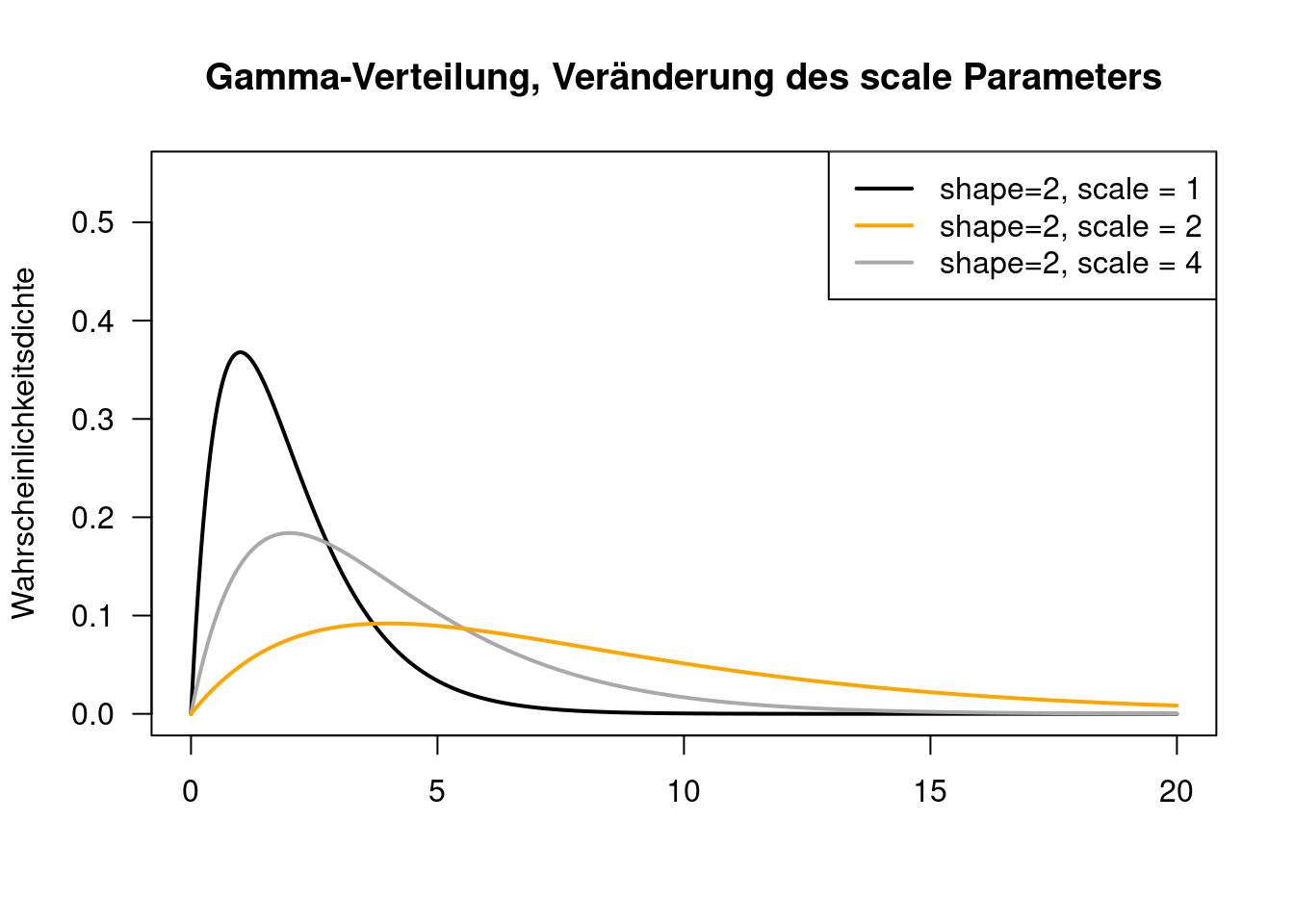
8.1.8 Gamma-Verteilung
Auch die Gamma-Verteilung ist rechtsschief und nimmt nur positive Werte an. Sie wird z.B. verwendet, um Wartezeiten zu modellieren, also z.B. wie lange wartet man an der Kasse im Supermarkt, wie lange dauert es, bis die Wirkung einer Behandlung einsetzt, wie lange dauert es, bis sich die Veränderungen im Klimageschehen in Veränderungen im Migrationsverhalten niederschlagen,…
Die Verteilung wird durch 2 Parameter \(k = shape\) und \(\Theta = scale\) definiert. Im deutschsprachigen Raum findet man auch eine alternative Parametrisierung durch \(p=k\) und \(q = \frac{1}{\Theta}\).
Der Erwartungswert der Gamma-Verteilung ergibt sich als \(E(X)= k\cdot\Theta\) bzw. \(E(X)= \frac{p}{b}\).
Die Varianz ergibt sich wie folgt: $Var(X)= k^2 $.
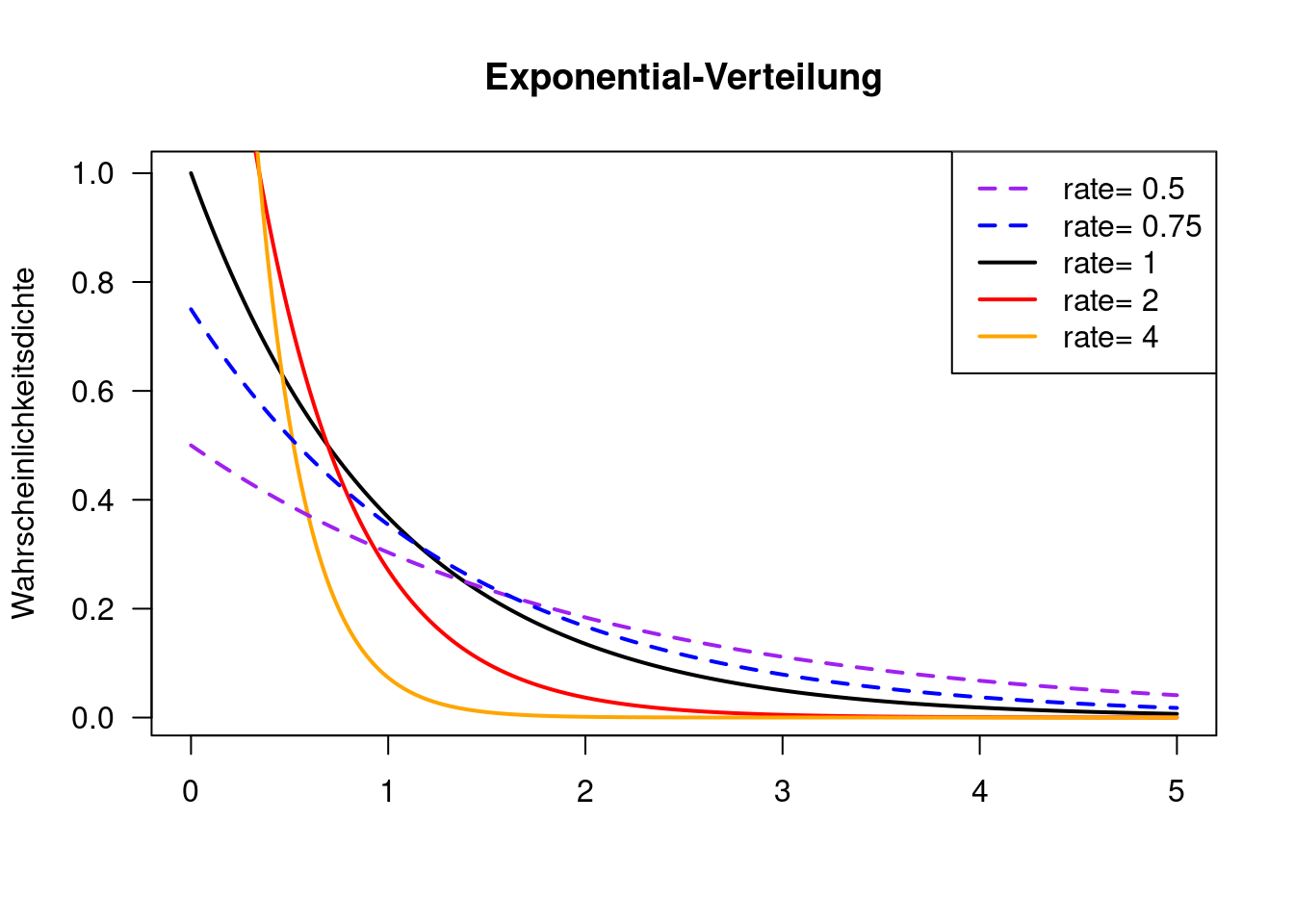
8.1.9 Exponential-Verteilung
Auch die Exponentialverteilung ist eine rechtsschiefe Verteilung, die nur positive Werte annehmen kann. Sie wird allgemein für die Modellierung von zufälligen Zeitintervallen benutzt. Sie ist ein Spezialfall der Gamma-Verteilung.
Fragestellungen umfassen z.B.:
- Zeit zwischen zwei Anrufen
- Lebensdauer von Atomen beim radioaktiven Zerfall
- Lebensdauer von Bauteilen, Maschinen und Geräten, wenn Alterungserscheinungen nicht betrachtet werden müssen.
- als grobes Modell für kleine und mittlere Schäden in der Versicherungsmathematik
- für die Modellierung von Extremwerten in Hydrologie und Klimatologie (Hochwasser, Extremniederschläge, Hagel,…)
Die Dichtefunktion ist für \(x\geq 0\) wie folgt definiert:35
\[ f(x) = \lambda e^{-\lambda x} \]
Der Erwartungswert berägt: \(E(X) = \frac{1}{\lambda}\). Der Erwartungswert berägt: \(Var(X) = \frac{1}{\lambda^2}\). Der Median berägt: \(median(X) = \frac{ln2}{\lambda}\).
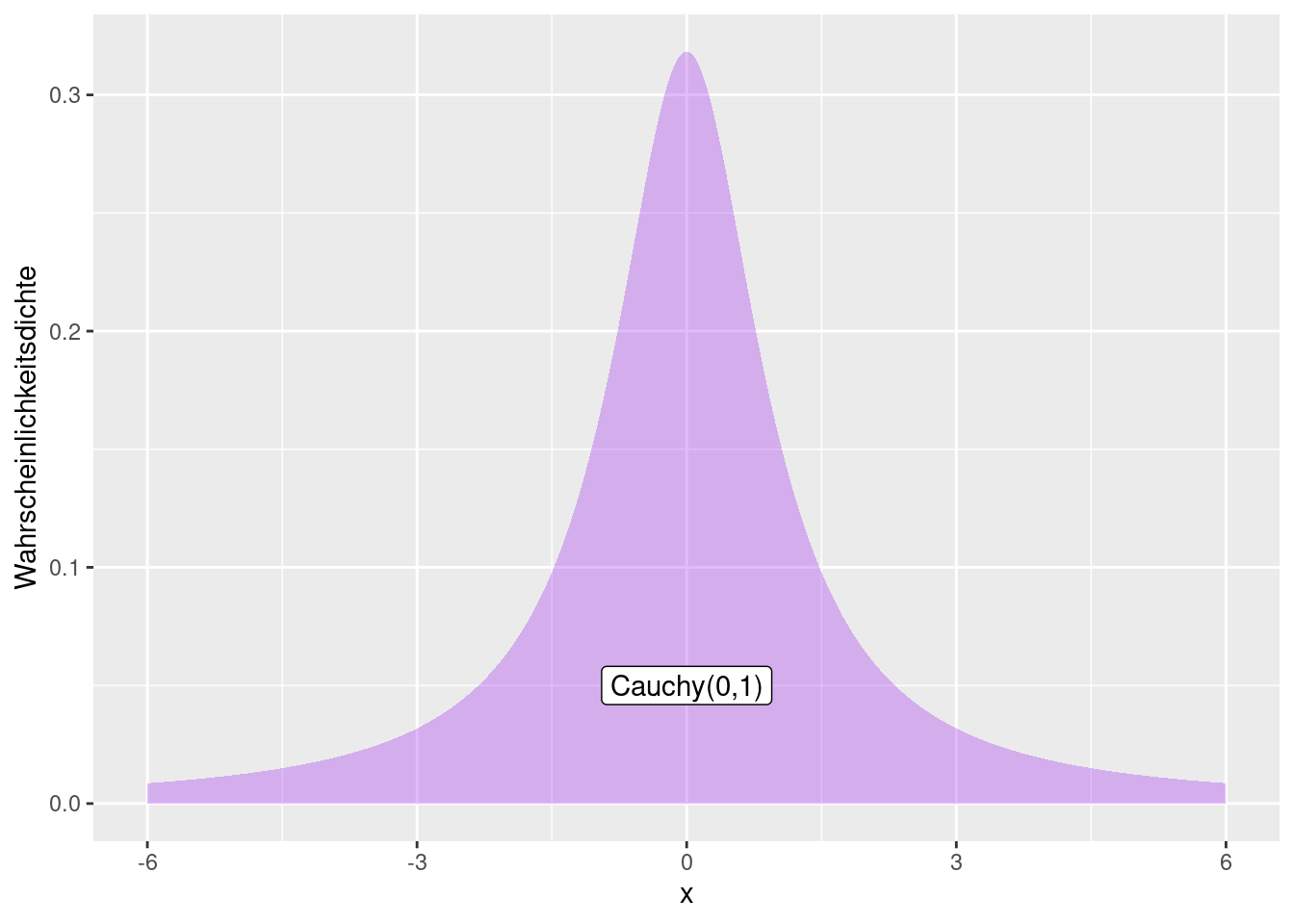
8.1.10 Cauchy-Verteilung
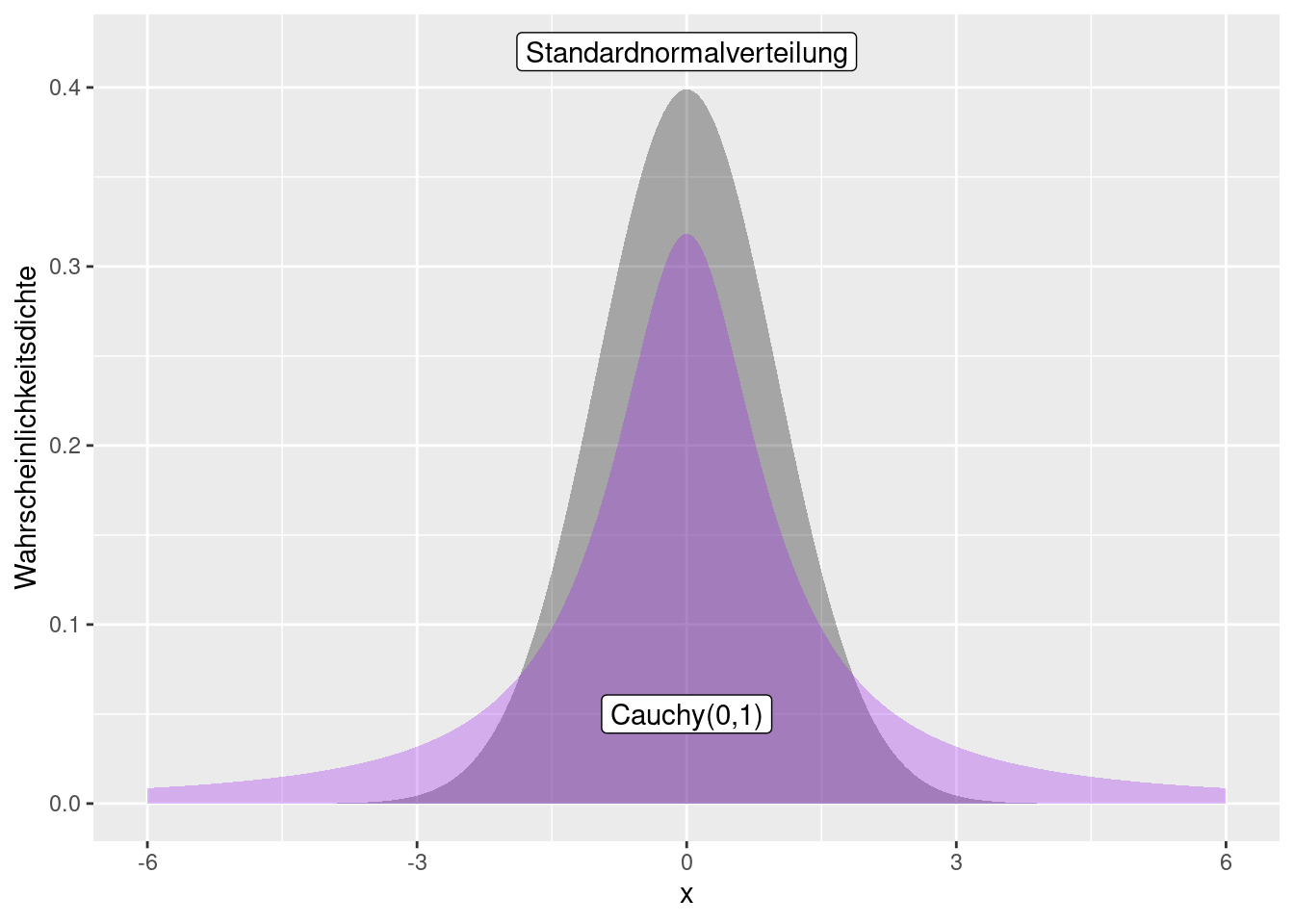
Die Cauchy-Verteilung ähnelt auf den ersten Blick einer Normalverteilung.
Allerdings hat sie deutlich mehr Wahrscheinlichkeitsmasse in den Enden der Verteilung. Die Cauchy-Verteilung wird deswegen verwendet, wenn man mehr Ausreißer modellierten möchte. Sie ergibt sich, wenn man eine Zufallsvariable \(Z\) als Verhältnis zweier unabhängiger zentrierter Normalverteilter Zufallsvariablen beschreibt.
Die Cauchy-Verteilung hat einige Eigenschaften, die man auf den ersten Blick nicht erwartet: sie besitzt keine endlichen Momente (Erwartungswert, Varianz, Schiefe, Wölbung,…). In Folge dessen trifft auf Cauchy-verteilte Daten auch nicht der Zentrale Grenzwertsatz oder die Gesetze der Großen Zahl zu.
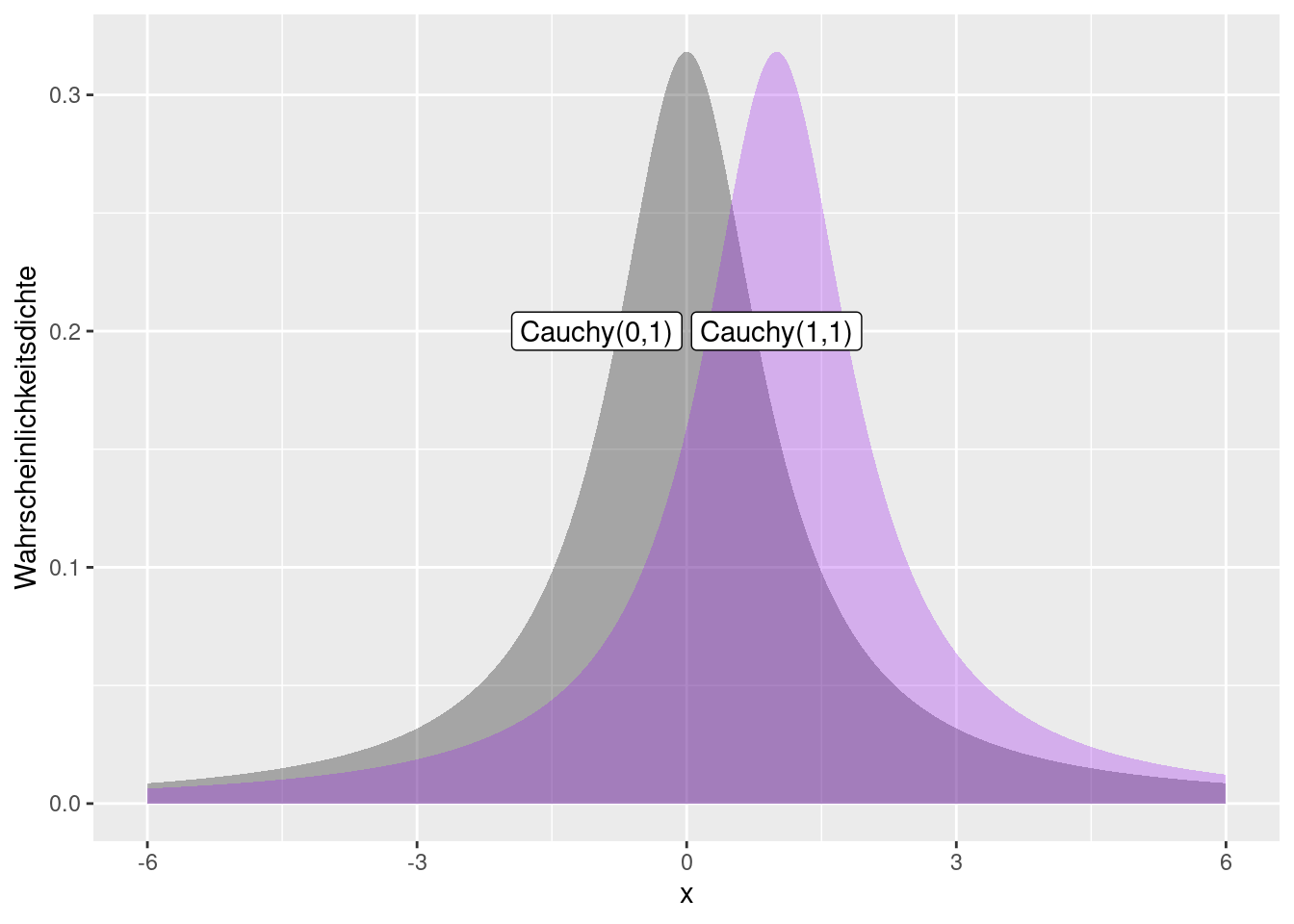
Die Verteilung wird durch zwei Parameter location und scale definiert. Der Parameter location translatiert die Kurve entlang der x-Achse. Dieser Parameter bestimmt den Median (und den Modus).
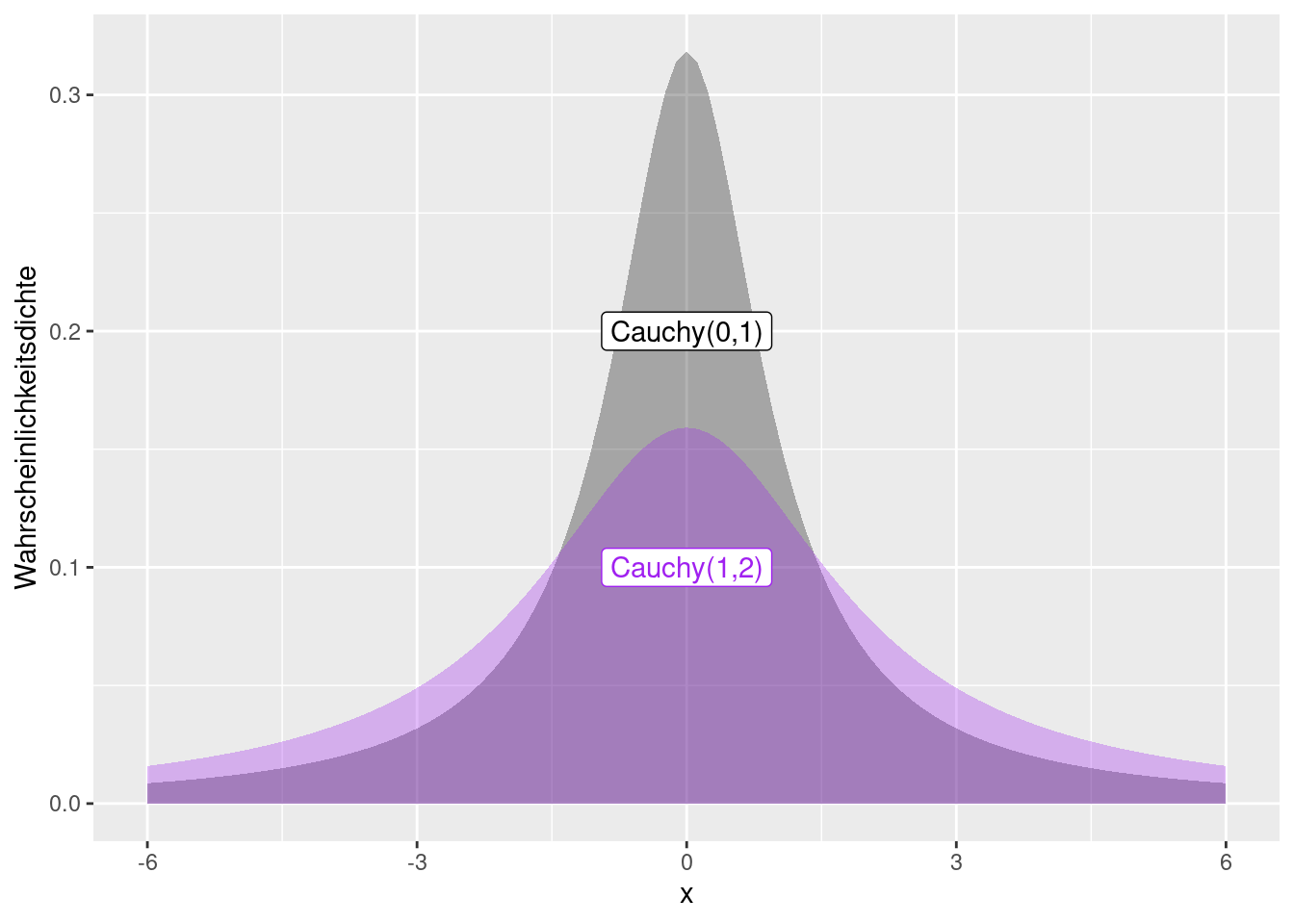
Der scale Parameter entspricht dem halben Interquantilsabstand.
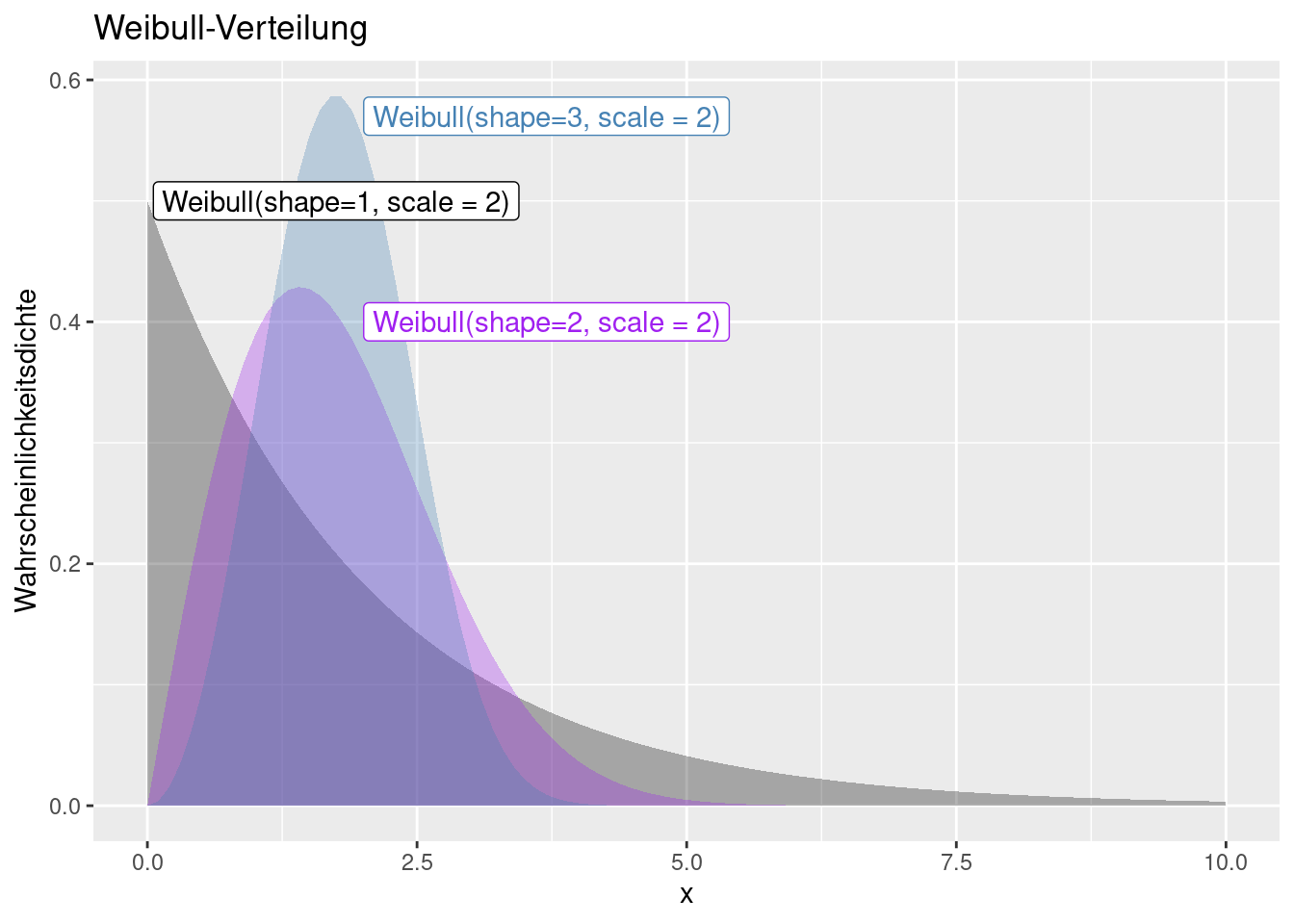
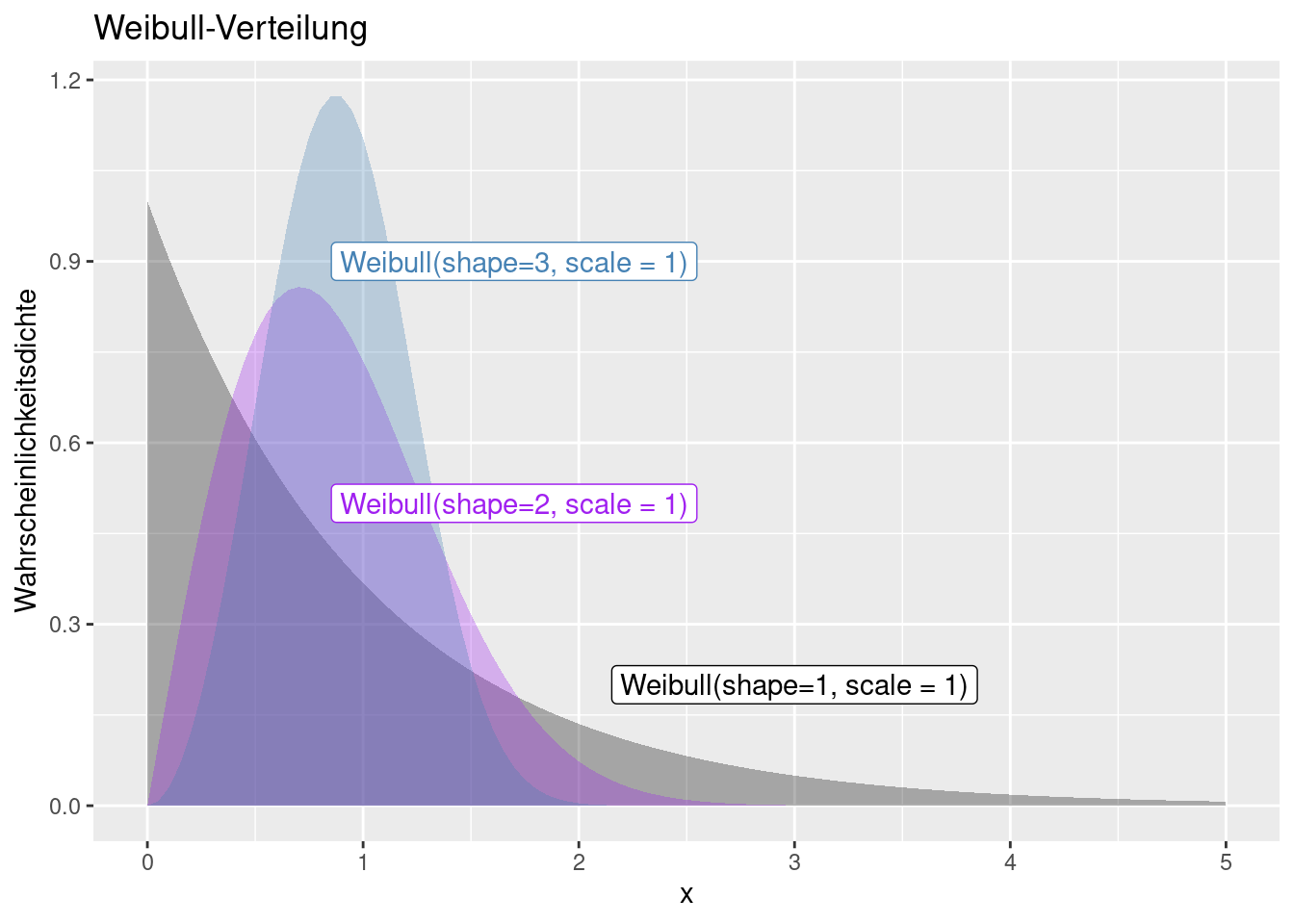
8.1.11 Weibull-Verteilung
Die Weibull-Verteilung kann zur Modellierung von Extremwerten verwendet werden (Extremwertverteilung) - also selten auftretenden Ereignissen wie bei Hochwasserereignissen oder Windstärken oder Ausfallhäufigkeiten von elektronischen Bauelementen. Sie ist nur für positive Werte definiert. Abhängig von ihren beiden Parametern ähnelt sie einer Normalverteilung oder schiefen Verteilungen wie der Exponentialverteilung. Anders als eine Exponentialverteilung berücksichtigt sie die Vorgeschichte eines Objekts, sie ist gedächtnisbehaftet.
Die Verteilung wird durch zwei Parameter beschrieben: den Skalen- (scale) und den Formparamter (shape)
Der Skalenparameter \(\lambda\) ist so definiert, dass sein Kehrwert stets größer Null ist: \(\frac{1}{\lambda}> 0\). In manchen Anwendungen wird \(\lambda\) durch seinen Kehrwert, die charakteristische Lebensdauer \(T\), ersetzt. Bei Lebensdauer-Analysen ist \(T\) jene Zeitspanne, nach der ca. 63,2 % der Einheiten ausgefallen sind.
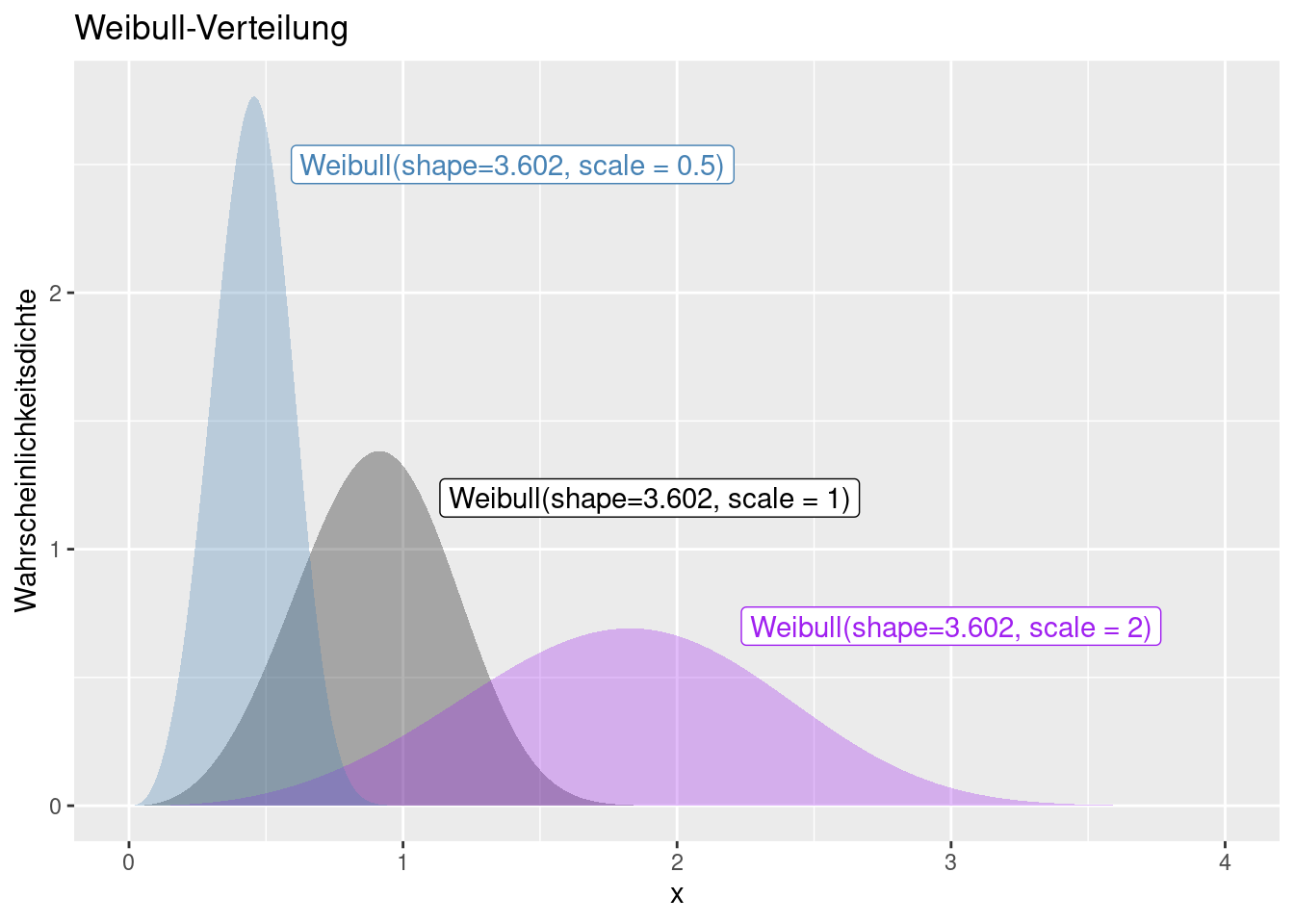
Der Formparameter (shape) der Weibull-Modul ist stets größer 0: \(k > 0\).
- Für k = 1 ergibt sich die Exponentialverteilung mit konstanter Ausfallrate.
- Für k = 2 ergibt sich die Rayleigh-Verteilung.
- Für \(k\approx 3{,}602\) ergibt sich eine Verteilung mit verschwindender Schiefe (ähnlich der Normalverteilung).
Während die Exponentialverteilung Probleme mit konstanter Ausfallrate \(\lambda\) beschreibt, kann man mittels der Weibullverteilung Fragestellungen mit steigender ( \(k > 1\)) oder fallender ( \(k < 1\)) Ausfallrate beschreiben. Man bezeichnet System mit \(k>1\) auch als ein alterndes System, bei dem die Ausfallrate mit der Zeit ansteigt.
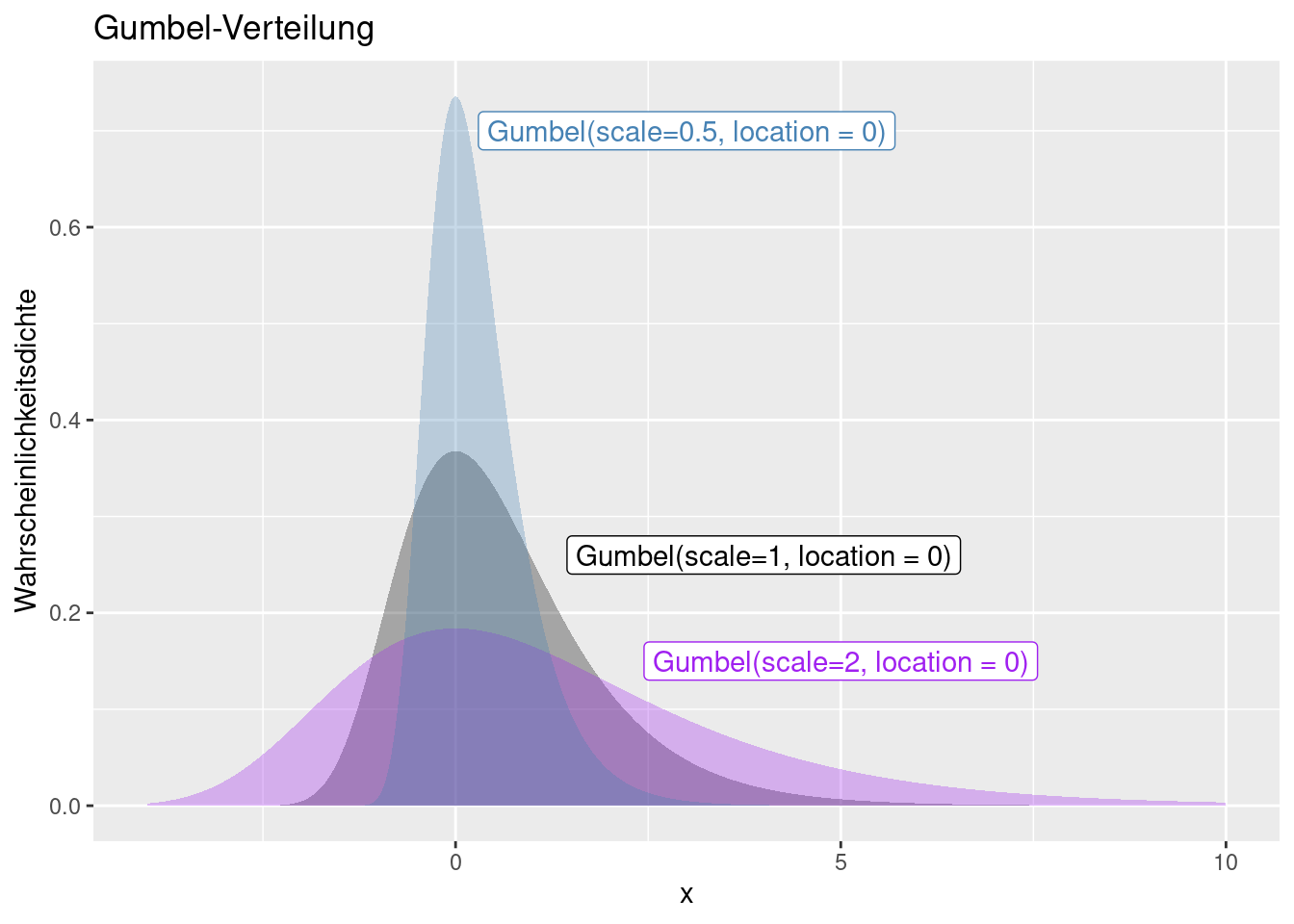
8.1.12 Gumbel Verteilung
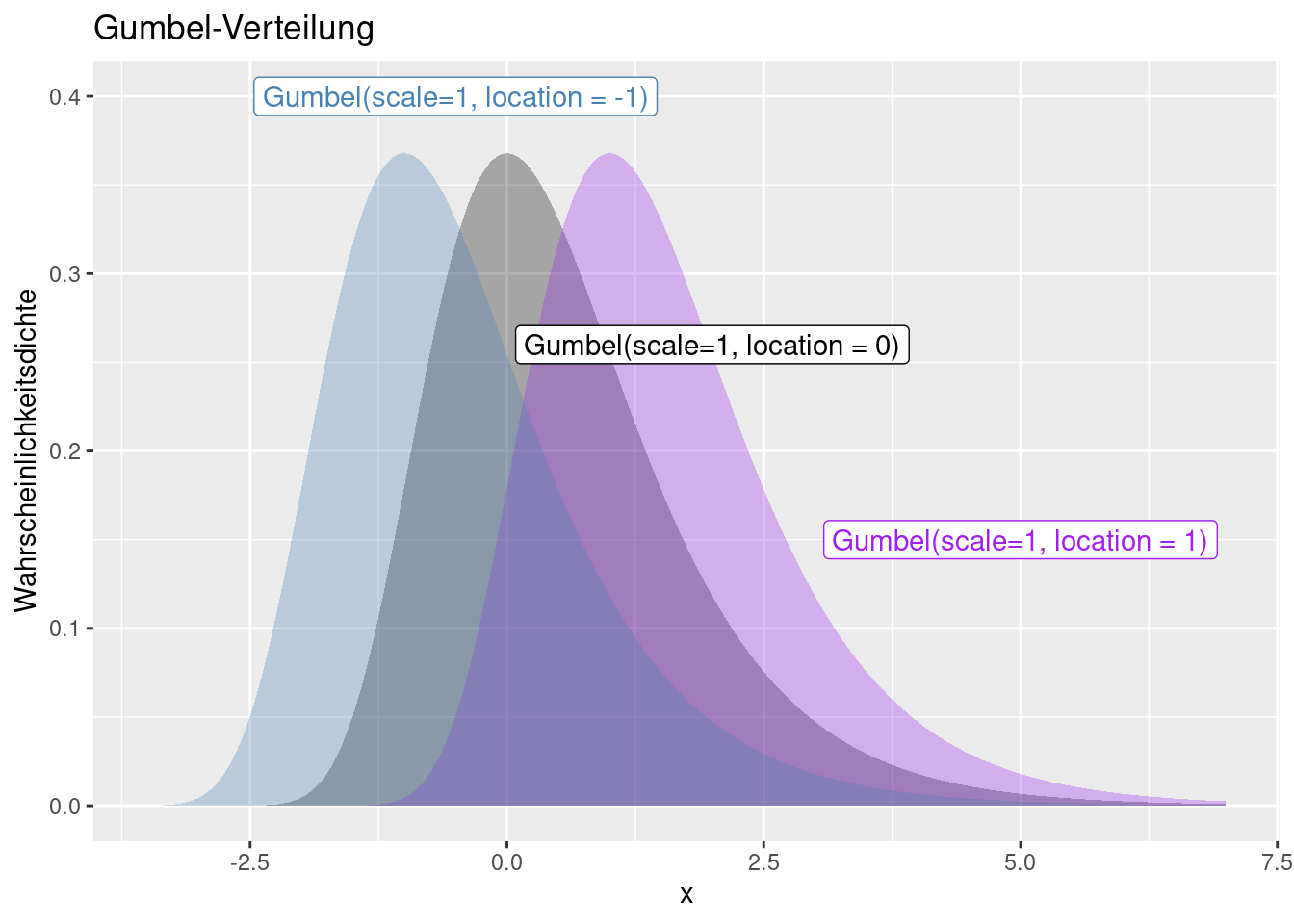
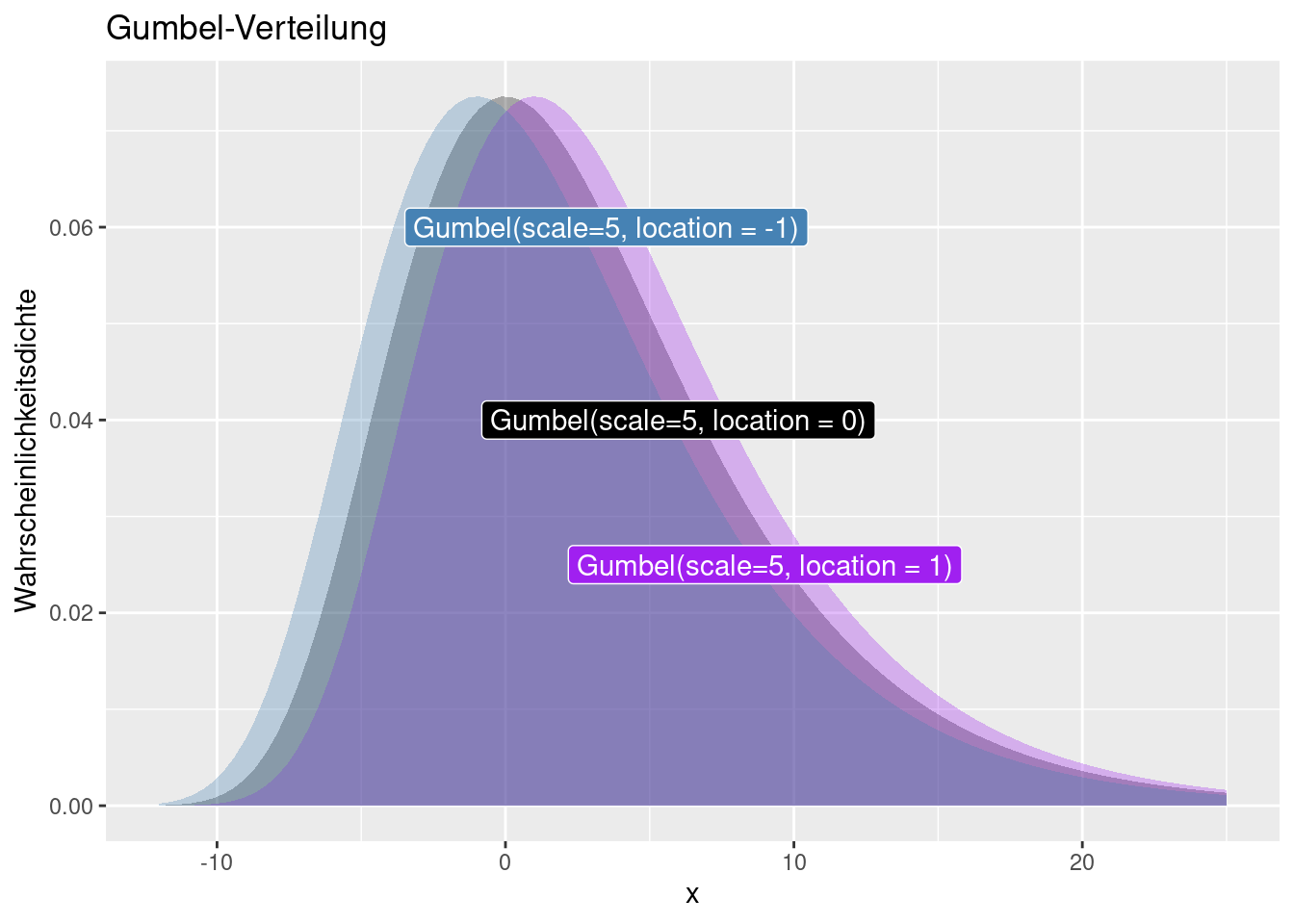
Auch bei der Gumbel handelt es sich um eine Extremwertverteilung. Die Funktion ist auch für negative Werte definiert. Die Verteilung wir durch einen Skalierungs- (scale) und eine Lageparameter (location) definiert. Der Lageparameter verschiebt die Funktion entlang der x-Achse (s. Abb. 8.13 und 8.12), während der Skalierungsparamter die Varianz beeinflusst (s. Abb. 8.11. Schiefe, Kurtosis und höhere zentrale Parameter werden durch beide Parameter nicht beeinflusse.´
## Loading required package: FAdist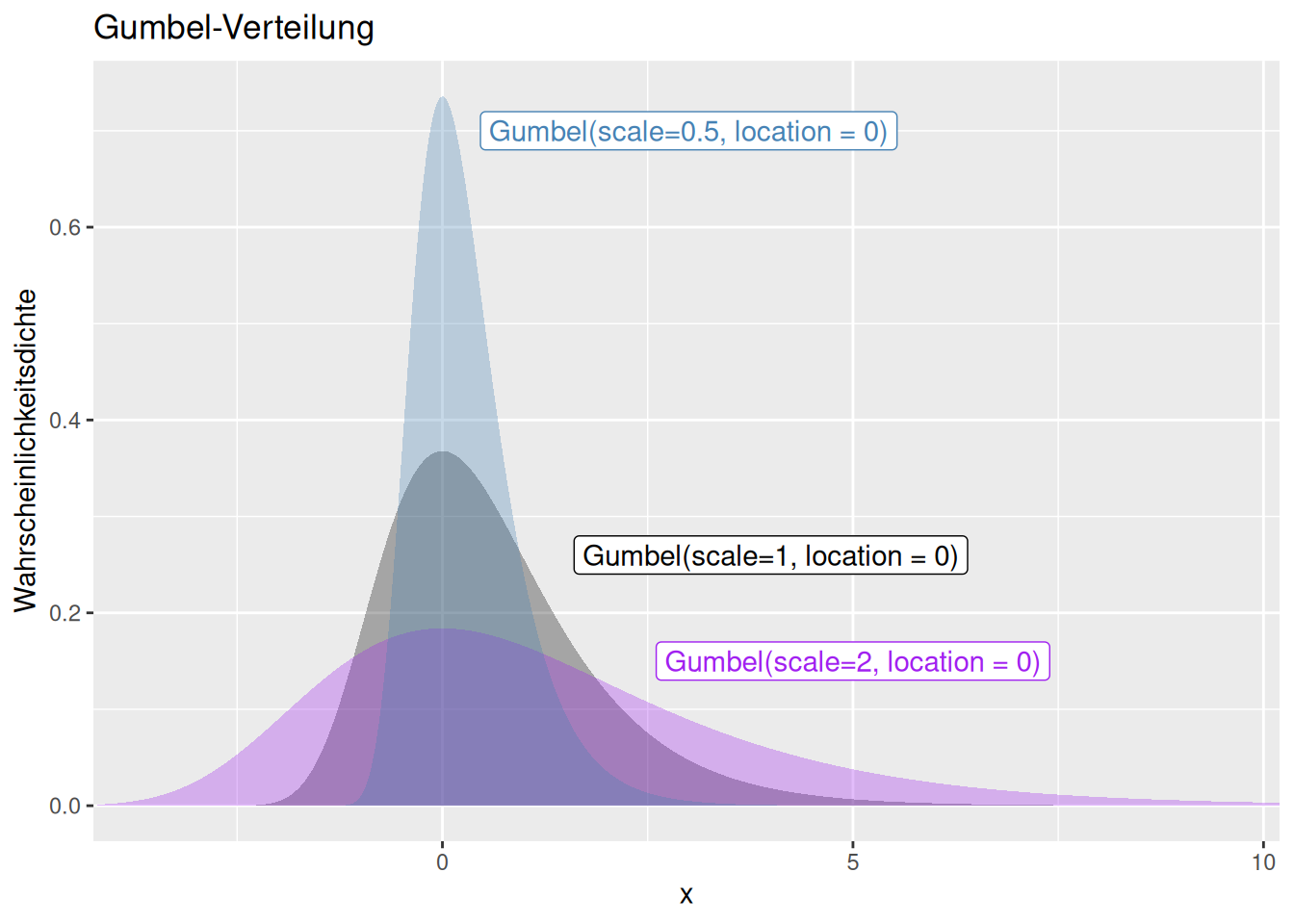
Figure 8.11: Wahrscheinlichkeitsdichtefunktion der Gumbel-Verteilung für verschiedene Werte für den Skalierungsparameter und konstanten Lageparameter von 0. Mit höherem Skalierungsparameter ändert sich die Streuung um den Lageparameter während sich die Schiefe und höhere zentrale Parameter nicht verändern.
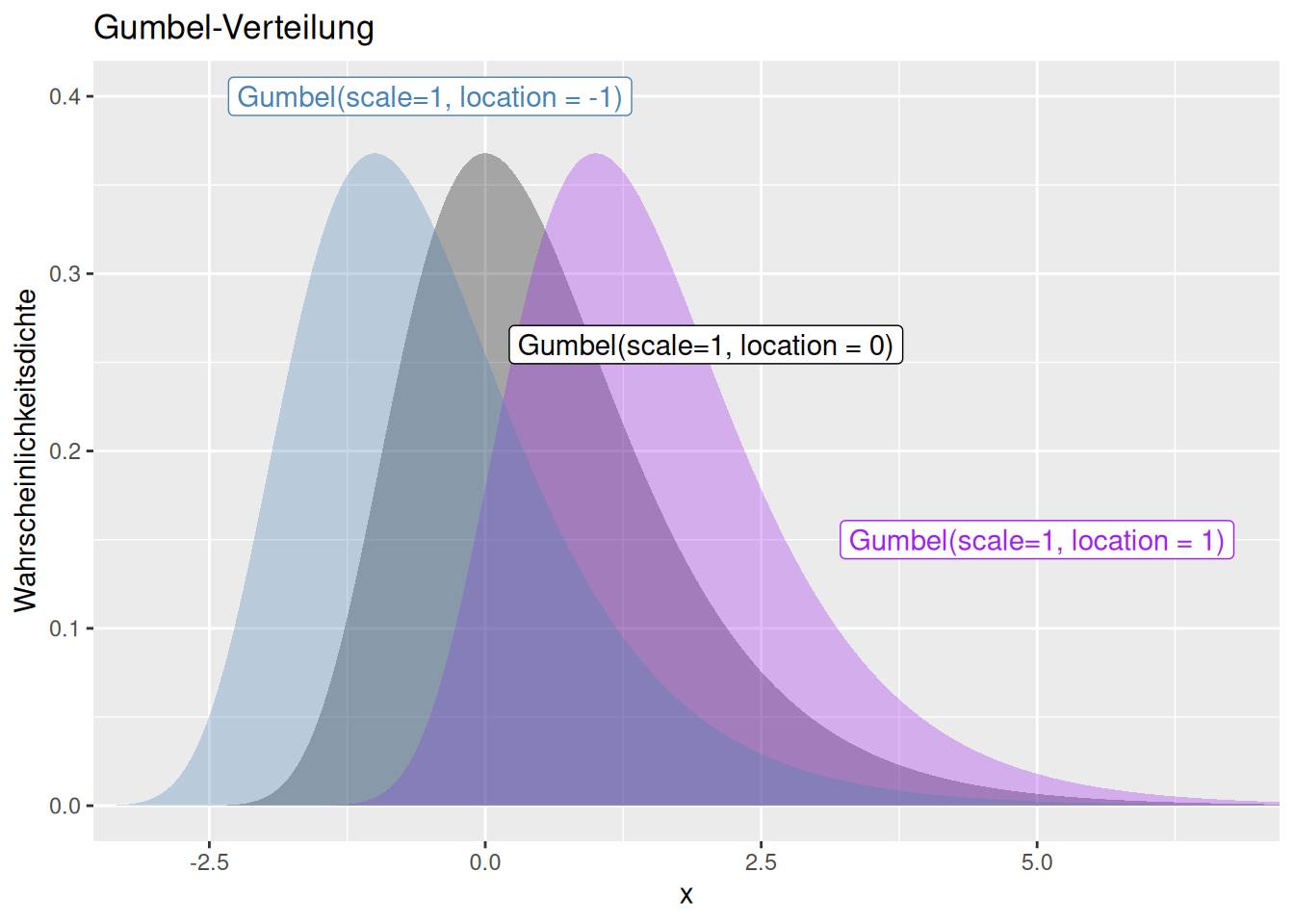
Figure 8.12: Wahrscheinlichkeitsdichtefunktion der Gumbel-Verteilung für verschiedene Werte für den Parameter location und konstanten scale Faktor von 1. Die gestrichelten Linien zeigen den location -Parameter der korrespondierenden Verteilungsfunktion an.
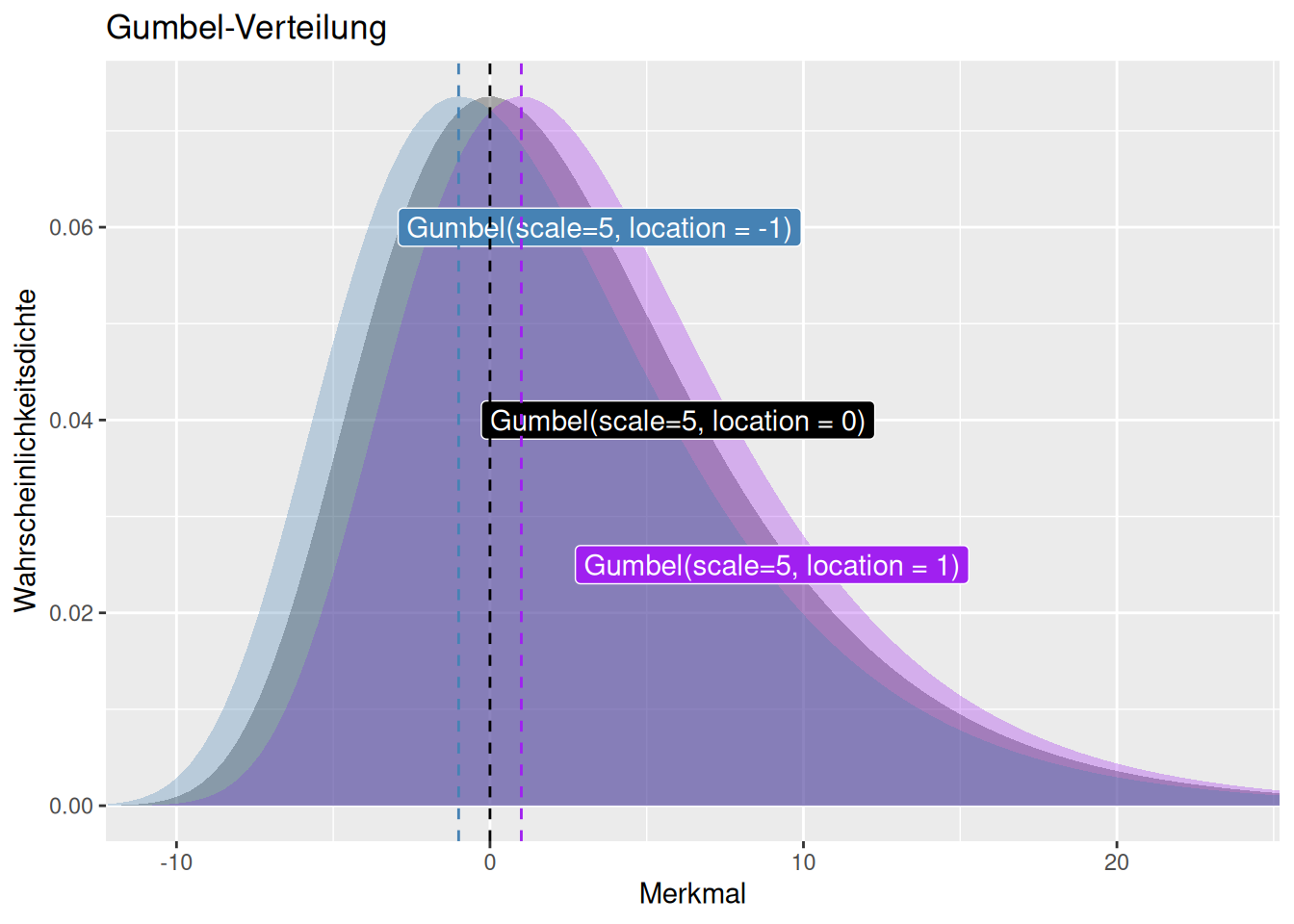
Figure 8.13: Wahrscheinlichkeitsdichtefunktion der Gumbel-Verteilung für verschiedene Werte für den Parameter location und konstanten scale Faktor von 5. Die gestrichelten Linien zeigen den location -Parameter der korrespondierenden Verteilungsfunktion an.
8.1.13 Inverse Gauss-/Normalverteilung
Die inverse Gauss- oder inverse Normalverteilung wird ähnlich wie die Gamma-Verteilung benutzt um die Verteilung strikt positiver Werte zu beschreiben. Der Name “inverse Normalverteilung” ist dahingehend irreführend, dass es sich nicht um die Verteilung 1/x (wenn x normalverteilt ist) handelt. Während die Noramlverteilung u.a. die Brownsche Molekülarbewegung beschreibt, beschreibt die inverse Normalverteilung den Zeitpunkt, bei dem ein bestimmtes Verteilungsniveau erreicht ist, wenn man eine Brownsche Molekülarbewegung mit positiver Drift (d.h. es gibt z.B. eine Strömung) und positivem Streungskoeffizienten betrachtet.
Die inverse Normalverteilung hat zwei Parameter: den Erwartungswert \(\mu\) und den Streuungskoeffizienten \(\lambda\).
\[P(x)=\sqrt{\frac{\lambda}{2 \pi x^3}} \cdot e^{-\frac{\lambda(x-\mu)^2}{2x\mu^2}}\]
mit \(\mu > 0\) und \(\lambda > 0\).
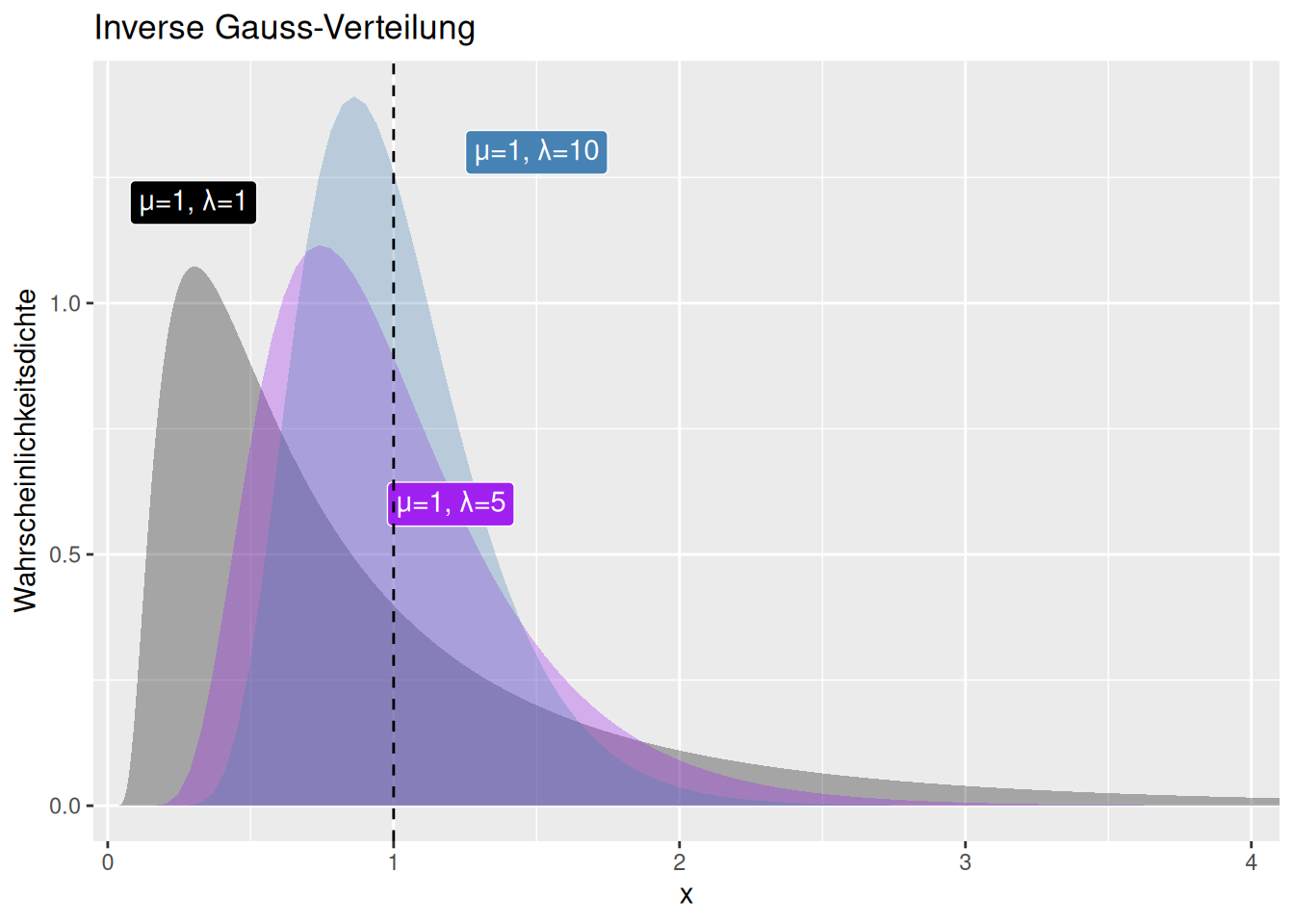
Figure 8.14: Veränderung der Form der inversen Gaussverteilung bei variablem Streuungskoeffizienten \(\lambda\) und konstantem Erwartungswert \(\mu\). Der als gestrichelte Linie eingezeichnete Erwartungswert ist bei allen drei dargestellten Parametrisierungen gleich.
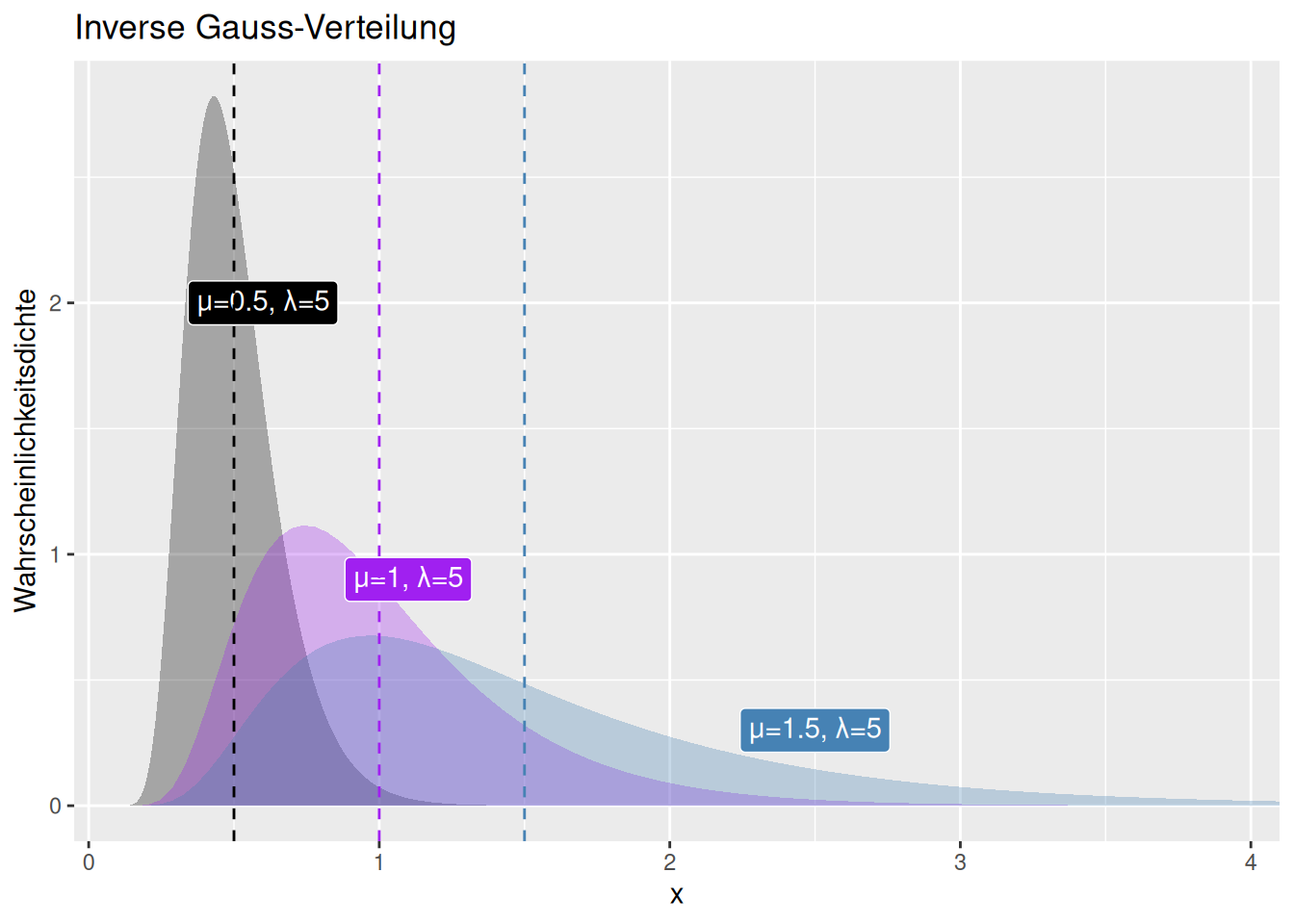
Figure 8.15: Veränderung der Form der inversen Gaussverteilung bei konstantem Streuungskoeffizienten \(\lambda\) und variablen Erwartungswert \(\mu\). Der Erwartungswert ist jeweils als gestrichelte Linie eingetragen.
Wie die Abbildungen 8.14) und 8.15) zeigen, verändern sich außer dem Mittelwert alle zentralen Momente mit beiden Parametern. Dabei ist der Effekt des Erwartungswertes \(\mu\) auf Varianz deutlich größer als der des Streuungskoeffizienten \(\lambda\).
Der Erwartungswert ist gleich \(\mu\). Die Varianz wächst in der dritten Potenz mit dem Erwartungswert und sinkt mit dem Streuungskoeffizienten: \(\sigma^2 = \frac{\mu^3}{\lambda}\). Die Schiefe wächst in Quadratwurzel mit dem Erwartungswert und dem Inversen des Streuungskoeffizienten: \(skewness = 3 \cdot\sqrt{\frac{\mu}{\lambda}}\) Der Exzess wächst mit dem Verhältnis aus Erwartungswert und Streuungskoeffizienten:: \(kurtosis= 15 \cdot\frac{\mu}{\lambda}\)
8.1.14 Bivariate Normalverteilung
Die bivariate Normalverteilung stellt eine Verallgemeinerung der Normalverteilung auf zwei Dimensionen dar - es sind auch multivariate Verteilungen höherer Dimensionalität gebräuchlich. Die Verteilung wird durch einen Erwartungswertvektor \(\mathbf{\mu}\) und die Kovarianzmatrix \(\mathbf{\Sigma}\) beschrieben, bei denen es sich um Verallgemeinerungen der Parameter der Normalverteilung handelt.
Die Hauptdiagonalelemente der Kovarianzmatrix beschreiben die Varianz in die beiden Richtungen. Die Elemente abseits der Hauptdiagonalen beschreiben die Kovarianz zwischen den beiden Dimensionen. Die Kovarianzmatrix ist stets symmetrisch, die Hauptdiagonalelemente sind stets positiv (da Varianzen nicht negativ und nicht null sein können).36 Wenn die Elemente der Nebendiagonalen alle Null sind, dann sind die Zufallsvariablen der beiden Dimensionen unkorreliert.
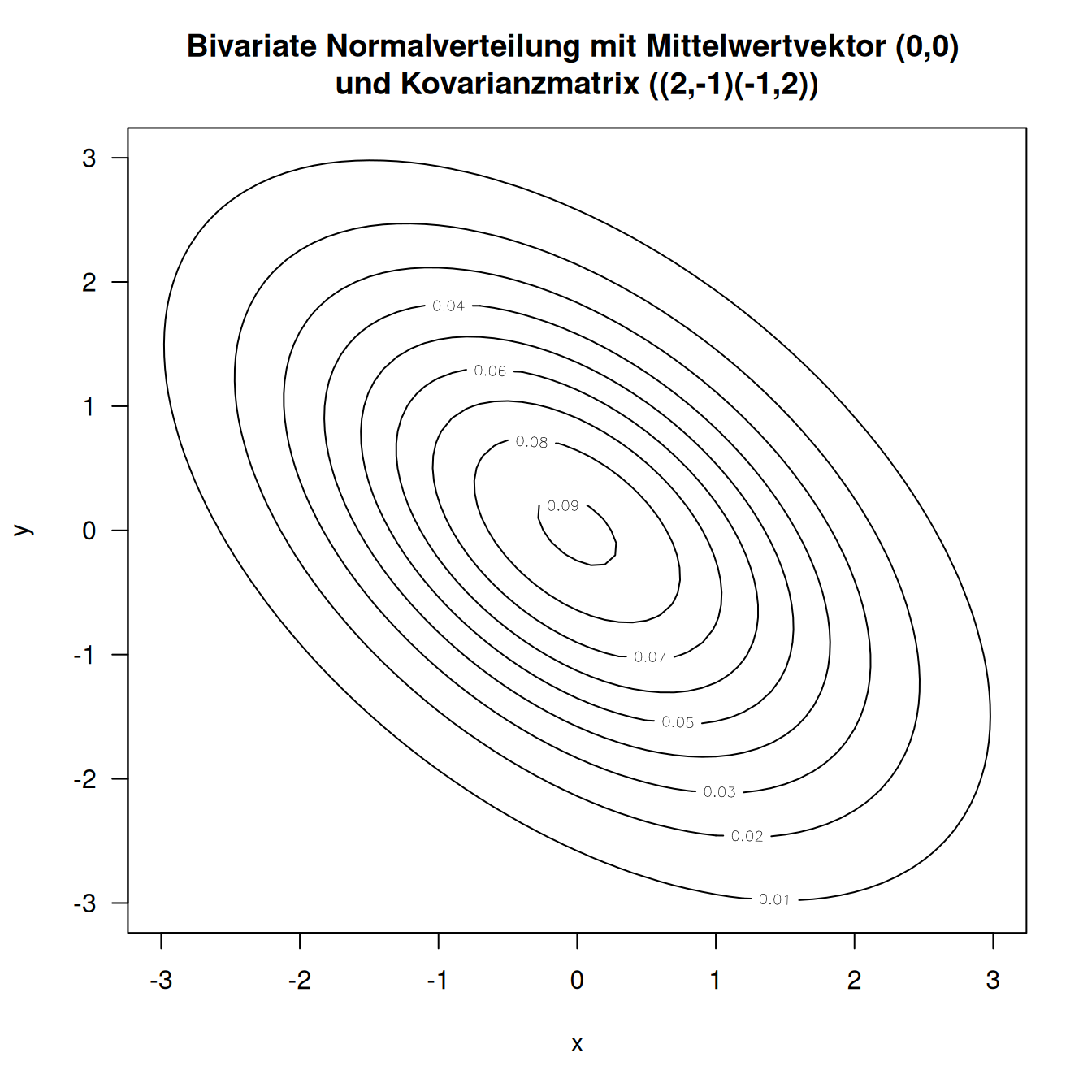
Figure 8.16: Kontourdarstellung einer bivariaten Normalverteilung. Die Isolinien stellen die Wahrscheinlichkeitsmasse dar. In diesem Beispiel sind die beiden Dimensionen nicht unabhängig voneinander sondern korreliert. Man erkennt dies daran, dass die Isolinien in eine Richtung schneller fallen, als in eine andere.
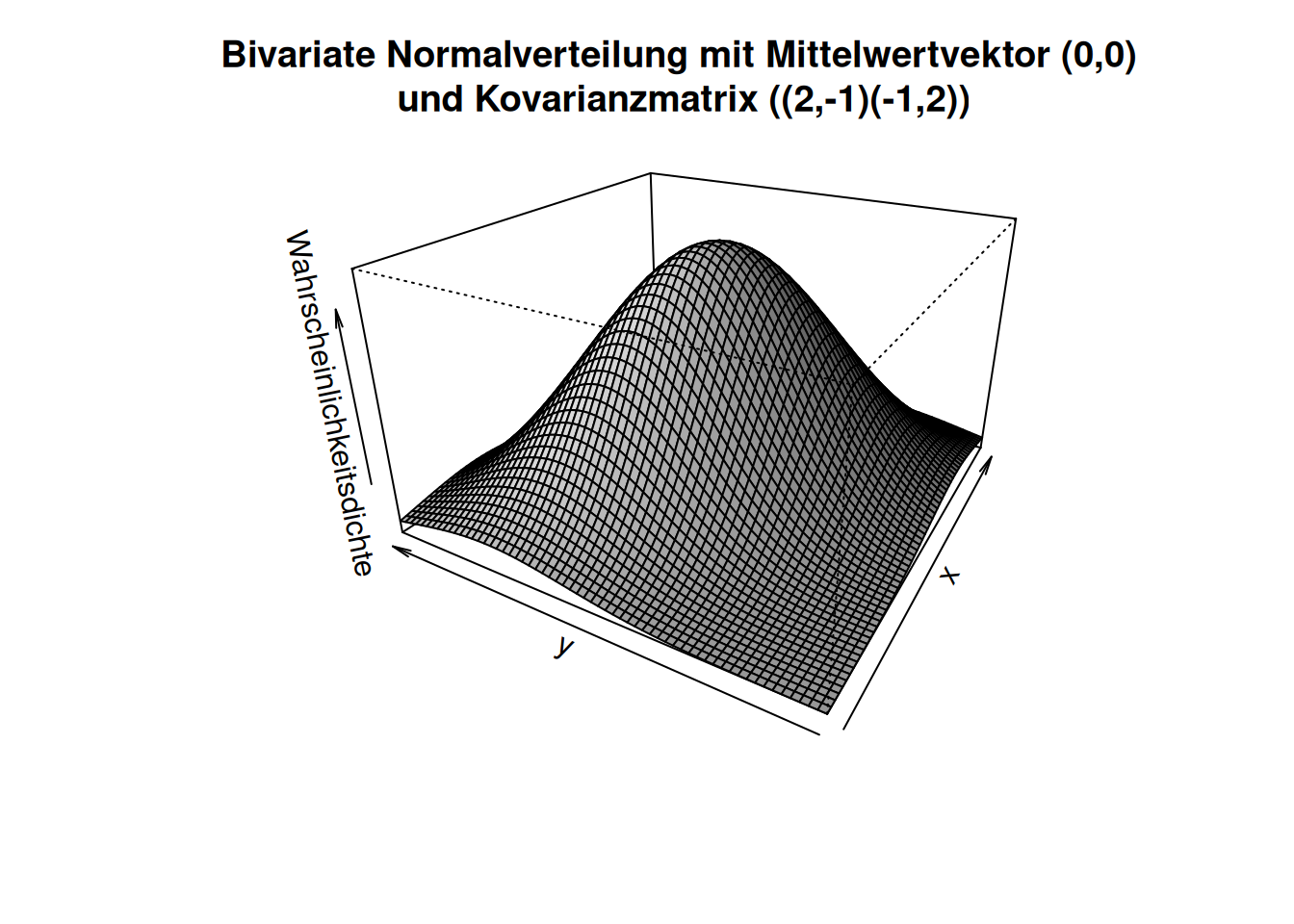
Figure 8.17: 3D-darstellung einer bivariaten Normalverteilung. Die z-Achse stellt die Wahrscheinlichkeitsmasse dar. In diesem Beispiel sind die beiden Dimensionen nicht unabhängig voneinander sondern korreliert.
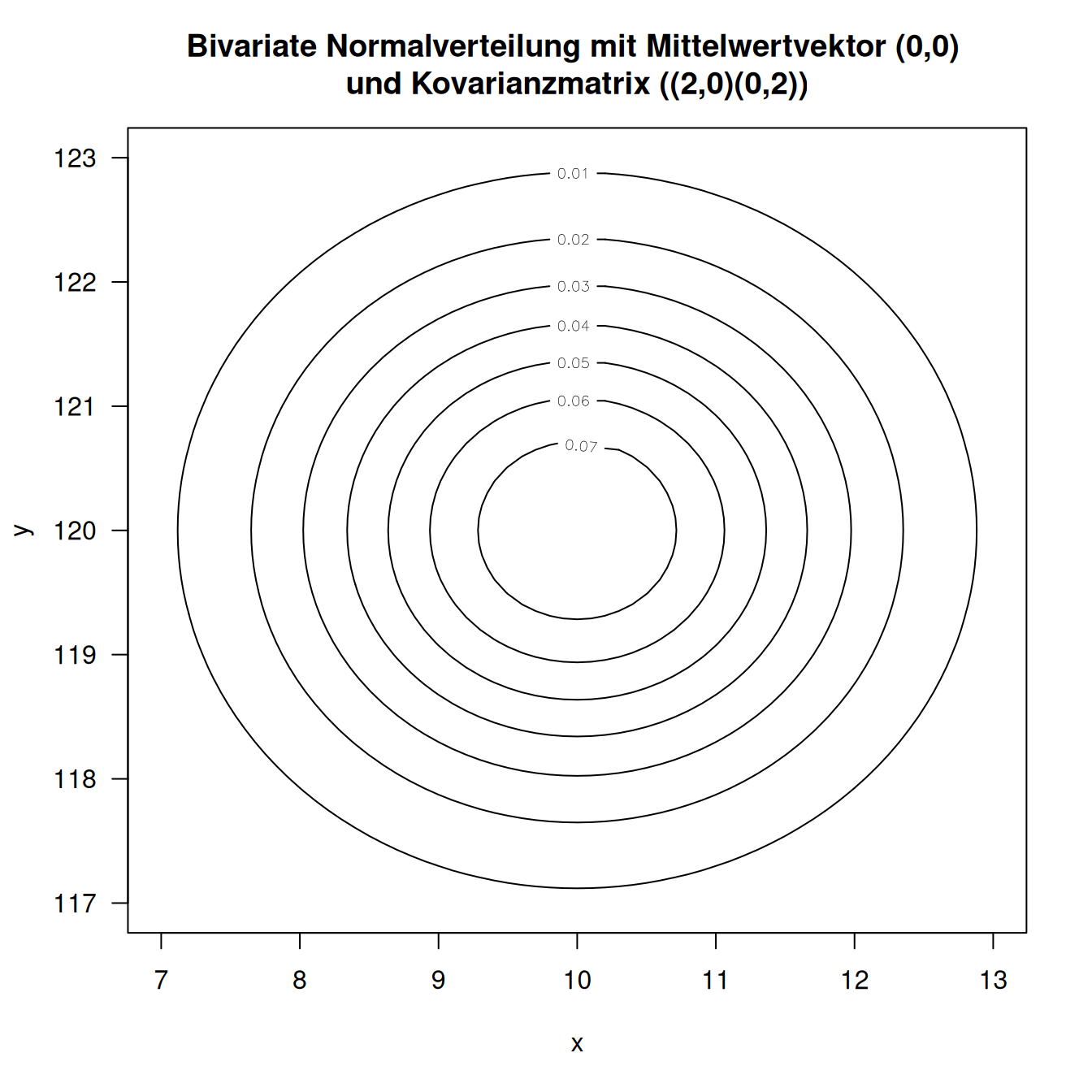
Figure 8.18: Kontourdarstellung einer bivariaten Normalverteilung. Die Isolinien stellen die Wahrscheinlichkeitsmasse dar. In diesem Beispiel sind die beiden Dimensionen unkorreliert.
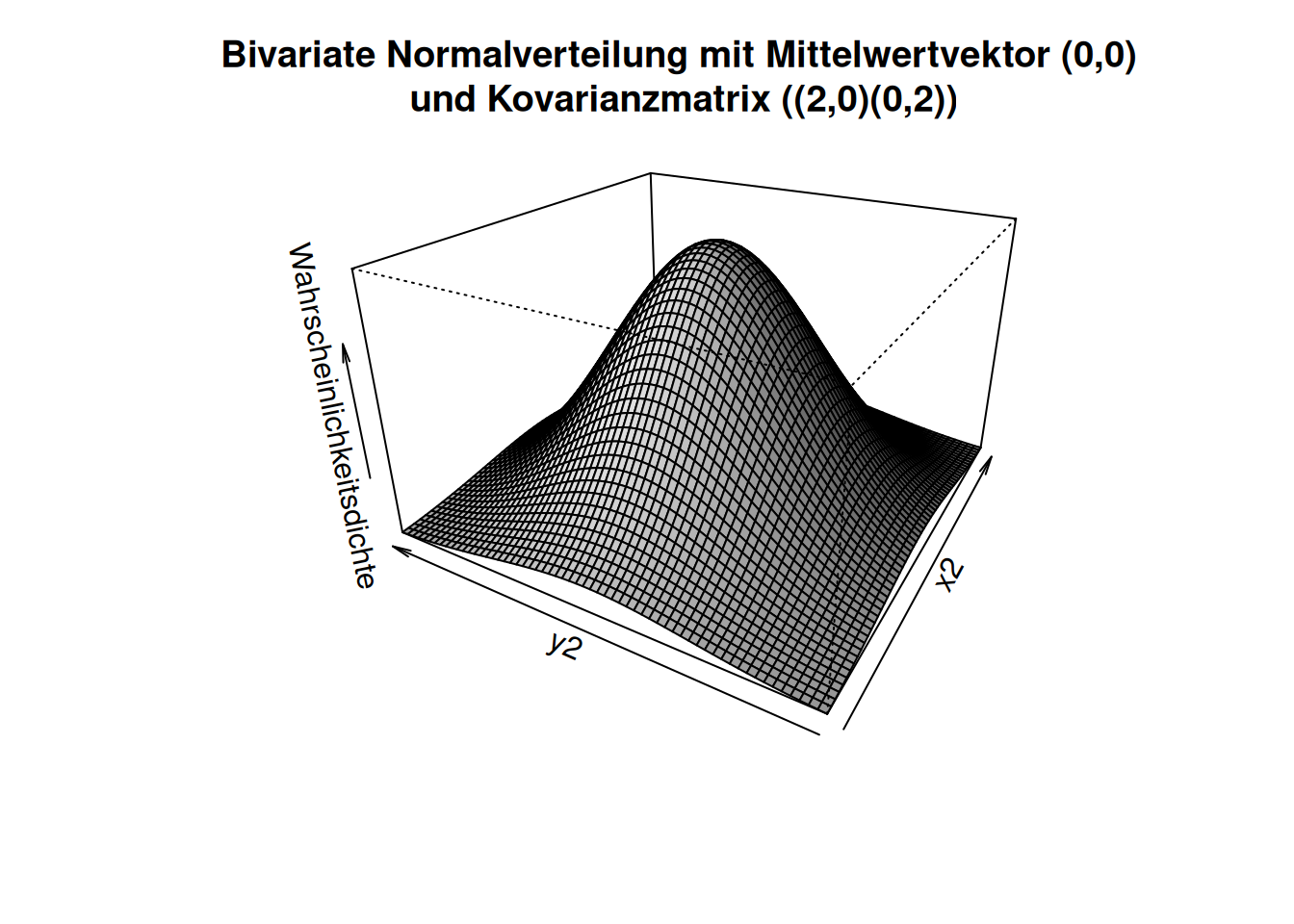
Figure 8.19: 3D-darstellung einer bivariaten Normalverteilung. Die z-Achse stellt die Wahrscheinlichkeitsmasse dar. In diesem Beispiel sind die beiden Dimensionen unkorreliert.
Die bivariate Normalverteilung ist z.B. interessant, wenn wir korrelierte Zufallsvariablen betrachten. Die Wahrscheinlichkeit für das Auftreten eines Wertes eines Merkmals hängt dann davon ab, welchen Wert das andere Merkmal angenommen hat.
## Warning in annotate(geom = "label", x = 35, y = 60, label =
## "Marginal-\nverteilung y\nfür x = 34\n(conditional on)", : Ignoring unknown
## parameters: `linetype`## Warning: The following aesthetics were dropped during statistical transformation: z.
## ℹ This can happen when ggplot fails to infer the correct grouping structure in
## the data.
## ℹ Did you forget to specify a `group` aesthetic or to convert a numerical
## variable into a factor?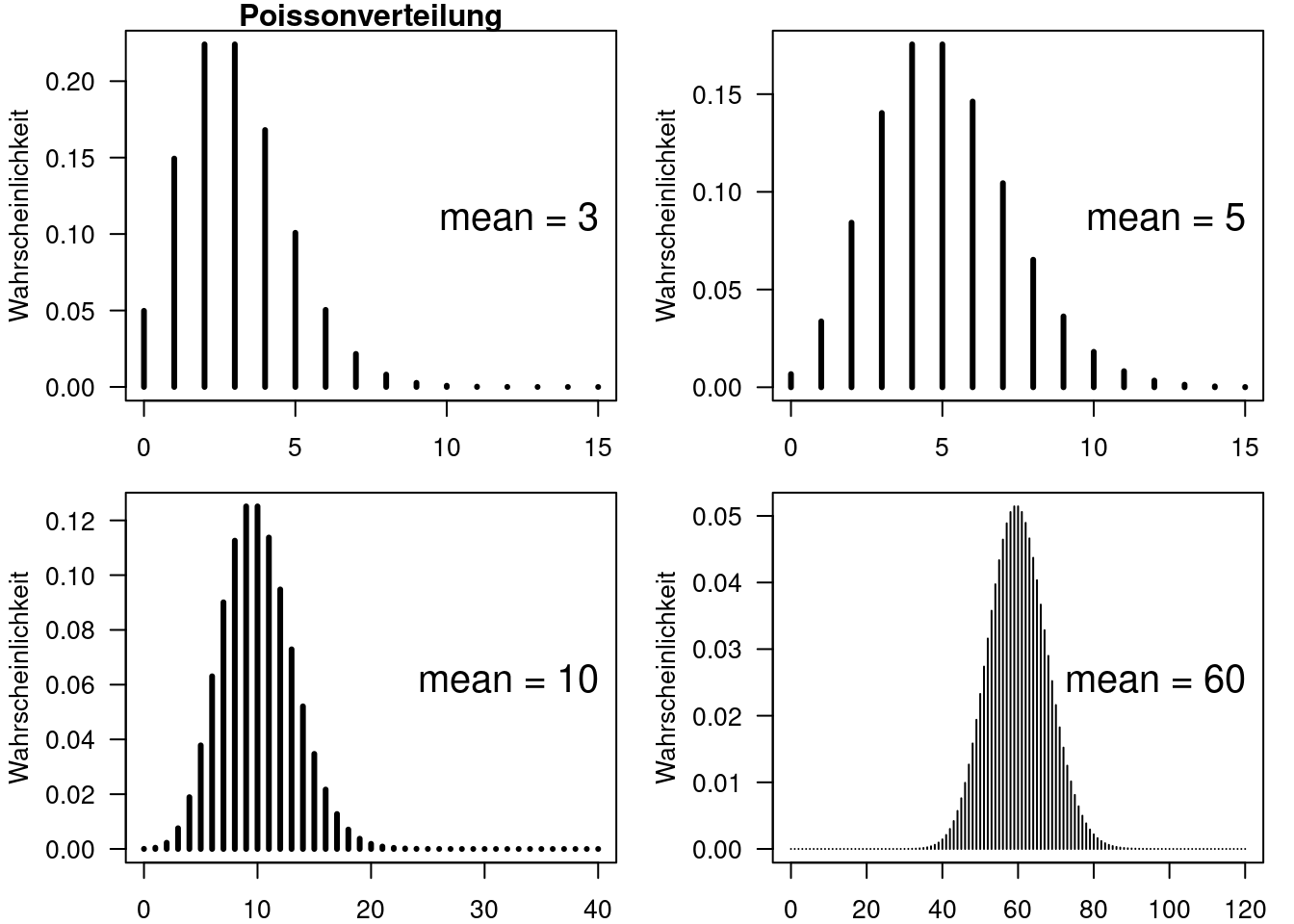
8.2 Diskrete-Verteilungen
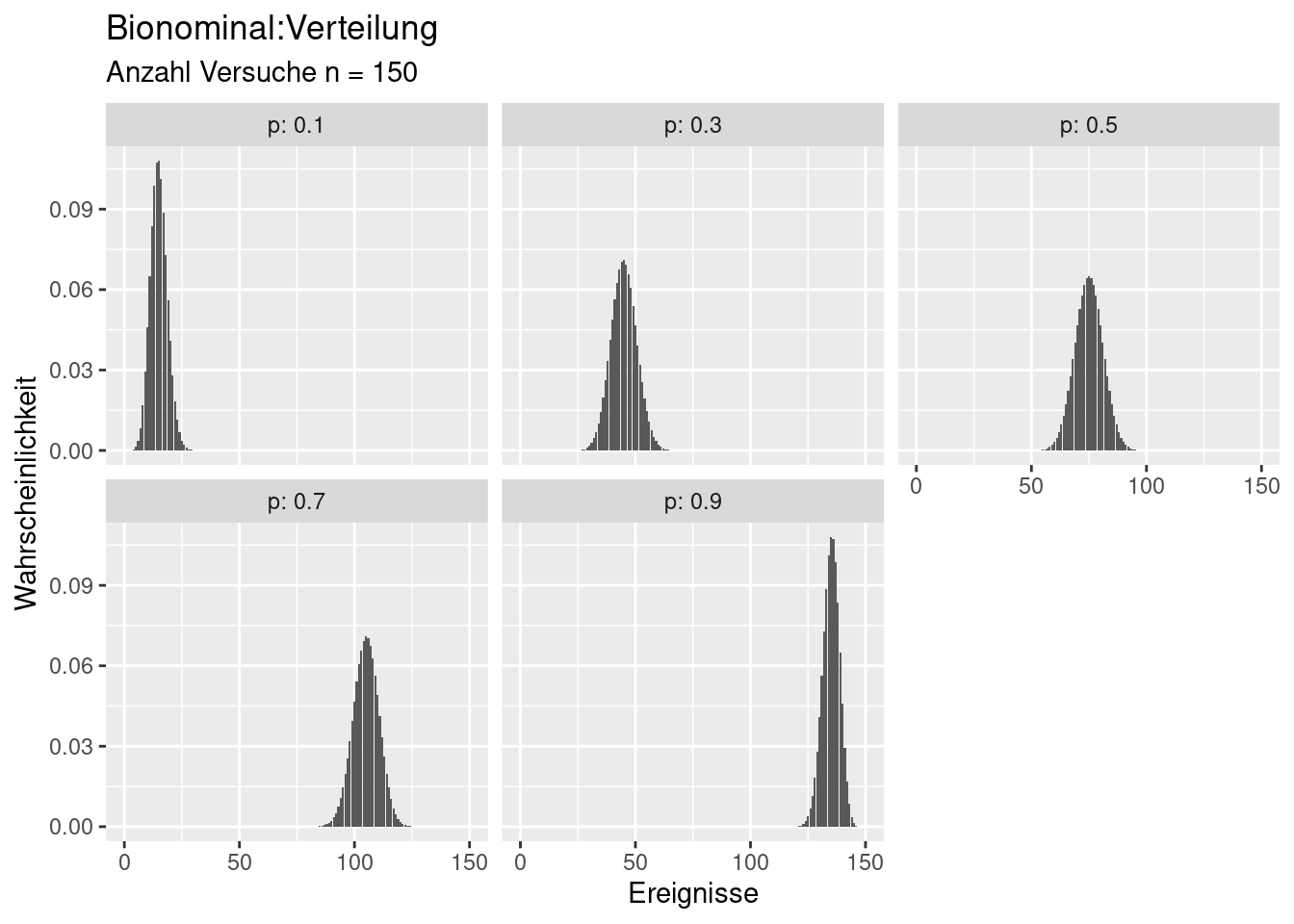
8.2.1 Binomial-Verteilung
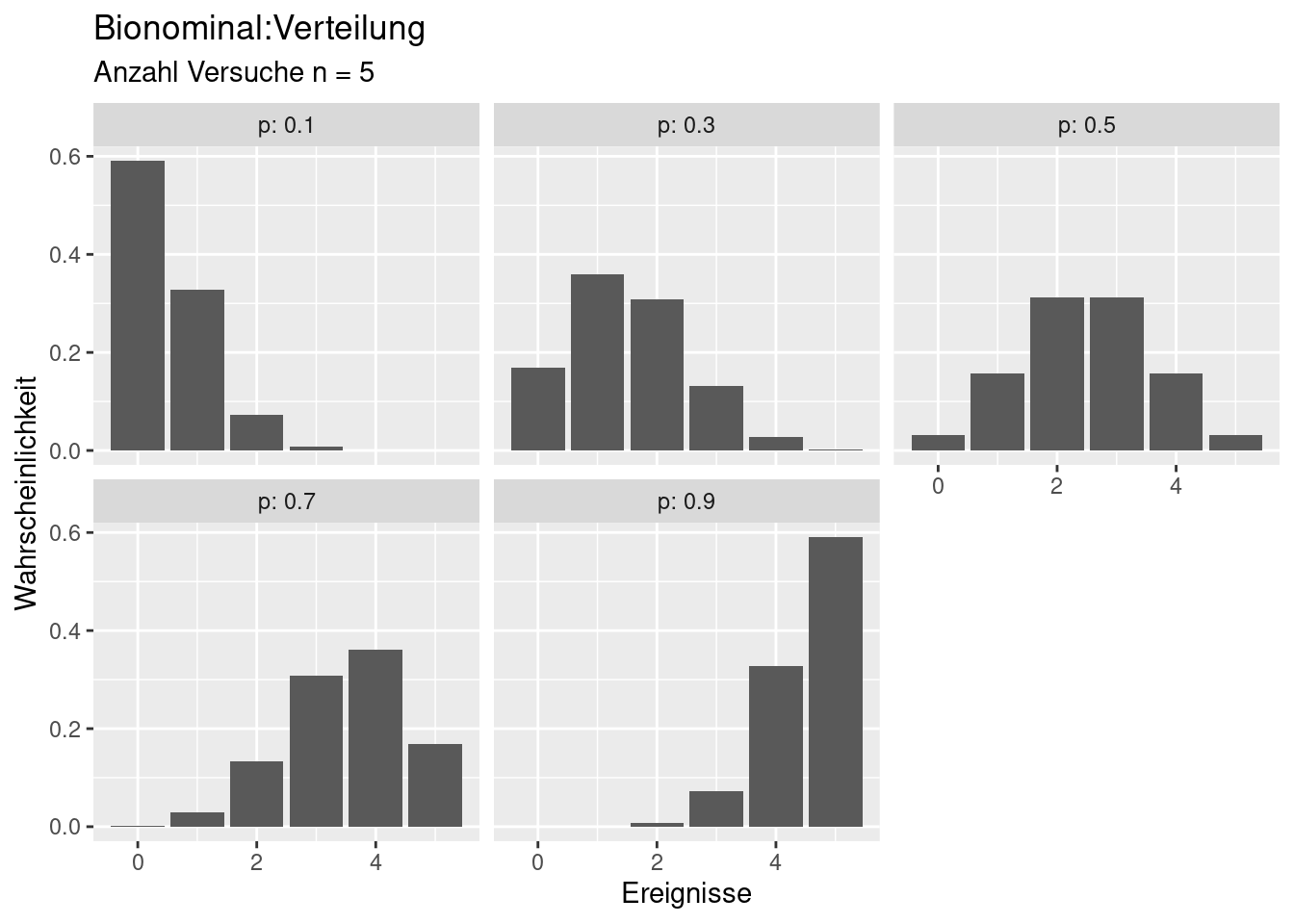
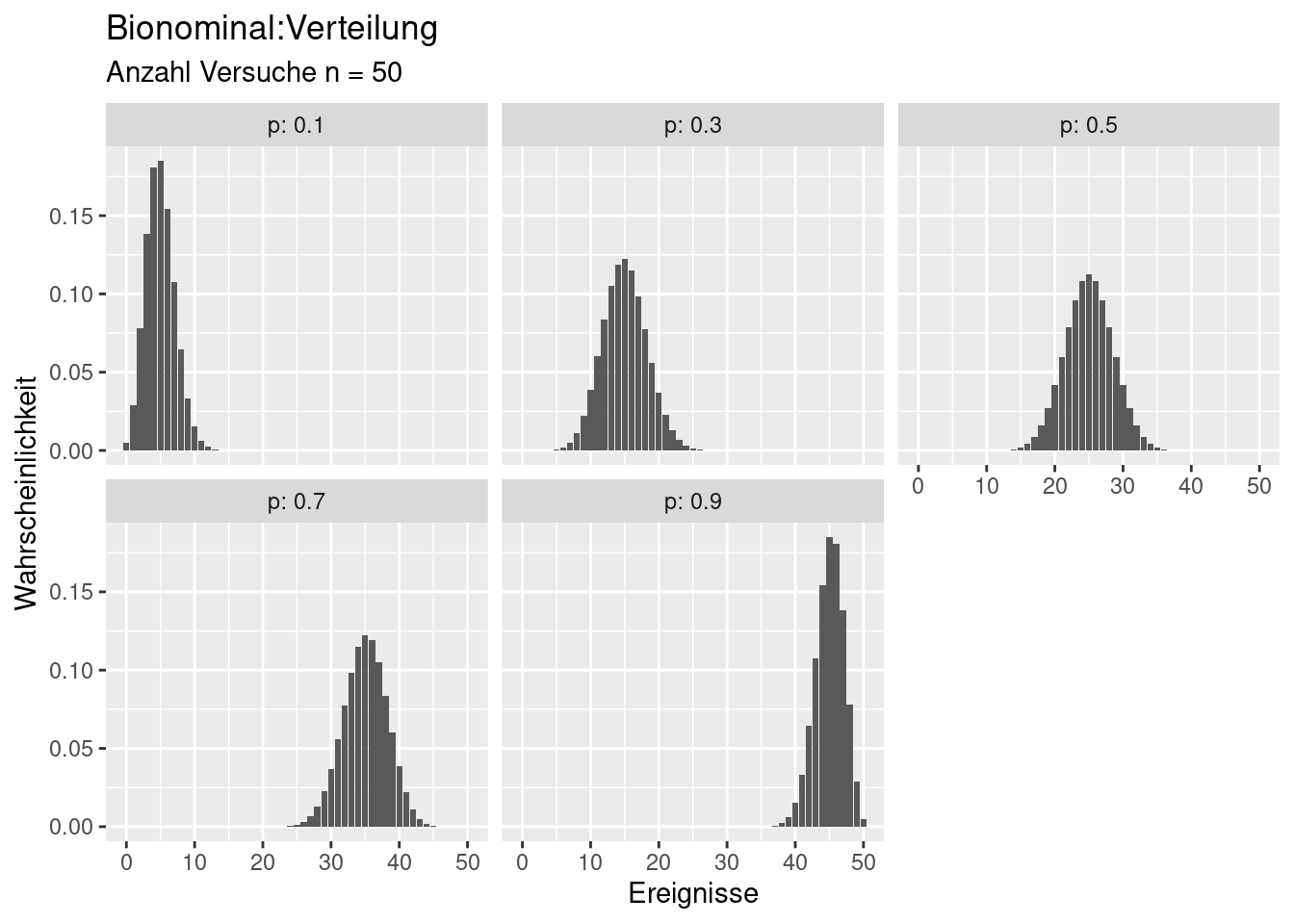
Die Binomial-Verteilung beschreibt, wie oft ein Ereigniss (success) bei einer definierten Anzahl \(n\) von Versuchen eintritt. Die Verteilung wird durch 2 Parameter beschrieben: \(n\) die Anzahl der Versuche und \(p\), die Wahrscheinlichkeit für das Eintreten des Ereignisses. Beispiele sind:
- Münzwurf
- Auftreten einer Art in einem bestimmten Gebiet
- Auftreten einer Landnutzungsveränderung wie Entwaldung, Baulandausweisung oder Aufgabe von Ackerland in einer Rasterzelle
- Anzahl des Auftretens einer Erkrankung (COVID-19, Dengue, Masern, Grippe,…) in einer Population (500 von 100.000 sind erkrankt)
- Anzahl der Wähler, die eine bestimmte Partei gewählt haben
Wenn \(n=1\) gilt, spricht man von der Bernoulliverteilung.
Verteilungsfunktion:
\[ Binom(k) = P(X=k|n,p) = \binom{n}{k}p^k(1-p)^{n-k} \]
Mittelwert: \(np\) Varianz: \(np(1-p)\)
Bei \(p=0.5\) ist die Verteilung symmetrisch. Für großes \(n\) ähnelt die Verteilung dann (\(p=0.5\)) einer diskreten Form der Normalverteilung.
8.2.2 Poisson-Verteilung
Die Poisson Verteilung wird für die Modellierung von Zähldaten, z.B. Artenzahlen, Anzahl Infizierter, Anzahl Wähler einer Partei,… verwendet. Die Verteilung kann nur Ganzzahlwerte, sogenannte Integer, annehmen. Im Gegensatz zur Binomial-Verteilung ist vorab nicht notwendigerweise bekannt, wieviel Ereignisse es maximal geben kann.
Charakterischtisch für die Verteilung ist, dass die Varianz mit dem Mittelwert zunimmt, genauer gesagt gilt: \[ Varianz = Mean \]. Dieses Merkmal ist für Zähldaten relevant: wenn man sich z.B. die Anzahl von Hochwasserereignissen für unterschiedliche Fließgewässer anschaut, dann ist für ein kleines Fließgewässer im Flachland ohne nennenswerte Zuflüsse vielleicht im Mittel mit einem Hochwasser in 50 Jahren zu rechnen. In diesem Fall kann man erwarten, dass in einem 50-Jahreintervall auch mal kein Hochwasser, zwei oder 3 Hochwasser auftreten. Das 5 Hochwasser auftreten ist sehr unwahrscheinlich. Stellen wir daneben ein Fließgewässer im Mittelgebirge, in dessen Einzugsgebiet viele Starkregenereignisse eintreten würden. Nehmen wir an, dass dort in 50 Jahren im statistischen Mittel 30 Hochwasser auftreten würden. Dann wäre es für ein 50-Jahresintervall nicht unwahrscheinlich, auch 25,26, 27,…33,34, 35 Hochwasser auftreten. Mit zunehmendem Mittelwert steigt also die Varianz.
Der Mittelwert ist der einzige Parameter der Poissonverteilung.
\[ Poisson(k) = P(X=k|\lambda) = \frac{\lambda^ke^{-\lambda}}{k!}\] Mittelwert: \(\lambda\) Varianz: \(\lambda\)
Die Poissionverteilung ist rechtsschief. Dies ist insbesondere für kleiner Mittelwerte der Fall. Mit größer werdendem Mittelwert wird die Verteilung zunehmend symmetrischer und nähert sich der Form einer Normalverteilung an - allerdings werden wie beschrieben nur diskrete Werte angenommen.
Schauen wir uns nochmal ein Beispiel an: Wie wahrscheinlich ist es bei einer Poissonverteilung auf einer Insel 10 Vogelarten zu beobachten, wenn wir im Mittel 7 Vogelarten erwarten?
## [1] 0.07098327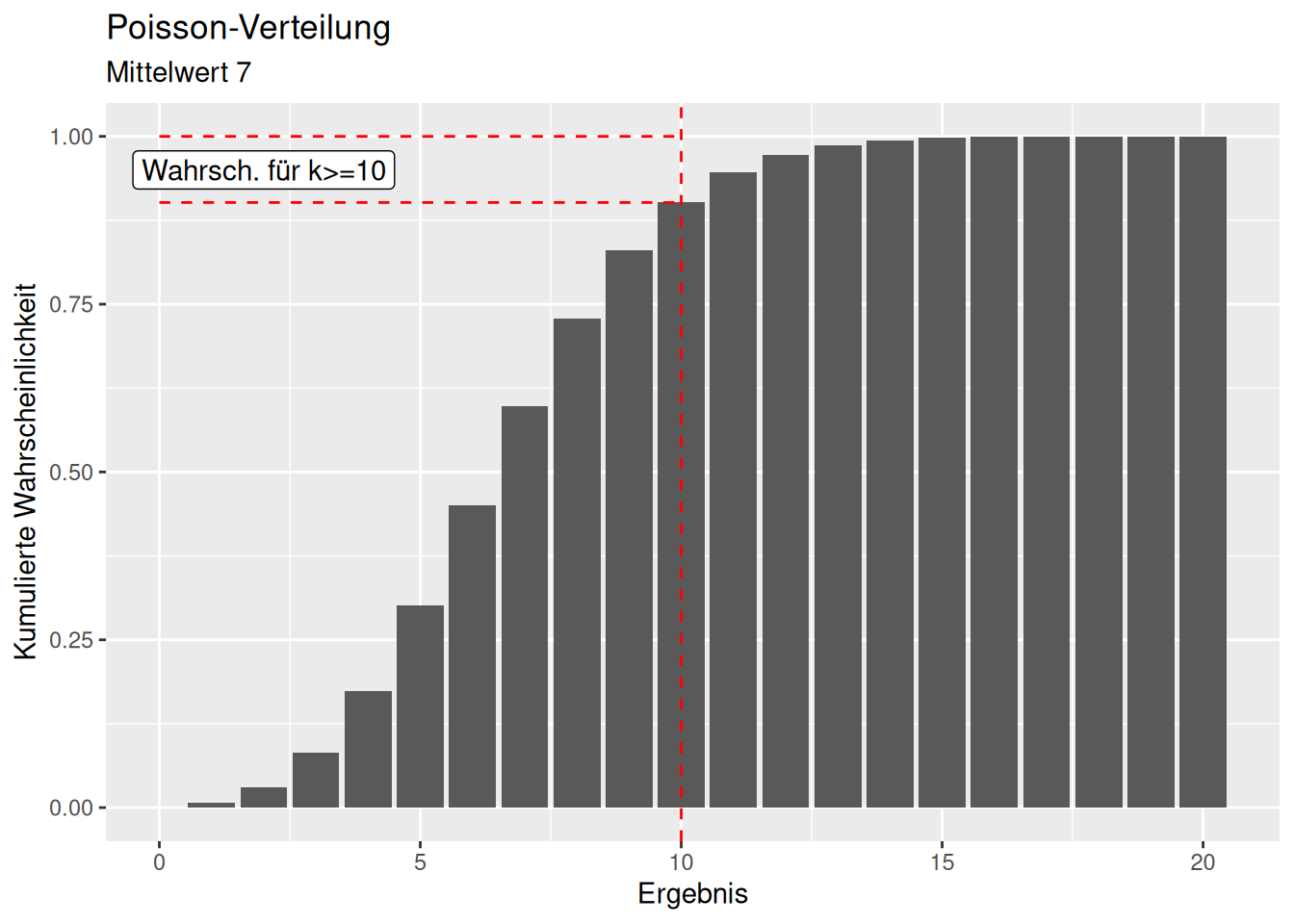
Wie wahrscheinlich ist es bei einer Poissonverteilung auf einer Insel 10 oder mehr Vogelarten zu beobachten, wenn wir im Mittel 7 Vogelarten erwarten?
## [1] 0.09852079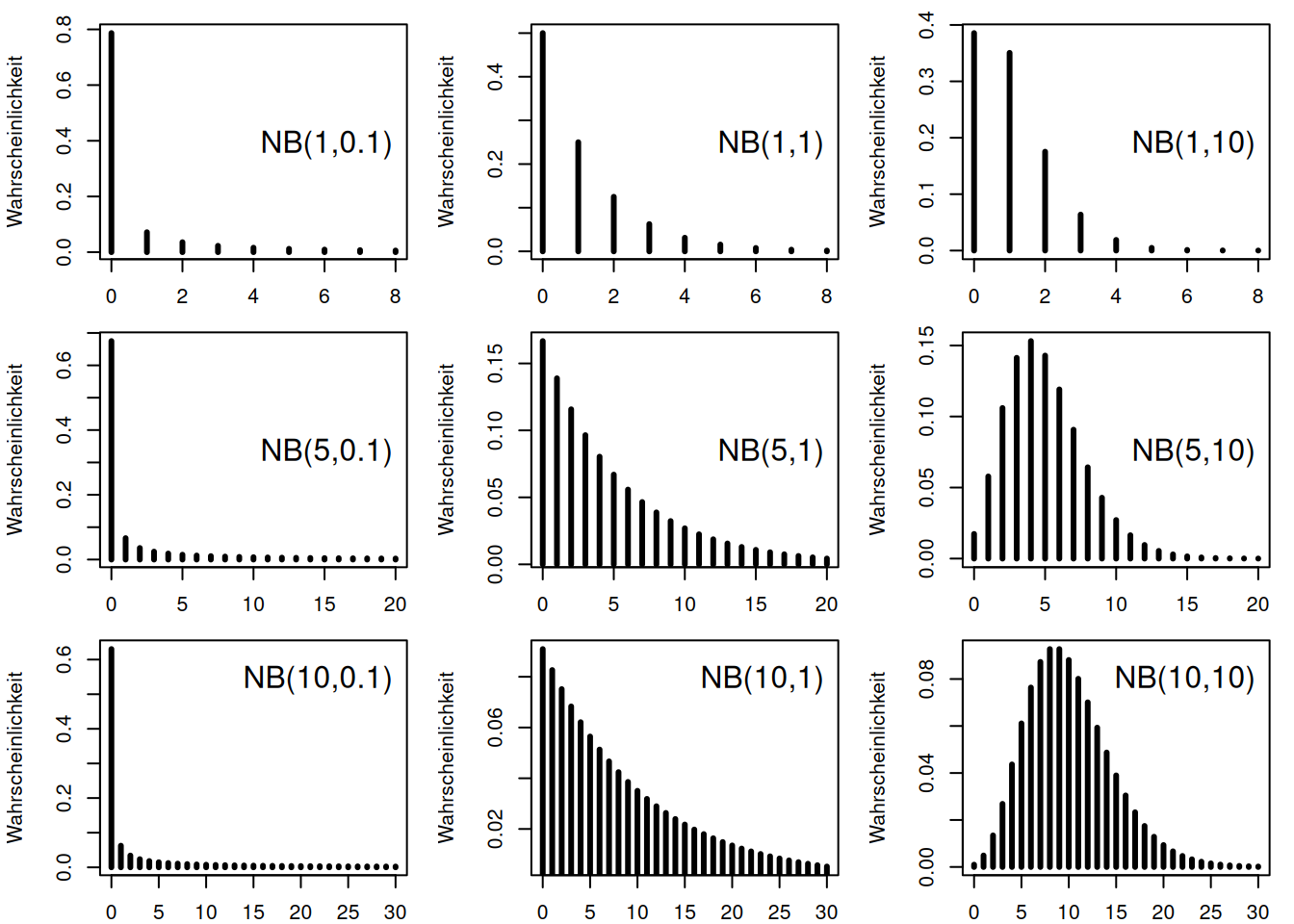
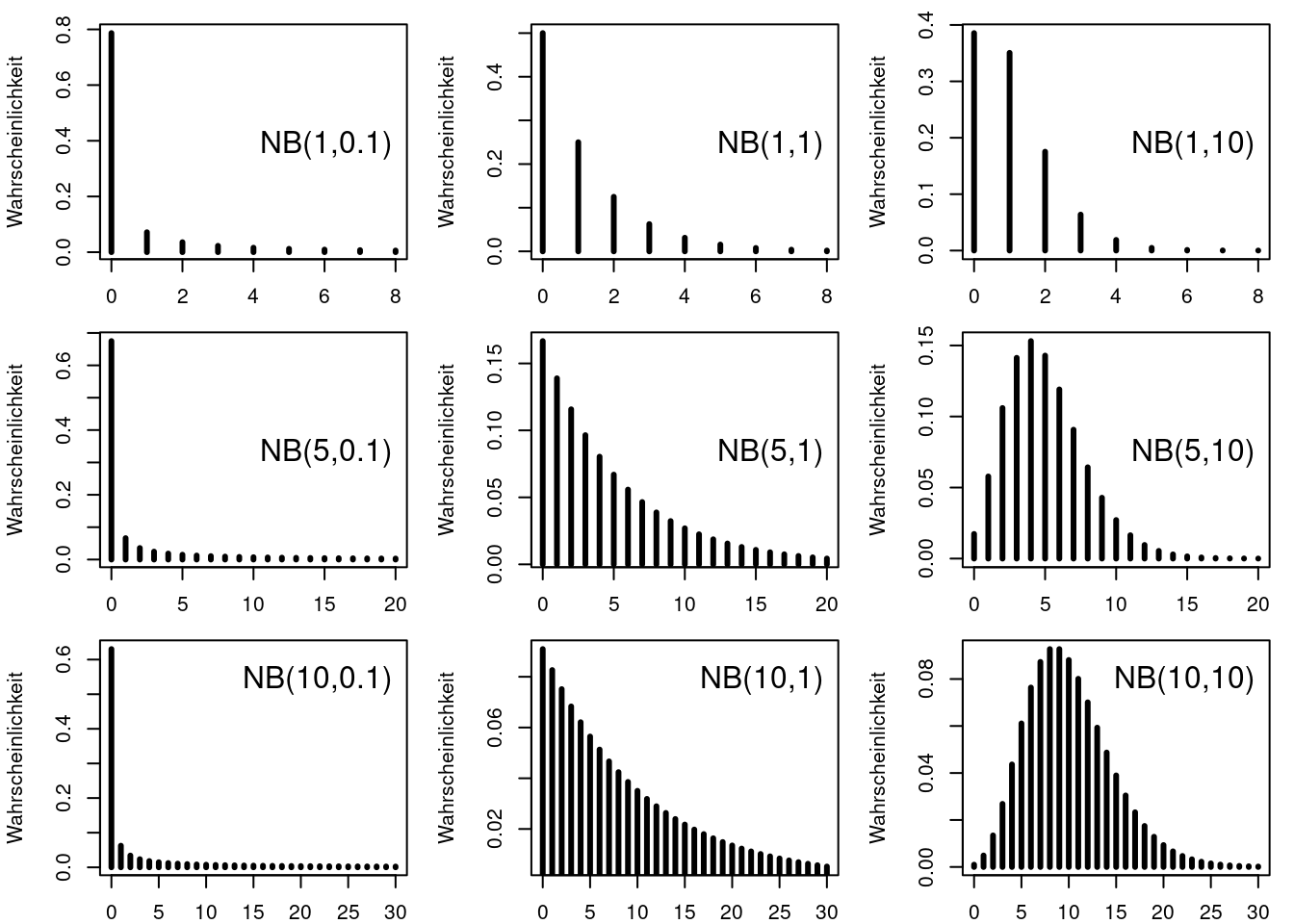
8.2.3 Negative Bionomial-Verteilung
Auch die negative Bionomial-Verteilung beschreibt Zähldaten. Allerdings kann sie auch Fälle beschreiben, bei denen die Varianz stärker (overdispersed) oder schwächer (underdispersed) als der Mittelwert ansteigt. Also ist die Varianz bei gleichem Mittelweret größer oder kleiner als bei der Poisssonverteilung. Bei dieser Herleitung wir die Verteilung anhand des Mittelwerte \(\mu\) (entspricht \(\lambda\) bei der Poissonverteilung) und des Dispersionsparameters \(size\) beschrieben.
Der Mittelwert ergibt sich dabei aus Wahrscheinlichkeit \(p\) für Eintreten des Ereignisses bei einem Versuch: \(\mu = \frac{r \cdot p}{1-p}\). Die Beziehung zwischen Mittelwert und Varianz wird hierbei über ein Polynom 2. Grades beschrieben: $ Varianz = + {size}$ bzw. $ $. Je kleiner der Dispersionsparameter, desto stärker wächst die Varianz mit dem Mittelwert.
Man kann die negative Bionmial-Verteilung auch über die Binomialverteilung herleiten. Dann beschreibt sie die Wahrscheinlichkeit, wann in einem Bernoulli-Prozess der r-te Erfolg erzielt wurde. Also z.B. nach wievielen Versuche man beim Münzwurf im Mittel achtmal Zahl erhalten hat oder wieviele Kraftfahrzeuge man im Mittel beobachten muss, um fünf falsche Abbiegevorgänge zu dokumentieren (falls die Abbiegevorgänge unabhängig voneinander sind).
Die Wahrscheinlichkeit für das Eintreten \(r\)-ten Ereignisse nach \(k\) Versuchen bei gegebener Wahrscheinlichkeit \(p\) für Eintreten des Ereignisses bei einem Versuch beträgt:
\[P(X=k|r,p) = \binom{k-1}{r-1}(1-p)^r p^{k-r}\]
In R wird eine leicht alternative Parametrisierung verwendet: hierbei wird die Anzahl von Fehlschlägen \(d = k -r\) bis zum \(r\)-ten Erfolg - bei gegebener Wahrscheinlichkeit \(p\) für Eintreten des Ereignisses bei einem Versuch - abgebildet:
\[P(X=d|r,p) = \binom{d + r-1}{r-1}(1-p)^r p^d\]
Beide Herleitungen sind einfach ineinander überführbar, da \(p = \frac{r}{r+\mu}\) bzw. \(\mu = \frac{r \cdot p}{1-p}\)
Die Poisson Verteilung ist ein Spezialfall für \(r \rightarrow \infty\): \[Poisson(\lambda)= \lim_{r \to \infty} NB(r, \frac{\lambda}{\lambda + r})\]
Verteilung für unterschiedliche Mittelwerte und k-Werte
Schauen wir uns einmal ein Beispiel an: Angenommen, wir haben Vogelbeobachtungsdaten bzgl. einer Art und fragen uns, ob einzelne Standorte auffällig sind, da die Zahlen höher oder niedriger als im Mittel sind. Wenn wir eine Poissonverteilung unterstellen, können wir die Wahrscheinlichkeit 5 Vögel der Art zu beobachten wenn wir im Gebiet im Mittel 4 Vögel erwarten wie folgt berechnen:
## [1] 0.1562935Eine Beobachtung von 5 Vögeln der Art erscheint also nicht unbedingt auffällig im Vergleich zum Gebietsmittel.
Was passiert, wenn wir davon ausgehen müssen, dass die Zähldaten eine stärkere Zunahme der Varianz mit dem Mittelwert aufweisen? Für einen Dispersionsparameter von 3 beträgt die Wahrscheinlichkeit 5 Vögel der Art zu beobachten, wenn wir im Gebiet im Mittel 4 Vögel erwarten:
## [1] 0.1007161Die Wahrscheinlichkeit ist geringer, trotzdem sind Standorte mit 5 Vögeln nicht wirklich auffällig.
Wenn wir einen Dispersionsparameter von 0,5 unterstellen verändert sich die Wahrscheinlichkeit 5 Vögel der Art zu beobachten, wenn wir im Gebiet im Mittel 4 Vögel erwarten wie folgt:
## [1] 0.04552152Nochmals deutlich kleiner, allerdings immer noch nicht unbedingt auffällig.
Schauen wir uns das einmal als Plots an:
Was passiert, wenn wir von einer Art ausgehen, welche im Gebiet im Mittel je Standort 40 mal beobachtet wird? Die Wahrsheinlichkeit 50 Vögel zu beobachten ist natürlich deutlich kleiner.
## [1] 0.01770702## [1] 0.01210818## [1] 0.004751823Im Vergleich dazu jeweils die Werte für die Beobachtung des Mittelwertes von 40 an einem Standort
## [1] 0.06294704## [1] 0.01620403## [1] 0.006011656Der Übersichtlichkeit halber als Tabelle:
birdSpotting <- data.frame(model=c("Poisson", rep("neg. binomail", 2)), mu=rep(40,3), dispersionsk = c(NA, 3, .5))
# Wahrscheinlichkeit für die Beobachtung von 40 Individuen
birdSpotting$p_40 <- c(dpois(x=40, lambda=40),
dnbinom(x=40,mu=40, size = 3),
dnbinom(x=40,mu=40, size = .5))
# Wahrscheinlichkeit für die Beobachtung von 50 Individuen
birdSpotting$p_50 <- c(dpois(x=50, lambda=40),
dnbinom(x=50,mu=40, size = 3),
dnbinom(x=50,mu=40, size = .5))
# Verhältnis Wahrscheinlichkeit für 50 zur Wahrscheinlichkeit für 40 Individuen
birdSpotting$rel_50_to_40 <- birdSpotting$p_50 / birdSpotting$p_40
birdSpotting## model mu dispersionsk p_40 p_50 rel_50_to_40
## 1 Poisson 40 NA 0.062947039 0.017707018 0.2813002
## 2 neg. binomail 40 3.0 0.016204028 0.012108176 0.7472325
## 3 neg. binomail 40 0.5 0.006011656 0.004751823 0.7904349Durch die höhere Varianz bei den beiden negativ-binominalverteilten Daten nimmt die Wahrscheinlichkeit der Beobachtung von 50 Vögeln im Verhältnis zur Wahrscheinlichkeit der Beobachtung von 40 Vögeln weniger stark ab als bei der Poissonverteilung.
Das Ganze noch einmal in Plotform:
x <- 1:150
p1 <- makePlot_pois(x, lambda=40, ylim=c(0,.2)) +
geom_vline(xintercept = 50, col="red", lty=2)
p4 <- makePlot_nb(x, mu=40, size = 50, ylim=c(0,.2)) +
geom_vline(xintercept = 50, col="red", lty=2)
p2 <- makePlot_nb(x, mu=40, size = 3, ylim=c(0,.2)) +
geom_vline(xintercept = 50, col="red", lty=2)
p3 <- makePlot_nb(x, mu=40, size = .5, ylim=c(0,.2)) +
geom_vline(xintercept = 50, col="red", lty=2)
ggarrange(p1, p4,p2, p3)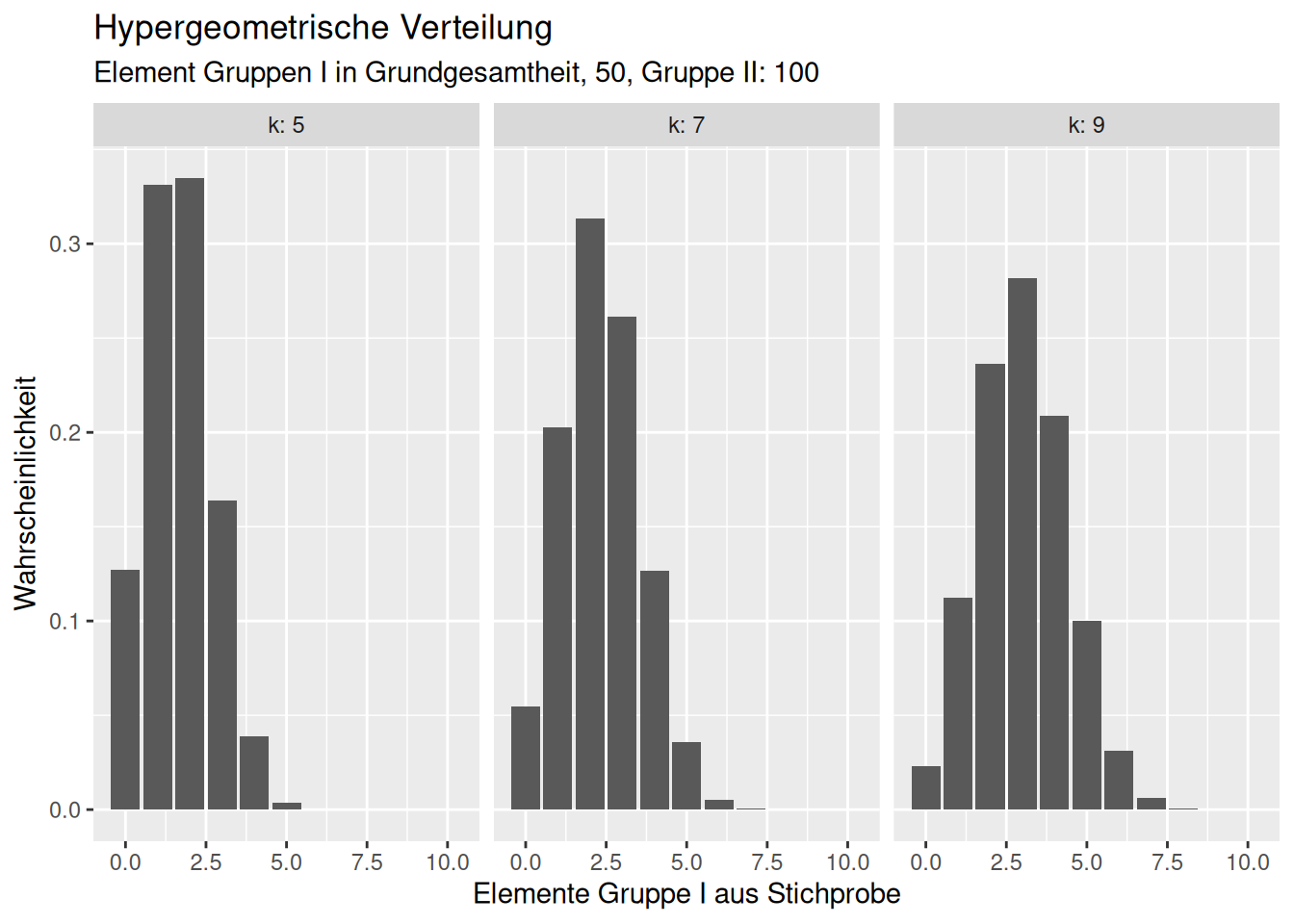
In der Praxis müssen wir den Dispersionsparameter i.d.R. nicht raten sondern können den Wert anhand der Daten schätzen.
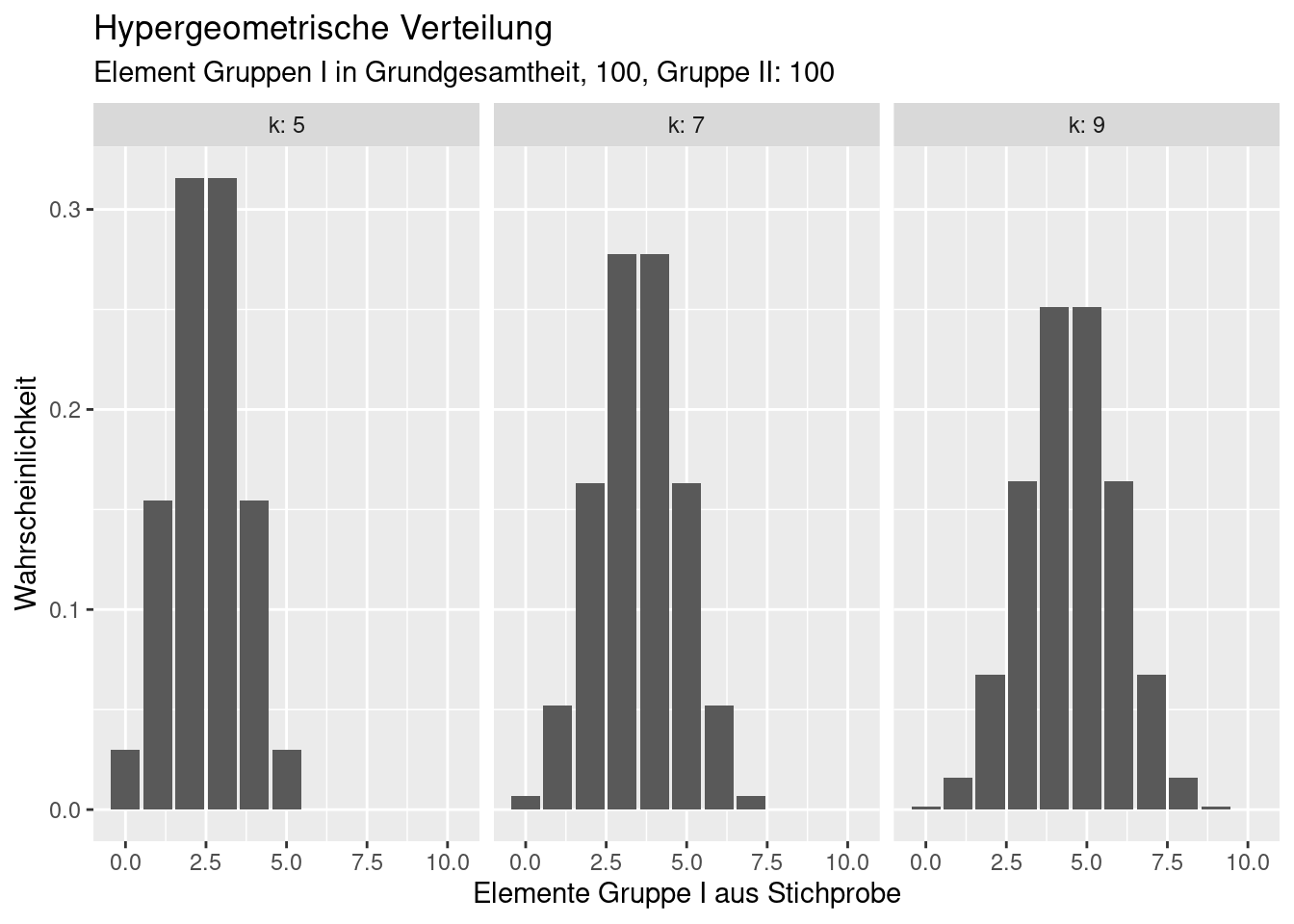
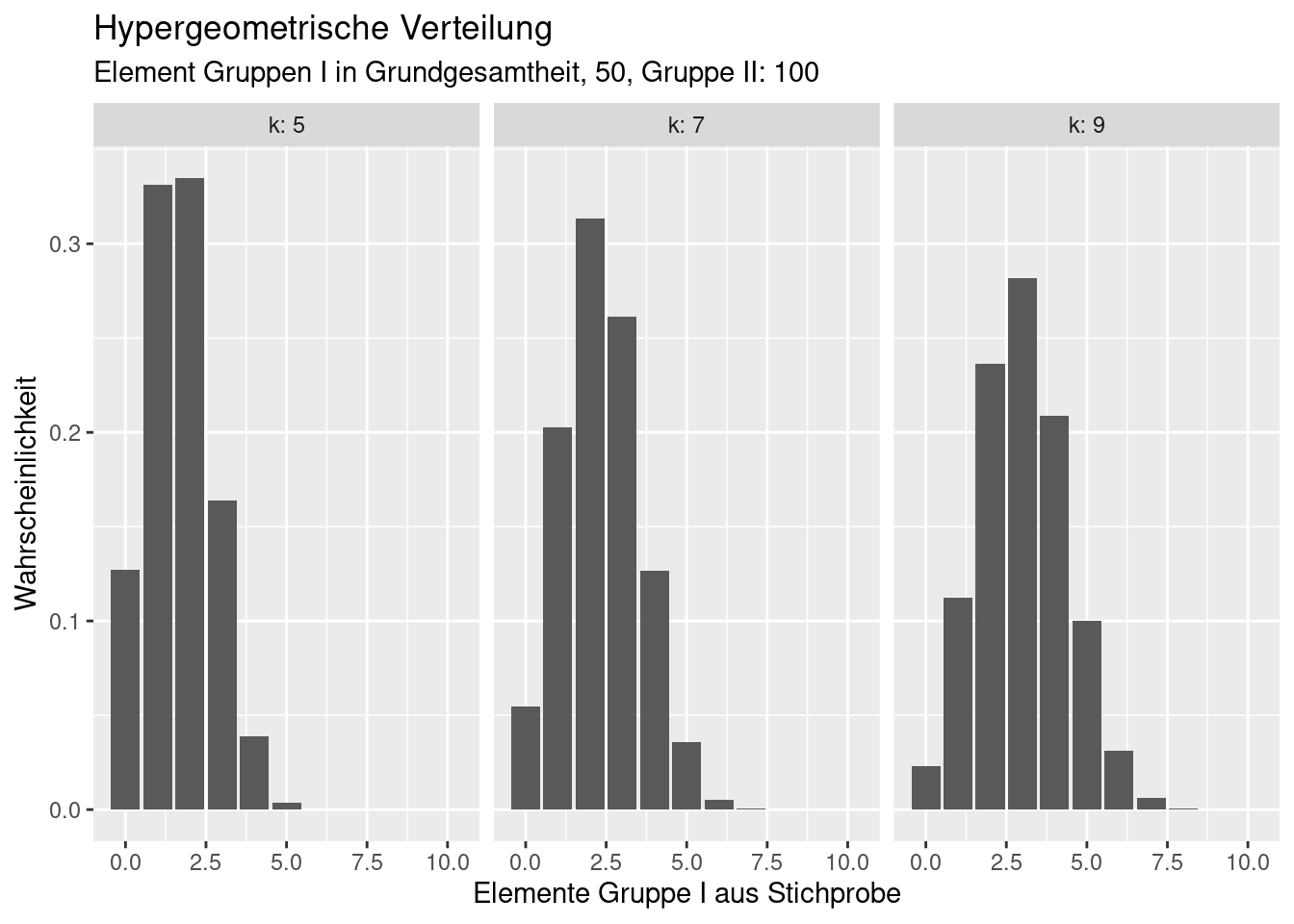
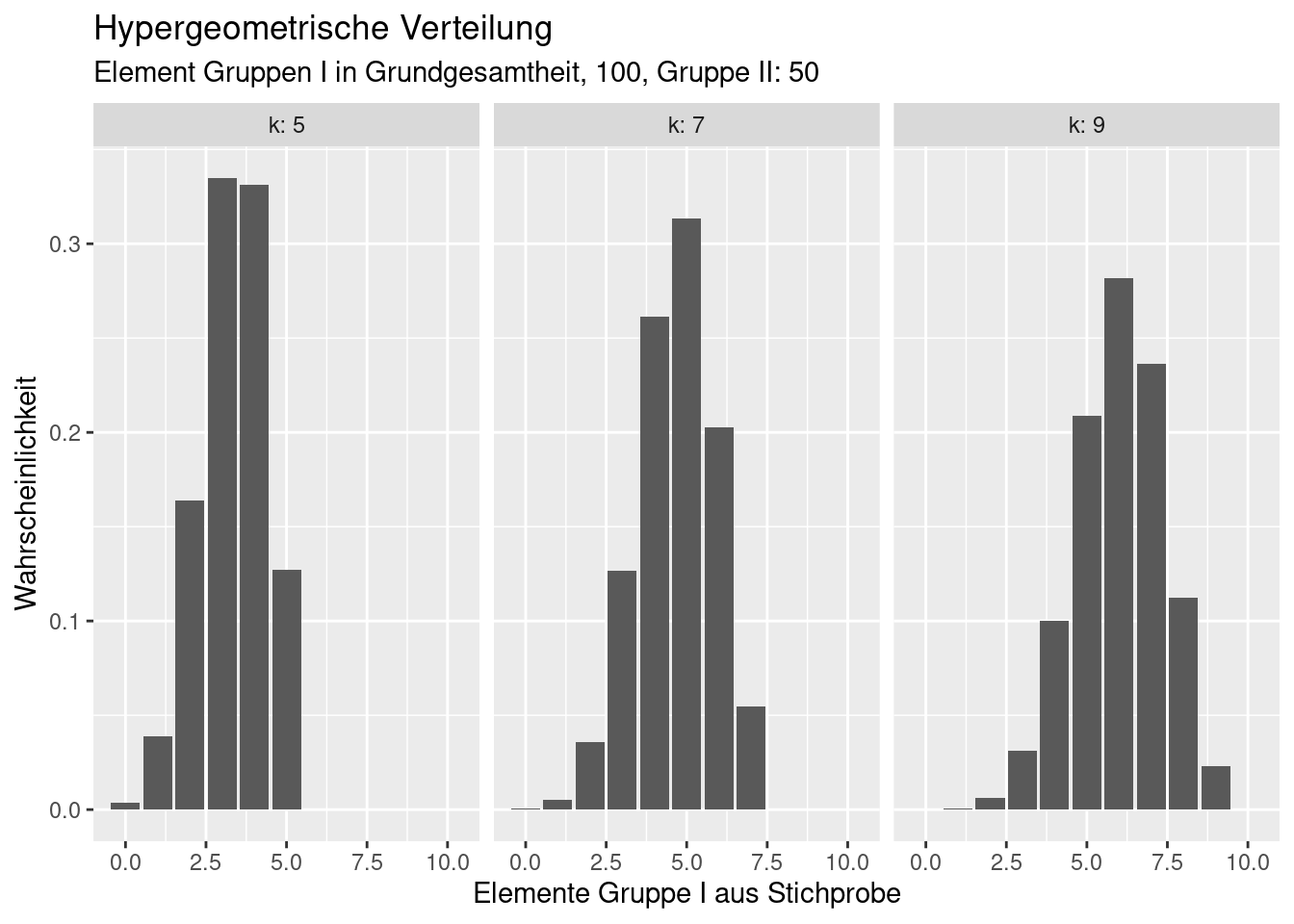
8.2.4 Hypergeometrische-Verteilung
Die hypergeometrische Verteilung beschreibt die Wahrscheinlichkeit dafür, dass bei \(N\) gegebenen Elementen („Grundgesamtheit des Umfangs N“), von denen \(M\) die gewünschte Eigenschaft besitzen, beim Ziehen einer Stichprobe des Umfanges \(n\) genau \(k\) Treffer erzielt werden, d.h. die Wahrscheinlichkeit für \(X = k\) Erfolge bei \(n\) Versuchen.
Sie hat z.B. in der Tierökologie Bedeutung, wenn z.B. 100 Individuen einer Art in einem Gebiet gefangen und markiert (z.B. beringt ) werden und bei einem zweiten Ausbringen von Fallen 30 von 100 gefangenen Exemplaren markiert sind, kann man mit der hypergeometrischen Verteilung die Abundanz (Anzahl Individuen) im Gebiet schätzen. Man einen ähnlichen Ansatz verfolgen, um Teilnehmer eines Großereignissen (z.B. Demonstration zu schätzen), indem man z.B. vorab eien Anzahl markanter Gegenstände (z.B. rote Hüte) ausgibt und dann einen Ausschnitt des Ereingnisses auszählt.
Die Verteilung ist durch 3 Parameter charakterisiert:
- die Anzahl m der Elemente einer Grundgesamtheit, die zu der Gruppe mit der gewünschten Eigenschaft gehören
- die Anzahl n der Elemente einer Grundgesamtheit, die nicht zu der Gruppe mit der gewünschten Eigenschaft gehören
- die Stichprobengröße \(k \leq (m+n)\)
Alternativ kann die Verteilung auch mit der Anzahl aller Elemente in der Grundgesamtheit (\(N\)) und \(m\) (oder \(n\)) und \(k\) definiert werden.
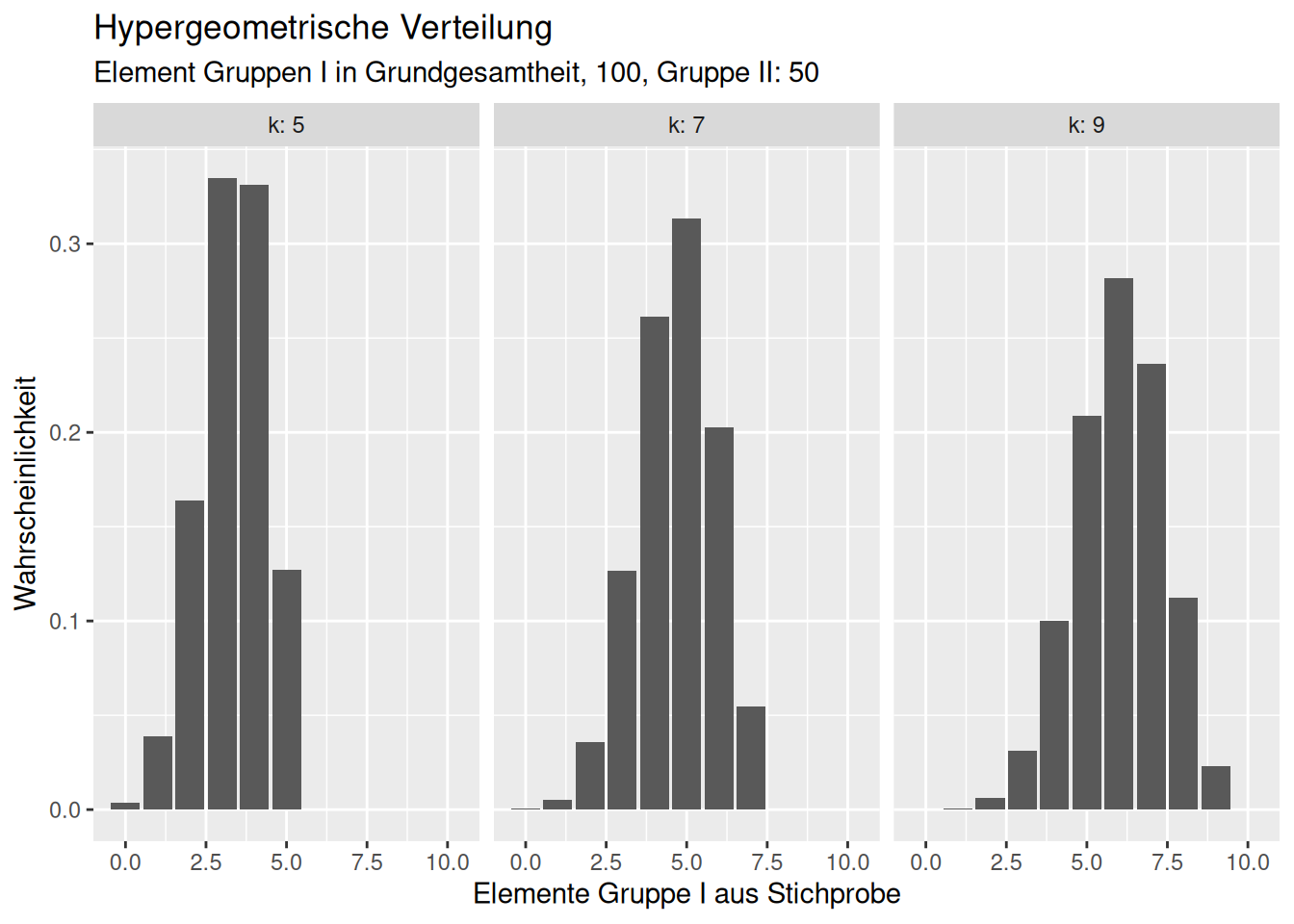
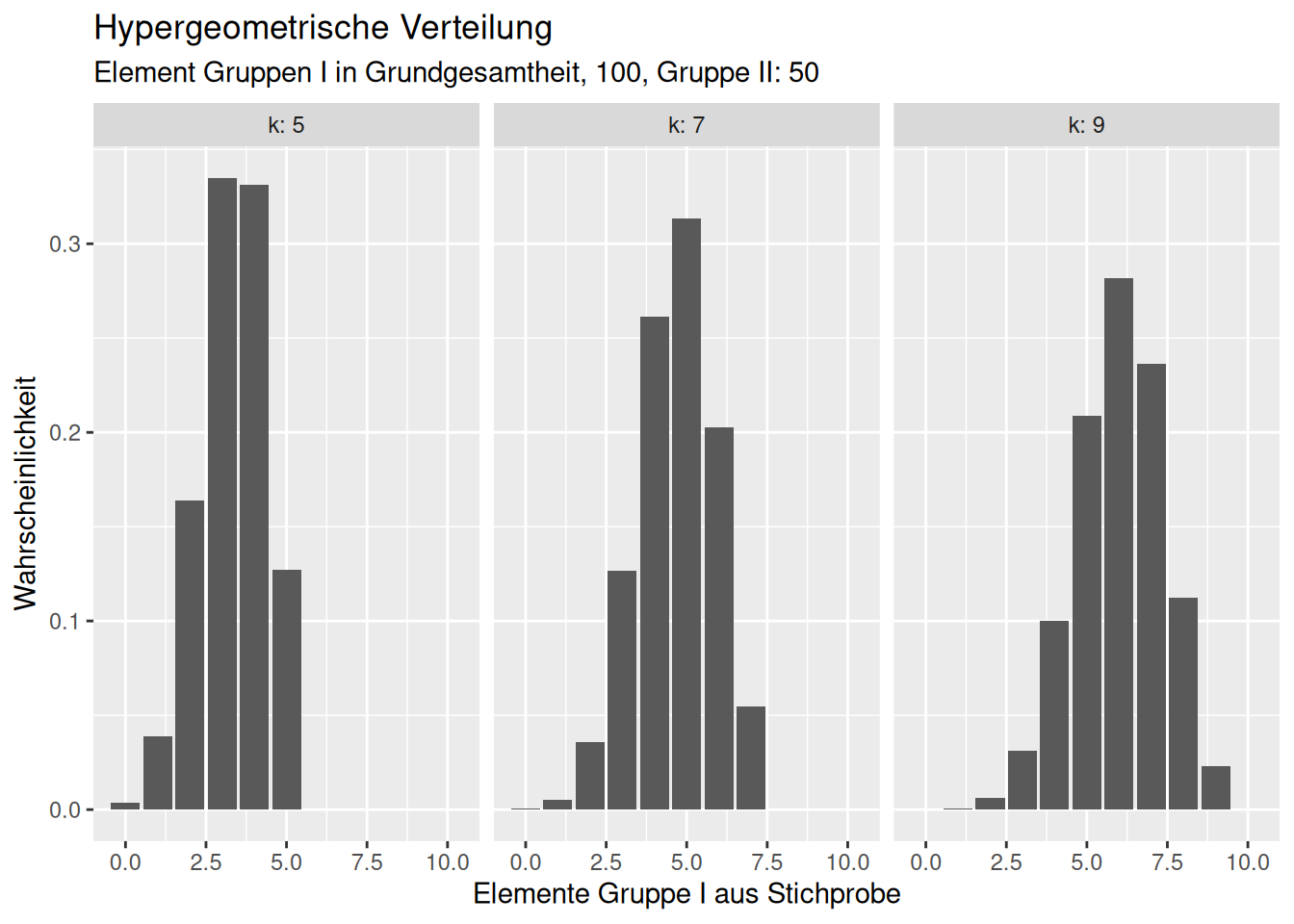
8.3 Welche Verteilung einet sich für welchen Zweck?
Grundsätzlich geht es draum, die Verteilung auszuwählen, die für einen bestimmten Anwendungszweck am besten geeignet ist. Dabei kann man sowohl empirisch vorgehen (welche Verteilung beschreibt die Stichprobe am besten?) als auch deduktiv vorgehen und sich z.B. Fragen, welche Eigenschaften eine Verteilung haben sollte. Oftmals wird man eine Kombination beider Vorgehensweisen verwenden um zum Ziel zu kommen.
Es lohnt sich auf jeden Fall zu überlegen, welche Eigenschaften man erwartet und dann zu prüfen, welche Verteilungen diese Eigenschaften erfüllen. Beispiele für solche Eigenschaften sind:
- diskret oder kontinuierlich
- will man diskrete Ereignisse modellieren (z.B. Anzahl von Krankheitsfällen, Anzahl von Unfällen zwischen Radfahrern und Autofahren) oder können die Daten Zwischenwerte annehmen (z.B. Temperaturwerte, Niederschlagsmenge, Schwermetallkonzentration im Auensediment)
- zulässiger Wertebereich
- sind positive und negative Werte zulässig oder nur positive Werte, ggf. auch nur strikt positive Werte (also ohne Null)?
- Beispiele für Daten, die nicht negativ sein können sind z.B. Stoff-Konzentrationen, Niederschlagsmengen, Temperaturen in °Kelvin oder Bevölkerungsdichte
- Schiefe und Neigung zu Ausreißern
- weiß man, dass der Prozess, der das Merkmal produziert mehr niedrige als hohe Werte produziert (oder umgekehrt?)
- weiß man ob der Prozess seltene Extremereignisse produziert? Beispiele sind Abfluss- und Niederschlagsmengen
- wie ist das Verhältnis von Mittelwert zu Varianz?
- kann man annehmen, dass die Variabilität unabhängig vom Mittelwert ist oder vermuten wir, dass sich die Variabilität mit dem Mittelwert erhöht oder erniedrigt?
- bei Messungenauigkeiten geht man oft davon aus, dass die Variabilität innerhalb eines sinnvollen Wertebereiches konstant ist
- bei anderen Prozessen muss man oft davon ausgehen, dass die Unsicherheit mit dem Erwartungswert steigt
- wenn wir die Anzahl von Studierenden in einem Studiengang betrachten und als Erwartungswert den Mittelwert der letzten Jahre annehmen, sollten wir davon ausgehen, dass der (absolute) Fehler bei großen Studiengängen höher ist als bei kleinen: Wenn im Mittel 10 Personen im 1. Mastersemester Ethnologie studieren, würden wir erwarten das in einem bestimmten Jahr vielleicht 5-12 Studierende das Studium begonnen haben. Bei einem Maschienenbau Bachelorstudiengang mit im Mittel 1000 Studierenden wird die Unsicherheit vermutlich höher ausfallen (vielleicht 950-1020)
8.3.1 Verhältnis von Mittelwert und Varianz
Die meisten Verteilungen besitzen einen Lage- und einen Streuungsparameter. Während bei der Gaussverteilung Mittelwert und Streung unabhängig voneinander sind, ist dies bei anderen Verteilungen nicht der Fall. So nimmt z.B. bei der Gamma und der inversne Gaussverteilung die Variabilität (bei ansonsten gleicher Parametrisierung) stark zu, wenn man den Erwartungswert von 1 auf 5 erhöht (bzw. bei der Gamma-Verteilung den shape Parameter bei konstantem scale Parameter so erhöht, dass sich der Erwartungswert von 1 auf 2 erhöht) - vergleiche Abb. 8.20. Im fall der Gamma-Verteilung steigt die Varianz quadratisch mit dem Erwartungswert, im Fall der inversen Gaussverteilung sogar in der dritten Potenz.
Daneben sieht man die ausgeprägte Schiefe von Gamma und inverser Gaussverteilung sowie das die Gaussverteilung bei einem Erwartungswert von \(\mu=1\) mit recht hoher Wahrscheinlichkeit negative Werte produziert.
Welche Verteilung zweckmäßig ist, hängt natürlich davon ab, welches Phänomen man modellieren möchte.
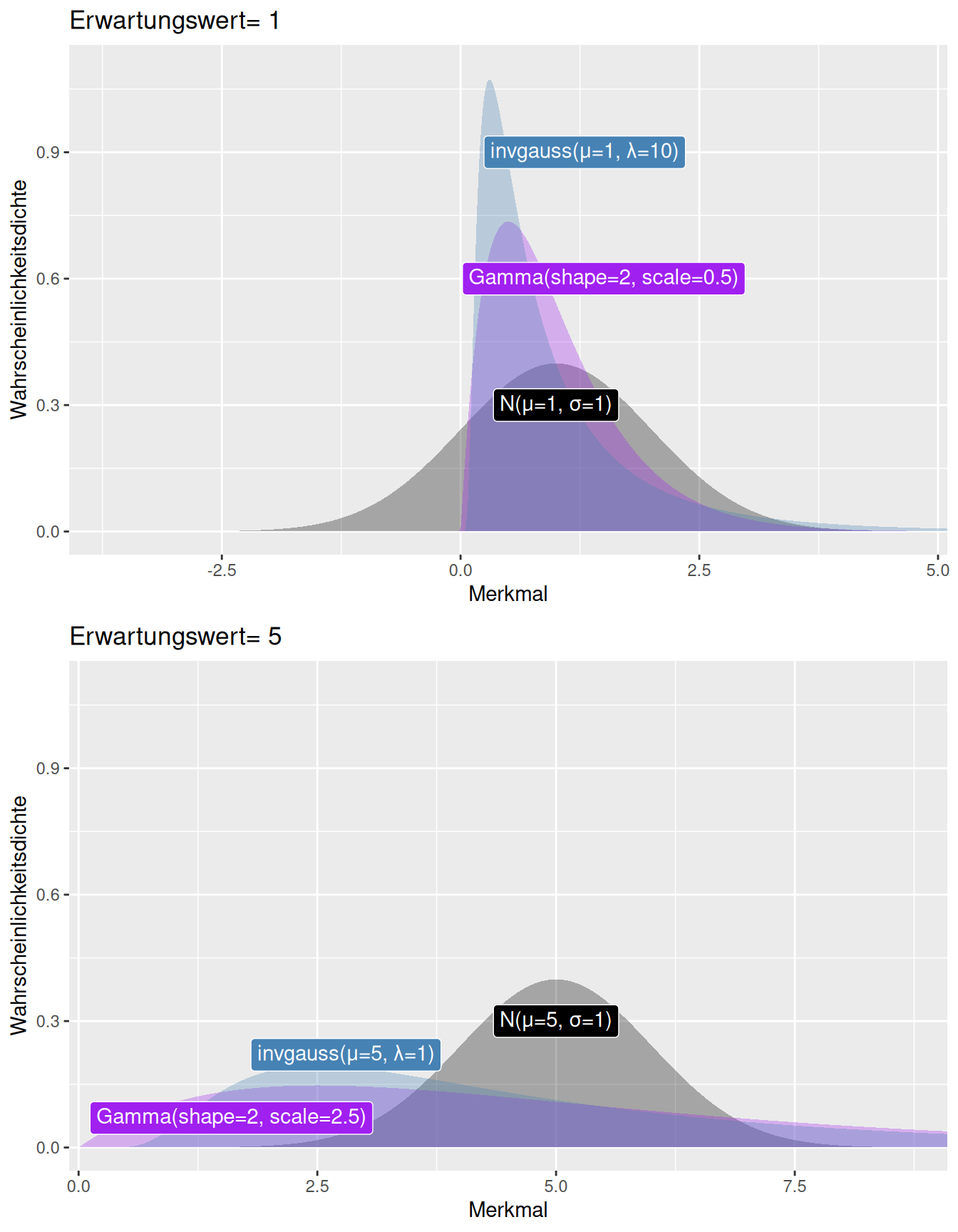
Figure 8.20: Veränderung der Variabilität mit dem Mittelwert für die Gauss-, Gamma und inverse Gaussverteilung. Die obere Abbildung zeigt die drei Verteilungen für einen Erwartungswert von 1, die untere (bei ansonsten gleicher Parametrisierung) für einen Erwartungswert von 5. Deutlich zu sehen ist, dass die Variabilität der Gamma und der inversen Gaussverteilung mit dem Mittelwert stark zunimmt. Die x-Achse ist auf der unteren Achse um 5 Einheiten translatiert (s. Achsenbeschriftung).
8.4 Schätzen von Verteilungsparametern mittels Maximum Likelihood
8.4.1 Likelihood
Die Likelihood ist so etwas wie die Umkehrung der Wahrscheinlichkeitsdichte. Die Wahrscheinlichkeitsdichte gibt an, wie wahrscheinlich eine Beobachtung bei der gegebenen Verteilung ist: \(P(x|\theta)\). Dabei ist \(x\) ein Datenpunkt und \(\theta\) sind die Parameter der Verteilung.
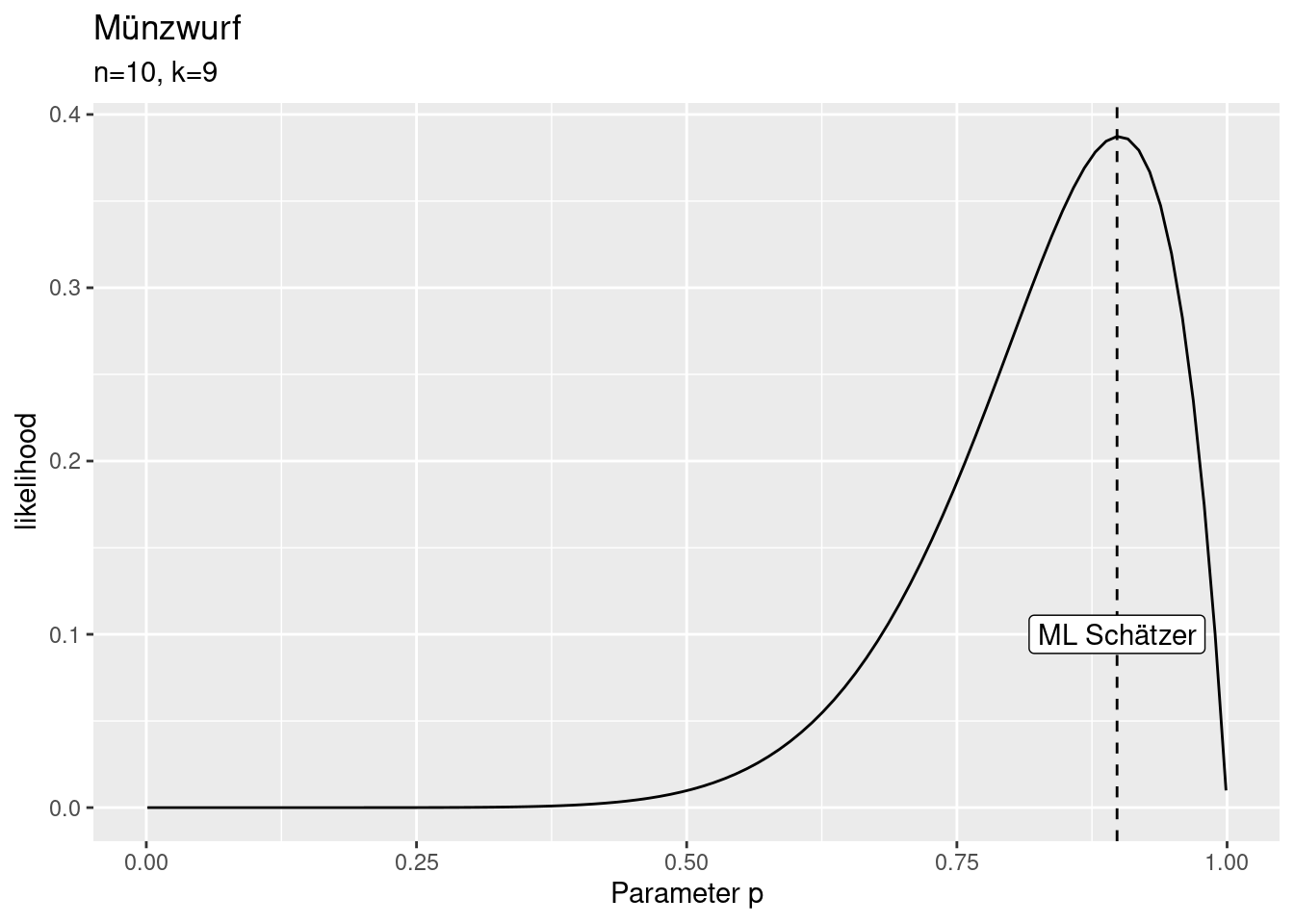
Die Likelihood dagegen gibt an, wie wahrscheinlich die Verteilungsparameter bei gegebenem Datenpunkt sind: \(L(\theta|x)\). Die Likelihood wird dabei eigentlich immer über mehrere Datenpunkte aggregiert. Sie beantwortet die Frage, wie wahrscheinlich bestimmte Verteilungsparameter für die beobachteten Daten sind - z.B. wie wahrscheinlich ist \(p=0.5\) (faire Münze), wenn wir aus Zehn Würfen neunmal Zahl geworfen haben? In dem Beispiel lässt sich die Wahrscheinlicheit ausrechnen - wir kennen ja die Verteilungsfunktion der Bionmialverteilung: \(P(X=10|p=0.5,n=10) = \binom{9}{10}0.5^9(1-p)^{10-9}\)
## [1] 0.009765625Also relativ unwahrscheinlich. Wie wahrscheinlich ist \(p=0.4\)?
## [1] 0.001572864Noch unwahrscheinlicher als \(p=0.5\). Was ist mit \(p=0.9\)?
## [1] 0.3874205Und \(p=0.95\)?
## [1] 0.3151247Wir sehen also, dass unterschiedliche Parameterwerte unterschiedlich wahrscheinlich sind bei den gegebenen Beobachtungen. Der Gedanke der Maximum Likelihood Schätzung ist es nun, den Parameterwert zu finden, der die höchste Wahrscheinlichkeit hat (bei gegebenen Daten).
Wir testen in einer Schleife (genauer gesagt mit Hilfe von sapply, was eine Funktion auf jedes Element eines Vektor mapped) hierfür einfach den ganzen Wertebereich durch und ermitteln den Wert mit der höchsten Likelihood. In Realität gibt es clevere Methoden, als alles durchzutesten, analystisch oder mit Hilfe von Optimierungsverfahren.
binomLik <- function(k,n, p)
{
choose(k=k,n=n)*p ^k * (1-p)^(n-k)
}
pvec <- seq(0.001, .999, length.out = 100)
theLik <- sapply(pvec, FUN= binomLik, k=9, n=10)
theLik <- data.frame(likelihood= theLik, p= pvec)
idx <- which.max(theLik$likelihood)
ggplot(theLik, aes(x=p, y= likelihood)) +
geom_line() +
xlab("Parameter p") +
labs(title="Münzwurf",
subtitle = "n=10, k=9") +
geom_vline(xintercept = theLik$p[idx], lty=2) +
annotate(geom= "label", x= theLik$p[idx],
y= 0.1, label= "ML Schätzer")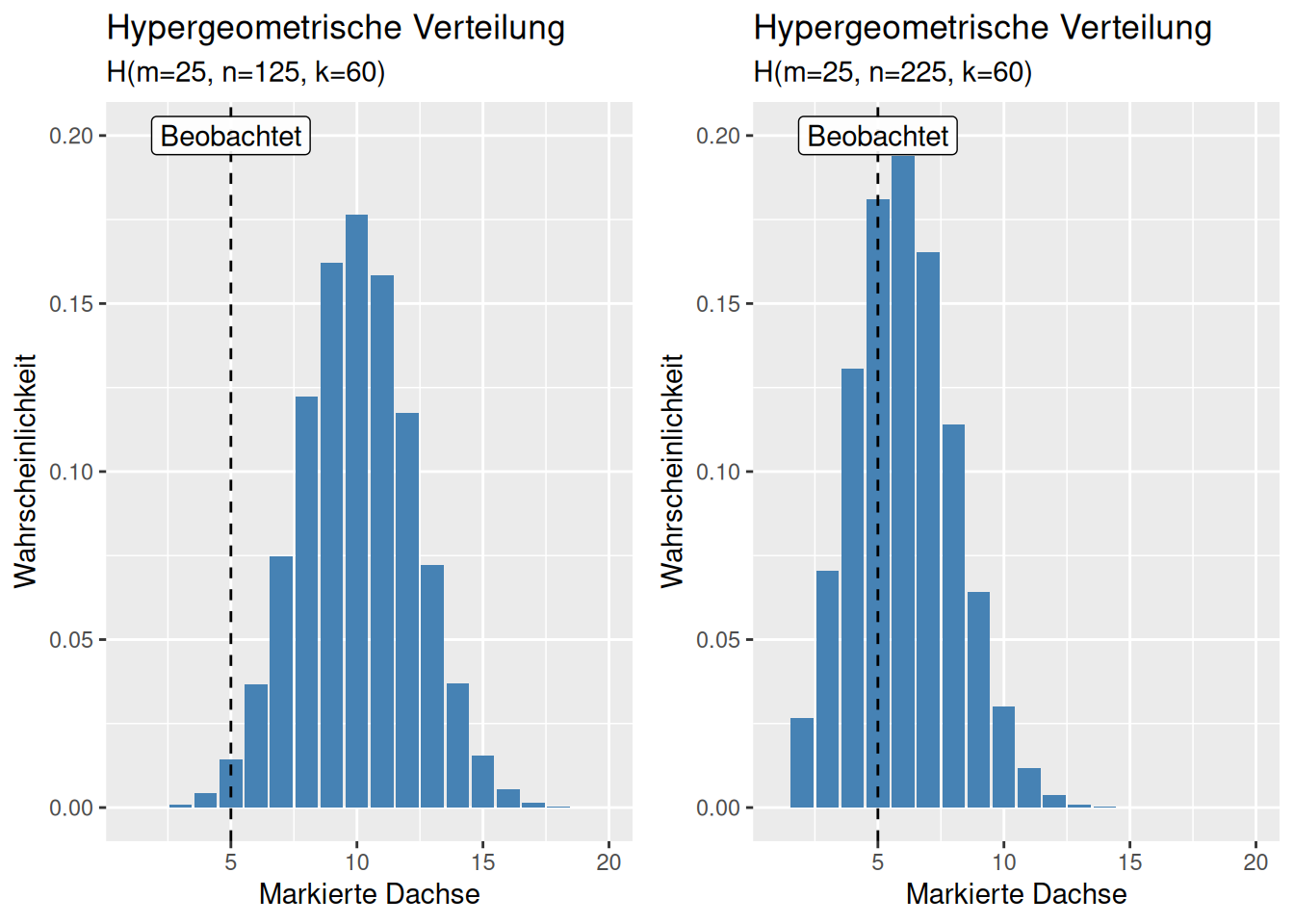
8.4.2 Beispiel aus der Ökologie (mark-recapture) mittels hypergeometrischer Verteilung
Mit Hilfe der Hypergeometrishcen Verteilung kann man anhand von mark-recapture Daten die Gesamtpopulation in einem Gebiet schätzen. Hierbei werden Individuen gefangen, markiert und wieder freigelassen. Später werden wieder Individuen gefangen. Anhand der Anzahl der bereits markierten Individuen kann man die Gesamtpopulation schätzen.
Wir haben in einem Gebiet in einer Feldsaison 25 Dachse gefangen, markiert und wieder frei gelassen (damit ist \(m\)= 25). In der nächsten Feldsaison haben wir 60 (\(k\)) Dachse im selben Gebiet gefangen. Von diesen waren 5 bereits markiert (\(x\)). Wie hoch schätzen wir die Dachspopulation (\(N\)) in der Region?
Als Verteilungsparameter der hypergeometrischen Verteilung ist die Dachspopulation \(n = N-m\), also \(N=n +25\) bzw. \(n= N - 25\).
Wie wahrscheinlich sind Populationen (\(N\)) von 150, 250, 500,… Dachsen?
- Parameter für
dhyper- \(x = 5\) (5 von 25 wurden wieder gefangen)
- \(m = 25\) (es gibt im Gebiet 25 Dachse, die markiert sind)
- \(k = 60\) (60 Dachse wurden als Stichprobe gefangen)
## [1] 0.01423138## [1] 0.1809279## [1] 0.1026143## [1] 0.1969146Wie sieht die zugehörige Wahrscheinlichkeitsverteilung aus?
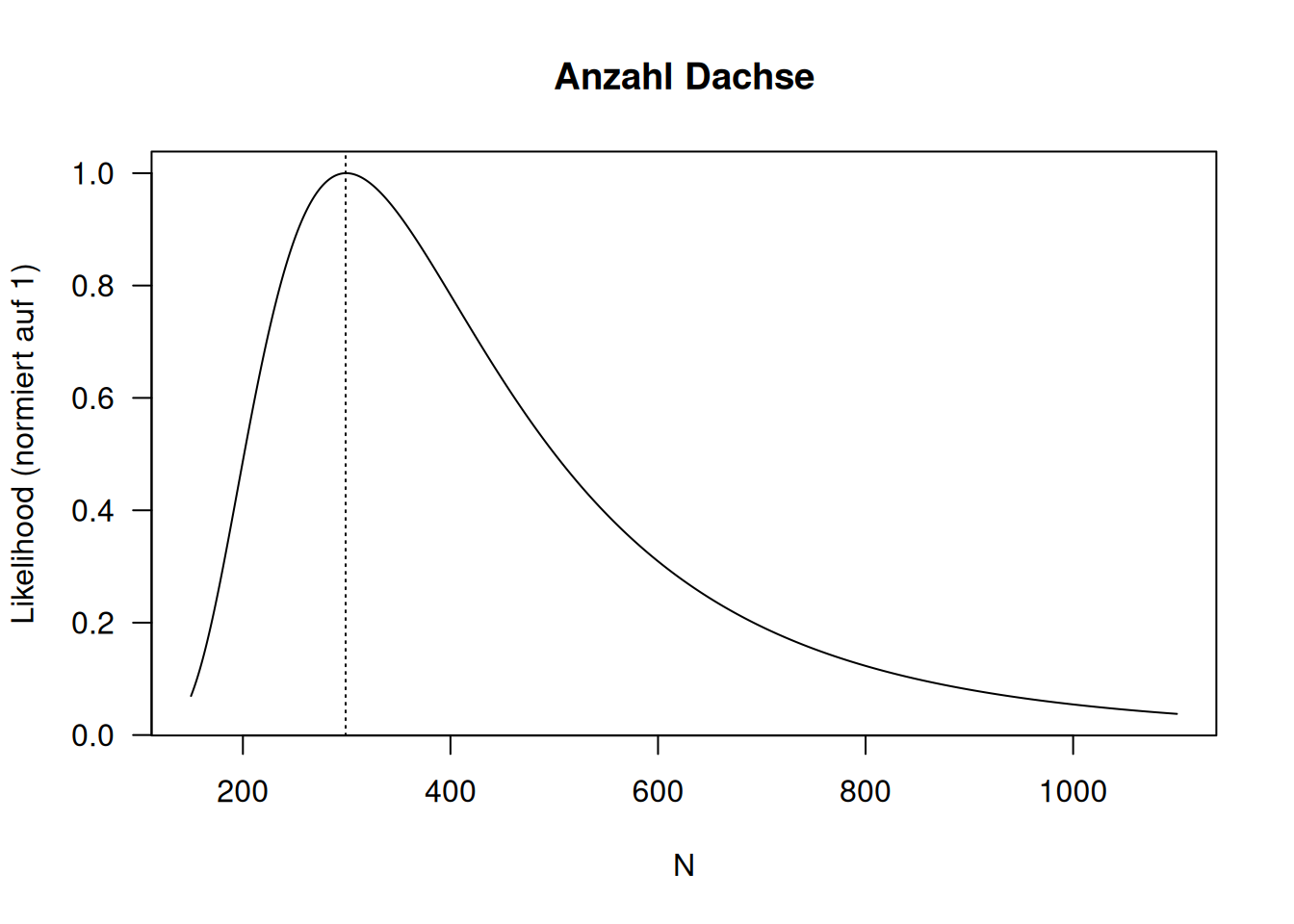
Wie sieht die Likelihhood der Anzahl Dachse im Beispiel aus?
Der Schätzwert für die Dachspopulation beträgt: 299. Aber wie wir anhand der Likelihoodfunktion sehen, sind auch Werte um 299 herum relativ wahrscheinlich. Allerdings fällt die likelihood mit zunehmendem Abstand stark (näherungsweise quadratisch) ab.
8.4.3 Schätzen mittels fitdistr
In R können Verteilungsparameter für eine Reihe von Verteilungen mittels der Funktion fitdistr() im package MASS(gehört zu den core packages und ist damit bereits installiert) geschätzt werden. Benötigt werden ein Vektor mit Werten (die beobachteten Realisierungen der Zufallsvariable), die Verteilung, die geschätzt werden soll und ggf. Startwerte für die Suche. Folgende Verteilungen können verwendet werden: “beta”, “cauchy”, “chi-squared”, “exponential”, “gamma”, “geometric”, “log-normal” (auch “lognormal”), “logistic”, “negative binomial”, “normal”, “Poisson”, “t” und “weibull”. Die Schätzung erfolgt auf Grundlage der Likelihood (genauer gesagt auf Grundlage der log-Likelihood, dem logarithmus aus der Likelihood) - fitdistr liefert also ML Schätzer der Verteilungsparameter bei gegebenen Daten.
Das Schätzen der Parameter passiert intern mittels der optim()Funktion.
8.4.4 Fallstudie Temperaturdaten
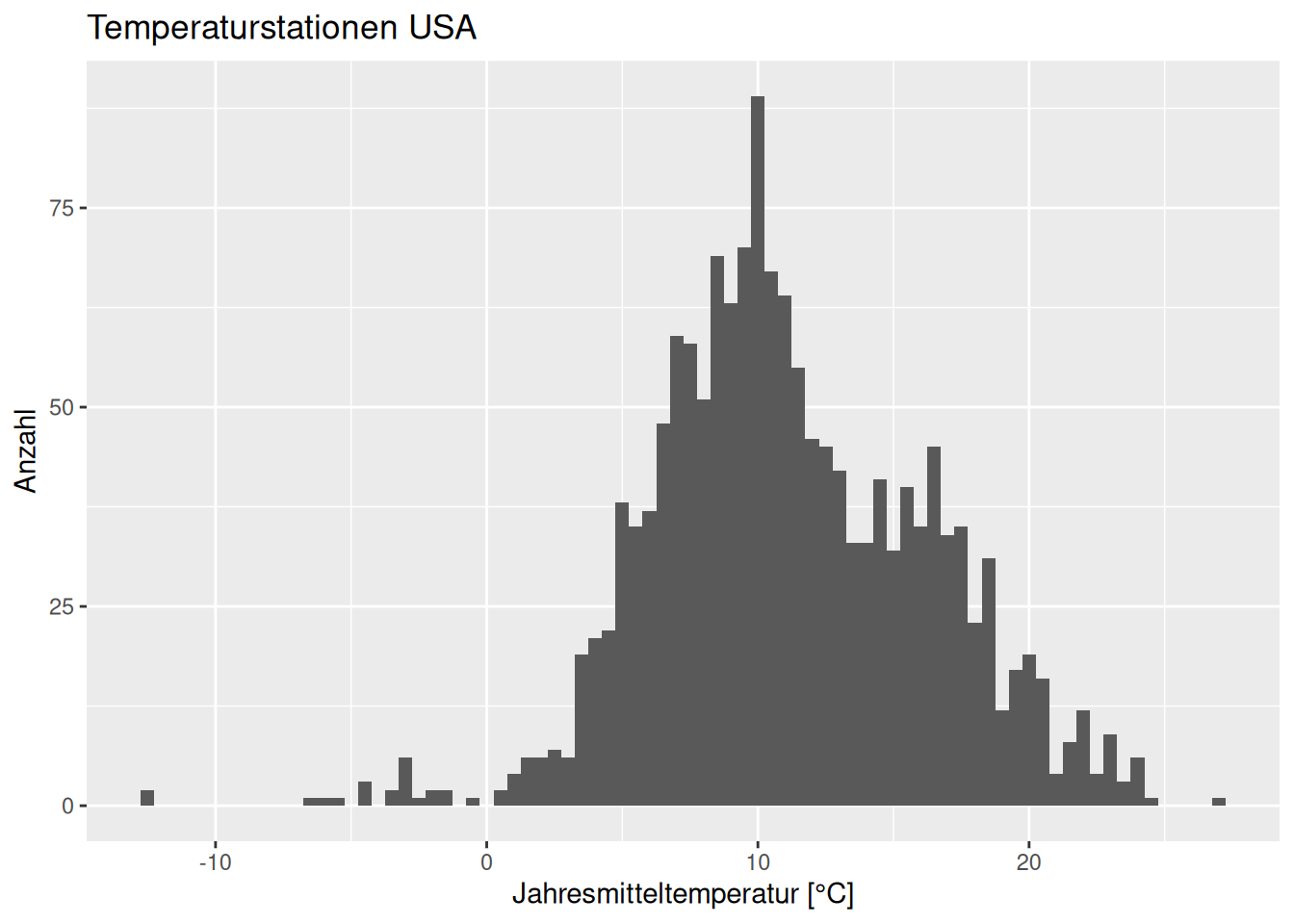
Wir wollen uns hier mit der Verteilungen der Jahresmitteltemperatur der Temperaturstationen der USA beschäftigen. Die Daten sind etwas älter und umfasst Temperaturdaten nur bis 1990.
Der Datensatz enthält neben den Koordinaten der Station die Höhe in müNN sowie den langjährigen Mittelwert der Jahrestemperatur (YEAR) sowie der einzelnen Monate. WIr filtern zunächst die Stationen, die sich in den USA befinden und plotten dann das Histogramm.
temp_us <- temp %>% filter(CNTRY_NAME == "United States")
ggplot(temp_us, aes(x= YEAR) ) +
geom_histogram(binwidth = .5) +
xlab("Jahresmitteltemperatur [°C]") +
ylab("Anzahl") + labs(title = "Temperaturstationen USA")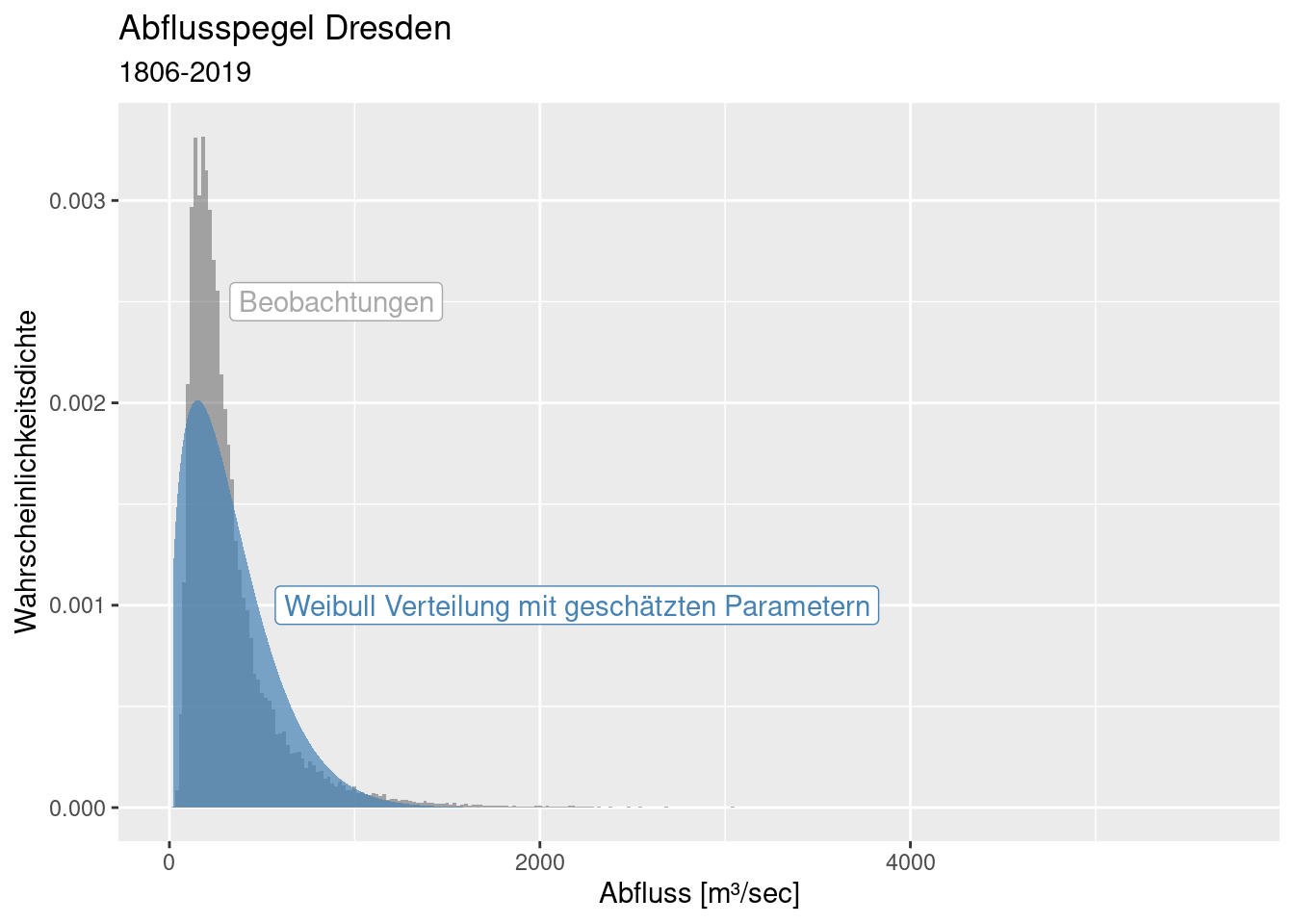
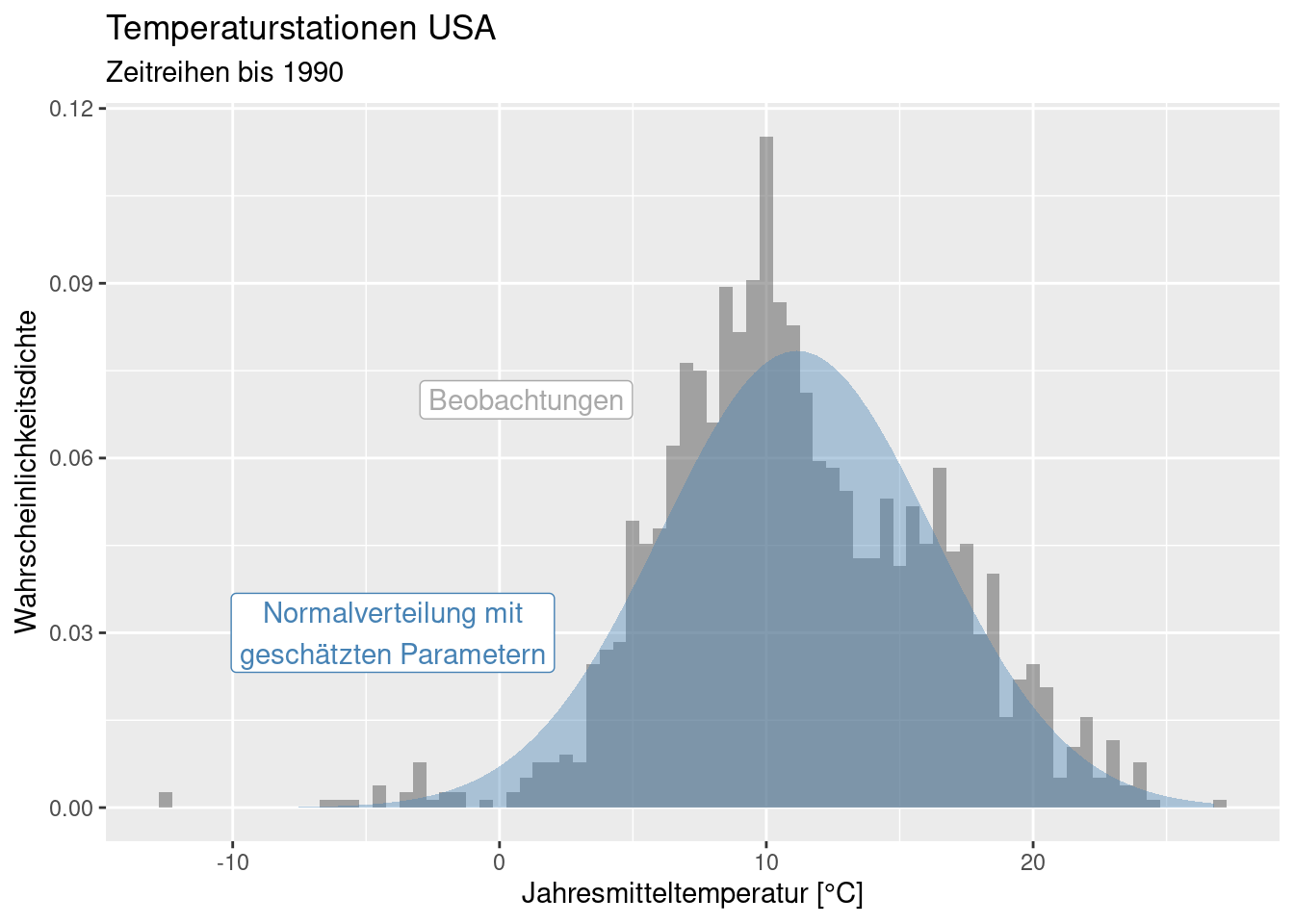
Die Daten sehen näherungsweise normalverteilt aus. Versuchen wir doch einmal, eine Normalverteilung an den Daten zu fitten.
## mean sd
## 11.15558288 5.08770286
## ( 0.12943672) ( 0.09152558)Die Normalverteilung, welche die Daten am besten beschreibt hat einen Mittelwert von 11.15°C (geschätzt mit einem Standardfehler von 0.13°C) und eine Standardabweichung von 5.1°C (geschätzt mit einem Standardfehler von 0.09°C).
tempUSGaussParam <- list( mean= tempUsGauss$estimate[1],
sd = tempUsGauss$estimate[2])
ggplot(temp_us, aes(x=YEAR)) +
geom_histogram(binwidth = 0.5, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dnorm,
geom = "area",
fill = "steelblue",
alpha = .4,
args = tempUSGaussParam
) +
xlab("Jahresmitteltemperatur [°C]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Temperaturstationen USA", subtitle = "Zeitreihen bis 1990") +
annotate(geom= "label", x=-4, y= 0.03, colour = "steelblue",
label = "Normalverteilung mit\ngeschätzten Parametern") +
annotate(geom= "label", x=1, y= 0.07, colour = "darkgrey",
label = "Beobachtungen")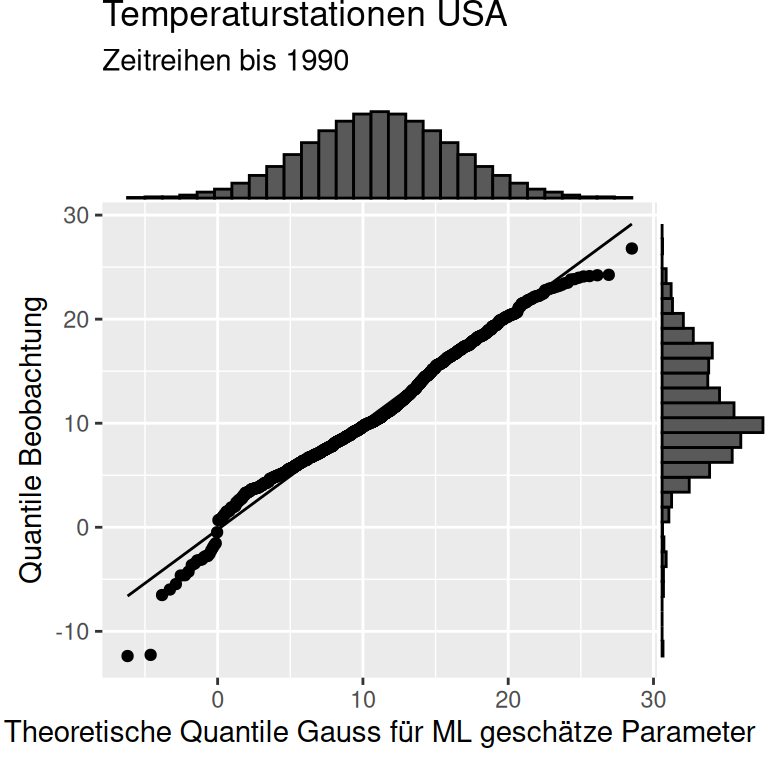
Wir sehen, dass die Normalverteilung die Daten recht anständig beschreibt, allerdings einige Aspekte nicht gut abbildet: das Histogramm zeigt einen deutlichen Peak, der nur teilweise wiedergegeben wird. Außerdem werden die extremen negativen Jahresmittelwerte nicht erfasst und die rechte Schulter der Verteilung nicht wirklich gut wiedergegeben. Wir werden uns später im Bereich Regression weiter mit diesen Daten beschäftigen und sehen, dass wir diese Abweichungen gut modellieren können.
Wir können die Güte der Anpassung der Verteilung an die Daten auch über einen sogenannten QQ-Plot bewerten. Dabei werden die Quantile der Beobachtungen gegen die Quantile einer Verteilung (hier der Normalverteilung) aufgetragen. stat_qq trägt beobachete gegen theoretische Werte auf, stat_qq_line zeichnet die Ideallinie dazu. Je näher die Punkte an der Linien liegen, desto besser werden die Daten durch die Verteilung beschrieben. In unserem Beispiel ist die Übereinstimmmung - aber auch die angesprochenen Abweichungen - deutlich zu erkennen. Die geschätzte Verteilung hat insbesondere Probleme bei den negativen Werten, da diese nach der Normalverteilung so nicht zu erwarten wären.
ggplot(temp_us, aes(sample = YEAR)) +
stat_qq(distribution = qnorm, dparams = tempUSGaussParam ) +
stat_qq_line(distribution = qnorm, dparams = tempUSGaussParam) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Gauss \nfür ML geschätze Parameter") +
labs(title = "Temperaturstationen USA", subtitle = "Zeitreihen bis 1990")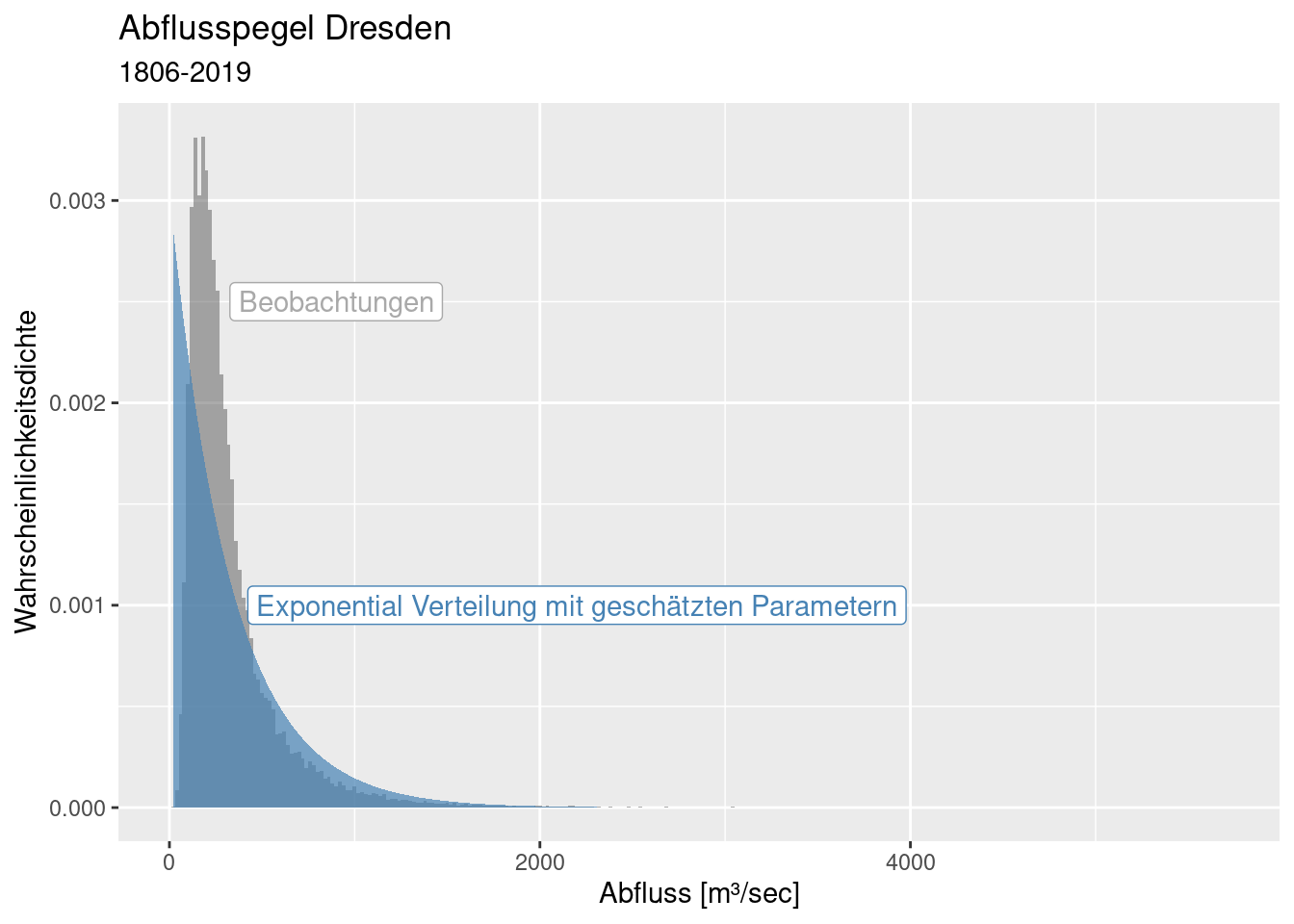
Man kann sich den QQ-Plot vielleicht etwas besser vorstellen, wenn man jeweils die Verteilung der Daten auf die x- und die y-Achse plottet wie in nachfolgender Abbildung. Auf der x-Achse ist das Histogramm einer Normalverteilung (mit den besten Parametern um die Daten zu beschreiben) dargestellt, an der y-Achse das Histogram der Beobachtungen. Man sieht z.B. , dass das empirische Histogramm im negativen Bereich mehr Masse hat, als man bei einer angepassten Normalverteilung erwarten würde. Die empirischen Werte sind hier kleiner, als die erwarteten - d.h. das Modell (Normalverteilung) überschätzt hier die Beobachtungen.
Auf der x-Achse werden wie gesagt die Werte der Quantile der geschätzten (theoretischen) Verteilung dargestellt, auf der y-Achse die Quantile der empirischen Beobachtungen. Zur verdeutlichung sind in Abbildung 8.21 jeweils das 10-, 50- und 90-Quantil beider Verteilungen dargestellt. Würden die geschätzten Verteilungen perfekt zu den Beobachtungen passen, würden alle Punkte auf der 1:1 Linie liegen, sich also alle Quantile beider Beobachtungen entsprechen. Dies ist im vorliegenden Beispiel nicht der Fall. Punkte unterhalb der 1:1 Linie zeigen an, dass das entsprechende Quantil der Beobachtungen (das was wir über die Realität wissen) aufgrund der Quantile der geschätzten theoretischen Verteilung überschätzt werden. Punkte oberhalb der Linie zeigen entsprechend an, dass die Quantile der Beobachtungen durch die geschätzte Verteilung unterschätzt werden.
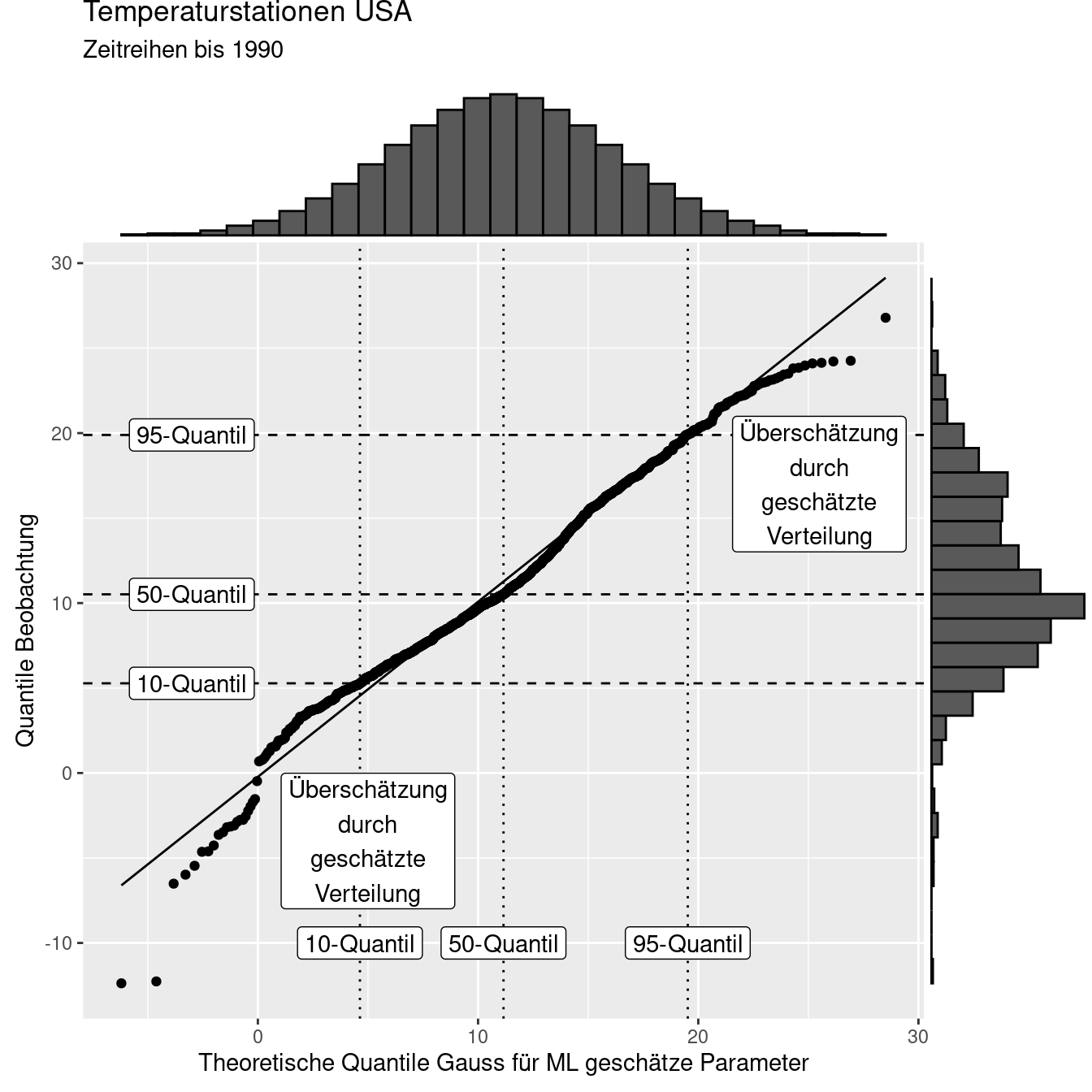
Figure 8.21: Die vertkalen Linien geben das 10-, 50- und 90-Quantil der geschätzten (theoretischen) Verteilung and, während die horizontalen Linien die entsprechenden Quantile der beobachteten Daten angeben.
Schauen wir uns das einmal beispielhaft für drei Quantile (1%, 7%, 50% und 99.9%) an:
theProbs <- c(.01, 0.07, .5, .999)
quantilesObs <- quantile(temp_us$YEAR, probs = theProbs)
quantileFittedDistr <- qnorm(p=theProbs,
mean = tempUSGaussParam$mean,
sd = tempUSGaussParam$sd)
data.frame(quantil = theProbs,
quantile_beobachtet = quantilesObs,
quantile_modelliert = quantileFittedDistr,
qmod_rel2_qobs = quantileFittedDistr / quantilesObs)## quantil quantile_beobachtet quantile_modelliert qmod_rel2_qobs
## 1% 0.010 -2.663895 -0.6801838 0.2553343
## 7% 0.070 4.666366 3.6471967 0.7815924
## 50% 0.500 10.515100 11.1555829 1.0609108
## 99.9% 0.999 24.236030 26.8777666 1.1090004Das 1-Quantil der modellierten Verteilung ist deutlich größer (~4-mal so groß) als das 1-Quantil der beobachteten Werte. Der Median der geschätzten Verteilung ist um 6.1% größer als der beobachtete Median. Das 99,9-Quantil ist - um 10.9% größer als das beobachtete 99,9-Quantil. Beim 7-Quantile wird das beobachte Quantil durch die geschätzte Verteilung unterschätzt - das 7-Quantil der geschätzten Verteilung ist um 21.8% kleiner als das 7-Quantil der Beobachtungen.
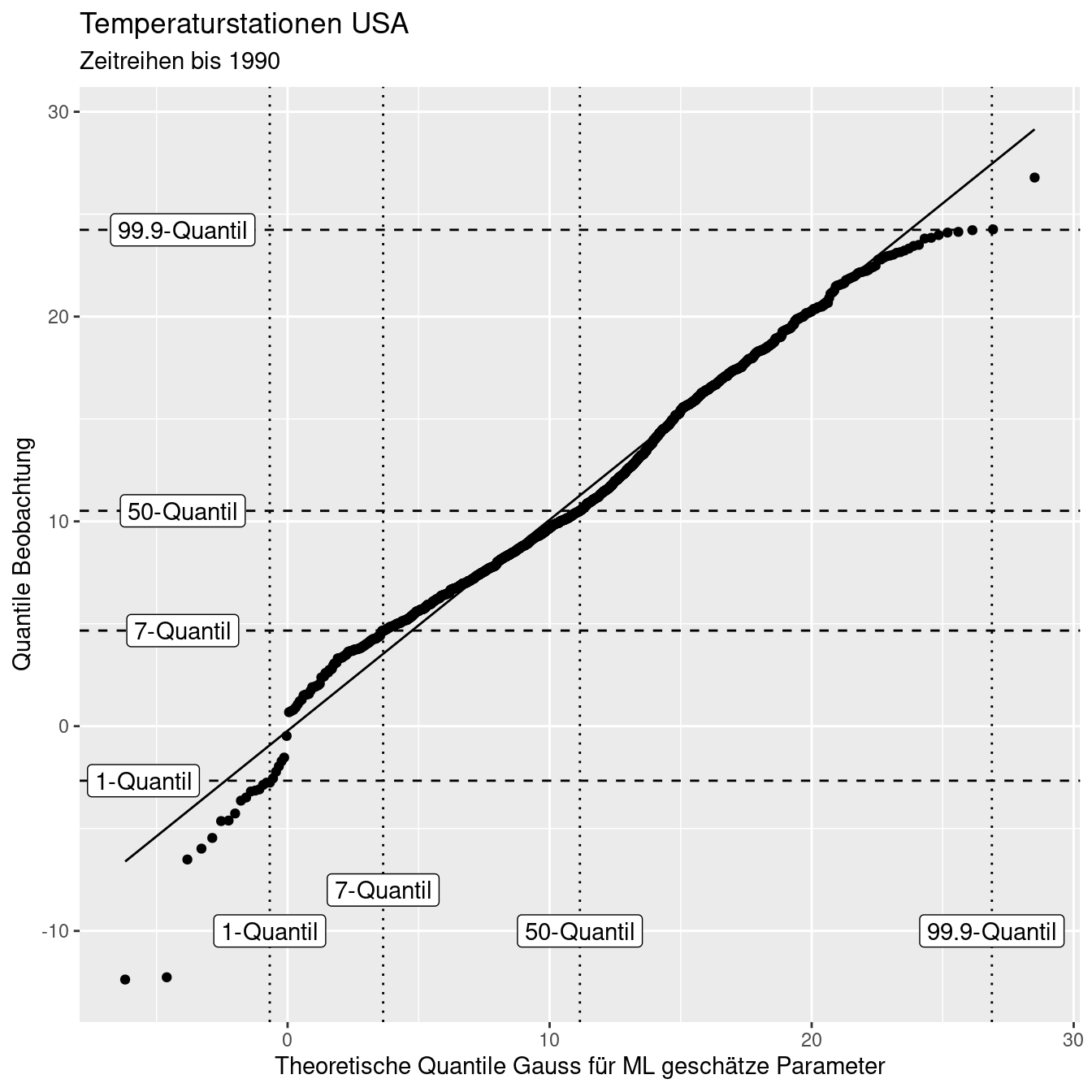
Figure 8.22: Die vertkalen Linien geben das 1-, 7-, 50- und 99.9-Quantil der geschätzten (theoretischen) Verteilung and, während die horizontalen Linien die entsprechenden Quantile der beobachteten Daten angeben.
8.4.5 Fallstudie Abflussganglinien
dresdenQ <- read.table(file = unzip(
"data/hydrologie/dresden_elbe.zip",
files = "6340120_Q_Day.Cmd.txt"),
header = TRUE, sep = ";")
summary(dresdenQ)## YYYY.MM.DD hh.mm Value
## Length:78162 Length:78162 Min. : 22.0
## Class :character Class :character 1st Qu.: 166.0
## Mode :character Mode :character Median : 249.0
## Mean : 328.7
## 3rd Qu.: 385.0
## Max. :5700.0Umwandeln der Datumsangaben in das Datumsformat mit Hilfe fun lubridate::as_date.
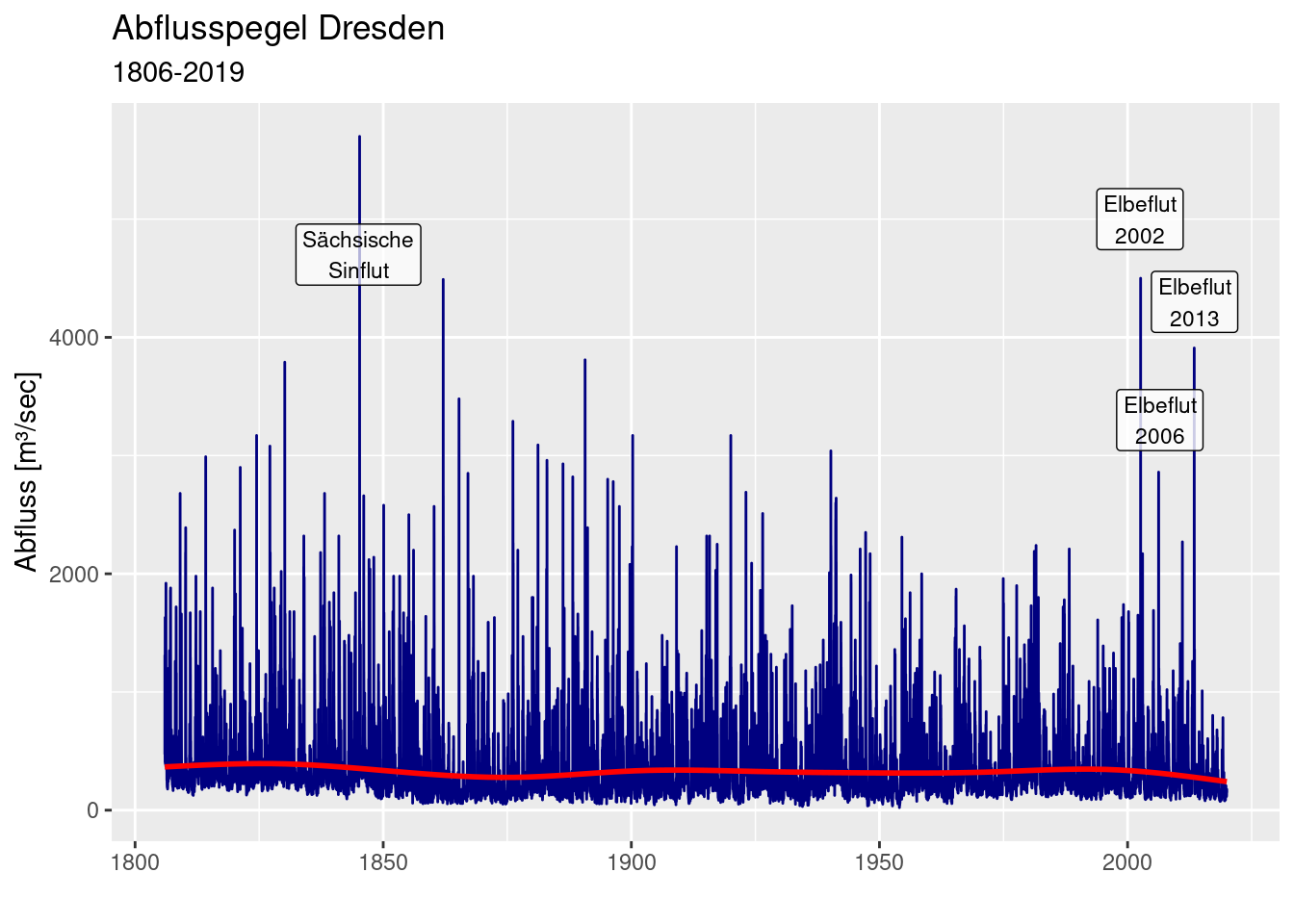
Wie bei Abflussganglinien in unseren Breiten nicht anders zu erwarten, schwanken die Pegeldaten recht stark. Die meiste Zeit herrschen Ablussbedingungen, die vor allem durch Grundwasserabfluss im tschechischen Teil des Einzugsgebietes gesteuert werden. Regenereignisse und oder Schneeschmelze führen zu Abflussspitzen. Deutlich zu erkennen sind die letzten extremen Hochwasser 2002, 2006 und 2013 und das Elbehochwasser von 1845, die sogenannte „Sächsische Sintflut“.
ggplot(dresdenQ, aes(y = Value, x = date)) +
geom_line(colour= "navy") +
geom_smooth(colour="red") +
ylab("Abfluss [m³/sec]") + xlab("") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=as_date("1845-01-01"), y= 4700,
label = "Sächsische\nSinflut", alpha=.7,
size=3) +
annotate(geom= "label", x=as_date("2002-07-01"), y= 5000,
label = "Elbeflut\n2002", alpha=.8,
size=3) +
annotate(geom= "label", x=as_date("2013-07-01"), y= 4300,
label = "Elbeflut\n2013", alpha=.7,
size=3) +
annotate(geom= "label", x=as_date("2006-07-01"), y= 3300,
label = "Elbeflut\n2006", alpha=.8,
size=3)## `geom_smooth()` using method = 'gam' and formula = 'y ~ s(x, bs = "cs")'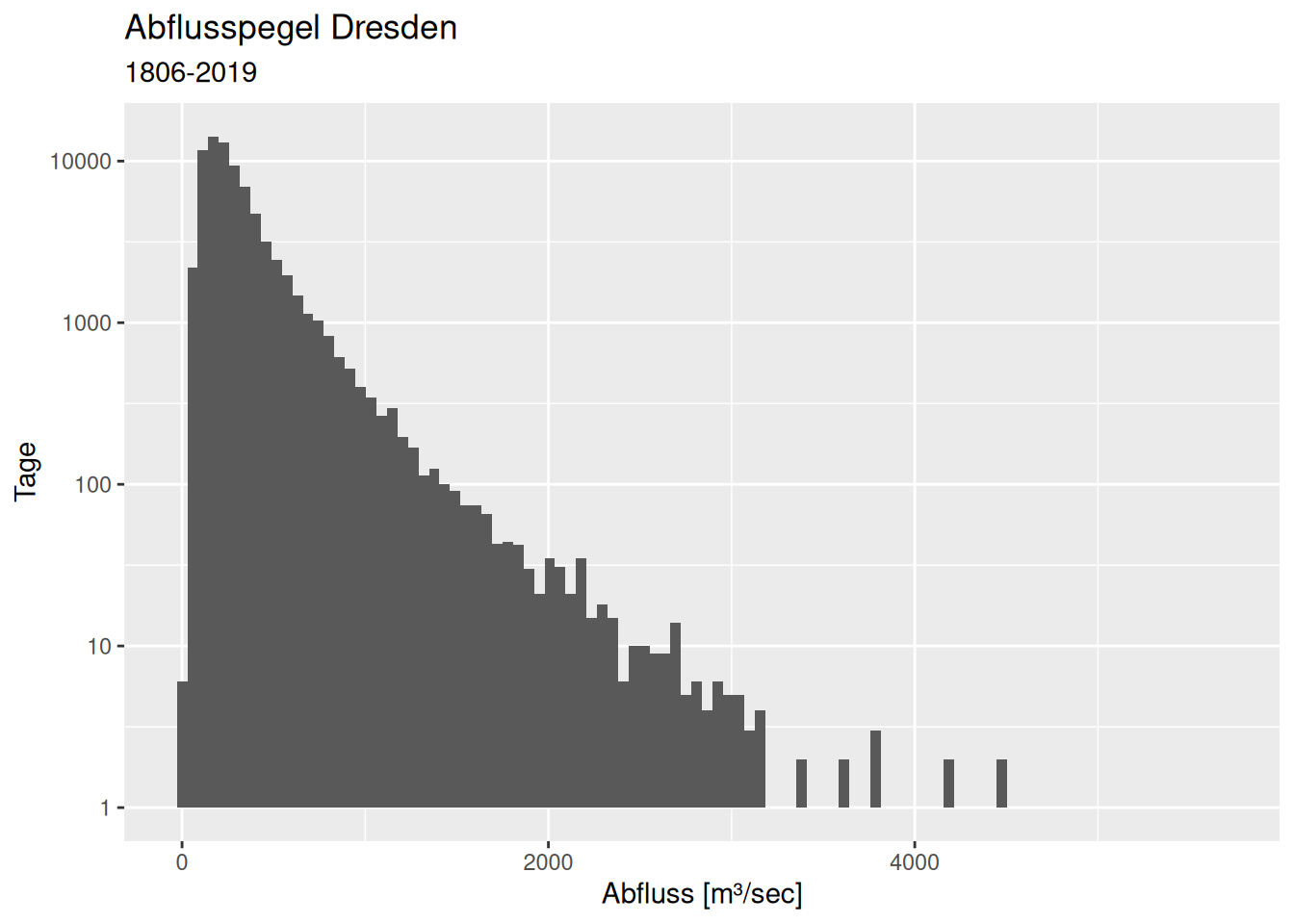
Die Verteilung der täglichen Abflusswerte ist - wie erwartet - rechtsschief. Es gibt wenige extreme Ereignisse mit entsprechenden Konsequenzen (Hochwasser).
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(bins = 100) + scale_y_log10() +
xlab("Abfluss [m³/sec]") + ylab("Tage") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")## Warning in scale_y_log10(): log-10 transformation introduced infinite values.## Warning: Removed 33 rows containing missing values or values outside the scale range
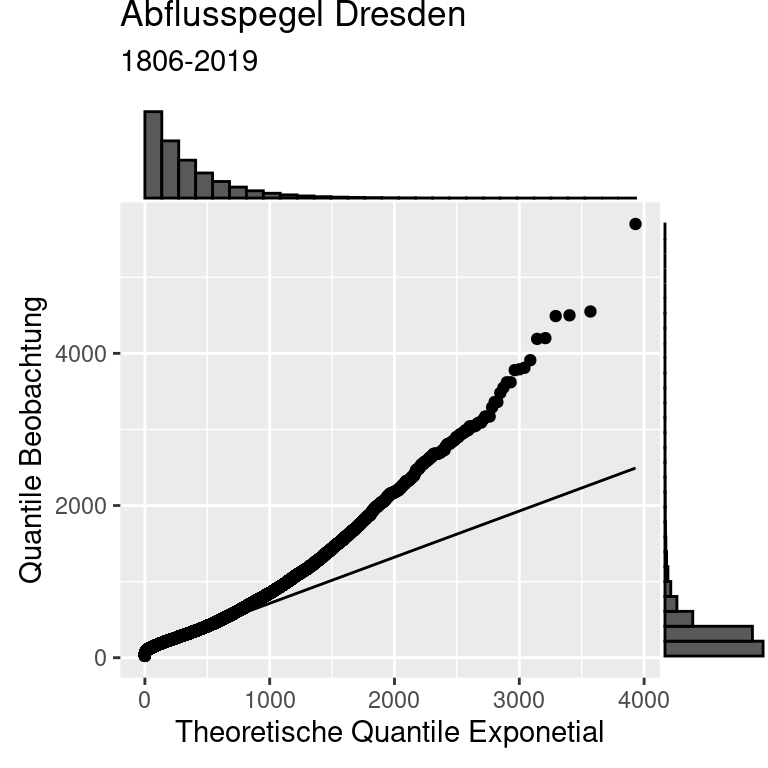
## (`geom_bar()`).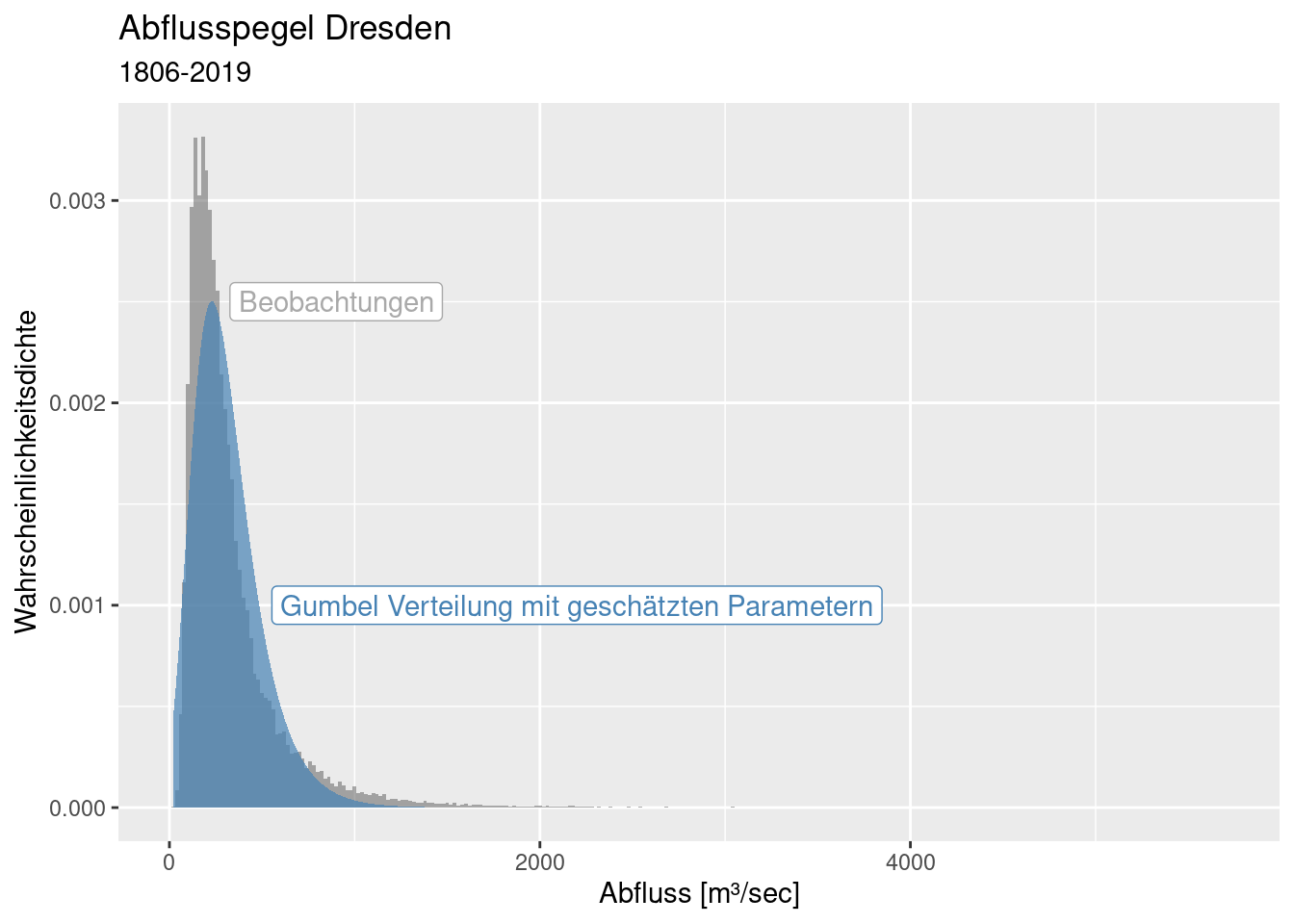
Es sollte klar sein, dass wir keine Normalverteilung verwenden können, um die Daten zu beschreiben. Wir brauchen eine Extremwertverteilung. Geeignete Kandidaten wären die Weibull, die Log-Normalverteilung oder die Gumbel-Verteilung, eventuell noch die Exponentialverteilung.
Einige Kennzahlen zur empirischen Verteilung der Daten
Mittelwert:
## [1] 328.7078Standardabweichung
## [1] 277.6336Variationskoeffizient
## [1] 0.8446212Schiefe
## [1] 3.518646Kurtosis
## [1] 24.92147Einige relevante Quantile
## 0% 2.5% 5% 25% 50% 75% 95% 97.5% 100%
## 22.0 84.4 99.0 166.0 249.0 385.0 832.0 1080.0 5700.08.4.5.1 Weibull-Verteilung
## shape scale
## 1.406177e+00 3.652393e+02
## (3.427007e-03) (9.873996e-01)ggplot() + xlim(0,4000) +
stat_function(
fun = dweibull,
geom = "area",
fill = "steelblue",
alpha = .3, n = 501,
args = list(shape=dresdenWeibullParams$estimate[1] ,
scale = dresdenWeibullParams$estimate[2])
)
ddWeiParamsList <- list( shape= dresdenWeibullParams$estimate[1],
scale = dresdenWeibullParams$estimate[2])
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(binwidth = 20, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dweibull,
geom = "area",
fill = "steelblue",
alpha = .7, n = 501,
args = ddWeiParamsList
) +
xlab("Abfluss [m³/sec]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=2200, y= 0.001, colour = "steelblue",
label = "Weibull Verteilung mit geschätzten Parametern") +
annotate(geom= "label", x=900, y= 0.0025, colour = "darkgrey",
label = "Beobachtungen")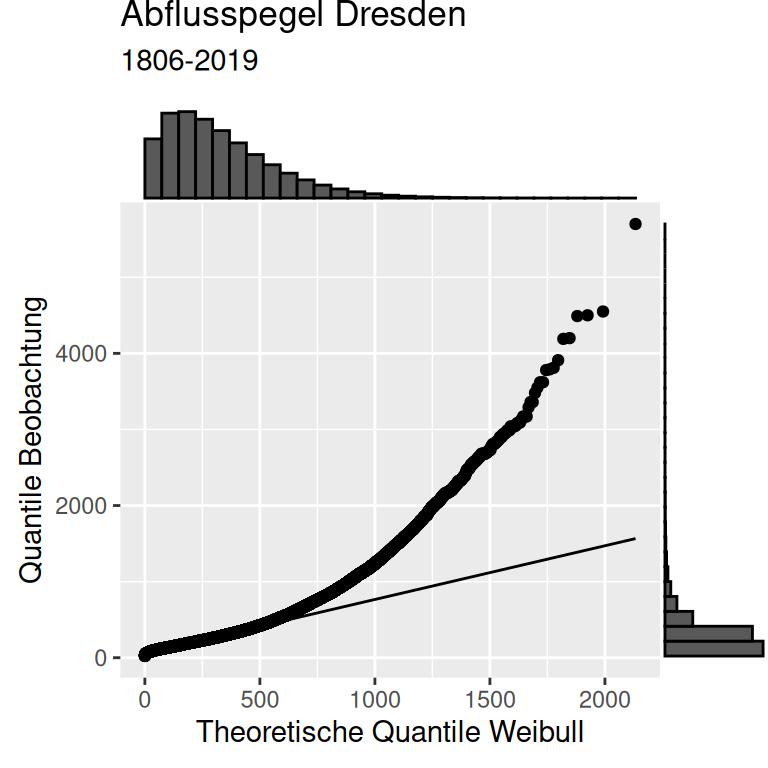
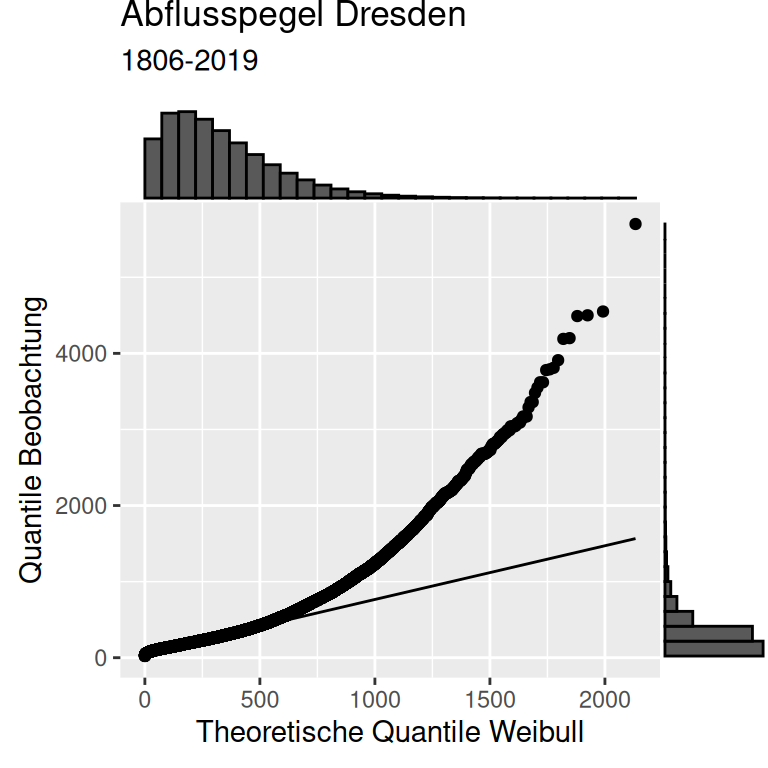
Wir können die Güte der Anpassung der Verteilung an die Daten auch über einen sogenannten QQ-Plot bewerten. Dabei werden die Quantile der Beobachtungen gegen die Quantile einer Verteilung aufgetragen.
Wie wir sehen, beschreibt die gefittete Weibull-Verteilung die Daten nicht wirklich gut. Während die Weibull-Verteilung die empirischen Daten gut für Tage mit Abflüssen bis etwa 600 \(m^3/sec\) beschreibt, unterschätzt die Weibull-Verteilung die seltenen Extrem-Hochwasser deutlich.
p1 <- ggplot(dresdenQ, aes(sample = Value)) +
stat_qq(distribution = qweibull, dparams = ddWeiParamsList ) +
stat_qq_line(distribution = qweibull, dparams = ddWeiParamsList) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Weibull") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")
ggMarginal(p1, type ="histogram")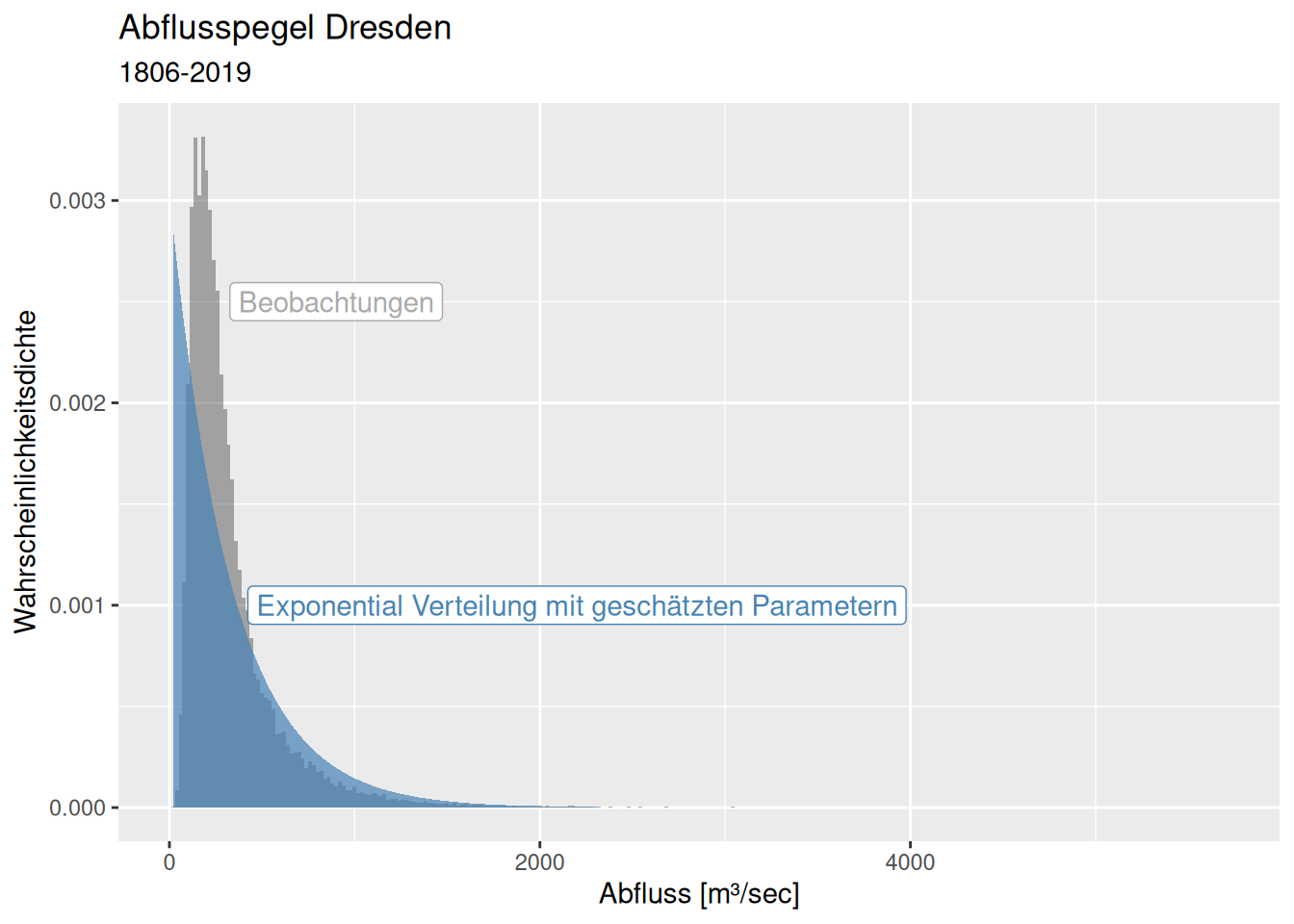
8.4.5.2 Exponential Verteilung
## rate
## 3.042215e-03
## (1.088158e-05)ddExpParamsList <- list( rate= dresdenExpParams$estimate[1])
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(binwidth = 20, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dexp,
geom = "area",
fill = "steelblue",
alpha = .7, n = 501,
args = ddExpParamsList
) +
xlab("Abfluss [m³/sec]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=2200, y= 0.001, colour = "steelblue",
label = "Exponential Verteilung mit geschätzten Parametern") +
annotate(geom= "label", x=900, y= 0.0025, colour = "darkgrey",
label = "Beobachtungen")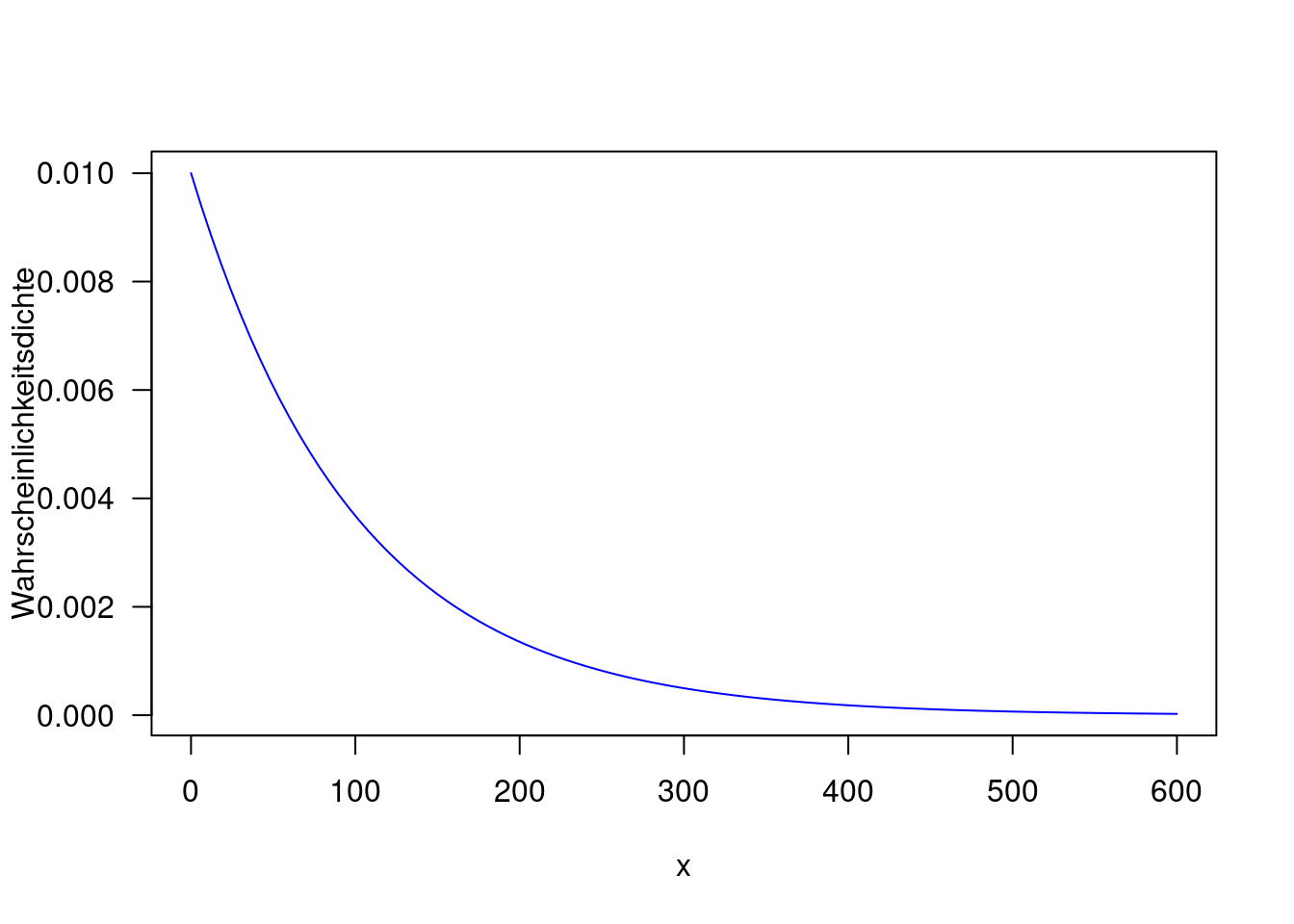
Die Exponentialverteilung schwächelt sowohl bei niedrigen als auch bei hohen Abflussmengen.
p1 <- ggplot(dresdenQ, aes(sample = Value)) +
stat_qq(distribution = qexp, dparams = ddExpParamsList ) +
stat_qq_line(distribution = qexp, dparams = ddExpParamsList) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Exponetial") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")
ggMarginal(p1, type ="histogram")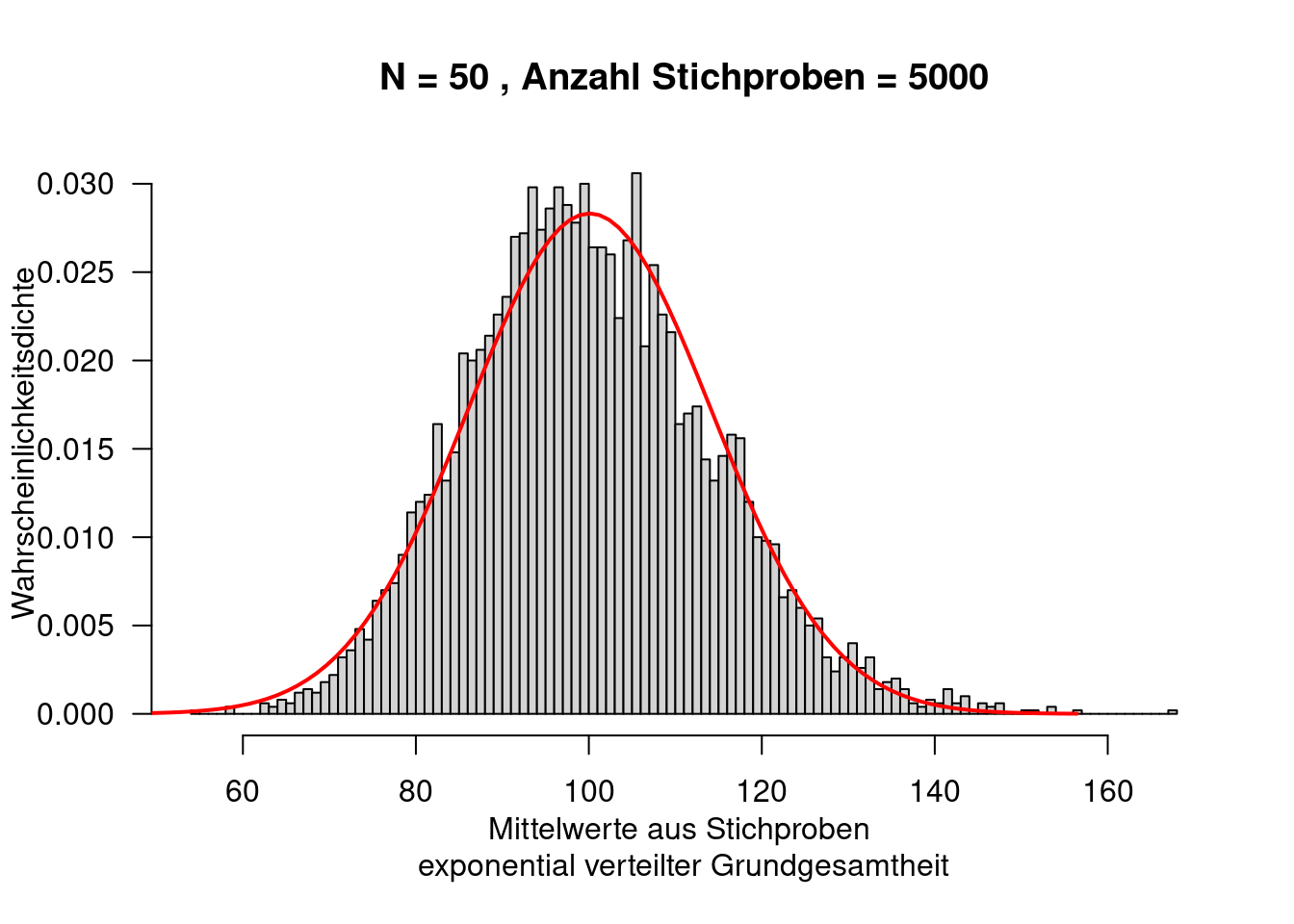
8.4.5.3 Log-Normal Verteilung
## meanlog sdlog
## 5.565069475 0.647300967
## (0.002315306) (0.001637169)ddLogNormParamsList <- list( meanlog= dresdenLogNormParams$estimate[1],
sdlog = dresdenLogNormParams$estimate[2])
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(binwidth = 20, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dlnorm,
geom = "area",
fill = "steelblue",
alpha = .7, n = 501,
args = ddLogNormParamsList
) +
xlab("Abfluss [m³/sec]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=2200, y= 0.001, colour = "steelblue",
label = "Log-Normalverteilung mit geschätzten Parametern") +
annotate(geom= "label", x=900, y= 0.0025, colour = "darkgrey",
label = "Beobachtungen")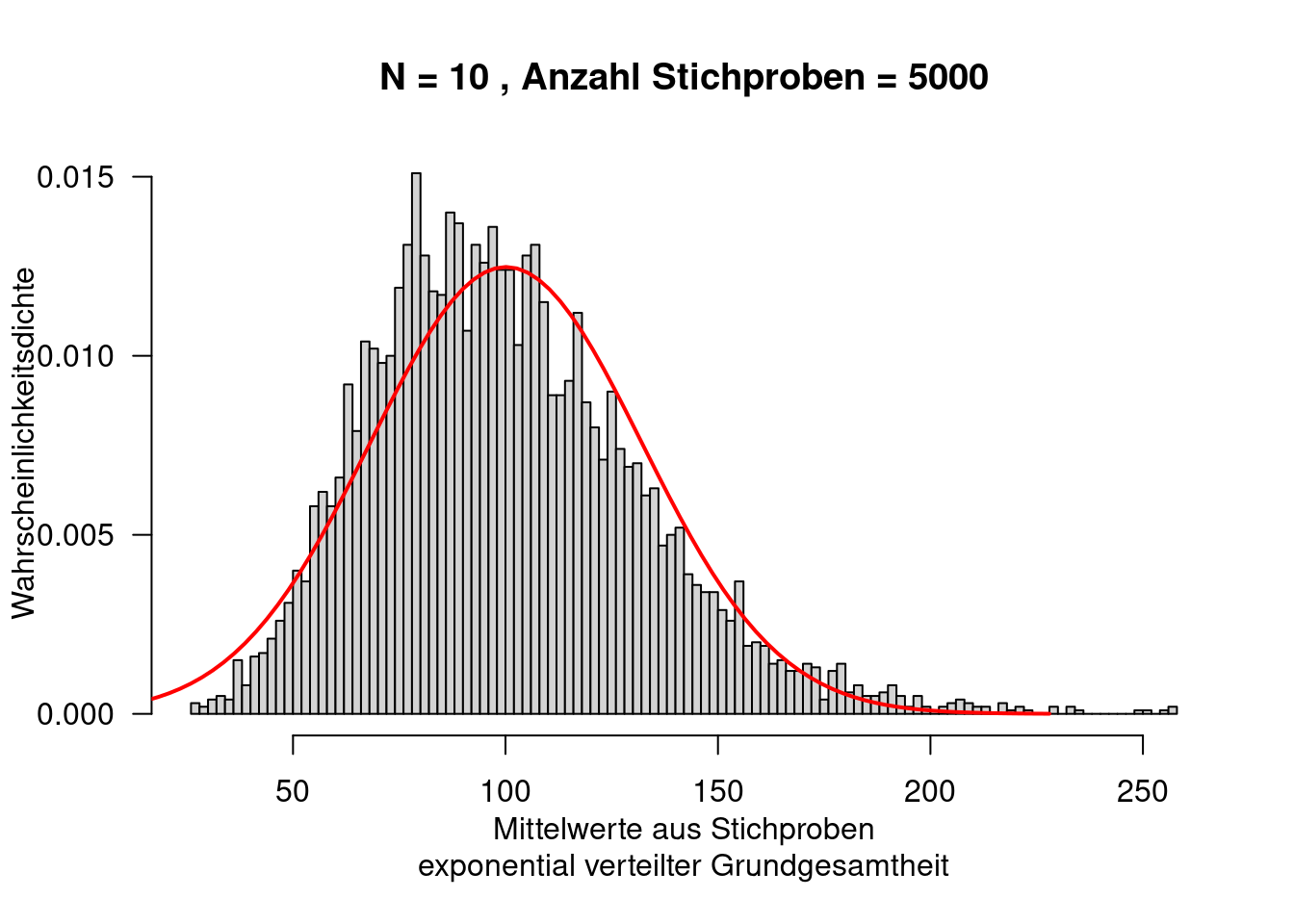
Die Log-Normalverteilung scheint die extremen Hochwasser bisher am besten abzubilden.
p1 <- ggplot(dresdenQ, aes(sample = Value)) +
stat_qq(distribution = qlnorm, dparams = ddLogNormParamsList ) +
stat_qq_line(distribution = qlnorm, dparams = ddLogNormParamsList) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Log-Normal") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")
ggMarginal(p1, type ="histogram")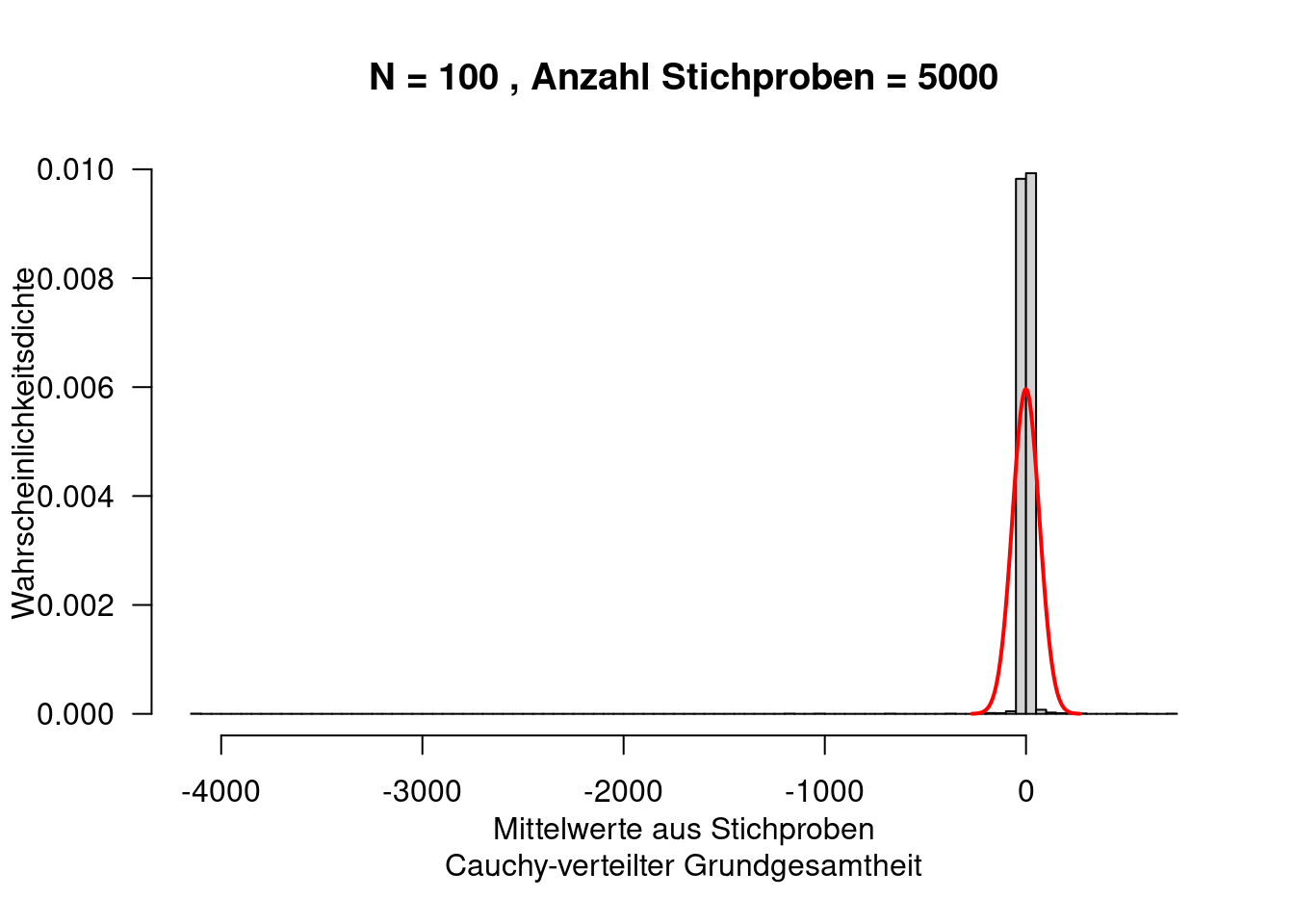
8.4.5.4 Gumbel
Die Gumbel-Verteilung ist nicht in den Core packages enthalten. Sie ist z.B. im package FAdist definiert (qgumbel, dgumbel, pgumbel, rgumbel), dass noch installiert werden muss. Ebenfalls benötigt - und installiert werden muss - wird das package fitdistrplus, dass es ermöglicht zusätzliche Verteilungen an Daten zu fitten.
## Loading required package: fitdistrplus## Loading required package: survivalDie Parameter sind anders benannt und wir müssen hier Startwerte angeben. Welche Parameter die Gumbel-Verteilung hat, finden wir raus, indem wir die Hilfe von qgumbel, dgumbel, pgumbel oder rgumbel anschauen. Geeignete Startwerte können wir durch Ausprobieren finden.
dresdenGumbelParams <- fitdist(dresdenQ$Value, distr = "gumbel",
start = list(scale = 10, location = 10))
dresdenGumbelParams## Fitting of the distribution ' gumbel ' by maximum likelihood
## Parameters:
## estimate Std. Error
## scale 146.9020 0.4485470
## location 228.9722 0.5449442ddGumbelParamsList <- list( scale= dresdenGumbelParams$estimate[1],
location = dresdenGumbelParams$estimate[2])
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(binwidth = 20, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dgumbel,
geom = "area",
fill = "steelblue",
alpha = .7, n = 501,
args = ddGumbelParamsList
) +
xlab("Abfluss [m³/sec]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=2200, y= 0.001, colour = "steelblue",
label = "Gumbel Verteilung mit geschätzten Parametern") +
annotate(geom= "label", x=900, y= 0.0025, colour = "darkgrey",
label = "Beobachtungen")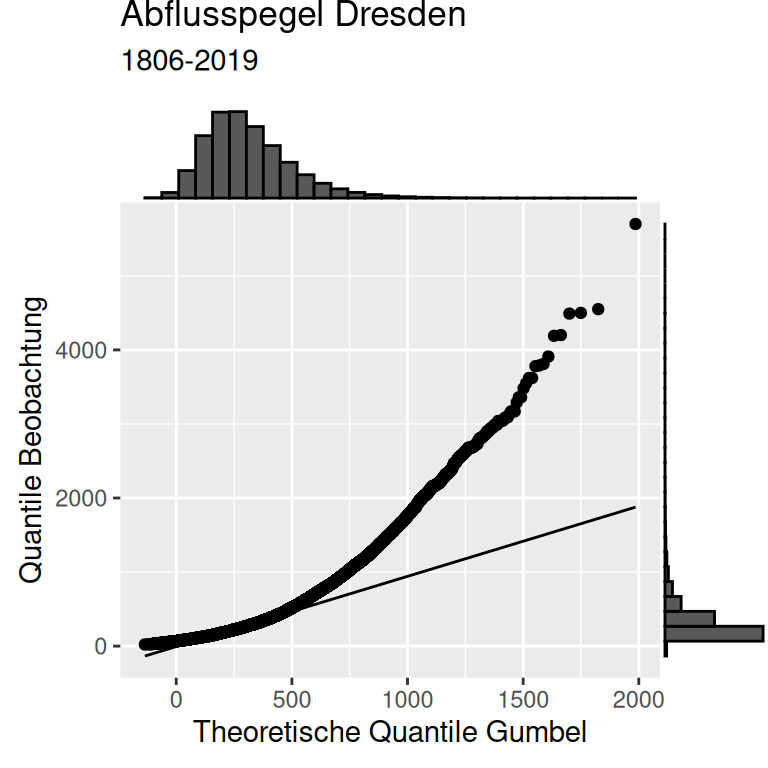
p1 <- ggplot(dresdenQ, aes(sample = Value)) +
stat_qq(distribution = qgumbel, dparams = ddGumbelParamsList ) +
stat_qq_line(distribution = qgumbel, dparams = ddGumbelParamsList) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Gumbel") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")
ggMarginal(p1, type ="histogram")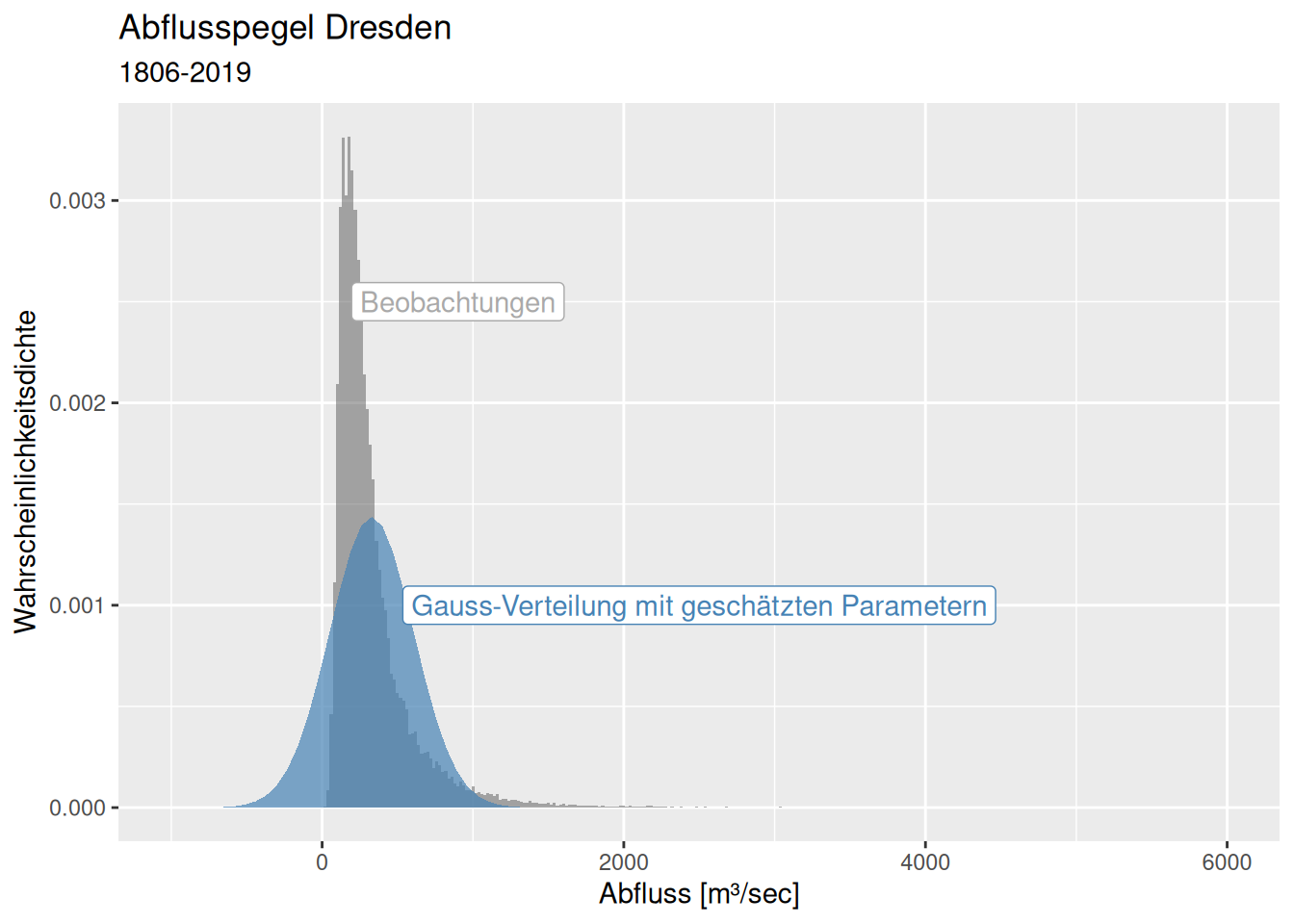
Auch die Gumbel-Verteilung hat Schwierigkeiten, die extremen Hochwasser gut abzubilden.
8.4.5.5 Normalverteilung
Nur um ein Gefühl dafür zu bekommen, wie es aussähe, wenn wir naiv eine Normalverteilung angenommen hätten.
## mean sd
## 328.7078312 277.6318279
## ( 0.9930507) ( 0.7021929)ddGaussParamsList <- list( mean= dresdenGaussParams$estimate[1],
sd = dresdenGaussParams$estimate[2])
ggplot(dresdenQ, aes(x=Value)) +
geom_histogram(binwidth = 20, mapping = aes(y = after_stat(density)),
alpha=.5) +
stat_function(
fun = dnorm,
geom = "area",
fill = "steelblue",
alpha = .7,
args = ddGaussParamsList
) +
xlab("Abfluss [m³/sec]") + ylab("Wahrscheinlichkeitsdichte") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019") +
annotate(geom= "label", x=2500, y= 0.001, colour = "steelblue",
label = "Gauss-Verteilung mit geschätzten Parametern") +
annotate(geom= "label", x=900, y= 0.0025, colour = "darkgrey",
label = "Beobachtungen") +
xlim(-1000, 6000)## Warning: Removed 2 rows containing missing values or values outside the scale range
## (`geom_bar()`).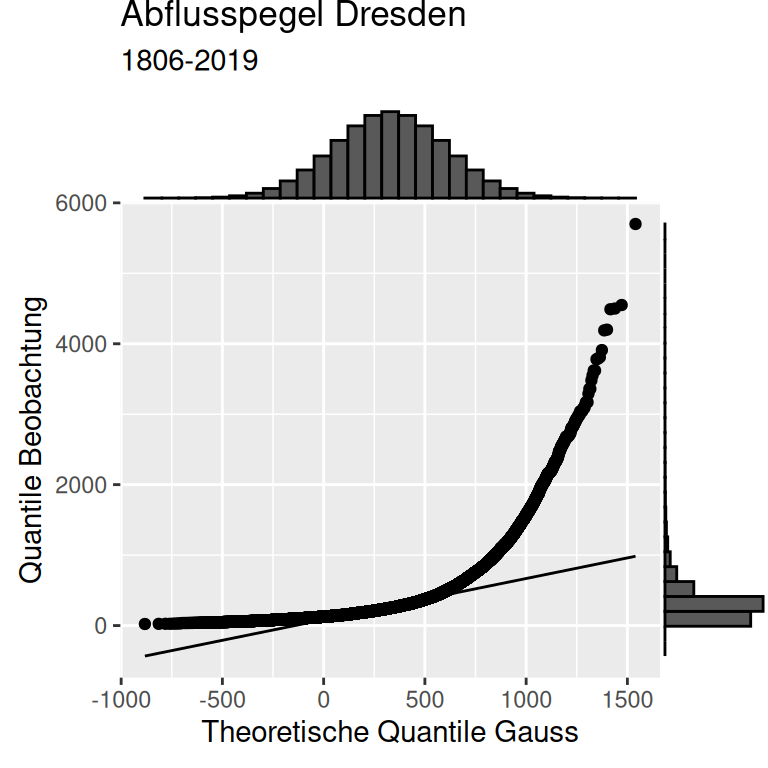
p1 <- ggplot(dresdenQ, aes(sample = Value)) +
stat_qq(distribution = qnorm, dparams = ddGaussParamsList ) +
stat_qq_line(distribution = qnorm, dparams = ddGaussParamsList) +
ylab("Quantile Beobachtung") +
xlab("Theoretische Quantile Gauss") +
labs(title = "Abflusspegel Dresden", subtitle = "1806-2019")
ggMarginal(p1, type ="histogram")
Die Gauss-Verteilung sagt negative Abflüsse voraus und unterschätzt extrme Hochwässer noch deutlich stärker als die anderen Verteilungen.
8.4.5.6 Vergleich der Verteilungen
Wir können die Verteilungen anhand ihrer Likelihood vergleichen. Je höher die Likelihood (bzw. die log-Likelihood), desto besser.37
## [1] -511887.9## [1] -521179.2## [1] -523369.6## [1] -531124## [1] -550669.6Die größte Likelihood hat die Lognormalverteilung, dann folgen die Gumbel, die Weibull und dann die Exponentialverteilung. Die Normalverteilung liegt wie erwartet deutlich am Ende der Anpassungsgüte.
Oder nocheinmal dieselben Zahlen aber als Plot:
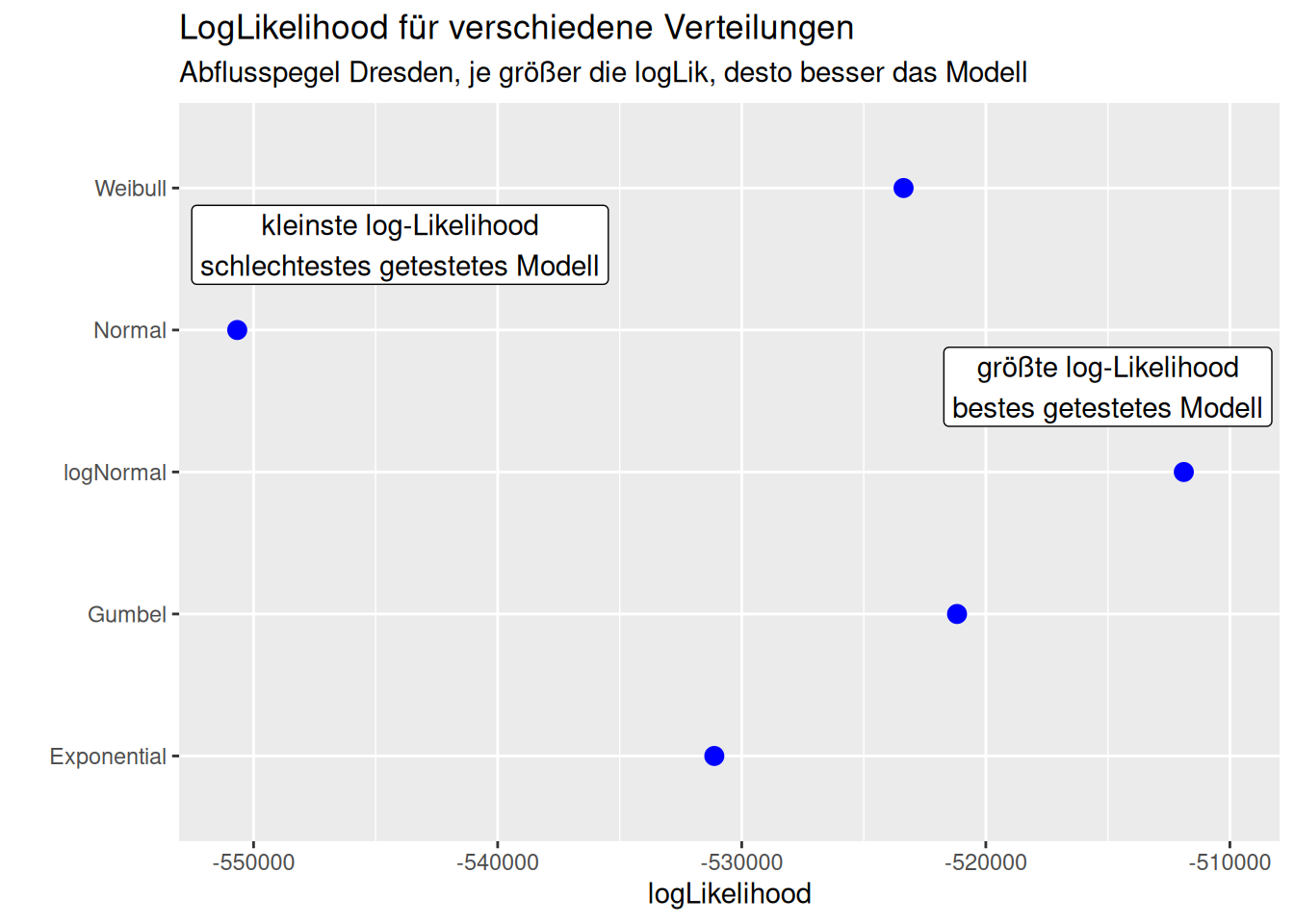
Schauen wir uns nun doch einmal an, was die unterschiedlichen Verteilungen für extreme Hochwasser an Wahrscheinlichkeiten angeben. Wir geben immer die Wahrscheinlichkeit für ein Ablussereignis an, dass so hoch wie der Schwellwert oder noch höher ist (lower.tail = FALSE).
Lognormalverteilung
qValues <- c(1000, 1500, 2000, 4000)
pValLogNorm <- plnorm(q = qValues, meanlog = ddLogNormParamsList$meanlog,
sdlog = ddLogNormParamsList$sdlog,
lower.tail = FALSE)
pValLogNorm## [1] 1.902649e-02 3.459924e-03 8.301209e-04 1.243715e-05Weibull-Verteilung
pValWeib <- pweibull(q = qValues, shape = ddWeiParamsList$shape,
scale = ddWeiParamsList$scale,
lower.tail = FALSE)
pValWeib## [1] 1.621430e-02 6.825421e-04 1.801458e-05 2.665613e-13Gumbel-Verteilung
pValGumb <- pgumbel(q = qValues, scale = ddGumbelParamsList$scale,
location = ddGumbelParamsList$location,
lower.tail = FALSE)
pValGumb## [1] 5.241162e-03 1.747241e-04 5.810481e-06 7.103984e-12Exponentialverteilung
## [1] 4.772904e-02 1.042735e-02 2.278061e-03 5.189562e-06Normalverteilung
pValNorm <- pnorm(q = qValues, mean = ddGaussParamsList$mean,
sd = ddGaussParamsList$sd,
lower.tail = FALSE)
pValNorm## [1] 7.804706e-03 1.227657e-05 8.730841e-10 3.206012e-40pValues <- data.frame(Q = qValues,
pNorm = pValNorm,
plNorm = pValLogNorm,
pExp = pValExp,
pGumb = pValGumb,
pWeib = pValWeib)
pValues %>%
pivot_longer(cols = -1, names_to = "Verteilung",
values_to = "p") %>%
ggplot(aes(x = Verteilung, y= p )) +
geom_point() + scale_y_log10() +
facet_wrap(~ Q, scale = "free", labeller = label_both) +
labs(title = "Pegel Dresden", subtitle = "Eintretenswahrscheinlichkeit für Q >= Abflusswert") +
ylab("Eintretenswahrscheinlichkeit")
Wir sehen, dass die Exponentialverteilung dazu neigt, die Wahrscheinlichkeit für Hochwasser bis 2000 \(m^3/sec\) zu überschätzen (wenn man die Log-Normalverteilung als Vergleich heranzieht), während die anderen Verteilungen sehr stark unterschätzen (die y-Achse ist logarithmisch skaliert). Die Normalverteilung unterschätzt die Eintrittswahrscheinlichkeit dramatisch.
8.4.6 Fallstudie aus der Ökologie - negative binomial Verteilung
In vergleichbaren Waldgebieten seinen Kamerafallen aufgestellt worden und anschließend hinsichtlich der auf den Bildern zu sehenden Arten ausgewertet worden. Hinsichtlich einer Art hätten wir die Anzahl von Beobachtungen counts für jedes Gebiet erhalten. Insgesamt haben wir für 18 Gebiete Kamerafallen aufgestellt (jeweils identisch viele, so dass wir die Gebiete vergleichen können). Die Gebiete unterscheiden sich dabei hinsichtlich der Art wie sie gemanaget werden management.
counts <- (c(67, 194, 155, 135, 146, 257, 114, 134, 111, 87,
62, 67, 85, 89, 63, 86, 97, 44))
management <- rep(LETTERS[1:3], each = 6)
dat <- data.frame(counts, management)
dat## counts management
## 1 67 A
## 2 194 A
## 3 155 A
## 4 135 A
## 5 146 A
## 6 257 A
## 7 114 B
## 8 134 B
## 9 111 B
## 10 87 B
## 11 62 B
## 12 67 B
## 13 85 C
## 14 89 C
## 15 63 C
## 16 86 C
## 17 97 C
## 18 44 Cggplot(dat, aes(x=counts)) +
geom_histogram(binwidth = 20) +
facet_wrap(~management, labeller = label_both) +
xlab("Anzahl Beobachtungen der Art je Gebiet") +
ylab("Anzahl der Gebiete") +
labs(title="Kamerafallendaten")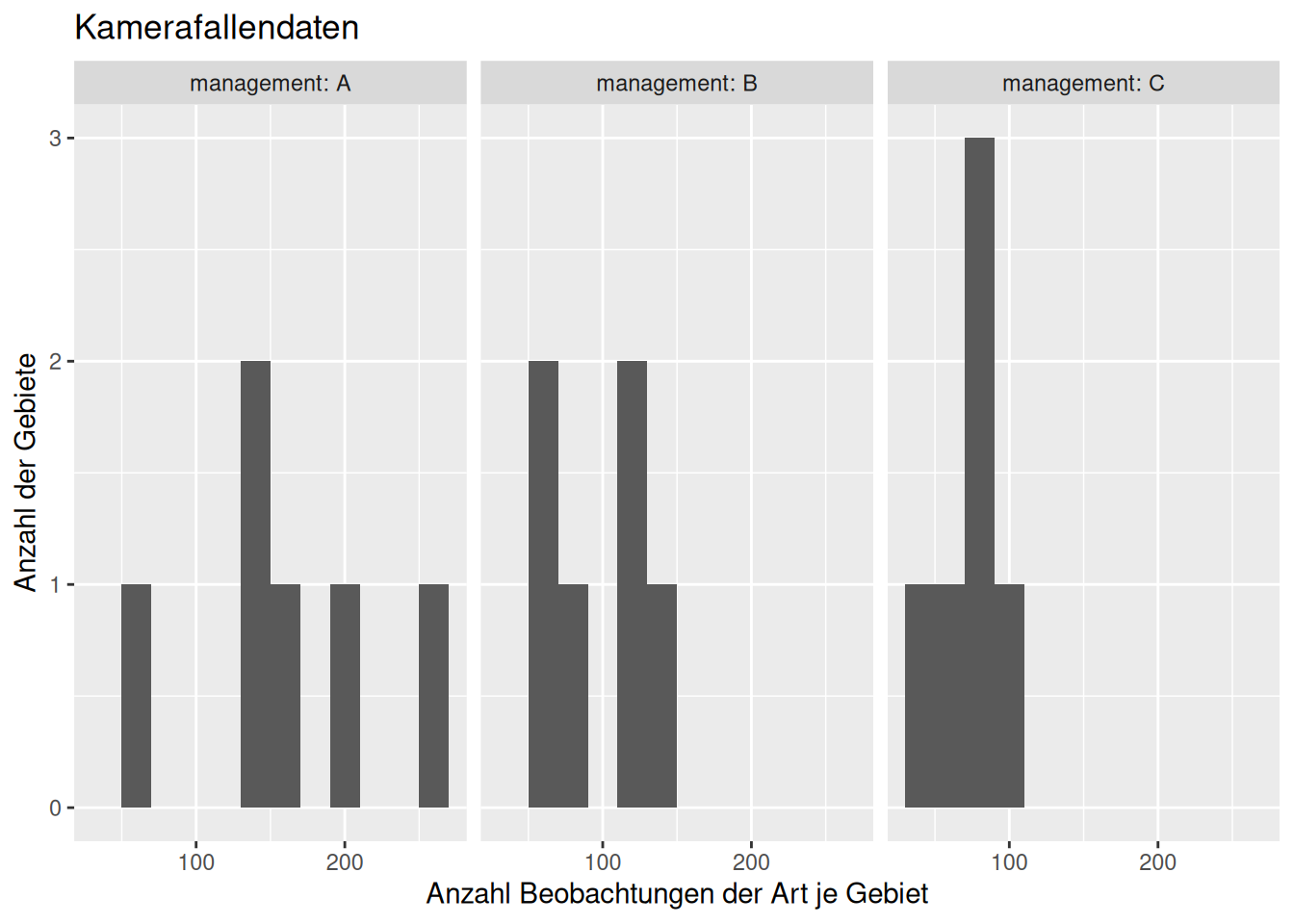
Die Frage sei nun, ob sich die Gebiete hinsichtlich der Artenzahlen nach Management unterscheiden. Wir wollen hierzu für alle Gebiete eines Managementstyps eine negative binomiale Verteilung schätzen. Hierzu benötigen wir das package fitdistrplus-
library(fitdistrplus)
# Management A
dat %>% filter(management=="A") %>% pull(counts) %>%
fitdistrplus::fitdist(distr = "nbinom")## Fitting of the distribution ' nbinom ' by maximum likelihood
## Parameters:
## estimate Std. Error
## size 7.051806 4.18428
## mu 159.010696 24.98339Um Platz zu sparen definieren wir eine Funktion und mappen sie mit sapply auf einen Vektor mit den Kürzeln für die 3 Managementtypen:
fitnb <- function(managementChar, data)
{
res <- data %>% filter(management==managementChar) %>%
pull(counts) %>%
fitdistrplus::fitdist(distr = "nbinom")
return(res$estimate)
}
sapply(c("A", "B", "C"), FUN= fitnb, data = dat)## A B C
## size 7.051806 15.08826 19.73955
## mu 159.010696 95.83560 77.32737Wie sehen die Verteilungen aus?
x <- 1:400
p1 <- makePlot_nb(x = x,size = 7.051806 , mu = 159.010696)
p2 <- makePlot_nb(x = x,size = 15.08826 , mu = 95.83560)
p3 <- makePlot_nb(x = x,size = 19.73955 , mu = 77.32737)
ggarrange(p1, p2, p3,
labels = c("A", "B", "C"))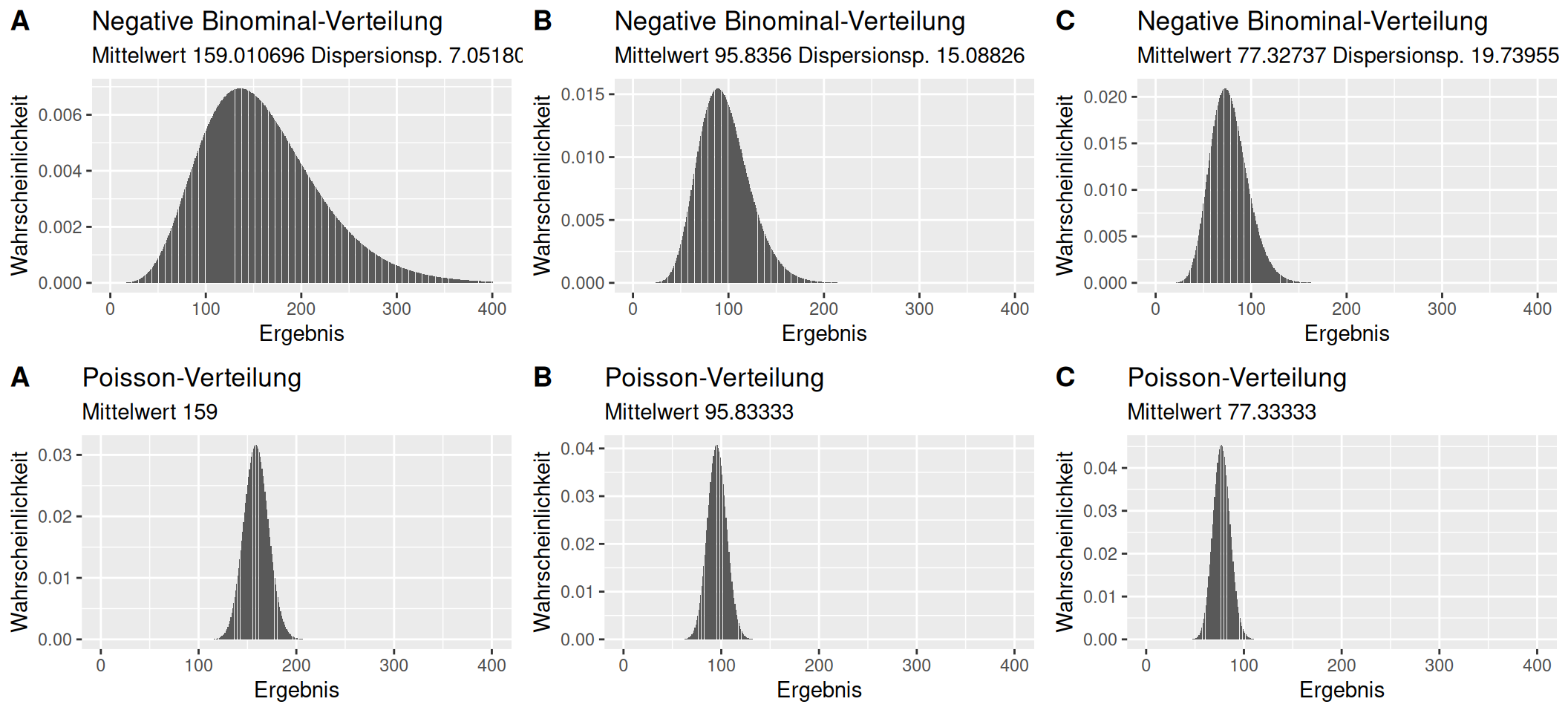
Die Verteilungen unterscheiden sich also durchaus, was darauf hin deutete, dass das Management der Gebiete eine relevante Rolle für die Abundanz der Art in der Region spielt.38
Falls wir eine Poissonverteilung annehmen würden (was nicht korrekt wäre, da die Daten stärker streuen), würden die Analyse wie folgt aussehen:
fitpois <- function(managementChar, data)
{
res <- data %>% filter(management==managementChar) %>%
pull(counts) %>%
fitdistrplus::fitdist(distr = "pois")
return(res$estimate)
}
sapply(c("A", "B", "C"), FUN= fitpois, data = dat)## A.lambda B.lambda C.lambda
## 159.00000 95.83333 77.33333x <- 1:400
p1pois <- makePlot_pois(x = x,lambda = 159)
p2pois <- makePlot_pois(x = x,lambda = 95.83333)
p3pois <- makePlot_pois(x = x,lambda = 77.33333)
ggarrange(p1, p2, p3,
p1pois, p2pois, p3pois,
ncol=3, nrow=2,
labels = rep(c("A", "B", "C"),2))
Welche der beiden Verteilungen beschreibt die Daten jeweils besser?
getLik4PoisNb <- function(managementChar, data)
{
theCounts <- res <- data %>% filter(management==managementChar) %>%
pull(counts)
fitPois <- fitdistrplus::fitdist(theCounts, distr = "pois")
fitNb <- fitdistrplus::fitdist(theCounts, distr = "nbinom")
return(list(logLik_pois = fitPois$loglik,
logLik_nb = fitNb$loglik))
}
sapply(c("A", "B", "C"), FUN= getLik4PoisNb, data = dat)## A B C
## logLik_pois -86.10071 -40.71461 -32.39105
## logLik_nb -32.90849 -28.04853 -26.27836Auf Basis der Log-Likelihood beschreibt die negative binomial Verteilung die Daten für alle Managementtypen besser als die Poisson Verteilung. Allerdings müssen wir für die negative binomial Verteilung 2 Parameter aus den Daten schätzen, während es für die Poissonverteilung nur einer ist. Hierzu später mehr, wenn wir uns anschauen, wie man Modelle mittels des AIC oder BICs vergleicht.39
8.4.7 Likelihood Funktionen für verschiedene Verteilungen
8.4.7.1 Normalverteilung
Die Likelihood, eine unabhängige, gleichmäßig verteilte (iid) Zufallsstichprobe \(x_1, x_2, \ldots x_n\) von einer Normalverteilung mit dem Mittelwert \(\mu\) und der Varianz \(\sigma^2\) zu beobachten ist gegeben durch folgende Likelihoodfunktion:
\[L(\mu, \sigma^2)= \prod_{i=1}^n (\frac{1}{\sqrt{2 \pi \sigma^2}} e^{- \frac{(x_i-\mu)^2}{2 \sigma^2}})\]
Bei der Log-Likelihood vereinfacht sich das Produkt zu einer Summe:
\[logL(\mu, \sigma^2)= \sum_{i=1}^n (-log(\sigma \sqrt{2 \pi}) - \frac{1}{2} \frac{(x_i-\mu)^2}{\sigma^2}) = -n\cdot log(\sigma \sqrt{2 \pi}) - \frac{n}{2}\sum_{i=1}^n \frac{(x_i-\mu)^2}{\sigma^2}\]
8.4.7.2 Poisson Verteilung
Die Likelihood, eine unabhängige, gleichmäßig verteilte (iid) Zufallsstichprobe \(x_1, x_2, \ldots x_n\) von einer Poissonverteilung mit dem Mittelwert \(\lambda\) zu beobachten ist gegeben durch folgende Likelihoodfunktion:
\[L(\lambda)= e^{-n\lambda}\cdot \lambda ^{\sum_i^{n}x_i}\]
8.4.7.3 Binomial Verteilung
Die Likelihood, eine unabhängige, gleichmäßig verteilte (iid) Zufallsstichprobe \(x_1, x_2, \ldots x_n\) aus einer Bernoulli-Verteilung mit \(P(X_i=1) = \theta\) und \(P(X_i=0) = 1-\theta\) zu beobachten ist gegeben durch folgende Likelihoodfunktion:
\[L(\theta)= \prod_{i=1}^n \theta^{x_i}(1-\theta)^{1-x_i}\]
Die Likelihood \(k\) Erfolgsereignisse aus \(n\) Versuchen für eine Binomial-verteilte Zufallsvariable \(X \widetilde{~} binomial(n,\theta)\) zu erhalten beträgt:
\[L(\theta)=\binom{n}{k}\theta^k(1-\theta)^{n-k}\]
8.5 Zentraler Grenzwertsatz
Der zentrale Grenzwertsatz (von Lindeberg-Lévy) (central limit theorem) liefert die Begründung dafür, dass sich bei der additiven Überlagerung vieler kleiner unabhängiger Zufallseffekte zu einem Gesamteffekt zumindest approximativ eine Normalverteilung ergibt, wenn keiner der einzelnen Effekte einen dominierenden Einfluss auf die Varianz besitzt.
Sei \(X_{1},X_{2},X_{3},\dots\) eine Folge von Zufallsvariablen, die auf demselben Wahrscheinlichkeitsraum mit dem Wahrscheinlichkeitsmaß \(P\) alle dieselbe Wahrscheinlichkeitsverteilung aufweisen und unabhängig sind (u.i.v. = unabhängig und identisch verteilt, engl. i.i.d. = independent and identically distributed). Weiterhin gelte, dass sowohl der Erwartungswert \(\mu\) als auch die Standardabweichung \(\sigma >0\) existieren und endlich sind. Für die \(n\)-te Teilsumme dieser Zufallsvariablen \(S_{n}=X_{1}+X_{2}+\cdots +X_{n}\) ist der Erwartungswert von \(S_{n}\) \(n\mu\) und die Varianz ist \(n\sigma ^{2}\). Standardisiert man die Zufallsvariable
\[Z_{n}={\frac {S_{n}-n\mu }{\sigma {\sqrt {n}}}}={\frac {{\frac {1}{n}}S_{n}-\mu }{\frac {\sigma }{\sqrt {n}}}}\]
dann besagt der Zentrale Grenzwertsatz, dass die Verteilungsfunktion von \(Z_{n}\) für \(n\to \infty\) punktweise gegen die Verteilungsfunktion \(\Phi\) der Standardnormalverteilung \(\mathcal N(0,1)\) konvergiert. Dies entspricht genau dem Begriff der Konvergenz in Verteilung in der Stochastik.
Anders formuliert konvergiert die Verteilung \(\sqrt{n}(\frac{S_n}{n}-\mu)\) gegen eine Normalverteilung.
Vereinfacht ausgedrückt folgen die Mittelwerte von Stichproben einer Normalverteilung, auch wenn die Verteilungsfunktion der Grundgesamtheit keine Normalverteilung ist. Dies gilt für die meisten Verteilungen. Die Cauchy-Verteilung ist mal wieder ein Gegenbeispiel, da weder Erwartungswert noch Varianz existieren.
Der zentrale Grenzwertsatz ist der Grund für die herausragende Bedeutung der Normalverteilung in der Statistik. Allerdings muss man sich klar machen, dass die Aussage nur für große Zahlen gilt. Was als groß angesehen wird ist dabei durchaus umstritten. Die bei Anwendern zu findende Aussage, dass 50 groß sei, kann man i.d.R. sicher als viel zu optimistisch bezeichnen. Stichprobenumfänge von zehntausend oder gar einhunderttausend kann man sicher als groß bezeichnen.
Wichtig ist weiterhin, dass die Beobachtungen unabhängig und identisch verteilt sind. Bei räumlicher oder zeitlicher Autokorrelation oder hierarchisch strukturierten Beobachtungen gilt der zentrale Grenzwertsatz nicht automatisch. Wenn weitere Bedingungen erfüllt sind, gilt der zentrale Grenzwertsatz trotzdem.
Schauen wir uns dies einmal für die Exponentialverteilung an, die klar alles andere als Normalverteilt ist.
# Plotten einer exponentiellen Verteilung
exp.rate <- 0.01
curve(dexp(x, rate=exp.rate), from=0, to=600, col="blue", ylab="Wahrscheinlichkeitsdichte", las=1)
Nun ziehen wir wiederholt Stichproben der Größe 50 und berechnen daraus jeweils den Mittelwert. Dannach plotten wir das entstehende Histogram und überlagern es mit einer Normalverteilung mit Mittelwert und Standardabweichung, die zuvor aus der Verteilung der Mittelwerte berechnet worden sind.
# Stichprobengröße, von der der Mittelwert berechnet wird
N <- 50
# Erzeugen eines leeren Vektors, um die Mittelwerte aufzunehmen
exp.means <- NULL
# Schleife über eine große Anzahl von Wiederholungen
for(i in 1:5000){
# Ziehen einer Stichprobe von der Expoentialverteilung
samp <- rexp(N, rate=exp.rate)
# Berechnen des Mittelwertes der Stichprobe und speichern im Vektor
exp.means[i] <- mean(samp)
}
# Berechnen von Mittelwert und Standardabweichung der Mittelwerte
mn.mn <- mean(exp.means)
sd.mn <- sd(exp.means)
# Plotten der Normalverteilung mit Mittelwert und Standardabweichung der Mittelwerte der Stichproben von der Exponentialfunktion
hist(exp.means, probability=T, breaks = 100,
main=paste("N =", N, ", Anzahl Stichproben = 5000"),
xlab="Mittelwerte aus Stichproben \nexponential verteilter Grundgesamtheit",
ylab="Wahrscheinlichkeitsdichte", las=1)
curve(dnorm(x, mean=mn.mn, sd=sd.mn), col='red', lwd=2,
from=(mn.mn - 4*sd.mn), to=(mn.mn + 4*sd.mn),
add = TRUE)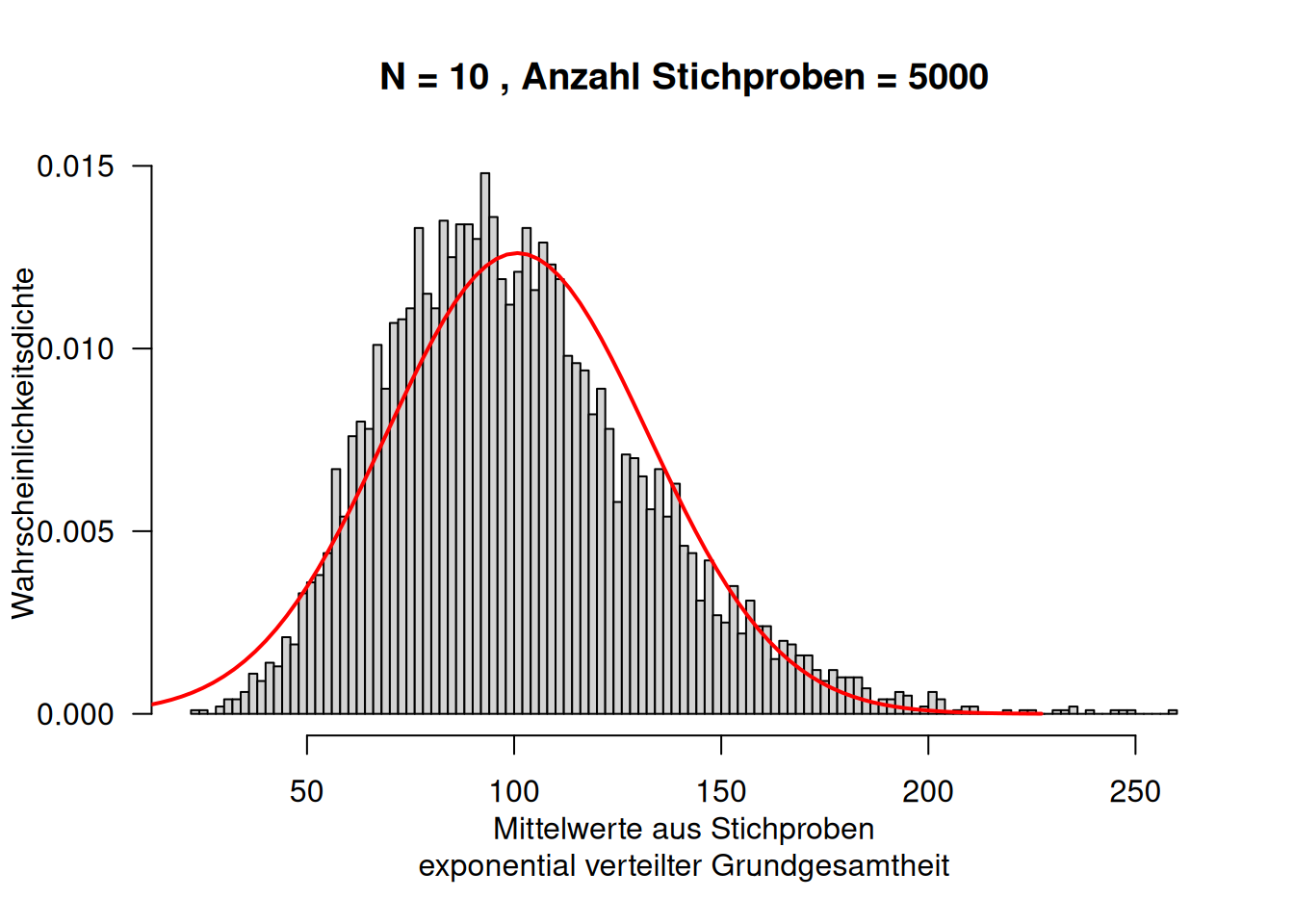
Wie wir sehen ähnelnt die Verteilung der Mittelwerte sehr stark einer Normalverteilung.
Wenn die Stichprobengröße sehr klein wählen (\(N =2\)), klappt das nicht mehr wirklich gut. Die Verteilung der Mittelwerte ähnelt nun sehr stark der Exponentialverteilung
# Stichprobengröße, von der der Mittelwert berechnet wird
N <- 2
# Erzeugen eines leeren Vektors, um die Mittelwerte aufzunehmen
exp.means <- NULL
# Schleife über eine große Anzahl von Wiederholungen
for(i in 1:5000){
# Ziehen einer Stichprobe von der Expoentialverteilung
samp <- rexp(N, rate=exp.rate)
# Berechnen des Mittelwertes der Stichprobe und speichern im Vektor
exp.means[i] <- mean(samp)
}
# Berechnen von Mittelwert und Standardabweichung der Mittelwerte
mn.mn <- mean(exp.means)
sd.mn <- sd(exp.means)
# Plotten der Normalverteilung mit Mittelwert und Standardabweichung der Mittelwerte der Stichproben von der Exponentialfunktion
hist(exp.means, probability=T, breaks = 100,
main=paste("N =", N, ", Anzahl Stichproben = 5000"),
xlab="Mittelwerte aus Stichproben\nexponential verteilter Grundgesamtheit",
ylab="Wahrscheinlichkeitsdichte", las=1)
curve(dnorm(x, mean=mn.mn, sd=sd.mn), col='red', lwd=2,
from=(mn.mn - 4*sd.mn), to=(mn.mn + 4*sd.mn),
add = TRUE)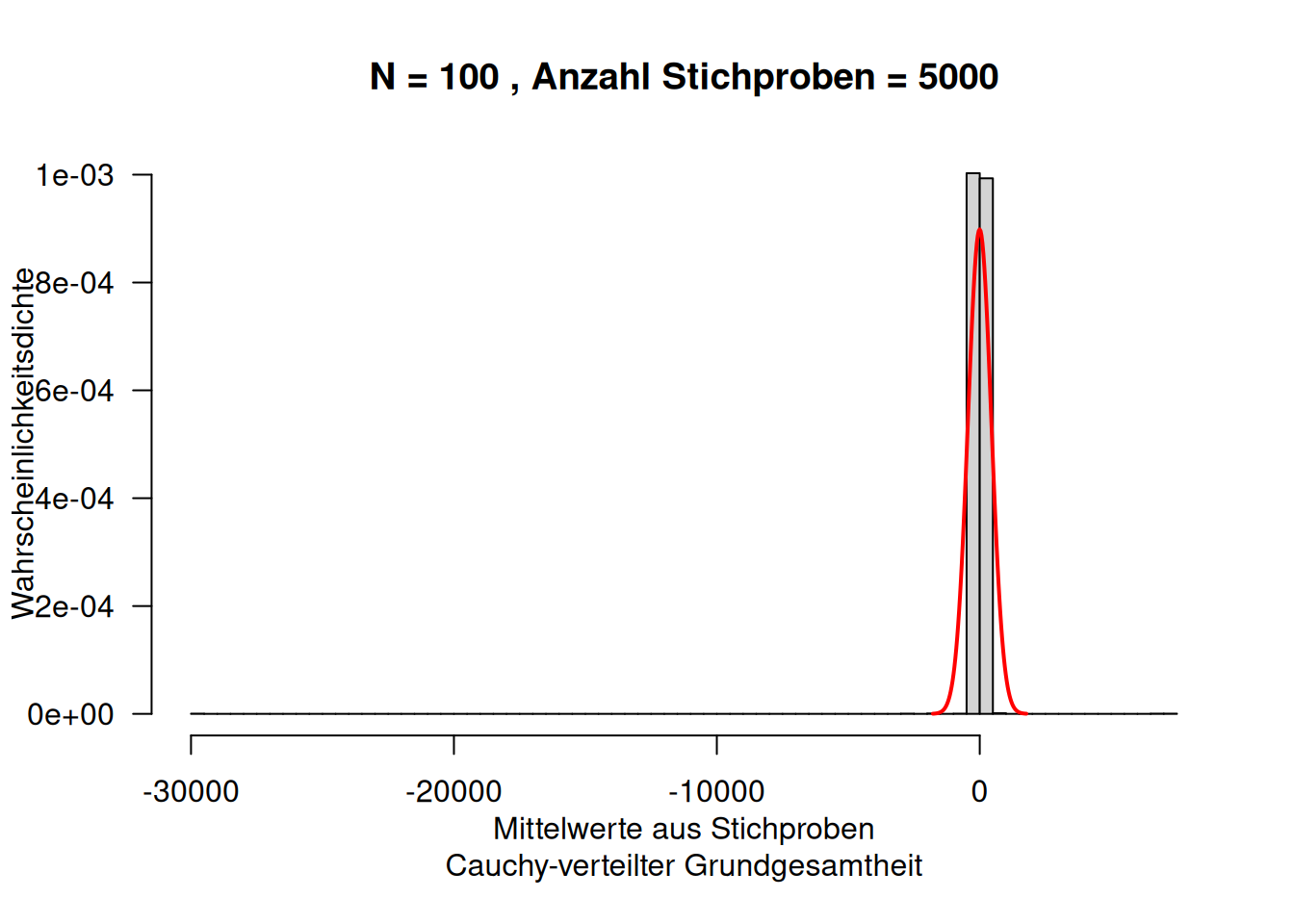
Wir brauchen also eine ausreichend große Stichprobengröße - sonst ist der Mittelwert als Schätzer des Erwartungswertes nicht gut genug. Auch bei einer Stichprobengröße von \(N=10\) ist die Verteilung der Mittelwerte noch nicht gut normalverteilt, allerdings bereits deutlich besser.
# Stichprobengröße, von der der Mittelwert berechnet wird
N <- 10
# Erzeugen eines leeren Vektors, um die Mittelwerte aufzunehmen
exp.means <- NULL
# Schleife über eine große Anzahl von Wiederholungen
for(i in 1:5000){
# Ziehen einer Stichprobe von der Expoentialverteilung
samp <- rexp(N, rate=exp.rate)
# Berechnen des Mittelwertes der Stichprobe und speichern im Vektor
exp.means[i] <- mean(samp)
}
# Berechnen von Mittelwert und Standardabweichung der Mittelwerte
mn.mn <- mean(exp.means)
sd.mn <- sd(exp.means)
# Plotten der Normalverteilung mit Mittelwert und Standardabweichung der Mittelwerte der Stichproben von der Exponentialfunktion
hist(exp.means, probability=T, breaks = 100,
main=paste("N =", N, ", Anzahl Stichproben = 5000"),
xlab="Mittelwerte aus Stichproben\nexponential verteilter Grundgesamtheit",
ylab="Wahrscheinlichkeitsdichte", las=1)
curve(dnorm(x, mean=mn.mn, sd=sd.mn), col='red', lwd=2,
from=(mn.mn - 4*sd.mn), to=(mn.mn + 4*sd.mn),
add = TRUE)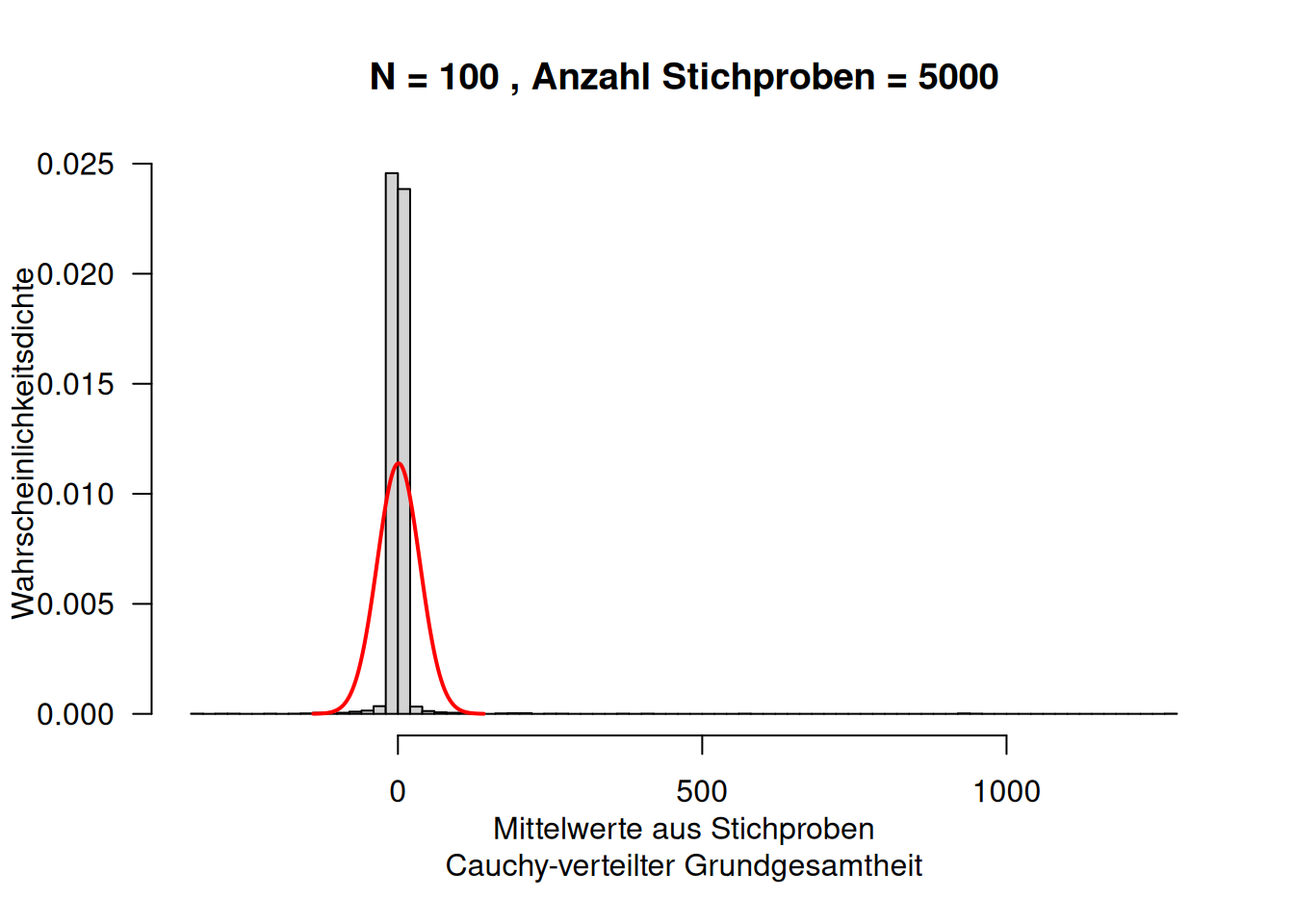
Schauen wir uns die Cauchy Verteilung als Beispiel an, für das der zentrale Grenzwertsatz nicht greift:
# Stichprobengröße, von der der Mittelwert berechnet wird
N <- 100
# Erzeugen eines leeren Vektors, um die Mittelwerte aufzunehmen
cau.means <- NULL
# Schleife über eine große Anzahl von Wiederholungen
for(i in 1:5000){
# Ziehen einer Stichprobe von der Expoentialverteilung
samp <- rcauchy(N, location = 0, scale = 1)
# Berechnen des Mittelwertes der Stichprobe und speichern im Vektor
cau.means[i] <- mean(samp)
}
# Berechnen von Mittelwert und Standardabweichung der Mittelwerte
mn.mn <- mean(cau.means)
sd.mn <- sd(cau.means)
# Plotten der Normalverteilung mit Mittelwert und Standardabweichung der Mittelwerte der Stichproben von der Exponentialfunktion
hist(cau.means, probability=T, breaks = 100,
main=paste("N =", N, ", Anzahl Stichproben = 5000"),
xlab="Mittelwerte aus Stichproben\nCauchy-verteilter Grundgesamtheit",
ylab="Wahrscheinlichkeitsdichte", las=1)
curve(dnorm(x, mean=mn.mn, sd=sd.mn), col='red', lwd=2,
from=(mn.mn - 4*sd.mn), to=(mn.mn + 4*sd.mn),
add = TRUE)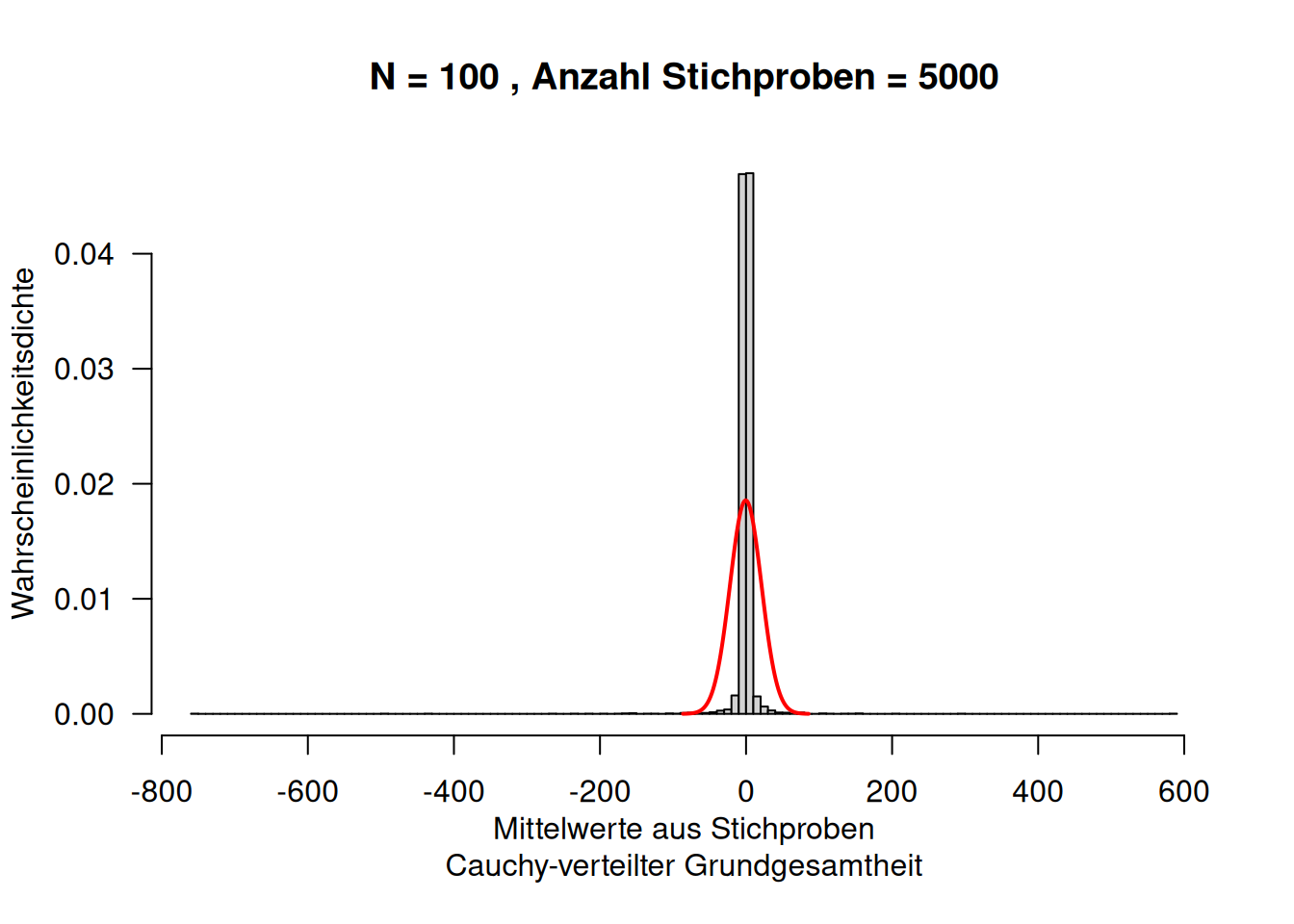
Die Mittelwerte der 5000 Stichproben streuen sehr stark und sind nicht normalverteilt. Es gibt viel mehr Wahrscheinlichkeitsmasse in den Ende der Verteilung der Mittelwerte, als aufgrund einer Normalverteilung zu erwarten wäre.
8.6 Kontrollfragen
- Welche Parameter beschreiben die Binomialverteilung
- Wie hängen Mittelwert und Varianz bei der Poisson-Verteilung zusammen?
- Wie kann man eine beliebige Normalverteilung in eine Standardnormalverteilung überführen?
- Was ist die Likelihood?
- Nennen Sie drei diskrete und drei kontinuierliche Verteilungen
- Beschreiben Sie, wie die Maximum Likelihood Schätzung von Verteilungsparametern funktioniert
- Nennen Sie zwei Test-Verteilungen
- Wie verändert sich die t-Verteilung, wenn sie den einzigen Verteilungsparameter verändern?
- Wie verändert sich die Form der Normalverteilung, wenn die Standardabweichung erhöht wird?
- Wie verändert sich die Form der Log-Normalverteilung, wenn die Standardabweichung erhöht wird?
In der Bayesischen Statistik wird oft eine alternative Form der Parametrisierung verwendet, bei der anstelle der Varianz die Präzison ($) verwendet wird.↩︎
Dieser quadratische Abfall ist der Grund, warum man die Methode der kleinsten Quadrate verwendet, um im linearen Modell Parameter zu schätzen.↩︎
Log steht hier für den natürlichen Logarithmus ln. Im Prinzip kann man den Zusammenhang aber auch durch den Logarithmus zu einer anderen Basis als der eulerschen Zahl e ausdrücken.↩︎
die Einkommen der unteren 95-98% folgen oftmals einer Log-Normalverteilung.↩︎
Es gibt auch eine alternative Parametrisierung über \(\mu = \frac{1}{\lambda}\), die vor allem im angelsächsischen Sprachraum verwendet wird: \(f(x) = \frac{1}{\mu} e^{-\frac{x}{\mu}}\).↩︎
Weiterhin ist die Kovarianzmatrix stets positiv semidefinit und damit stets mittels Hauptachsentransformation transformierbar.↩︎
Noch besser, wenn wir das über der AIC oder BIC vergleichen, da die Verteilungen eine unterschiedliche Anzahl von Parametern verwenden. Aber dazu später mehr.↩︎
Korrekt würden wir dies durch ein generalisiertes lineares Modell testen. Dazu später mehr. Der Code wäre wie folgt:
g <- MASS::glm.nb(counts~management, data=dat); summary(g)↩︎Außerdem sollten wir berücksichtigen, dass der Datensatz sehr klein ist, was die Unsicherheit der Schätzer erhöht. Allerdings ist dies in der Praxis häufig der Fall, da Untersuchungen geld- und zeitintensiv sind und wir oftmals mit kleinen Datensätzen umgehen müssen.↩︎