Kapitel 14 Lineares Modell - Unsicherheit
## Warning in library(package, lib.loc = lib.loc, character.only = TRUE,
## logical.return = TRUE, : there is no package called 'AICcmodavg'14.1 Vorbereitung
Daten einlesen und Selektion von nicht NA Werten für Russland
temp <- read.table("data/temperatur.csv", header=TRUE)
temp.ru <- subset(temp, ELEV > -20 & CNTRY_NAME == "Russia")Fitten des Regressionsmodells:
14.2 Unsicherheit
Konfidenzintervalle der Regressionskoeffizienten geben uns an, in welchem Bereich wir 95% der Regressionskoeffizienten erwarten würden, wenn wir eine andere Stichprobe aus der Selben zugrundeliegenden Grundgesamtheit ziehen würden.69
Die Konfidenzintervalle berechnen sich dabei wie folgt:
Schätzer \(\pm\) Kritischer Wert * Standardfehler des Schätzers
oder im linearen Modell:
\[ \hat{\beta}_i \pm t^{\frac{\alpha}{2}}_{n-p}\hat{\sigma}\sqrt{(X^TX)^{-1}_{ii}} \]
## 2.5 % 97.5 %
## (Intercept) -0.8300 0.1400
## ELEV -0.0057 -0.0038
## LAT.cent -0.8400 -0.7100
## LON.cent -0.1300 -0.0850Nun kann man sich fragen, ob die Unsicherheit der Schätzung auch von anderen Koeffizienten beeinfluss wird. Die Antwort ist ein klares ja.
Die sogenannten 100*(1-\(\alpha\)) Konfidenzregionen sind wie folgt definiert:
\[ (\hat{\beta} - \beta)^T X^T X (\hat{\beta} - \beta) \leq p \hat{\sigma}^2 F^{\alpha}_{p,n-p} \]
\(n\) ist die Anzahl der Beobachtungen im Modell und \(p\) die Anzahl der Parameter im Modell. \(F\) bezeichnet die F-Verteilung mit den beiden angebenen Freiheitsgraden. \(X\) ist die Modelmatrix des Modells, \(\beta\) der wahre - unbekannte - Regressionskoeffizient und \(\hat{\beta}\) der anhand der Stichprobe geschätze Regressionskoeffizient.
Da die Regionen im mehrdimensionalen Raum schlecht darstellbar sind, wollen wir hier zweidimensionale Projektionen darstellen.70 Die Punkte zeigen die Schätzer, die Ellipsen die Projektionen der Konfidenzintervalle. Die gestrichelten Linien zeigen die eindimensionalen Konfidenzintervalle - wie wir erkennen sind die individuellen Konfidenzintervalle für die Koeffizienten etwas zu schmal. Da der Ursprung stets außerhalb der Ellipsen liegt, sind unsere Koeffizienten signifikant von Null verschieden, auch wenn wir die Konfidenzregion betrachten (joint test).
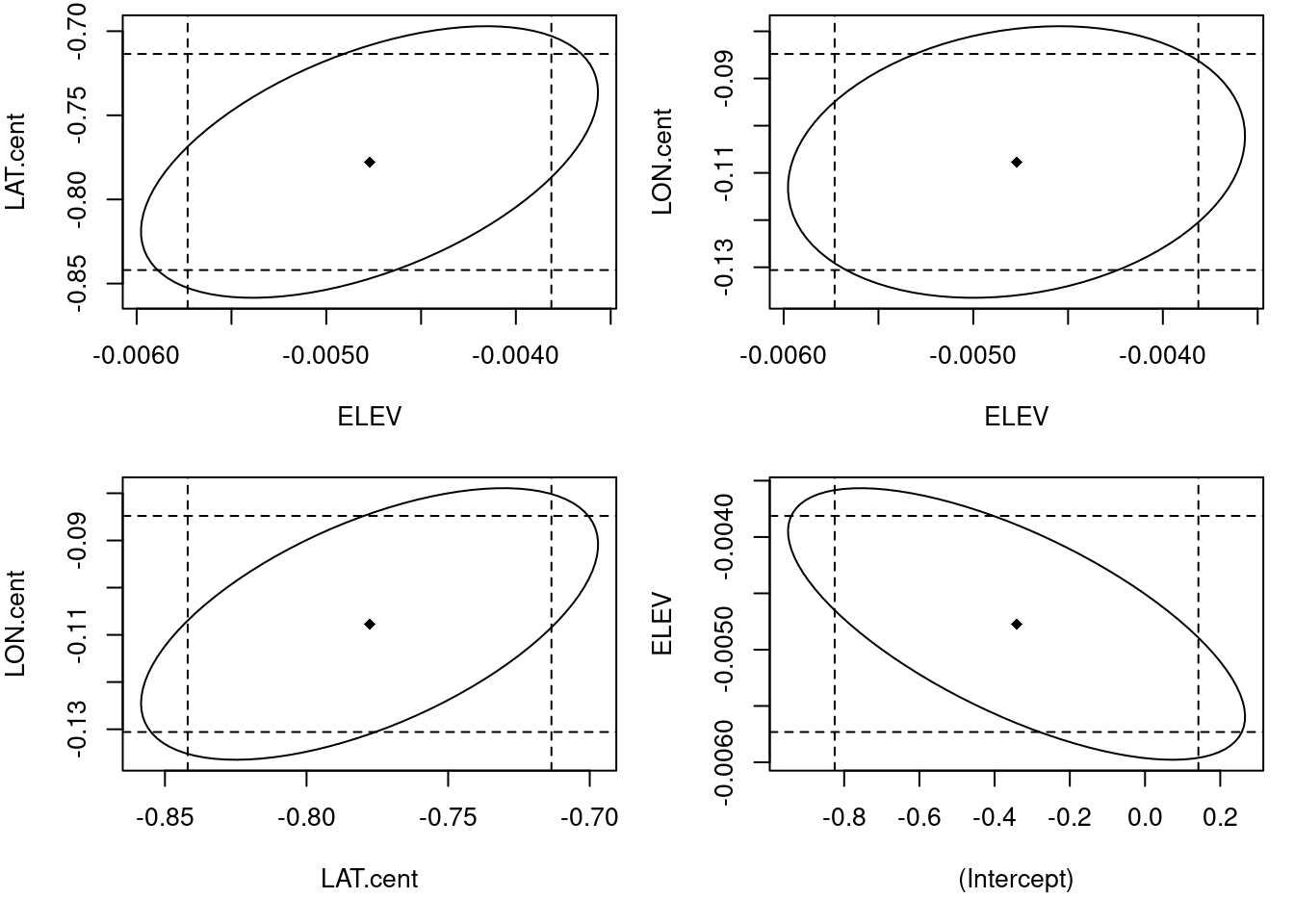
Was wir den Plots weiterhin entnehmen können ist, dass die Koeffizienten korreliert sind. Dies könnten wir auch wie folgt einsehen:
## (Intercept) ELEV LAT.cent LON.cent
## (Intercept) 1.00 -0.68 -0.35 -0.13
## ELEV -0.68 1.00 0.51 0.19
## LAT.cent -0.35 0.51 1.00 0.59
## LON.cent -0.13 0.19 0.59 1.00Der Parameter corr=TRUE bei summary.lm liefert die Korrelationsmatrix der geschätzten Parameter. Hier habe ich die Korrelationskoeffizienten (Pearson’s r) auf zwei signifikante Stellen gerundet dargestellt.
Oftmals haben die Korrelationen zwischen Prädiktoren und die Korrelationen der Regressionskoeffizienten dieser Prädiktoren entgegengesetzte Vorzeichen. Ins Unreine gesprochen wirken korrelierte Prädiktoren in dieselbe Richtung und gleichen sich teilweise aus: wenn der eine Koeffizient größer wird, muss der andere kleiner werden. Bei negativen Korrelationen ist es umgekehrt.
## ELEV LAT.cent LON.cent
## ELEV 1.00 -0.50 0.16
## LAT.cent -0.50 1.00 -0.58
## LON.cent 0.16 -0.58 1.00Latitide und Longitude sind schwach negativ korreliert (Stationen, die bei unserer Stichprobe weiter im Norden liegen liegen tendenziell weiter im Westen), entsprechend sind ihre Regressionskoeffizienten positiv korreliert. Stationen, die höher gelegen sind, liegen tendenziell eher weiter südlich (negativ korreliert), entsprechend sind ihre Regressionskoeffizienten positiv korreliert.
14.3 Unsicherheit der Vorhersage
Die Unsicherheit der Schätzung der Koeffizienten wirkt sich auch auf die Unsicherheit der Vorhersage aus. Wir können uns vorstellen, dass wir immer wieder neue Daten aus der Selben Grundgesamtheit erheben und immer wieder Regressionsmodelle schätzen. Überlagern wir dann all diese Regressionsmodelle, können wir daraus die Konfidenzbänder um die Vorhersage ableiten. Der Bereich, innerhalb dessen 95% der Regressionsmodelle liegen, definiert den 95% Konfidenzbereich. Da die Daten an den Rändern der Verteilung stärker streuen als um den Mittelwert, sind die Konfidenzbänder am engsten um den Mittelwert der Verteilung und gehen zu den Rändern hin auseinander.
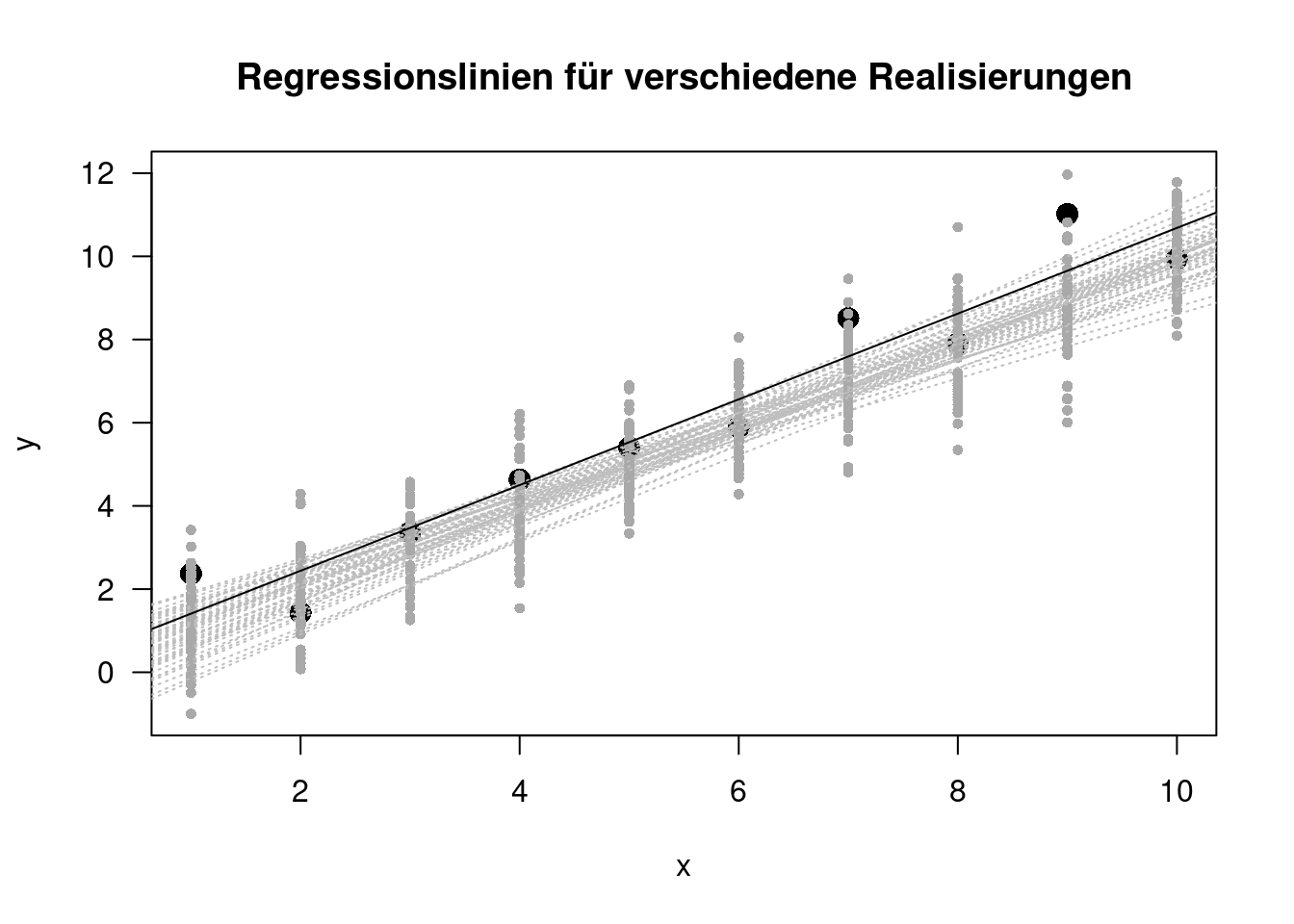
Figure 14.1: Die Konfidenzbänder geben die Unsicherheit der Regressionslinie aufgrund des Fehlers auf dem Response an. Gezeigt sind verschiedene Realisierungen des Response bei fixem Prädiktor (Annaheme fehlerfrei gemessen) sowie die dazugehörigen (grau-gestrichelt) Regressionslinien. EIne Realisierung und die dazugehörige Regressionslinie sind in schwarz hervorgehoben. Es ist deutlich zu sehen, dass die Unsicherheit der Lage der Regressionsline zu den Rändern hin größer wird und am Mittelwert der Stichprobe des Prädiktors (gestichelte vertikale Linie) am geringsten ist.
Der Bereich, der durch die durch die Unsicherseit entstehenden Regressionsgeraden überlagert wird nennt man das Konfidenzband. Ähnlich wie beim Konfidenzintervall gibt man das für ein bestimmtes Konfidenzniveau an, gebräuchlich ist auch hier das 95%-Konfidenzband, also der Bereich, in dem bei hoher Anzahl von Wiederholungen des Experimentes inklusive Schätzen der Regressionsparameter 95% der Regressionslinien liegen. Berücksichtigt wird dabei simultan die Unsicherheit der Schätzung des Achsenabschnittes und des oder der Steigungen für die unterschiedlichen Prädiktoren im Modell. Die Unsicherheit nimmt dabei vom Mittelwert der Daten (in den verschiedenen Dimensionen) aus nach außen zu. In Abbildung 14.1 ist der Mittelwert als gestirchelte schwarze Linie dargestellt.
Das Konfidenzband verbindet die Konfidenzintervalle um einen bestimmten Prädiktorwert x:
\[\hat{y}_{ci}=\hat{y}\pm t_{n-2}^{\alpha/2} \cdot \sqrt{ \frac{\sum_{i=1}^n(y_i-\hat{y})^2}{n-2}}\cdot \sqrt{\frac{1}{n} + \frac{(x-\bar{x})^2}{\sum_{i=1}^n(x_i- \bar{x})^2}}\]
In der zweiten Wurzel findet sich der Ausdruck \((x-\bar{x})^2\) - je weiter wir also vom Mittelwert des Prädiktors \(x\) entfernt sind, desto breiter das Konfidenzintervall für einen Prädiktorwert \(x\). \(t_{n-2}^{\alpha/2}\) gibt den Wert der t-Statistik bei \(n-2\) Freiheitsgraden und dem Signifikanzniveau \(\alpha\) (bei zweiseitigem Test) an. Die erste Wurzel gibt den Standardfehler der Schätzung von \(y\) gegeben \(x\) an. Die zweiter Wurzel stellt die Unsicherheit aufgrund der Entfernung zum Mittelwert der Stichprobe hinsichtlich des Prädiktors \(x\) dar.
Wir können das Konfidenzintervall je Vorhersage über predict erhalten, wenn wir interval="confidence" spezifizieren. Mittels level kann man das Intervall spezifizieren - standardmäßig liefert predict.lm das 95%-Intervall zurück.
new.ru.3 <- data.frame(ELEV=seq(min(temp.ru$ELEV), max(temp.ru$ELEV),
length.out=100),
LAT.cent=mean(temp.ru$LAT.cent),
LON.cent=mean(temp.ru$LON.cent))
g.pred <- as.data.frame(predict(g, newdata = new.ru.3,
interval="confidence"))plot (YEAR ~ ELEV, data=temp.ru, pch=16, col="grey",
cex=2, xlab="Geländehöhe [m]",
ylab="Jahresmitteltemperatur [°C]",
las = 1)
lines(g.pred$fit ~ new.ru.3$ELEV)
lines(g.pred$upr ~ new.ru.3$ELEV, lty=2)
lines(g.pred$lwr ~ new.ru.3$ELEV, lty=2)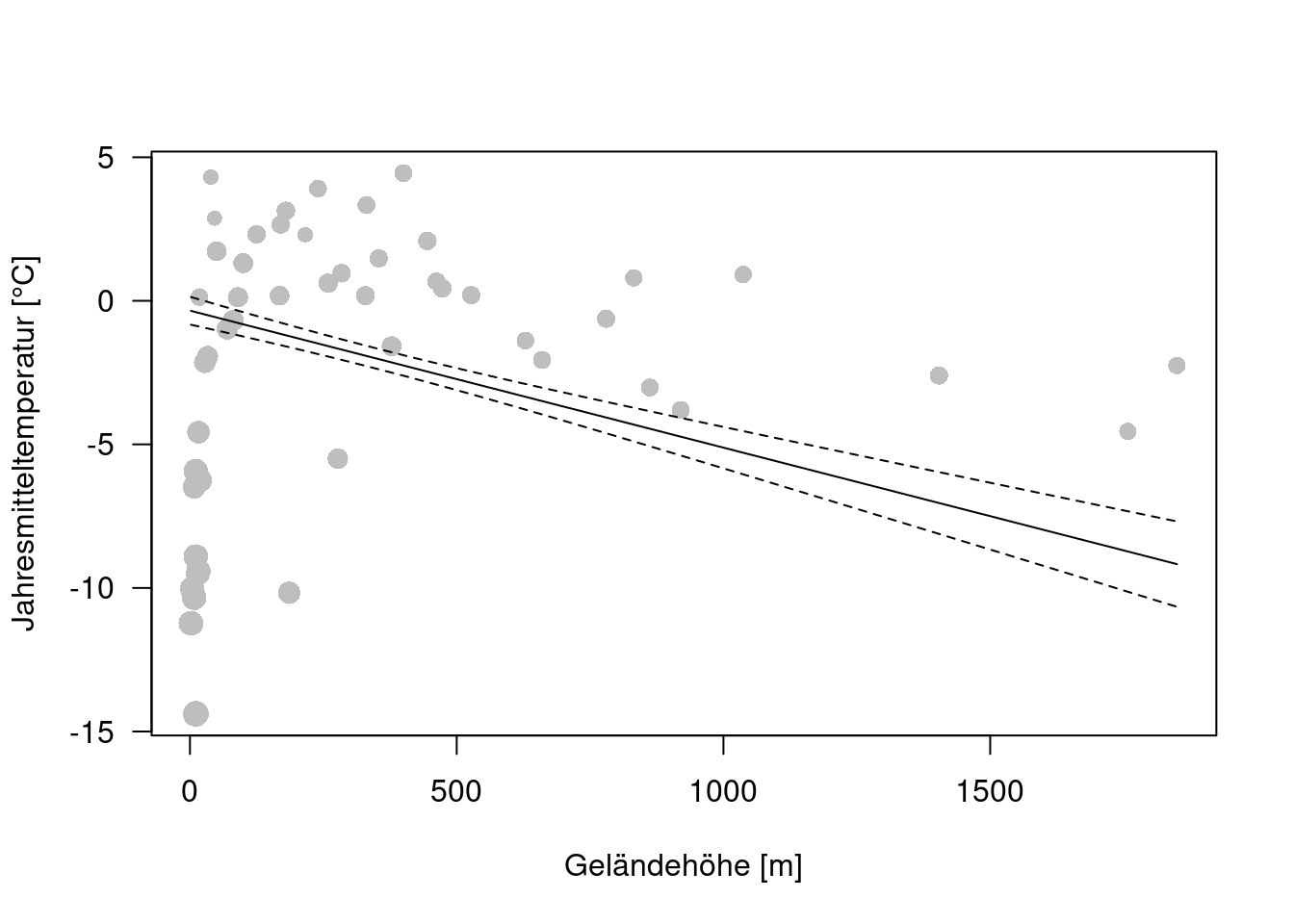
Figure 14.2: Vorhersage und 95% Konfidenzband für die russischen Klimastationen die Höheninformationen besitzen.
In dieser Abbildung sieht das zunächst nicht wirklich nach einem guten fit aus. Wir wollen deswegen den Längenkreis über die Punktgröße visualisieren:
# express lattitude by point size
plot (YEAR ~ ELEV, data=temp.ru, pch=16, col="grey",
cex=LAT/40, las = 1,
xlab="Geländehöhe [m]",
ylab="Jahresmitteltemperatur [°C]")
lines(g.pred$fit ~ new.ru.3$ELEV)
lines(g.pred$upr ~ new.ru.3$ELEV, lty=2)
lines(g.pred$lwr ~ new.ru.3$ELEV, lty=2)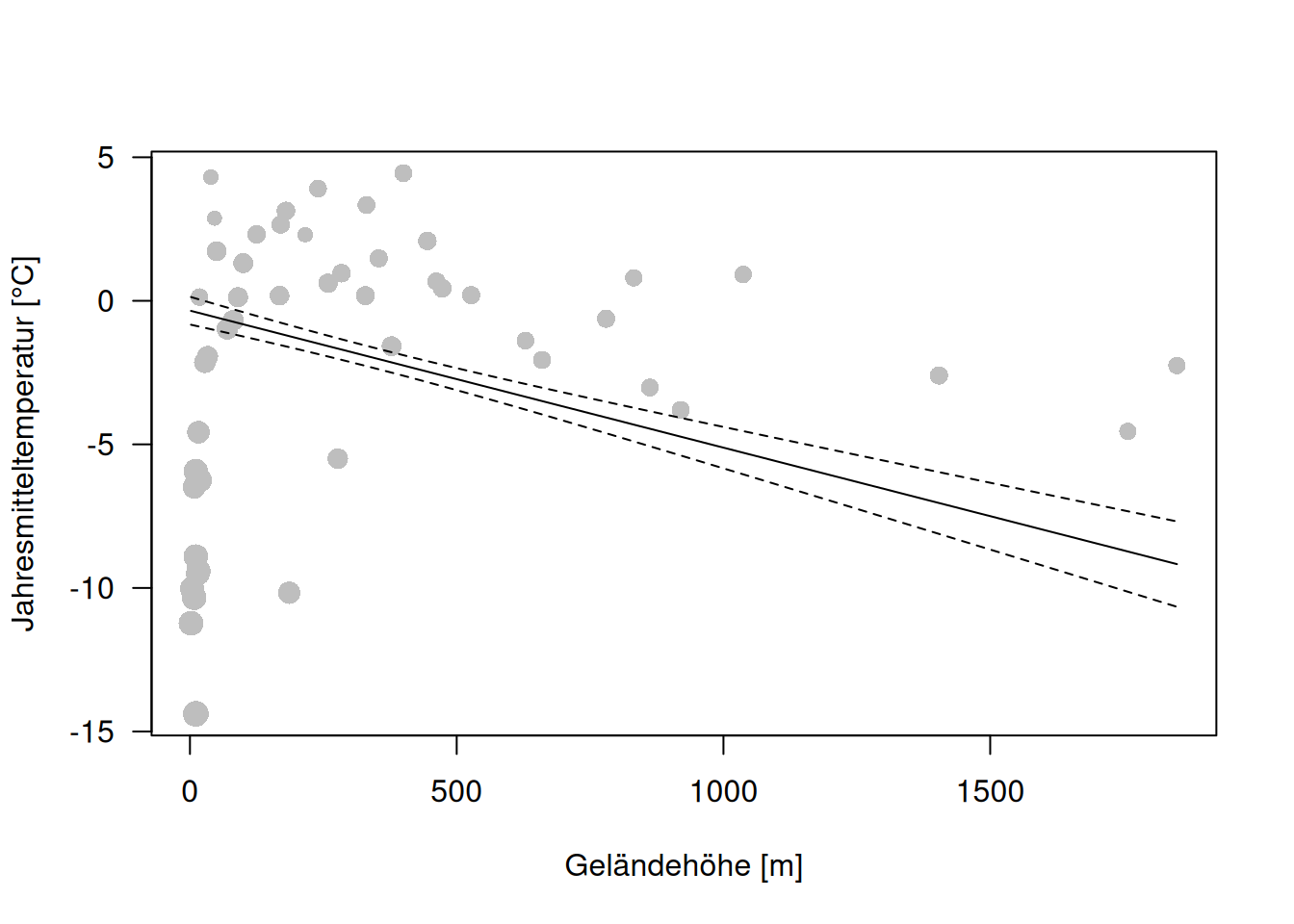
Figure 14.3: Vorhersage und 95% Konfidenzband für die russischen Klimastationen die Höheninformationen besitzen. Punktgröße symbolisiert den Längenkreis der Klimstation.
Wir sehen, dass die große Streuung in Meeresspiegelhöhe durch einen Nord-Süd-Gradienten erklärt wird und das viele der Punkte oberhalb der Regressionsgeraden in südlicheren Breiten liegen.
Wenn wir den Plot entlang von LAT plotten sollte der Fit deutlich besser aussehen:
new.lat <- data.frame(ELEV=100,
LAT.cent = seq(min(temp.ru$LAT.cent),
max(temp.ru$LAT.cent)),
LON.cent = 0 )
g.pred.lat <- predict(g, newdata= new.lat, se=TRUE)plot (YEAR ~ LAT.cent, data=temp.ru, pch=16,
col="grey", cex=2, las = 1,
xlab="zentrierte geographische Breite [°]",
ylab="Jahresmitteltemperatur [°C]")
lines(g.pred.lat$fit~ new.lat$LAT.cent, lwd=2)
lines(g.pred.lat$fit + 1.96* g.pred.lat$se.fit ~ new.lat$LAT.cent, lty=2)
lines(g.pred.lat$fit - 1.96* g.pred.lat$se.fit ~ new.lat$LAT.cent, lty=2)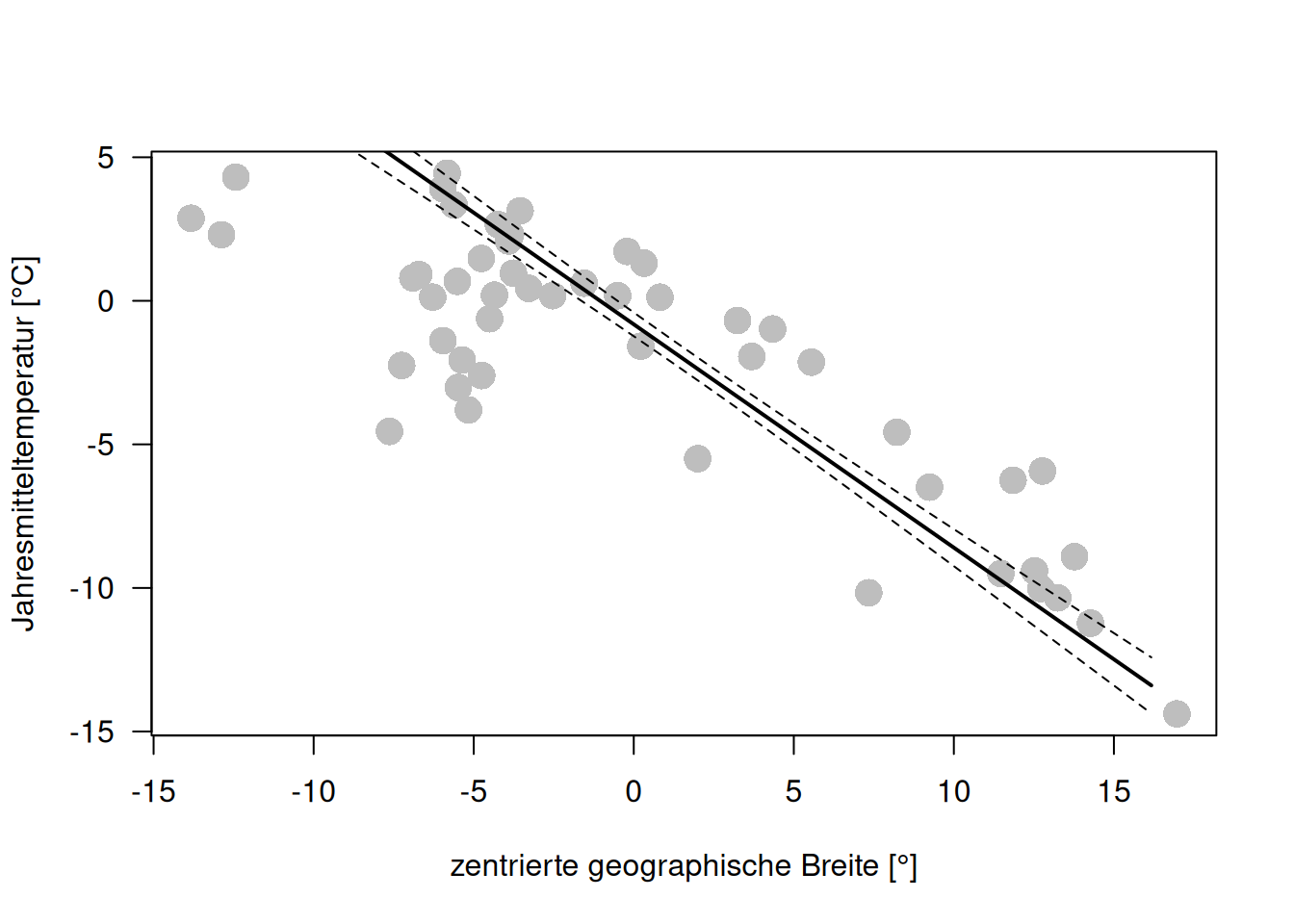
Wie würden die Ergebnisse aussehen, wenn wir nur LAT als Prädiktor hätten und die anderen beiden Prädiktoren aus dem Modell entfernen würden?
##
## Call:
## lm(formula = YEAR ~ LAT.cent, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -6.317 -1.926 0.107 2.291 3.602
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.98438 0.36334 -5.461 1.65e-06 ***
## LAT.cent -0.49200 0.04628 -10.630 3.30e-14 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.569 on 48 degrees of freedom
## Multiple R-squared: 0.7019, Adjusted R-squared: 0.6957
## F-statistic: 113 on 1 and 48 DF, p-value: 3.297e-14new.lat.2 <- data.frame( LAT.cent = seq(min(temp.ru$LAT.cen),
max(temp.ru$LAT.cen),
length.out = 100) )
g.pred.lat.2 <- predict(g.lat, newdata= new.lat.2, se=TRUE)plot (YEAR ~ LAT.cent, data=temp.ru, pch=16,
col="grey", cex=2, las = 1,
xlab="zentrierte geographische Breite [°]",
ylab="Jahresmitteltemperatur [°C]")
lines(g.pred.lat.2$fit~ new.lat.2$LAT.cent, lwd=2)
lines(g.pred.lat.2$fit + 1.96* g.pred.lat.2$se.fit ~
new.lat.2$LAT.cent, lty=2)
lines(g.pred.lat.2$fit - 1.96* g.pred.lat.2$se.fit ~
new.lat.2$LAT.cent, lty=2)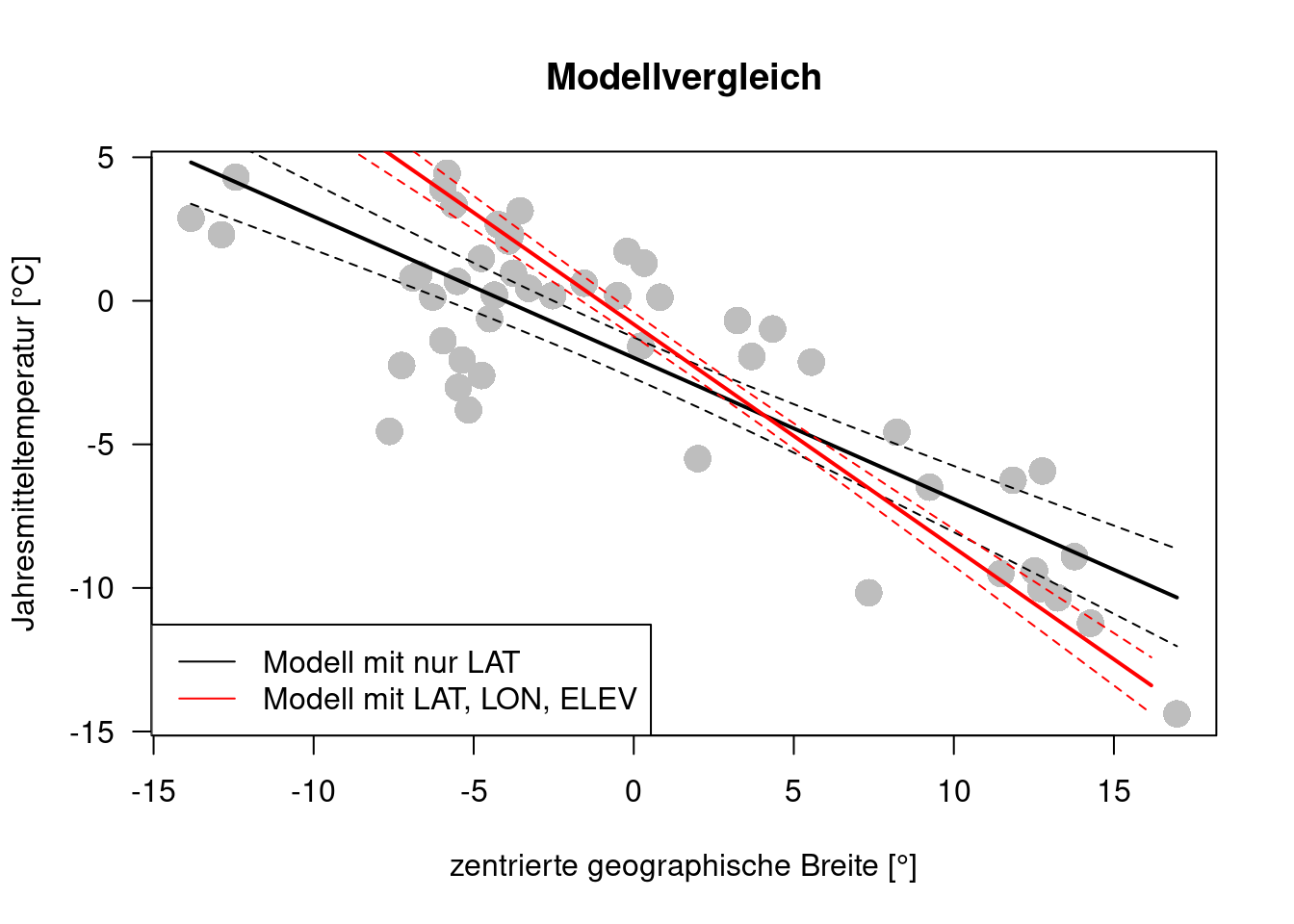
Wir sehen, dass sich die Lage der Regressionsgeraden verschiebt und das die Unsicherheit deutlich größer wird.
Modellvergleich in einem Plot:
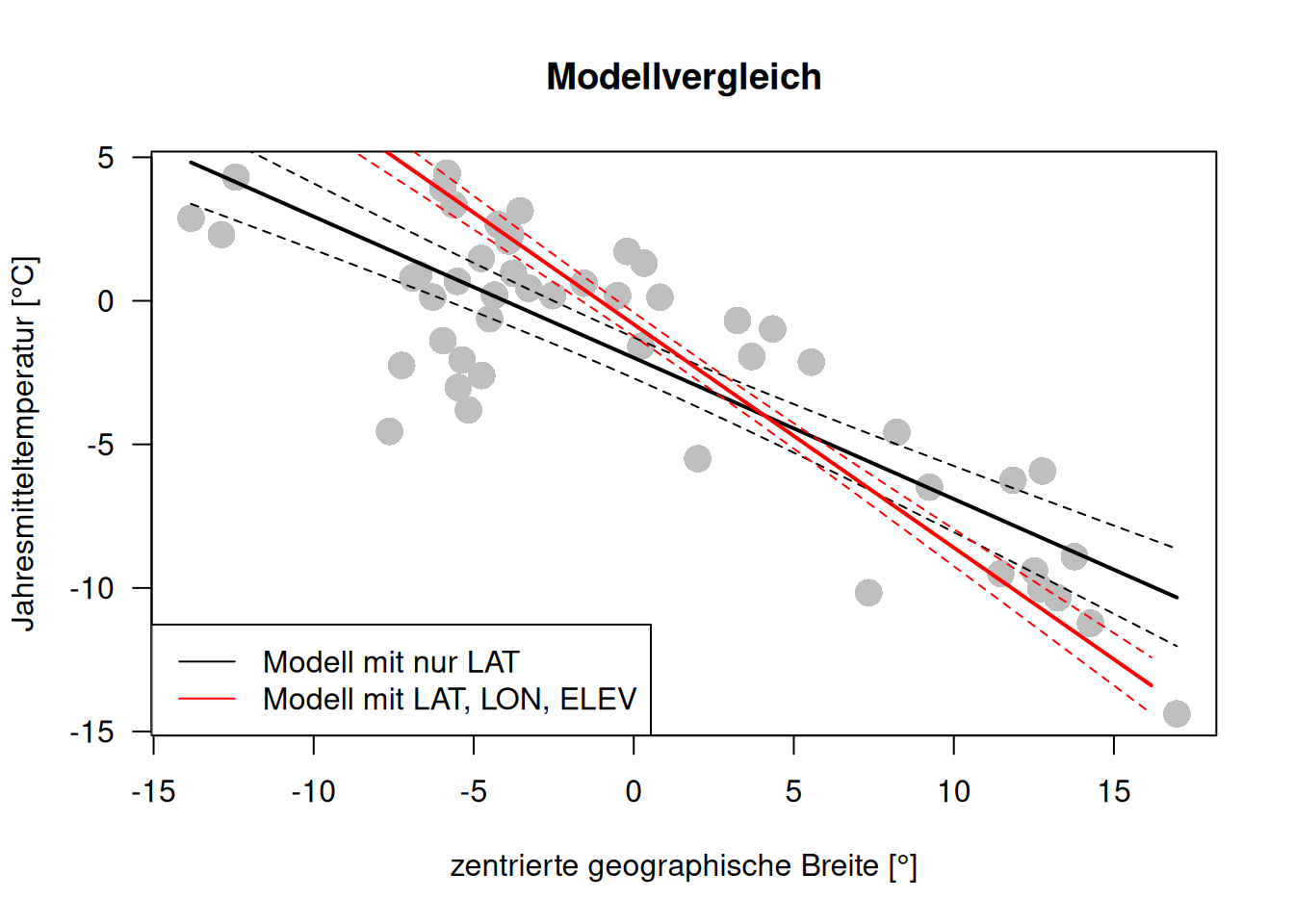
14.4 Konfidenz- und Vorhersagebänder
Während die Konfidenzbänder die Unsicherheit für die Vorhersage im Mittel angeben, ist die Unsicherheit höher, wenn wir eine Vorhersage für ein ganz bestimmtes Objekt machen wollen. Wenn wir nicht vorhersagen wollen, die die Jahresmitteltemperatur auf 500m Höhe auf einer beliebigen ist, sondern die Jahresmitteltemperatur für eine ganz bestimmte Station vorhersagen wollen, ist die Unsicherheit klar größer.
Die zusätzliche Unsicherheit wird im linearen Modell durch die Residuenvarianz bzw. -standardabweichung angegeben: \(\hat{\sigma}^2\). Diese quantifiziert die zusätzliche Variabilität zwischen Stationen und damit die zusätzliche Unsicherheit, wenn wir eine Vorhersage für ein ganz bestimmtes Objekt (oder einen bestimmten Zeitpunkt, eine bestimmte Person,…) treffen wollen.
Vorhersage des mittleren Effektes an der Stelle \(x_0\):
\[\hat{y_0} = x_0^T\hat{\beta} + \epsilon\] \[E(\epsilon)=0\] Konfidenzbereich für \(x_0\):
\[\hat{y_0}\pm t_{n-p}^{\frac{\alpha}{2}}\hat{\sigma} \sqrt{x_0^T(X^TX)^{-1}x_0}\]
Vorhersagebereich für \(x_0\):
\[\hat{y_0}\pm t_{n-p}^{\frac{\alpha}{2}}\hat{\sigma} \sqrt{1 + x_0^T(X^TX)^{-1}x_0}\]
Wir die individuelle Unsicherheit mit berücksichtigt, spricht man von Vorhersagebändern. Man erhält diese in predict mittels interval="confidence". Mittels level kann man das Intervall spezifizieren - standardmäßig liefert predict.lm das 95%-Intervall zurück.
g.pred.pred <- as.data.frame(predict(g, newdata= new.ru.3,
interval="predict", level=0.95))
g.pred.conf <- as.data.frame(predict(g, newdata= new.ru.3,
interval="confidence", level=0.95))plot(g.pred.pred$fit~ new.ru.3$ELEV,
xlab="Geländehöhe [müNN]", las = 1,
ylab="Jahresmitteltemperatur [°C]", type="l",
lwd=2, main=paste("Für geogr. Länger:", round(mean(temp.ru$LON),2),
", geogr. Breite:" , round(mean(temp.ru$LAT),2)))
lines( g.pred.pred$lwr ~ new.ru.3$ELEV, lty=2, lwd=2)
lines(g.pred.pred$upr ~ new.ru.3$ELEV, lty=2, lwd=2)
lines( g.pred.conf$lwr ~ new.ru.3$ELEV, lty=3, col="blue", lwd=2)
lines(g.pred.conf$upr ~ new.ru.3$ELEV, lty=3, col="blue", lwd=2)
legend(x="topright", legend=c("Vorhersage","95% Vorhersageband","95% Konfidenzband"),
lty=1:3, col=c("black","black", "blue") )
points(YEAR ~ ELEV, data=temp.ru)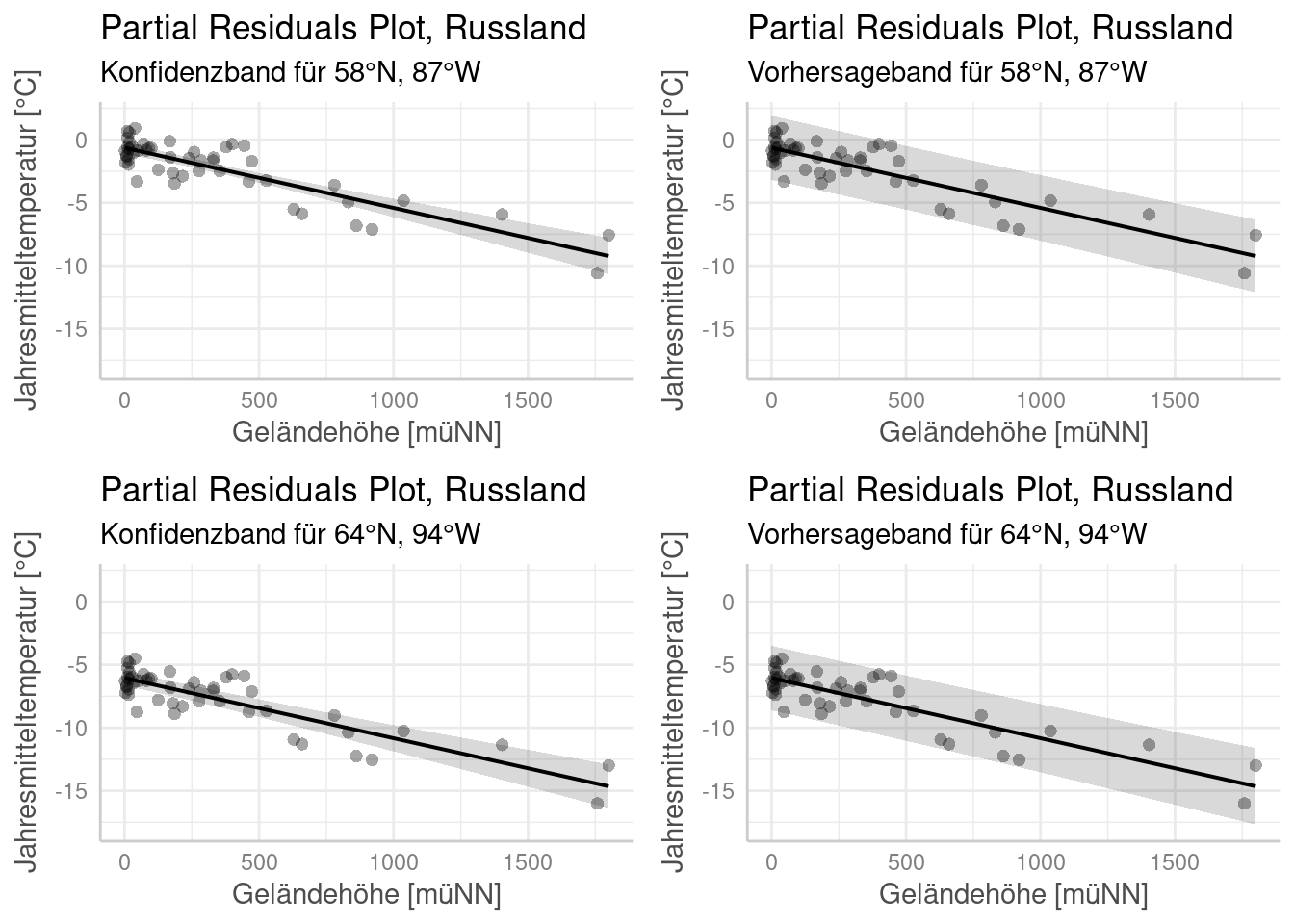
Figure 14.4: 95%-Vorhersage- und Konfidenzband für russische Klimastationen mit Höheninformation.
Bei der Interpretation sollte man im Kopf behalten, dass wir eine einfache Projektion in den 2d-Teilraum aus einem Prädiktor und dem Response betrachten und nicht einen Added Variable oder Partial Residuals Plot.
Um einen Partial Residuals Plot einfach zu erzeugen, kann man sich der Funktionaliät von ggeffects::ggpredict bedienen. Wenn man ein vom Befehl zurückgegebenes Objekt plottet, kann man sich mittels show_residuals die partiellen Residuen anzeigen lassen. Es ist hilfreich, den Bereich, über den geplottet wird explizit zu definieren, da sonst die Residuen gruppiert werden.
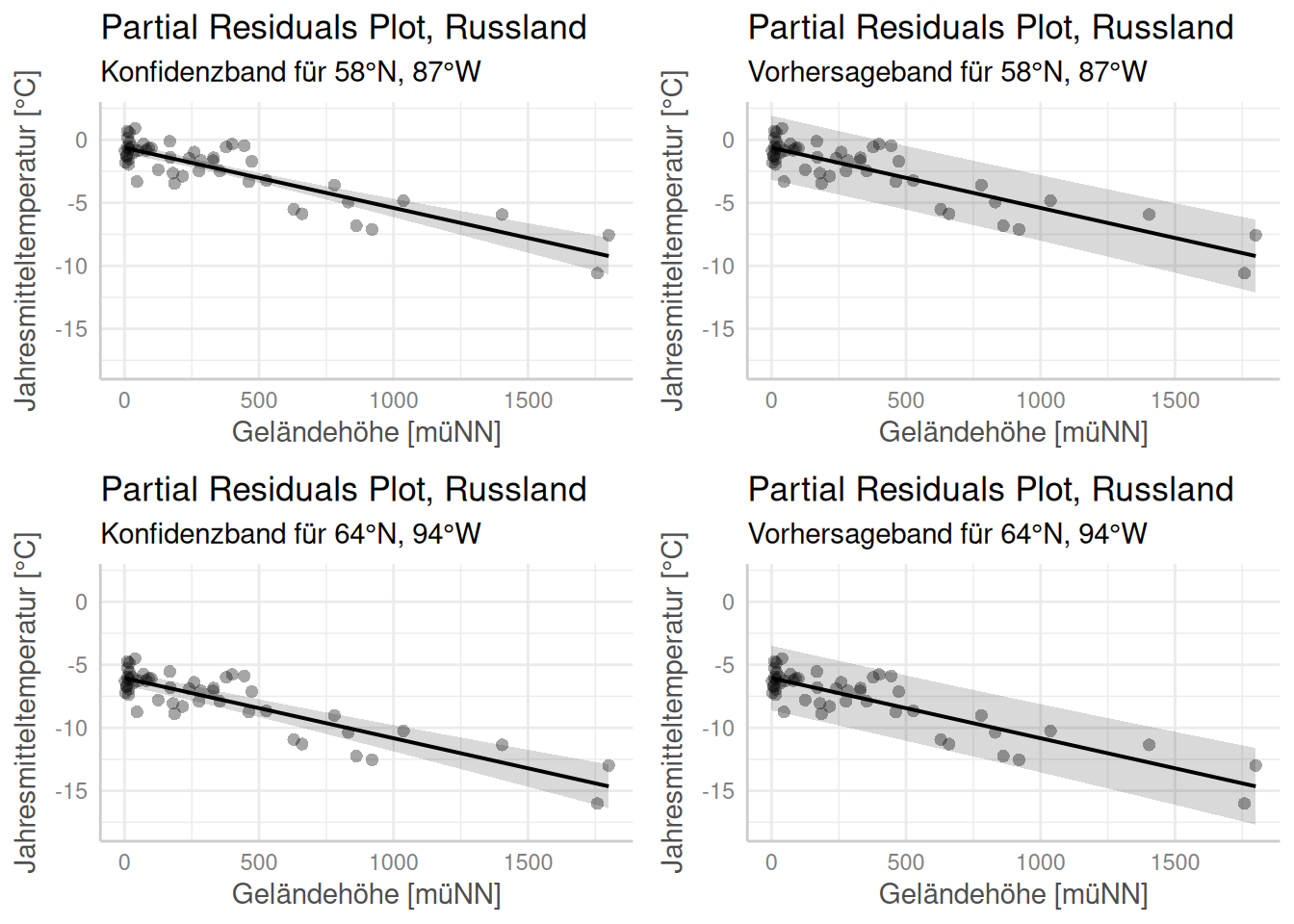
Wir plotten nachfolgend jeweils für zwei verschiedene Werte für Längengrad und Breitengrad den Zusammenhang zwischen Jahresmitteltemperatur und Geländehöhe (erste Zeile: Werte nahe dem Mittelwert der Klimastationen in Russland, die Geländehöheninformationen besitzen, 2. Zeile Werte die eher dem 75-Quantil entsprechen). Die linke Spalte zeigt jeweils das Konfidenzband, die rechte das Vorhersageband. Man sieht, wie sich sowohl die Lage der Regressionsgeraden verändert und wie insbesondere das Konfidenzband weiter wird, wenn wir uns bei Längengrad und Breitengrad stärker vom Zentrum der Daten entfernen.
library(ggeffects)
g.ru <- lm(YEAR ~ ELEV + LAT + LON, data=temp.ru)
p1<- ggpredict(g.ru, terms = c("ELEV[0:1800]", "LAT[58]", "LON[87]")) %>%
plot(show_residuals=TRUE) +
labs(title="Partial Residuals Plot, Russland", subtitle= "Konfidenzband für 58°N, 87°W") +
xlab("Geländehöhe [müNN]") + ylab("Jahresmitteltemperatur [°C]") + ylim(-18,2)
p2 <- ggpredict(g.ru, terms = c("ELEV[0:1800]", "LAT[58]", "LON[87]"), interval = "prediction") %>%
plot(show_residuals=TRUE) +
labs(title="Partial Residuals Plot, Russland", subtitle= "Vorhersageband für 58°N, 87°W")+
xlab("Geländehöhe [müNN]") + ylab("Jahresmitteltemperatur [°C]")+ ylim(-18,2)
p3<- ggpredict(g.ru, terms = c("ELEV[0:1800]", "LAT[64]", "LON[94]")) %>%
plot(show_residuals=TRUE) +
labs(title="Partial Residuals Plot, Russland", subtitle= "Konfidenzband für 64°N, 94°W") +
xlab("Geländehöhe [müNN]") + ylab("Jahresmitteltemperatur [°C]") + ylim(-18,2)
p4 <- ggpredict(g.ru, terms = c("ELEV[0:1800]", "LAT[64]", "LON[94]"), interval = "prediction") %>%
plot(show_residuals=TRUE) +
labs(title="Partial Residuals Plot, Russland", subtitle= "Vorhersageband für 64°N, 94°W")+
xlab("Geländehöhe [müNN]") + ylab("Jahresmitteltemperatur [°C]") + ylim(-18,2)
ggpubr::ggarrange(p1,p2, p3, p4)