Kapitel 13 Multivariates Lineares Modell
13.1 Anwendungsbeispiel - Temperaturdaten in Russland
Schauen wir uns einmal den Zusammenhang zwischen Höhe und Jahresmitteltemperatur für die Klimastionen in Russland an:
Selektion von Stationen in Russland:
Die -9999 Werte zeigen fehlende Werte, d.h. wir wissen nicht, wie hoch die Station liegt. Deswegen eliminieren wir diese Stationen:
## [1] 50 36Wir hätten den gleichen Voprgang auch in einem Rutsch erledigen können:
temp.ru <- subset(temp, ELEV > -20 & CNTRY_NAME == “Russia”)
Wie sehen die Daten aus:
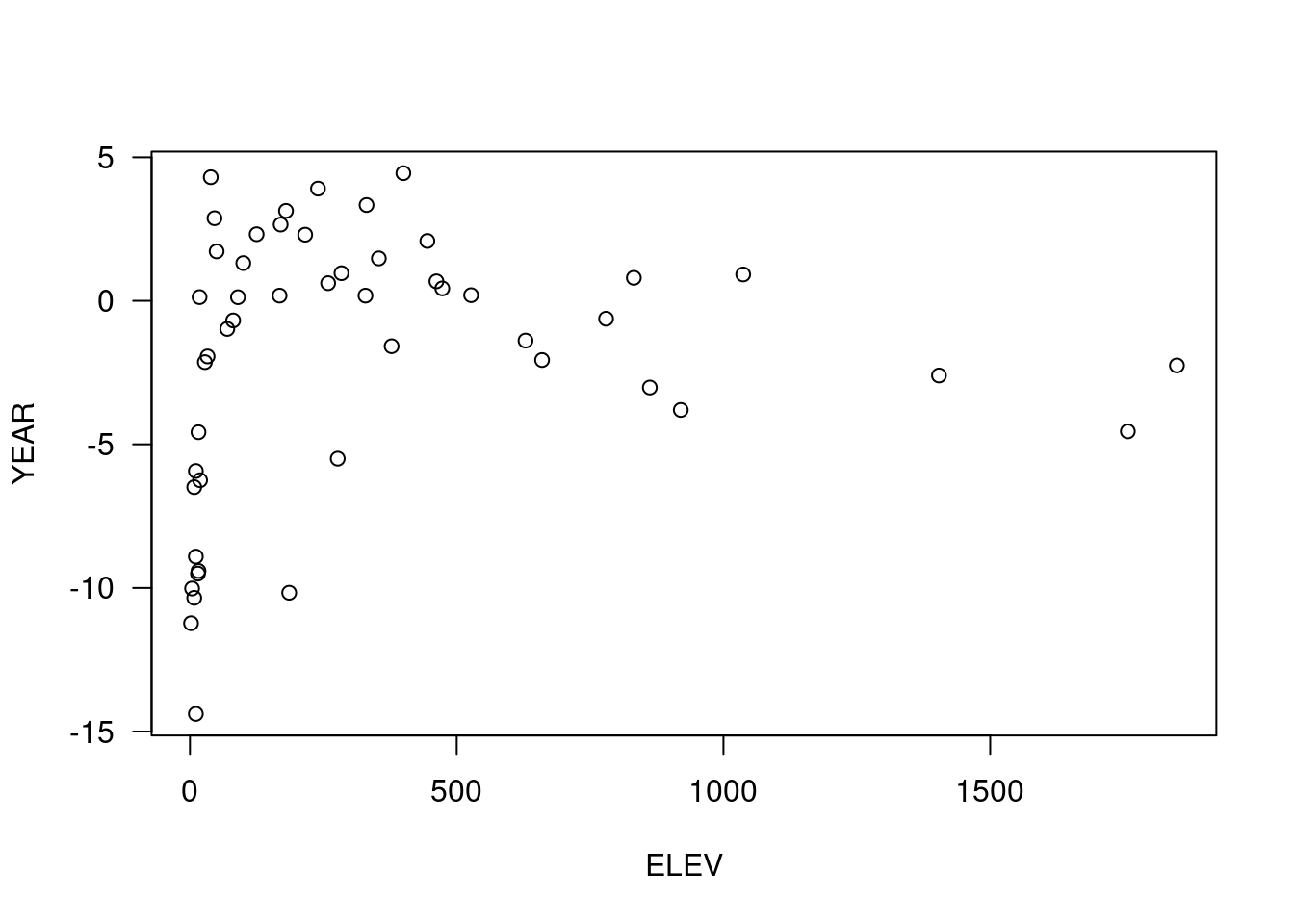
plot( YEAR ~ ELEV, data=temp.ru, xlab="Höhe [m]", ylab="Jahresmitteltemperatur [°C]", main="", las=1)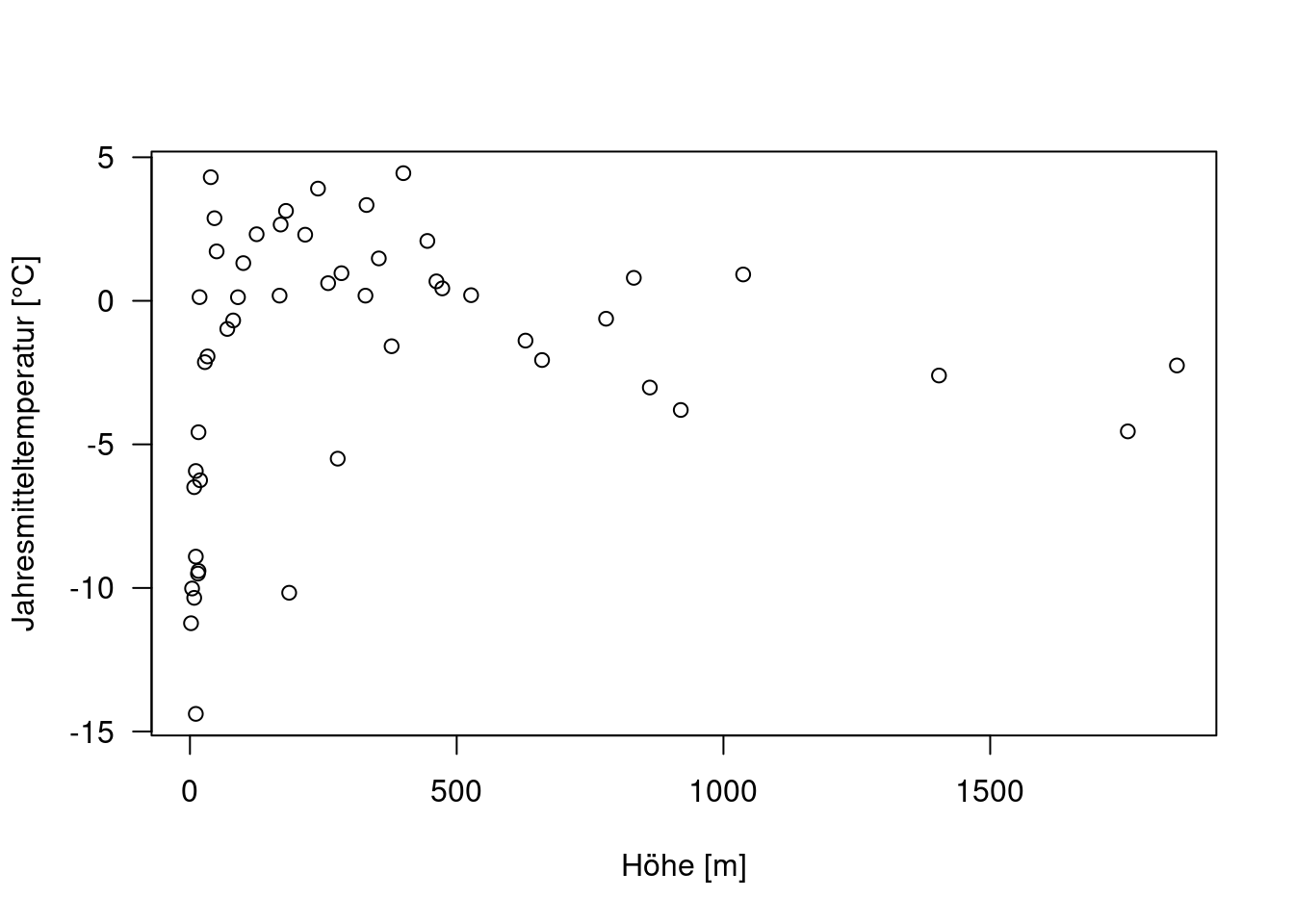
Der Zusammenhang sieht nicht so aus, wie erwartet. Ein lineares Regressionsmodell bestätigt, dass der Zusammenhang zwischen Temperatur und Höhe nicht signifikant ist.
##
## Call:
## lm(formula = YEAR ~ ELEV, data = temp.ru)
##
## Coefficients:
## (Intercept) ELEV
## -2.518695 0.001552##
## Call:
## lm(formula = YEAR ~ ELEV, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -11.884 -3.234 1.570 3.345 6.764
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.518695 0.840156 -2.998 0.0043 **
## ELEV 0.001552 0.001516 1.024 0.3112
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.655 on 48 degrees of freedom
## Multiple R-squared: 0.02136, Adjusted R-squared: 0.0009722
## F-statistic: 1.048 on 1 and 48 DF, p-value: 0.3112plot( YEAR ~ ELEV, data=temp.ru, xlab="Höhe [m]", ylab="Jahresmitteltemperatur [°C]", main="", las=1)
abline(g0)
Woran könnte es liegen, dass wir den zu erwartenden Zusammenhang hier nicht finden?
Die Stationen sind über einen recht großen Bereich verteilt - deswegen spielt die Lage der Stationen nun im Vergleich zu Deutschland eine viel stärkere Rolle. Wir bekommen einen Eindruck davon, wenn wir die Stationen nach Länge und Breite plotten und die Punktgröße von der Jahrestemperatur und die Punktfarbe vom Vorzeichen abhängig machen. Um sich überlappende Punkte kenntlich zu machen, werden die Farben halbtransparent definiert.
ggplot(temp.ru, aes(x= LON, y = LAT, size = abs(YEAR), color = as.factor(sign(YEAR)))) +
geom_point(alpha=.5) +
ylab("Längengrad") +
xlab("Breitengrad")+
labs(title = "Temperaturstationen in Russland") +
scale_size_binned_area(name = "Absolutwert\nJahresmittel-\ntemperatur") +
scale_color_manual(values=c("blue", "red"),
labels = c("negative", "positive"),
name= "Vorzeichen\nJahresmittel-\ntemperatur")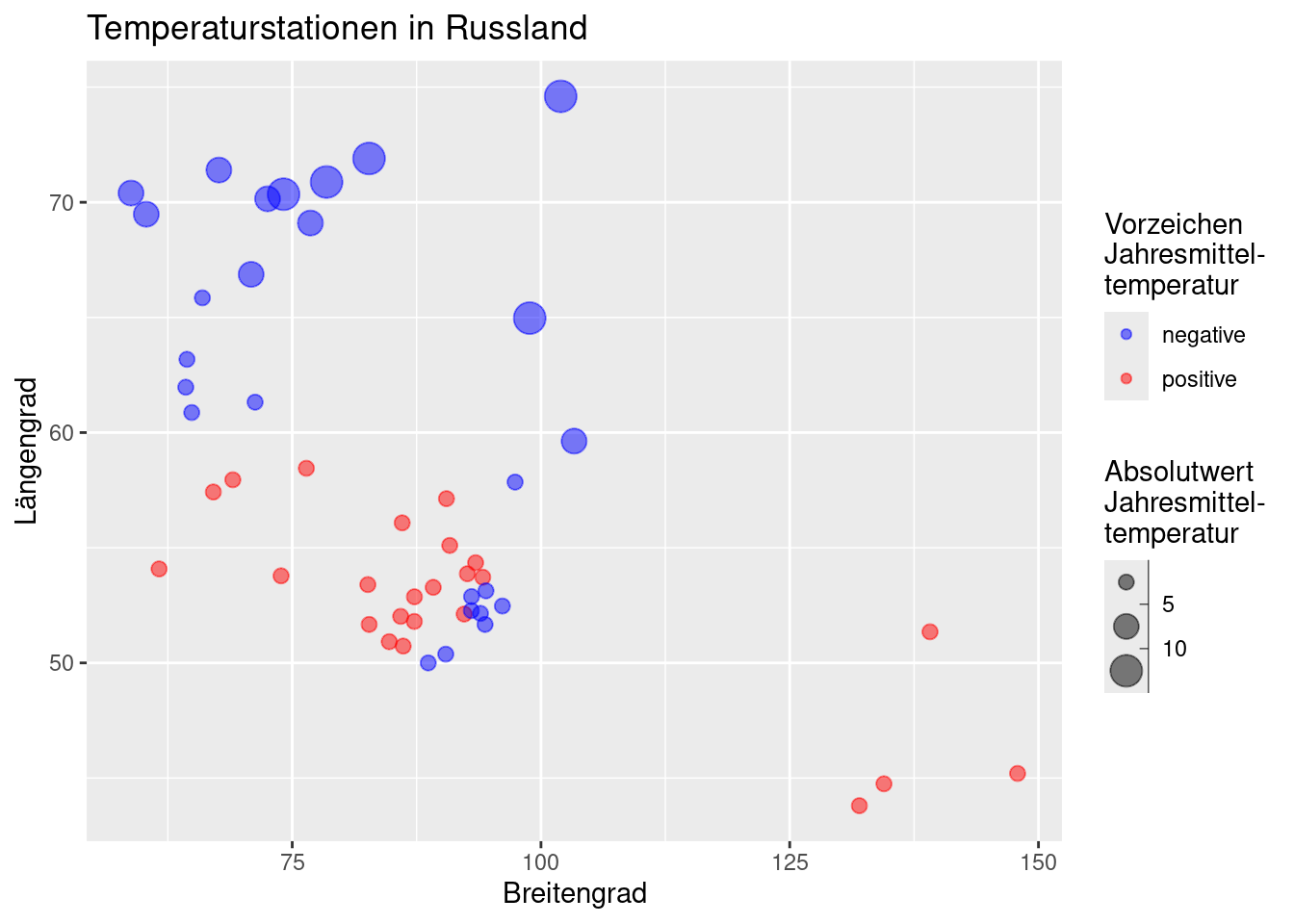
Wir sehen dies auch, wenn wir uns die Residuen etwas genauer anschauen. Wir tragen dabei die Residuen des Modells gegen die 3 potentiellen Prädiktoren auf.
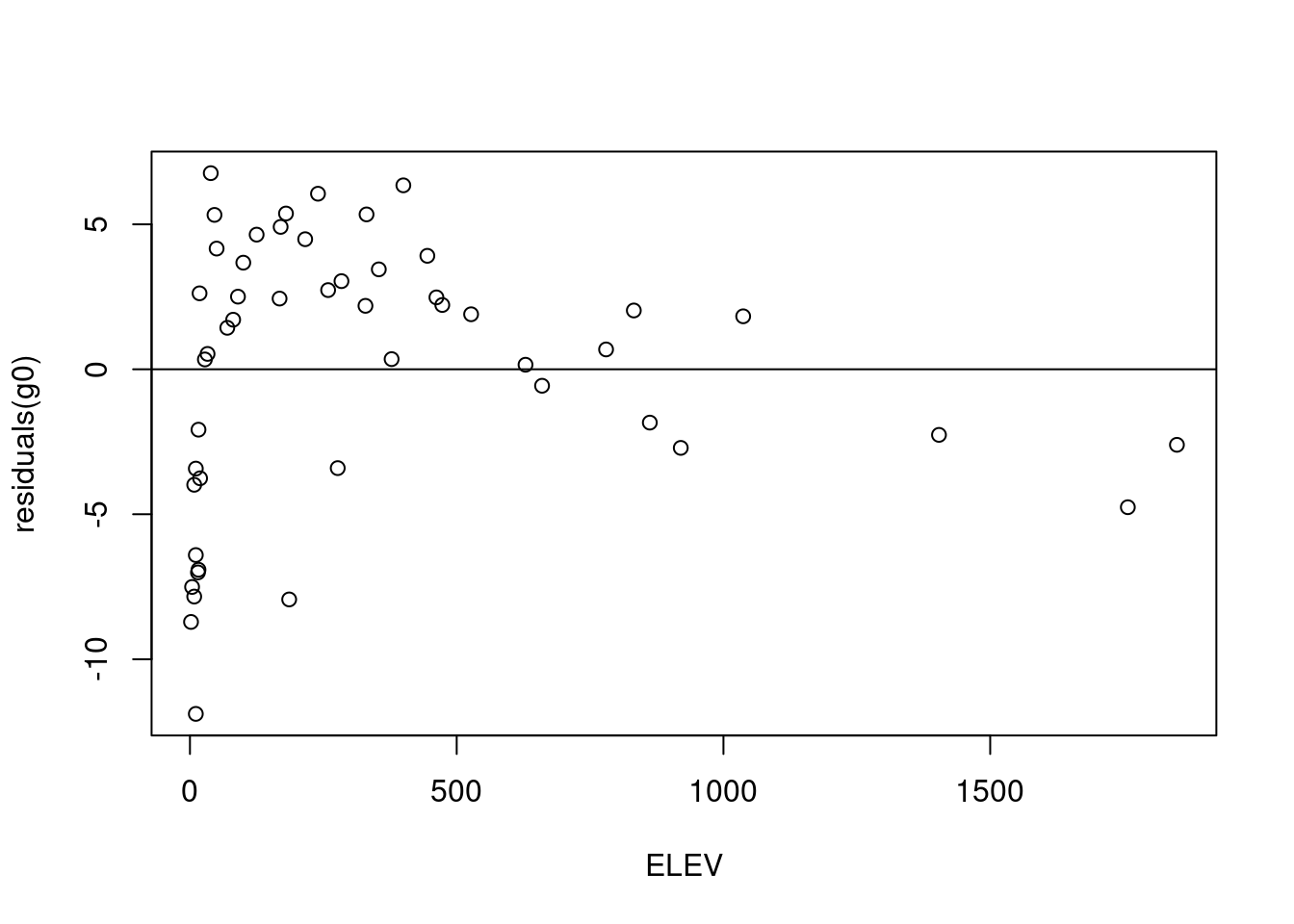

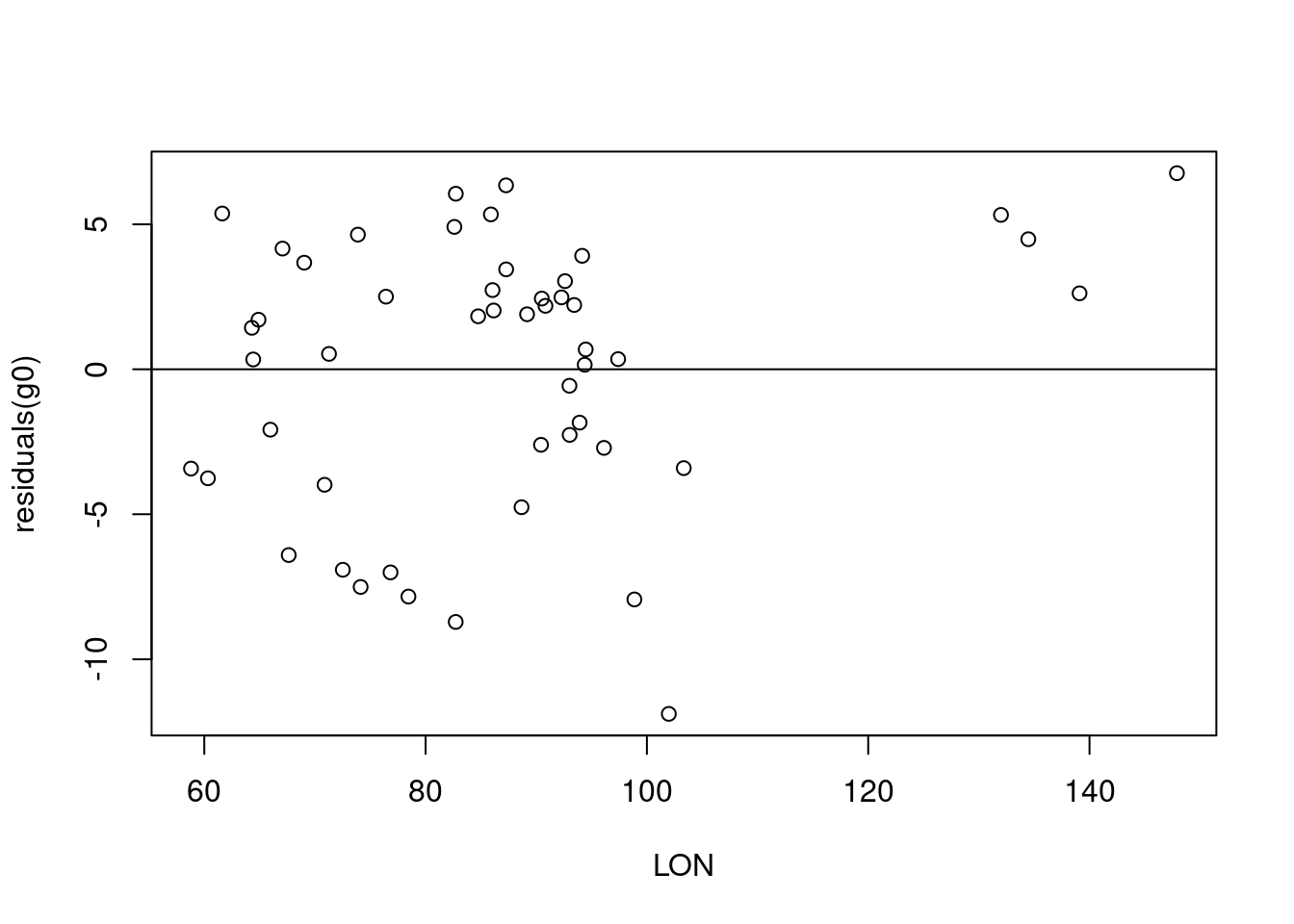
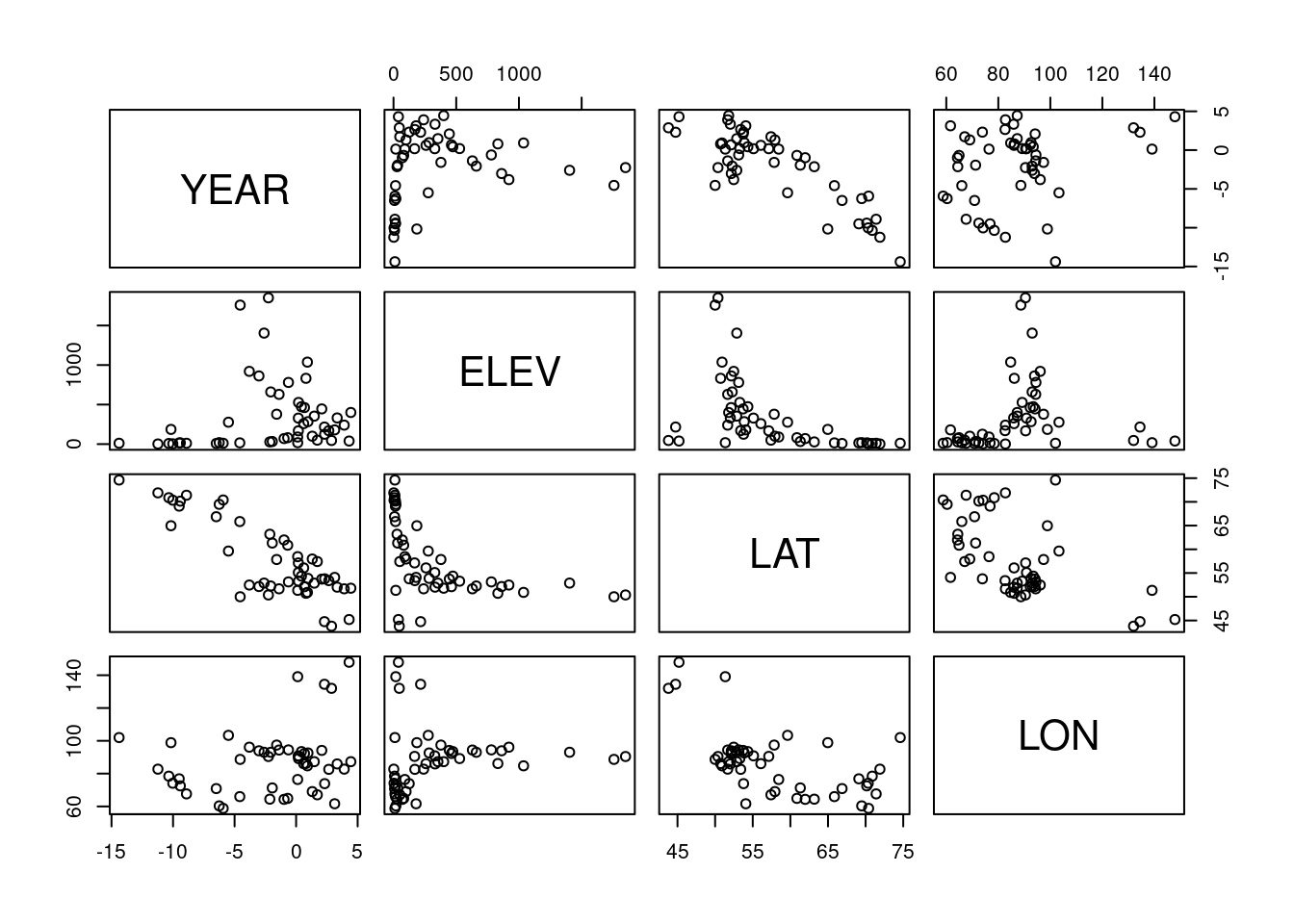
Insbesondere beim Breitengrad sehen wir einen starken negativen Zusammenhang der Residuen mit zunehmendem Breitengrad.
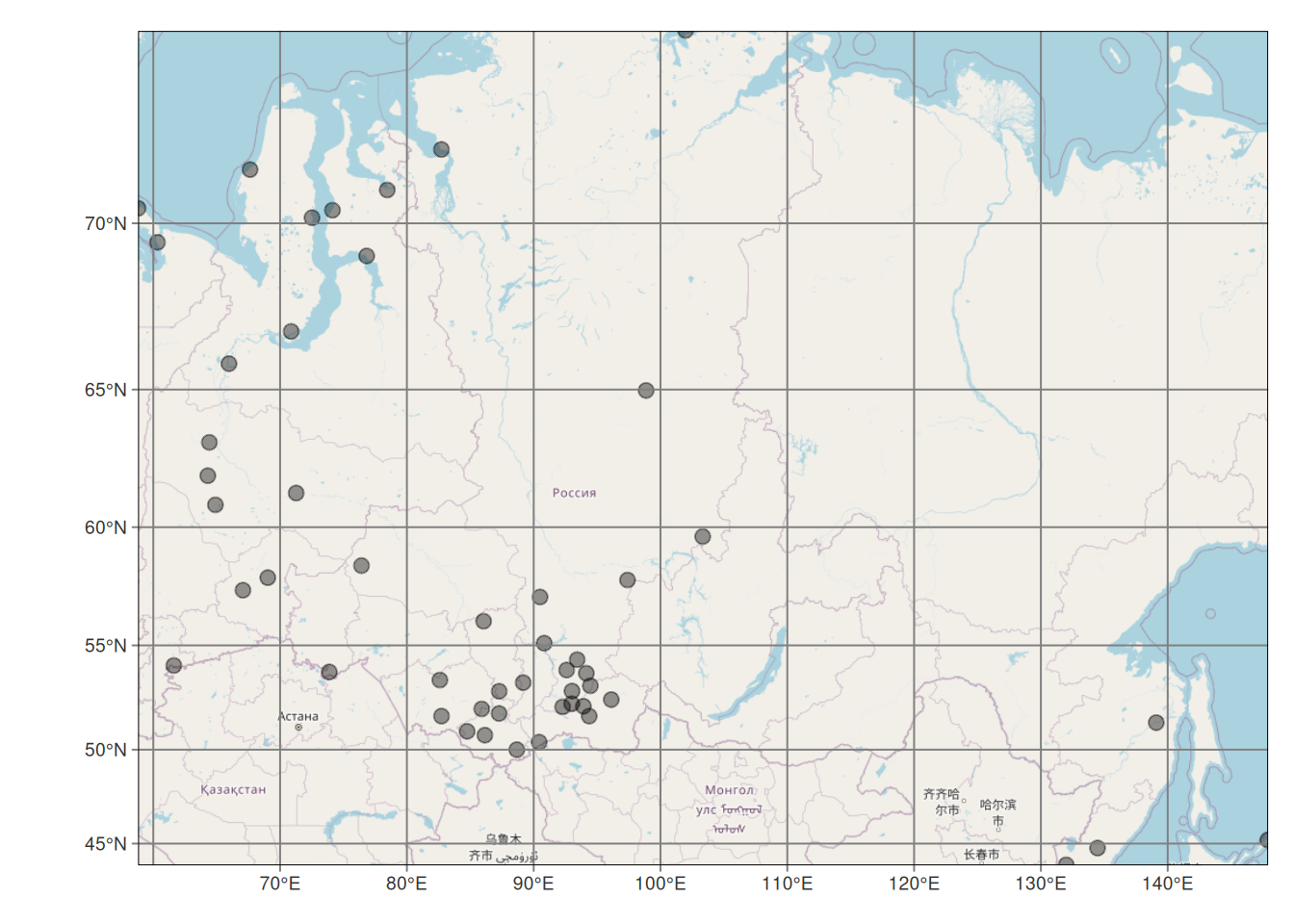
Figure 13.1: Lage der russischen Klimastationen mit Höheninformationen.
Wie wir sehen, sind die russischen Klimastationen mit Höhenangaben (Abbildung 13.1) etwas ungünstig verteilt. Die Verteilung aller russischer Klimastationen (Abbildung 13.2) ist etwas homogener, zeigt jedoch auch eine starke Clusterbildung und schlecht abgedeckte Gebiete.
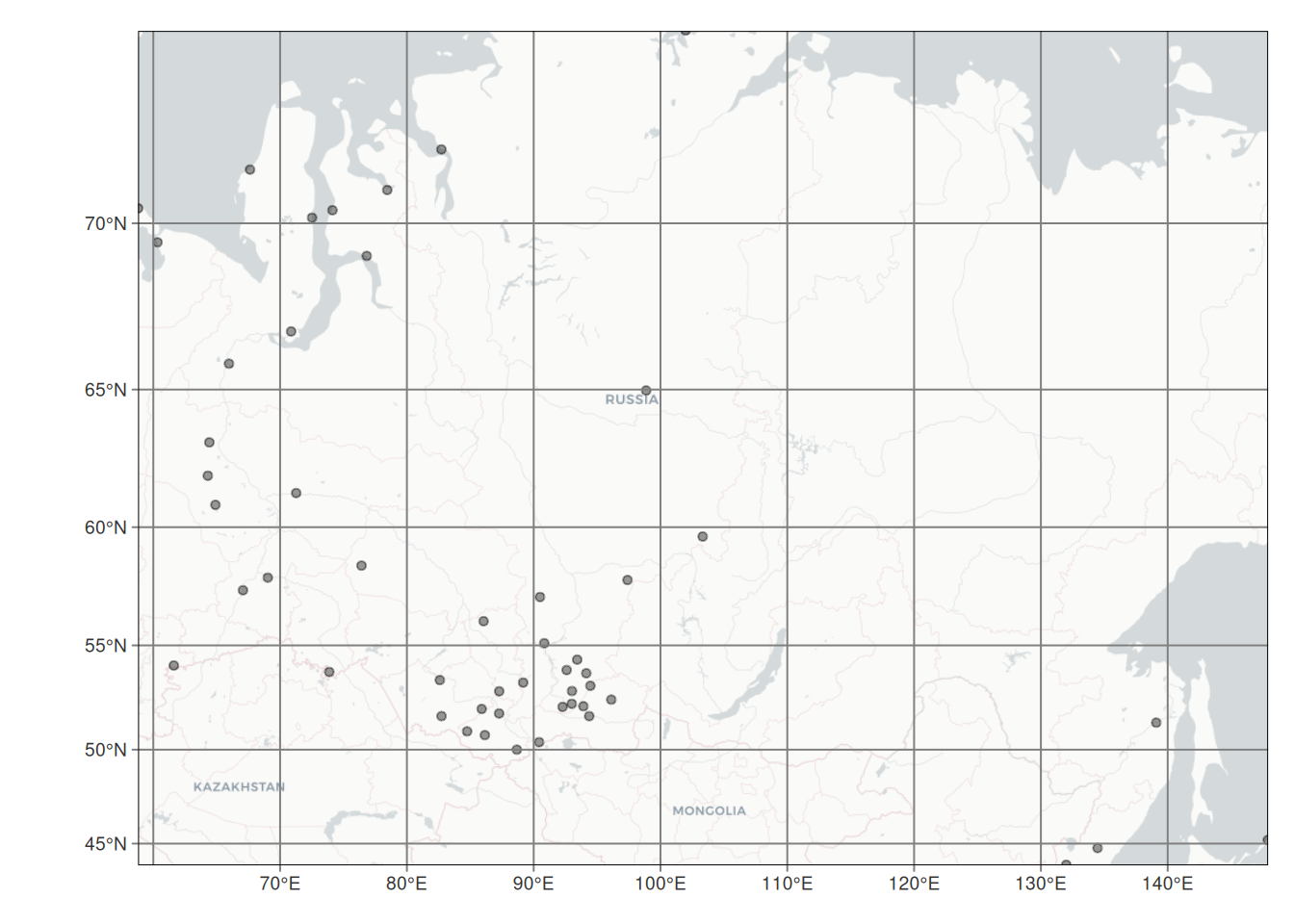
Figure 13.2: Lage aller russischer Klimastationen - mit und ohne Höheninformationen.
Entsprechend wollen wir das Modell um Längengrad und Breitengrad als zusätzliche Prädiktoren erweitern:
##
## Call:
## lm(formula = YEAR ~ ELEV + LAT + LON, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 53.8410350 2.6293965 20.477 < 2e-16 ***
## ELEV -0.0047720 0.0004765 -10.015 3.88e-13 ***
## LAT -0.7777441 0.0319038 -24.378 < 2e-16 ***
## LON -0.1076918 0.0113755 -9.467 2.26e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.241 on 46 degrees of freedom
## Multiple R-squared: 0.9333, Adjusted R-squared: 0.929
## F-statistic: 214.7 on 3 and 46 DF, p-value: < 2.2e-16Das Modell erklärt nun 93% der Varianz in den Daten. Die Temperatur fällt mit 0.48°C je 100 Höhenmeter, die Temperatur steigt nach Norden hin an und fällt nach Osten hin ab (zunehmende Kontinentalität). Alle Koeffizienten sind hochsignifikant von Null verschieden. Dies scheint alles plausibel.
Wichtig ist, sich klar zu machen, dass die Koeffizienten so interpretiert werden, dass sie die Veränderung des Response in Abhängigkeit einer Änderung eine Prädiktors um eine Einheit ausmachen, wenn alle andern Prädiktoren konstant bleiben.
Allerdings gibt es ein Problem: der Achsenabschnitt. Am Äquator wird demnach auf Meereshöhe eine durchschnittliche Jahrestemperatur von 54°C vorausgesagt, was nicht sehr plausibel ist.
Dies liegt daran, dass der Achsenabschnitt sehr weit von unseren Daten entfernt liegt und entsprechend nur sehr unsicher geschätzt werden kann - grundsätzlich sollten wir Extrapolation immer vermeiden!
Wir sehen das, wenn wir uns mit predict nicht nur den fit sondern auch das 95% Konfidenzintervall ausgeben lassen. Wir müssen nun natürlich Werte für alle 3 Prädiktoren im Modell definieren. Da LAT den stärksten Einfluss hat lassen wir diesen Wert variieren und halten die anderen Werte auf ihrem Mittelwert fest.
plot(YEAR ~ LAT, data=temp.ru, xlim=c(0, 90), ylim=c(-15,55),
xlab="Breitengrad", ylab="Jahresmitteltemperatur [°C]",
main = "Russische Stationen mit Höheninformation", las = 1)
new.ru.2 <- data.frame(ELEV=mean(temp.ru$ELEV), LAT=seq(0, max(temp.ru$LAT), length.out=100), LON=mean(temp.ru$LON))
g.pred.2 <- as.data.frame(predict(g, newdata = new.ru.2, interval="confidence"))
lines(g.pred.2$fit~ new.ru.2$LAT, col="red")
lines(g.pred.2$upr~ new.ru.2$LAT, col="red", lty=2)
lines(g.pred.2$lwr~ new.ru.2$LAT, col="red", lty=2)
legend(x="topright", legend= c("Vorhersage", "95%-Konfidenzband"), lty=1:2, col = "red")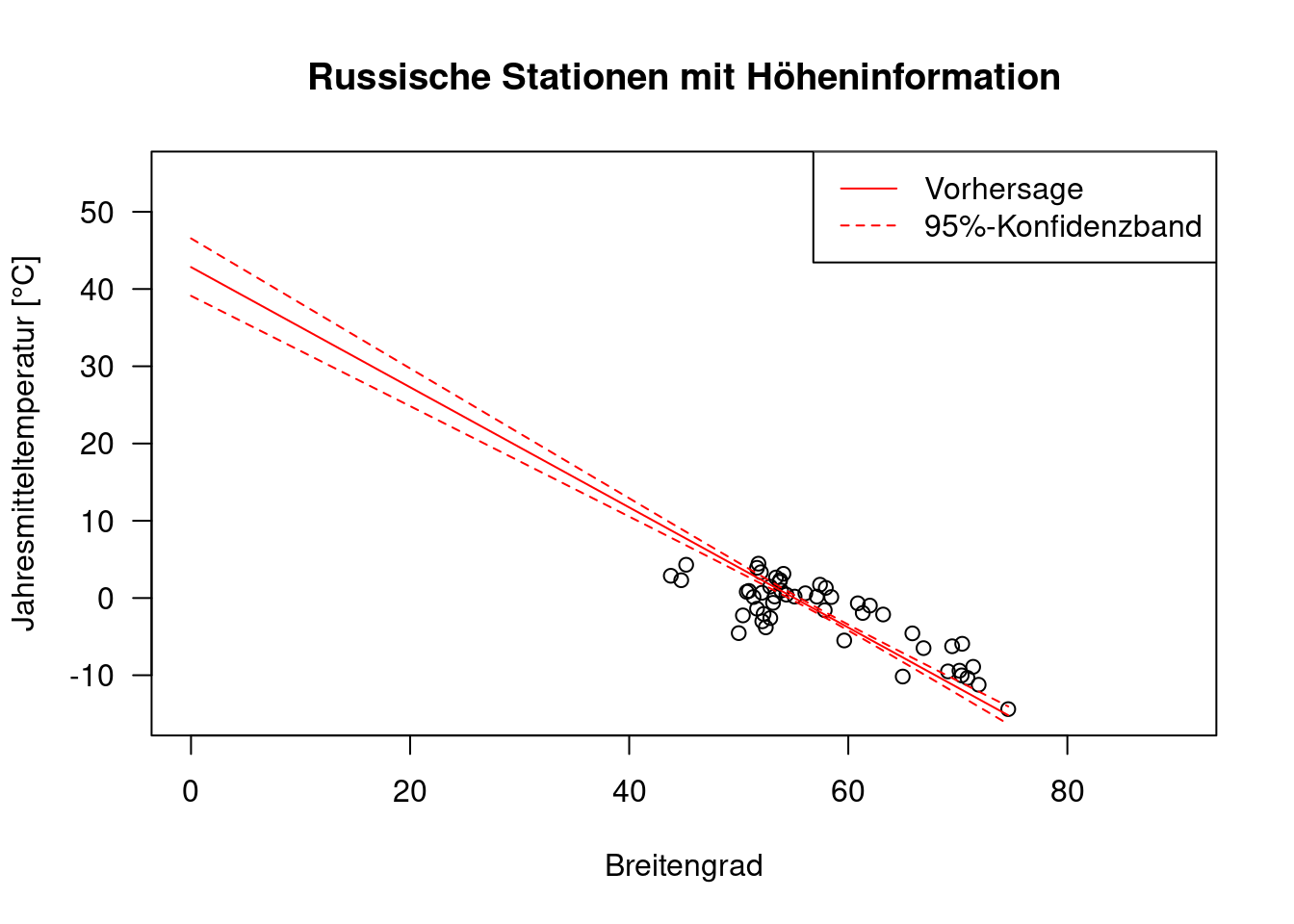
Einerseits stört uns das für Vorhersagen in Russland nicht wirklich, andererseits möchten wir auch keinen offensichtlich falschen Achsenabschnitt im Modell haben. Wir können das lösen, indem wir LAT und LON zentrieren, d.h. den Mittelwert abziehen.
## [1] 57.6312## [1] 86.9182temp.ru$LAT.cent <- temp.ru$LAT - mean(temp.ru$LAT)
temp.ru$LON.cent <- temp.ru$LON - mean(temp.ru$LON)
g <- lm(YEAR ~ ELEV+ LAT.cent + LON.cent, data=temp.ru)
summary(g)##
## Call:
## lm(formula = YEAR ~ ELEV + LAT.cent + LON.cent, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.3416690 0.2402221 -1.422 0.162
## ELEV -0.0047720 0.0004765 -10.015 3.88e-13 ***
## LAT.cent -0.7777441 0.0319038 -24.378 < 2e-16 ***
## LON.cent -0.1076918 0.0113755 -9.467 2.26e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.241 on 46 degrees of freedom
## Multiple R-squared: 0.9333, Adjusted R-squared: 0.929
## F-statistic: 214.7 on 3 and 46 DF, p-value: < 2.2e-16Wie wir sehen ändern sich die Regressionskoeffizienten für die 3 Pädiktoren nicht - eine einfache Translation hat nur einen Einfluß auf den Achsenabschnitt. Auch die Standardfehler sind - bis auf den Achsenabschnitt - unverändert.
Das Modell sagt voraus, dass wir auf Meereshöhe in der Mitte Sibiriens eine Jahresmitteltemperatur von etwa 0°C zu erwarten haben - das klingt nicht so unplausibel. Wenn wir etwas recherchieren finden wir heraus, dass Novosibirsk in der Nähe der mittleren Längen- und Breitengradangaben liegt: auf 145m üNN wird dort eine Jahresmitteltemperatur von 2,4°C berichtet. Wir liegen also relativ nahe an der Realität.
Wenn wir wissen wollen, wie groß der Effekt der einzelnen Prädiktoren (sogenannte effect size) auf die Vorhersage ist, müssen wir die Größe der Eingangsdaten mit einbeziehen. Eine einfache Möglichkeit ist es, alle Prädiktoren zu standardisieren, d.h. den Mittelwert abzuziehen und dann durch die Standardabweichung zu teilen um dann mit den standardisierten Variablen das Modell erneut zu fitten.
## [1] "matrix" "array"## $dim
## [1] 50 3
##
## $dimnames
## $dimnames[[1]]
## [1] "1024" "1025" "1028" "1072" "1073" "1075" "1078" "1079" "1080" "1086"
## [11] "1092" "1098" "1103" "1107" "1113" "1124" "1136" "1255" "1267" "1293"
## [21] "1300" "1308" "1316" "1325" "1335" "1355" "1366" "1374" "1376" "1379"
## [31] "1381" "1382" "1383" "1384" "1385" "1386" "1387" "1390" "1393" "1398"
## [41] "1496" "1522" "1529" "1542" "1666" "1667" "1668" "1669" "1670" "1672"
##
## $dimnames[[2]]
## [1] "LAT" "LON" "ELEV"
##
##
## $`scaled:center`
## LAT LON ELEV
## 57.6312 86.9182 344.2400
##
## $`scaled:scale`
## LAT LON ELEV
## 7.930248 19.463288 438.522545temp.ru$LAT.scale <- scaled.pred[,1]
temp.ru$LON.scale <- scaled.pred[,2]
temp.ru$ELEV.scale <- scaled.pred[,3]
g.scale <- lm(YEAR ~ ELEV.scale+ LAT.scale + LON.scale, data=temp.ru)
summary(g.scale)##
## Call:
## lm(formula = YEAR ~ ELEV.scale + LAT.scale + LON.scale, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -1.9844 0.1755 -11.306 7.11e-15 ***
## ELEV.scale -2.0926 0.2089 -10.015 3.88e-13 ***
## LAT.scale -6.1677 0.2530 -24.378 < 2e-16 ***
## LON.scale -2.0960 0.2214 -9.467 2.26e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.241 on 46 degrees of freedom
## Multiple R-squared: 0.9333, Adjusted R-squared: 0.929
## F-statistic: 214.7 on 3 and 46 DF, p-value: < 2.2e-16Wir sehen, dass sich - natürlich - sowohl die Koeffizenten als auch die Standardfehler verändert haben. Die Signifikanzniveaus für die 3 Prädiktoren sind unverändert geblieben - Schätzer und Standardfehler ändern sich ja um denselben Faktor, weswegen ihr Verhältnis gleich bleibt. Wir können nun ablesen, wie stark der Effekt der Veränderung eines der standardisierten Prädiktoren um eine Einheit ist (wenn wir die anderen konstant halten - ceteris paribus wie die Ökonomen sagen). Der Breitengrad hat den stärksten Effekt während die Höhe und der Längengrad in etwa gleich stark wirken.
Dieses Regressionsmodell ist zwar sehr gut geeignet, um einen Vergleich hinsichtlich der Wichtigkeit der unterschiedlichen Prädiktoren zu erstellen, aber es ist nun nicht mehr so einfach zu interpretieren, da wir mit den standardisierten Einheiten argumentieren müssen: wenn sich die standardisierte Höhenlage um eine Einheit erhöht, dann sinkt die Temperatur um… wieviel war nochmal eine standardisierte Höheneinheit?
Besser, wir verwenden zur Kommunikation wieder das unstandardisierte Modell. Wie so oft ist es hilfreich, aus verschiedenen Perspektiven auf das gleiche Problem zu blicken.
13.2 Modellselektion
Müssen wir eigentlich den Breitengrad im Modell haben oder ist der Effekt dieses Prädiktors auf die Modellgüte nicht signifikant? Diese Frage können wir nicht mittels des \(R^2\) und auch nicht unbedingt mittels der Signifikanztests der Koeffizienten beantworten.
Wenn wir ein Modell ohne LON.cent fitten, sinkt das \(R^2\) erheblich - aber genug, um für den Verbleib des Terms im Modell zu plädieren?
##
## Call:
## lm(formula = YEAR ~ ELEV + LAT.cent, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -4.6191 -1.8325 0.6108 1.5827 3.1444
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.6359966 0.4046355 -1.572 0.123
## ELEV -0.0039170 0.0007947 -4.929 1.07e-05 ***
## LAT.cent -0.6009944 0.0439463 -13.676 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 2.108 on 47 degrees of freedom
## Multiple R-squared: 0.8035, Adjusted R-squared: 0.7951
## F-statistic: 96.07 on 2 and 47 DF, p-value: < 2.2e-16##
## Call:
## lm(formula = YEAR ~ ELEV + LAT.cent + LON.cent, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -0.3416690 0.2402221 -1.422 0.162
## ELEV -0.0047720 0.0004765 -10.015 3.88e-13 ***
## LAT.cent -0.7777441 0.0319038 -24.378 < 2e-16 ***
## LON.cent -0.1076918 0.0113755 -9.467 2.26e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.241 on 46 degrees of freedom
## Multiple R-squared: 0.9333, Adjusted R-squared: 0.929
## F-statistic: 214.7 on 3 and 46 DF, p-value: < 2.2e-16Grundsätzlich gilt der gute alte Satz von Box, dass alle Modelle falsch sind, manche aber nützlich. Mit nützlich meint man oft, dass das Modell wesentliche Zusammenhänge beschreibt und/oder gute Vorhersagen liefert. Der Unterschied zwischen beiden Kriterien ist der, ob man bereit ist zu akzeptieren, dass das Modell aus den falschen Gründen gute Vorhersagen macht. Online Shops wie z.B. Amazon ist es z.B. recht egal, warum ihre Association Rule Mining Algorithmen Produkte vorschlagen (“Andere Kunden interessierten sich auch für…”), solange das im Mittel passt und sich Gewinne erziehlen lassen. Im wissenschaflichen Kontext steht dagegen das Aufdecken von Wirkungszusammenhängen im Vordergrund: man will verstehen, wie eine System reagiert um z.B. Vorhersagen über zukünftiges Systemverhalten treffen zu können. Wie wollen z.B. verstehen, wie sich Information auf klimarelevantes Verhalten auswirkt, wie stark die Abundanz einer Art durch vermehrte Düngung oder das Anlegen von Blühstreifen oder durch eine steigende Besucherzahl beeinflusst wird und dabei für Faktoren wie das Wetter korrigieren.
Wenn Regressionsmodelle Prädiktoren enthalten, die nur einen zufälligen Effekt ausweisen, tragen diese nichts zur Erklärung bei, sondern verstellen ggf. den Blick auf die relevanten Wirkungszusammenhänge. Wenn wir in obiges Modell z.B. noch das Alter der Großmutter des Stationsleiters mit ins Modell integrieren würden, hätte dies nur einen zufälligen Effekt. Der geschätzte Regressionskoeffizient hätte eine hohe Unsicherheit. Würden wir das Modell verwenden, um für eine unbekannte Station die Jahresmitteltemperatur vorherzusagen, dann hätte das Alter der Großmutter einen zufälligen Effekt, der die Vorhersagegüte verschlechtern dürfte.
Solche Überlegungen finden sich im Prinzip der Sparsamkeit auch bekannt als Ockhams Skalpell (Ockhams razor) wieder, das auf Wilhelm von Ockham (1288–1347) zurückgeht. Vereinfacht ausgedrückt besagt es:
-Von mehreren möglichen hinreichenden Erklärungen für ein und denselben Sachverhalt ist die einfachste Theorie allen anderen vorzuziehen. - Eine Theorie ist einfach, wenn sie möglichst wenige Variablen und Hypothesen enthält und wenn diese in klaren logischen Beziehungen zueinander stehen, aus denen der zu erklärende Sachverhalt logisch folgt.
Übertragen auf unser lineares Modell für die Jahresmitteltemperatur in Deutschland heißt das wir versuchen das Modell mit möglichst wenigen Parameter zu finden, dass die Daten gut beschreibt.
\(R^2\) ist dafür ungeeignet, da es (eben so wie die Residual Sum of Squares oder der mittlere Fehler oder der root mean square error) nicht zwangsläufig schlechter wird, wenn wir weitere Prädiktoren ins Modell aufnehmen, selbst wenn diese keinen Effekt haben. Wenn wir das Alter der Großmutter des Stationsleiters mit ins Modell aufnehmen, verändert sich \(R^2\) vermutlich nur wenig. Vielleicht wird es zufällig etwas schlechter, vielleicht aber auch zufällig etwas besser. Was wir benötigen ist ein Maß oder einen Test dafür, ob die Veränderung des Modells durch das Hinzunehmen bzw. Hinwegnehmen eines Faktors mehr als zufällig besser oder schlechter wird.
Eingesetzt werden hierfür Likelihood-Ratio Tests für genestete Modelle und Informationsmaße wie das Akaike-Informationskriterium (Aikaike Information Criterion, AIC) oder das Bayessches Informationskriterium (BIC).
Likelihood-Ratio Tests setzen die Likelihhod zweier Modell miteinander in Beziehung und ermitteln ob der Unterschied rein zufällig zustande gekommen sein kann. Sie können nur auf genestete Modelle angewandt werden - d.h. wir können nur Modelle vergleichen, wenn eines davon eine Teilmenge der Prädiktoren eines anderen ist. Sprich: wir können z.B. YEAR ~ ELEV + LAT.cent + LON.cent mit YEAR ~ ELEV + LAT.cent vergleichen, nicht aber YEAR ~ LAT.cent + LON.cent mit YEAR ~ ELEV + LAT.cent. Und wir dürfen auch nur Modelle vergleichen, die auf die Selben Daten angewandt worden sind - die Likelihood hängt ja direkt von den verwendeten Daten ab.
Schauen wir uns einen Likelihood-Ratio Test für ein Modell mit und ohne Längengrad als Prädiktor an:
Wie wir sehen, unterscheiden sich die log-Likelihoods nicht unerheblich.
## 'log Lik.' -79.65949 (df=5)## 'log Lik.' -106.6906 (df=4)Der LR-Test erfolgt so, dass die skalierte Differenz der Residual Sum of Squares verwendet wird62 mit einer \(\chi^2\)-Verteilung verglichen wird. Als Anzahl der Freiheitsgrade der \(\chi^2\)-Verteilung wird die Differenz der Freiheitsgrade beider Modell (jeweils n-p) verwendet.
Anzahl Beobachtungen:
## [1] 50Verbleibende Freiheitsgrade beider Modelle
## [1] 46## [1] 47LR-Test mittels anova.lmlist
## Analysis of Variance Table
##
## Model 1: YEAR ~ ELEV + LAT.cent + LON.cent
## Model 2: YEAR ~ ELEV + LAT.cent
## Res.Df RSS Df Sum of Sq Pr(>Chi)
## 1 46 70.847
## 2 47 208.882 -1 -138.03 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1\(H_0\) ist dabei, dass beide Modell dieselbe Likelihood haben. Dies wird vom Modell klar abgelehnt. Zusammen mit der Information, dass das die \(RSS\) im komplexeren Modell kleiner (und damit \(R^2\) höher) ist können wir schließen, dass es besser ist, das komplexere Modell zu verwenden.
Persönlich favorisiere ich den AIC bzw. den BIC für die Modellselektion. Beide Maße verwenden zusätzlich zur Likelihood (die ja durch weitere Prädiktoren nicht schlechter wird, selbst wenn diese keinen Effekt haben) einen Strafterm (penalty) \(k\) .
\[AIC = -2 \cdot max( \mathcal{logL}) + 2 k\] \[BIC = -2 \cdot max( \mathcal{logL}) + log(n) * k\]
\(loglik\) ist der natürliche Logarithmus der Likelihood, \(log(n)\) der natürliche Logarithmus aus der Stichprobengröße63 und \(k\) die Anzahl der Parameter im Modell. Beim linearen Modell ergibt sich \(k\) als die Anzahl der Regressionskoeffizienten (inklusive des Achsenabschnitts) plus 1, da auch \(\sigma^2\) aus den Daten geschätzt werden muss.
Der Wert \(2*k\) beim AIC mag zufällig erscheinen, beruht jedoch auf einer solide theoretische Herleitung.
Je kleiner der AIC bzw. der BIC, desto besser das Modell, das komplexere Modell ist in unserem Fall deutlich überlegen.
## df AIC
## g 5 169.3190
## g2 4 221.3812Der BIC lässt sich über den gleichen Befehl aufrufen, nur der Strafterm k mus entsprechend modifiziert werden:
## df AIC
## g 5 178.8791
## g2 4 229.0293Wieder das klare Signal, dass das komplexere Modell zu bevorzugen ist.
Alternativ auch
## df BIC
## g 5 178.8791
## g2 4 229.0293Hinweis: Weder AIC, AICC noch BIC sind (wie ja auch die Likelihood) über den Datensatz hinweg interpretierbar. Es macht keinen Sinn, einen AIC Wert zu kommunizieren. “Ich habe ein Modell mit einem AIC von -212” ist aussagelos, wenn man damit Datensätze vergleichen will. Weder AIC noch BIC sind skaliert. Will man ein absolutes Maß für die Modellgüte haben, sollte man \(R^2\) verwenden, dass allerdings nicht für die Modellselektion verwendet werden kann.
AIC und BIC sind nur bis auf eine additive Konstante genau bestimmt. Unterschiedliche Funktionen unterscheiden sich in der Art und Weise, wie mit dieser additiven Konstante umgegangen wird. Deswegen kann man AIC bzw. BIC Werte, die von verschiedenen Funktionen berechnet wurden i.d.R. nicht miteinander vergleichen.
Der höhere Strafterm beim BIC 64 führt dazu, dass der BIC kleinere Modelle bevorzugt, also einen höheren Selektionsdruck ausübt. Der Strafterm beim BIC ist im Gegensatz zum AIC von der Stichprobengröße abhängig. Dies korrigiert dafür, dass bei großen Stichproben Verbesserungen der log-Likelihood bzw. der Residualvarianz „leichter“ möglich sind, weshalb der AIC bei großen Stichproben tendenziell Modelle mit verhältnismäßig vielen Parametern vorteilhaft erscheinen lässt.
AIC und BIC unterscheiden sich auch hinsichtlich ihrer Zielsetzung: Während das BIC versucht dasjenige Modell auszuwählen, das a-posteriori die größte Plausibilität besitzt das wahre Modell zu sein, geht das AIC davon aus, dass es kein wahres Modell gibt.
Für kleine Stichprobengrößen wird beim AIC eine korrigierte Version empfohlen, der AICc:
\[AICc = -2 \cdot max(\mathcal{logL}) + 2 \cdot p \cdot \frac{n}{n-k-1} \]
Der AICc ist im package AICcmodavg als AICc implementiert.65.
Der Vollständigkeit halber sei noch das adjustierte \(R^2\) genannt (\(\bar{R}^2\) oder auch \(R^2_{adj}\)), dass ebenfalls versucht über einen Strafterm eine Korrektur vorzunehmen. Für die Modellselektion ist jedoch der AIC/BIC vorzuziehen, da \(\bar{R}^2\) auch marginal-signifikante Parameter 66 im Modell belässt.
\[\bar{R}^2 = 1 - (1-R^2)\frac{n-1}{n-p} \]
\(n\) ist dabei die Stichprobengröße (hier n= 50) und \(p\) die Anzahl Regressionskoeffizienten (inklusive dem Achsenabschnitt. hier p=4)67. \(R^2\) wird bei summary als Multiple R-squared angegeben, \(\bar{R^2}\) als Adjusted R-squared.
Wenn sich zwei Modelle um weniger als 2 AIC oder BIC Einheiten unterscheiden (sogenannter \(\Delta AIC\) bzw. \(\Delta BIC\)), dann sind die Modelle von gleicher Qualität - d.h. man muss anhand einer zusätzlichen Argumentation entscheiden, welches Modell man bevorzugt, oder ob man ggf. auch mit beiden Modell weiterrechnet indem man z.B. die Modellvorhersagen mittelt.
13.2.1 Hilfsfunktionen für die Modellselektion
Um nicht dutzende von Modellen manuell spezifizieren und vergleichen zu müssen gibt es die drop1 Funktion. Diese Funktion gibt den AIC/BIC für das komplette Modell aus und für alle Modelle, in denen jeweils 1 Term weggelassen wurde.
AIC
## Single term deletions
##
## Model:
## YEAR ~ ELEV + LAT.cent + LON.cent
## Df Sum of Sq RSS AIC
## <none> 70.85 25.425
## ELEV 1 154.48 225.33 81.277
## LAT.cent 1 915.28 986.13 155.088
## LON.cent 1 138.03 208.88 77.487Wenn wir keinen Term entfernen (none) liegt der AIC bei 25.425. Entfernen wir ELEV (d.h. YEAR ~ LAT.cent + LON.cent) liegt der AIC bei 81.277, das Modell ist also deutlich schlechter. Lassen wir LAT.cent weg (d.h. YEAR ~ ELEV + LON.cent), so liegt der AIC bei 155.088 und falls wir LON.cent weglassen (d.h. YEAR ~ ELEV + LAT.cent) liegt der AIC bei 77.487. Das heißt wir behalten das Modell mit drei Termen.
BIC
## Single term deletions
##
## Model:
## YEAR ~ ELEV + LAT.cent + LON.cent
## Df Sum of Sq RSS AIC
## <none> 70.85 33.073
## ELEV 1 154.48 225.33 87.013
## LAT.cent 1 915.28 986.13 160.824
## LON.cent 1 138.03 208.88 83.223Auch der BIC kommt zu gleichen Ergebnis. Nicht verwirren lassen: die Funktion gibt immer AIC als Spaltenüberschrift aus; hier ist es aber der BIC, der ausgegeben wird.
Wenn wir mit transformierten Werten rechen, kann das direkt in der Gleichung angegeben werden. Beim Vorhersagen mit predict ist R clever genug, dass direkt umzusetzen. Nicht, dass das hier großen Sinn machen würde, aber da Sie das in der Hausaufgabe benötigen werden möchte ich das kurz demonstrieren.
##
## Call:
## lm(formula = YEAR ~ sqrt(ELEV) + LAT.cent + LON.cent, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.2875 -0.9646 0.2051 0.7953 2.8667
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.14938 0.41667 2.759 0.0083 **
## sqrt(ELEV) -0.20747 0.02438 -8.511 5.27e-11 ***
## LAT.cent -0.83634 0.04011 -20.851 < 2e-16 ***
## LON.cent -0.11413 0.01284 -8.886 1.51e-11 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.379 on 46 degrees of freedom
## Multiple R-squared: 0.9177, Adjusted R-squared: 0.9123
## F-statistic: 170.9 on 3 and 46 DF, p-value: < 2.2e-16Nun die Vorhersage mit predict und anschließendes plotten des Zusammenhanges, wie er im Modell abgebildet wird.
new.ru.3 <- data.frame(ELEV=seq(min(temp.ru$ELEV), max(temp.ru$ELEV), length.out=100),
LAT.cent=mean(temp.ru$LAT.cent), LON.cent=mean(temp.ru$LON.cent))
g.pred.trans <- as.data.frame(predict(g.trans, newdata = new.ru.3, interval="confidence"))
plot(YEAR ~ ELEV, data=temp.ru, las = 1)
lines(g.pred.trans$fit~ new.ru.3$ELEV, col="red")
lines(g.pred.trans$upr~ new.ru.3$ELEV, col="red", lty=2)
lines(g.pred.trans$lwr~ new.ru.3$ELEV, col="red", lty=2)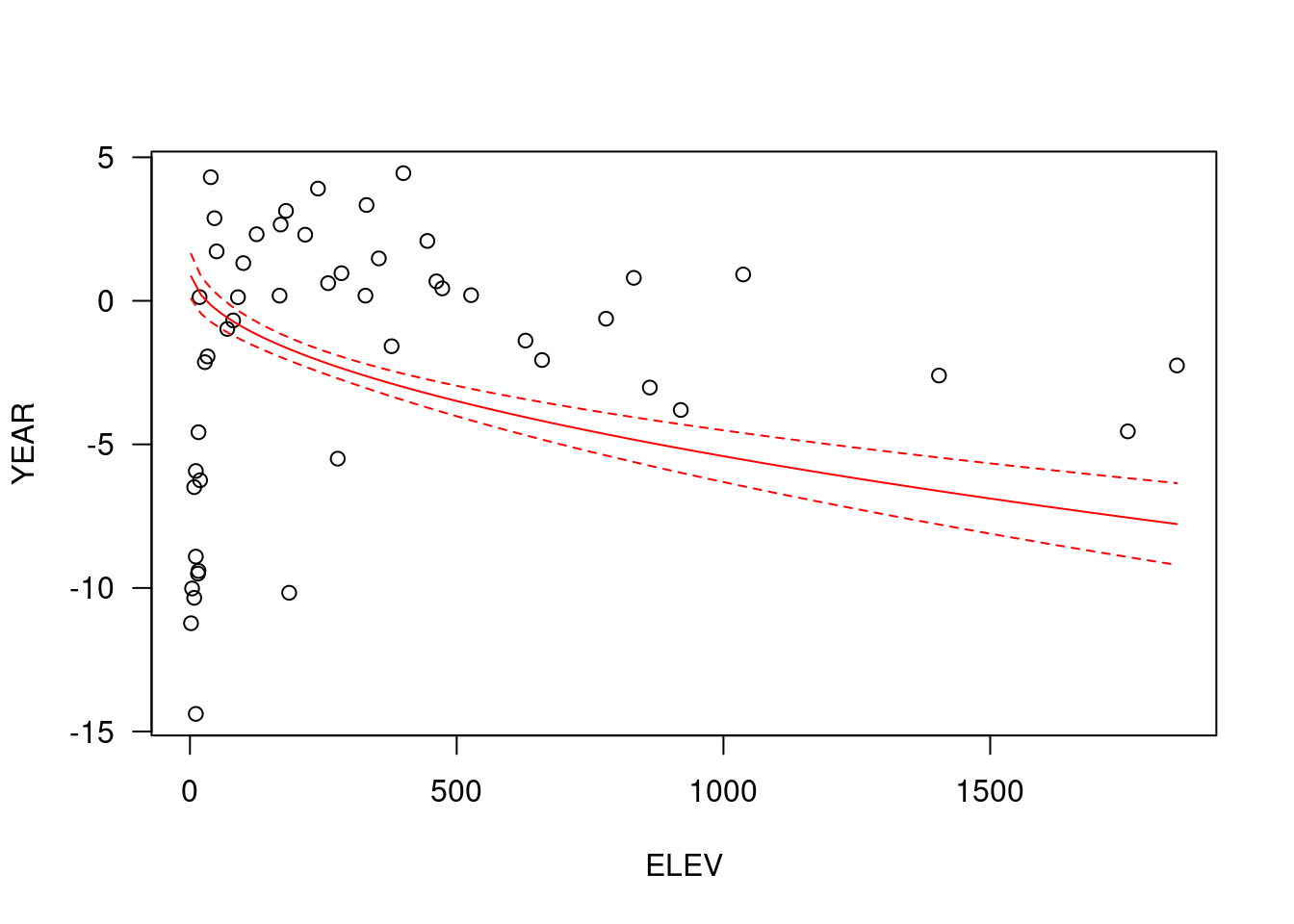
Wie Sie sehen, wird die Transformation on-the-fly umgesetzt.
13.4 Plots für ein verbessertes Verständnis multivariater Modelle
Die mehrdimensionalität erschwert es, Zusammenhange zu erkennen. Deswegen möchte ich im folgenden eine Reihe von Plots vorstellen, die helfen, tiefere Einsichten in die Zusammenhänge zu erhalten.
13.4.1 Conditioning Plots
Diese Form von Plots plotten den Zusammenhang zwischen zwei Variablen in Abhängigkeit (conditional on) von weiteren Variablen. Hierfür werden die Daten anhand der zusätzlichen Variablen in Teilmengen gepackt und dann separat geplottet. Nachfolgendes Beispiel zeigt dies für den Zusammenhang zwischen Geländehöhe und Temperatur abhängig vom Längengrad.
Der obere Teilplot in nachfolgender Abbildung 13.3 zeigt die Intervalle, in welche die Variable LON (Längengrad) unterteilt worden ist. Standardmäßig überlappen sich die Intervalle dabei.68 Die Breite der Intervalle richtet sich dabei nach der Anzahl der Datenpunkte in dem Bereich. Die Teilplot zeigen den Zusammenhang zwischen Jahresmitteltemperatur und Längengrad für die Stationen, die in der jeweiligen Längengradzone liegen. Das erste Intervall von 58.795 bis 73.885 ist unten links dargestellt, das zweite (67.065 bis 82.735) rechts daneben (2. Zeile, 2. Spalte), das vierte Intervall (84.745 bis 93.025) in der ersten Zeile, ersten Spalte. Über panel = panel.smooth legen wir eine Art gleitenen Mittelwert (lowess-smoother) über die Daten (rote Linie), die uns (insbesondere bei vielen Datenpunkten) hilft, den mittleren Zusammenhang zu erkennen.
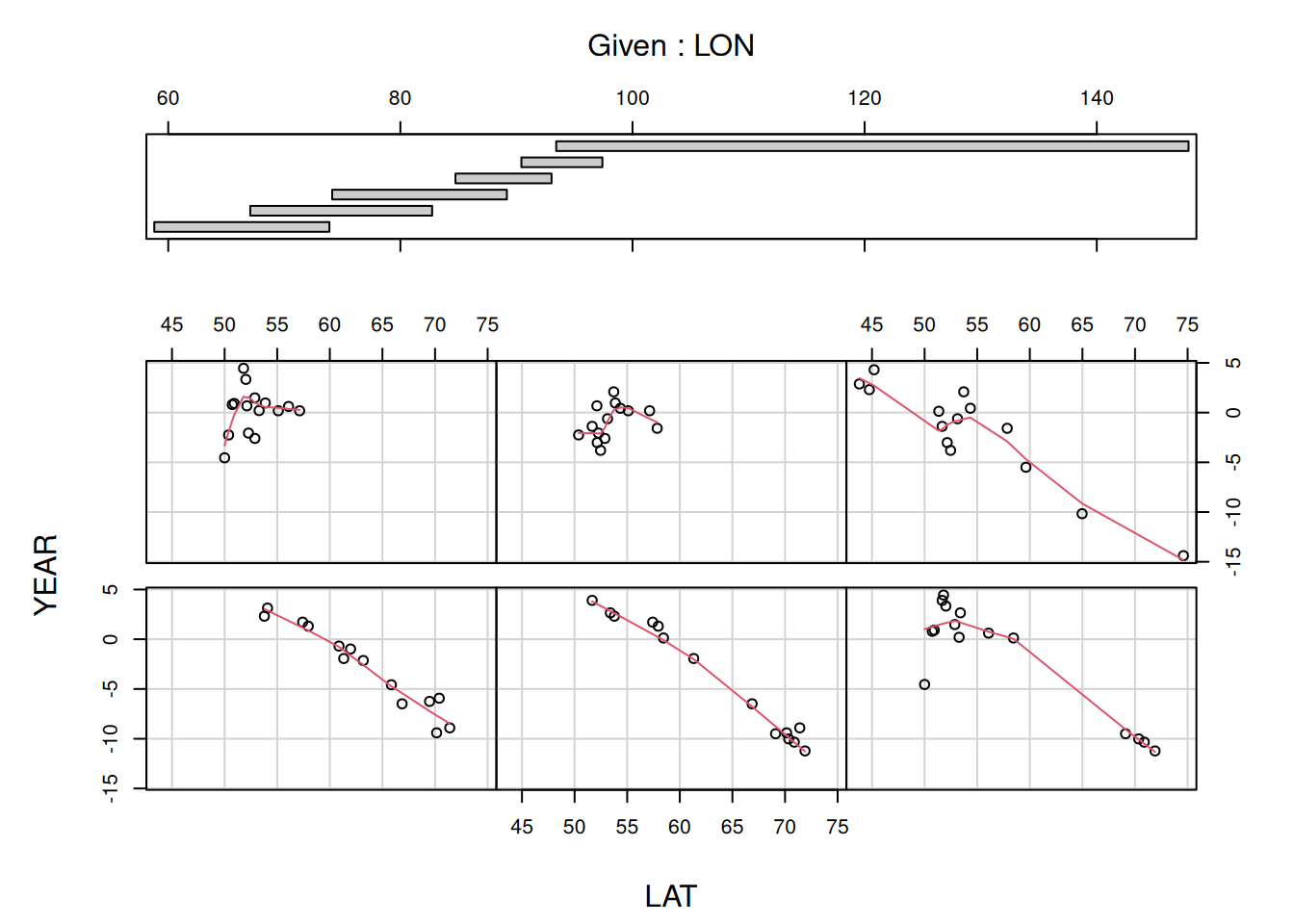
Figure 13.3: Conditioning Plot für den Zusammenhang zwischen Jahresmitteltemperatur und Breitengrad in Abhängigkeit vom Längengrad. Dargestellt für die historischen Temperaturdaten für die Stationen in der Russischen Föderation.
Für die Intervalle 1-3 und 6 sehen wir einen ähnlichen Zusammenhang: je nördlicher die Station, desto kälter ist es im Jahresmittel. Das 4. und 5. Intervall scheinen diesen Zusammenhang nicht zu zeigen und auch im 3. und 6. Intervall gibt es Abweichungen. Dies liegt vermutlich an der Geländehöhe als zusätzliche Einflussgröße. Ein Blick auf die topographische Karte der Russischen Föderation zeigt, dass wir im Bereich 60-90°E das westsibirische Tiefland haben, in dem die Geländehöhe (bis auf das schmale Uralgebirge) einen geringeren Einfluss hat, während östlich davon die Stationen im zentralasiatischen Gebirsgürtel liegen, was relevante Reliefunterschiede bedingt. Interessanterweise haben wir keine Klimastationen westlich des Urals.
Man kann die Plots auch von mehr als einer zusätzlichen Variablen abhängig machen (s. Abbildung 13.4).
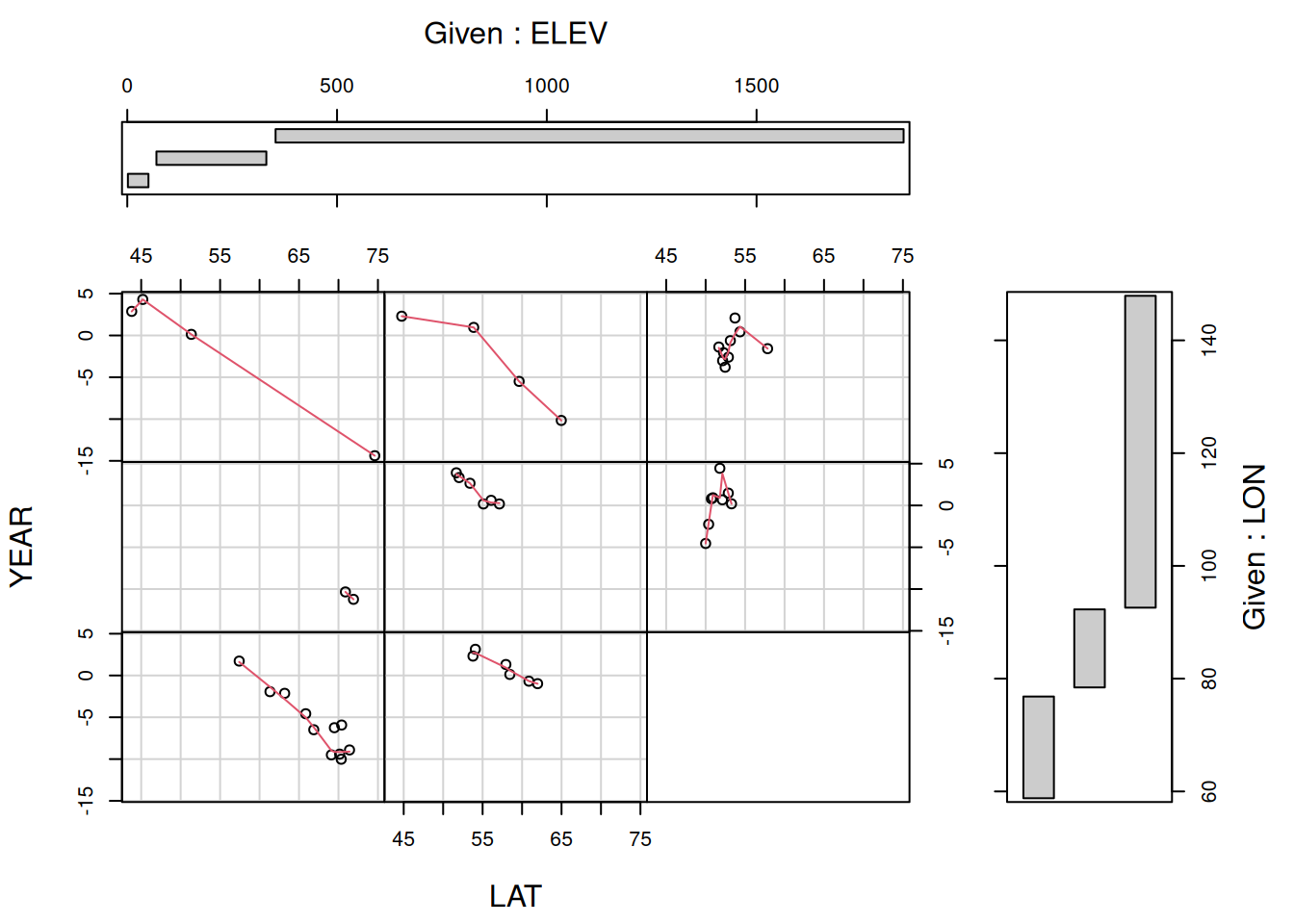
Figure 13.4: Conditioning Plot für den Zusammenhang zwischen Jahresmitteltemperatur und Breitengrad in Abhängigkeit vom Längengrad und Geländehöhe. Dargestellt für die historischen Temperaturdaten für die Stationen in der Russischen Föderation. An den Rändern sind jeweils die Intervalle der beiden zusätzlichen Variablen für die Teilplots angegeben.
Die Klimastationen mit Höheninformationen in Russland verteilen sich nicht nur etwas ungünstig hinsichtlich der Abdeckung der Längengrade, sondern auch hinsichtlich der Höhenlagen. Wir müssen also aufpassen, dass wir nicht durch eine ungünstige Verteilung der Stationen in einem der Teilplots in die Irre geführt werden.
13.4.2 Zusätzliches Modellverständnis durch Added Variable und Partial Residual Plots
Wenn wir verstehen wollen, wie ein Modell die Daten beschreibt, hatten wir ja schon gesehen, wie wir mittels predict den Verlauf der Regressionsline darstellen können. Problematisch ist allerdings immer, dass die anderen Vorhersagevariablen ebenfalls die Lage des Fits beeinflussen und wir somit Schwierigkeiten haben, den Effekt eines Prädiktors zu isolieren. Durch Verwendung von Added Variable und Partial Residual Plots kann man dieses Problem etwas umgehen. Diese werden auch im Bereich der Modelldiagnose - also beim Überprüfen der Modellannahmen - eingesetzt.
13.4.2.1 Partial Regression oder Added Variable Plots
In Added Variable Plots versuchen wir den Effekt eines Prädiktors \(x_i\) auf \(y\) zu isolieren. Zunächst berechnen wir die Residuen \(\hat{\delta}\) wenn wir \(y\) mit allen Prädiktoren im Modell ohne \(x_i\) erklären. Dies ergibt den \(y\)-Wert, wenn man den Effekt aller anderen Variablen herausgerechnet hat. Dann regressieren wir \(x_i\) mit allen anderen Prädiktoren im Modell und erhalten die Residuen \(\hat{\gamma}\). Diese beschreiben \(x_i\), nachdem alle Effekte der anderen Prädiktoren herausgerechnet wurden.
Der added variable plot ist nun der Plot den wir erhalten, wenn wir \(\hat{\delta}\) gegen \(\hat{\gamma}\) plotten. Wir sollten hier in der Modelldiagnose nach Ausreißern, einflußreichen Punkten und nicht-Linearität Ausschau halten.
13.4.2.1.1 Added Variable Geländehöhe
Schauen wir uns einmal den added variable plot für Geländehöhe am Beispiel der russischen Temperaturstationen an.
Residuen der Regression von der Jahresmitteltemperatur mit allen Prädiktoren im Modell ohne Geländehöhe: \(\hat{\delta}\).
Residuen der Regression von Geländehöhe gegen die anderen Prädiktoren im Modell: \(\hat{\gamma}\).
Added Variable von Geländehöhe:
Normales Regressionsmodell mit allen 3 Prädiktoren und Modellvorhersage mittels predict um die Regressionsfunktion zu plotten,
g.ru <- lm(YEAR~ELEV + LAT + LON, data=temp.ru)
newDat.ru <- data.frame(ELEV=seq(min(temp.ru$ELEV), max(temp.ru$ELEV), length.out=100), LAT=mean(temp.ru$LAT), LON=mean(temp.ru$LON))
pred.ru.elev <- predict(g.ru, newdata = newDat.ru)par(mfrow=c(1,2))
plot(d~m, xlab="Residuen für Geländehöhe", ylab="Residuen von Temperatur", main="added variable plot \nfür Geländehöhe", pch=21, bg="orange", las=1)
abline(g.addedValueElev)
plot(YEAR~ELEV, data=temp.ru, main="Original Plot", xlab="Geländehöhe [m]", ylab="Mittlere Jahrestemperatur [°C]", pch=21, bg="orange", las=1)
lines(pred.ru.elev ~ newDat.ru$ELEV)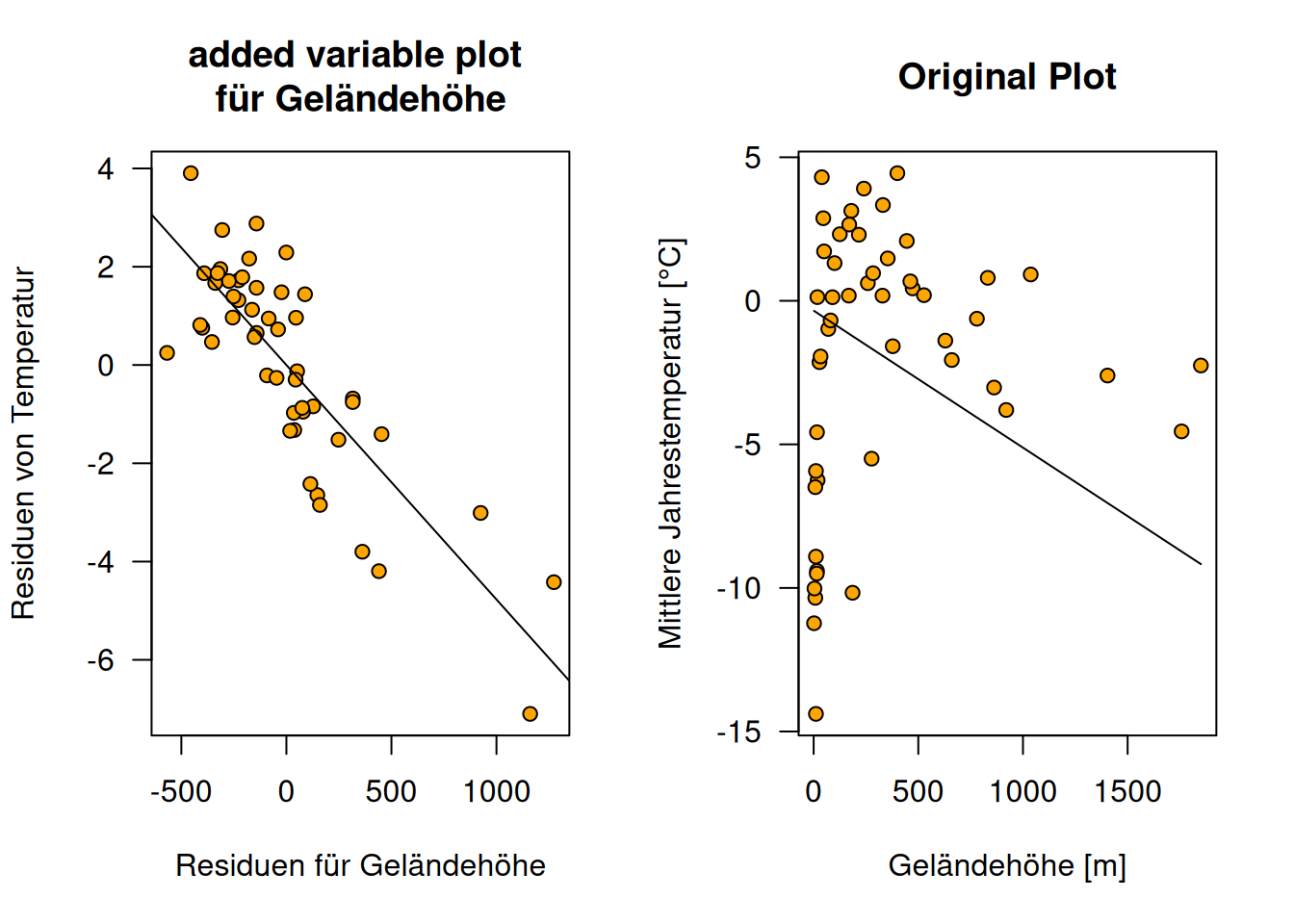
Figure 13.5: Verleich des Added Variable Plot für Geländehöhe versus den naviven Plot der einfach nur die Regressionsgerade in die Projektion von Geländehöhe gegen Jahrestemperatur zeigt und den Einfluss von geographischer Länge und Breite nicht berücksichtigt. Die Plots beruhen auf den russischen Temperaturstationen, die Höheninformationen haben.
Den Effekt von Geländehöhe auf Temperatur können wir deutlich einfacher im added variable plot ablesen, als in der einfachen Projektion der Daten und der Regressionsgleichung in den durch Response und Geländehöhe aufgespannten zweidimensionalen Teilraum (s. Abbildung 13.5). Der Effekt von geographischer Breite und Länge wird im rechten Teilplot ausgeklammert, weswegen wir keinen Zusammenhang zwischen Geländehöhe und Temperatur sehen können. Im added variable plot ist der Zusammenhang klar zu erkennen.
Der Added Variable Plot zeigt hier keine Besonderheiten einzelner Punkte hinsichtlich der Geländehöhe.
Wenn wir den Regressionskoeffizienten von \(\hat{\delta}\) gegen \(\hat{\gamma}\) mit dem Koeffizienten der Geländehöhe des vollen Regressionsmodells vergleichen, sehen wir, dass die Koeffizienten und die Standardfehler sehr ähnlich sind.
##
## Call:
## lm(formula = d ~ m)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.227e-17 1.718e-01 0.00 1
## m -4.772e-03 4.664e-04 -10.23 1.19e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.215 on 48 degrees of freedom
## Multiple R-squared: 0.6856, Adjusted R-squared: 0.679
## F-statistic: 104.7 on 1 and 48 DF, p-value: 1.195e-13##
## Call:
## lm(formula = YEAR ~ ELEV + LAT + LON, data = temp.ru)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 53.8410350 2.6293965 20.477 < 2e-16 ***
## ELEV -0.0047720 0.0004765 -10.015 3.88e-13 ***
## LAT -0.7777441 0.0319038 -24.378 < 2e-16 ***
## LON -0.1076918 0.0113755 -9.467 2.26e-12 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.241 on 46 degrees of freedom
## Multiple R-squared: 0.9333, Adjusted R-squared: 0.929
## F-statistic: 214.7 on 3 and 46 DF, p-value: < 2.2e-1613.4.2.1.2 Added Variable Plot geographische Breite
Da geographische Breite den stärksten Effekt der 3 Prädiktoren hat, sind die Abbweichungen zwischen dem einfachem Scatterplot im 2d-Teilraum und dem added variable plot nicht so stark. Man erkennt trotzdem deutlich, dass die Variabilität um die Regressionsgerade im added variable plot geringer ist (s. Abbildung 13.6).
d.lat <- residuals(lm(YEAR ~ LON + ELEV, data=temp.ru))
m.lat <- residuals(lm(LAT ~ LON + ELEV, data=temp.ru))
g.addedValueLat <- lm(d.lat ~ m.lat)
newDat.ru.lat <- data.frame(LAT=seq(min(temp.ru$LAT), max(temp.ru$LAT), length.out=100),
LON=mean(temp.ru$LON), ELEV=mean(temp.ru$ELEV))
pred.ru.Lat <- predict(g.ru, newdata = newDat.ru.lat)par(mfrow=c(1,2))
plot(d.lat ~ m.lat, xlab="Residuen für geographische Breite", ylab="Residuen von Temperatur", main="added variable plot \nfür geographische Breite", pch=21, bg="orange", las=1)
abline(g.addedValueLat)
plot(YEAR ~ LAT, data=temp.ru, main="Original Plot", xlab="Geographische Breitet [°]", ylab="Mittlere Jahrestemperatur [°C]", pch=21, bg="orange", las=1)
lines(pred.ru.Lat ~ newDat.ru.lat$LAT)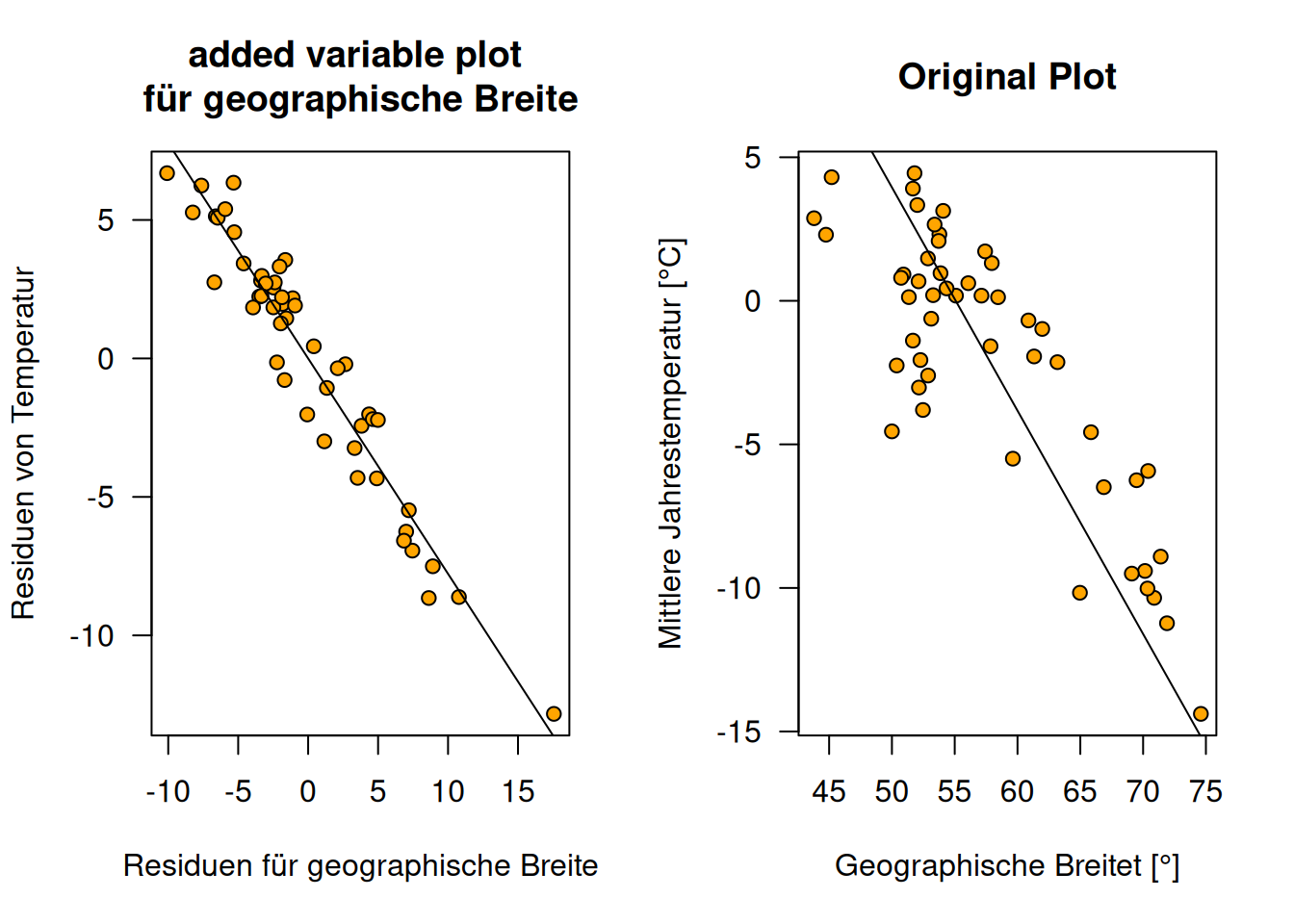
Figure 13.6: Verleich des Added Variable Plot für geographische Breite versus den naviven Plot der einfach nur die Regressionsgerade in die Projektion von geographischer Breite gegen Jahrestemperatur zeigt und den Einfluss von geographischer Länge und Geländehöhe nicht berücksichtigt. Die Plots beruhen auf den russischen Temperaturstationen, die Höheninformationen haben.
13.4.2.1.3 Added Variable Plot geographische Länge
d.lon <- residuals(lm(YEAR ~ LAT + ELEV, data=temp.ru))
m.lon <- residuals(lm(LON ~ LAT + ELEV, data=temp.ru))
g.addedValueLon <- lm(d.lon ~ m.lon)
newDat.ru.lon <- data.frame(LON=seq(min(temp.ru$LON), max(temp.ru$LON), length.out=100),
LAT=mean(temp.ru$LAT), ELEV=mean(temp.ru$ELEV))
pred.ru.Lon <- predict(g.ru, newdata = newDat.ru.lon)par(mfrow=c(1,2))
plot(d.lon ~ m.lon, xlab="Residuen für geographische Länge", ylab="Residuen von Temperatur", main="added variable plot \nfür geographische Länge", pch=21, bg="orange", las=1)
abline(g.addedValueLon)
plot(YEAR~LON, data=temp.ru, main="Original Plot", xlab="Geographische Länge [°]", ylab="Mittlere Jahrestemperatur [°C]", pch=21, bg="orange", las=1)
lines(pred.ru.Lon ~ newDat.ru.lon$LON)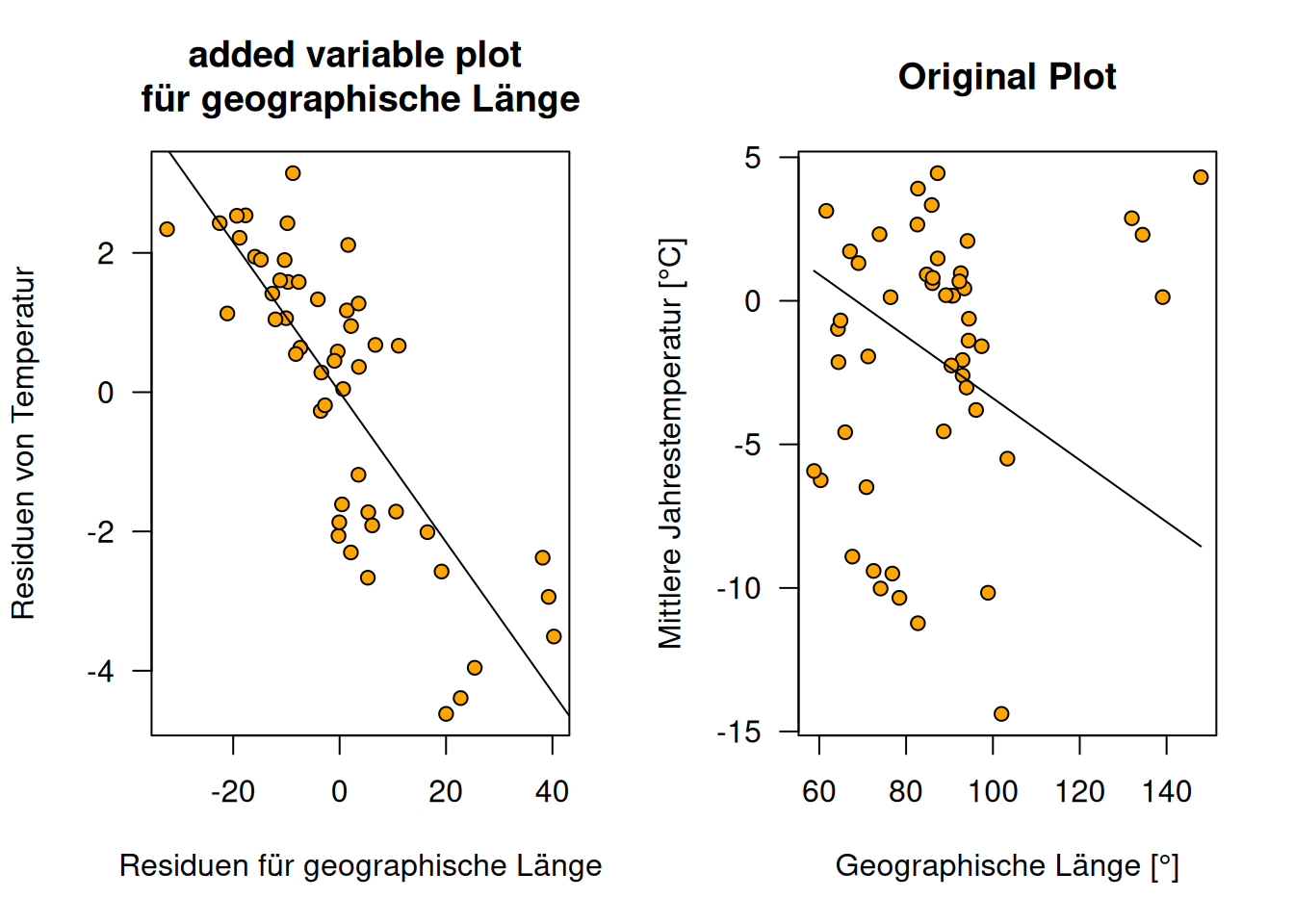
Figure 13.7: Verleich des Added Variable Plot für geographische Länge versus den naviven Plot der einfach nur die Regressionsgerade in die Projektion von geographischer Länge gegen Jahrestemperatur zeigt und den Einfluss von geographischer Breite und Geländehöhe nicht berücksichtigt. Die Plots beruhen auf den russischen Temperaturstationen, die Höheninformationen haben.
13.4.2.1.4 Vergleich zwischen Ländern
Die Vorteile des Added Variable Plots kommen ebenfalls zum tragen, wenn wir die Regressiosnmodelle zwischen mehreren Ländern - z.B. Deutschland und Russland - vergleichen wollen. Während die normalen Vorhersageplots - aufgrund der sehr unterschiedlichen Wertebereiche für geographische Position nicht vergleichbar sind, wird dieser Effekt in den Added Variable Plots herausgerechnet.
temp.de <- subset(temp, CNTRY_NAME == "Germany")
g.de <- lm(YEAR~ELEV + LAT + LON, data=temp.de)
newDat.de <- data.frame(ELEV=seq(min(temp.de$ELEV),
max(temp.de$ELEV),
length.out=100),
LAT=mean(temp.de$LAT),
LON=mean(temp.de$LON))
pred.de.elev <- predict(g.de, newdata = newDat.de)
d.de <- residuals(lm(YEAR ~ LAT + LON, data=temp.de))
## Added Variable Geländehöhe
# Residuen der Regression von Geländehöhe gegen die anderen Prädiktoren im Modell
m.de <- residuals(lm(ELEV ~ LAT + LON, data=temp.de))
# Added Variable von Geländehöhe:
g.addedValueElev.de <- lm(d.de~m.de)par(mfrow=c(1,2))
plot(YEAR ~ ELEV, data=temp.ru, main="Original Plot, Russland",
xlab="Geographische Breite [°]",
ylab="Mittlere Jahrestemperatur [°C]",
pch=21, bg="orange", las=1)
lines(pred.ru.elev ~ newDat.ru$ELEV)
plot(YEAR ~ ELEV, data=temp.de, main="Original Plot, Deutschland",
xlab="Geographische Breite [°]",
ylab="Mittlere Jahrestemperatur [°C]",
pch=21, bg="orange", las=1)
lines(pred.de.elev ~ newDat.de$ELEV)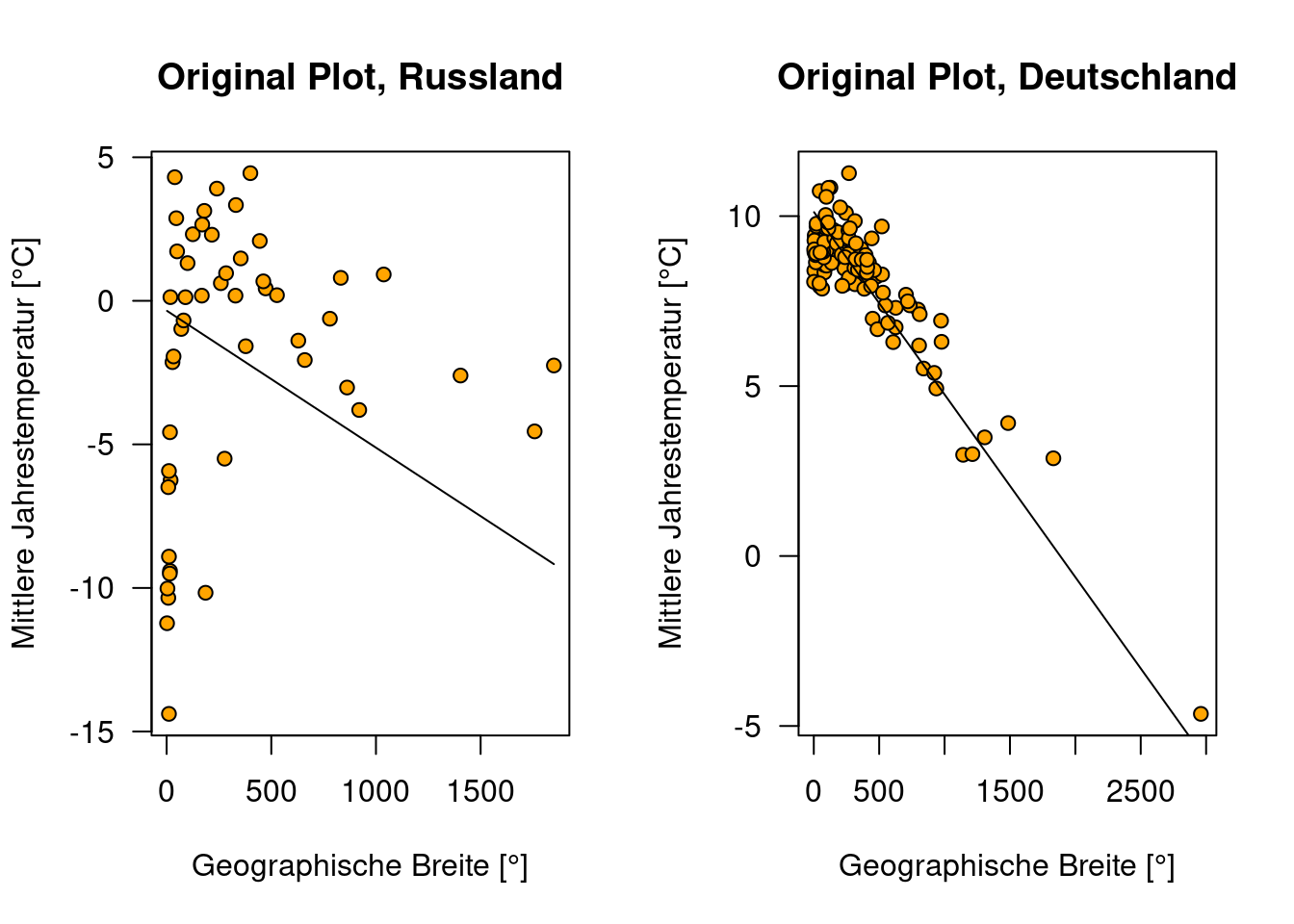
par(mfrow=c(1,2))
plot(d~m, xlab="Residuen für Geländehöhe",
ylab="Residuen von Temperatur",
main="Added Variable Plot \nfür Geländehöhe, Russland",
pch=21, bg="orange", las=1)
abline(g.addedValueElev)
plot(d.de~m.de, xlab="Residuen für Geländehöhe",
ylab="Residuen von Temperatur",
main="Added Variable Plot \nfür Geländehöhe, Deutschland",
pch=21, bg="orange", las=1)
abline(g.addedValueElev.de)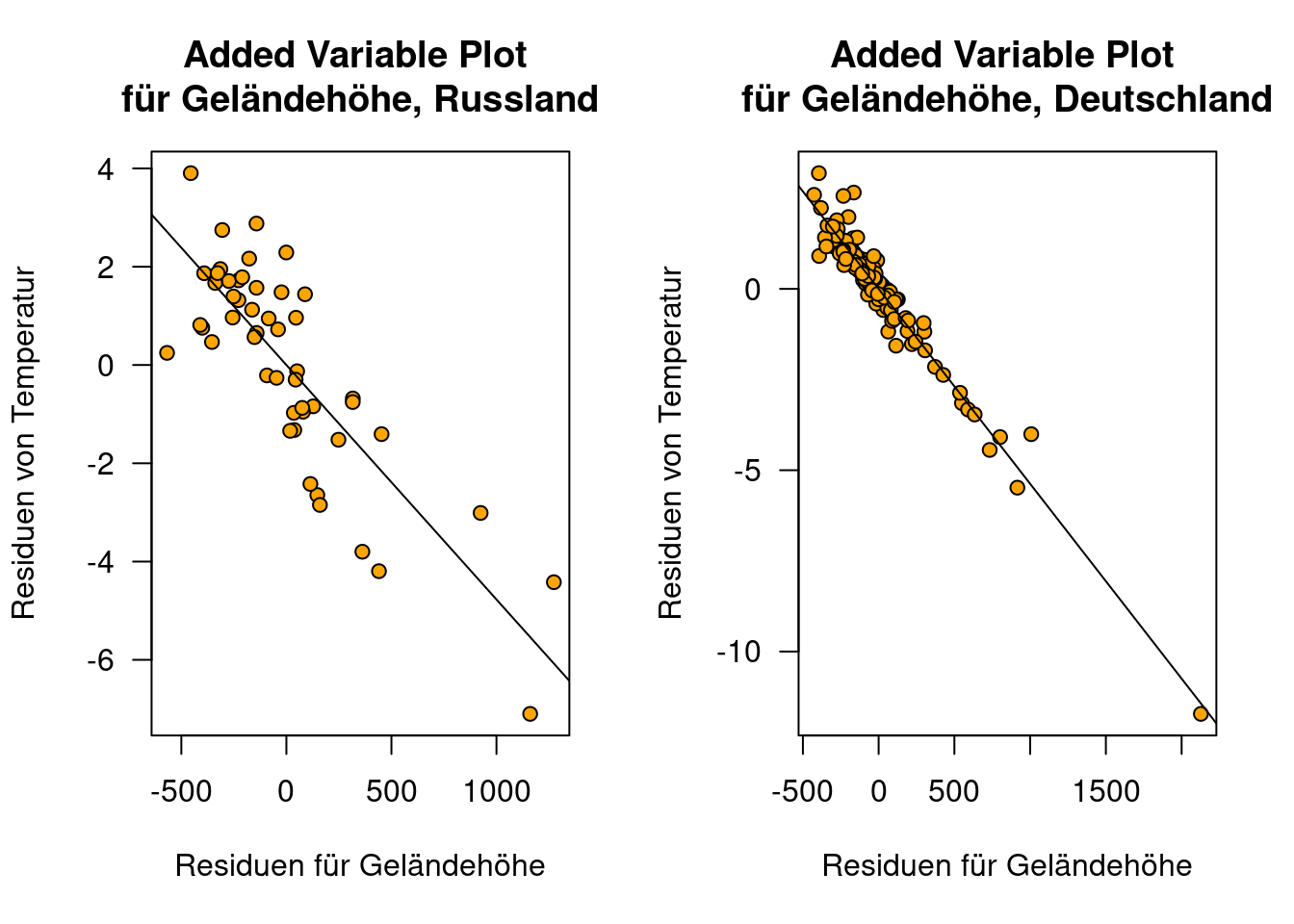
13.4.2.2 Partial Residual Plot
Beim Partial Residual Plot plottet man \(\hat{\epsilon} + \hat{\beta}_i x_i\) gegen \(x_i\). \(\hat{\epsilon} + \hat{\beta}_i x_i\) ist dabei genau das, was wir erhalten, wenn wir den vorhergesagten Effekt von allen anderen Prädiktoren im Modell vom Response abziehen:
\[ y - \sum_{j \neq i}{x_j \hat{\beta}_j} = \hat{y} + \hat{\epsilon} - \sum_{j \neq i}{x_j \hat{\beta}_j} = x_j \hat{\beta}_j + \hat{\epsilon} \]
Die Steigung im Plot von \(\hat{\epsilon} + \hat{\beta}_i x_i\) gegen \(x_i\) ist wieder \(\hat{\beta}_i\). Auch die Interpretation des Plots ist ähnlich wie beim added variable plot.
Im Allgemeinen kann man in Partial Residual Plots besser nicht-Linearitäten erkennen, während im added variable plot Ausreißer oder einflußreiche Punkte besser zu erkennen sind.
Einmal händisch durchgeführt:
par(mfrow=c(1,2))
plot(partResid4Elev.ru ~ temp.ru$ELEV, xlab="Geländehöhe", ylab="Partial Residuals", main="Partial Residual Plot\nfür Geländehöhe", las=1, pch=21, bg="purple")
abline(lm(partResid4Elev.ru ~ temp.ru$ELEV))
plot(YEAR~ELEV, data=temp.ru, main="Original plot", xlab="Geländehöhe [m]", ylab="Mittlere Jahrestemperatur [°C]", pch=21, bg="purple", las=1)
lines(pred.ru.elev ~ newDat.ru$ELEV)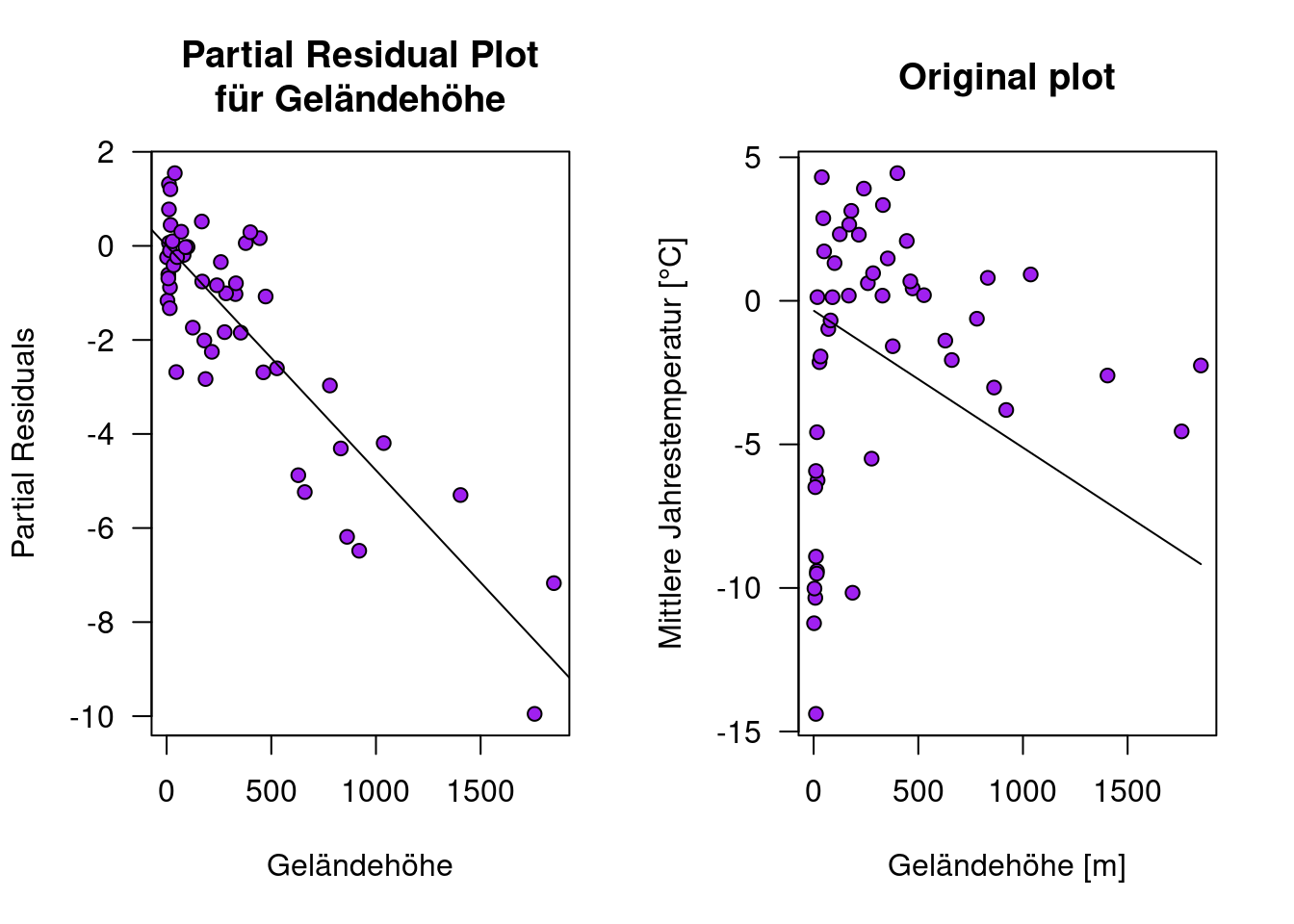
Die Regression der partiellen Residuen gegen Geländehöhe liefert auch hier wieder Schätzer und Standardfehler, die sehr ähnlich zu denen im Ausgangsregressionsmodell sind.
##
## Call:
## lm(formula = partResid4Elev.ru ~ temp.ru$ELEV)
##
## Residuals:
## Min 1Q Median 3Q Max
## -2.46384 -0.76645 0.08496 0.77674 2.28727
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -5.071e-17 2.193e-01 0.00 1
## temp.ru$ELEV -4.772e-03 3.958e-04 -12.06 3.93e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 1.215 on 48 degrees of freedom
## Multiple R-squared: 0.7518, Adjusted R-squared: 0.7466
## F-statistic: 145.4 on 1 and 48 DF, p-value: 3.929e-16Partial Residual Plots kann man auch einfach mittels der prplot Funktion aus dem Package faraway erzeugen, man muss die darzustellende erklärende Variable anhand ihres Index (ihre Position im formula Objekt der Regressionsgleichung) auswählen. Verschönern kann man die Plots allerdings nicht ohne weiteres.
## Loading required package: faraway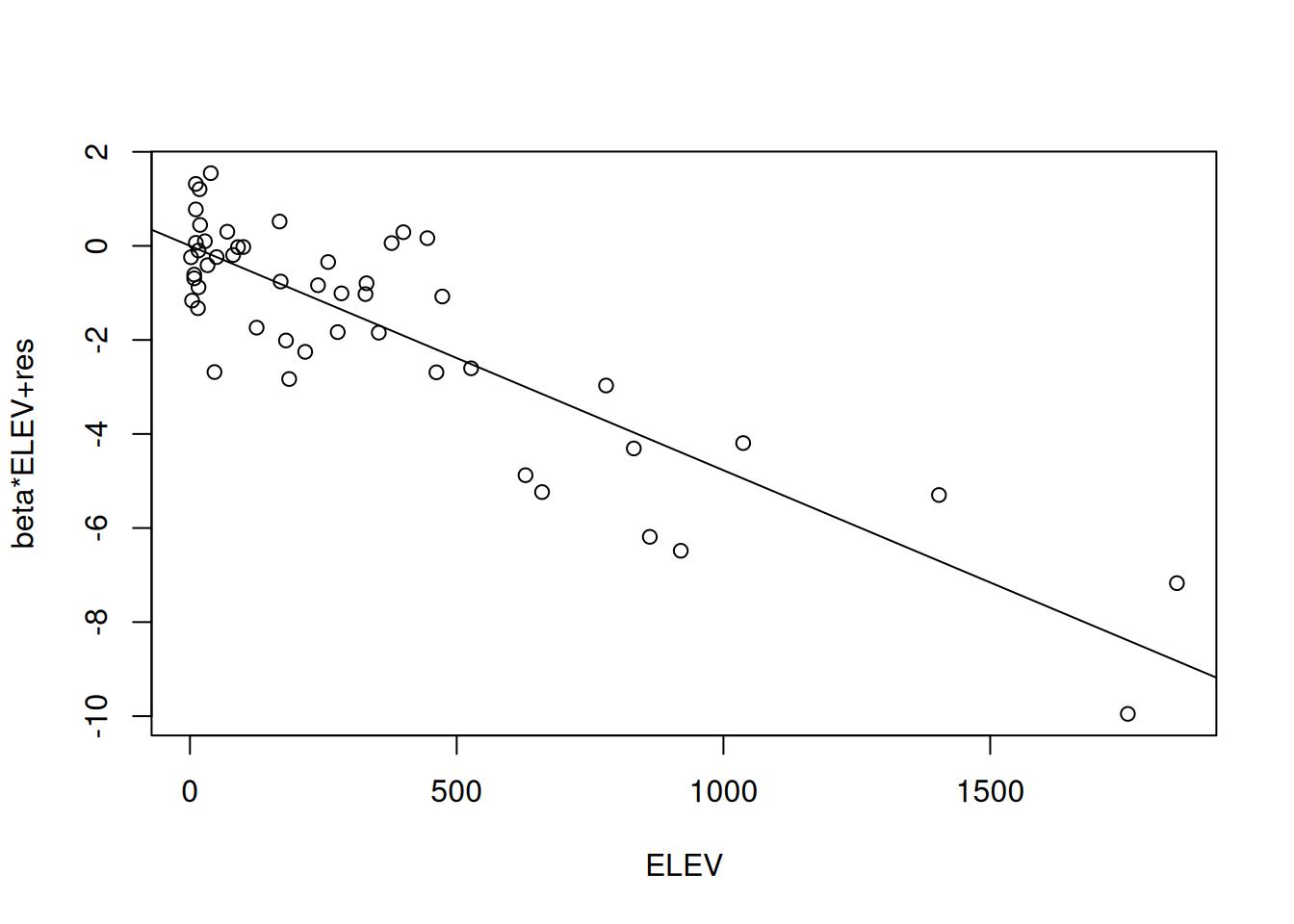
Figure 13.8: Partial Residual Plot für Geländehohe. Der Plot beruht auf den russischen Temperaturstationen, die Höheninformationen haben.
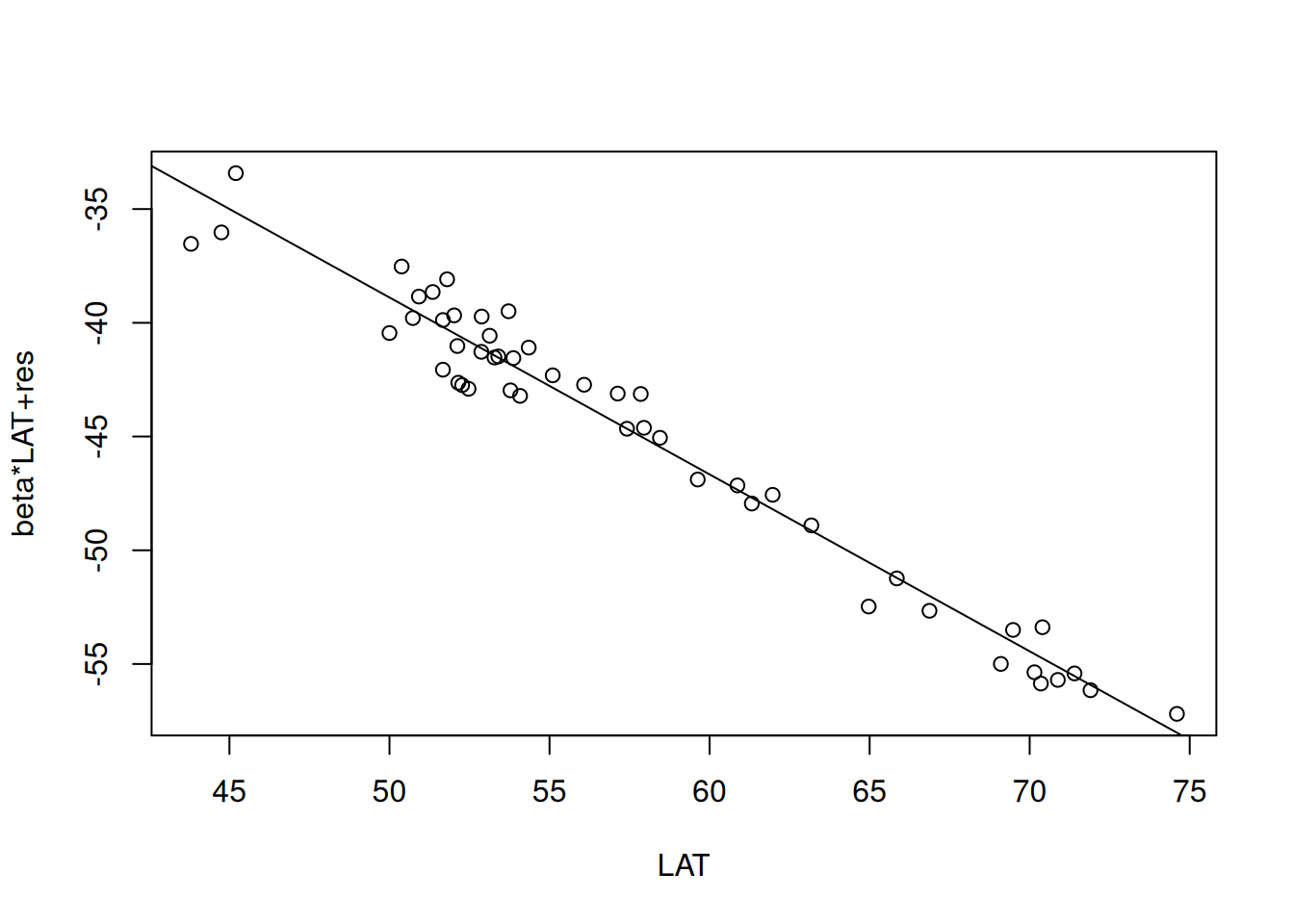
Figure 13.9: Partial Residual Plot für geographische Breite Der Plot beruht auf den russischen Temperaturstationen, die Höheninformationen haben.
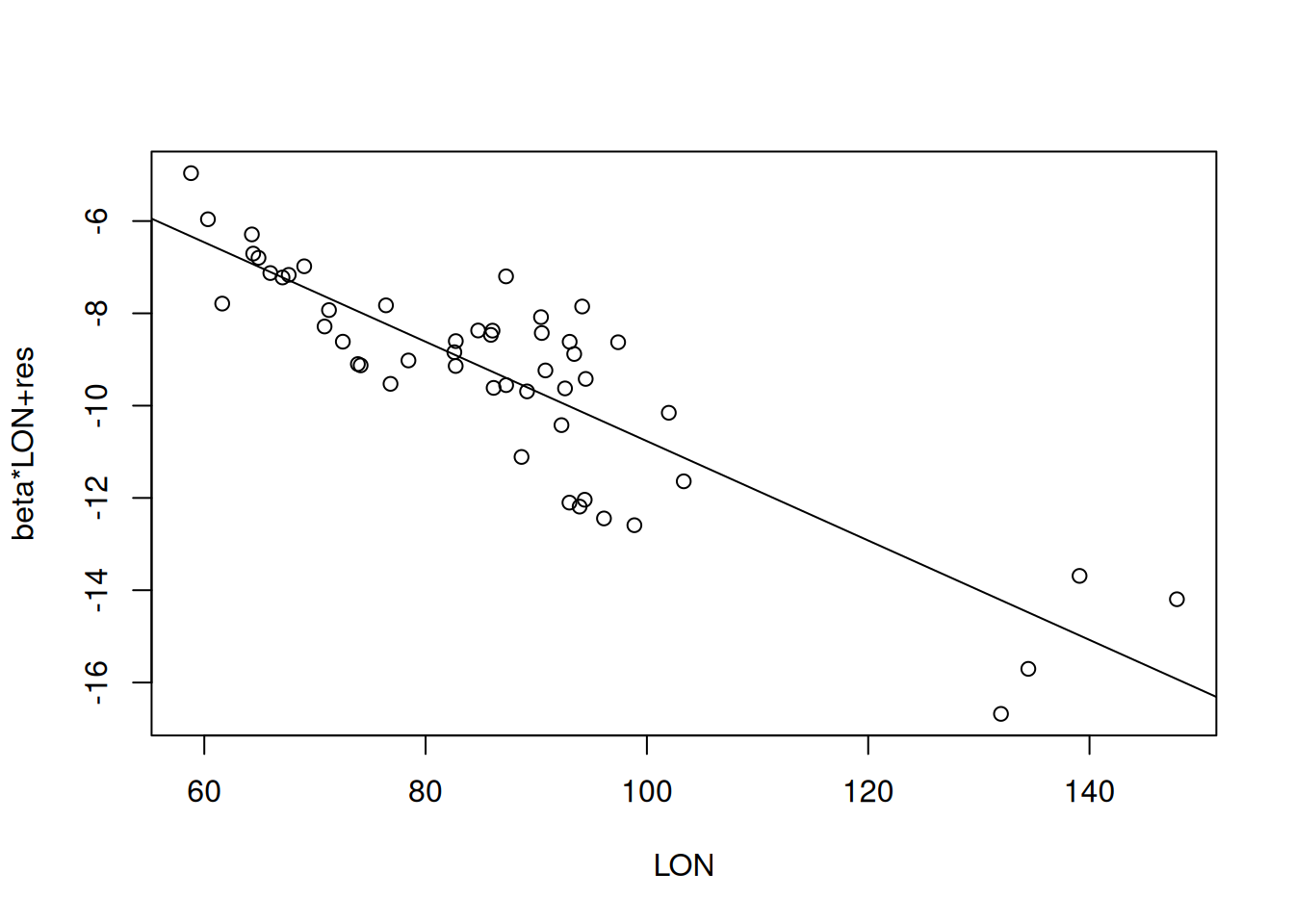
Figure 13.10: Partial Residual Plot für geographische Länger. Der Plot beruht auf den russischen Temperaturstationen, die Höheninformationen haben.
13.4.2.2.1 Vergleich zwischen Ländern
Ein Vergleich der Partial Residual Plots zeigt für Kanada deutliche Abweichungen gegenüber den andern ausgewählten Ländern im Hinblick auf den Zusammenhang zwischen den Partial Residuals und Geländehöhe (Abbildung 13.11). Schaut man sich die Partial Residuals Plots für den Prädiktor Längengrad an (Abbildung 13.12), erkennt man für Kanada einen quadratischen Effekt. Möglicherweise spielen maritime Prozesse eine Rolle bei den hier beobachteten Abweichungen.
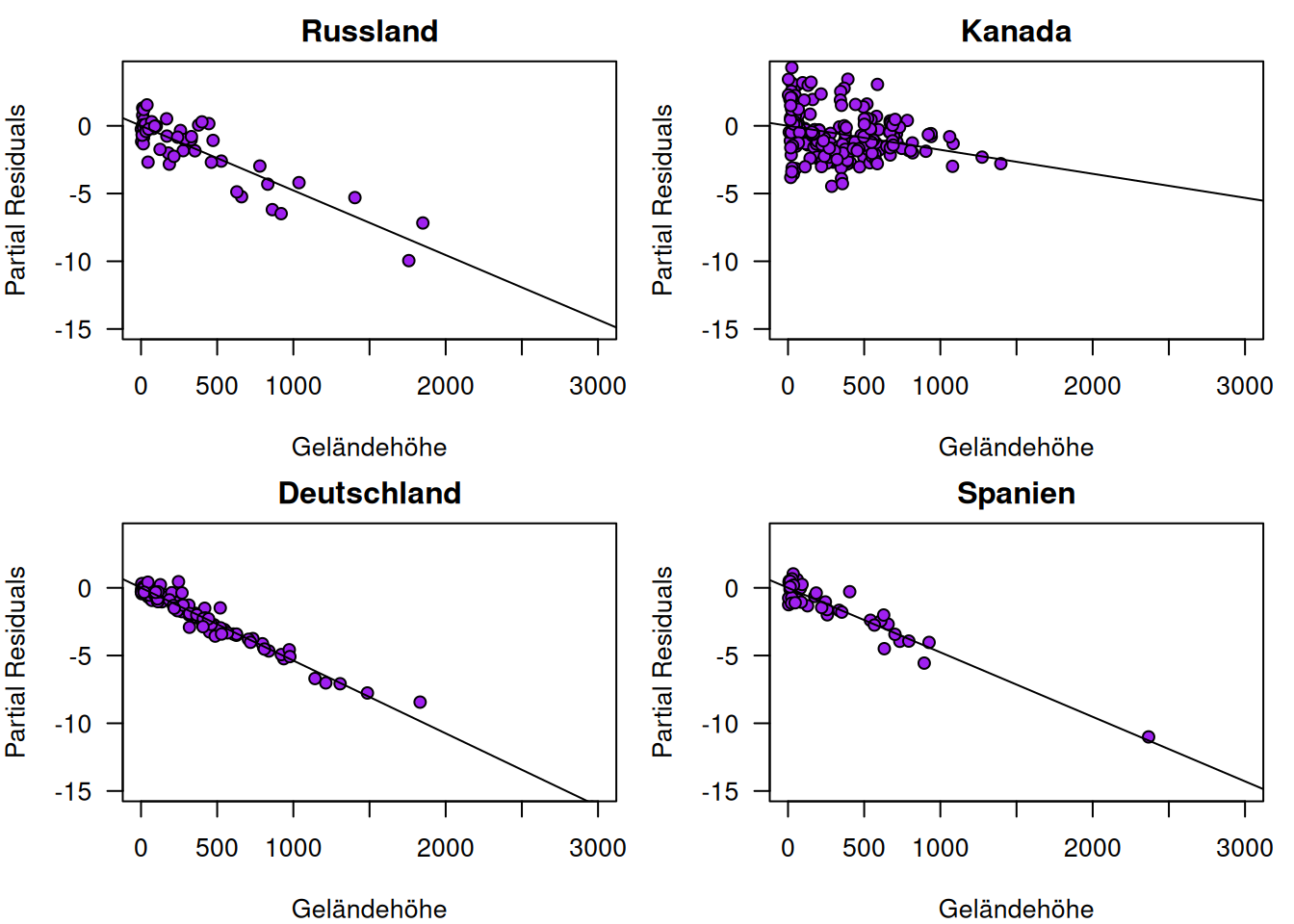
Figure 13.11: Partial Residual Plots für den Effekt von Geländehöhe auf Jahresmitteltemperatur anhand vier ausgewählter Länder.
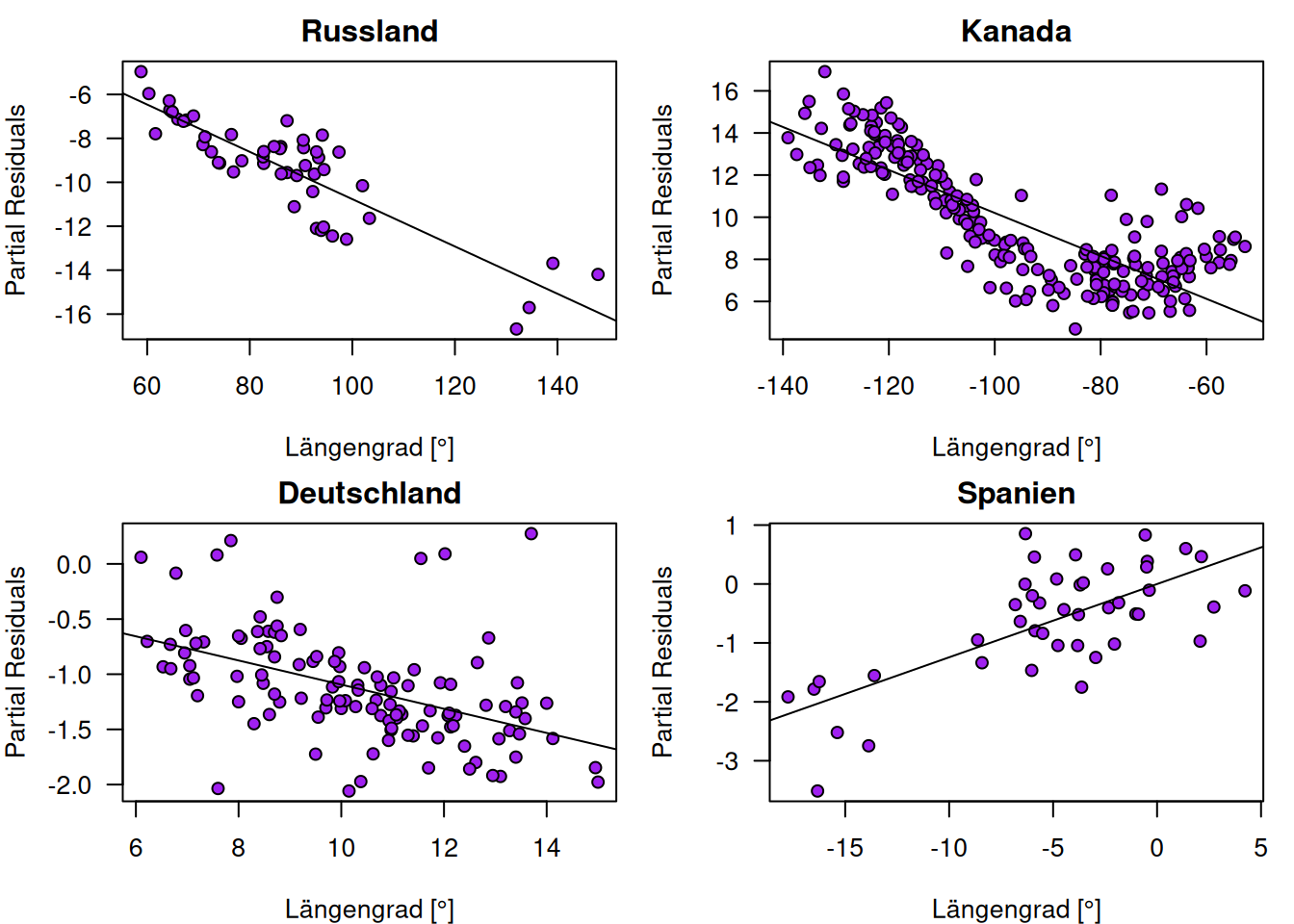
Figure 13.12: Partial Residual Plots für den Effekt des Längengrades auf Jahresmitteltemperatur anhand vier ausgewählter Länder.
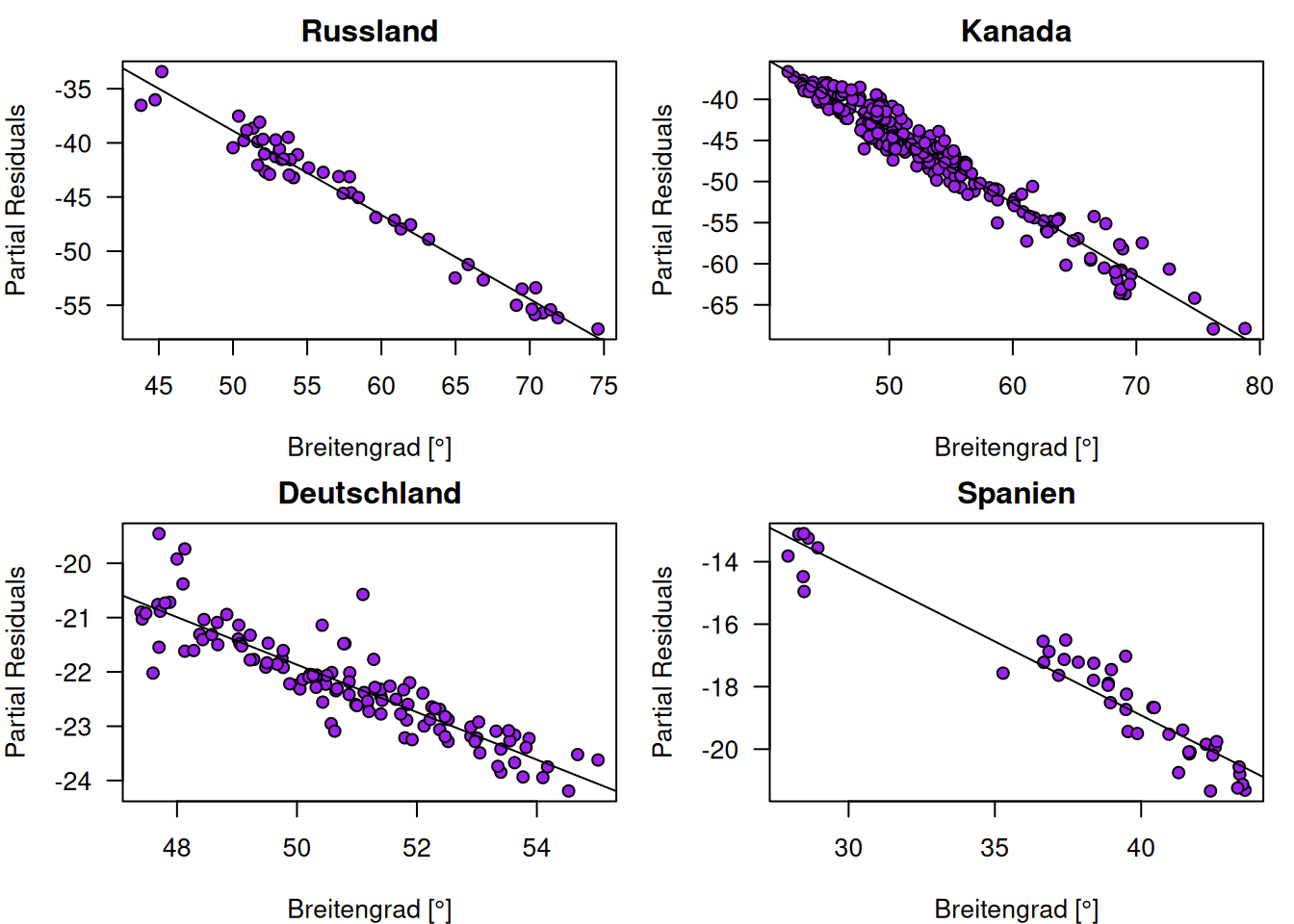
Figure 13.13: Partial Residual Plots für den Effekt des Breitengrades auf Jahresmitteltemperatur anhand vier ausgewählter Länder.
Der Partial Residual Plot für Kanada für den Prädiktor Längengrad an (Abbildung 13.12) zeigt die Abweichung vor allem für den Bereich zwischen 100 und 80° westlicher Breite. Eine mögliche Erklärung könnte der Hudson Bay sein, dessen große Wasserfläche einen ausgleichenden Effekt auf die Lufttemperatur haben dürfte (vergleiche Abbildung ??).
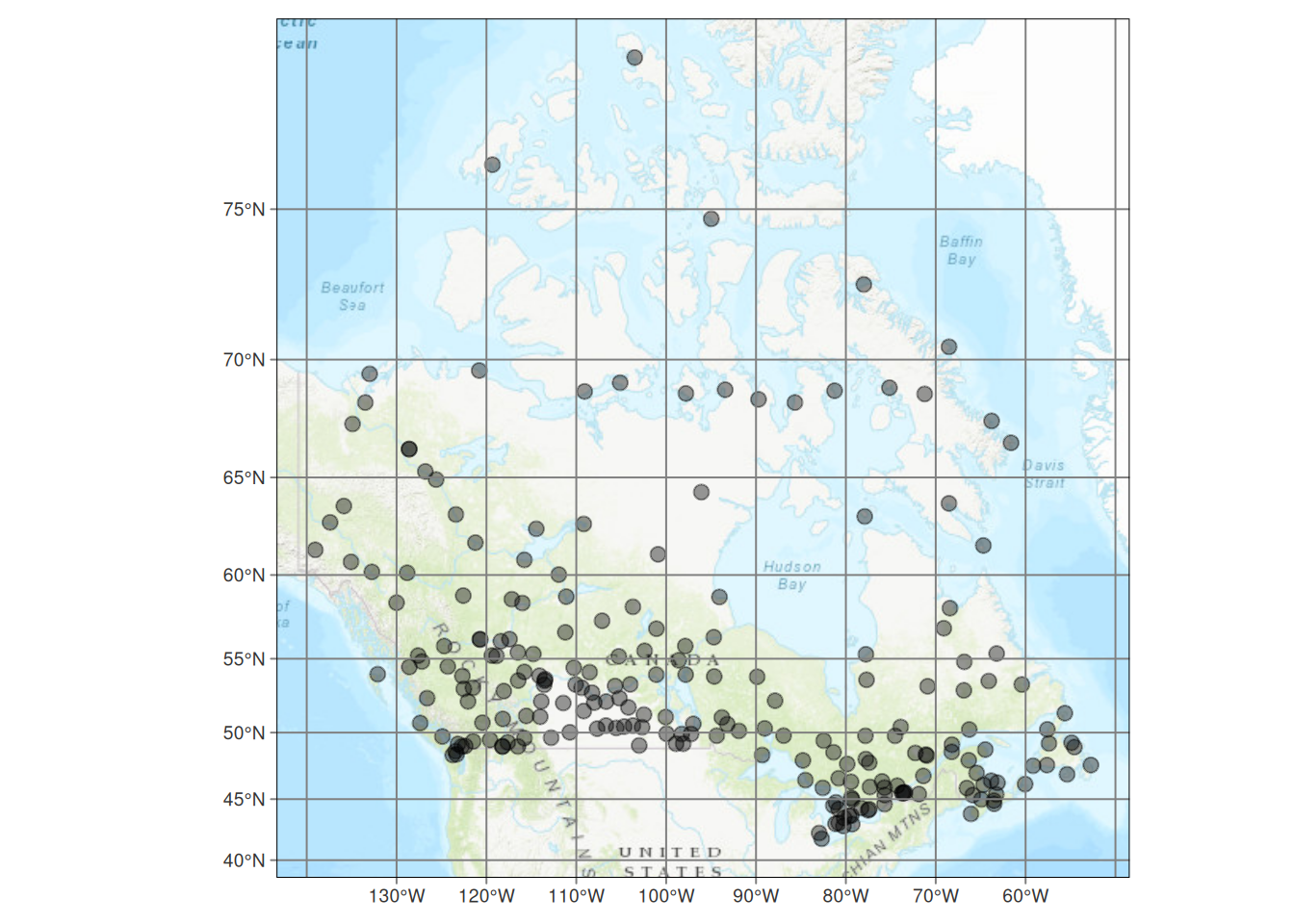
Figure 13.14: Lage der kanadischen Klimastationen.
Ein Vergleich zwischen Added Variable und Partial Residuals Plot zeigt für Kanada bgzl. dem Effekt von Längengrad Unterschiede: der nichtlineare Effekt ist beim Partial Residuals Plot deutlich besser zu erkennen.
g.ca <- lm(YEAR~ELEV + LAT + LON, data=temp.ca)
newDat.ca <- data.frame(ELEV=seq(min(temp.ca$ELEV),
max(temp.ca$ELEV),
length.out=100),
LAT=mean(temp.ca$LAT),
LON=mean(temp.ca$LON))
pred.ca.elev <- predict(g.ca, newdata = newDat.ca)
d.ca <- residuals(lm(YEAR ~ LAT + LON, data=temp.ca))
## Added Variable Geländehöhe
# Residuen der Regression von Geländehöhe gegen die anderen Prädiktoren im Modell
m.ca <- residuals(lm(ELEV ~ LAT + LON, data=temp.ca))
# Added Variable von Geländehöhe:
g.addedValueElev.ca <- lm(d.ca~m.ca)
par(mfrow=c(1,2))
plot(partResid4Elev.ca ~ temp.ca$ELEV, xlab="Geländehöhe",
ylab="Partial Residuals",
main="Partial Residuals Kanada",
las=1, pch=21, bg="purple")
abline(lm(partResid4Elev.ca ~ temp.ca$ELEV))
plot(d.ca~m.ca, xlab="Residuen für Geländehöhe",
ylab="Residuen von Temperatur",
main="added variable plot - Kanada",
pch=21, bg="orange", las=1)
abline(g.addedValueElev.ca)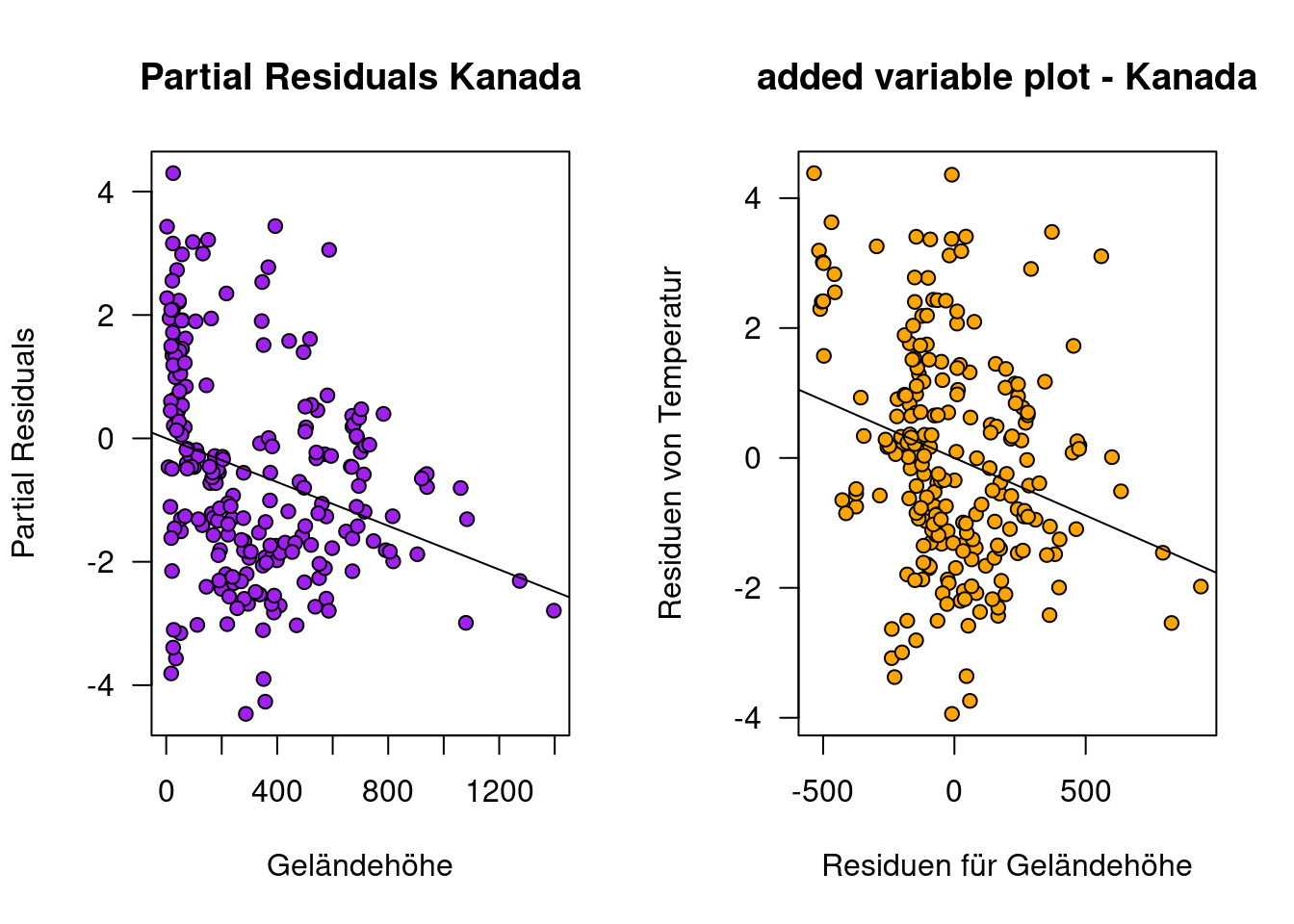
newDat.ca.lon <- data.frame(LON=seq(min(temp.ca$LON),
max(temp.ca$LON),
length.out=100),
LAT=mean(temp.ca$LAT),
ELEV=mean(temp.ca$ELEV))
pred.ca.lon <- predict(g.ca, newdata = newDat.ca.lon)
d.ca.lon <- residuals(lm(YEAR ~ LAT + ELEV, data=temp.ca))
## Added Variable Längengrad
# Residuen der Regression von Längengrad gegen die anderen Prädiktoren im Modell
m.ca.lon <- residuals(lm(LON ~ LAT + ELEV, data=temp.ca))
# Added Variable von Geländehöhe:
g.addedValueLon.ca <- lm(d.ca.lon~m.ca.lon)
par(mfrow=c(1,2))
plot(partResid4Lon.ca ~ temp.ca$LON, xlab="Längengrad",
ylab="Partial Residuals",
main="Partial Residual Plot - Kanada",
las=1, pch=21, bg="purple")
abline(lm(partResid4Lon.ca ~ temp.ca$LON))
plot(d.ca.lon~m.ca.lon, xlab="Residuen für Längengrad",
ylab="Residuen von Temperatur",
main="added variable plot - Kanada",
pch=21, bg="orange", las=1)
abline(g.addedValueLon.ca)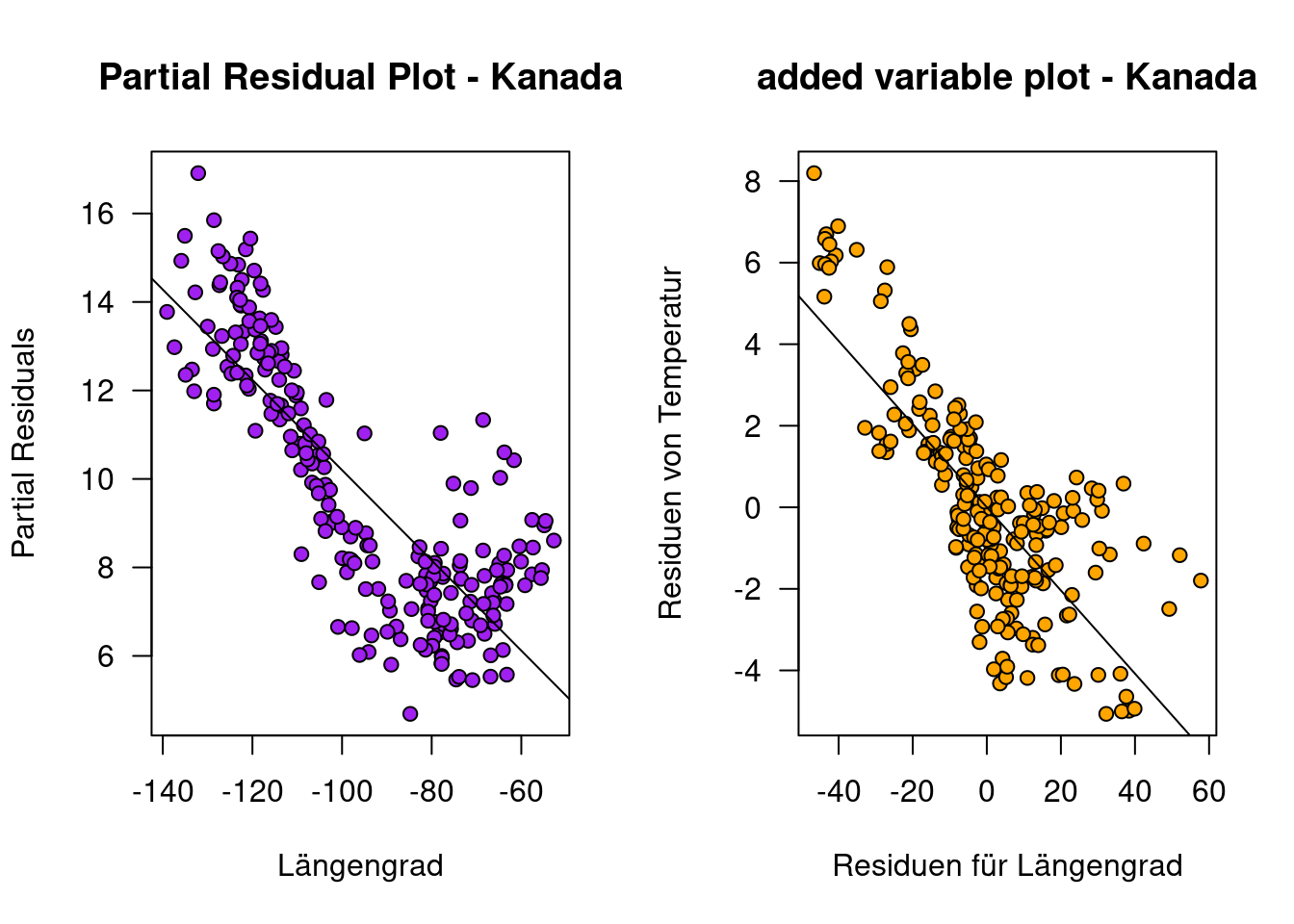
Dies erfolgt bei
anova.lmlistmittest = "LRT".lmtest::lmrtestberuht dagegen auf der Differenz der log-Likelihoods. Daneben unterscheiden sich die Tests darin, ob ML oder REML Schätzer verwendet werden sowie weiteren Details, s. https://stats.stackexchange.com/questions/155474/why-does-lrtest-not-match-anovatest-lrt.↩︎Genauer gesagt der limitierende Stichprobenumfang. Bei kontinuierlichem Response ist dies der Stichprobenumfang, bei binärem (Bernoulli: 0 oder 1) Response ist \(n= min(\text{Anzahl 0}, \text{Anzahl 1})\).↩︎
Wenn die Stichprobengröße größer als 8 ist, ist log(n) > 2.↩︎
Um die
drop1Funktionalität nutzen zu können, muss zusätzlicher Code genutzt werden, der Teil der von von Christoph Scherber geschriebenen Funktion stepAICc ist: http://wwwuser.gwdg.de/~cscherb1/statistics.html↩︎Irrtumswahrscheinlichkeit beim t-Test ~ 0.12 bis 0.15.↩︎
Damit entspricht \(p\) nicht \(k\) beim AIC, bei dem auch \(\sigma^2\) mitgezählt wird.↩︎
Mittels
overlapkann man die Stärke des Überlappens einstellen oder ganz ausschaltenoverlap = 0.↩︎