Kapitel 4 How to do it in R
In diesem Kapitel möchte ich relevante und immer wieder auftauchende Arbeitsvorgänge (wie lädt man eine CSV Datei, wie filtert man Daten,…) kurz vorstellen. Gedacht ist dies als eine Art Kochbuch: die Befehle werden kurz vorgestellt, so dass man hoffentlich schnell das gewünschte findet. Sie werden hier i.d.R. keine tiefergehenden Erklärungen finden, dafür dienen die nachfolgenden Kapitel.
4.1 Daten laden
4.1.1 Textdateien
Textdateien mit tabellarischen Daten lädt man mit read.table.
Wichtiger Parameter:
filedefiniert den Dateinamen inklusive (relativem oder absolutem) Pfad. Der Dateiname muss in (doppelten oder einfachen) Anführungszeichen stehen. Wichtig: als Dateipfadtrennzeichen müssen Sie in R immer den Slash “/” verwenden, nicht den Backslash “", auch wenn der unter Windows gebräuchlich ist.- enthält die erste Zeile die Spaltennamen? Falls ja, verwenden Sie den Parameter
header=TRUE(Groß-/Kleinschreibung ist wichtig), ansonstenheader=FALSE. - welches Trennzeichen wird verwendet um die einzelnen Spalten voneinander abzugrenzen? Wenn es sich um Whitespace (Leerzeichen und/oder Tabulatoren) handelt, müssen Sie nichts angeben, sonst müssen Sie dass Trennzeichen mittels
sep=""angeben. Übliche Trennzeichen sindsep=";",sep=",",sep="/",… - wird der Punkt oder das Komma als Dezimaltrennzeichen verwendet? Suchen Sie nach Nummerischen Werte und schauen Sie, mit was Nachkommastellen beschrieben sind. Falls das Komma verwendet wird, kann es sein, dass die Zahlenwerte jeweils in Anführungszeichen gepackt sind um sie als String zu kennzeichen. Falls das Trennzeichen das Komma ist, müssen sie dies der Funktion mittels
dec=","mitteilen. Falls der Punkt verwendet wird, müssen Sie nichts weiter machen.
4.2 Data wrangling
4.2.1 Daten erzeugen
Mitunter möchte man Daten in R anlegen. I.d.R: verwendet man dazu einer der folgenden Datenstrukturen: vector, list, matrix oder data.frame (bzw. im tidyverse tibble).
4.2.1.1 Vektoren anlegen
4.2.1.1.1 Sequenz von Werten
Integerwerte zwischen Start und Endwert mittels des : Operators
## [1] 5 6 7 8 9 10Zahlen zwischen Start- und Endwert mit fester Schrittweite:
## [1] -2.1 -1.6 -1.1 -0.6 -0.1 0.4 0.9 1.4 1.9 2.4 2.9 3.4 3.9 4.4 4.9
## [16] 5.4 5.9 6.4 6.9 7.4 7.9 8.4 8.9 9.4 9.9 10.4 10.9 11.4 11.9 12.4
## [31] 12.9 13.4 13.9 14.4 14.9Zahlen zwischen Start- und Endwert mit definierter Anzahl von Zwischenschritten:
## [1] 100.0000 116.6667 133.3333 150.0000 166.6667 183.3333 200.0000 216.6667
## [9] 233.3333 250.0000Wert wiederholen
## [1] "A" "A" "A" "A" "A"4.2.1.2 Leeren Vektor bestimmten Datentyps anlegen:
## [1] 0 0 0 0 0 0 0 0 0 0## [1] "" "" "" "" "" "" "" "" "" ""4.2.1.6 data.frame anlegen
data.frame erzeugt einen data.frame. Felder kann man mittel feldname=werte anlegen, die längste Anzahl von Werten gibt die Anzahl Zeilen des data.frames vor. Vektorlängen müssen dabei übereinstimmen. Einzelne Werte werden ggf. wiederholt.
## feld1 feld2 feld3 name4
## 1 NA 1 2 1
## 2 NA 2 2 3
## 3 NA 3 2 5
## 4 NA 4 2 7
## 5 NA 5 2 9Als Ergebnis erhält man dann einen data.frame mit den angegebenen Feldnamen und Elemente.
Man kann natürlich einen data.frame aus in Variablen gespeicherten Vektoren anlegen.
vec1 <- 1:3
vec2 <- c("Saudi-Arabien", "VAE", "Ägypten")
myDat <- data.frame(vec1, vec2)
print(myDat)## vec1 vec2
## 1 1 Saudi-Arabien
## 2 2 VAE
## 3 3 Ägypten## ID Land
## 1 1 Saudi-Arabien
## 2 2 VAE
## 3 3 Ägypten4.2.1.7 Leeres Objekt anlegen
Mnachmal benötigt man nur ein benanntes Objekt, das man dann im folgenden verändert (z.B. bei Simulationsexperimenten). Dies geschieht, indem man der Variablen einfach NULL zuweist.
#leeres Objekt anlegen
res <- NULL
for(i in 1:500)
{
theSample <- rlnorm(17)
res[i] <- median(theSample) # Objekt wird implizit als Vektor angelegt, wenn man den Klammer-Operator verwendet
}
hist(res, main="Median aus normalverteilter Stichprobe der Größe 17",
xlab="Stichprobenmedian",
ylab="Anzahl",
las=1)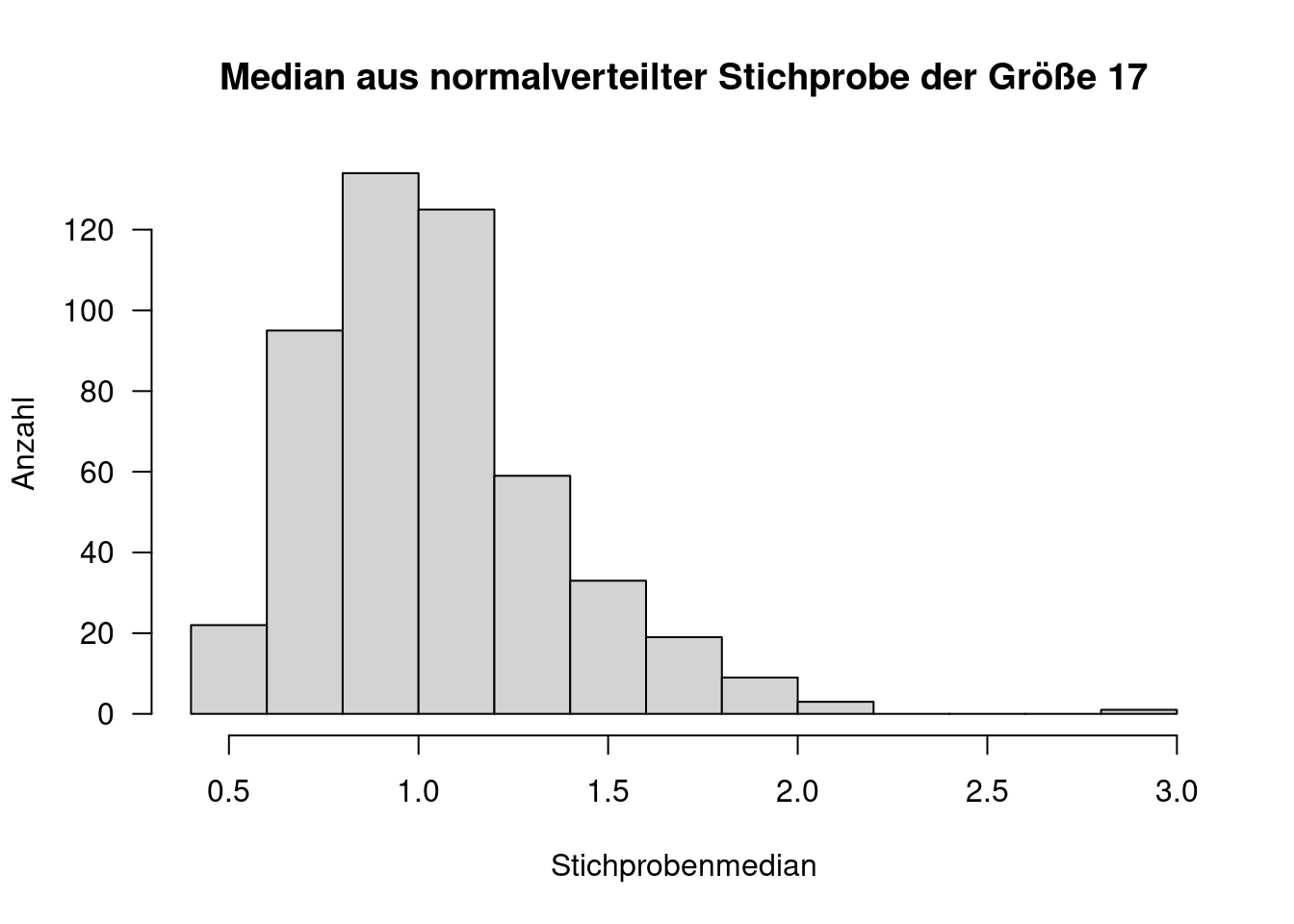
4.2.2 Filtern und Selektieren
4.2.2.1 Subset
subset kann eine Teilmenge eines data.frames anhand eines logischen Ausdrucks filtern, der sich auf die Felder des data.frames bezieht
# Stationen in Dtld.
temp.de <- subset(temp, CNTRY_NAME == "Germany")
# Station mit Jahresmitteltemperatur > 25°C
temp.hot <- subset(temp, YEAR > 25)
# Stationen in Dtld. oder Italien
temp.de <- subset(temp, CNTRY_NAME == "Germany" | CNTRY_NAME == "Italy")
# oder
temp.deit <- subset(temp, CNTRY_NAME %in% c("Germany", "Italy"))Der %in%-Operator erlaubt es dabei, einen Vektor von zulässigen Werten (hier Ländernamen) anzugeben. Abfragen lassen sich auch mit logischen Operatoren wir ODER (|) UND (&) oder NICHT (!) verknüpfen. Ggf- ist es dabei notwendig die einzelnen Ausdrücke zu klammern um den Vorrang der einzlenen Operatore korrekt wiederzugeben.12
4.2.2.2 Der $-Operator
Der $-Operator erlaubt es auf eine einzelne Spalte in einem data.frame zuzugreifen. Zurückgegeben wird ein Vektor
## [1] 8.927 5.600 7.690 6.320 6.530 6.385 7.680 7.790 7.660 7.978
## [11] 7.320 6.792 7.830 7.620 8.106 7.942 8.220 7.760 6.980 1.167
## [21] 7.383 8.260 8.045 8.061 8.400 9.745 7.833 7.406 6.142 5.300
## [31] 3.470 7.374 7.450 6.000 7.350 6.890 7.320 1.215 6.610 6.259
## [41] 8.030 7.670 7.384 7.650 7.343 7.800 7.500 7.740 8.440 8.250
## [51] 8.192 8.440 8.007 8.100 8.417 9.420 8.720 8.400 8.628 3.980
## [61] 8.050 8.257 8.110 4.840 8.850 5.930 8.830 9.800 6.320 8.770
## [71] 8.010 3.970 9.319 7.044 4.920 9.561 9.365 9.761 8.790 8.370
## [81] 7.910 8.240 6.040 7.440 8.220 7.680 8.763 10.040 9.900 8.489
## [91] 9.613 8.850 7.930 8.149 8.650 1.740 10.380 5.760 5.340 6.400
## [101] 7.730 7.700 8.920 7.535 7.990 8.360 1.520 8.500 8.257 6.580
## [111] 6.050 -7.344 5.354 7.090 0.380 7.936 4.870 12.440 0.430 -0.422
## [121] 7.440 11.652 -8.570 11.609 9.680 11.235 5.460 11.580 12.626 11.220
## [131] 12.050 12.109 12.570 12.248 12.300 13.890 6.060 -0.520 13.313 12.330
## [141] 12.434 13.330 11.430 11.530 11.915 12.668 12.665 2.110 12.430 13.360
## [151] 13.704 10.410 13.220 13.760 13.397 9.675 14.115 13.462 14.294 13.405
## [161] 14.280 13.990 16.010 15.087 14.716 14.650 9.100 14.861 15.660 13.464
## [171] 13.004 13.7364.2.2.3 Der []-Operator - Zeilen und Spalten selektieren
Der []-Operator erlaubt es auf eine Bereiche, die über Zeilen und Spalten definiert werden in einem data.frame zuzugreifen.
dataframe[zeilen, spalten]
## [1] 11.42Will man alle Spalten haben, lässt man das zweite Argument leer
## TEMP_STA_1 FID_1 AREA PERIMETER TEMP_STATI COUNTRY_ID NAME LAT LON
## 529 916200 5275 0 0 5276 618 SCHWERIN 53.63 11.42
## ELEV FIRST LAST MISSING DISC FID_2 ISO_3DIGIT ISO_NUM CNTRY_NAME
## 529 59 1981 1990 1.7 0 148 DEU 276 Germany
## LONG_NAME SQKM SQMI centerX centerY JAN FEB MAR
## 529 Federal Republic of Germany 355246 137160.5 10.39365 51.10656 0.14 0.5 3.97
## APR MAI JUN JUL AUG SEP OCT NOV DEC YEAR
## 529 7.69 13.03 15.11 17.36 17.18 13.77 10.06 4.722 1.589 8.76008Will man alle Zeilen haben, lässt man das erste Argument leer
## [1] 7.60 13.43 11.42 12.08 12.62 13.40 10.68 11.73 11.93 12.82 13.20 13.10
## [13] 14.00 11.40 11.58 13.07 13.52 14.12 10.32 10.62 10.77 11.30 12.23 12.40
## [25] 12.65 13.70 13.58 14.95 10.38 10.15 10.77 10.97 11.30 11.18 12.13 12.13
## [37] 12.87 12.95 8.42 9.55 8.58 8.70 10.00 10.70 7.20 8.80 9.83 11.13
## [49] 7.32 8.05 8.30 8.75 9.70 10.45 13.40 6.78 6.22 6.53 6.97 8.48
## [61] 8.83 9.45 9.95 10.60 6.10 6.95 7.17 7.58 7.97 8.70 9.72 9.95
## [73] 6.67 7.05 8.45 8.00 8.60 8.70 9.97 10.08 10.95 10.92 11.88 12.18
## [85] 6.68 7.05 7.12 8.37 8.55 9.22 9.20 9.52 10.97 11.08 12.10 13.28
## [97] 7.85 8.42 8.75 9.87 9.97 10.93 11.55 11.70 12.50 13.47 8.00 9.18
## [109] 9.50 10.33 10.28 10.98 11.02 11.07 12.02 15.00 10.53 11.33 11.78 11.03
## [121] 13.58 13.03 7.70 7.65 7.73 8.73 9.07 9.70 9.28 9.73 10.28 10.87
## [133] 12.10 12.33 13.48 8.85 9.93 10.70 11.30 12.62 10.38 11.20 12.73 12.50
## [145] 13.37 13.50 11.07 12.98 14.20 12.60 12.23 14.65 15.72 16.78 14.30 15.80
## [157] 17.95 16.88 17.30 17.07 18.35 16.25 13.10 15.55 12.50 14.22 14.30 15.05
## [169] 15.13 8.28 8.60 9.05Man kann auch auf Elemente eines Vektors zugreifen:
## [1] 5.6Mit dem :Operator kann man einen Bereich definieren
## [1] 5.600 7.690 6.320 6.530 6.385 7.680 7.790 7.660 7.978 7.320 6.792Das funktioniert auch bei data.frames:
## NAME LAT LON
## 350 BASEL/BINNINGEN 47.60 7.60
## 527 ARKONA 54.68 13.43
## 529 SCHWERIN 53.63 11.42Man kann auch einen Vektor mit Spaltennamen (in Anführungszeichen) angeben, um auf einzelne Spalten zuzugreifen.
## NAME YEAR
## 350 BASEL/BINNINGEN 8.92892
## 527 ARKONA 8.27375
## 529 SCHWERIN 8.760084.2.2.4 Daten filtern mit which() und []
Man kann sich mit dem which Befehl die Indizes der Zeilen ausgeben lassen, die eine Bedingung erfüllen. Den Vektor, der zurück gegeben wird kann man dann zusammen mit dem []Operator verwenden, um Zeilen eines data.frames zu selektieren.
Wir können z.B. alle Temperaturstationen suchen, die in einem bestimmten Bereich hinsichtlich Längengrad und Breitengrad liegen. Der & Operator steht für eine logisches AND, der | Operator für ein logisches OR. Ggf. muss man die einzelnen Ausdrücke Klammern.
Die Position der Klimastationen im Datensatz (der Index), die zwischen 53 und 55° geographischer Breite und zwischen dem 20-ten und dem 25-ten Längengrad liegen:
## [1] 703 704 708 709 1192 1197 1201Die Feldwerte für 4 Attribute an den Positionen im data.frame, die eben ausgewählt worden sind.
## NAME YEAR LAT LON
## 703 KETRZYN 7.35917 54.07 21.37
## 704 SUWALKI 6.13833 54.13 22.95
## 708 MLAWA 7.45433 53.10 20.35
## 709 BIALYSTOK 6.80008 53.10 23.17
## 1192 KAUNAS 6.38892 54.88 23.88
## 1197 KALININGRAD 7.05017 54.70 20.62
## 1201 GRODNO 6.88267 53.68 23.834.2.2.5 Spalten selektieren mit dplyr::select
Das package dplyr bietet viele Optionen um Daten zu manipulieren. Mit select kann man Spalten selektieren:
## [1] "YEAR" "LAT" "LON"dplyr::select kennt eine ganze Reihe mächtiger Konstrukte, die das Selektieren vereinfachen, z.B. kann man nebeneinander stehende Spalten über den :Operator adressieren. Möchte man den Stationsnamen, Längen- und Breitengrad sowie die Monats- und Jahresmittelwerte selektieren, kann man das ausnützen:
## [1] "TEMP_STA_1" "FID_1" "AREA" "PERIMETER" "TEMP_STATI"
## [6] "COUNTRY_ID" "NAME" "LAT" "LON" "ELEV"
## [11] "FIRST" "LAST" "MISSING" "DISC" "FID_2"
## [16] "ISO_3DIGIT" "ISO_NUM" "CNTRY_NAME" "LONG_NAME" "SQKM"
## [21] "SQMI" "centerX" "centerY" "JAN" "FEB"
## [26] "MAR" "APR" "MAI" "JUN" "JUL"
## [31] "AUG" "SEP" "OCT" "NOV" "DEC"
## [36] "YEAR"## [1] "NAME" "LAT" "LON" "JAN" "FEB" "MAR" "APR" "MAI" "JUN" "JUL"
## [11] "AUG" "SEP" "OCT" "NOV" "DEC" "YEAR"4.2.3 Runden von Ergebnissen
Wichtig: wir rechnen nicht mit gerundeten Werten sondern immer mit den original berechneten Werten. R stellt Zahlen mittels print & co mit einer einstellbaren Anzahl von Nachkommastellen dar, rechnet aber i.d.R. 13 mit höherer Genauigkeit. D.h. verwenden SIe das Ergebnis einer Berechnung - das Sie z.B. in einer Variablen gespeichert haben - und nicht copy & paste der Ausgabe des Ergebnisses.
Generell runden wir nur, um die Ergebnisse zu präsentieren. Einerseits aufgrund der besseren Lesbarkeit, andererseits auch um klar zu machen, welche Genauigkeit wir für vertrauenswürdig halten. Wenn man z.B. die Differenz zwischen 2 Mittelwerten hinsichtlich der Unterschiede der Zahlunsbereitschaft zweier Gruppen mit \(10.34197348933333311114\)€ angibt, zeigt man klar, dass man nicht verstanden hat, was diese Zahl bedeutet. Nur weil man auf 54 Stellen hinter dem Dezimalseparator rechnen kann heißt das nicht, dass man diese Genauigkeit in den Ergebnissen wirklich hat. Sind die Messgeräte genau genug, um diese Genauigkeit zu ermitteln,… Das übliche Vorgehen ist, dass man implizit angibt, wie “gut” eine Zahlenwert ist, indem man nur die Stellen angibt, die mit Gewissheit bekannt sind plus eine Stelle mehr.
Es macht oftmals Sinn die Zahlen auf signifikante Stellen zu runten (s. unten) und nicht \(0.0000271\) als \(0\) darzustellen. Insbesondere bei p-Werten und Regressionskoeffizienten sollte auf signifikante Stellen gerundet werden.
Entsprechend rundet man die Werte für die Ergebnispräsentation. Dabei sind verschiedene Fälle zu unterscheiden.
Hinweis: für die Übung sind die Fragen in Moodle zu beantworten, die automatisch angewandt werden. Verwenden Sie bitte immer die angegebene Methode zum Runden - auch wenn man sich teilweise auch für eine andere Methode entscheiden könnte. Die vorgeschlagene Methode ist als so erfolgt die Auswertung in Moodle und nicht notwendigerweise als so ist die einzig richtige Vorgehensweise zu interpretieren.
4.2.3.1 round
Das aus der Schule bekannte Runden erfolgt in R mittels round(x=zahl, digits=nachkommastellen). Dabei wird der Ansatz go to the even digit (auchr round to even genannt)t nach dem IEC 60559 bzw. IEEE 754 Standard angewandt: für Fälle bei denen die letzte signifikante Zahl gleich 5 ist wird zur nächsten geraden Zahl gerundet.14 digitsgibt an, wieviele Nachkommastellen man möchte. Es sind negative Werte erlaubt.
## [1] 2## [1] -2## [1] -2## [1] 2## [1] 2.5Negative Zahlenangaben für die Anzahl der Nachkommastellen führen zu Runden vor dem Dezimalseparator.
## [1] 20604.2.3.2 Runden zur nächsten kleineren größeren ganzen Zahl
Mittels ceiling(zahl) bzw. floor rundet man zur nächsten größeren bzw. kleineren ganzen Zahl.
## [1] 1## [1] 0## [1] 14.2.3.3 Runden auf signifikante Stellen
Manchmal hat man Ergenisse, die sich sehr stark in der Größenordnung unterscheiden. Dies tritt insbesondere bei p-Werten und Regressionskoeffizienten auf. Der Einsatz von round() ist hierbei i.d.R. irreführend und damit abzulehnen. Man verwendet stattdessen den Ansatz, dass man auf eine Anzahl signifikanter Stellen rundet- d.h. die letzten aussagekräftigen Ziffern. Dazu müssen mögliche Abweichungen dieser Zahl innerhalb der Grenzen der Abweichung der letzten Stelle liegen - führende Nullen sind nicht aussagekräftig. Es wird ggf. auch vor dem Dezimalseparator gerundet.
## [1] 0.031## [1] 0.03## [1] -3.45e-07 2.02e+03 1.00e+06 -1.26e+01Die Notation e+03und e-07 ist dabei als \(*10^3\) bzw. \(10^{-7}\) zu lesen.
## [1] -3.45e-07 2.02e+03 1.00e+06 -1.26e+01 1.00e+06## [1] -3e-07 2e+03 1e+06 -1e+01 1e+064.3 Arbeiten mit Faktoren
Für das Arbeiten mit kategorialen Variablen, müssen diese in Faktoren konvertiert werden. Im Hintergrund wird eine sogenatnne dummy Variable erzeugt, die mit 0 oder 1 anzeigt, ob die Beobachtung in die Kategorie fällt. Intern erhält jedes Level eines Faktors eine fortlaufende Integernummer sowie dazu ein Label, der in Plots etc. auftaucht. Die Reihenfolge, in der die Level angeordnet sind ist wichtig, da sie festlegt, was als Referenzlevel angesehen wird (ANOVA; ANCOVA) und für z.B. polyseriale Korrelation die Reihung (also die Ordnung bei ordinal skalierten Variablen15). Wenn man nichts angibt, verwendet R immer eine alphabetische Sortierung.
## [1] "character"## [1] "männlich" "weiblich"Erzeugen wir eine Faktorvariable und setzen wir weiblich als Referenzlevel.
Verwenden wir englische Label:
dat$geschlechtFeng <- factor(dat$geschlecht,
levels = c("weiblich", "männlich"),
labels = c("female", "male"))## [1] "factor"Die interne Kodierung sehen wir, wenn wir uns mittels str die Struktur des Vektors ausgeben lassen. Hier einmal für den Charakter-Vektor:
## chr [1:62] "männlich" "weiblich" "männlich" "männlich" "männlich" ...Und hier für den Faktorvektor:
## Factor w/ 2 levels "female","male": 2 1 2 2 2 2 2 2 1 1 ...Intern sind die Einträge mit 1 und 2 kodiert. Dazu gibt es eine lookup table mit den Labeln der Faktorlevel.
4.4 Plotten
4.4.1 ggplot2
ggplot2` folgt folgender Logik:
ggplot()spezifiziert über den Parameterdata =den data.frame (tabellarischen Datensatz), aus dem die zu plottenden Daten stammen. Mittelmapping = aes()werden die Felder des data.frames auf graphische Variablen gematcht.- dann werden mittels (überladenem)
+Operator weitere Manipulationen vorgenommen. - relevant ist vor allem die Definition wie die Variablen dargestellt werden sollen. Für einen Scatterplot ist das
geom_point(), Linien kann man übergeom_line()darstellen, Histogramme übergeom_histogramm()und vieles viels mehr. - dann können z.B. die Achsenbeschriftungen überarbeitet werden, ein Titel vergeben werden, die Skalierung der Achsen geändert werden oder Text in der Abbildung platziert werden.
4.4.1.1 Scatterplot
Plotten zweier Merkmale gegeneinander. Dient dazu, Assoziationen zwischen Variablen zu erkennen. Falls die Reihung der Werte relevant sein sollte, würde sich einen Linienplot ggf. besser eignen.
# Mapping graphische Variablen auf Feldnamen aus data
ggplot(data= temp.deit, mapping = aes(x=ELEV, y= YEAR)) +
# erstelle Scatterplot, halbtransparentes Punktsymbol
geom_point(alpha = 0.5) +
# ein Plot je Land
facet_wrap(~ CNTRY_NAME) +
# Spezifikation der Achsenbeschriftung
xlab("Geländehöhe [müNN]") +
ylab("Mittlere Jahrestemperatur [°C]")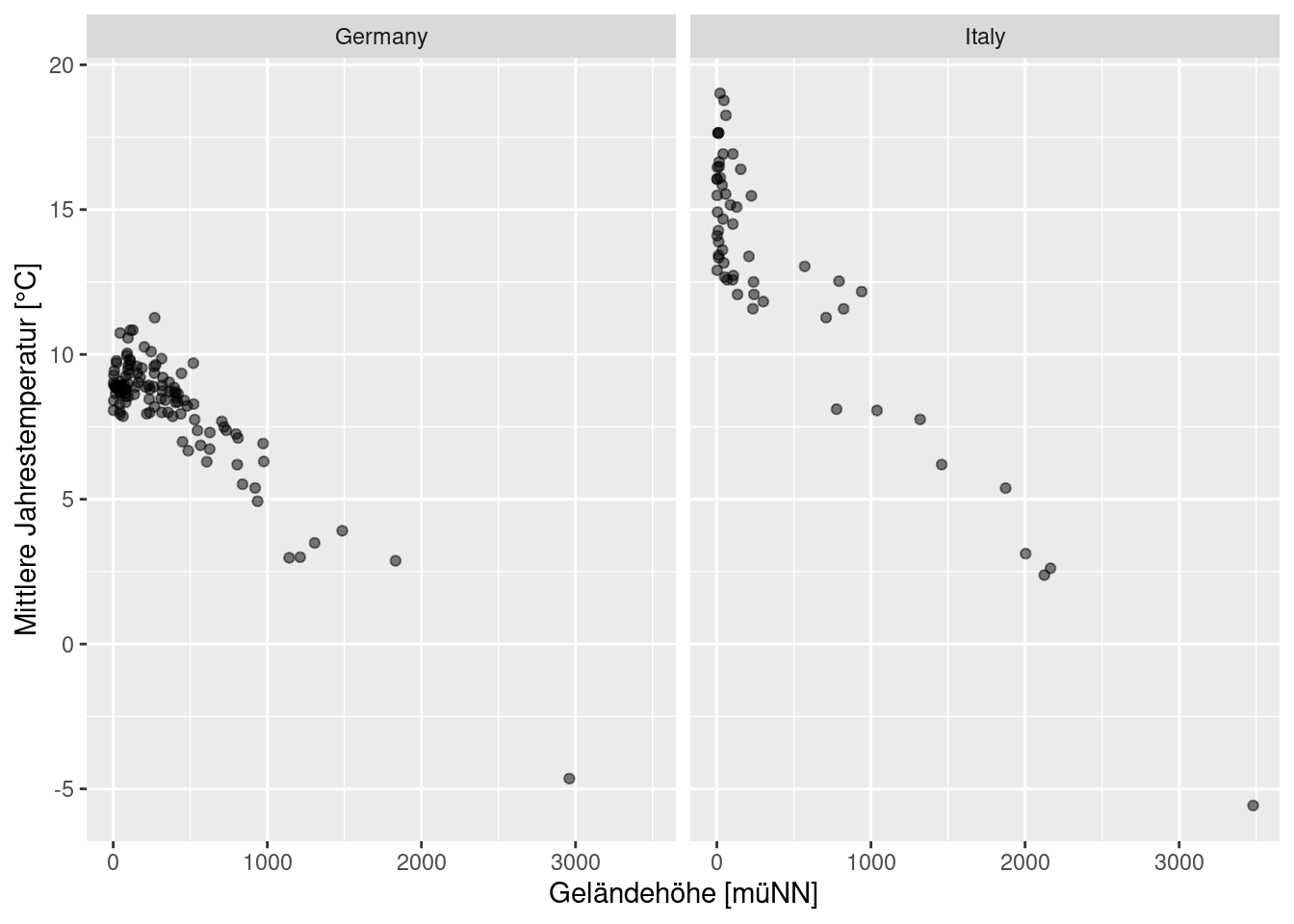
4.4.1.2 Histogram
Zeigt die Verteilung der Daten. Unterstützt die Interpretation statistischer Kennzahlen wie Mittelwert, Standardabweichung, Quantile,…
# Mapping graphische Variablen auf Feldnamen aus data
ggplot(data= temp.deit, mapping = aes(x= YEAR)) +
# erstelle histogramm, Intervallgröße 1°C
geom_histogram(binwidth = 1, fill = "navy") +
# ein Plot je Land
facet_wrap(~ CNTRY_NAME) +
# Spezifikation der Achsenbeschriftung
ylab("Anzahl Messstationen") +
xlab("Mittlere Jahrestemperatur [°C]")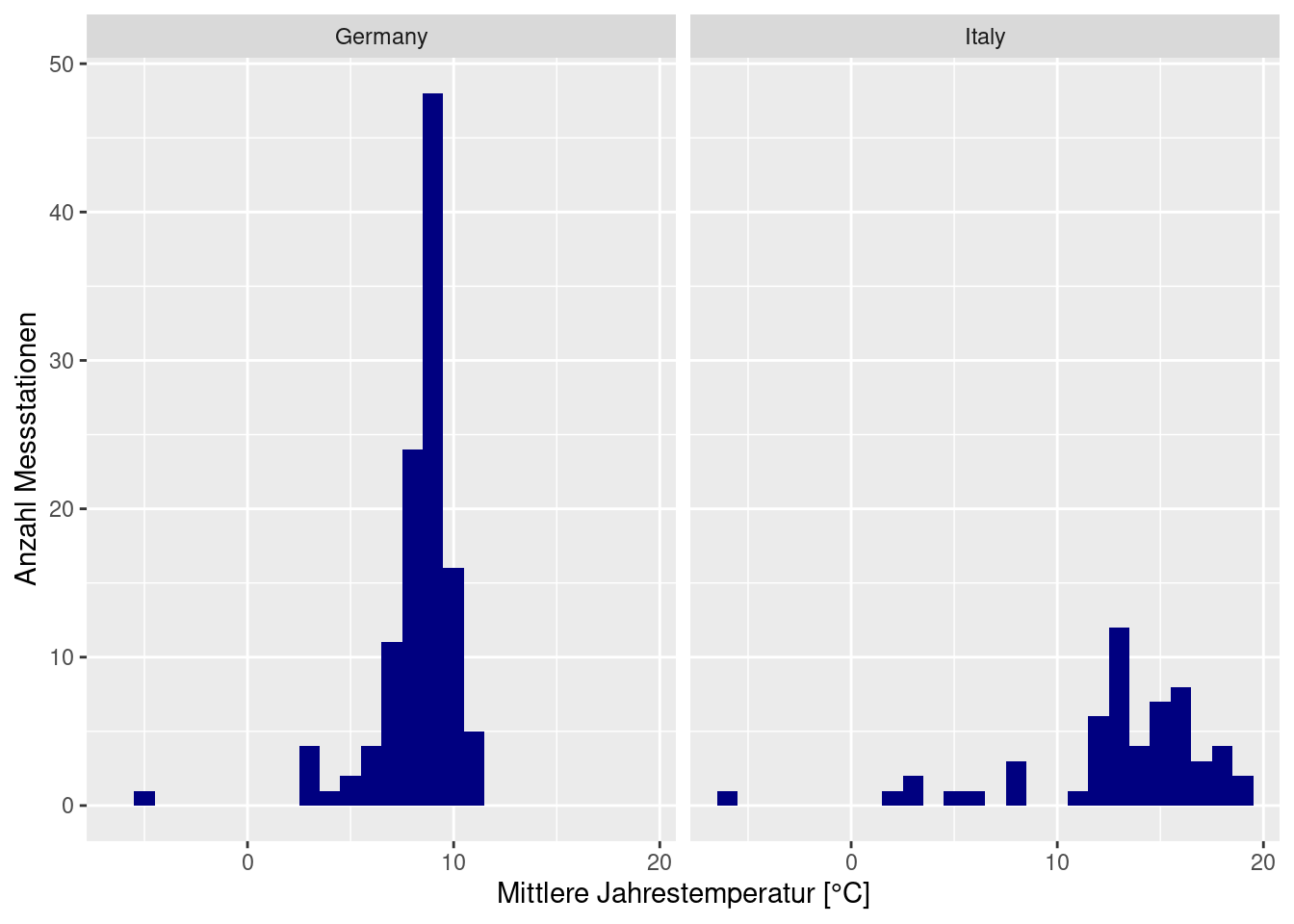
4.4.1.3 Boxplot
Dient der Darstellung der Verteilung von einer kontinuierlichen Variablen für verschiedene Level einer kategorialen Variable
ggplot(data= temp.deit, mapping = aes(x= CNTRY_NAME, y= YEAR)) +
geom_boxplot() +
ylab("Mittlere Jahrestemperatur [°C]") +
xlab("") +
annotate(geom = "label",
x= c(1.5, 2.5, 2.5, 1.2, 2.2),
y= c(13.5, 12.2, 16, -4.8, 7),
label= c("Q50", "Q25", "Q75", "Ausreißer", "Whisker"))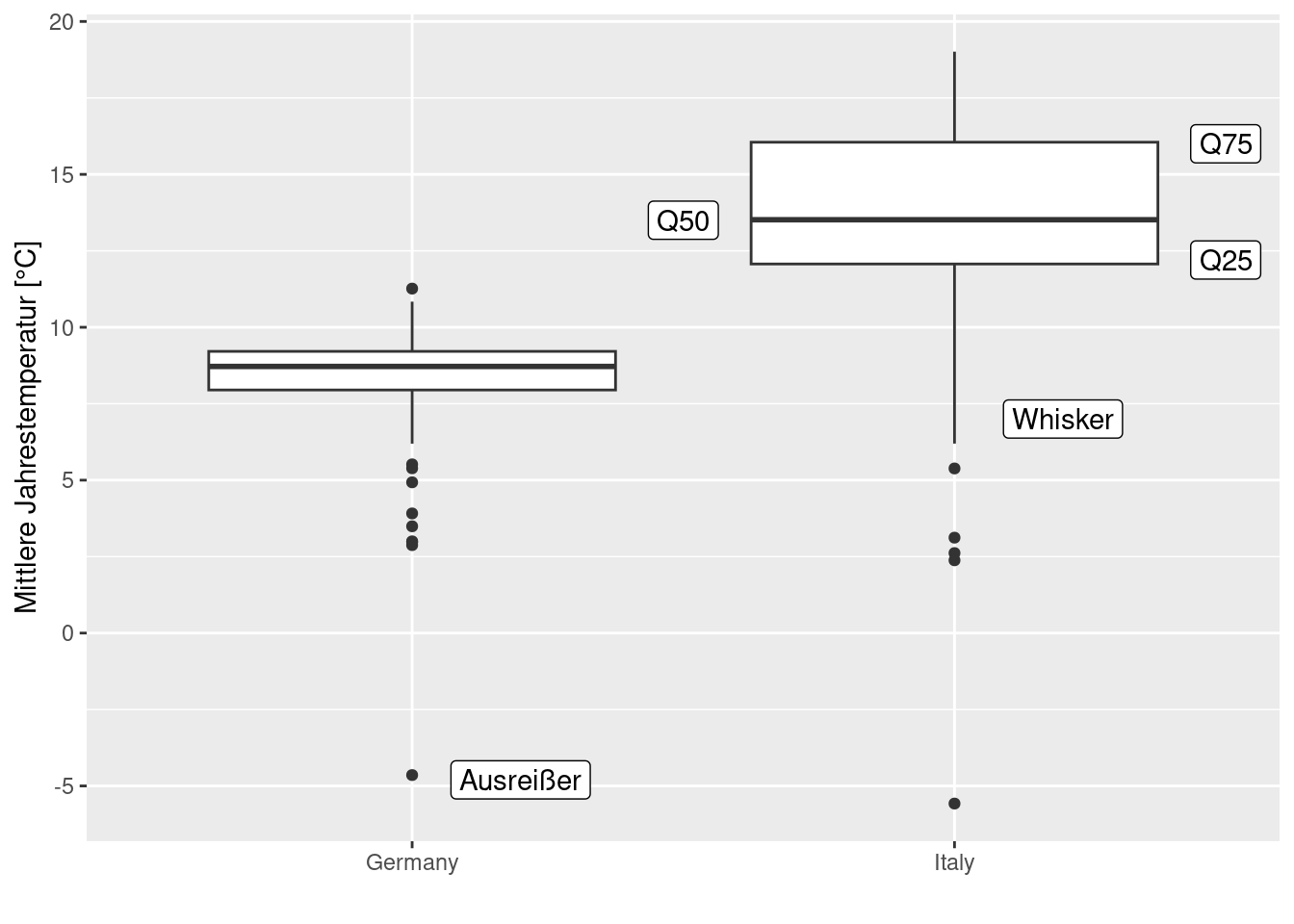
Der Boxplot zeigt das 25, 50 und 75-Quantil (Box, der Median ist der Strich in der Mitte, die Striche für 25 und 75-Quantil werden im Englischen als hinges bezeichnet) sowie die sogenannten Whiskers, die standardmäßig bis maximal 1,5 mal dem IQR reichen (aber durch die Werteverteilung beschränkt werden, d.h. liegt der maximal Wert bei 1.2IQR, dann reicht der Whisker auf der einen Seite auch nur bis 1.2 IQR). Werte außerhalb dieses Bereiches werden als Punkte dargestellt.
Mitte notch=TRUE kann man Einkerbungen einzeichnen, die eine Einschätzung erlauben, ob sich die zwei Klassen unterscheiden. Überlappen sich die Einkerbungen zweier Klassen nicht, kann man davon ausgehen, dass die Mittelwerte beider Klassen auf dem 5-% Niveau signifikant unterschiedlich sind.
ggplot(data= temp.deit, mapping = aes(x= CNTRY_NAME, y= YEAR)) +
geom_boxplot(notch=TRUE) +
ylab("Mittlere Jahrestemperatur [°C]") +
xlab("")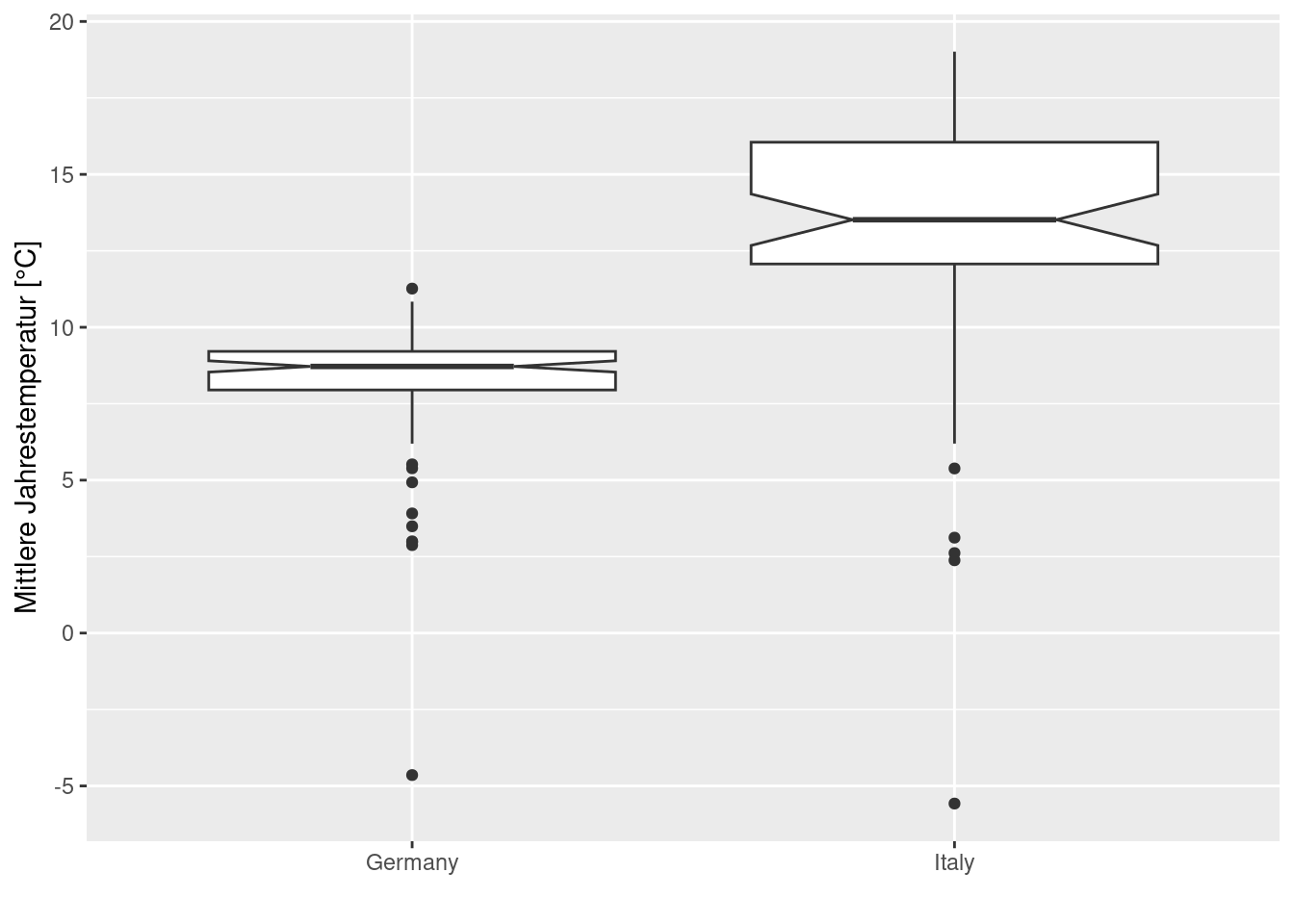
Generell empfiehlt sich auch der Parameter varwidth= TRUE, der die Breite der Boxen abhängig von der Stichprobengröße macht.
ggplot(data= temp.deit, mapping = aes(x= CNTRY_NAME, y= YEAR)) +
geom_boxplot(notch=TRUE, varwidth = TRUE) +
ylab("Mittlere Jahrestemperatur [°C]") +
xlab("")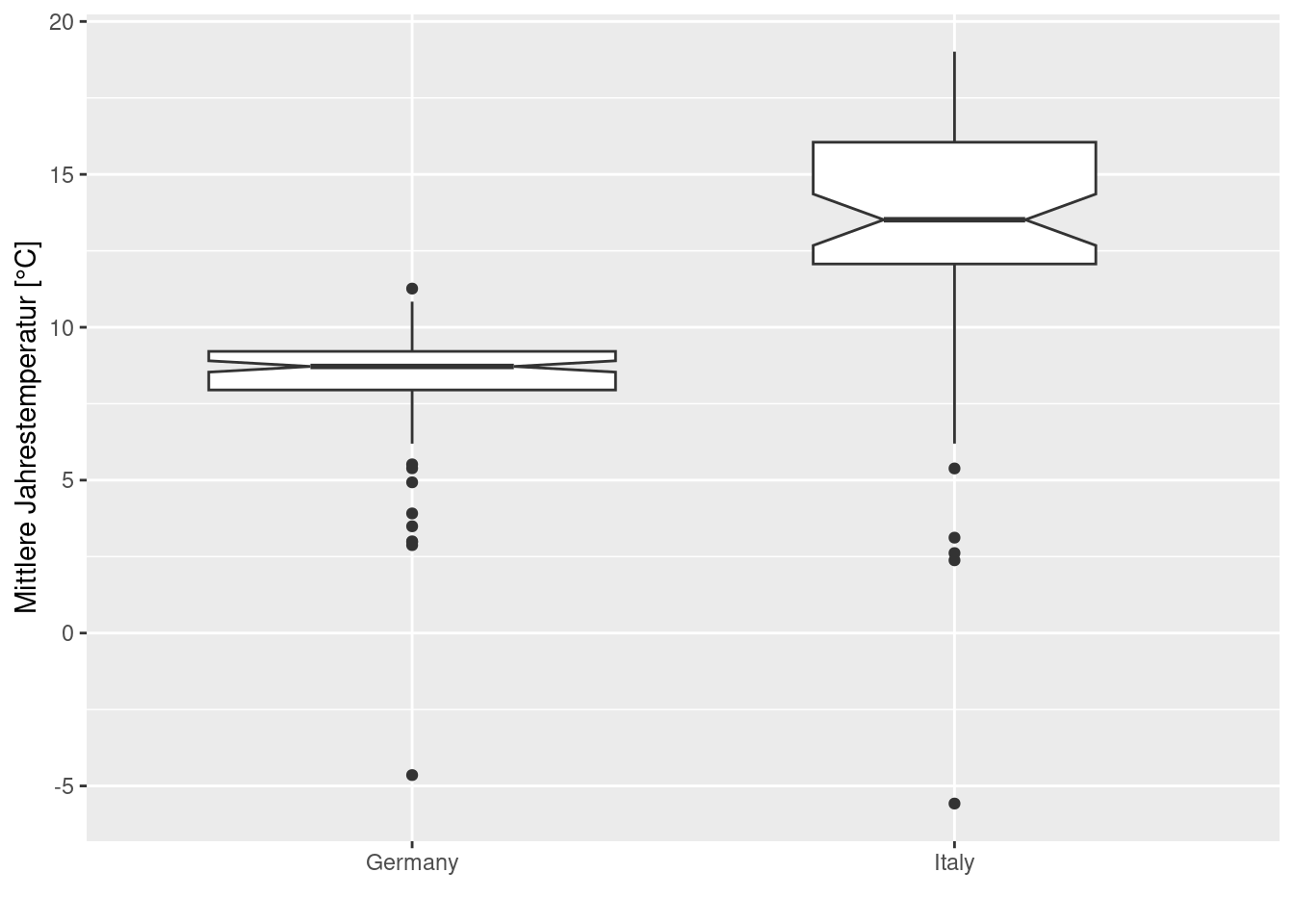
4.7 Kontrollstrukturen
4.7.2 For-Schleifen
Eine For-Schleife dient dazu, dieselbe Sequenz von Befehlen auf einen Vektor oder eine Liste von Objekten anzuwenden. Die Operation bleibt gleich, nur das Objekt an dem sie ausgeführt wird ändert sich.
Stellen wir uns als einfaches Beispiel vor, wir wollten für alle Zahlen eines Vektors die Quadratwurzel berechnen, dann könnten wir die wie folgt tun:16
## [1] 3.464102
## [1] 4.84768
## [1] 3.464102
## [1] 0.5890671Der Schleifenkopf gibt an, über welchen Vektor oder welche Liste wir iterieren wollen (hier myValues) und wie die Schleifenvariable heißen soll (hier aZahl). Die Schleifenvariable verändert ihren Wert in jedem Schleifendurchlauf. Alles was innerhalb der gescheiften Klammern steht, wird in jeem Schleifendurchlauf ausgeführt.
Ein leicht komplexeres Beispiel:
for(aZahl in myValues)
{
paste("Die Quadratwurzel aus ", aZahl, "lautet:",sqrt(aZahl), "\n" ) %>% cat()
}## Die Quadratwurzel aus 12 lautet: 3.46410161513775
## Die Quadratwurzel aus 23.5 lautet: 4.84767985741633
## Die Quadratwurzel aus 12 lautet: 3.46410161513775
## Die Quadratwurzel aus 0.347 lautet: 0.589067059000926Oftmals sieht man auch Konstrukte, bei denen wir die Schleife einfach eine bestimmte Anzahl von Malen durchlaufen wollen: for(i in 1:20){...}. Das kann man z.B. verwenden, wenn man wissen will, die stark Mittelwerte einer Stichprobe von 20 um den wahren Mittelwert streuen, wenn wir von einer Standardnormalverteilung ausgehen.
n <- 500 # Anzahl der Durchläufe
# anlegen eines leeren Vektors um die Ergebnisse aufzunehmen
vecOfMeans <- numeric(n)
for(i in 1:n)
{
# ziehen zufallsstichprobe aus Standardnormalverteilung
mySample <- rnorm(20)
# Mittelwert berechnen
theMean <- mean(mySample)
# Mittelwert an der i-ten Position des Ergebnisvektors speichern
vecOfMeans[i] <- theMean
}hist(vecOfMeans, las=1,
main="Mittelwerte einer Stichprobe von 20 aus N(0,1)")
abline(v=0, lty=2, col="red", lwd=2)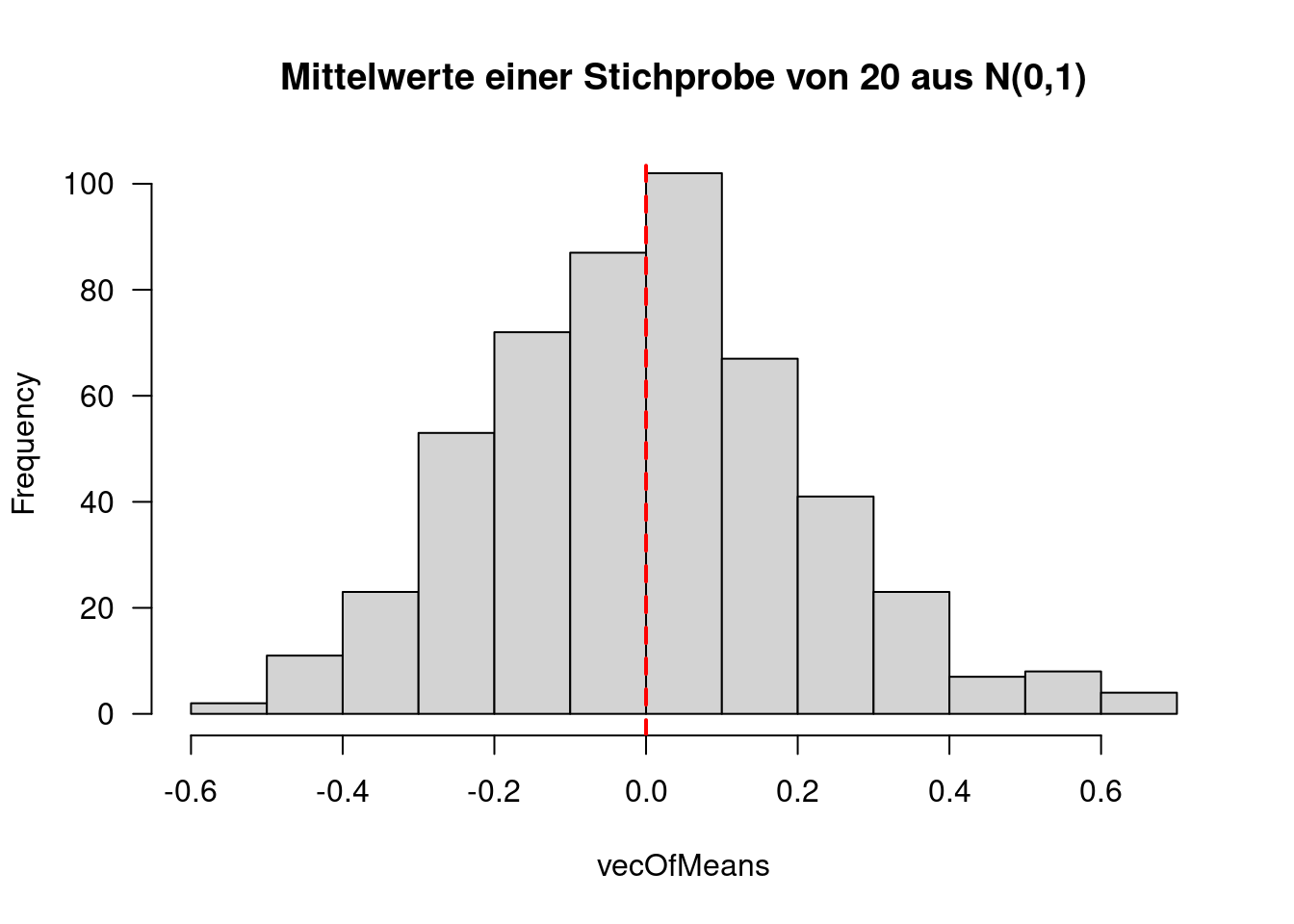
Wir benutzen das Konstrukt der For-Schleife im Kursbuch z.B. um das Gesetz der großen Zahlen oder den Standardfehler (##stderr) nachvollziehbar zu machen.