Kapitel 10 Statistische Tests - Überblick

library(ggplot2)
library(MASS)
library(tidyverse)
library(ggpubr)
library(FAdist)
inkar <- read.table("data/inkar_ue2_all.csv", header = TRUE, sep = ";")

10.1 Parametrische Tests

Parametrische Tests beruhen darauf, dass man eine berechnete Test-Statistik mit einer theoretischen Verteilung der Test-Statistik vergleicht. Man tut dies, um zu ermitteln, wie wahrscheinlich ein zufälliges Auftreten des beobachteten Test-Statistik-Wertes ist. Die Zuverlässigkeit der Aussage beruht darauf, ob die theoretische (parametrische) Verteilung zu den Stichprobendaten passt. Sind die Annahmen verletzt, dann kann man dem p-Wert nicht trauen.

10.1.1 Vergleich von Mittelwerten

In vielen Situationen wollen wir Gruppen hinsichlich ihres Mittelwertes miteinander vergleichen: wird die CDU/CSU von Wählern in ländlichen Wahlkreisen vermehrt gewählt, ist die Bodenerosion auf Schlägen mit Zwischenfrucht reduziert gegenüber solchen ohne?

10.1.1.1 t-Test

Den t-Test haben wir schon kennengelernt (s. hier). Der Test stell den einfachsten Fall eines (generalisierten) linearen Regressionsmodells dar. Es handelt sich um die Regression für eine normalverteilte Zufallsvariable mit einem kategorialen Prädiktor mit einem oder zwei Faktor-Leveln.

Im Kern basiert der t-Test auf dem Vergleich eines Schätzwertes mit seinem Standardfehler (vergleiche hier). Wenn der Wert groß ist, relativ zu seinem Standardfehler, dann ist er signifikant. Bei der Test-Statistik kann es sich dabei um den Mittelwert einer Stichprobe handeln, um die Differenz zweier Stichproben oder auch eine andere Statistik, solange sie näherungsweise normalverteilt ist. Die t-Verteilung wird dabei als Testverteilung verwendet. Die Anzahl der (unabhängigen) Datenpunkte minus 1 gibt die Anzahl der Freiheitsgrade (Parameter der Verteilung) an.

10.1.1.2 Vergleich einer Stichprobe mit Referenzwert (one sampled t-test)

Diese Variante des t-Tests wird angewandt, wenn wir nur eine Stichprobe haben und diese mit einem Referenzwert vergleichen wollen. Wir könnten zum Beispiel daran interessiert sein, ob die mittlere Zahlungsbereitschaft für Klimawandel in Form von zusätzlichen Steuern von Geographiestudierenden (s. hier) von 220€/Jahr abweicht. Wir gehen davon aus, hätten 20 zufällig ausgewählte Studierende der Geographie befragt³⁵. Die Frage sei nun, ob dieser Wert von einem Referenzwert - hier z.B. 220 €/Jahr - abweicht.

Wir sehen im Beispiel, dass der Mittelwert der Verteilung recht nah an dem Referenzwert von 220 €/Jahr liegt, allerdings ist die Streuung nicht unerheblich.

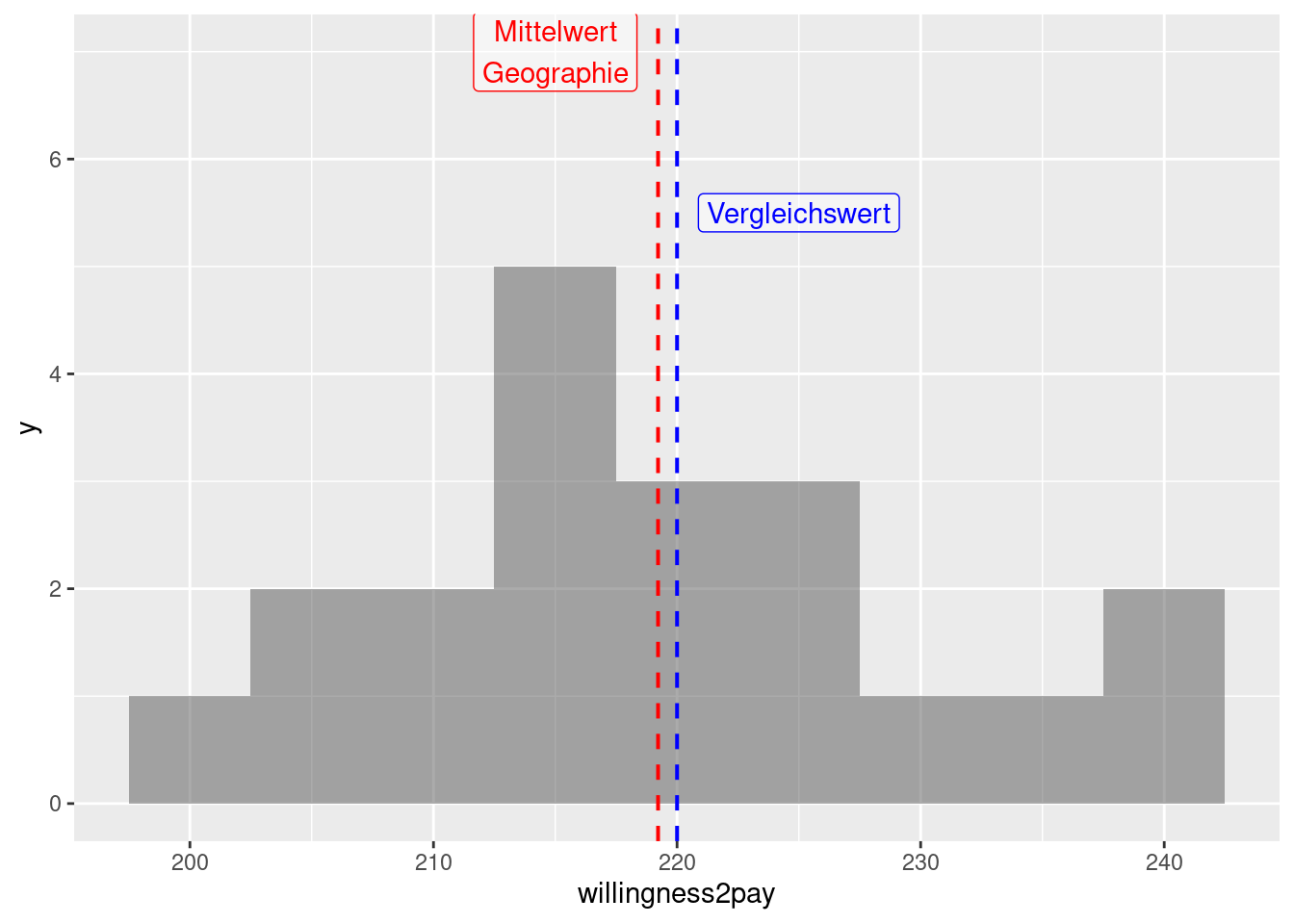
Falls wir davon ausgehen können, dass die Daten normalverteilt sind, können wir folgende Test-Statistik benutzen:

\[ t = \frac{\bar{x} - A} {\mathrm{SE}_{\bar{x}}} = \frac{\bar{x} - A} {\sigma_x / \sqrt{n}} \] Wobei \(A\) der Referenzwert ist, \(\bar{x}\) der Mittelwert der Stichprobe und \(\mathrm{SE}_{\bar{x}}\) der Standardfehler des Mittelwertes.

In unserem Fall also:

meanGeog <- mean(tTestDat1$willingness2pay)
ref <- 220
sdGeog <- sd(tTestDat1$willingness2pay)
n <- nrow(tTestDat1)

tStat <- (meanGeog - ref)/(sdGeog / sqrt(n))
print(tStat)

## [1] -0.3134383

Der zugehörige p-Wert:

pt(tStat, df = n-1, lower.tail = TRUE) * 2

## [1] 0.7573626

Die Freiheitsgrade ist \(n-1\), wir müssen mit 2 multiplizieren, wenn wir den zweiseitigen Test verwenden. Da der Mittelwert kleiner als der Referenzwert ist, suchen wir nach p[X<x], was wir durch lower.tail = TRUE spezifizieren.

Einfacher geht es mit der Funktion t.test. Wir geben nur einen Vektor an und mittels mu den Vergleichswert.

t.test(tTestDat1$willingness2pay, mu = 220)

## 
##  One Sample t-test
## 
## data:  tTestDat1$willingness2pay
## t = -0.31344, df = 19, p-value = 0.7574
## alternative hypothesis: true mean is not equal to 220
## 95 percent confidence interval:
##  214.0117 224.4284
## sample estimates:
## mean of x 
##    219.22

Wir sehen, dass wir auf Grundlage des zweiseitigen Tests die Nullhypothese, dass der wahre Mittelwert gleich 220 €/Jahr ist aufgrund der hohen Irrtumswahrscheinlichkeit nicht verwerfen können. Das 95% Konfidenzintervall schließt 220 ein, was ebenfalls zeigt, das wir die Nullhypothese nicht verwerfen können.

10.1.1.3 Vergleich zweier gepaarter Stichproben (paired sample t-test)

Bei gepaarten Stichproben sind die Elemente der beiden Stichproben miteinander verbunden. Dies kann z.B. der Fall sein, wenn wir dieselbe Person vor und nach einer Intervention befragen - wenn wir z.B. herausfinden wollen, ob eine zusätzliche Information zum Klimawandel die Zahlungsbereitschaft erhöht. Andere Beispiele sind: (i) die Anzahl Moosarten auf der Nord- und der Südseite desselben Baumes oder (ii) die Mittlere Monatstemperatur an derselben Messstation im Januar und im Februar oder die Messung einer Stoffkonzentration an der Einleitung eines Emittenten in ein Fließgewässer und eine Messung 200m flussabwärts davon. Wichtig ist, dass es sich immer zwei Messungen je Einheit/Objekt/Subjekt haben, aber eben die Messung/Befragung an einer Vielzahl von Einheiten/Objekten/Subjekten durchgeführt haben.

Untersuchen wir noch einmal eine hypothetische Zahlungsbereitschaftsbefragung einer Zielgruppe. Die 20 Teilnehmer werden jeweils vorab befragt und dann noch einmal, nachdem Ihnen Informationen zu den Auswirkungen des Klimawandels präsentiert worden sind.³⁶. Wenn wir die Paarung ignorieren, können wir zwei Verteilungen (vorher/nachher) vergleichen. Allerdings wissen wir ja, dass es sich jeweils um gepaarte Befragungen handelt, weswegen wir die Daten auch daraufhin auswerten können. Wir betrachten zunächst den Scatterplot der Beobachtungen (Zahlungsbereitschaft vorher und nachher) und berechnen dann die Verteilung der Differenzen der Zahlungsbereitschaftsbefragung.

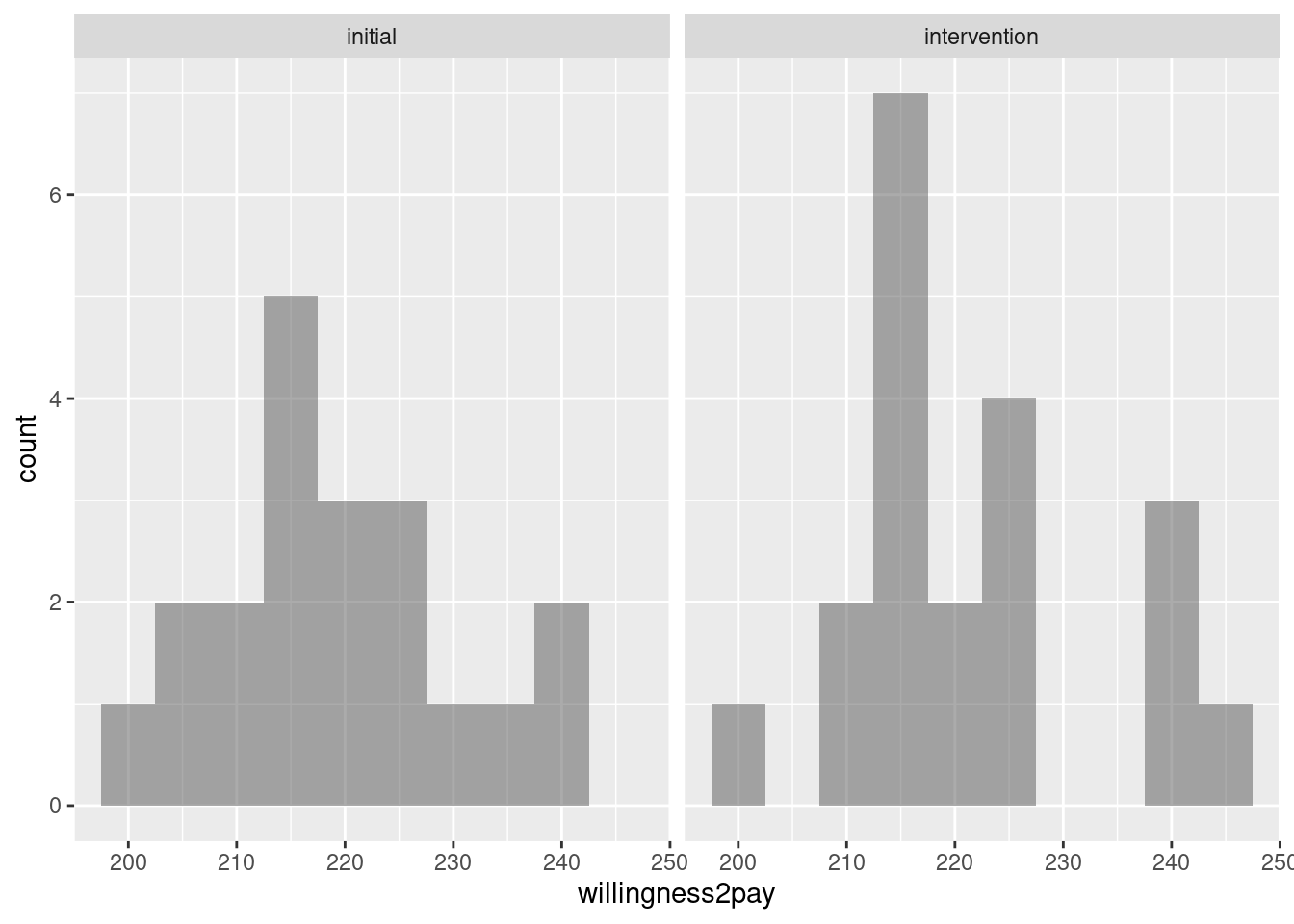
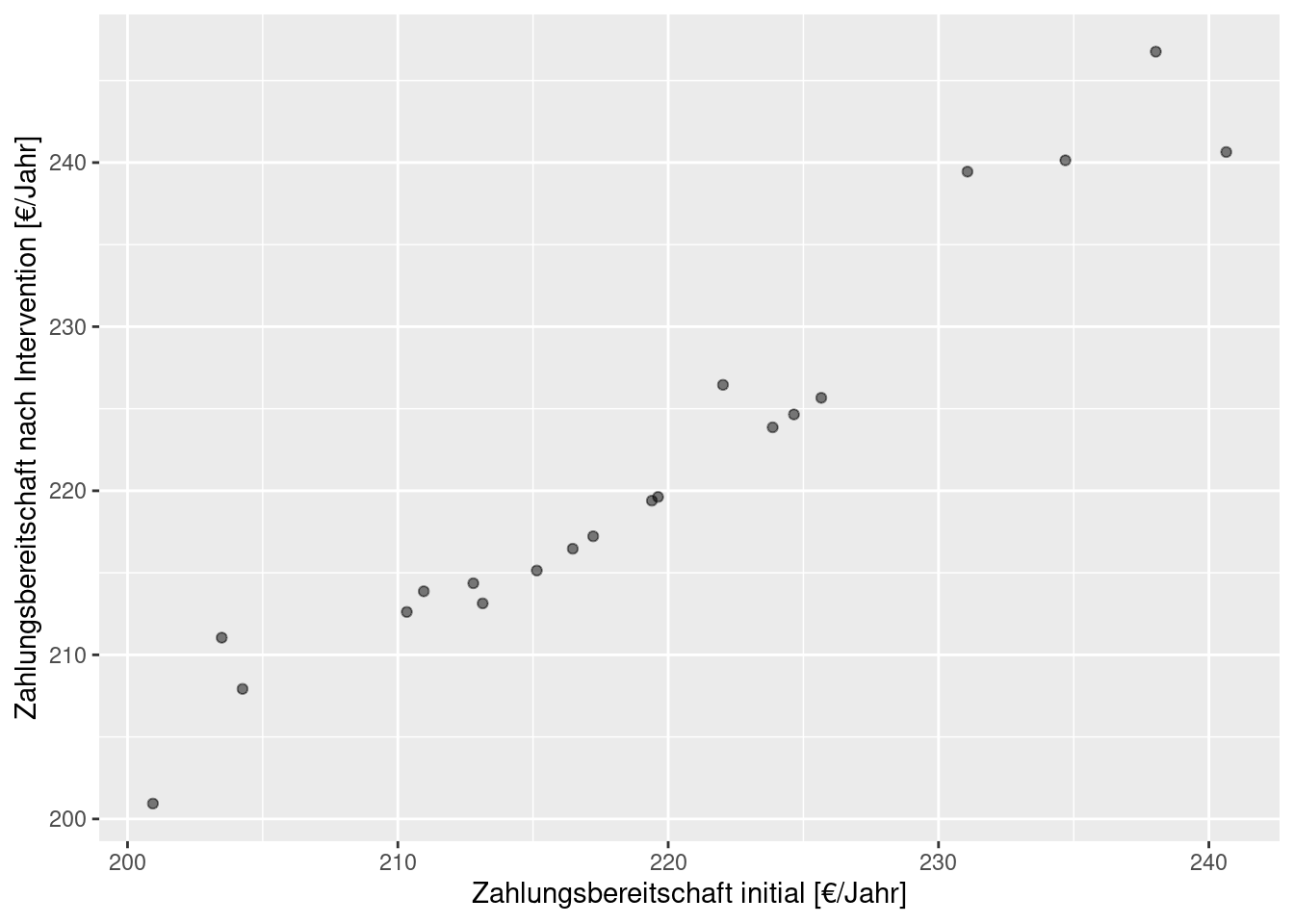
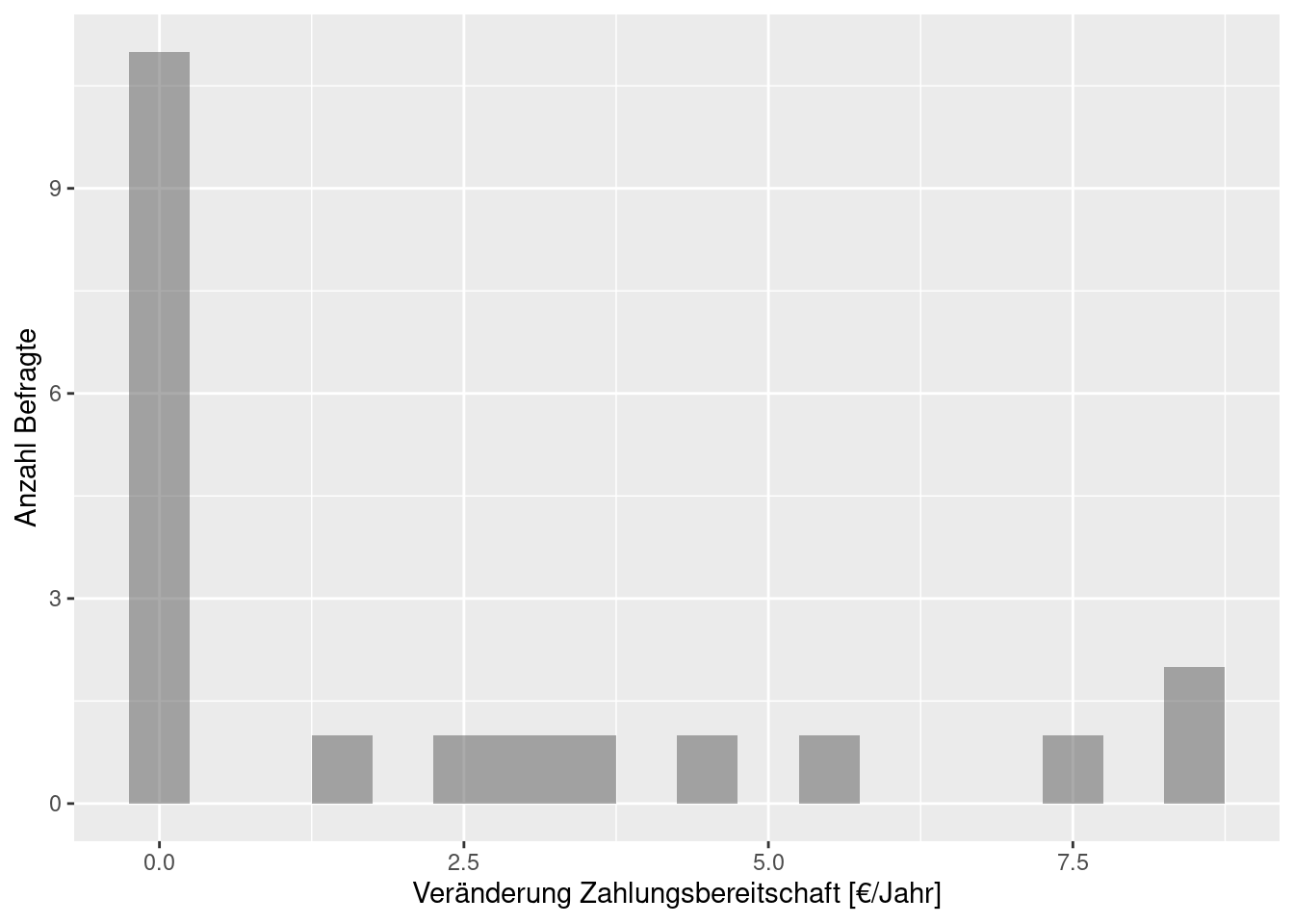
Unsere Test-Statistik für den t-Test sieht wie folgt aus:

\[ t = \frac{1}{n} \frac{\sum_{i=1}^n(x_{1i}- x_{2i})} {\mathrm{SE}_{x_1-x_2}} = \frac{\bar{x}_1-\bar{x}_2} { \frac{\sigma_{x_1 - x_2}} {\sqrt{n}}} \]

Hierbei wird angenommen, dass die Standardabweichung beider Stichproben gleich ist. Ist sie das nicht, muss dafür korrigiert werden (Welsch, s. unten).

Wir rechnen also nicht mehr mit der Differenz zwischen dem Stichprobenmittelwert und einem Referenzwert, sondern wir berechnen den Mittelwert der Differenzen. Wir testen also auf die Differenz der Stichproben. Der Standardfehler, mit dem wir die Differenzen vergleichen ist der Standardfehler des Mittelwertes der Differenzen. Wichtig ist, dass unsere Stichprobengröße \(n\) nicht 2*20 (20 Teilnehmer), sondern 20. Nach der Umrechnung und Korrektur rechnen wir quasi wie beim Vergleich einer Stichprobe mit dem Referenzwert Null.

diffWillingness2pay <- tTestDat2paired$willingness2payAfter - tTestDat2paired$willingness2pay

Mittelwert der Differenzen - es hat sich die Zahlungsbereitschaft durch die Intervention im Mittel erhöht:

mean(diffWillingness2pay)

## [1] 2.248636

Standardabweichung der Differenzen: so stark schwanken die Veränderungen durch die Intervention um ihren Mittelwert:

sd(diffWillingness2pay)

## [1] 3.087995

Standardfehler der Differenzen

n <- length(diffWillingness2pay)
sd(diffWillingness2pay) / sqrt(n)

## [1] 0.6904967

Test-Statistik:

tTestStat <- mean(diffWillingness2pay) / (sd(diffWillingness2pay) / sqrt(n))
tTestStat

## [1] 3.256548

2* pt(tTestStat, df = n-1, lower.tail = FALSE)

## [1] 0.004152154

t.test(y = tTestDat2paired$willingness2pay,
       x= tTestDat2paired$willingness2payAfter,
      paired = TRUE, var.equal = TRUE)

## 
##  Paired t-test
## 
## data:  tTestDat2paired$willingness2payAfter and tTestDat2paired$willingness2pay
## t = 3.2565, df = 19, p-value = 0.004152
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  0.8034094 3.6938617
## sample estimates:
## mean difference 
##        2.248636

Wir können - falls die Annahmen erfüllt sind - die Nullhypothese dass die Differenzen gleich Null sind mit einer Irrtumswahrscheinlichkeit von knapp 2% ablehnen.

Der einseitige Test darauf, dass die Differenzen positiv sind, ist erwartungsgemäß stärker siginifikant.

t.test(y = tTestDat2paired$willingness2pay,
       x= tTestDat2paired$willingness2payAfter,
      paired = TRUE, var.equal = TRUE,
      alternative= "greater")

## 
##  Paired t-test
## 
## data:  tTestDat2paired$willingness2payAfter and tTestDat2paired$willingness2pay
## t = 3.2565, df = 19, p-value = 0.002076
## alternative hypothesis: true mean difference is greater than 0
## 95 percent confidence interval:
##  1.054675      Inf
## sample estimates:
## mean difference 
##        2.248636

10.1.1.4 Vergleich zweier ungepaarter Stichproben (two sample t-test)

Im Gegensatz zum Vergleich gepaarter Stichproben gibt es hierbei keine Beziehung zwischen den Stichproben. Wir haben z.B. 20 Personen ohne und 20 Personen mit Intervention hinsichtlich ihrer Zahlungsbereitschaft befragt, aber unterschiedliche Personen. Oder wir haben an 10 Einleitungen die Schadstoffkonzentration gemessen und an 10 weiteren Orten 200m flussabwärts einer Einleitung, aber an insgesamt 20 Einleitungen. Oder wir haben 400 Bäume auf der Südseite und 400 Bäume an der Nordseite untersucht, aber jeweils unterschiedliche Bäume. Da wir hierbei die individuelle Variabilität (zwischen Personen, zwischen Einleitern, zwischen Bäumen) nicht kontrollieren, ist diese Form des Tests weniger trennscharf.

Die Test-Statistik sieht wie folgt aus:

\[ t = \frac{\bar{x}_1-\bar{x}_2} {\mathrm{SE}_\mathrm{Differenzen}} = \frac{\bar{x}_1-\bar{x}_2} {\sqrt{ \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} }}\]

Die Berechnung ist bis auf den Standardfehler gleich. Der Standardfehler der Differenzen der beiden Stichproben ist größer als der Standardfehler, den wir beim gepaarten Zweistichproben t-Test verwenden. Entsprechend ist der Test weniger trennscharf.

t.test(y = tTestDat2paired$willingness2pay,
       x= tTestDat2paired$willingness2payAfter,
      paired = FALSE, var.equal = TRUE,
      alternative= "greater")

## 
##  Two Sample t-test
## 
## data:  tTestDat2paired$willingness2payAfter and tTestDat2paired$willingness2pay
## t = 0.61077, df = 38, p-value = 0.2725
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  -3.958413       Inf
## sample estimates:
## mean of x mean of y 
##  221.4687  219.2200

10.1.1.5 Welch-Satterhaite Korrektur für ungleiche Stichprobenvarianz

Der Welch oder Welch-Satterhaite Test (Welch 1938) korrigiert den Zweistichprobentest dahingehend, dass ungleiche Varianzen erlaubt sind. Allerdings sollten die Stichproben normalverteilt sein und eine ähnliche Stichprobengröße aufweisen.

Die Test-Statistik entspricht der beim ungepaarten Zwei-Stichproben t-Test:

\[ t = \frac{\bar{x}_1-\bar{x}_2} {\mathrm{SE}_\mathrm{Differenzen}} = \frac{\bar{x}_1-\bar{x}_2} {\sqrt{ \frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2} }}\]

Der Unterschied liegt darin, dass sich die Freiheitsgrade anders berechnen es ist nun nicht mehr \(df = (n_1+n_2)-2\), sondern:

\[df= \frac{(\frac{\sigma_1^2}{n_1} + \frac{\sigma_2^2}{n_2})^2}{\frac{(\sigma_1^2/n_1)^2}{n_1-1} + \frac{(\sigma_2^2/n_2)^2}{n_2-1}}\] Dieser Wert ist kleiner als bei der Annahme gleicher Varianz. Entsprechend ist die Irrtumswahrscheinlichkeit etwas größer.

Hier mit der korrekten Berücksichtigung der ungleichen Stichprobenvarianz.

t.test(y = tTestDat3$willingness2pay1,
       x= tTestDat3$willingness2pay2,
      paired = FALSE, var.equal = FALSE,
      alternative= "greater")

## 
##  Welch Two Sample t-test
## 
## data:  tTestDat3$willingness2pay2 and tTestDat3$willingness2pay1
## t = 5.4319, df = 26.465, p-value = 5.098e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  7.997647      Inf
## sample estimates:
## mean of x mean of y 
##  230.3940  218.7391

Hier mit der nicht korrekten Annahme gleicher Stichprobenvarianz.

t.test(y = tTestDat3$willingness2pay1,
       x= tTestDat3$willingness2pay2,
      paired = FALSE, var.equal = TRUE,
      alternative= "greater")

## 
##  Two Sample t-test
## 
## data:  tTestDat3$willingness2pay2 and tTestDat3$willingness2pay1
## t = 5.4319, df = 38, p-value = 1.711e-06
## alternative hypothesis: true difference in means is greater than 0
## 95 percent confidence interval:
##  8.037467      Inf
## sample estimates:
## mean of x mean of y 
##  230.3940  218.7391

Der Ansatz von Welch beruht darauf, die sogenannten effektiven Freiheitsgrade (effective degrees of freedom) zu schätzen.

Schauen wir uns einmal etwas genauer an, wie die Korrektur wirkt, in dem wir für eine Reihe von Unterschiedlichen Stichprobenvarianzen und Stichprobengrößen die Freiheitsgrade berechnen. Anschließend schauen wir uns die kritischen Werte für bestimmte Irrtumswahrscheinlichkeiten an und welche Mittelwertdifferenzen wir bei verschiedenen Irrtumswahrscheinlichkeiten noch unterscheiden können.

ZUnächst erzeugen wir einen dat.frame, der alle Kombinationen der Werte die wir untersuchen wollen enthält.- Hierzu verwenden wir expand.grid - der Befehl erzeugte automatisch alle Kombinationsmöglichkeiten.

dat <- expand.grid(n1=c(20,30), n2=20, sigma1 = 1, 
                   sigma2 = seq(0.1,10, by=.1),
                   pval=seq(.001, 0.05, by=.001))

Dann berechnen wir die Freiheitsgrade anhand der oben angegebenen Formeln:

dat <- mutate(dat, df_normal= n1+n2 -2,
              df_Welch = ((sigma1^2)/n1 + (sigma2^2)/n2)^2 / ( ((sigma1^2/n1)^2)/ (n1-1) + ((sigma2^2/n2)^2)/ (n2-1) ),
              se_differences = sqrt((sigma1^2/n1)+ (sigma2^2/n2)) )

head(dat)

##   n1 n2 sigma1 sigma2  pval df_normal df_Welch se_differences
## 1 20 20      1    0.1 0.001        38 19.37996      0.2247221
## 2 30 20      1    0.1 0.001        48 29.86627      0.1839384
## 3 20 20      1    0.2 0.001        38 20.51757      0.2280351
## 4 30 20      1    0.2 0.001        48 32.40634      0.1879716
## 5 20 20      1    0.3 0.001        38 22.39252      0.2334524
## 6 30 20      1    0.3 0.001        48 36.34744      0.1945079

Um mit ggplot einfacher Plots erzeugen zu können pivotieren wir den data.frame. Anschließend sind die Freiheitsgrade in der Spalte df und die Korrekturmethode in der Spalte method enthalten.

dat <- pivot_longer(dat, cols= c(df_Welch, df_normal), values_to = "df", names_to = "method")

head(dat)

## # A tibble: 6 × 8
##      n1    n2 sigma1 sigma2  pval se_differences method       df
##   <dbl> <dbl>  <dbl>  <dbl> <dbl>          <dbl> <chr>     <dbl>
## 1    20    20      1    0.1 0.001          0.225 df_Welch   19.4
## 2    20    20      1    0.1 0.001          0.225 df_normal  38  
## 3    30    20      1    0.1 0.001          0.184 df_Welch   29.9
## 4    30    20      1    0.1 0.001          0.184 df_normal  48  
## 5    20    20      1    0.2 0.001          0.228 df_Welch   20.5
## 6    20    20      1    0.2 0.001          0.228 df_normal  38

NUn berechnen wir je Parameterkombination den Kritischen Wert je Irrtumswahrscheinlichkeit und die sich aus der multiplikation mit dem Standardfehler (s. Formel oben) ergebende minimale Mittelwertdifferenz die auf dem Irrtumswahrscheinlichkeitsniveau gerade noch detektiert werden kann.

dat <- mutate(dat, criticalValue = qt(p=pval, df= df))

dat <- mutate(dat, meandiff4criticalValue = criticalValue * se_differences)

Da die Korrektrmethoden automatisch in der Legende verwendet werden benennen wir sie mittels gsub um. gsub sucht und ersetzt Teile eines Strings. Da die Funktion vektorisiert ist, können wir sie auf die ganze Spalte anwenden.

dat$method <- gsub(pattern="df_", 
                   replacement = "", 
                   x= dat$method)
dat$method <- gsub(pattern="normal", 
                   replacement = "unkorrigiert", 
                   x= dat$method)

Nun noch der Plot.

dat %>% 
ggplot(mapping = aes(x=sigma2, y=df, col= method)) +
  geom_line() + facet_wrap(~n1 , labeller = label_both) +
  labs(title="Vergleich der Freiheitsgrade", 
       subtitle= "n2 = 20, sigma1 =1" )+
  xlab(parse(text="sigma[2]")) +
  ylab("Effektive Freiheitsgrade") +
  scale_color_discrete(name="Korrekturmethode")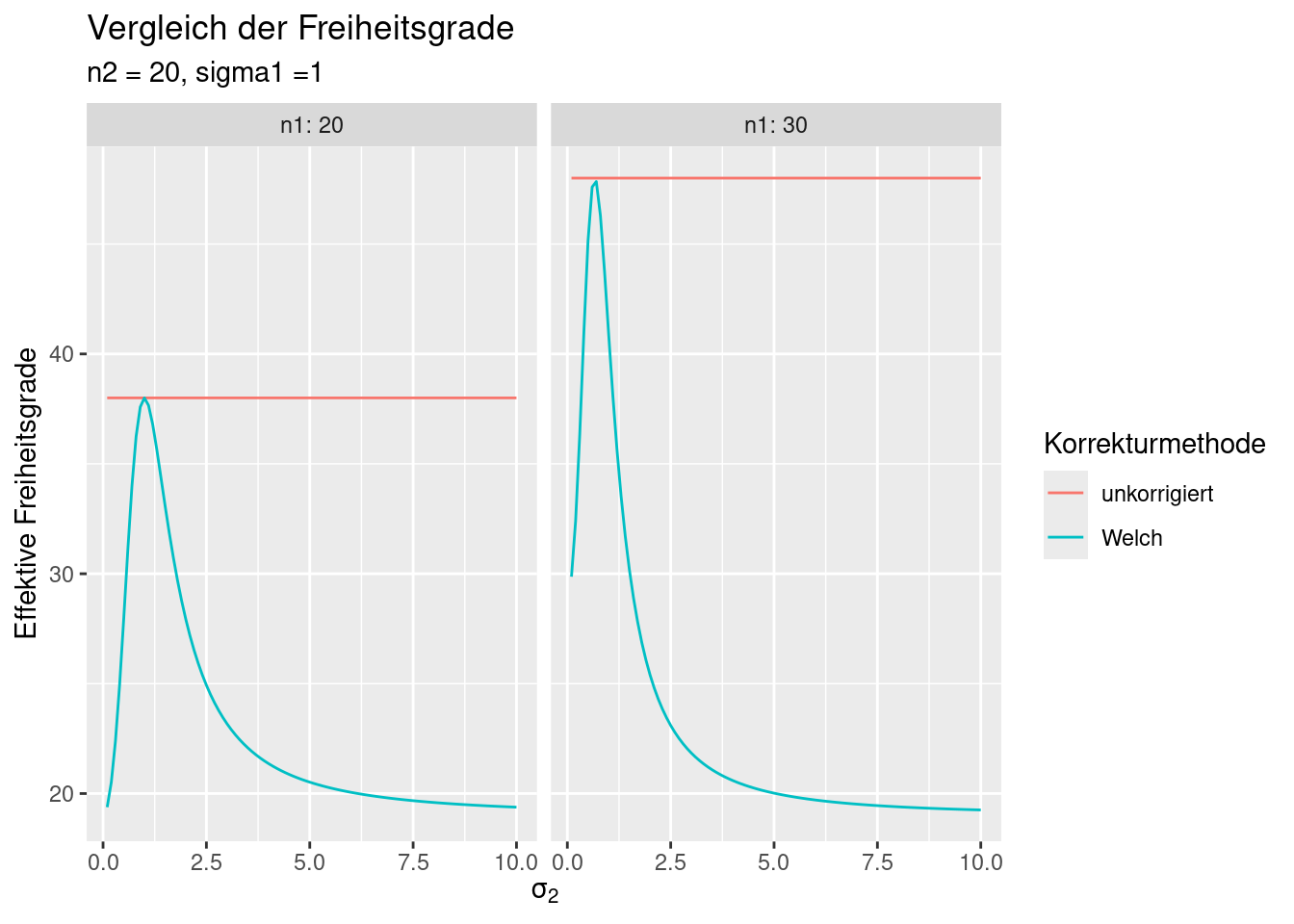

Wie wir sehen, sind die effektiven Freiheitsgrade, die mittels der Welsch-Saitterhaite Methode errechnet werden immer kleiner gleich den unkorrigierten Werten. Nur wenn die Stichprobenvarianzen gleich sind, entsprechen sich die Freiheitsgrade.

Ist die Standardabweichung der zweiten Stichprobe z.B. doppelt so groß wie die erste, dann betragen die effektiven Freiheitsgrade nur noch anstelle von .

Dies wirkt sich auch auf die kritischen Werte der t-Verteilung aus (s. Abbildung 10.1).

dat %>% filter(sigma2 %in% c(.05, 1, 2, 4, 8)) %>%
ggplot(mapping = aes(x=pval, y=criticalValue, col= method)) +
  geom_line() + facet_wrap(~n1 + sigma2, labeller = label_both, ncol=4) +
  scale_x_continuous(breaks= c(.01, .03, .05)) +
  labs(title="Kritischer Wert der t-Verteilung in Abhängigkeit vom Korrekturverfahren", 
       subtitle="n2=20, sigma1= 1") +
  xlab("p-Wert") +
  ylab("Kritischer Wert der t-Verteilung")+
  scale_color_discrete(name="Korrekturmethode")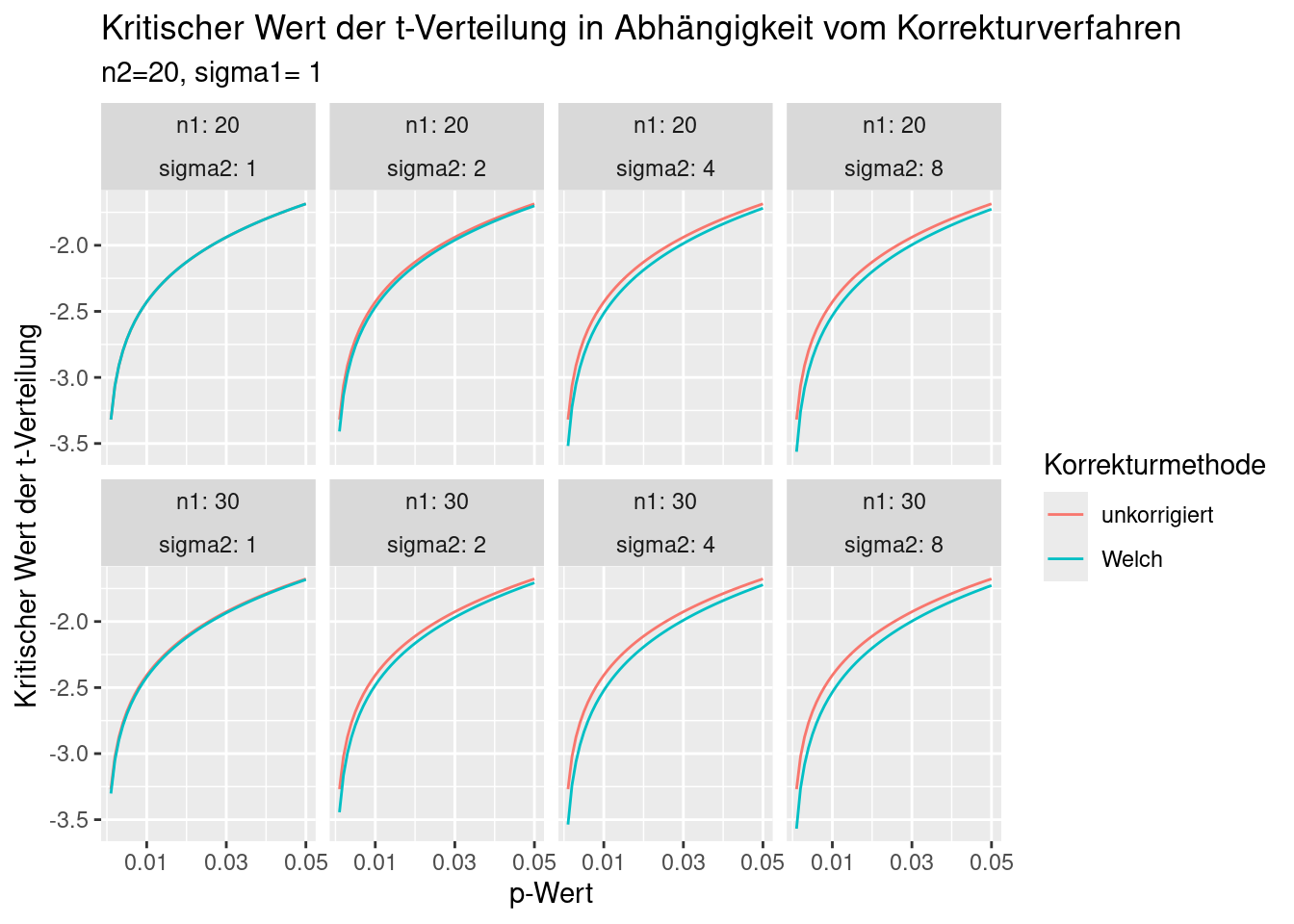

Figure 10.1: Kritischer Wert der t-Verteilung in Abhängigkeit vom Korrekturverfahren. Die Korrektur nach Welch ist die korrekte Vorgehensweise. Die unkorrigierten Werte werden nur zum Vergleich gezeigt.

Schauen wir uns die aufgrund der Unterschiede in den Freiheitsgraden resultierenden t-Verteilungen einmal an (s. Abbildung 10.2). Die Unterschiede der Verteilungen sind klein und schwer zu erkennen. Allerdings sind die resultierenden Unterschiede im Hinblick auf die kritischen Werte der jeweiligen t-Verteilung für die Irrtumswahrscheinlichkeit von 2% merkbar.

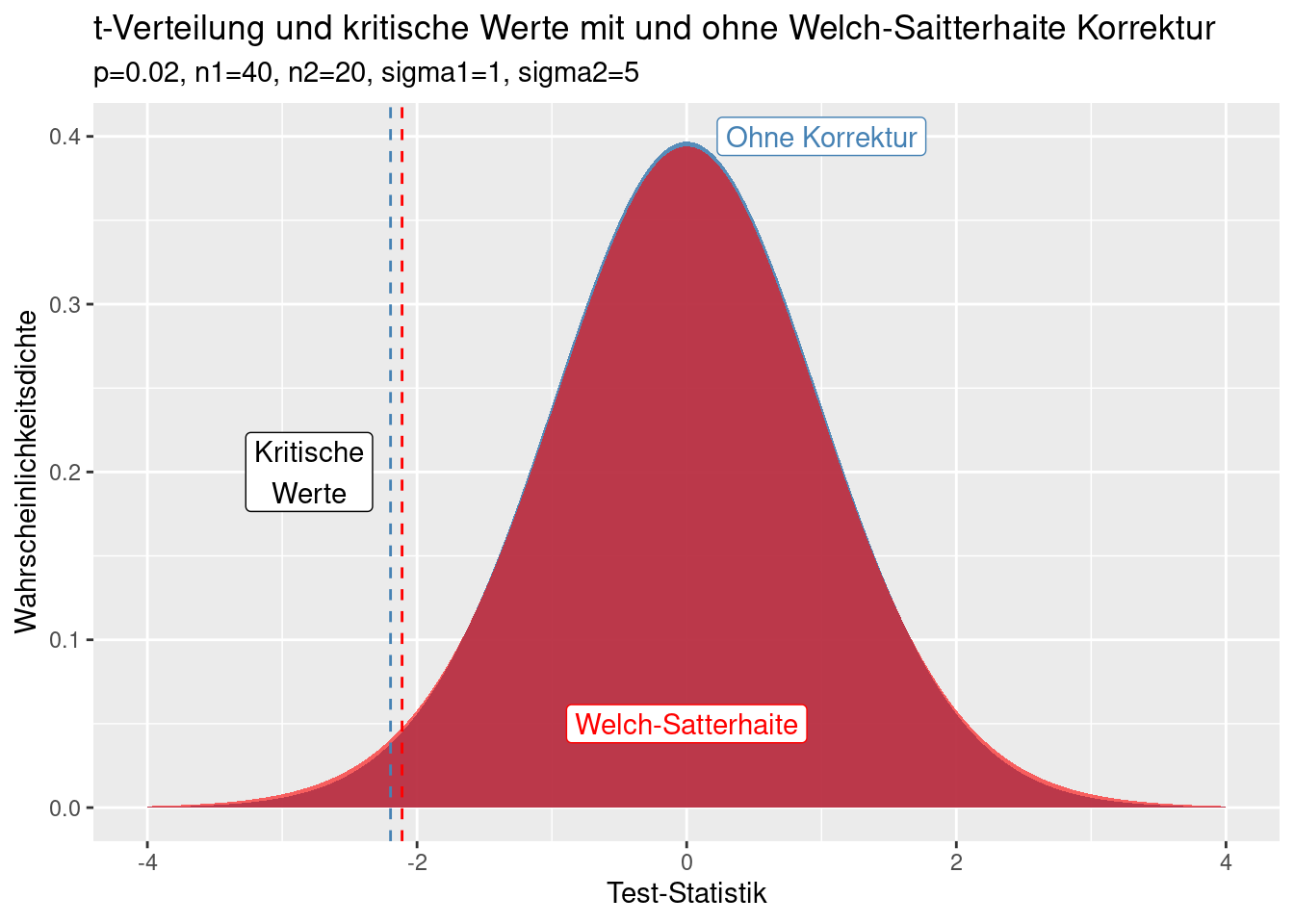
Figure 10.2: Effekt der Welch-Saitterhaite Korrektur auf die für den t-Test verwendete t-Verteilung. Gezeigt sind zusätzlich die kritischen Werte für p=0.02. Die Korrektur nach Welch ist die korrekte Vorgehensweise. Die unkorrigierten Werte werden nur zum Vergleich gezeigt.

Zuletzt schauen wir uns noch an, wie sich die minimal detektierbaren Unterschiede für unterschiedliche Irrtumswahrscheinlichkeiten verändern, wenn wir die Korrektur anwenden oder (fälschlicherweise) nicht anwenden (s. Abbildung ??).

dat %>% filter(sigma2 %in% c(2,4,8)) %>%
ggplot(mapping = aes(x=pval, y=meandiff4criticalValue, col= method)) +
  geom_line() + facet_wrap(~n1 + sigma2, labeller = label_both, ncol=3, scale="free_y") +
  scale_x_continuous(breaks= c(.01, .03, .05)) +
  labs(title="Bei kritischem Wert der t-Verteilung unterscheidbarer Unterschied\nzwischen den Mittelwerten", 
       subtitle="n2=20, sigma1=1") +
  xlab("p-Wert") +
  ylab("Minimal detektierbarer Mittelwert")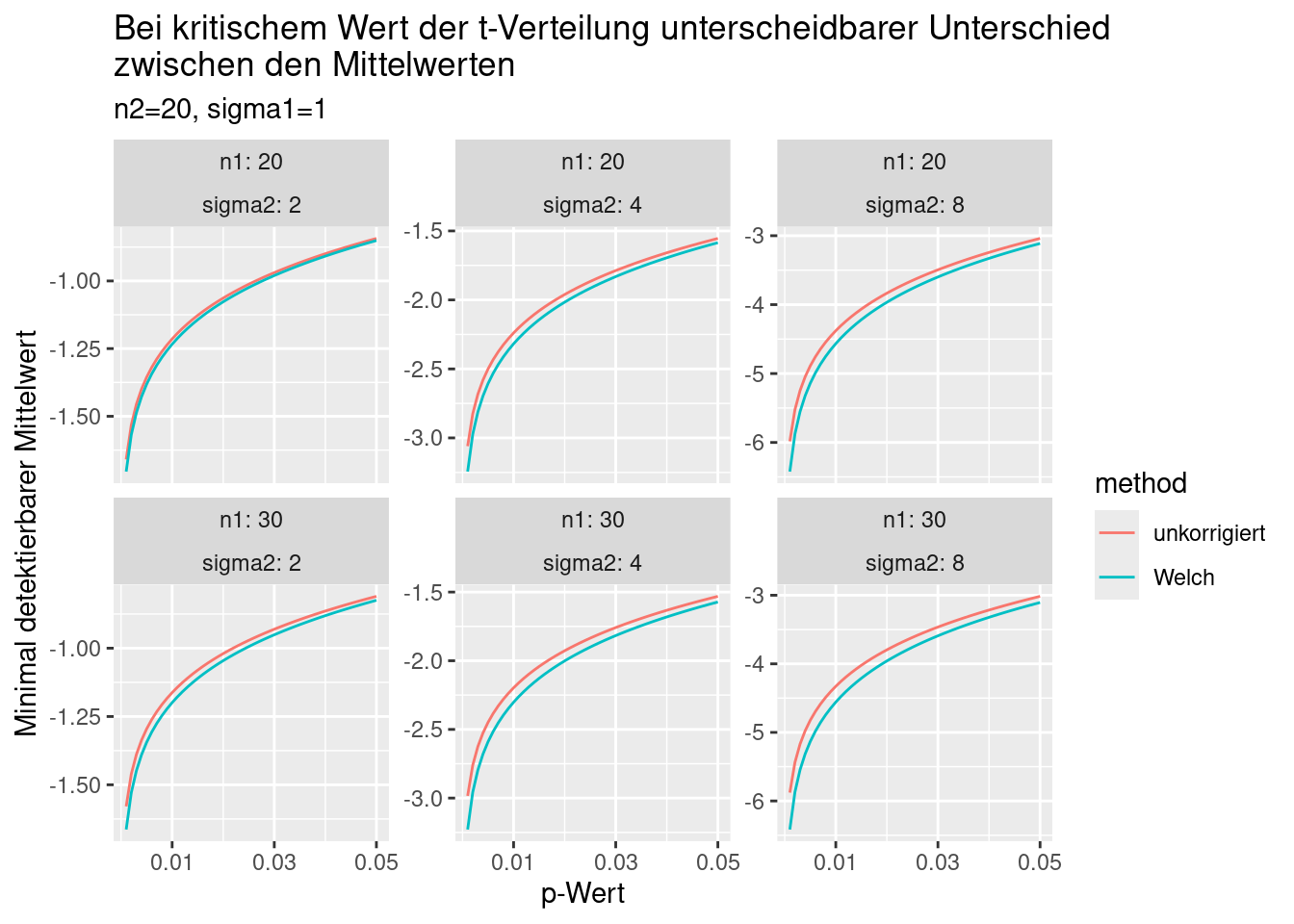

Figure 10.3: Minimal - auf angegebenem Irrtumswahrscheinlichkeitsniveau - detektierbare Differenz der Mittelwerte der beiden Stichproben für angegebenen Stichprobengrößen und Stichprobenvarianzen. Die Korrektur nach Welch ist die korrekte Vorgehensweise. Die unkorrigierten Werte werden nur zum Vergleich gezeigt.

Je größer die Unterschiede in den Standardabweichungen der Stichproben, desto ausgeprägter die Unterschiede. Der Zusammenhang mit der Irrtumswahrscheinlichkeit ist erwartungsgemäß nicht-linear (ergibt sich aus der Form der t-Verteilung). Am größten sind die Unterschied hinsichtlich der minimal detektierbaren Mittelwertdifferenz für kleine p-Werte.

Die Korrektur führt zu Unterschieden, die üblicherweise nicht allzu groß sind. Jedoch kann dieser Unterschied für die Interpretation relevant sein, je nachdem, ob der Unterschied der Mittelwerte als gerade noch signifkant oder eben nicht eingeschätzt wird. Die Korrektur sollte im Zweifelsfall immer angewandt werden. Falls die Stichprobenvarianzen gleich sind ist der Effekt 0. Falls es Unterschiede bei den Stichprobenvarianzen gibt, sind wir auf der sicheren Seite.

10.1.2 Varianzanalyse mittels F-Test

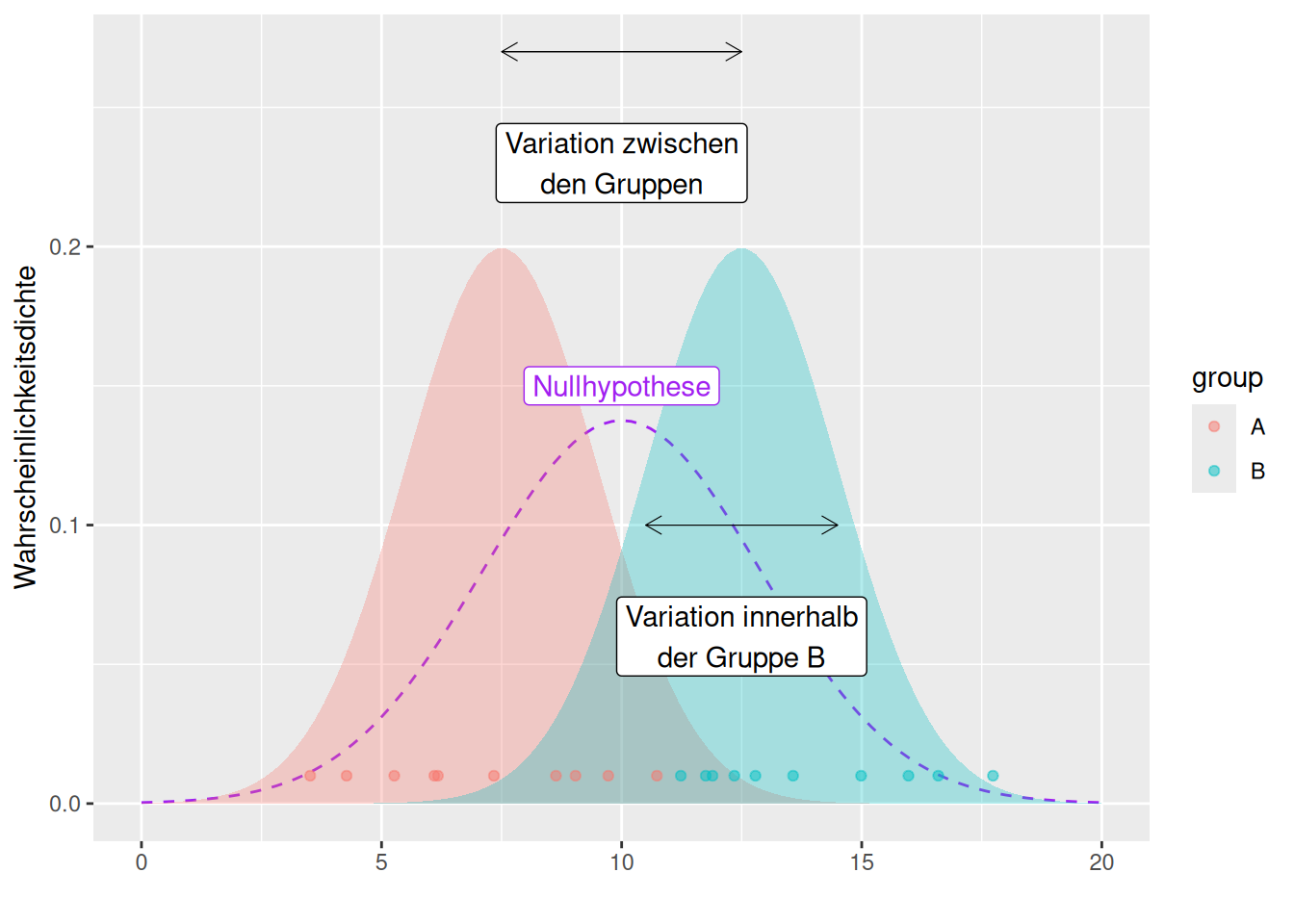
Auch die Varianzanalyse mittels F-Test testet auf Unterschiede zwischen Stichproben. Allerdings wird hierbei auf eine Unterschiedlichkeit der Varianzen getestet. Die Nullhypothese ist, dass beide Stichproben aus der Selben Grundgesamtheit stammen. Die Alternativhypothese ist, dass die Stichproben aus unterschiedlichen Grundgesamtheiten stammen. Die Annahme ist, dass die Grundgesamtheiten normalverteilt sind.

Man testet:

\[ F = \frac{\textrm{Variation zwischen den Gruppen}}{\textrm{Variation innerhalb der Gruppen}} \]

Wenn die Variabilität zwischen den Gruppen klein ist im Verhältnis zur Variation innerhalb der Gruppen (hier Annahme das alle Stichproben aus der Selben Gruppe entstammen), dann ist die Wahrscheinlichkeit für das zufällige Auftreten dieser Variabilität hoch (und damit zufällig zu erwarten).

Getestet wird die Teststatistik gegen eine F-Verteilung mit den Freiheitsgraden \(df_1 = n_1-1\) und \(df_2 = n_2-1\) mit \(n_1\) und \(n_2\) die Stichprobengröße der ersten und der zweiten Stichprobe.

Der Test wird in R mittel der Funktion var.test durchgeführt. x und y geben die beiden Stichproben (als Vektoren) an, ratio das zu testende Verhältnis zwischen der Varianz beider Stichproben (wenn gleiche Varianz getestet wird: ratio = 1) und alternative die Art des Tests (zweiseitig, größer, kleiner als).

Für den Fall, dass wir \(H_0: \sigma^2_1 = \sigma^2_2\) gegen \(H_q: \sigma^2_2 > \sigma^2_1\) ergibt sich die Teststatistik als:

\[F = \frac{S_2^2}{S_1^2} = \frac{\frac{1}{n_2-1}\sum_{i=1}^{n_2}(X_{2,i}-\bar{X}_2)^2} {\frac{1}{n_1-1}\sum_{i=1}^{n_1}(X_{1,i}-\bar{X}_1)^2} \]

Wir schauen uns das hier an einem Beispiel an. Wir wollen untersuchen, ob die Arbeitslosenquote der Neuen und der Alten Bundesländer dieselbe Varianz besitzen.

ggplot(inkar, aes(x=Arbeitslosenquote, fill = ow)) + 
  geom_histogram(binwidth = .5, alpha=.7,
                 mapping = aes(y = after_stat(density)))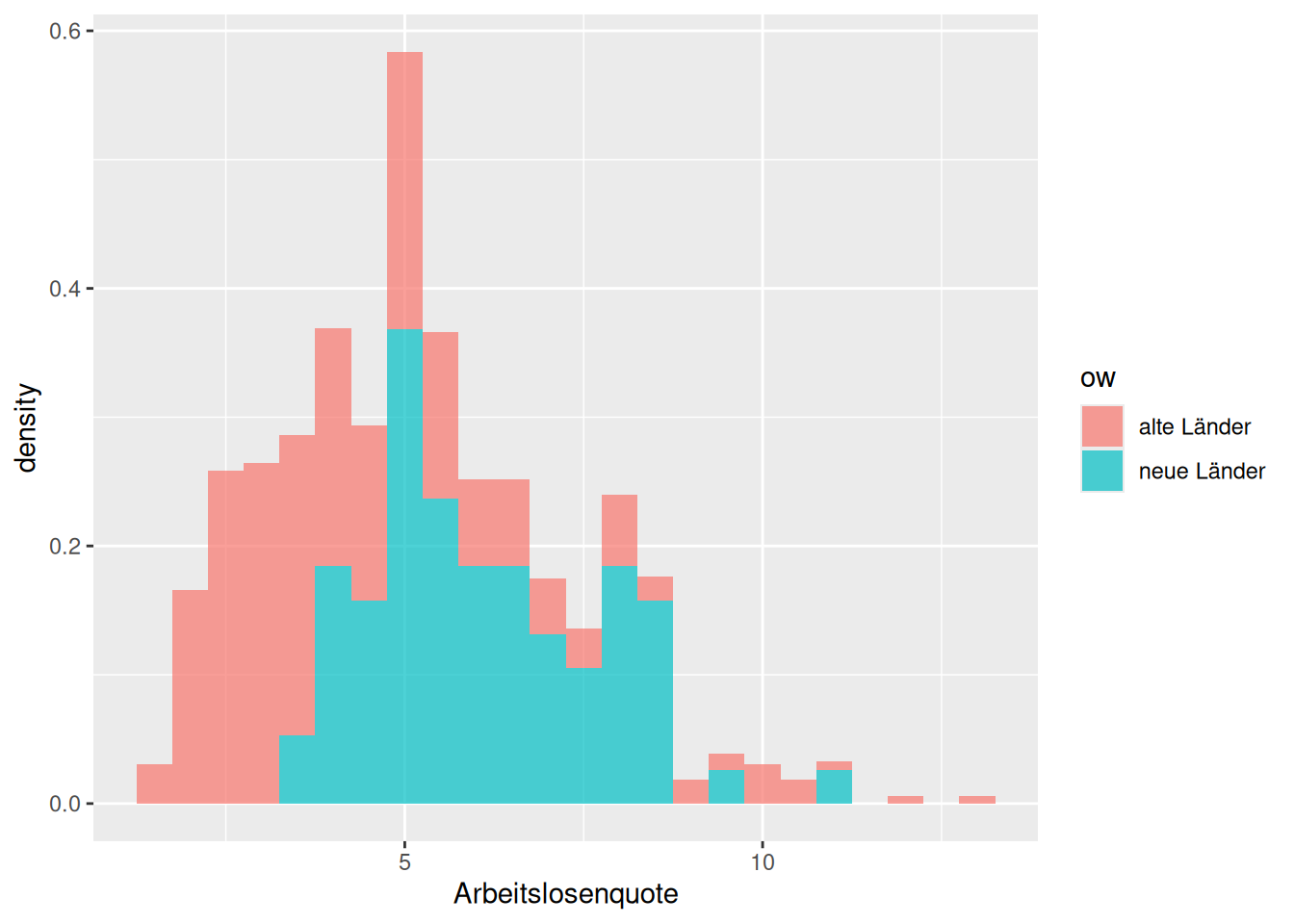

Wie wir sehen, ist die Varianz in den Neuen Ländern geringer als in den Alten Bundesländern.

var(subset(inkar, ow== "alte Länder")$Arbeitslosenquote)

## [1] 4.308633

var(subset(inkar, ow== "neue Länder")$Arbeitslosenquote)

## [1] 2.512992

Die Frage ist nun, ob diese Unterschiede zufällig zu erwarten sind.³⁷

var.test(subset(inkar, ow== "alte Länder")$Arbeitslosenquote,
       subset(inkar, ow== "neue Länder")$Arbeitslosenquote,
       ratio = 1, alternative = "two.sided")

## 
##  F test to compare two variances
## 
## data:  subset(inkar, ow == "alte Länder")$Arbeitslosenquote and subset(inkar, ow == "neue Länder")$Arbeitslosenquote
## F = 1.7145, num df = 324, denom df = 75, p-value = 0.00567
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  1.175527 2.402126
## sample estimates:
## ratio of variances 
##           1.714543

Der zweiseitige F-Test zeigt an, dass wir die Nullhypothese, dass beide Varianzen gleich groß sind (das beide Gruppen der Selben Grundgesamtheit entstammen) mit geringer Irrtumswahrscheinlichkeit verwerfen können.

Der einseitiger Test mit \(H_1: \sigma^2_{AL} > \sigma^2_{NL}\) ist erwartungsgemäß trennschärfer.

var.test(subset(inkar, ow== "alte Länder")$Arbeitslosenquote,
       subset(inkar, ow== "neue Länder")$Arbeitslosenquote,
       ratio = 1,
       alternative = "greater")

## 
##  F test to compare two variances
## 
## data:  subset(inkar, ow == "alte Länder")$Arbeitslosenquote and subset(inkar, ow == "neue Länder")$Arbeitslosenquote
## F = 1.7145, num df = 324, denom df = 75, p-value = 0.002835
## alternative hypothesis: true ratio of variances is greater than 1
## 95 percent confidence interval:
##  1.250266      Inf
## sample estimates:
## ratio of variances 
##           1.714543

Hat man mehrere Stichproben, könnte man diese jeweils paarweise vergleichen. So möchte man z.B. die Zahlungsbereitschaft von 10 verschiedenen Studiengängen hinsichtlich der Mittelwerte oder hinsichtlich der Varianzen vergleichen. Das mehrfache Testen ist allerdings problematisch, denn die Wahrscheinlichkeit, irrtümlich Unterschiede zu detektieren, die gar nicht existieren steigt mit der Anzahl der paarweisen Vergleiche. Bei 10 Gruppen hat man \(10 \choose 2\) = 45 Vergleiche, bei jedem Vergleich hat der Test die angenommene Irrtumswahrscheinlichkeit (z.b. 5%). Damit ist es relativ wahrscheinlich, dass wir zufällig mehrere Unterschiede detektieren, die gar nicht real sind.

Oftmals ist man allerdings gar nicht an den paarweisen unterschieden interessiert, sondern daran, ob sich die Gruppen unterscheiden - z.B. von einer Referenzgruppe. Dann nutzt man weiterhin die Varianzanalyse (ANOVA - analysis of variance), die sich auch auf den Fall mehrerer Gruppen übertragen lässt. Die ANOVA stellt einen Spezialfall des linearen Regressionsmodells dar und begegnet uns dort noch im Detail.

10.1.3 Wald Test

Der Wald-Test beruht ähnlich wie der t-Test auf dem Vergleich der Abweichung zwischen Schätzer und Vergleichswert und der Unsicherheit der Schätzung. Der Grundgedanke ist hier wieder die Abweichung in Bezug zur Unsicherheit zu setzen: ist die Abweichung bei der (geschätzten) Unsicherheit groß genug, dass sie nicht zufällig aufgetreten sein kann?

\[W=\frac{(\hat{\Theta}- \Theta_0)^2}{var(\hat{\Theta})}\]

\[\sqrt{W}=\frac{\hat{\Theta}-\Theta_0}{se(\hat{\Theta})}\] Im Gegensatz zum t-Test ist die Teststatistik \(W\) unter der Nullhypothese asymptotisch \(\chi^2\)-verteilt mit einem Freiheitsgrad, bzw. \(\sqrt{W}\) asymptotisch z-verteilt³⁸.

Der Wald-Test begegnet uns u.a. beim Signifikanztest von Regressionskoeffizienten beim generalisiertem linearem Modell (GLM).

Wald-Tests beruhen auf der Annahme, dass die likelihood normalverteilt ist (Zentraler Grenzwertsatz) und Schätzen anhand des Standardfehlers die Konfidenzintervalle. Genauer gesagt ist es ausreichend, dass die Likelihood Funktion quadratisch ist. Die Aussagekraft der Tests ist stark eingeschränkt, falls die Annahme verletzt ist.

Nachfolgende Abbildung symbolisiert wie der Wald-Test durchgeführt wird: die Differenz zwischen dem ML Schätzer und einem gewählten Parameter wird durch den Standardfehler der Schätzung geteilt um daraus die Irrtumswahrscheinlichkeit zu ermitteln.

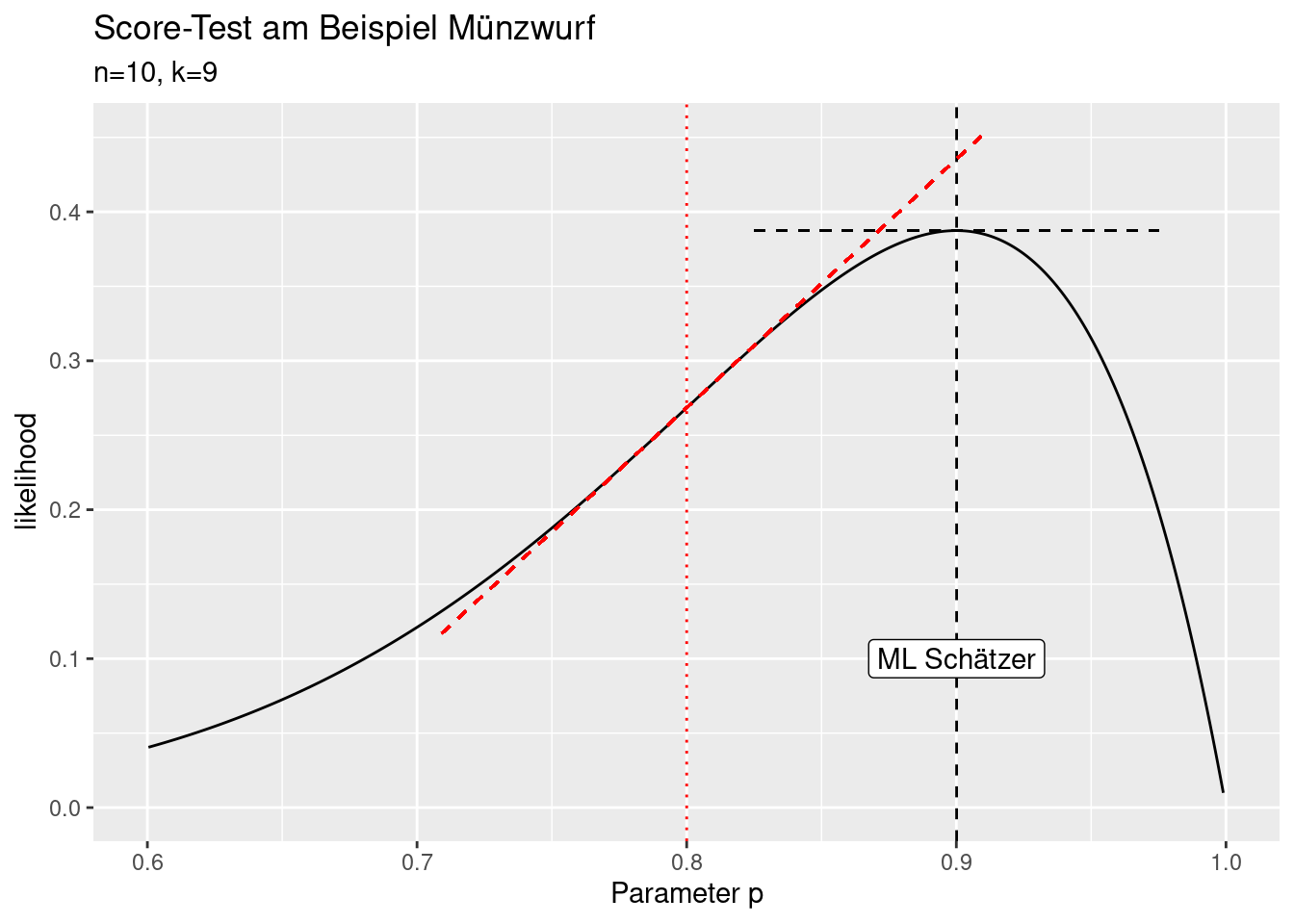
10.1.4 Likelihood Ratio Test

Likelihood-Ratio Tests beruhen auf dem Verhältnis der Likelihoods von Modellen mit unterschiedlichem Parameterwerten (oder Parametern). Sie sind im Allgemeinen verlässlicher als Wald- oder Score-Tests.

Es geht also im Gegensatzu zum Wald-Test nicht um das Verhältnis der Differenz der Parameterwerte in Relation zum Standardfehler, sondern um das Verhältnis der beiden Likelihoods. Die Test-Statstik berechnet sich für den ein-Parameter Fall und \(H_0: \Theta = \Theta_0\) als:

\[W= -2log\frac{L(\Theta_0)}{L(\hat{\Theta})} = 2log\frac{L(\hat{\Theta})}{L(\Theta_0)}\]

Die Teststatistik folgt asymptotisch einer \(\chi^2\)-Verteilung. Die Herleitung beruht auf dem Theorem von Wilk, das besagt das das Verhältnis von log-Likelihoods asmyptotisch normalverteilt ist. ³⁹ Die Anzahl Freiheitsgrade der \(\chi^2\)-Verteilung ergibt sich - in den meisten Fällen - als Differenz zwischen den Anzahl Parametern beider Modelle.

Mit dem ML Schätzer von 0.9000991 können wir z.B. testen, ob der wahre Wert nicht auch 0.8491502 sein könnte. Da wir für den ML Schätzer einen Parameter schätzen, während wir für den Vergleichswert keinen Parameter schätzen müssen ist die Differenz der Freiheitsgrade 1, d.h. wir verwenden ein \(\chi^2\)- Verteilung mit df=1 als Testverteilung. Die Irrtumswahrscheinlichkeit zeigt, dass wir die Nullhypothese, dass der wahre Wert gleich 0.8491502 sein könnte nicht ablehnen können. Dies liegt daran, das die Likelihood Funktion in diesem Bereich recht flach ist, was an der geringen Stichprobengröße (n=10) liegt.

testStat <- -2*log(binomLik(p=theta_0,k=9, n=10)/
        binomLik(p= 0.9000991, k= 9, n= 10))

1- pchisq(q=testStat, df=1)

## [1] 0.6355371

LR-Tests werden uns z.B. beim Vergleich von genesteten GLM begegnen.

10.1.5 Lagrange Multiplier oder Score-Tests

Lagrange Multiplier oder Score-Tests beruhen auf dem Vergleich der Steigung der Likelihood-Funktion an der Stelle des Parameters \(\Theta_0\) mit der Steigung an der maximum Likelihodschätzung (die 0 ist). Der Power der Tests ist geringer als beim LR und beim Wald-Test, sie werden angewandt, wenn die Likelihoodfunktion sich nur aufwendig berechnen lässt.

Die Teststatistik ergibt sich aus dem Verhältnis der quadrierten Score-Funktion \(U(\Theta)\), welche die Ableitung der Likelihood-Funktion an der Stelle \(\Theta\) beschreibt und der Fisher Information, welche die 2. Ableitung der Likelihood-Funktion an der Stelle \(\Theta\) beschreibt, was die Varianz der Score-Funktion angibt.

Auch beim Score-Test vergleicht man die Teststatistik mit einer \(\chi^2\)-Verteilung.

Der Score Test begegnet uns z.B. bei den Lagrange Multiplier Tests für räumliche Abhängigkeit und räumliche Heterogenität (s. z.B. Kursbuch Spatial Data Science).

10.1.6 Weitere parametrische Tests

Im Kapitel Assoziation werden wir uns mit Assoziationstests wie dem \(\chi^2\)-Test beschäftigen.

10.2 Verteilungstests

Bei dieser Kategorie von Tests geht es darum zu beurteilen, ob Beobachtungen zu einer Verteilung passen oder nicht. Das ist z.B. dann notwendig, wenn man entscheiden muss, ob die Voraussetzungen für die Anwendungen eines t-Tests oder F-Tests im Hinblick auf die Normalverteilungsannahme erfüllt sind.

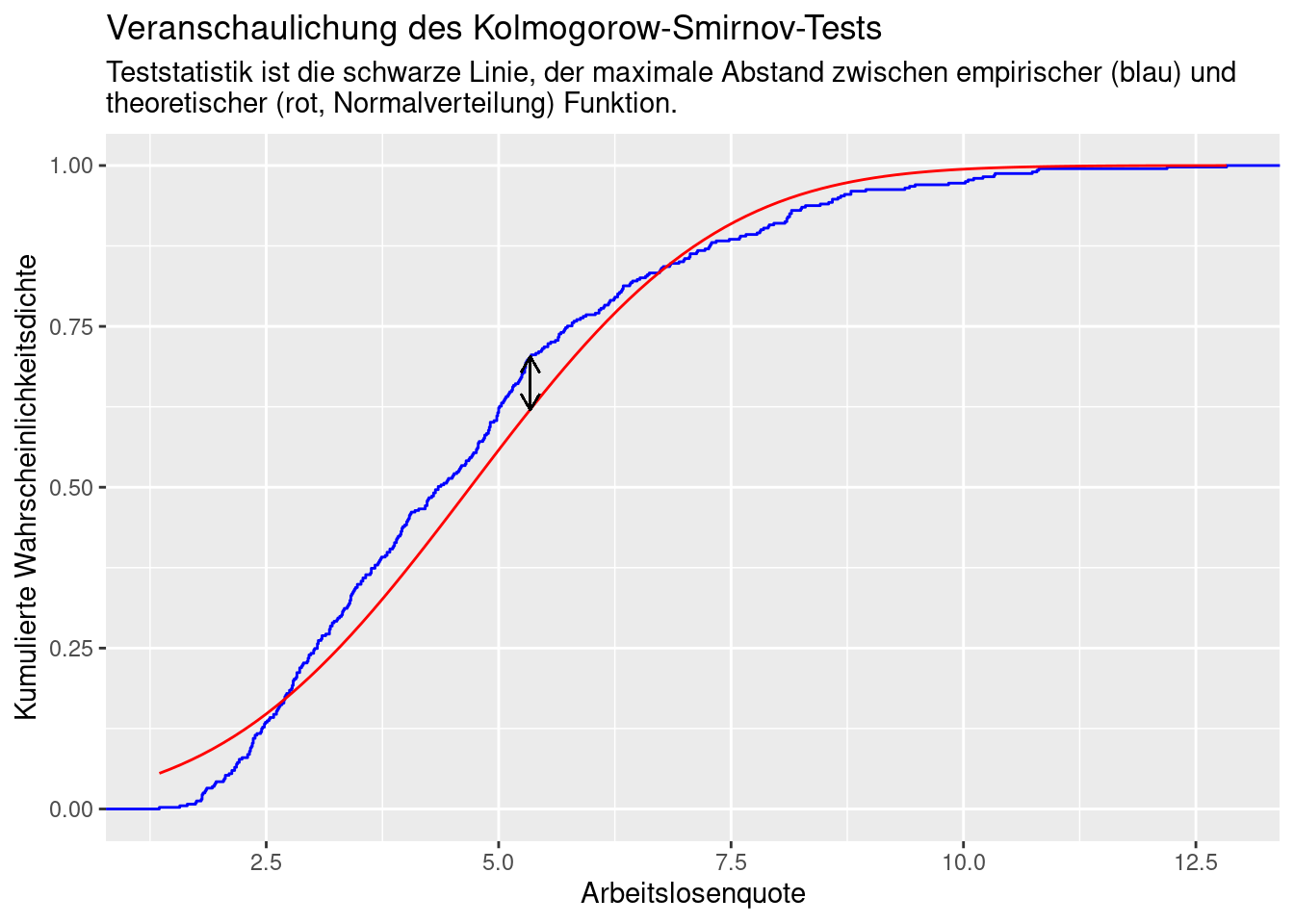
10.2.1 Vergleich von Verteilungen mittels des Kolmogorow-Smirnoff Tests

Der Kolmogorow-Smirnow-Test testet die Übereinstimmung zweier Wahrscheinlichkeitsverteilungen. Dies kann sowohl den Test ob zwei Zufallsvariablen eine identische Verteilung besitzen oder oder eine Zufallsvariable einer bestimmten Wahrscheinlichkeitsverteilung folgt umfassen.

Der Test testet ob die Zufallsvariable \(X\) die Verteilung \(F_0\) besitzt: \(H_0: F_X(x) = F_0(x)\).

\(H_1: F_X(x) \neq F_0(x)\)

Dabei wird die empirische Verteilungsfunktion \(F_n\) mit \(F_0\) anhand der Teststatistik \(d_n\) verglichen.

\[d_n = ||F_n-F_0|| = \sup_x|F_n(x) - F_0(x)| \] Wobei \(\sup_x\) das Supremum von \(x\) (die obere Schranke von x) angibt. Anschaulich gesprochen, nimmt \(d_n\) den Wert der größten absoluten Abweichung zwischen den beiden Verteilungen für alle Werte von \(x\) an.

Die empirische Verteilungsfunktion ist wie folgt definiert:

\[F_n = \frac{\textrm{Anzahl Elemente}\leq x}{n} = \frac{1}{n}\sum_{i=1}^nI_{(-\infty,x]}(X_i) \]

Wobei \(I_{(-\infty,x]}(X_i)\) die Indikatorfunktion definiert, die 1 annimmt, wenn \(X_i\leq x\) und 0 sonst.

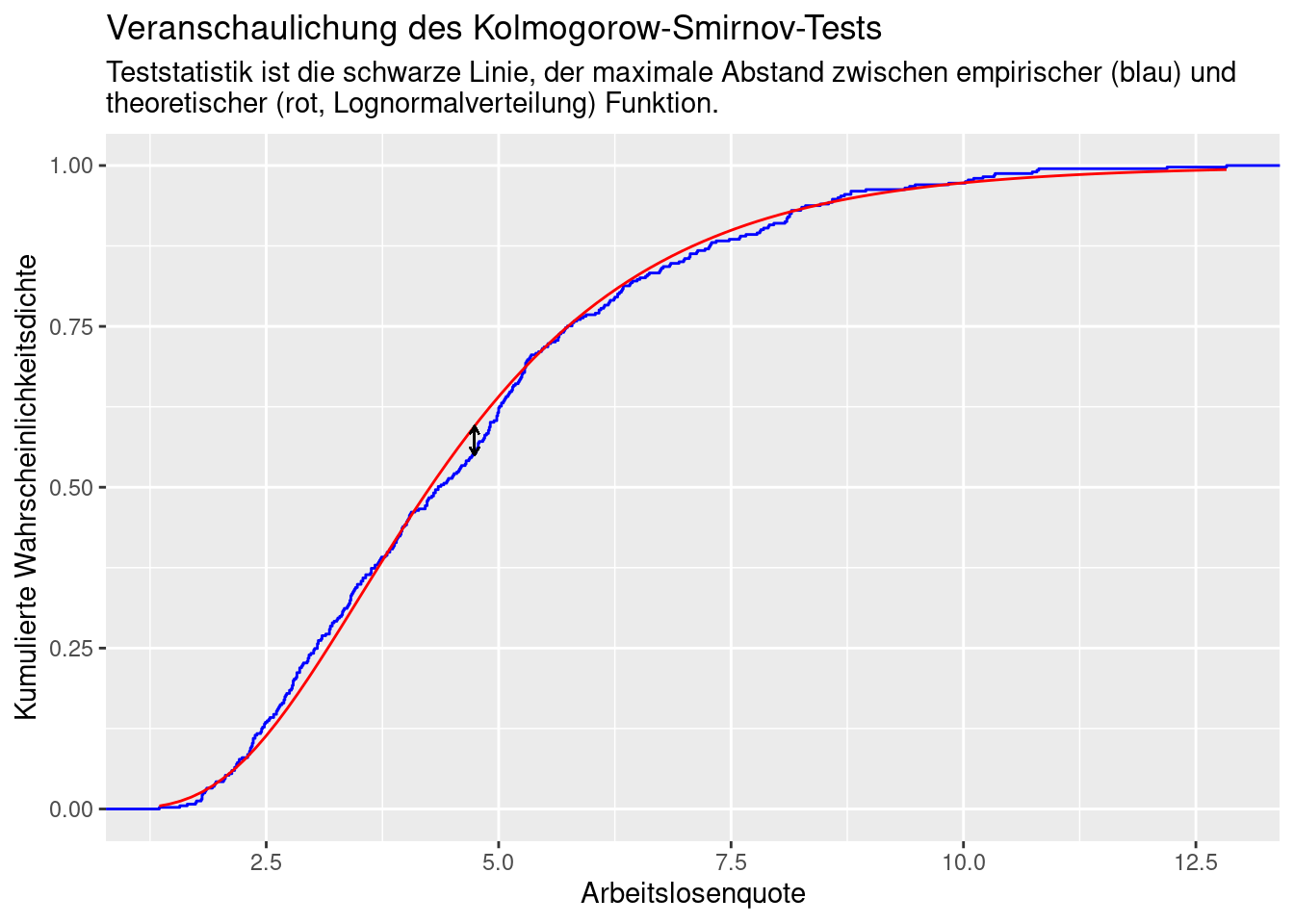
In R wird der Test mittels ks.test durchgeführt. Da wir gegen eine parametrisierte Verteilung testen möchten, fitten wir die Verteilungsparameter mittels fitdistr. Für die Funktion in y sind nur kontinuierliche Funktionen zulässig.

aqNorm_params <- fitdistr(inkar$Arbeitslosenquote, densfun = "normal")

ks.test(x = inkar$Arbeitslosenquote, 
        y= pnorm, mean = aqNorm_params$estimate[1],
                            sd = aqNorm_params$estimate[2])

## Warning in ks.test.default(x = inkar$Arbeitslosenquote, y = pnorm, mean =
## aqNorm_params$estimate[1], : ties should not be present for the one-sample
## Kolmogorov-Smirnov test

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  inkar$Arbeitslosenquote
## D = 0.083085, p-value = 0.007882
## alternative hypothesis: two-sided

Der Test zeigt an, dass wir die Nullhypothese, dass die Arbeitslosenquote der Kreise in Deutschland einer Normalverteilung folgt mit geringer Irrtumswahrscheinlichkeit verworfen werden kann. Das die Daten unter Annahme der Normalverteilung (\(H_0\)) zustande gekommen sind ist unwahrscheinlich, weswegen wir \(H_0\) ablehnen.

Die Warnung zeigt, dass wir dem Test nur eingeschränkt vertrauen werden können, da der selbe Wert mehrfach vorkommt (ties). Der Plot der empirischen Wahrscheinlichkeitsdichtefunktion weiter oben zeigt allerdings, dass das Problem hier nicht sehr groß sein dürfte.

aq_params <- fitdistr(inkar$Arbeitslosenquote, densfun = "lognormal")

ks.test(x = inkar$Arbeitslosenquote, 
        y= plnorm, meanlog = aq_params$estimate[1],
                            sdlog = aq_params$estimate[2])

## Warning in ks.test.default(x = inkar$Arbeitslosenquote, y = plnorm, meanlog =
## aq_params$estimate[1], : ties should not be present for the one-sample
## Kolmogorov-Smirnov test

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  inkar$Arbeitslosenquote
## D = 0.044971, p-value = 0.392
## alternative hypothesis: two-sided

Bei einer Lognormalverteilung können wir die Nullhypothese nicht verwerfen. Es ist gut möglich, dass die Daten aus einer log-normalverteilten Grundgesamtheit entstammen (s. p-Wert). Deswegen sollten wir die Nullhypothese (die Daten entstammen einer Log-Normalverteilung) nicht ablehen.

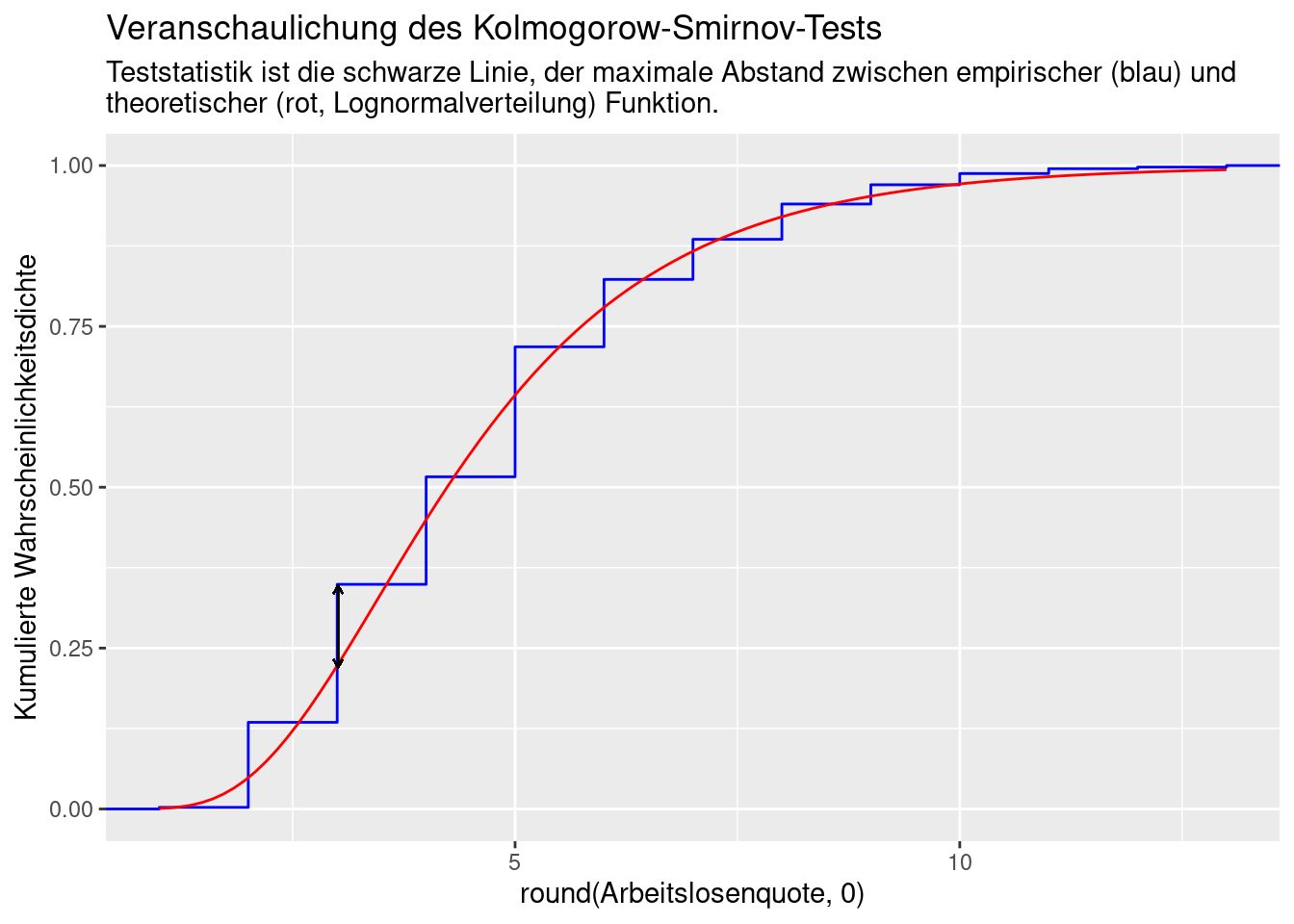
Damit steht aber auch die Aussagekraft der obigen Varianzanalyse über den F-Test in Frage.

10.2.1.0.1 Effekt von Rundung auf Ergebnis des KS-Tests

Der KS-Test reagiert sensitiv auf Datenbindungen. Diese können z.B. durch Rundungen entstehen. Wir schauen uns für das Beispiel der Arbeitslosenquote beim Vergleich mit der Lognormalverteilung an. Runden wir die Werte auf eine Nachkommastelle (die Originaldaten sind auf zwei Nachkommastellen gerundet), dann können wir die Nullhypothese nicht ablehnen. Bei Rundung auf Null Nachkommastellen lehnen wir die Nullhypothese dagegen ab.

aqRound1_params <- fitdistr(round(inkar$Arbeitslosenquote,1), 
                      densfun = "lognormal")

ks.test(x = round(inkar$Arbeitslosenquote,1), 
        y= plnorm, meanlog = aqRound1_params$estimate[1],
                            sdlog = aqRound1_params$estimate[2])

## Warning in ks.test.default(x = round(inkar$Arbeitslosenquote, 1), y = plnorm, :
## ties should not be present for the one-sample Kolmogorov-Smirnov test

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  round(inkar$Arbeitslosenquote, 1)
## D = 0.05238, p-value = 0.2212
## alternative hypothesis: two-sided

aqRound0_params <- fitdistr(round(inkar$Arbeitslosenquote,0), 
                      densfun = "lognormal")

ks.test(x = round(inkar$Arbeitslosenquote,0), 
        y= plnorm, meanlog = aqRound0_params$estimate[1],
                            sdlog = aqRound0_params$estimate[2])

## Warning in ks.test.default(x = round(inkar$Arbeitslosenquote, 0), y = plnorm, :
## ties should not be present for the one-sample Kolmogorov-Smirnov test

## 
##  Asymptotic one-sample Kolmogorov-Smirnov test
## 
## data:  round(inkar$Arbeitslosenquote, 0)
## D = 0.127, p-value = 4.823e-06
## alternative hypothesis: two-sided

Der Plot der empirischen Verteilung zeigt sehr deutlich die Datenbindungen, was zu sprunghafen anstelle von kontinuierlichen Anstiegen in der empirischen Verteilungsfunktion führt. Dies führt zu größeren Abstände zur Log-Normalverteilung, damit einem größeren Wert der Testverteilung und damit einem kleineren p-Wert (es wird unwahrscheinlicher, dass die Beobachtungen einer log-normalverteilten Grundgesamtheit entstammen).

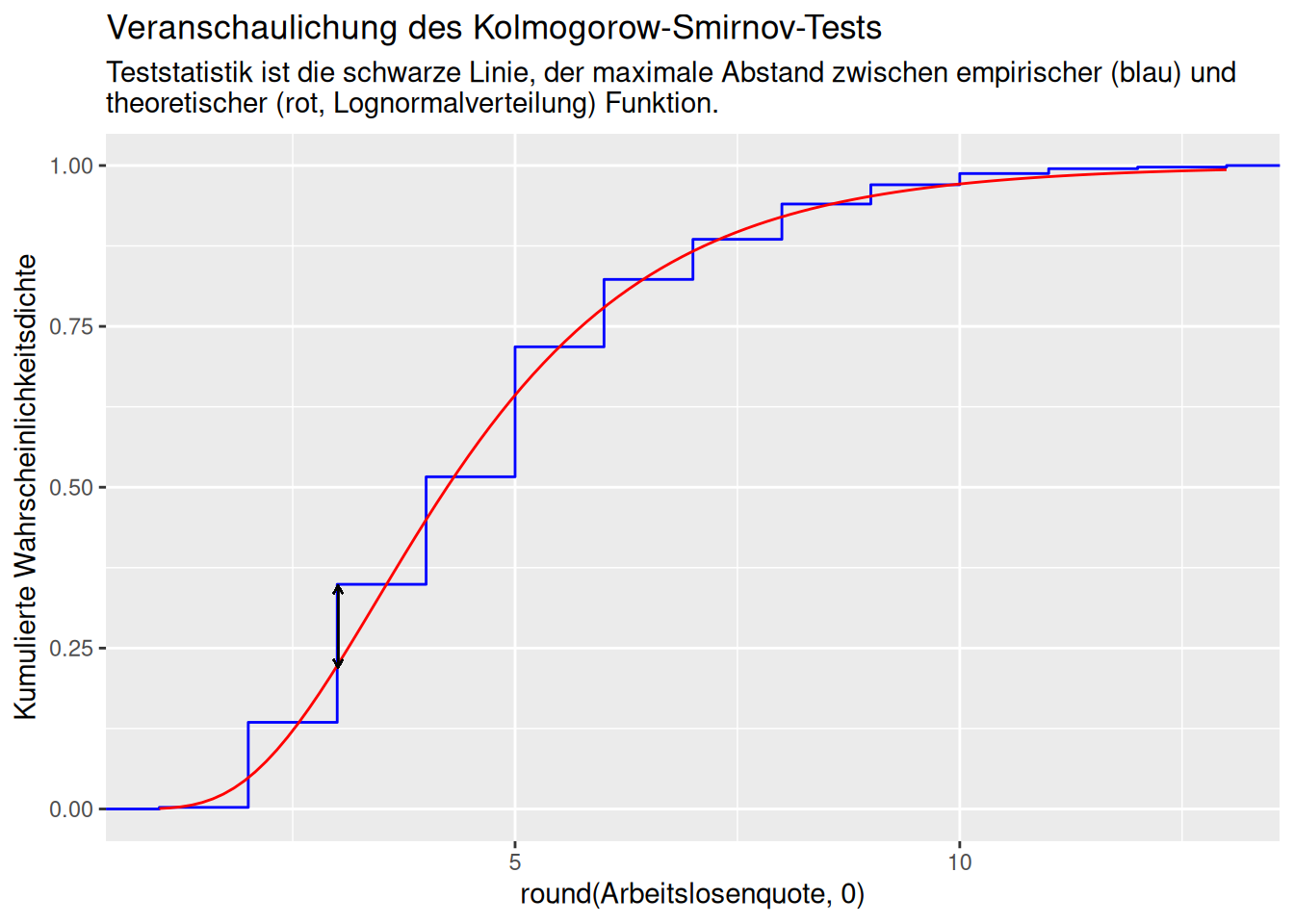
Deswegen ist es wichtig, den QQ-Plot zu betrachten und aufmerksam im Hinblick auf die Warnmeldungen des KS-Tests zu sein. Wie Abbildung @ref(fig:qqPlotsAqKS_rounding) zeigt folgen die beobachteten Quantile der Log-Normalverteilung relativ gut. Allerdings treten bei höhren Quantilen größere Abweichungen auf, die aber tendenziell noch in Ordnung sind. Die Rundung auf keine Nachkommastelle (Teilabbildung c) überlagert den Zusammenhang, allerdings wird hier deutlich, dass die Abweichung nicht so bedeutend ist wie sie der KS-Test suggeriert.

aqRound0_paramsList <- list(meanlog = aqRound0_params$estimate[1],
                            sdlog = aqRound0_params$estimate[2])
aqRound1_paramsList <- list(meanlog = aqRound1_params$estimate[1],
                            sdlog = aqRound1_params$estimate[2])
aq_paramsList <- list(meanlog = aq_params$estimate[1],
                            sdlog = aq_params$estimate[2])

pqqRound0 <- ggplot(inkar, aes(sample = round(Arbeitslosenquote,0))) +
  stat_qq(distribution = qlnorm, dparams =   aqRound0_paramsList) +
  stat_qq_line(distribution = qlnorm, dparams = aqRound0_paramsList) +
  ylab("Quantile Beobachtung") +
  xlab("Theoretische Quantile Log-Normalverteilung") +
  labs(title = "Arbeitslosenquote", subtitle = "gerundet auf keine Nachkommastelle")

pqqRound1 <- ggplot(inkar, aes(sample = round(Arbeitslosenquote,1))) +
  stat_qq(distribution = qlnorm, dparams =   aqRound1_paramsList) +
  stat_qq_line(distribution = qlnorm, dparams = aqRound1_paramsList) +
  ylab("Quantile Beobachtung") +
  xlab("Theoretische Quantile Log-Normalverteilung") +
  labs(title = "Arbeitslosenquote", subtitle = " gerundet auf eine Nachkommastelle")

pqq <- ggplot(inkar, aes(sample = Arbeitslosenquote)) +
  stat_qq(distribution = qlnorm, dparams =   aq_paramsList) +
  stat_qq_line(distribution = qlnorm, dparams = aq_paramsList) +
  ylab("Quantile Beobachtung") +
  xlab("Theoretische Quantile Log-Normalverteilung") +
  labs(title = "Arbeitslosenquote", subtitle = "keine Rundung")

ggarrange(ggExtra::ggMarginal(pqq, type="histogram", size=5),
          ggExtra::ggMarginal(pqqRound1, type="histogram", size=5),
          ggExtra::ggMarginal(pqqRound0, type="histogram", size=5), labels = "auto"
)

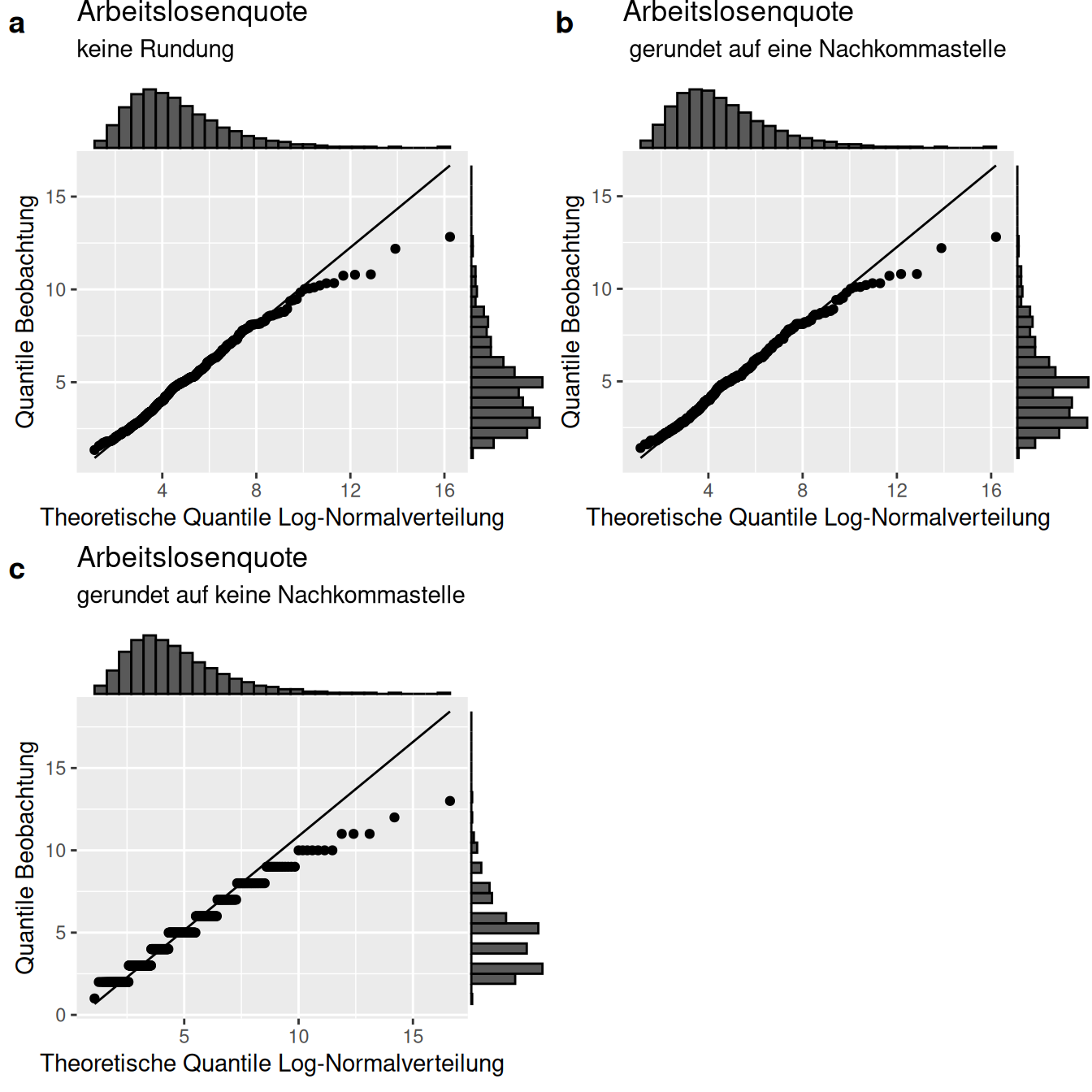
(#fig:qqPlotsAqKS_rounding)Effekt von Rundungen am Beispiel der Arbeitslosenquote auf Kreisbasis (INKAR Daten). Gezeigt sind jeweils die QQ-Plots gegen die Log-Normalverteilung. Die Werte wurden in den Teilabbildungen b) und c) auf eine bzw. keine Nachkommastelle gerundet um den Effekt gerundeter Daten auf die Verteilung deutlich zu machen.

Ein Blick auf den QQ-Plot der ungerundeten Werte gegen die Normalverteilung (??) zeigt stärkere Abweichungen bei kleinen und bei großen Werten. Die Normalverteilung unterschätzt in beiden Bereichen die auf Grundlage der beobachteten Werte geschätzten Quantile.

aqNorm_paramsList <- list(mean = aqNorm_params$estimate[1],
                            sd = aqNorm_params$estimate[2])
pqqNormal <- ggplot(inkar, aes(sample = Arbeitslosenquote)) +
  stat_qq(distribution = qnorm, dparams =   aqNorm_paramsList) +
  stat_qq_line(distribution = qnorm, dparams = aqNorm_paramsList) +
  ylab("Quantile Beobachtung") +
  xlab("Theoretische Quantile Normalverteilung") +
  labs(title = "Arbeitslosenquote", subtitle = "keine Rundung")

ggExtra::ggMarginal(pqqNormal, type="histogram", size=5)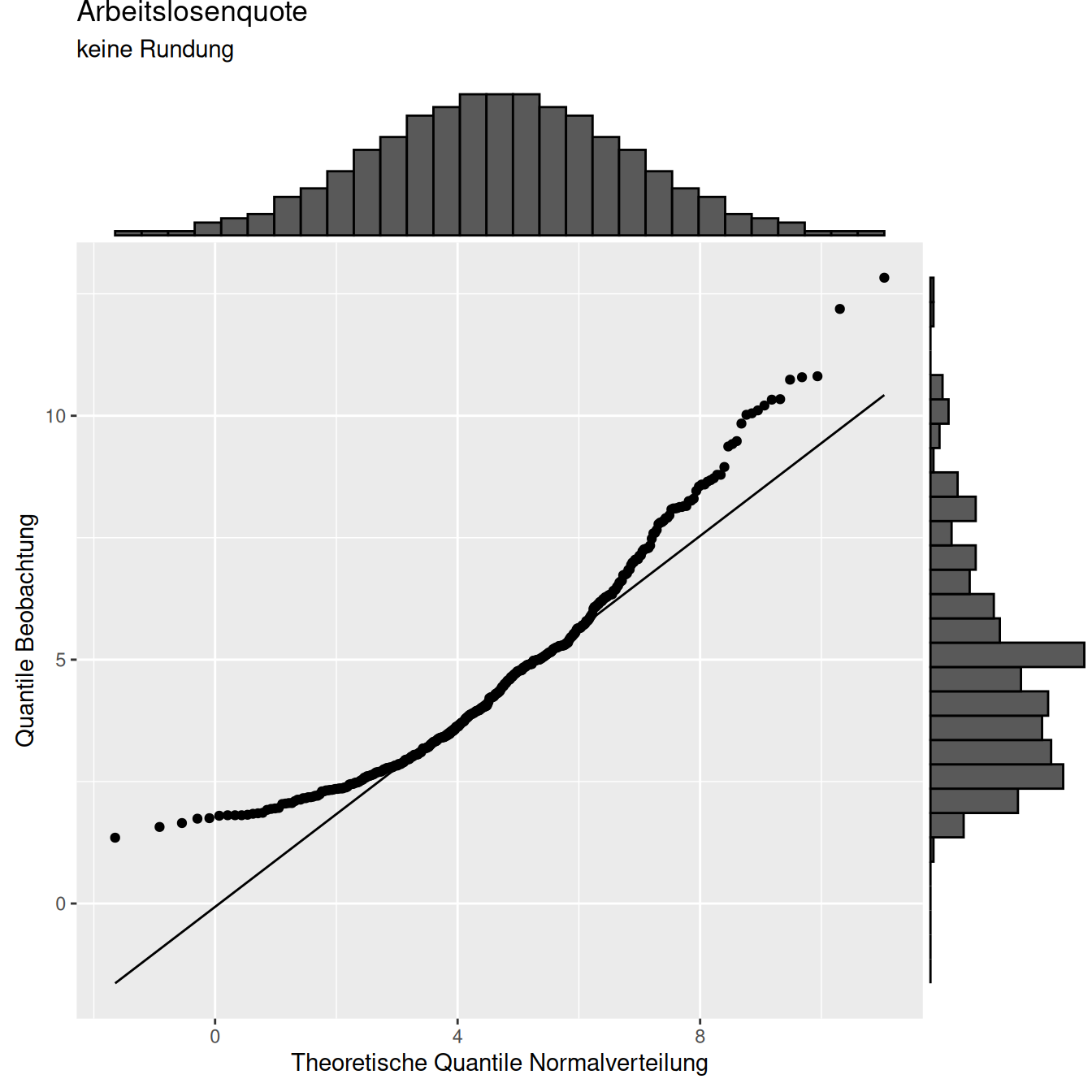

Figure 10.4: QQ-Plot der (ungerundeten) Arbeitslosenquote der Kreise der BRD gegen die Quantile der (bestangepassten) Normalverteilung.

10.2.1.1 Weitere Verteilungstests

Neben dem KS Test gibt es eine Vielzahl von Tests auf Übereinstimmung der Verteilung von Beobachtungen mit theoretischen Verteilungen. Aufgrund der großen Bedeutung der Normalverteilung in vielen Anwendungen - bzw. der fehlenden Bereitschaft, sich mit anderen Verteilungen auseinanderzusetzen - gibt es viele Tests, die explizit nur auf die Annahme normalverteilter Daten testen.

Will man die Verteilung von Daten bzw. Residuen⁴⁰ auf Normalverteilung testen, dann sind von den angesprochenen Tests der Anderson-Darling-Test und der Shapiro-Wilk-Test in den meisten Fällen vorzuziehen, da sie die größte Teststärke aufweisen.

10.2.1.1.1 Lilliefors-Test

Der Lilliefors-Test (nortest::lillie.test) ist eine für die Normalverteilung korrigierte Version des Kolmogorow-Smirnov-Tests. \(H_0\) lautet wieder: Die Stichprobe ist normalverteilt.

10.2.1.1.2 Anderson-Darling goodness of fit Test

Der Anderson-Darling goodness of fit Test (Anderson and Darling 1952) testet auf Übereinstimmung mit kontiuierlichen Verteilungen (ADGofTest::ad.test). Der Test beruht auf einer Transformation der nach Größe sortierten Werte in der Stichprobe in eine Gleichverteilung anhand der Verteilungsfunktion der vorgegebenen hypothetischen Wahrscheinlichkeitsverteilung. Als Prüfgröße fungiert der Abstand der transformierten Stichprobendaten zur Verteilungsfunktion der Gleichverteilung. \(H_0\) lautet wieder: Die Stichprobe ist normalverteilt.

10.2.1.1.3 Shapiro und Wilks Test

Der Shapiro und Wilks Test [shapiro_analysis_1965] testet eine empirische Verteilung auf Übereinstimmung mit der Normalverteilung (shapiro.test). Im Kern beruht der Test auf einer Varianzanalyse. Die verwendete Teststatistik berechnet, wie die Varianz einer Stichprobe aussehen müsste, wenn sie aus einer normalverteilten Grundgesamtheit stammte, und vergleicht diese erwartete Varianz mit einem zweiten Schätzer für die tatsächliche Varianz der Stichprobe. \(H_0\) ist, dass die Daten einer Normalverteilung folgen. Folgende Vorraussetzungen müssen erfüllt sein:

• unabhängige Beobachtungen
• Stichprobenumfang zwischen 3 und 5000
• metrisch skalierte Beobachtungen
• Abwesenheit von Datenbindungen

10.2.1.1.4 Jarque-Bera-Test

Der Jarque-Bera-Test (Jarque and Bera 1980) vergleicht die Schiefe und Kurtosis der empirischen Verteilung mit denen einer Normalverteilung (moments::jarque.test oder tseries::jarque.bera.test). Die Teststatistik \(JB\) ist \(\chi^2\)-verteilt mit zwei Freiheitsgraden. \(H_0\) lautet wieder: Die Stichprobe ist normalverteilt.

\[JB= \frac{n}{6}(\gamma^2+\frac{(\omega-3)^2}{4})\] wobei \(\gamma\) die Schiefe und \(\omega\) die Kurtosis der empiritschen Daten sind.

10.2.1.2 Kritische Anmerkungen zu Verteilungstests

In der Praxis ist man an der Verteilung der Residuen interessiert, nicht an der Verteilung der Rohdaten, d.h. die Verteilung der Werte, nachdem man strukturelle Effekte berücksichtigt hat.

Bei kleinen Stichproben sind die Tests i.d.R. nicht trennscharf genug, während bei sehr großen Stichproben werden auch kleine / unwichtige Abweichungen als signifikant erkannt werden. Generell gesprochen helfen Tests alleine oft nicht, eine Problem anzugehen, da sie zwar die Anwesenheit eines Problems anzeigen können, jedoch die Ursache i.d.R. nicht wirklich eingrenzen können (sogenannte Omnibus Tests). Sie sollten darum immer durch graphische Verfahren wie QQ-Plots ergänzt werden.

Schauen wir uns das einmal für den Kolmogorov-Smirnov Test an. Wir simulieren 10.000 Stichproben für 4 verschiedene Stichprobengrößen (7,20, 50 und 500) für drei verschiedene Verteilungen (Standardnormalverteilung, Lognormalverteilung und Cauchsverteilung) und berechnen jeweils den p-Wert und speichern den in einem dat.frame.

set.seed(17)
nRep <- 10^3
theSampleSizes <- c(7, 20, 50, 500)
nSizes <- length(theSampleSizes)
nDist <- 3
ksSim <- data.frame(pval=rep(NA,nRep*nSizes*nDist),n=NA, popDistr=NA )

# function that evaluates the test and returns the pvalue
# currently only for normal distribution
getKSpval4norm <- function(sample)
{
  params <- fitdistr(sample, densfun = "normal")
  testres <- ks.test(x = sample, 
        y= pnorm, mean = params$estimate[1],
        sd = params$estimate[2])
  return(testres$p.value)
}

counter <- 0
for(i in 1:nRep)
{
  for(j in 1:nSizes)
  {
    n <- theSampleSizes[j]
    
    counter <- counter +1
    theSample <- rnorm(n=n, mean=0, sd=1)
    ksSim$pval[counter] <- getKSpval4norm(theSample)
    ksSim$n[counter] <- n
    ksSim$popDistr[counter] <- "N(0,1)"
    
    counter <- counter +1
    theSample <- rlnorm(n=n, meanlog =0, sdlog=1)
    ksSim$pval[counter] <- getKSpval4norm(theSample)
    ksSim$n[counter] <- n
    ksSim$popDistr[counter] <- "logN(0,1)"

    counter <- counter +1
    theSample <- rcauchy(n=n, location =0, scale = 1)
    ksSim$pval[counter] <- getKSpval4norm(theSample)
    ksSim$n[counter] <- n
    ksSim$popDistr[counter] <- "Cauchy(0,1)"    
     
  }
}

Wie oft wir die Nullhypothese abgelehnt?

ksSimAgg <- ksSim %>%
  mutate(h0rejected = ifelse(pval <0.05, 1,0)) %>%
  group_by(popDistr, n) %>%
  summarise(h0rejected = sum(h0rejected)/10^4) 

## `summarise()` has grouped output by 'popDistr'. You can override using the
## `.groups` argument.

knitr::kable(ksSimAgg)

popDistr	n	h0rejected
Cauchy(0,1)	7	0.0047
Cauchy(0,1)	20	0.0519
Cauchy(0,1)	50	0.0937
Cauchy(0,1)	500	0.1000
N(0,1)	7	0.0000
N(0,1)	20	0.0000
N(0,1)	50	0.0000
N(0,1)	500	0.0000
logN(0,1)	7	0.0004
logN(0,1)	20	0.0213
logN(0,1)	50	0.0820
logN(0,1)	500	0.1000

Wir sehen, dass für kleine Stichprobengrößen die Nullhypothese sowohl für die Cauchy als auch für die Lognormalverteilung deutlich zu selten abgelehnt wird. Selbst bei einer Stichprobengröße von 50 wird die Nullhypothese (“Die Stichprobe stammen von einer normalverteilten Grundgesamtheit”) nur in 81% der Fälle abgelehnt. Wir sehen auch, dass Stichproben, die einer Normalverteilung entspringen sehr sich als solche erkannt werden.

Wie verteilen sich die p-Werte?

ggplot(ksSim, aes(x=pval)) +
  geom_histogram() + 
  geom_vline(xintercept = 0.05, lty=2, col="red") +
  facet_wrap(~popDistr +n, scale="free_y") +
  xlab("Irrtumswahrscheinlichkeit") +
  ylab("Häufigkeit") +
  labs(title="Irrtumswahrscheinlichkeit beim KS Test auf Normalverteilung",
       subtitle="Test auf Normalverteilung bei verschiedenen Stichprobengrößen und Verteilungen")

## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.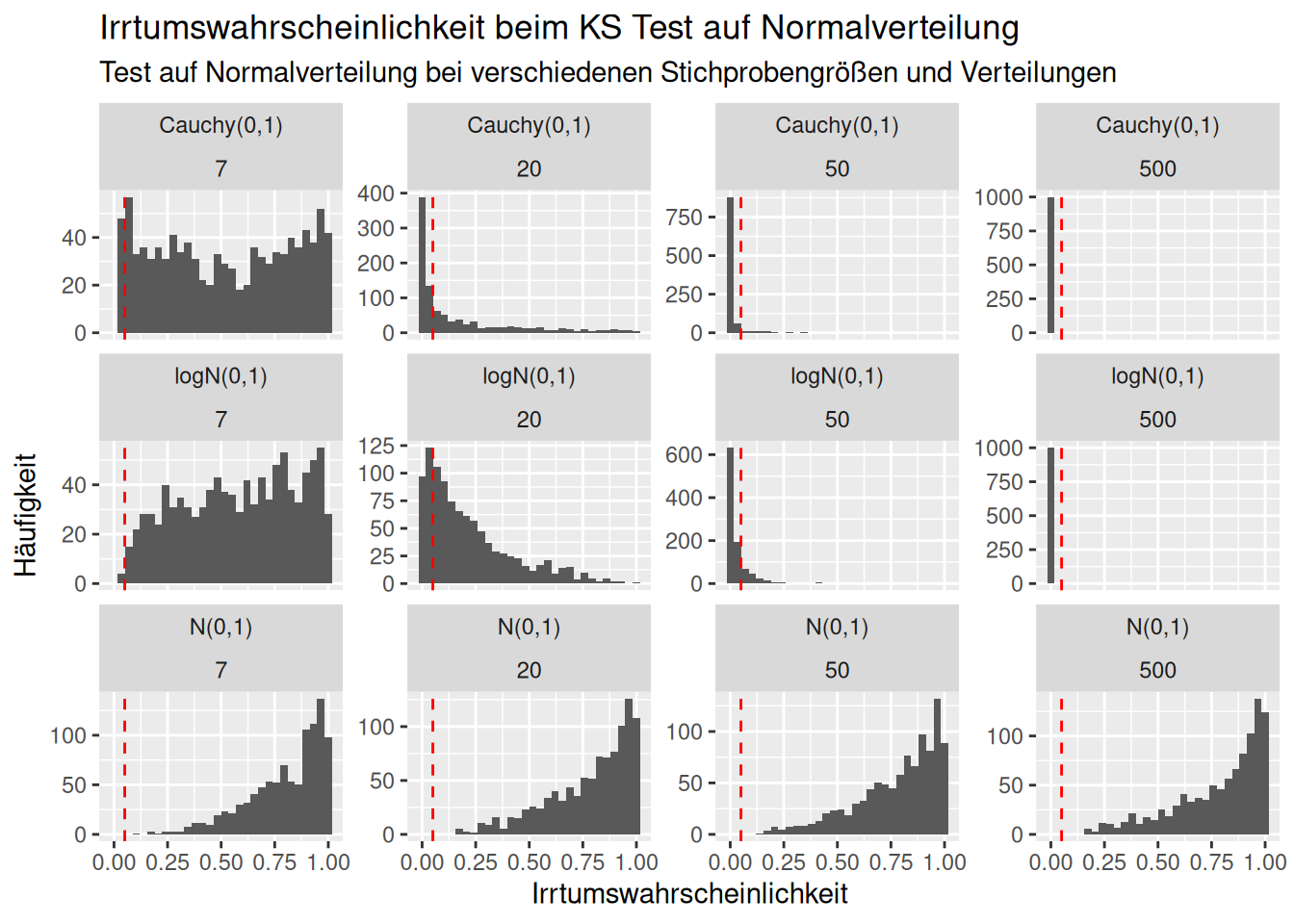

10.3 Nicht-parametrische Tests

Nicht parametrische Test machen sie keine Annahmen über die Wahrscheinlichkeitsverteilung der untersuchten Variablen und sind deswegen auch anwendbar, wenn die bei vielen statistischen Aussagen notwendigen Verteilungsvoraussetzungen nicht erfüllt sind. Die Ergebnisse parameterfreier Tests sind invariant - d.h. sie ändern sich nicht - gegenüber Transformationen der Variablen mit beliebigen streng monotonen Funktionen.

Bei parameterfreien Modellen wird im Gegensatz zu parametrischen Modellen die Modellstruktur nicht a priori festgelegt wird, sondern aus den Daten bestimmt wird. Der Begriff parameterfrei bedeutet somit nicht, dass solche Modelle überhaupt keine Parameter besitzen. Die Art und Anzahl der Parameter ist flexibel und nicht von vornherein festgelegt.

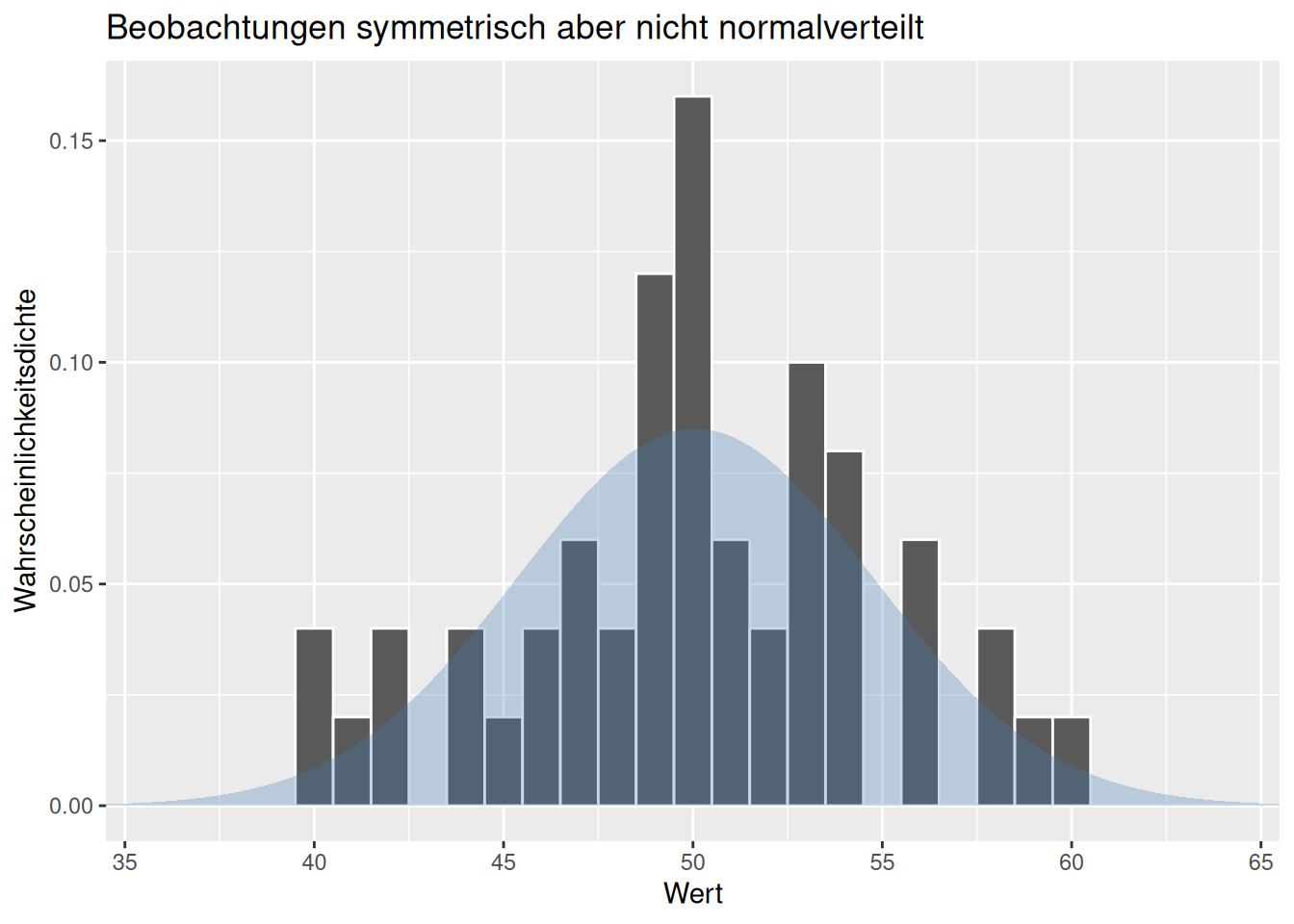
Im folgenden werden Alternativen für den gepaarten und den ungepaarten t-Test gezeigt um an diesem einfachen Beispiel zu demonstrieren, wie das Vorgehen ist. Falls die Voraussetzungen für den t-Test nicht erfüllt sind, können möglicherweise die Rangtransformationsstests (Wilcoxon-Mann-Whitney-Test und Wilcoxon-Vorzeichen-Rang-Test) angewandt werden, da diese nur die Voraussetzung symmetrisch verteilter Daten haben. Dies ist weniger streng als die Annahme normalverteilter Daten beim t-Test (s. Abbildung @ref(fig:dataSymNotNoraml}).

Eine weitere Familie von nicht-parametrischen Test sind die Permutationstest, welche darauf beruhen, anhand einer Permutation der Daten zu überprüfen, wie wahrscheinlich die Teststatistik unter der Nullhypothese auftritt.

10.3.1 Wilcoxon-Vorzeichen-Rang-Test

Der Wilcoxon-Vorzeichen-Rang-Test ist eine Alternative zum gepaartem t-Test, wenn die Vorraussetzungen (kontinuierliche Daten, annähernd normalverteilt) nicht erfüllt sind, die allerdings symetrisch verteilt sind. Er wird deswegen oftmals bei ordinal skalierten Variablen eingesetzt. Der Test setzt voraus, dass wir es mit gepaarten Daten zu tun haben.

Der Grundgedanke ist, dass je Paar die Differenz des Merkmals je Paar berechnet wird (z.B. für vorher/nachher). Die Absolutwerte der Differenzen werden gereiht dann gereiht und die Ränge berechnet. Der Rang wird jeweils mit dem Vorzeichen versehen, je nachdem ob die Differenz negativ oder positiv ist. Differenzen von 0 werden ignoriert. Wir berechnen dann Summe der negativen und positiven Ränge und verwenden den mit dem kleineren Absolutwert (Erwartungswert) sowie dessen Standardfehler und testen ähnlich wie beim t-Test (Vergleich des Mittelwertes mit dem Standardfehler). Wenn wir die Differenzen nicht gegen Null vergleichen (Einstichprobentest), sondern für zwei Gruppen, berechnen wir jeweils den Mittelwert und den Standardfehler je Gruppe und testen dann, ob sich diese signigikant unterscheiden.

Der Test verwendet anstelle der Mittelwerte (wie beim t-Test) die Mediane der Grundgesamtheit und testet, ob diese gleich sind. Der Test vergleicht dabei nicht die Mediane der Stichproben, sondern den Median der Differenzen der gepaarten Werte.

\[H_0: median(x_1 - x_2) = 0\]

\[H_A: median(x_1 - x_2) \neq 0\] (für den zweiseitigen Test)

Die Teststatistik beruht auf den Differenzen der gepaarten Wertepaare \(D_i = X_i - Y_i\). Diese werden dann sortiert und der Rang von \(D_i\) (\(R_i\)) bestimmt.

Die Teststatistik berechnet sich wie folgt:

\[T = \sum_{i=1}^n sgn(D_i)\cdot R_i\]

Wobei \(sgn(x)\) die Vorzeichenfunktion ist:

\[ sgn(x) = \left \{ \begin{array}{rr} 1 & x > 0\\\ 0 & x = 0 \\ -1 & x < 0\\ \end{array} \right.\]

Der Wert der Teststatistik wird dann mit der Verteilung unter der Nullhypothese verglichen. Unter \(H_0\) erwartet man asymptotisch eine Normalverteilung, wobei Korrekturfaktoren für kleine Stichprobengrößen zusätzlich zur Anwendung kommen.

Oft führt man noch eine z-Transformation durch um dann mit der Standardnormalverteilung agieren zu können: Wir berechnen den Mittelwert \(\bar{T} = \frac{n(n+1)}{4}\). Die Formel \(\bar{T} = \frac{n(n+1)}{4}\) ergibt sich einfach wenn wir uns überlegen, dass wir bei \(n\) Elementen die Ränge von 1 bis n haben. Wenn wir die Summe von \(n\) Zahlen berechnen, so ist die \(\sum_{i=1}^{k}= \frac{n(n+1)}{2}\) (Gaußsche Summenformel). Wenn negative und positive Differenzen zufällig auftreten, erwarten wir, dass die Summe der Ränge der negativen und der positiven Differenzen gleich groß ist, d.h. wir erwarten, dass die Summe der Ränge der positiven und negativen Ränge \(\frac{n(n+1)}{2} \cdot \frac{1}{2} = \frac{n(n+1)}{4}\) ist.

Der Standardfehler dieses Erwartungswertes berechnet sich als \(\text{SE}_{\bar{T}} = \sqrt{\frac{n(n+1)(2n+1)}{24}}\).

\(\frac{T-\bar{T}}{\text{SE}_{\bar{T}}}\) ist dann standardnormalverteilt. Damit können wir dann direkt sagen, dass die Wahrscheinlichkeit, einen Wert von \(|T| > 1.96\) zu erhalten bei 5% liegt.

Wenn Differenzen von 0 auftreten, ändert sich die Verteilung unter der Nullhypothese, so dass keine exakten p-Werte (Irrtumswahrscheinlichkeiten) angegeben werden können.

In R wird der Test mittels wilcox.test(x,y, paired=TRUE) berechnet.

Wenden wir dies auf die Daten aus den gepaarten Zahlungsbereitschaftsbefragungen an - z.B. weil wir Zweifel an der Normalverteilung der Daten haben.

wilcox.test(y= tTestDat2paired$willingness2payAfter, 
            x= tTestDat2paired$willingness2pay,
            paired = TRUE)

## Warning in wilcox.test.default(y = tTestDat2paired$willingness2payAfter, :
## cannot compute exact p-value with zeroes

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  tTestDat2paired$willingness2pay and tTestDat2paired$willingness2payAfter
## V = 0, p-value = 0.009152
## alternative hypothesis: true location shift is not equal to 0

Wir können also die Nullhypothese, dass der Median der Differenzen gleich Null ist mit kleiner Irrtumswahrscheinlichkeit (p-value = 0.009152) verwerfen.

Es ist möglich über den optionalen Parameter mu bei wilcox.test eine andere Differenz zu testen.

Schauen wir uns einmal den nachfolgenden Datensatz an, der symmetrisch aber nicht normalverteilt sind. Gehen wir davon aus, dass die Werte die Differenzen gepaarter Daten sind, können wir den Wilcoxon-Vorzeichen-Rang-Test anwenden:

set.seed(48)
theSample <- data.frame(x = crch::rtt(n = 23, location = 46.6, scale=, left=40, right=60, df=2),
                        y = crch::rtt(n = 23, location = 45, scale=3, left=35, right=55, df=3))

fittedGaussX <- fitdistr(theSample$x, densfun="normal")
fittedGaussY <- fitdistr(theSample$y, densfun="normal")

p1 <- ggplot(theSample, aes(x=x)) +
  geom_histogram(binwidth = 1,  mapping = aes(y = after_stat(density)),
                 col="white") +
   stat_function(
    fun = dnorm,
    geom = "area",
    fill = "steelblue",
    alpha = .3,
    args = list(mean= fittedGaussX$estimate[1] , 
                sd = fittedGaussX$estimate[2])
  ) +
  scale_x_continuous(expand = expansion(add=0),
                     limits=c(34.5,65.5)) +
  xlab("Wert X ") + ylab("Wahrscheinlichkeitsdichte") 

p2 <- ggplot(theSample, aes(x=y)) +
  geom_histogram(binwidth = 1,  mapping = aes(y = after_stat(density)),
                 col="white") +
   stat_function(
    fun = dnorm,
    geom = "area",
    fill = "steelblue",
    alpha = .3,
    args = list(mean= fittedGaussY$estimate[1] , 
                sd = fittedGaussY$estimate[2])
  ) +
  scale_x_continuous(expand = expansion(add=0),
                     limits=c(30.5,60.5)) +
  xlab("Wert Y") + ylab("Wahrscheinlichkeitsdichte") 

ggpubr::ggarrange(p1, p2)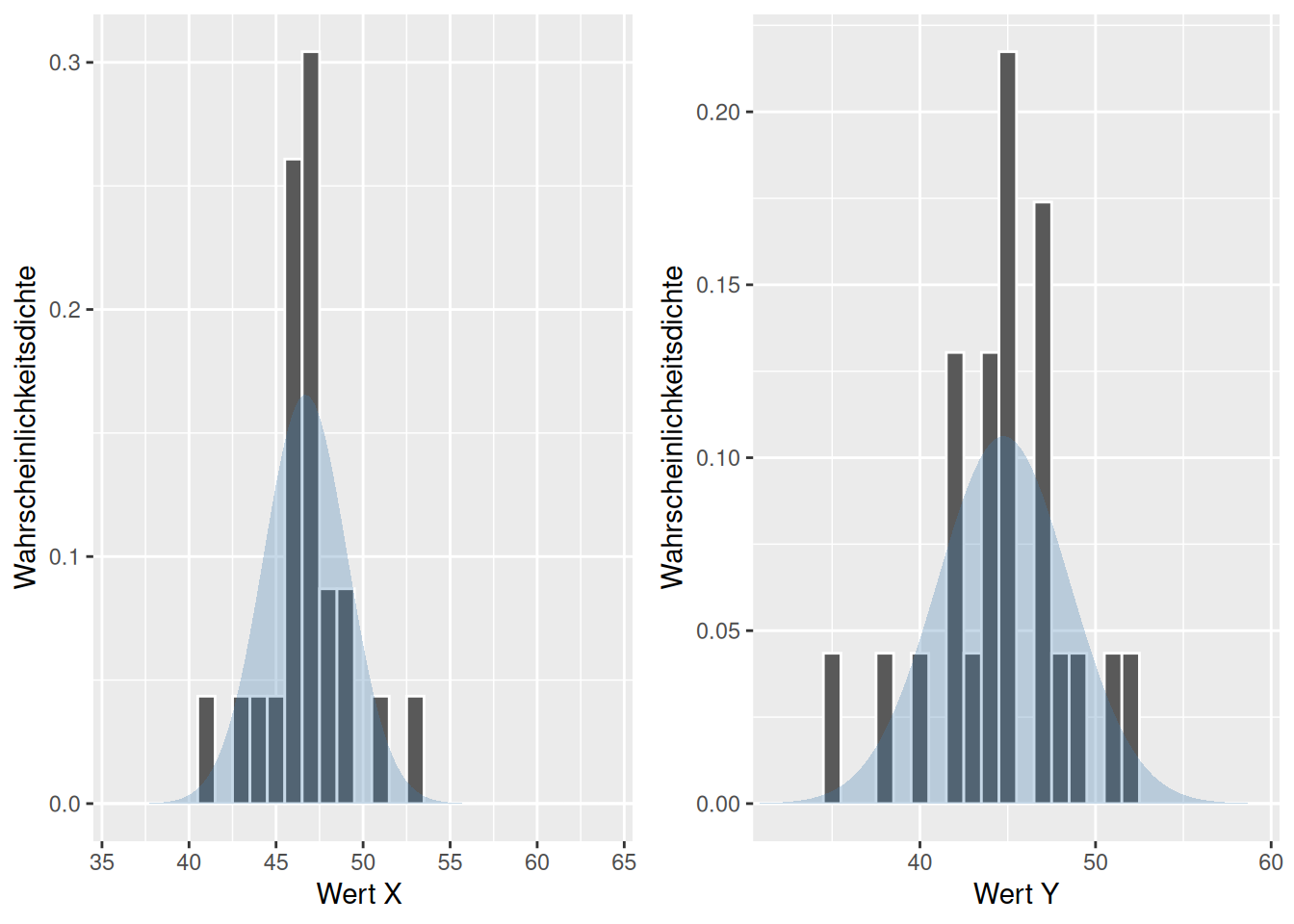

wilcox.test(x= theSample$x, 
            y= theSample$y,
            paired = TRUE)

## 
##  Wilcoxon signed rank exact test
## 
## data:  theSample$x and theSample$y
## V = 203, p-value = 0.04844
## alternative hypothesis: true location shift is not equal to 0

Der Wilcoxon-Vorzeichen-Rang-Test gibt hier also einen - marginal- signifikanten Unterschied der Mediane an.

Verwenden wir fälschlicherweise den t-Test, so zeigt dieser an, dass die Mittelwerte sich nicht signifikant unterscheiden.

t.test(x= theSample$x, 
            y= theSample$y,
            paired = TRUE)

## 
##  Paired t-test
## 
## data:  theSample$x and theSample$y
## t = 1.8362, df = 22, p-value = 0.07988
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -0.2499746  4.1119697
## sample estimates:
## mean difference 
##        1.930998

10.3.2 Wilcoxon-Mann-Whitney-Test

Dieser Rangsummen-Test ist die Übertragung des Wilcoxon-Vorzeichen-Rang-Tests auf ungepaarte Daten. Konzeptionell ähnelt er damit dem ungepaarten zwei-Stichproben t-Test. Er wird angewandt, falls die Werte nicht metrisch skaliert sind, oder die Normalverteilungs-Annahme verletzt sein könnte. Der Test testet, ob ein aus einer Grundgesamtheit stammender Wert im Mittel größer oder kleiner ist als ein aus einer anderen Grundgesamtheit stammender Wert. Der Test erfolgt wie üblich auf Grundlage zweier Stichproben.

Der Grundgedanke beruht auf dem Vergleich eines Merkmal zwischen zwei Gruppen. Wir sortieren hierfür die Beobachtungen anhand des Merkmals - ohne Berücksichtigung der Gruppen - und notieren den Rang (kleinster Wert, zweitkleinester Wert,…). Wir erwarten hinsichtlich der Summe der Ränge, wenn es einen Effekt, dass die Summe der Ränge für eine Gruppe deutlich größer als die andere ist. Wenn es keinen Effekt gibt erwarten wir dagegen, dass die Summe der Ränge für beide Gruppen in etwa gleich sind.

Unter der Nullhypothese wird davon ausgegangen, dass beide Grundgesamtheiten identisch sind. Falls die Nullhypothese abgelehnt wird, kann man davon ausgehen, dass die Mediane der Grundgesamtheiten unterschiedlich sind.

\(H_0:\) Es ist gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population (\(P( X > Y ) = P ( X < Y )\)) \(H_A:\) Es ist nicht gleich wahrscheinlich, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population \(P( X > Y ) \neq P ( X < Y )\)

Die Teststatistik ist wie folgt definiert:

\[U = \sum_{i=1}^n\sum_{j=1}^m S(X_i, Y_j)\]

wobei \[S(X_i, Y_j) = \left \{ \begin{array}{rr} 1 & X > Y\\\ 0.5 & X = Y \\ 0 & X < Y\\ \end{array} \right.\]

Unter der Nullhypothese ist \(U\) asymptotisch normalverteilt, wobei für kleine Stichprobengrößen die exakten Werte tabelliert vorliegen. Wenn Wertepaare mit identischen Werten für \(X_i\) und \(Y_j\) auftreten, kann der p-Wert nicht exakt bestimmt werden, sondern muss geschätzt werden.

Der Test ist auch unter den Namen Mann-Whitney-U-Test, U-Test, Wilcoxon-Rangsummentest gebräuchlich.

In R wird der Test mittels wilcox.test(x,y, paired=FALSE) berechnet. Hier wird die Teststatitik mit W bezeichnet.

wilcox.test(y = tTestDat2paired$willingness2pay,
            x= tTestDat2paired$willingness2payAfter,
            paired = FALSE,
            alternative= "greater")

## Warning in wilcox.test.default(y = tTestDat2paired$willingness2pay, x =
## tTestDat2paired$willingness2payAfter, : cannot compute exact p-value with ties

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  tTestDat2paired$willingness2payAfter and tTestDat2paired$willingness2pay
## W = 218.5, p-value = 0.3131
## alternative hypothesis: true location shift is greater than 0

Der Wilcoxon-Mann-Whitney-Test kommt hier (bei etwas größerem p-Wert) zum gleichen Ergebnis wie der ungepaarte t-Test, den wir oben durchgeführt haben - allerdings wäre er auch anwendbar, wenn die Annahme des t-Testes hinsichtlich der Normalverteilung der Werte nicht gegeben wären. Damit können wir also die Nullhypothese - dass es gleich wahrscheinlich ist, dass ein zufällig aus der einen Population ausgewählter Wert größer oder kleiner ist als ein zufällig ausgewählter Wert aus der anderen Population ist - verworfen werden. Der Wer W=218.5 gibt hier die Teststatistik an.

Der Test nimmt, wie der Wilcoxon-Vorzeichen-Rang-Test an, dass die Verteilungen der Populationsverteilungen sich nur in ihrer Parametrisierung unterscheiden, aber es sich um die Selbe Verteilung handelt. Falls diese Annahme verletzt ist, sollte der Test nicht angewandt werden.

10.3.2.1 Kritische Anmerkungen zu Rangtransformationstests

Rangtransformationstests sind gebräuchlich, nicht nur für für ordinalverteilte Werte, sondern auch, um mit Verletzungen der Verteilungsannahmen parametrischer Tests umgehen zu können. Durch die Rangtransformation wird die Annahmenverletzung sozusagen geheilt. Dies ist praktisch, weswegen sich die Tests großer Beliebtheit erfreuen. Allerdings sollte man sich klar machen, dass bei der Rangtransformation Information verworfen wird. Entsprechend verlieren diese Tests an Trennschärfe.

10.3.3 Permutationstests

Permutationstests beruhen darauf, dass man die Daten unter der Annahme der Nullhypothese permutiert und die statistische Kennzahl, die von Interesse ist auf Grundlage der Permutation neu berechnet. Dies macht man sehr oft und vergleicht die Verteilung der so zustande gekommenen statistischen Kennzahl mit dem Wert, der sich aus den beobachteten Daten ergibt. Daraus lässt sich abschätzen, wie wahrscheinlich das Auftreten des beobachten Wertes unter der Nullhypothese ist.

Schauen wir uns das einmal für die Zahlungsbereitschaftsbefragung an, die wir oben beim ungepaarten t-Test verwendet haben.

Unter der Nullhypothese stammen alle Beobachtungen aus derselben Grundgesamtheit bzw. es besteht kein Unterschied zwischen den beiden Gruppen. D.h. wir können unter der Nullhypothese die Zahlungsbereitschaften beliebig den beiden Gruppen zu ordnen.

head(tTestDat3)

##   willingness2pay1 willingness2pay2
## 1         238.8236         229.3548
## 2         215.8552         230.1349
## 3         210.8594         229.6985
## 4         225.4849         232.7226
## 5         211.9161         233.9047
## 6         225.2874         224.0037

Differenz der Mittelwerte beider Gruppen:

obsMeanDiff <- mean(tTestDat3$willingness2pay1) - mean(tTestDat3$willingness2pay2)
obsMeanDiff

## [1] -11.65496

Nun packen wir alle Daten in einen Vektor und ordnen Sie zufällig den beiden Gruppen zu.

willingness2payAll <- c(tTestDat3$willingness2pay1, tTestDat3$willingness2pay2)
n <- length(willingness2payAll)

Zur Zuordnung ziehen wir aus den Zahlen 1 bis 40 (soviele Beobachtungen haben wir) 20 zufällig. Diese verwenden wir als Gruppe 1, den Rest als Gruppe 2. Wir machen uns dabei zu nutze, dass man mit dem Klammeroperator nicht nur Elemente an den gegebenen Positionen auswählen kann, sondern auch Elements ausschließen kann, wenn man den Minus Operator anwendet.

idx <- sample(1:40, size = 20)
mean(willingness2payAll[idx]) - mean(willingness2payAll[-idx])

## [1] -0.2151482

Nun wiederholen wir das 999 mal und speichern die Differenzen in einem Vektor:

nPerm <- 9999
simMeanDiff <- numeric(nPerm)
for(i in 1:nPerm)
{
  idx <- sample(1:40, size = 20)
  simMeanDiff[i] <-  mean(willingness2payAll[idx]) - mean(willingness2payAll[-idx])
}

Die Frage ist, wie sich der beobachtete Wert im Verhältnis zu diesen simulierten Werten einsortiert.

hist(simMeanDiff, xlim = c(-12,12), las= 1,
     xlab = "Differenz der Mittelwerte", 
     main = "Zahlungsbereitschaftsbefragung")
abline(v= obsMeanDiff, col= "red", lty=2)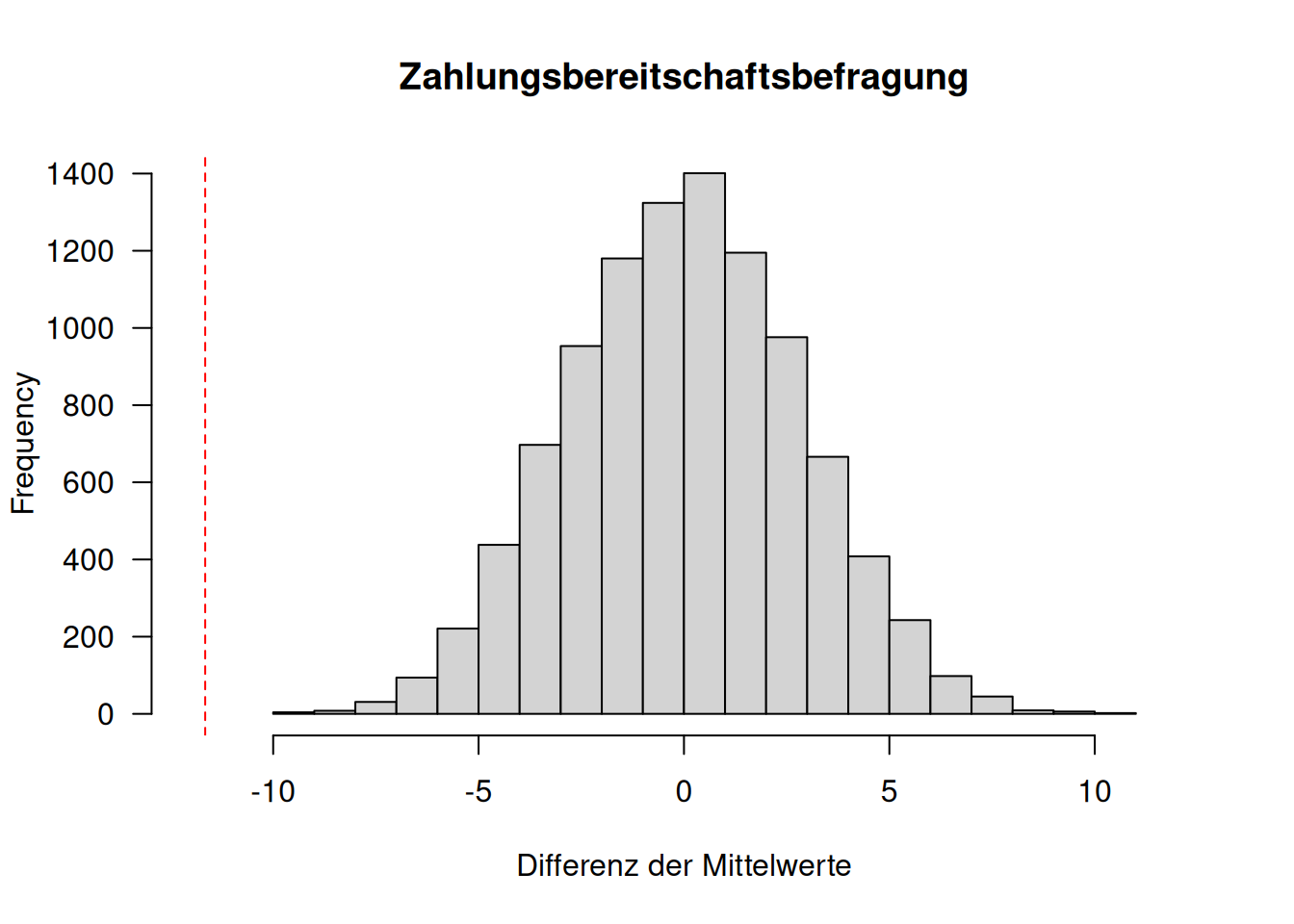

Der beobachtete Wert ist also unter der Nullhypothese sehr unwahrscheinlich. Wir können auch den p-Wert berechnen: wir sortieren alle simulierten und den beobachteten Wert und ermitteln die Position des simulierten Wertes. Geteilt durch 999+1 ergibt dies den p-Wert.

allMeanDiffs <- sort(c(simMeanDiff, obsMeanDiff))
position <- which(allMeanDiffs == obsMeanDiff)
position / (nPerm +1)

## [1] 1e-04

Solange die Daten unabhängig voneinander sind, können wir mit Permutationstests agieren. Das Schöne ist, dass wir dabei keinerlei Verteilungsinformationen benötigen, sondern direkt mit der Verteilung der Beobachtungen agieren. Wichtig ist nur, dass unsere Stichproben groß genug sind - haben wir zu wenige Datenpunkte, kann kein statistischer Test belastbare Ergebnisse liefern.

Schauen wir uns einmal ein Beispiel mit schief verteilten Werten an. Wir sind wieder daran interessiert, ob sich die Mittelwerte der beiden Verteilungen voneinander unterscheiden.

set.seed(32)
theSample <- data.frame(x= rgumbel(n=60, scale=30, location=500),
                        y= rgumbel(n=60, scale=30, location=532.5))
theSample_long <- pivot_longer(theSample, col=1:2)

ggplot(theSample_long, aes(x=value)) +
  geom_histogram(binwidth = 10,  mapping = aes(y = after_stat(density)),
                 col="white") +
  facet_wrap(~name) +
  xlab("Werte ") + ylab("Wahrscheinlichkeitsdichte")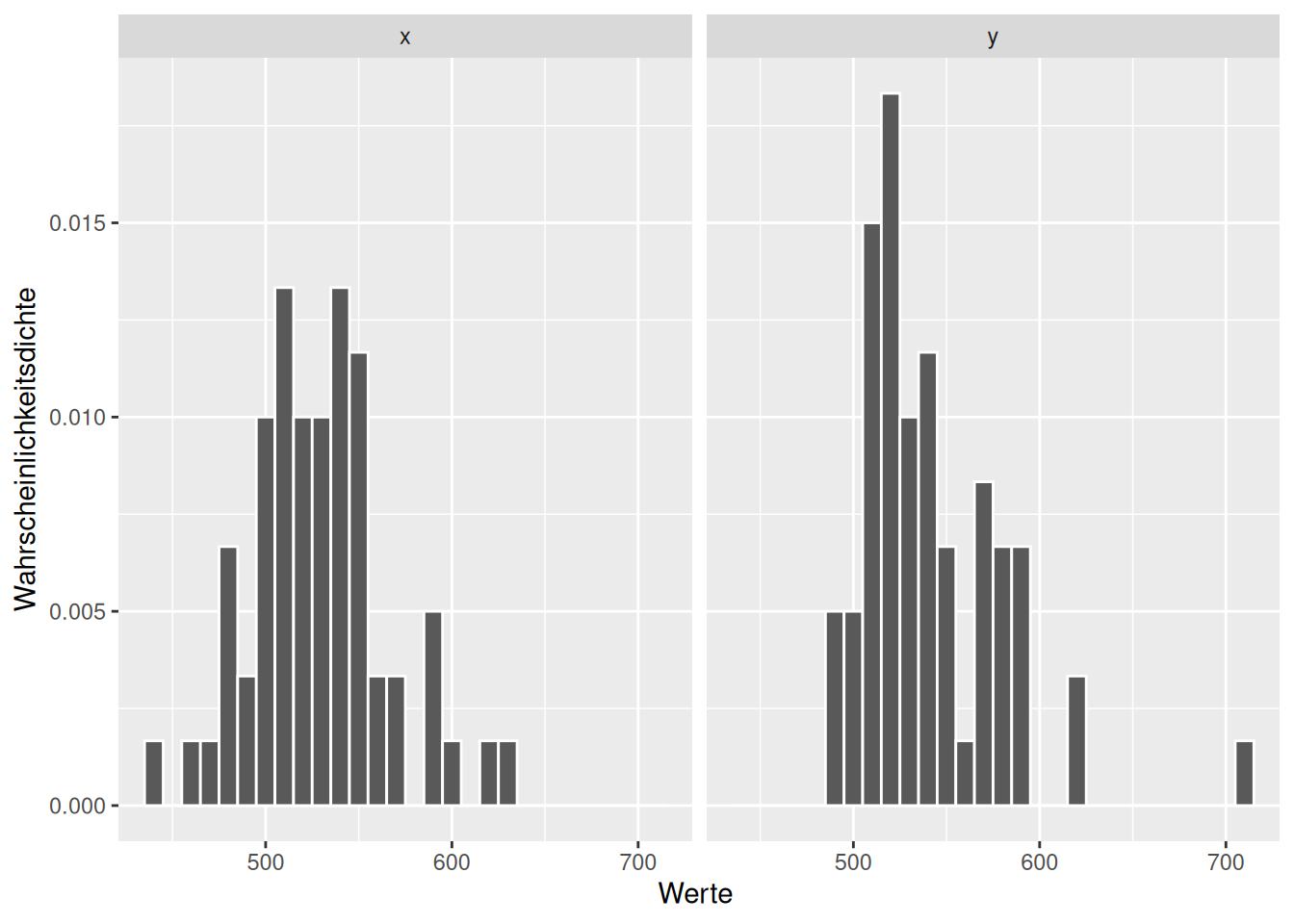

Figure 10.5: Beispieldatensatz mit merklicher Schiefe der beiden Stichproben. Zu testen ist die Nullhypothese, dass die Mittelwerte der beiden Grundgesamtheiten gleich sind.

# t-Test
t.test(x=theSample$x,
            y=theSample$y,
            paired= TRUE)

## 
##  Paired t-test
## 
## data:  theSample$x and theSample$y
## t = -1.7818, df = 59, p-value = 0.07992
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -25.426626   1.473043
## sample estimates:
## mean difference 
##       -11.97679

# wilcoxon
wilcox.test(x=theSample$x,
            y=theSample$y,
            paired= TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  theSample$x and theSample$y
## V = 697, p-value = 0.1093
## alternative hypothesis: true location shift is not equal to 0

# Permutationstest
obsMeanDiff <- mean(theSample$x - theSample$y)
sampleSize <- nrow(theSample)
nPerm <- 9999
simMeanDiff <- numeric(nPerm)
for(i in 1:nPerm)
{
  idx <- sample(1:(sampleSize*2), size = sampleSize)
  simMeanDiff[i] <-  mean(theSample_long$value[idx]) - mean(theSample_long$value[-idx])
}
allMeanDiffs <- sort(c(simMeanDiff, obsMeanDiff))
position <- which(allMeanDiffs == obsMeanDiff)
position / (nPerm +1)

## [1] 0.042

Während der Permutationstest - korrekterweise - anzeigt, dass die beiden Mittelwerte der Grundgesamtheiten verschieden sind, können dies der t-Test und der Wilcoxon-VOrzeichen-Rnag-Test hier auf dem 5% Signifikanzniveau nicht anzeigen.

10.4 Kontrollfragen

• wie unterscheiden sich der besprochenen F-Test zur Varianzanalyse und dem ungepaarten t-Test?
• wie funktioniert der KS-Test?
• was sind Datenbindungen
• was ist das Grundprinzip von Rangtransformationstests?
• was ist das Grundprinzip von Permutationstests?
• welche Varianten des t-Test gibt es?
• wann wird die Welch-Saitterhaite Korrektur angewandt?

## Loading required package: ggExtra