Kapitel 9 Von der Stichprobe zur Grundgesamtheit - schließende Statistik

Wir wollen uns hier mit einigen grundlegenden Konzepten beschäftigen, die uns immer wieder begegnen werden, wenn wir versuchen auf Grundlage einer Stichprobe auf die Grundgesamtheit zu schließen.

9.1 Gesetz der großen Zahlen

Das Gesetz der großen Zahlen beschreibt, dass Durchschnitte der Ergebnisse bei wachsender Anzahl der Experimente gegen den Erwartungswert streben, bzw. wie die Stichprobenmittelwerte bei wachsender Stichprobengröße gegen den Erwartungswert konvergieren.

Eine Folge von Zufallszahlen \(x_1, x_2,...\) konvergiert unter bestimmen Voraussetzungen gegen den Erwartungswert. Konvergenz ist hierbei allerdings nicht so zu verstehen, dass der Stichprobenmittelwert sich dem Erwartungswert monoton annähert. Vielmehr kann sich der Stichprobenmittelwert zwischenzeitlich auch vom Erwartungswert entfernen. Man sagt, der Stichprobenmittelwert konvergiert in Wahrscheinlichkeit gegen den wahren Wert.

Schwaches Gesetz der großen Zahlen (Konvergenz in Wahrscheinlichkeit):

Eine Folge von Zufallszahlen \(x_1, x_2,...\) mit \(E[|X_i|] < \infty\) genügt dem schwachen Gesetz der großen Zahlen, wenn für

\[\bar{X}_n = \frac{1}{n}\sum_{i=1}^n(x_i - E[x_i]) \]

für alle positiven Zahlen \(\epsilon\) gilt:

\[ \lim_{x \to \infty} P(|\bar{X}_n| > \epsilon) = 0 \] Die Zufallszahlen müssen dafür paarweise unabhängig und identisch Verteilt sein und der Erwartungswert endlich sein oder die Zufallszahlen müssen paarweise unkorreliert sein und die Varianz von \(X_i\) endlich.

Einfach ausgedrückt: wenn unsere Stichprobe groß genug ist (und die Zufallszahlen unabhängig sind), dann können wir daraus den Erwartungswert sehr genau schätzen.

Schauen wir uns das einmal anhand eins Beispiels an. Hierzu ziehe ich eine große Anzahl von Normalverteilten Zufallszahlen und speichere diese in einem data.frame. Dann berechnen ich in einer Schleife den Mittelwert der ersten \(i\) Elemente. Dann plotte ich diesen auf Grundlage der stetig wachsenden Stichprobe berechneten Mittelwert gegen die Anzahl der Elemente in der Stichprobe.

set.seed(42)
n <- 10^4
popMean <- 30
popSd <- 2
theSample <- data.frame(x= rnorm(n, mean = popMean, sd = popSd))
theSample$idx <- 1:n
for(i in 1:n)
{
  theSample$mean[i] <- mean(theSample$x[1:i])
}

ggplot(theSample, mapping = aes(x=idx, y= mean)) +
  geom_line() + 
  geom_hline(yintercept = popMean, col="red") +
  xlab("Stichprobengröße") +
  ylab("Mittelwert") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Mittelwert aus wachsender normalverteilter Stchprobe")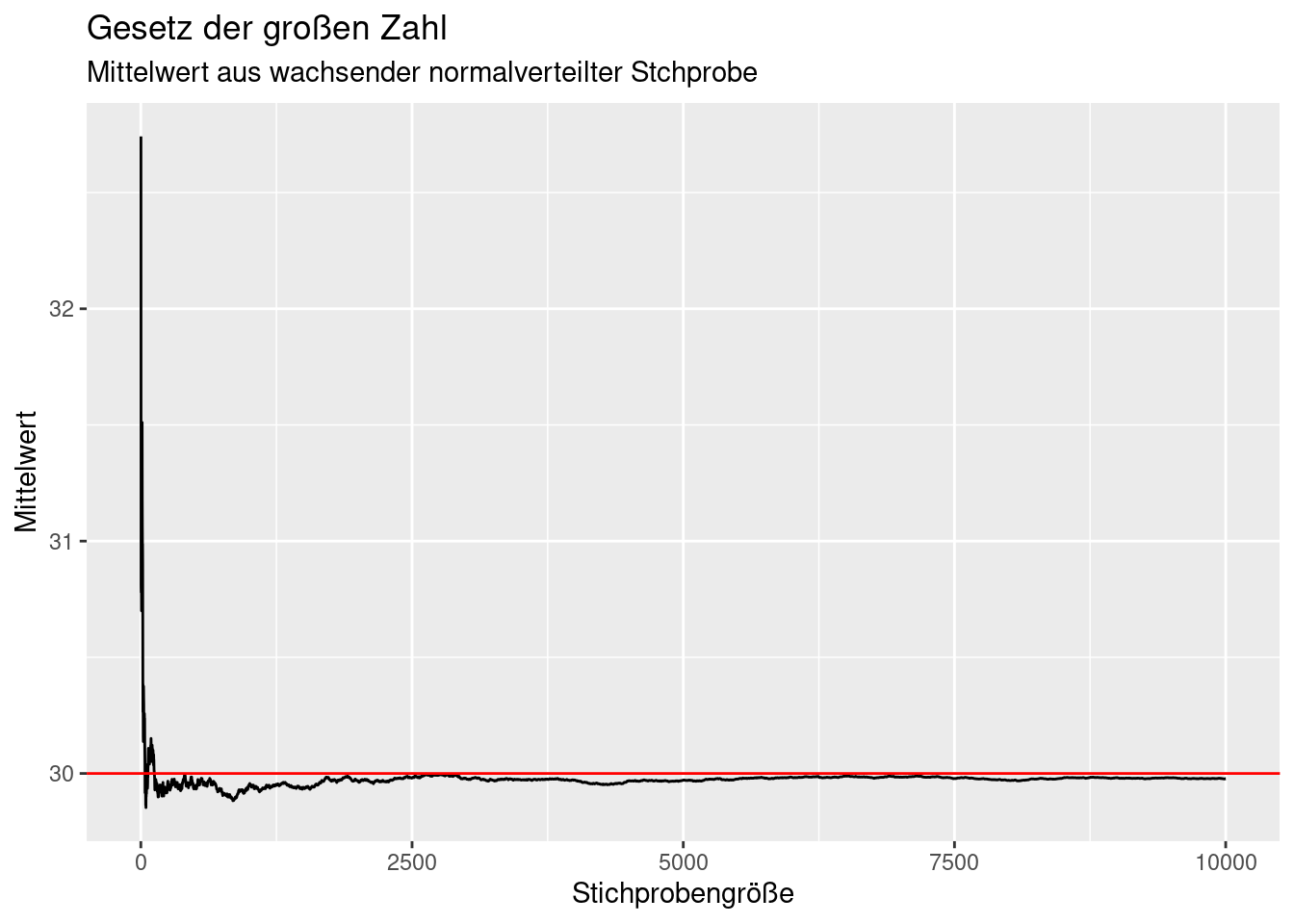

Wie wir sehen, konvergiert der Stichprobenmittelwert relativ schnell gegen den wahren Mittelwert (rot). Allerdings ist die Konvergenz nicht monoton: es gibt immer wieder Perioden, in denen sich der Stichprobenmittelwert sich vom wahren Wert der Grundgesamtheit entfernt.

Wenn wir das Experiment wiederholen, erhalten wir natürlich einen etwas anderen Verlauf. Ich habe hier über set.seeds den Zufallszahlengenerator eingefroren, so dass immer das gleiche Ergebnis herauskommt.

Da for Schleifen in R recht langsam sind, können wir die Berechnung mit zwei Funktionen deutlich beschleunigen.´

set.seed(4)
theSample <- data.frame(x= rnorm(n, mean = popMean, sd = popSd))
theSample$idx <- 1:n
# much faster variant
theSample$mean <- cumsum(theSample$x) / seq_along(theSample$x)

ggplot(theSample, mapping = aes(x=idx, y= mean)) +
  geom_line() + 
  geom_hline(yintercept = popMean, col="red") +
  xlab("Stichprobengröße") +
  ylab("Mittelwert") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Mittelwert aus wachsender normalverteilter Stchprobe")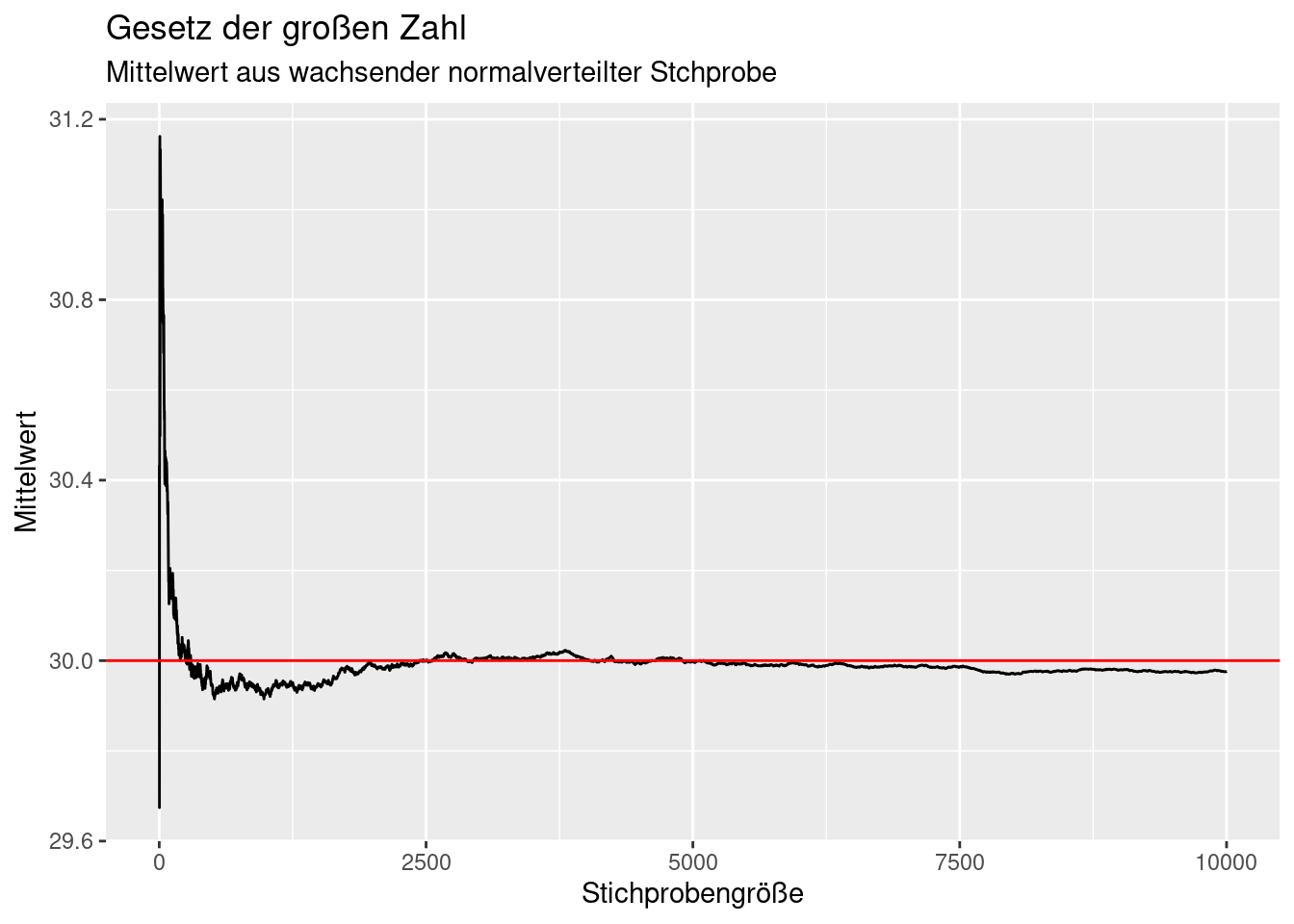

Ein Beispiel für Verteilungen ohne bestimmten Erwartungswert ist die Cauchy-Verteilung. Hierbei konvergiert das Stichprobenmittel leider nicht.

set.seed(4)
n <- 10^5
theSample <- data.frame(x= rcauchy(n, location = popMean, scale =  popSd))
theSample$idx <- 1:n
theSample$mean <- cumsum(theSample$x) / seq_along(theSample$x)

ggplot(theSample, mapping = aes(x=idx, y= mean)) +
  geom_line() + 
  geom_hline(yintercept = popMean, col="red", lty=2) +
  xlab("Stichprobengröße") +
  ylab("Mittelwert") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Standardabweichung aus wachsender chauchyverteilter Stchprobe")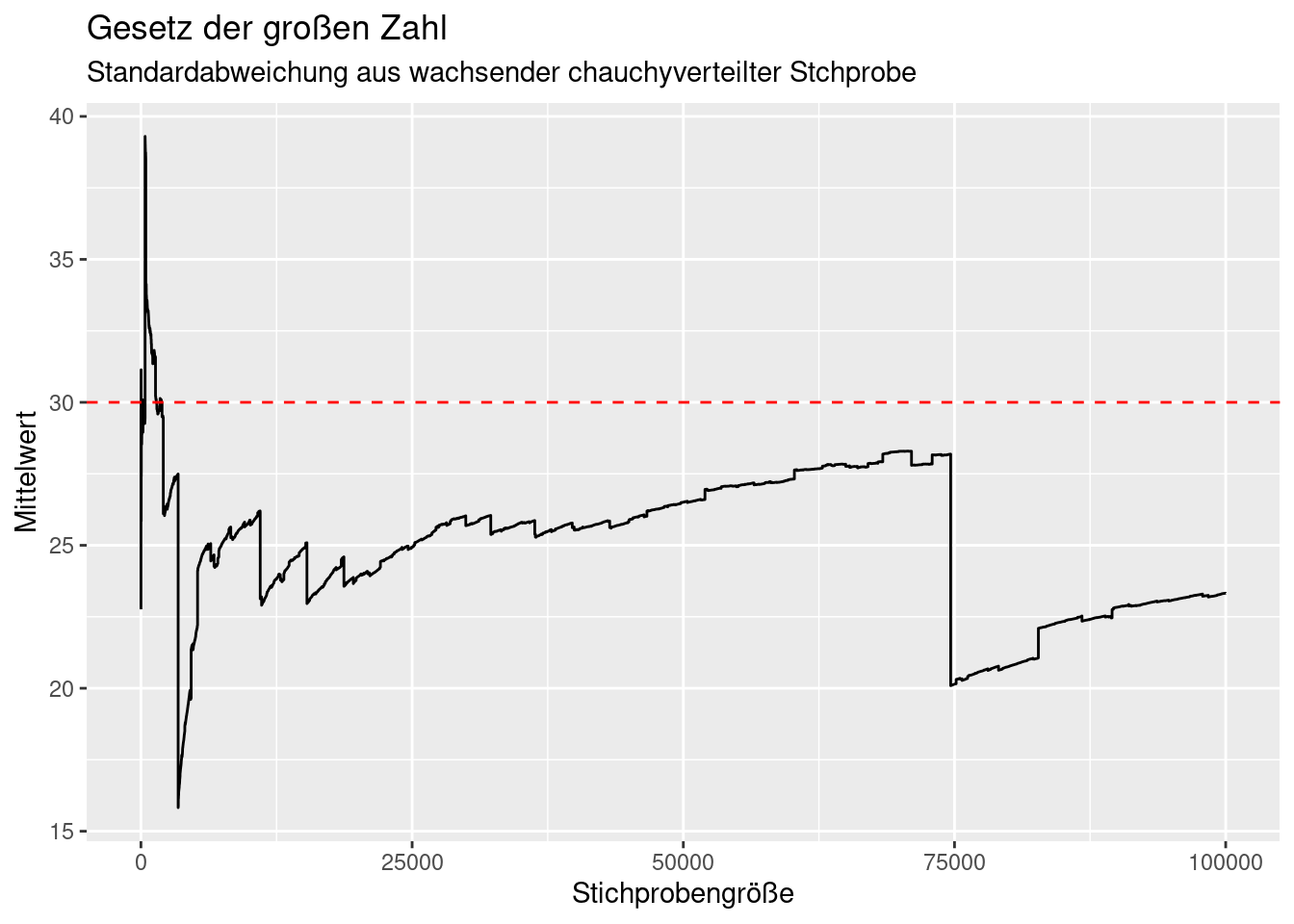

Wählt man dagegen den Median, konvergiert dieser auch bei der Cauchy-Verteilung.

set.seed(4)
n <- 10^4
theSample <- data.frame(x= rcauchy(n, location = popMean, scale =  popSd))
theSample$idx <- 1:n
theSample$mean <- cumsum(theSample$x) / seq_along(theSample$x)


theSample$median <- sapply(seq_along(theSample$x), FUN = 
                            function(z) 
                            {
                              median(theSample$x[1:z])
                            }
                          )

ggplot(theSample, mapping = aes(x=idx, y= median)) +
  geom_line() + 
  geom_hline(yintercept = median(theSample$x), col="red", lty=2) +
  xlab("Stichprobengröße") +
  ylab("Median") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Media aus wachsender chauchyverteilter Stchprobe")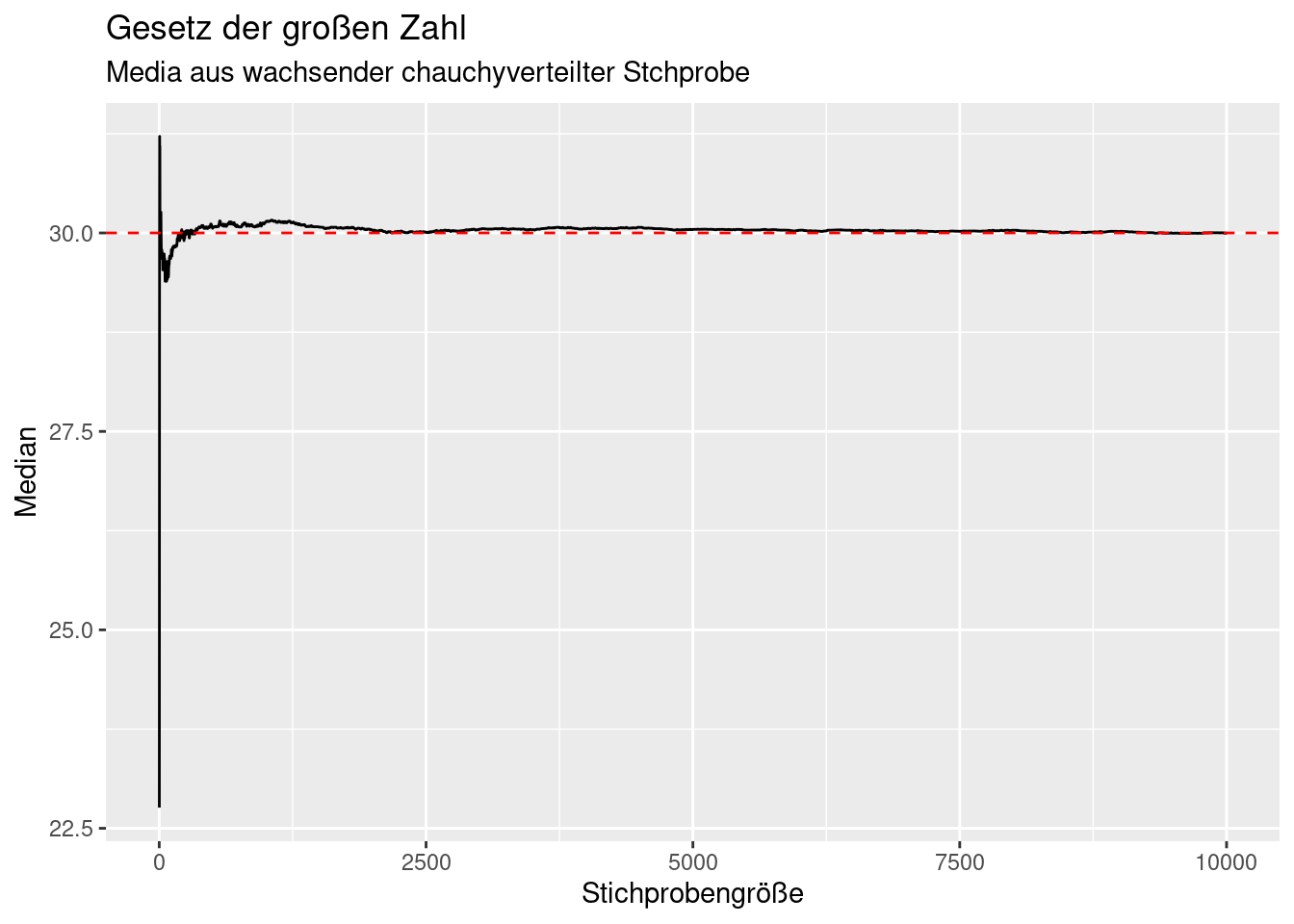

Neben Mittelwert und Median unterliegen auch andere Statistiken wie die Standradabweichung dem Gesetz der großen Zahlen.

set.seed(42)
n <- 10^4
popMean <- 30
popSd <- 2
theSample <- data.frame(x= rnorm(n, mean = popMean, sd = popSd))
theSample$idx <- 1:n
theSample$sd <- NA # wir können sd für n= 1 nicht berechnen
for(i in 2:n)
{
  theSample$sd[i] <- sd(theSample$x[1:i])
}

ggplot(theSample, mapping = aes(x=idx, y= sd)) +
  geom_line() + 
  geom_hline(yintercept = popSd, col="red") +
  xlab("Stichprobengröße") +
  ylab("Standardabweichung") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Standardabweichung aus wachsender normalverteilter Stchprobe")

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).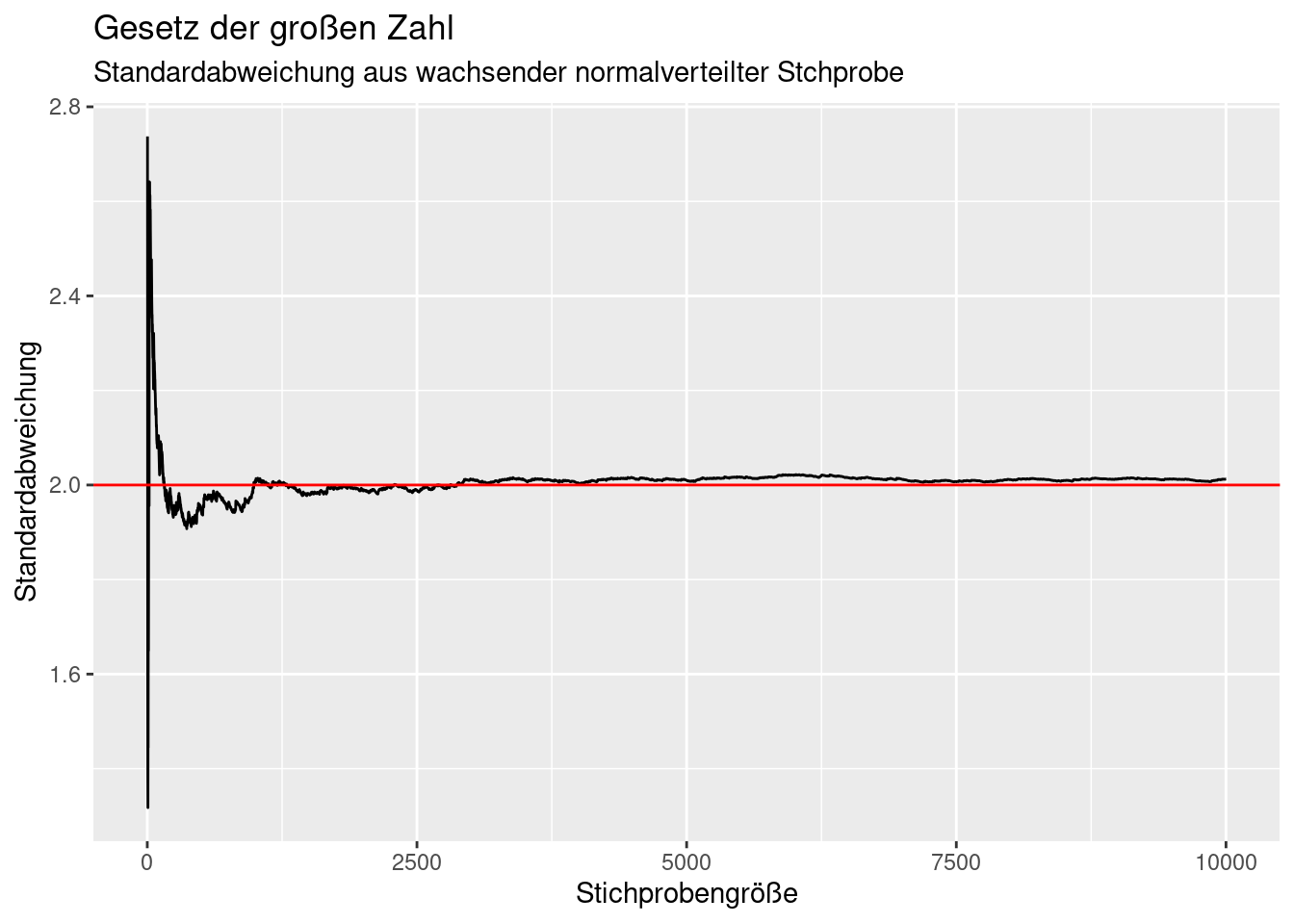

9.2 Standardfehler

Der Standardfehler quantifiziert die Unsicherheit, mit der man auf Grundlage der Stichprobe auf die Grundgesamtheit schließen kann. Der Standardfehler ist die Standardabweichung der Schätzung der statistischen Kenngröße. Damit ist er auch ein Gütemaß: je kleiner der Standardfehler, desto genauer kann man den unbekannten Parameter der Grundgesamtheit anhand der Stichprobe schätzen.

Für manche Kombinationen aus statistischer Kenngröße und der Wahrscheinlichkeitsverteilung, der die Kenngröße vermutlich folgt, gibt es einfache Formeln. Oftmals sind die Formeln jedoch recht kompliziert oder existieren nicht. In diesen Fällen kann man sich mit Verfahren wie dem Bootstrap (Efron and Tibshirani 1994) behelfen, dass auf einem Resamplingverfahren mit Zurücklegen beruht - dies führt hier jedoch aktuell zu weit.

9.2.1 Standardfehler des Mittelwertes

Bekanntester Standardfehler ist der Standardfehler des Mittelwertes. Wenn man anhand einer Stichprobe den Mittelwert der zugrundeliegenden Grundgesamtheit bestimmen will:

\[ st.err = \sigma_{\bar{x}} = \frac{\sigma}{\sqrt{n}} \] Dabei ist n die Stichprobengröße und \(\sigma\) die Standardabweichung der Grundgesamtheit. Da \(\sigma\) nicht bekannt ist, wird die Standardabweichung der Stichprobe \(\sigma_x\) verwendet. Entsprechend kann man den Standardfehler nicht exakt bestimmen, sondern ihn nur schätzen. Deswegen wird der Standardfehler des Mittelwertes oft wie folgt angegeben (der Hat Operator zeigt an, dass es sich um eine Schätzung handelt):

\[ \hat{\sigma}_{\bar{x}} = \frac{\sigma_x}{\sqrt{n}} \] Wir schätzen also den Standardfehler auf Grundlage der Informationen aus der Stichprobe (Standardabweichung der Stichprobe). Dieser geschätzte Standardfehler gibt wiederum die Güte der Schätzung des Mittelwertes der Grundgesamtheit an - genauer gesagt ist er die Standardabweichung der Schätzung. Um die Verwirrung noch größer zu machen, spricht man oft vom Standardfehler, meint jedoch den Schätzer des Standardfehlers.

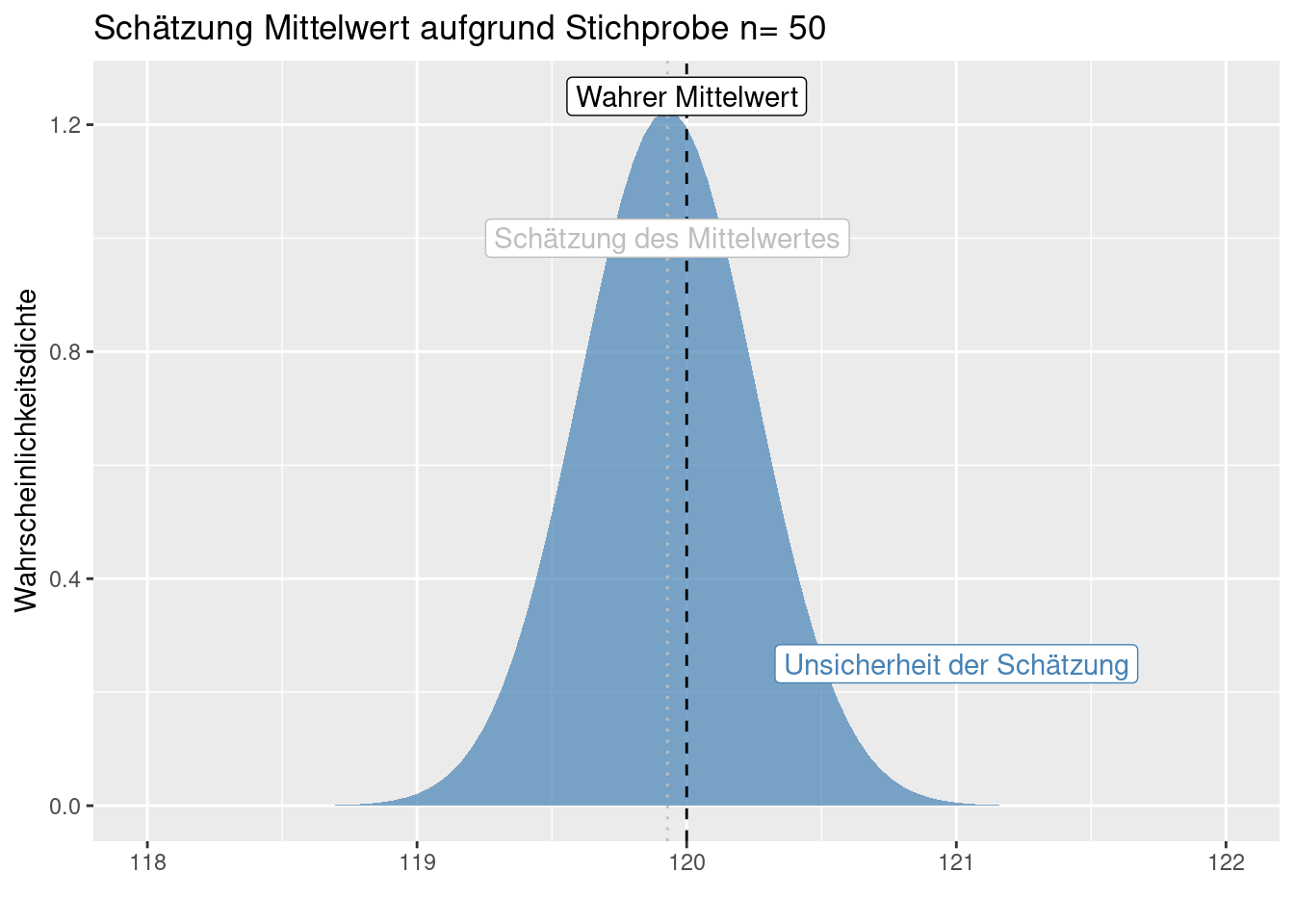
Der (Schätzer des) Standardfehler des Mittelwertes hängt davon ab, wie stark die Werte in der Stichprobe streuen und wie groß die Stichprobe ist. Letzteres ist mit dem Gesetz der großen Zahlen verknüpft, da mit zunehmender Stichprobengröße statistische Kenngrößen gegen den Erwartungswert streben. Da die Stichprobe innerhalb der Wurzel im Nenner steht bedeutet dies, dass man eine 100-mal größere Stichprobe benötigt um einen 10-mal kleineren (Schätzer des) Standardfehlers des Mittelwertes zu bekommen.

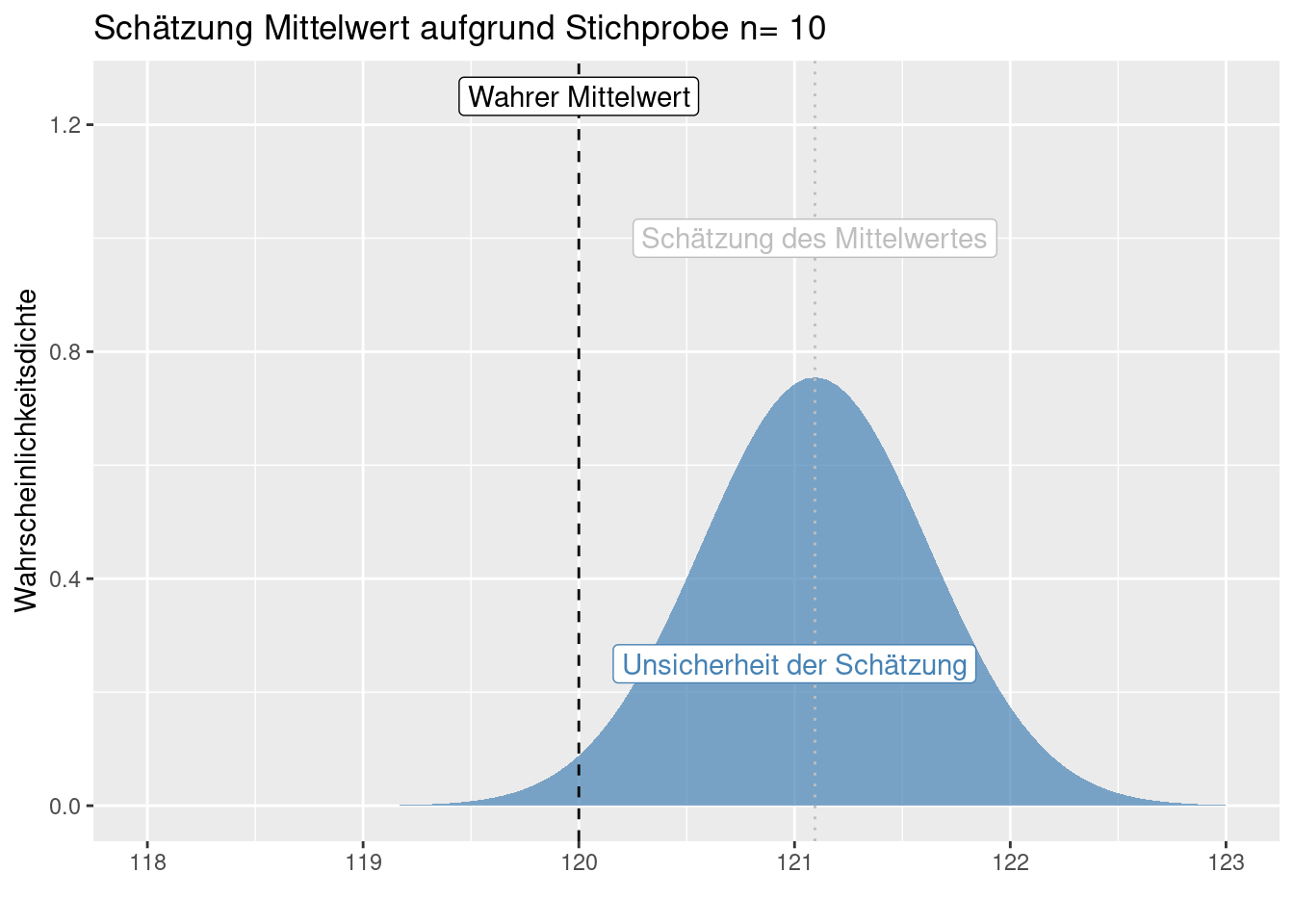
Da es sich bei der Stichprobe ja um eine Zufallsstichprobe handelt, erhält man bei unterschiedlichen Experimenten natürlich unterschiedliche Schätzungen für Mittelwert und Stadradfehler des Mittelwertes.

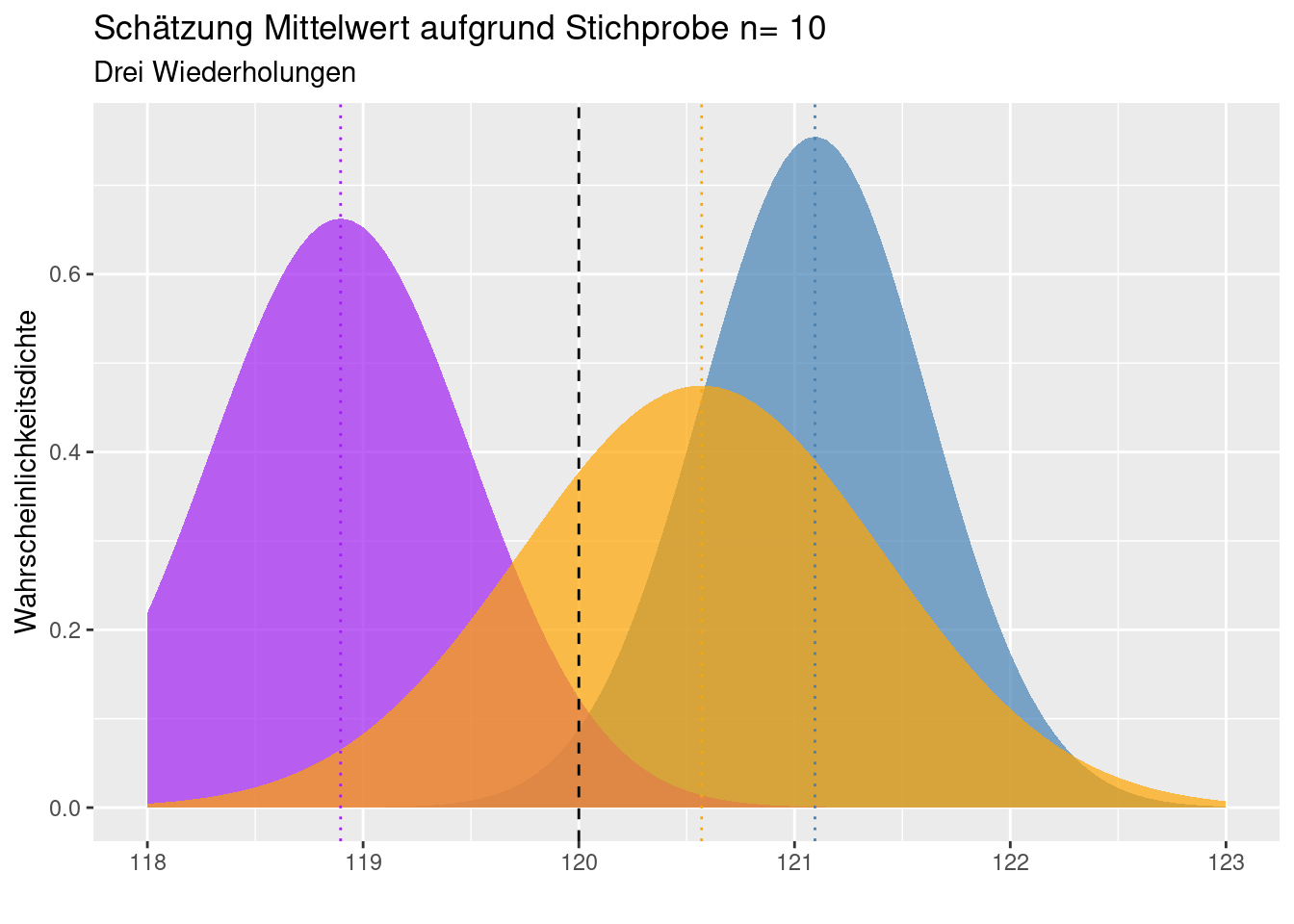
Hinweis: Die Schätzung der Standardabweichung der Grundgesamtheit auf Grundlage der Stichproben-Standardabweichung unterschätzt bei kleinen Stichproben die Standardabweichung der Grundgesamtheit systematisch. Hierfür gibt es Korrekturfaktoren, z.B. (Gurland and Tripathi 1971).

9.2.2 Standardfehler für andere statistische Kennzahlen

Ein oft gemachter Fehler ist es, den Standardfehler des Mittelwertes allgemein mit dem Begriff Standardfehler zu verbinden. Standardfehler gibt es für alle Schätzungen von Parametern aus einer Stichprobe: für den Median, die Varianz, die Standardabweichung, die Schiefe, den Variationskoeffizient, Korrelations- und Regressionskoeffizienten. Leider gibt es keine einfachen Formeln für die Standardfehler der meisten statistischen Kennzahlen.

Unter Annahme normalverteilter Daten (s. Kapitel Verteilungen), kann der Standardfehler des Medians aus der Stichprobe wie folgt geschätzt werden:

\[ \hat{\sigma}_{median(x)} = \sqrt{\frac{\pi}{2}} \cdot \frac{\sigma_x}{\sqrt{n}} \]

Die Konstante \(\frac{\pi}{2}\) ist dabei eine Schätzung der Varianz auf Basis der Normalverteilung. Für andere Verteilungen und für andere Quantile ändert sich die Formel und wird komplexer.

9.2.3 Simulation des Standardfehlers

Wir wollen im folgenden den Standardfehler über Simulationen ermitteln. Zunächst für den Mittelwert, dann für andere Statistiken. Warum tun wir das? Um besser zu verstehen, was der Standardfehler ist.

Was wir benötigen wir für das Experiment?

eine Grundgesamtheit, in userem Fall eine Wahrscheinlichkeitsverteilung, von der wir ziehen. Wiur beginnen mit der simpelsten, der Normalverteilung
eine Stichprobe - wir können einfach mit rnorm eine Stichprobe der Verteilung ziehen
eine Statistik, die wir berechnen wollen - hier den Mittelwert mean
einen Ort, wo wir den Mittelwert speichern

Und dann wiederholen wir das z.B. 100 mal. Das Programmierkonstrukt dafür ist eine for-Schleife. Wir legen einen Vektor der Länge k = 100 an und ziehen in jedem Schleifendurchlauf eine neue Stichprobe, berechnen den Mittelwert und legen das an der Position \(i\) (Schleifenvariable) ab. Die Schleifenvariable wird in jedem Durchgang um eins hochgezählt, i =1, i = 2, … i = k.

Anschließend berechnen wir die Standardabweichung der Mittelwerte - voila, da ist der Standardfehler der Statistik (hier des Mittelwertes).

n <- 20 # Stichprobengröße
k <- 1000 # Anzahl Wiederholungen
mu <- 100 # Erwartungswert der Grundgesamtheit
sigma <- 5 # die Standardabweichung der Grundgesamtheit
theStats <- numeric(k) # mit 0 initialisierter Vektor der Länge k
for(i in 1:k)
{
  theSample <- rnorm(n = n, mean = mu, sd = sigma)
  theStats[i] <- mean(theSample)
}

# Standardfehler
sd(theStats)

## [1] 1.096362

Im Vergleich dazu der Standardfehler des Mittelwertes anhand der Formel aus der letzten Stichprobe

sd(theSample)/sqrt(n)

## [1] 0.809132

theStderr <- sd(theStats)
theMeanEst <- mean(theStats)

ggplot(data = data.frame(mean = theStats),
       mapping = aes(x=mean)) +
  geom_histogram(binwidth = 0.25, fill = "steelblue",
                 alpha = 0.6) +
  xlab("Mittelwerte der Stichproben") +
  ylab("Anzahl Stichproben") +
  geom_vline(xintercept = c(mu, theMeanEst),
             col = c("red", "purple"), lty=2) +
  annotate(geom = "label", x = mu, y= 100, alpha=.6,
           col = "red", label = "Mittelwert\nGrundgesamtheit") +
  annotate(geom = "label", x = theMeanEst, y= 80, alpha=.6,
           col = "purple", label = "Schätzer des\nMittelwertes\n über Stichproben") +
  annotate(geom = "segment", x = theMeanEst - theStderr, xend = theMeanEst + theStderr,
           y=5, yend = 5, col = "purple") +
  annotate(geom = "label", x = mu, y= 20, alpha=.6,
           col = "purple", label = "Standardfehler der Schätzung des Mittelwertes") +
  labs(title = "Schätzung des Mittelwertes normalverteilte Stichprobe",
       subtitle = paste("Anzahl Stichproben =", k))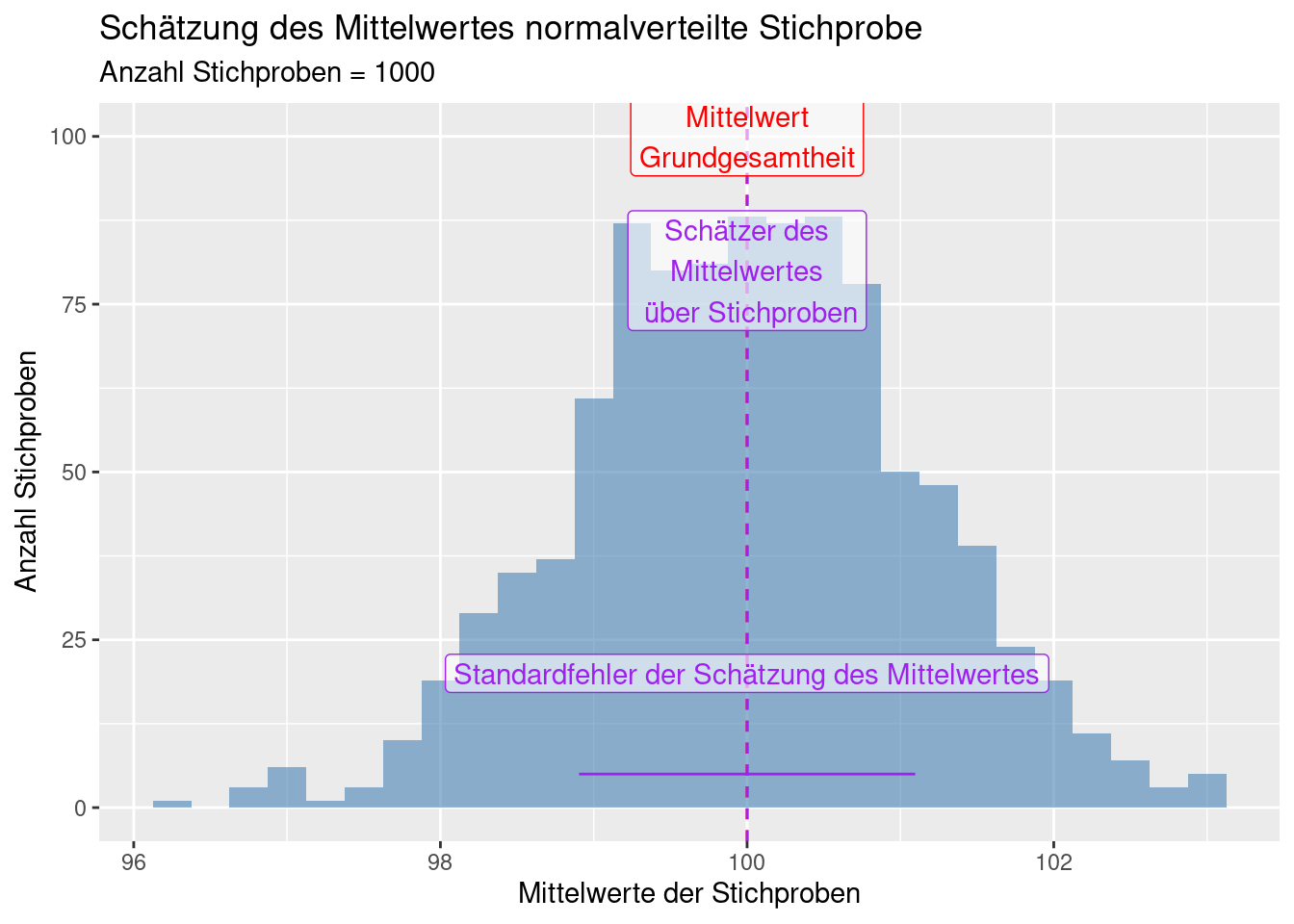

Wie oft liegt der wahre Mitelwert bei verschiedenen Stichprobengrößen außerhalb des 95% Konfidenzintervalls?

n <- 10 # Stichprobengröße
k <- 10^4 # Anzahl Wiederholungen
mu <- 100 # Erwartungswert der Grundgesamtheit
sigma <- 5 # die Standardabweichung der Grundgesamtheit


testN10 <- 0
testN50 <- 0
testN100 <- 0

popMeanIncluded <- function(mu, sigma, n)
{
  qt025 <- qt(p=0.025, df = n-1)
  qt975 <- qt(p=0.975, df = n-1)
  theSample <- rnorm(n = n, mean = mu, sd = sigma)
  meanSample <- mean(theSample)
  sdSample <- sd(theSample)    
  
  res <- 0
  
  if( ((meanSample + qt025 *sdSample / sqrt(n))<= mu) &
      ((meanSample + qt975 *sdSample / sqrt(n))>= mu))
    res <- 1
  return(res)
}

for(i in 1:k)
{
  
  testN10 <- testN10 + popMeanIncluded(mu, sigma, n= 10)  
  testN50 <- testN50 + popMeanIncluded(mu, sigma, n= 50)  
  testN100 <- testN100 + popMeanIncluded(mu, sigma, n= 100)  
}

testN10/k

## [1] 0.9496

testN50/k

## [1] 0.9516

testN100/k

## [1] 0.9479

Wie wir sehen, het die Stichprobengröße keinen Einfluss auf den Prozentsatz der außerhalb liegt. Das Konfidenzintervall wird einfach nur kleiner. Abweichungen zwischen den Prozentzahlen sind rein zufällig. Wenn die Stichprobengröße allerdings zu klein ist, wird der Standradfehler ungenau geschätzt - entsprechend liegt das Konfidenzintervall falsch und die Anzahl der Ereignisse, die außerhalb liegen sind ebenfalls zu optimistisch. Deswegen gibt es Korrekturfaktoren (s. oben).

9.2.4 Entwicklung des Standardfehlers für wachsende Stichprobengröße

set.seed(42)
n <- 10^3
popMean <- 30
popSd <- 2
theSample <- data.frame(x= rnorm(n, mean = popMean, sd = popSd))
theSample$idx <- 1:n

for(i in 1:n)
{
  theSample$mean[i] <- mean(theSample$x[1:i])
  theSample$stderr[i] <- ifelse(i < 2, NA, 
                                sd(theSample$x[1:i]) / sqrt(i)
                               )
}


p1 <- ggplot(theSample, mapping = aes(x=idx, y= stderr)) +
  geom_line() + 
  xlab("Stichprobengröße") +
  ylab("Standardfehler des Mittelwertes") +
  labs(title= "Standardfehler",
       subtitle = "Standardfehler des Mittelwertes aus wachsender normalverteilter Stichprobe")
p2 <- ggplot(theSample, mapping = aes(x=idx, y= mean)) +
  geom_line() + 
   geom_hline(yintercept = popMean, col="red") +
  xlab("Stichprobengröße") +
  ylab("Mittelwert") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Mittelwert aus wachsender normalverteilter Stchprobe")

ggpubr::ggarrange(p1,p2, nrow=2)

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).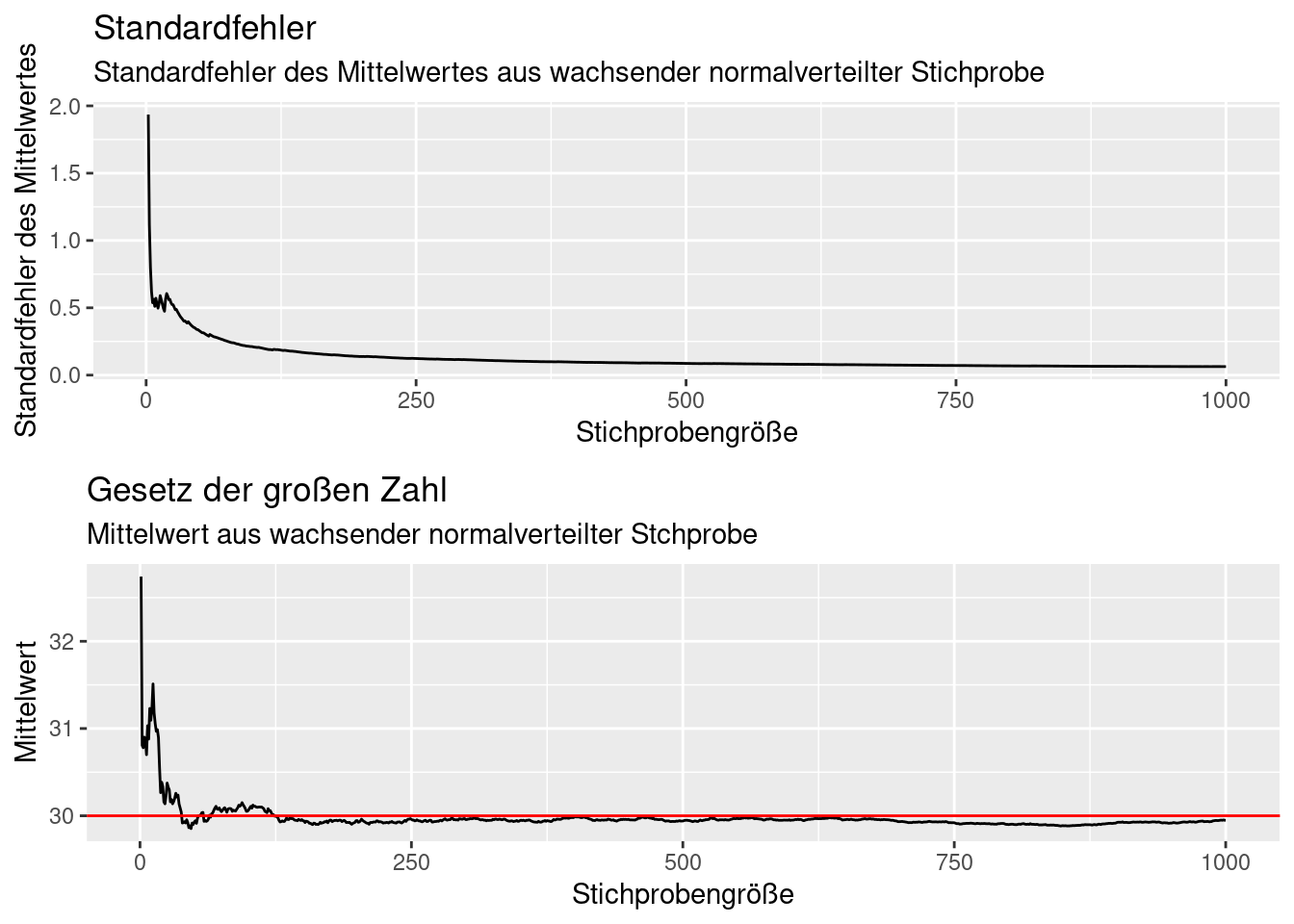

9.3 Konfidenzintervall

Ein anderes Maß, um die Unsicherheit der Schätzung eines Parameters anzugeben ist das Konfidenzintervall (auch Vertrauensbereich genannt). Das Maß fußt konzeptionell auf der frequentistischen Statistik: wenn man aus der selben Grundgesamtheit wiederholt Zufallsstichproben nach dem gleichen Verfahren zieht (gleiche Stichprobengröße) und daraus jeweils den Schätzer berechnet, dann liegen beim x% Konfidenzintervall x% der Schätzwerte innerhalb des x% Konfidenzintervalls.

Dies ist etwas anderes, als zu sagen dass der wahre Wert der Stichprobe mit x%-iger Wahrscheinlichkeit innerhalb des x-% Konfidenzintervalls liegt. Diese nicht korrekte Behauptung findet man leider immer wieder. Wichtig ist, sich klar zu machen, dass das Konfidenzintervall keine Eigenschaft des Schätzers, sondern des Verfahrens ist.

In der bayesischen Statistik gibt es den Begriff des Glaubwürdigkeitsintervalls (credibility interval), dass das dem entspricht, was sich viele unter dem Begriff des Konfidenzintervalls vorstellen.

Je breiter das Konfidenzintervall, (bei gleichem Konfidenzniveau, z.B. 95%), desto unsicherer ist die Parameterschätzung. Die Breite hängt mit der Stichprobengröße und der Variabilität der Daten zusammen. Je geringer die Stichprobe, desto breiter das Konfidenzintervall. Je variabler die Daten, desto breiter das Konfidenzintervall.

9.3.1 Schätzung des Konfidenzintervalls des Mittelwertes für normalverteilte Daten

Für den Mittelwert normalverteilter Zufallsdaten kann man das Konfidenzintervall auf Grundlage der [t-Verteilung] {#t-verteilung} schätzen. Bei einer Stichprobengröße von \(n\), verwenden wir eine t-Verteilung mit \(n-1\) Freiheitsgraden.

Die Statistik \(T = \frac{\bar{x}-\mu}{\frac{s_x}{\sqrt{n}}}\) ist t-verteilt mit \(n-1\) Freiheitsgraden. \(\mu\) ist dabei der unbekannte Erwartungswert der Grundgesamtheit, \(\bar{x}\) und \(s_x\) sind der Stichprobenmittelwert und die Stichprobenstandardabweichung.

Sei \(c\) das 97.5-Quantil von T, dann ist das theoretische 95%-Konfidenzintervall wie folgt definiert³³:

\[ P(-c \leq T \leq c) = 0.95\]

\[ P(\bar{x}-\frac{cs_x}{\sqrt{n}} \leq \mu \leq \bar{x}-\frac{cs_x}{\sqrt{n}}) = 0.95 \] Anders ausgedrückt:

\[ P(\bar{x}-t_{n-1,1- \alpha /2}*stderr \leq \mu \leq \bar{x}-t_{n-1,1- \alpha /2}*stderr) = 0.95 \]

9.3.2 Beispiel mit simulierten Daten

Ähnlich wie beim Standardfehler können wir ein einem Zufallsexperiment wiederholt Stichproben ziehen und dann das 2,5 und das 97.5-Quantil berechen - das ist dann das 95% Konfidenzintervall.

Der Einfachheit verwenden wir einfach die oben simulierten Werte für eine normalverteilte Grundgesamtheit.

q25 <- quantile(theStats, probs = .025)
q975 <- quantile(theStats, probs = .975)

ggplot(data = data.frame(mean = theStats),
       mapping = aes(x=mean)) +
  geom_histogram(binwidth = 0.25, fill = "steelblue",
                 alpha = 0.6) +
  xlab("Mittelwerte der Stichproben") +
  ylab("Anzahl Stichproben") +
  geom_vline(xintercept = c(mu, theMeanEst),
             col = c("red", "purple"), lty=2) +
  annotate(geom = "label", x = mu, y= 100, alpha=.6,
           col = "red", label = "Mittelwert\nGrundgesamtheit") +
  annotate(geom = "label", x = theMeanEst, y= 80, alpha=.6,
           col = "purple", label = "Schätzer des\nMittelwertes\n über Stichproben") +
  annotate(geom = "segment", x = q25, xend = q975,
           y=5, yend = 5, col = "purple") +
  annotate(geom = "label", x = mu, y= 20, alpha=.6,
           col = "purple", label = "95%-Konfidenzintervall der Schätzung des Mittelwertes") +
  labs(title = "Schätzung des Mittelwertes normalverteilte Stichprobe",
       subtitle = paste("Anzahl Stichproben =", k))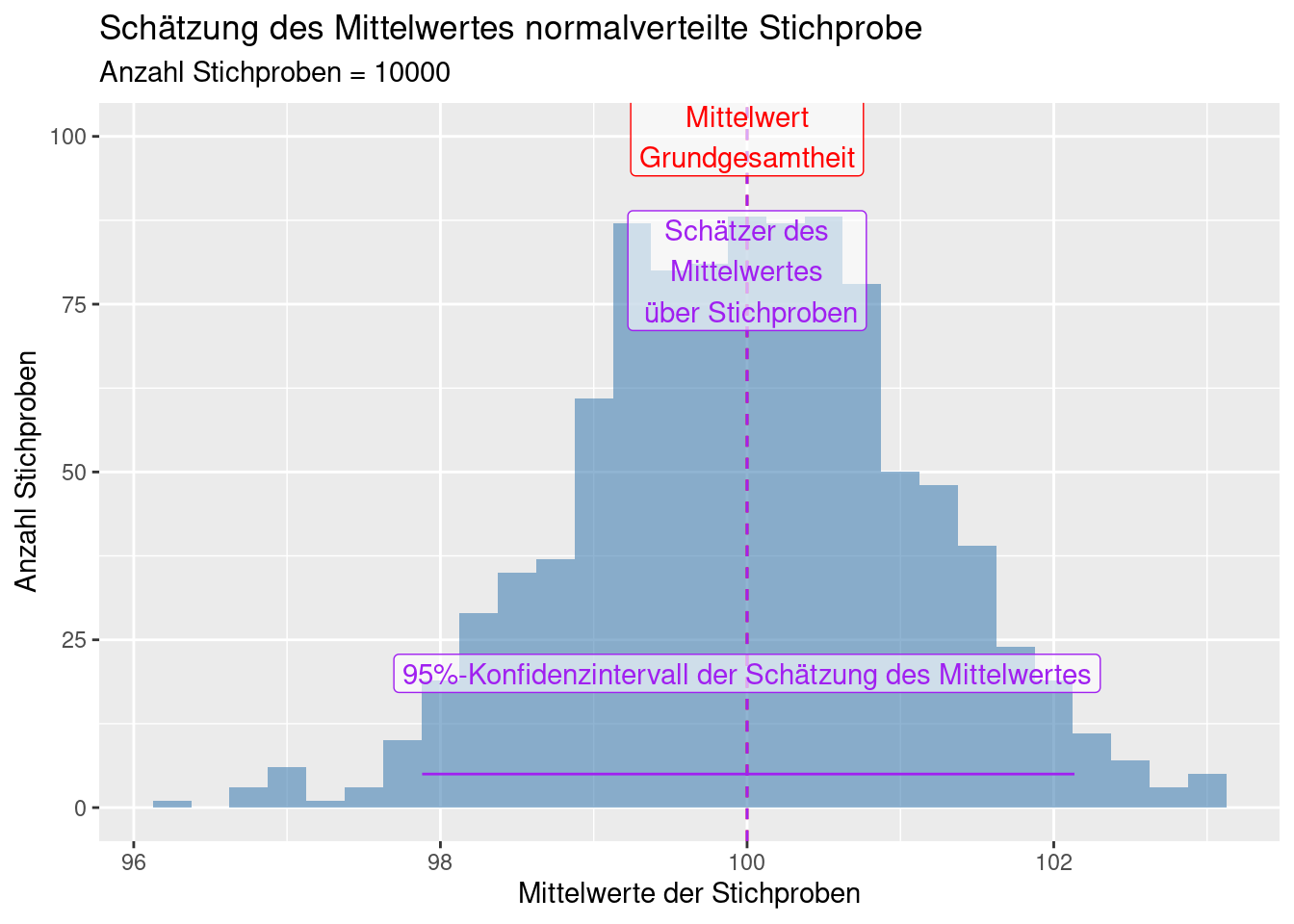

9.3.2.1 Simulation der t-basierten Konfidenzintervalle je Stichprobe

In der Realität kennen wir die Grundgesamtheit ja gerade nicht und wir können i.d.R. auch nicht einfach beliebig viele zusätzliche Stichproben ziehen. In der Regel müssen wir mit der einen Stichprobe leben, die wir gezogen haben und schätzen daraus das Konfidenzintervall.

Wenn wir mit simulierten Daten arbeiten, können wir mehrfach von der selben zugrundeliegenden Grundgesamtheit ziehen und jeweils das Konfidenzintervall berechnen.

n <- 20 # Stichprobengröße
k <- 100 # Anzahl Wiederholungen
mu <- 100 # Erwartungswert der Grundgesamtheit
sigma <- 5 # die Standardabweichung der Grundgesamtheit

qt025 <- qt(p=0.025, df = n-1)
qt975 <- qt(p=0.975, df = n-1)


ciDat <- data.frame(meanEst = rep(NA,k), ci025 = NA, ci975 = NA, sample = 1:k)

for(i in 1:k)
{
  theSample <- rnorm(n = n, mean = mu, sd = sigma)
  meanSample <- mean(theSample)
  sdSample <- sd(theSample)    
  
  ciDat$meanEst[i] <- meanSample
  
   ciDat$ci025[i] <- meanSample + qt025 *sdSample / sqrt(n)
   ciDat$ci975[i] <- meanSample + qt975 *sdSample / sqrt(n)
    
}

ggplot(ciDat, mapping = aes(y= sample) ) +
  geom_crossbar(aes(x= meanEst,  xmin = ci025, xmax = ci975),
                fill = "steelblue", alpha= .5) +
  xlab("Werte") + ylab("Stichprobe") + 
  labs(title = "Geschätze Konfidenzintervalle je Stichprobe",
       subtitle = "Stichprobengröße = 20") +
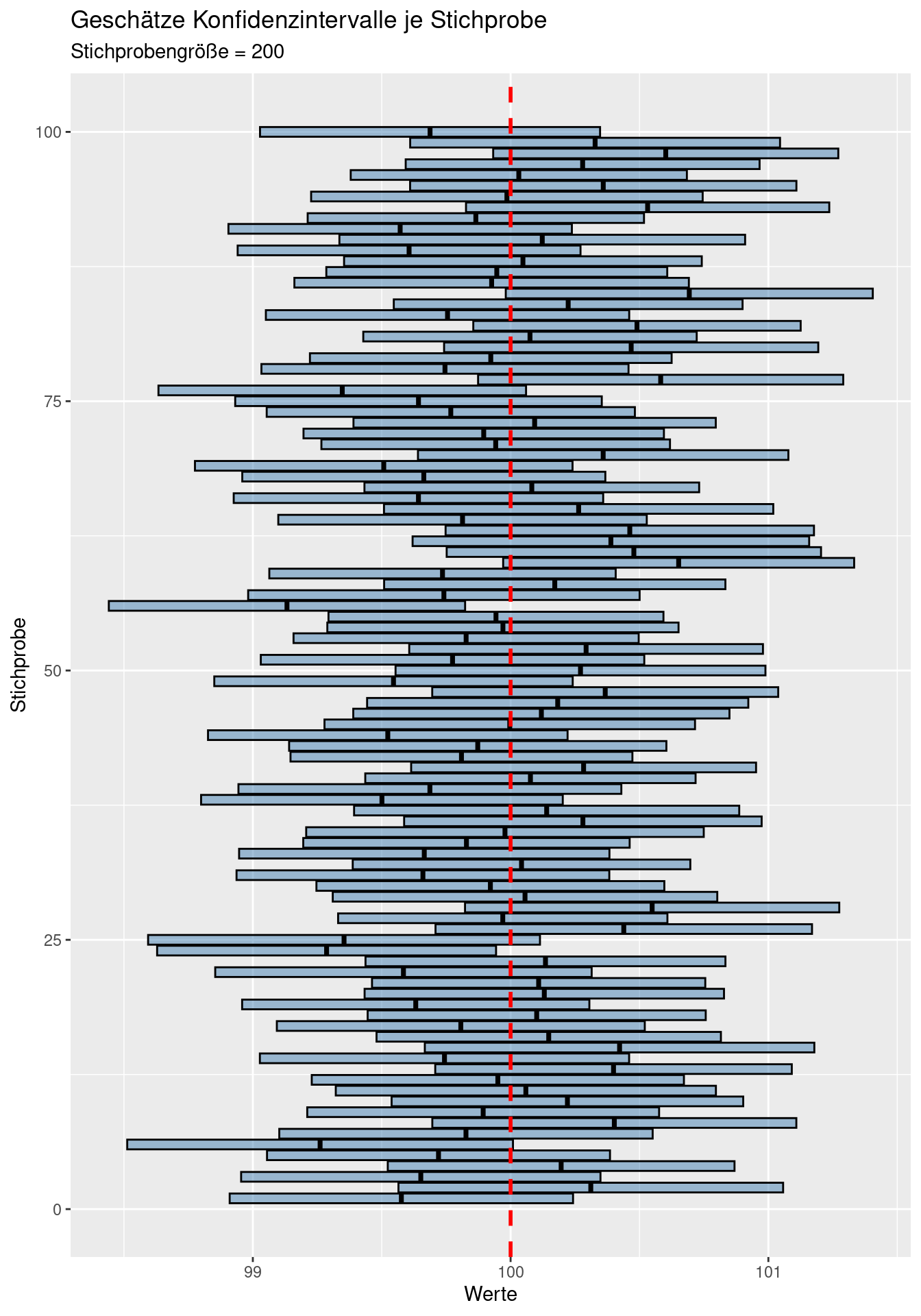
  geom_vline(xintercept = mu, col = "red", lty=2, lwd=1)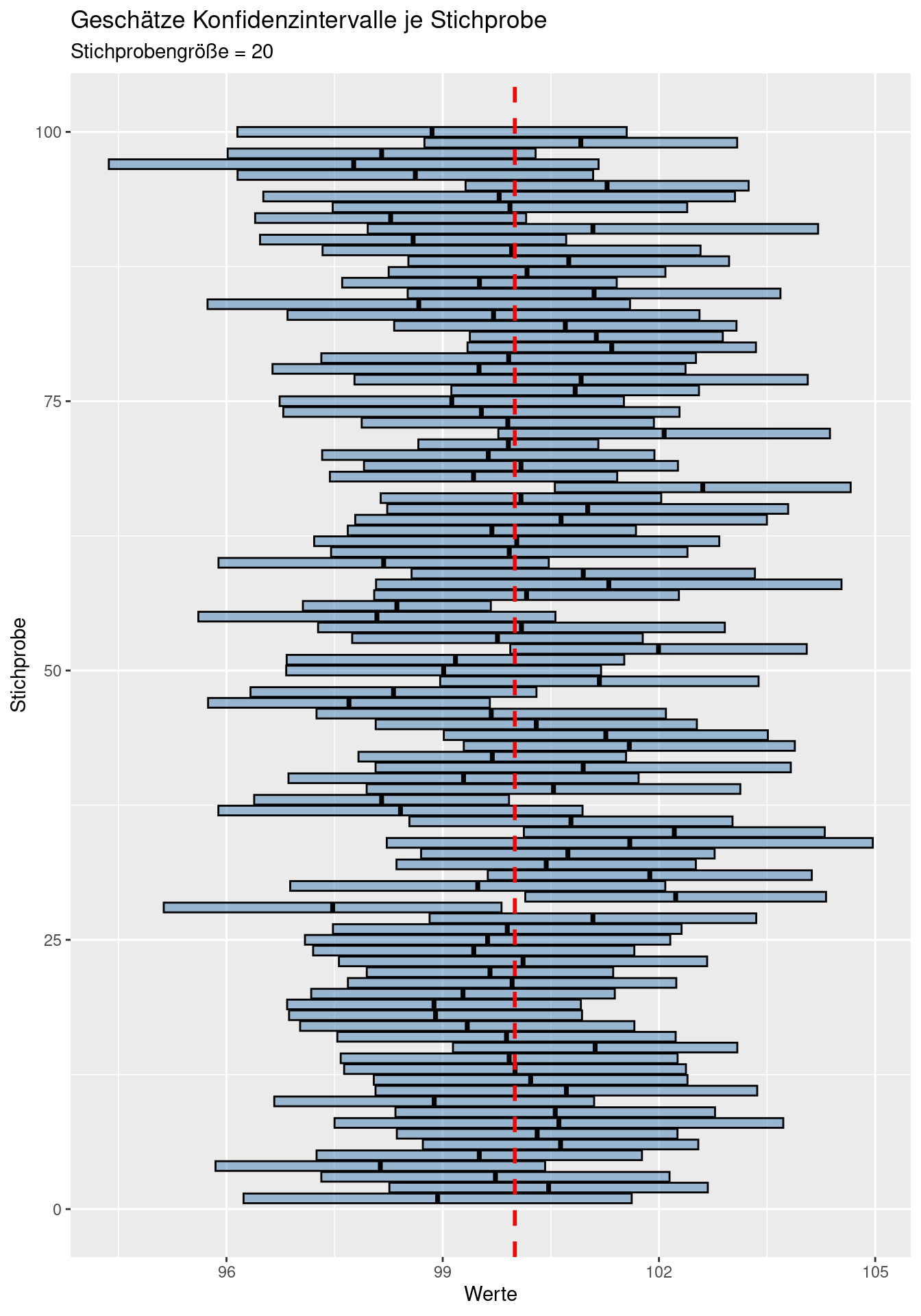

Wie wir sehen, schließen bei 100 Stichproben einige 95%-Konfidenzintervalle auf Basis der Stichprobe nicht den wahren Mittelwert (rote gestichelte Linie) ein - im Mittel sind es 5 von 100 Stichproben, bei denen dies der Fall ist. In der Realität schätzen wir das Konfidenzintervall ja aufgrund der Stichprobe. Der wahre Mittelwert kann außerhalb liegen - wir können nicht wissen, ob dies der Fall ist oder nicht.

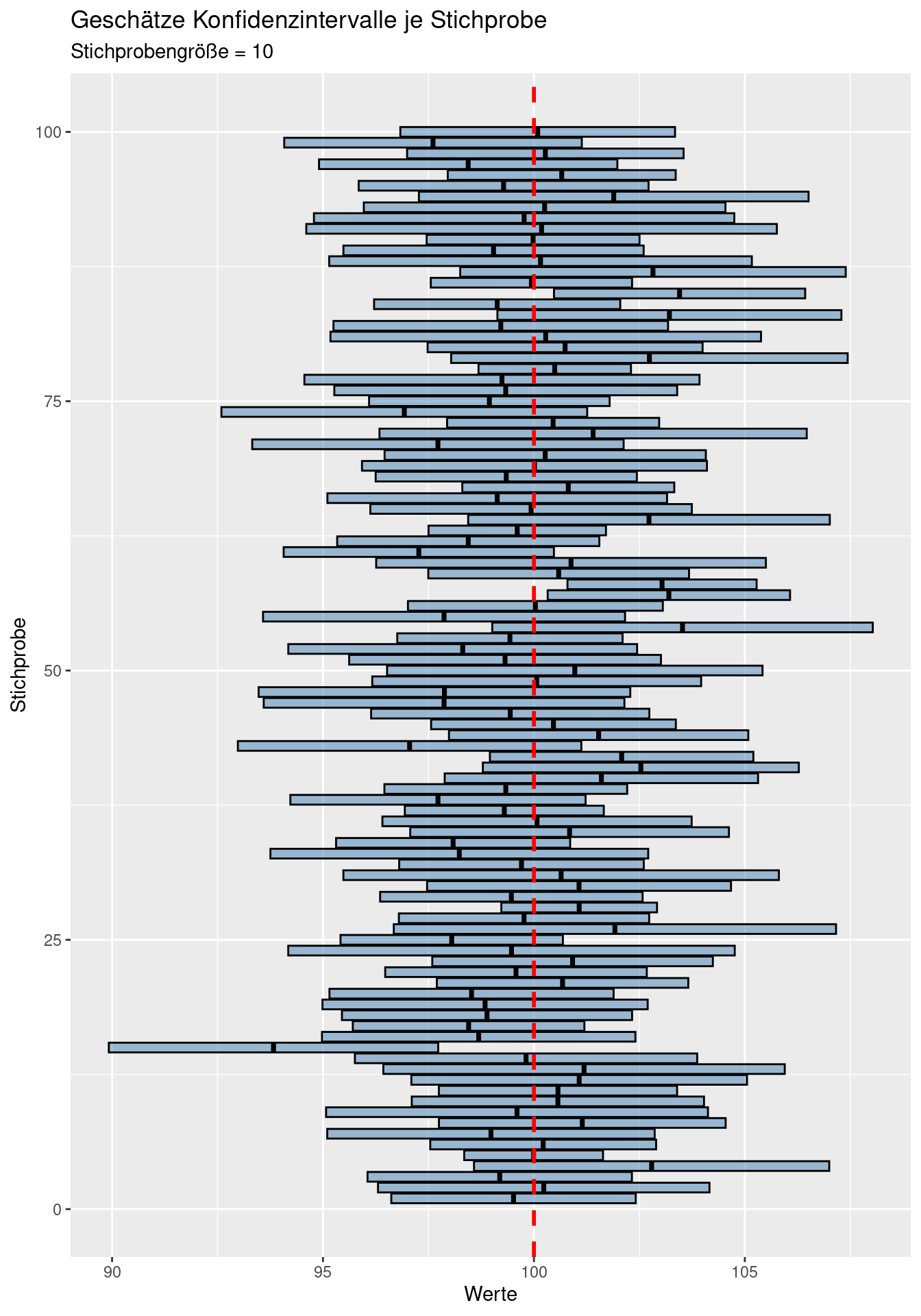
Bei kleinen Stichprobengrößen werden die Konfidenzintervalle breiter, bei größeren schmäler, da sich der Standardfehler vergößert bzw. verringert und zudem die Unsicherheit zunimmt bzw. abnimmt.

9.3.3 Entwicklung des Konfidenzintervalls für wachsende Stichprobengröße

Mit wachsender Stichprobengröße konvergiert der Standardfehler des Mittelwertes gegen Null, da die (zunehmend besser geschätzte) Standardabweichung gegen die Standardabweichung der Grundgesamtheit konvergiert und durch die Quadratwurzel der stetig wachsenden Stichprobengröße geteilt wird (s. oben). Entsprechend wird das Konfidenzintervall kleiner, da dabei ein fester Wert (kritischer t-Wert) mit dem immer kleiner werdenden Standardfehler multipliziert wird.

set.seed(42)
n <- 2*10^3
popMean <- 30
popSd <- 2
theSample <- data.frame(x= rnorm(n, mean = popMean, sd = popSd))
theSample$idx <- 1:n

for(i in 1:n)
{
  theSample$mean[i] <- mean(theSample$x[1:i])
  theSample$stderr[i] <- ifelse(i < 2, NA, 
                                sd(theSample$x[1:i]) / sqrt(i)
                               )
}

theSample$ci025 <- theSample$mean + qt025 * theSample$stderr
theSample$ci975 <- theSample$mean + qt975 * theSample$stderr

ggplot(theSample, mapping = aes(x=idx, y= mean)) +
  geom_line() + 
  geom_line(mapping = aes(x=idx, y= ci025), lty=3, col= "darkgrey") +
  geom_line(mapping = aes(x=idx, y= ci975), lty=3, col= "darkgrey") +
   geom_hline(yintercept = popMean, col="red") +
  xlab("Stichprobengröße") +
  ylab("Mittelwert + 95% CI") +
  labs(title= "Gesetz der großen Zahl",
       subtitle = "Mittelwert + 95% Konfidenzintervall aus wachsender normalverteilter Stchprobe")

## Warning: Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).
## Removed 1 row containing missing values or values outside the scale range
## (`geom_line()`).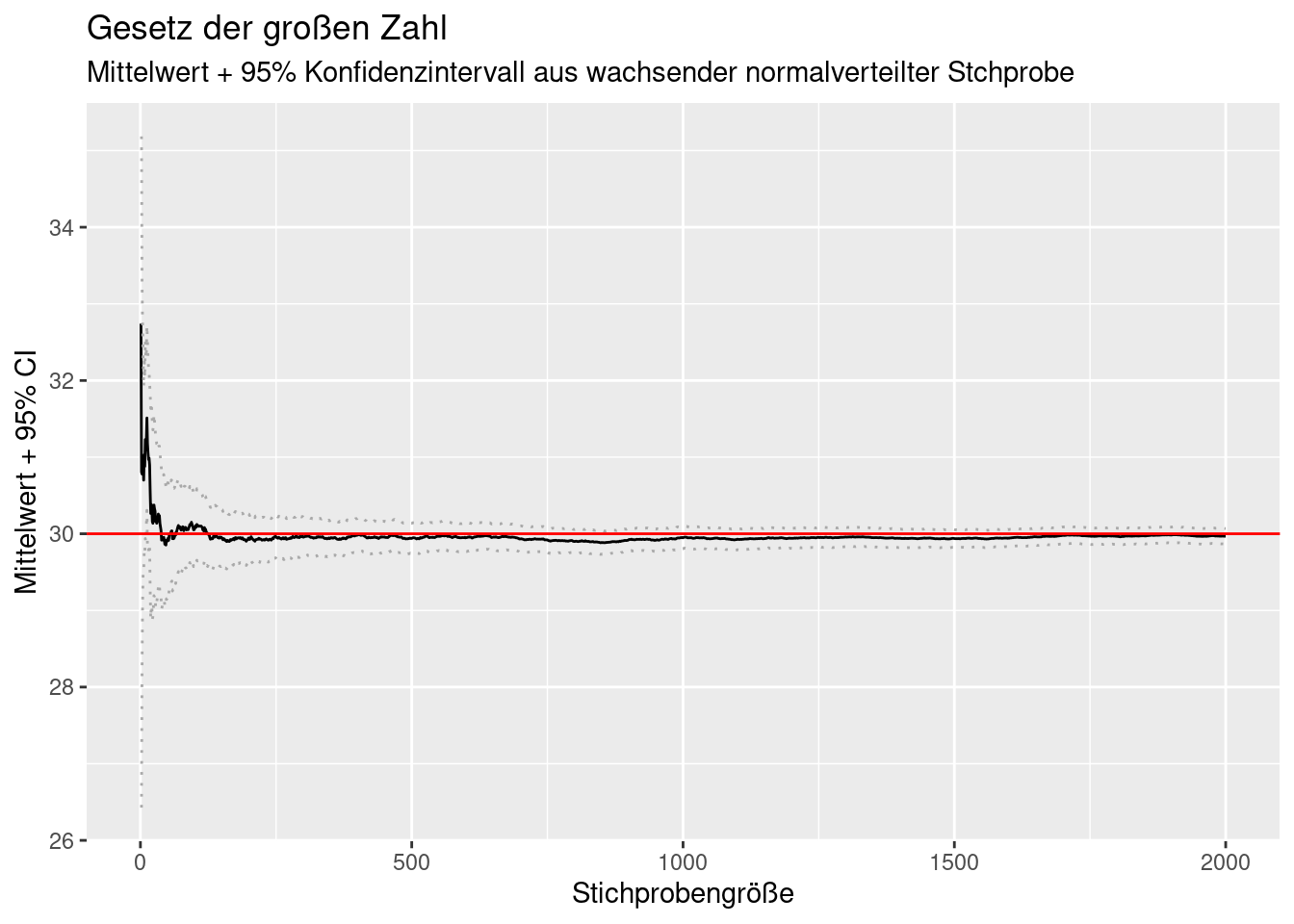

9.4 Kontrollfragen

wie ist der Standardfehler einer statistischen Kenngröße definiert
wie das 99%-Konfidenzintervall einer statistischen Kenngröße definiert
was besagt das Gesetz der großen Zahlen
was besagt der zentrale Grenzwertsatz

Weiterführende/zitierte Literatur

Efron, Bradley, and Robert J. Tibshirani. 1994. An Introduction to the Bootstrap. CRC Press.

Gurland, John, and Ram Tripathi. 1971. “A Simple Approximation for Unbiased Estimation of the Standard Deviation.” The American Statistician 25 (4): 30–32.

Ja, 97.5 und 95 ist korrekt: es gibt eine 2.5% Wahrscheinlichkeit, dass \(T \leq c\) und eine 2.5% Wahrscheinlichkeit, dass \(T \geq -c\) ist.↩︎